Abstract
With the increasingly serious eutrophication of inland water, the frequency and scope of harmful cyanobacteria blooms are increasing, which affects the ecological balance and endangers human health. The aim of this study was to propose an alternative method for the quantification of cyanobacterial concentrations in water by correlating multispectral data. The research object was the cyanobacteria in Erhai Lake, Dali, China. Ten monitoring sites were selected, and multispectral images and cyanobacterial concentrations were measured in Erhai Lake from September to November 2021. In this study, multispectral data were used as independent variables, and cyanobacterial concentrations as dependent variables. We performed curve estimation, and significance analysis for the independent variables, and compared them with the original variable model. Here, we chose about four algorithms to establish models and compare their applicability, including Multivariable Linear Regression (MLR), Support Vector Regression (SVR), Long Short-Term Memory (LSTM), and Extreme Learning Machine (ELM). The prediction performance was evaluated by the coefficient of determination (R2), Root-Mean-Square Error (RMSE), and Mean Relative Error (MRE). The results showed that the variable analysis model outperformed the original variable model, the ELM was superior to other algorithms, and the variable analysis model based on the ELM algorithm achieved the best results (R2 = 0.7609, RMSE = 4197 cells/mL, MRE = 0.044). This study confirmed the applicability of cyanobacterial concentrations prediction using multispectral data, which can be characterized as a quick and easy methodology, and the deep neural network has great potential to predict the concentration of cyanobacteria.
1. Introduction
Since the eutrophication of inland lakes appeared in the 1930s, about 40–50% of lakes and reservoirs in the world have been affected by eutrophication to different degrees. Lake eutrophication has become one of the most intractable water environment problems [1]. Eutrophication of water bodies will cause the rapid growth of phytoplankton, especially those algae with floating or moving ability, as well as over-propagation of algae which forms algal blooms on the water surface. Cyanobacteria blooms will excessively consume oxygen in water, which may lead to the death of aquatic plants and fish [2]. Harmful Algal Blooms (HABs) are dangerous to aquatic organisms and water ecosystems, and may cause mild skin irritation to humans and even cause public health risks of serious diseases [3]. Therefore, a timely grasp of the outbreak of cyanobacteria blooms in water bodies is important for precaution and management.
Currently, the remote sensing monitoring of cyanobacteria mainly involves the spatial characteristics of harmful cyanobacteria and remote sensing inversion of the phytoplankton pigment concentration, including chlorophyll-a (chl-a) and phycocyanin (PC). The main basis is that the outbreak of cyanobacteria will cause changes in physical properties such as water color and transparency, and then lead to changes in the spectral reflection characteristics of water bodies [4]. The research data sources mainly include GF-1, Sentinel-3a, Landsat8, MODIS, AVHRR, and other multisource satellite remote sensing data. The study area comprises mainly inland lakes such as Taihu Lake in China and Lake Erie in North America [5].
In research on the spatial characteristics of harmful cyanobacteria, there are two main aspects: false color composite maps composed of appropriate spectral bands and water color indices. On the false color composite map composed of appropriate spectral bands, the water bloom is different from clean water bodies, turbid water bodies, and clouds. Single-band threshold [6], D-value algorithms [7], and ratioing algorithms [8], which are relatively simple can roughly identify water blooms. The water color index also provides a new idea for this problem [9]. Among many water color indices, the normalized difference vegetation index (NVDI) method has high accuracy in monitoring low concentrations of cyanobacteria [10,11]. The enhanced vegetation index (EVI) method can effectively restrain the interference of background water and sediment [12]. The baseline subtraction method used by the floating algae index (FAI) can effectively remove cloud and geometry contamination and is more stable for extracting a long-term series of cyanobacteria blooms [13,14]. In addition, the maximum characteristic peak height (MPH) and maximum chlorophyll index (MCI) are also applied in water bloom monitoring [15,16]. Through the above findings, research on the spatial characteristics of harmful cyanobacteria can indicate the range of cyanobacteria blooms, but they will be affected by clouds, aquatic plants, and turbid water [17,18].
In research on remote sensing inversion of the phytoplankton pigment concentration, the single-band threshold [19], band interpolation algorithms, and band ratio algorithms [20] of chl-a are simple and suitable for areas with high chlorophyll concentrations. The three-band method [21,22] and four-band method [23] weaken the influence of turbid water on chl-a, and improve the accuracy of the model. Neural network algorithms have high accuracy, but they need large data support [24,25]. For phycocyanin, remote sensing inversion uses mostly empirical models, semi-analytical models, and so on [26,27,28,29]. Currently, the remote sensing inversion of the cyanobacteria pigment concentration is mainly based on empirical algorithms and semi-empirical and semi-analytical algorithms of multispectral and hyperspectral data [30,31].
With the development of artificial intelligence, machine learning has become an important technology in water quality inversion, such as Multiple Linear Regression (MLR), Support Vector Machine (SVM), Extreme Learning Machine (ELM), Long Short-Term Memory (LSTM), ANN, Backpropagation Neural Network (BP-NN), Catboost model (CB), Random Forest (RF), etc. [32]. In chlorophyll remote sensing inversion, SVM and ELM algorithms outperform CB [33], BP-NN [34], RF [35], and other algorithms [36,37,38,39]. For SVM, it is characterized by robustness, and has a good ability to interpret a nonlinear relationship. Satisfactory results have also been obtained in salinity estimation [40,41]. ELM has a simple working principle and high computational efficiency. Especially in the estimation of organic carbon, ELM has good reliability and accuracy [42]. In the estimation of suspended solids, total nitrogen and total phosphorus, the performance of SVM and MLR algorithm is better than that of ANN and other algorithms [43,44,45,46]. In water quality temperature estimation, MLR produced promising outcomes [47,48]. MLR is a flexible method of data analysis that may be appropriate whenever a quantitative variable is to be examined in relationship to any other factors and it has been widely used in various fields. LSTM has good performance in long-term water quality monitoring [49,50]. However, the estimation effect of these algorithms on cyanobacteria concentrations are still unknown. Therefore, we chose MLR, SVM, LSTM, and ELM algorithms to establish models for estimating the concentration of cyanobacteria from multispectral data in this study. Their applicability in cyanobacteria concentration prediction will be compared.
The spatial characteristics of harmful cyanobacteria can reflect the spatial distribution of cyanobacteria and other phytoplankton, but it is difficult to quantitatively evaluate the concentration of cyanobacteria in water [51,52]. The remote sensing inversion of phytoplankton pigment concentrations can reflect the eutrophication degree of water bodies. However, it cannot represent the specific concentration of cyanobacteria. They are affected by other phytoplankton.
Cyanobacteria treatment stations have been built in Erhai Lake. Physical adsorption of cyanobacteria by adsorbent and mechanical filtration can achieve the effect of water purification. When treating cyanobacteria with different concentrations, the dosage and proportion of adsorption are also different. Therefore, it is necessary to identify and analyze the concentration of cyanobacteria in water to improve the treatment efficiency and avoid waste and pollution.
Given the above, this study monitored cyanobacterial concentrations and multispectral data in Erhai Lake. The regression prediction model between multispectral data and cyanobacterial concentrations was established by MLR, SVR, LSTM, and ELM. This study provides a theoretical basis for the rapid and efficient treatment of cyanobacteria.
2. Materials and Methods
2.1. Study Area
The study area is located northwest of Erhai Lake. Erhai Lake, the seventh largest freshwater lake in China, is located in Dali, Yunnan Province (25°36′–25°58′ N, 100°06′–100°18′ E, 1972 m above sea level). Its water surface coverage is approximately 251 km2, and it has a shallow mean water depth of 10.5 m. It is a national nature reserve and the only centralized water source in Dali. It is responsible for the drinking water supply of more than 600,000 residents and a large number of tourists. The quality of water is related to the social and economic development of Dali. From 1999 to 2014, cyanobacteria blooms occurred many times in summer and autumn in Erhai Lake, mainly in small-scale blooms (the area of blooms is within 10 km2). The large-scale water blooms mainly occurred in 2003, 2006, and 2013, among which the area of water blooms in 2006 was the largest, reaching 42 km2. The nearshore lake bay area is prone to cyanobacterial accumulation, and the large-scale cyanobacteria blooms in Erhai Lake mainly occur in the northern area of Erhai Lake. The accumulation of cyanobacteria in the nearshore area starts in spring, and blooms in the central water area occur in late summer and autumn (August–November), among which large-scale water blooms mainly occur in October.
Combined with the distribution of cyanobacteria blooms in previous years, the blooms on the northern shore of Erhai Lake are relatively serious. Therefore, 100 m away from the shore, one sampling point every 120 m, and a total of 10 sampling and monitoring points were selected to form a sampling belt distributed along the coast for monitoring. The specific area is shown in Figure 1.
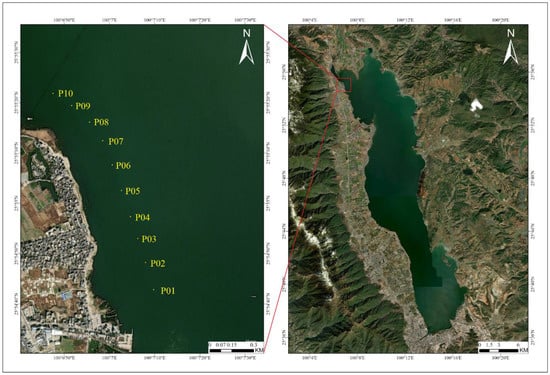
Figure 1.
Study Area.
2.2. Field Data Collection
From September to November 2021, field data collection and sampling analysis were conducted. The main objective was to obtain multispectral data and lake water samples from 10 monitoring points and analyze them in the laboratory. A total of 60 days of monitoring and 135 groups of effective data were collected. The experiment was conducted 18 times, and 2 times were affected by rain, strong wind, and other factors, which affected the safety of the experiment, so it was impossible to sample on the spot. In addition, the UAV is affected by the wind during the flight and there are ships on the water surface, which makes the image inaccurate. Finally, 135 sets of complete data were obtained.
The multispectral camera carried by DJI·P4M was used for image acquisition in this experiment. The camera was equipped with six lenses, namely RGB visible light and five spectral channels of R, G, B, RE, and NIR. Parameters of multispectral camera are shown in Table 1. And this multispectral camera is shown in Figure 2.

Table 1.
Multispectral camera parameters.

Figure 2.
Multispectral camera.
According to the selected sampling points, the multispectral image of the actual water surface was taken vertically downward 10 m above each point (photo resolution: 1600 × 1300), and the accuracy of each pixel was approximately 0.53 cm/pixel.
This experiment was designed to be sampled and tested every three days. Each experiment started at 1 p.m., when the temperature is the highest and the light is the strongest. Multispectral images were taken at each sampling point at 1:00 p.m., water samples were collected at 2:00 p.m., and water samples were collected at a depth of 20 cm with a water sampler. Water was taken 10 times near each sampling point, to a total of 10 L. After mixing, 500 mL for detection was taken. Immediately after collection, the water sample was sent to the laboratory to test the cyanobacterial concentrations, chlorophyll concentration, turbidity and temperature and other parameters, in order to complete the detection before 7 p.m. of the same day.
2.3. Data Preprocessing
For water samples, we used the multi parameter cyanobacteria concentration module of HX-200 multi parameter controller produced by Beijing Hongxinhengce Technology Co., Ltd. (Beijing, China) to analyze the cyanobacterial concentration. It makes use of the characteristics of cyanobacteria with absorption peaks and reflection peaks in the spectrum. The monochromatic light at the absorption peak band of the cyanobacteria spectrum was emitted into the water. The cyanobacteria in the water absorb the energy of the light and reflect monochromatic light with another wavelength. The light intensity reflected by cyanobacteria is directly proportional to the content of cyanobacteria in water to detect the concentration of cyanobacteria.
The gray value of the nonreflective strong area in the middle of different band multispectral images was extracted by MATLAB. Multispectral images are a group of images with different bands at the same position, so the coordinates of the extracted pixels in the same group of images are consistent. The gray values of the extracted images in different bands are taken as independent variables in the regression model.
2.4. Modeling Techniques
2.4.1. Multivariable Linear Regression
MLR is a statistical analysis technique to find the functional relationship between multiple independent variables and a dependent variable. It can estimate the model parameters by the least square method, find the function by minimizing the sum of squares of errors, and solve the coefficient matrix by matrix operation. MLR is the most widely used regression model. Its prediction model is as follows:
where is the predicted value, is the input argument vector, is the vector of coefficients, and is the random error term, . The error term should be independent and have a normal distribution [53].
2.4.2. Support Vector Regression
SVR is the implementation of support vector machine (SVM) in regression. SVM is a kind of generalized linear classifier for binary classification of data according to supervised learning, and its decision boundary is the maximum margin hyperplane for solving learning samples [54]. SVM uses the hinge loss function to calculate the empirical risk and adds the regularization term to the solution system to optimize the structural risk. It is a sparse and robust classifier. SVM can be used for nonlinear classification by the kernel method, which is one of the common kernel learning methods.
2.4.3. Long Short-Term Memory
LSTM is a commonly used recurrent neural network (RNN). Compared with RNN, its essence lies in the introduction of the concept of the cell state. The cell state of LSTM will determine which states should be left behind and which states should be forgotten. The problem of the disappearance of the RNN gradient was solved [55]. The LSTM network has three gates in the hidden layer (input gates, output gates, and forget gates). Input gates control the input flow of the memory cell, and output gates control the output flow into other cells. The role of forget gates is to selectively forget the information in the state of the cell.
2.4.4. Extreme Learning Machine
ELM proposed a single-hidden layer feedforward network (SLFNs) that randomly selects the input weights and analytically determines the output weights of SLFNs [56]. One key principle of the ELM is that one may randomly choose and fix the hidden node parameters. After the hidden node parameters were chosen randomly, the SLFN becomes a linear system where the output weights of the network can be analytically determined using a simple generalized inverse operation of the hidden layer output matrices [57]. The applications of ELM include computer vision and bioinformatics. It is also applied to regression problems in some Earth Sciences and Environmental Sciences [58].
2.5. Modeling Strategy and Validation Metrics
The model dataset was randomly divided into a training set and test set at a ratio of 3:1, and the independent variable of the model was the gray value of images in different bands. As the image was in TIF format, it was a 16-bit grayscale image with a grayscale value range of 0–65,535. The unit of the input independent variable is cells/mL, and the magnitude was also large, so they are normalized, put into the model for analysis, and then inverse normalization is carried out after the results are output.
In this study, different forecasting models were evaluated using the following three evaluation metrics: coefficient of determination of use (R2), root mean square error (RMSE), and mean relative error (MRE). The larger the R2 and the smaller the RMSE and MRE are, the better the prediction accuracy of the model:
where is the measured value, is the predicted value, is the average of the measured values, and denotes the number of samples.
3. Results
3.1. Descriptive Statistics
A total of 135 groups of data were collected. The measured minimum concentration of cyanobacteria was 1303 cells/mL and the maximum concentration was 45,373 cells/mL. The distribution range of all cyanobacterial concentrations is shown in Figure 3.
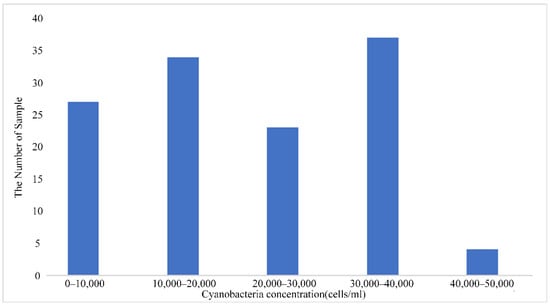
Figure 3.
Concentration distribution range of cyanobacteria detected in the experiment.
The statistical values of the training and test datasets for cyanobacterial concentrations prediction are shown in Table 2. We used the Maximum, Minimum, Median, Mean, and Standard Deviation for analysis. The final statistics indicated that the distribution of the whole dataset and the training and testing datasets were similar. Therefore, the samples in the training and test datasets were representative of the whole sample and could be used to build and test accurate models.

Table 2.
Descriptive statistics of the whole dataset, the training dataset, and the test dataset.
3.2. Analysis of the Importance of Variables
3.2.1. Curve Estimation
To improve the accuracy of linear regression, we estimated the curve for each variable, and the estimated R2 value is shown in Table 3.

Table 3.
R2 value estimated by variable curve.
According to the results in the above table, the R2 value of quadratic and cubic was maximum. Therefore, we added quadratic and cubic functions of variables and the interaction of multiplication between variables to transform and expand the variables.
3.2.2. Significance Test
Each independent variable had a different influence on the dependent variable, so the significance test is conducted for the expanded variables in 3.2.1, taking p ≤ 0.05, that is, the confidence interval was 95%. SPSS was used to analyze the significance of each variable. The analysis results are shown in Table 4. Finally, eight variables with p ≤ 0.05 were obtained: G, NIR, B × RE, B × NIR, G × RE, G × NIR, R × RE, and R × NIR.

Table 4.
Variables with p ≤ 0.05 in significance analysis.
3.3. Comparison of the Performances of Different Models
To compare the prediction accuracy of four algorithms (MLR, SVR, LSTM, ELM) and the influence of variable analysis on the results, two combinations of original variables and variables after variable analysis are used to model with four algorithms. As shown in Figure 4, among the models established by using the original variables, the model trained with the LSTM algorithm had the best prediction performance (R2 = 0.9996), and its effect was much higher than that of the other algorithms. However, in the model test, the ELM algorithm had the best performance (R2 = 0.7409), and its accuracy is slightly higher than that of the SVR algorithm (R2 = 0.6998). Additionally, the LSTM algorithm had the worst effect in the model test (R2 = 0.5632).
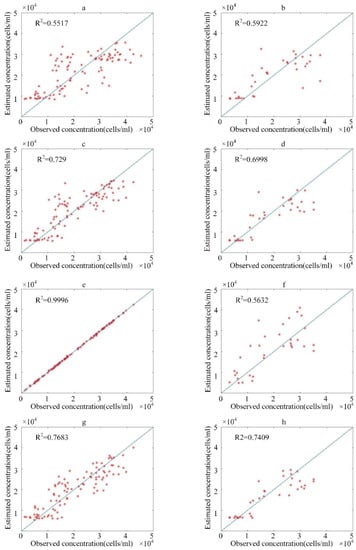
Figure 4.
Prediction performance of the original variable model: (a,b) is the training and testing of MLR; (c,d) is the training and testing of SVR; (e,f) is the training and testing of LSTM; (g,h) is the training and testing of ELM.
As shown in Figure 5, in the modeling after variable analysis, the model trained using the LSTM algorithm also had the best prediction performance. In the model test, the ELM algorithm had the best performance (R2 = 0.7409), and the LSTM algorithm had the worst effect in the model test (R2 = 0.5632). Compared with the models established by the original variables, the performance of all models was improved, especially MLR and SVR (training R2 increased by 0.1047 and 0.0317, respectively, and test R2 increased by 0.0857 and 0.0592, respectively).
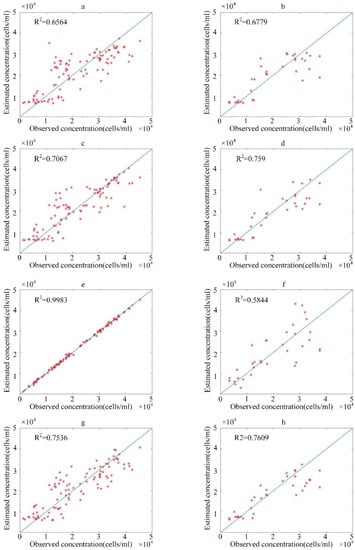
Figure 5.
Prediction performance of the model after variable analysis: (a,b) is the training and testing of MLR; (c,d) is the training and testing of SVR; (e,f) is the training and testing of LSTM; (g,h) is the training and testing of ELM.
The evaluation indexes of all models established by the original variables and variables obtained after variable analysis are shown in Table 5 and Table 6. From the RMSE and MRE of different algorithm models, due to the overfitting phenomenon of the LSTM model, the training error is the smallest, but the test error is the largest. The ELM model test error is the smallest. From the model established by different variable combinations, variable analysis reduces the error of the MLR algorithm model and increases the error of the SVR algorithm. The errors of RMSE trained by LSTM algorithm and MRE tested by ELM algorithm have increased, while the other errors have decreased. All in all, the reduction of error is more obvious, and the range of increase is small.

Table 5.
Prediction results of the original variable model.

Table 6.
Model performance after variable analysis.
Overall, ELM algorithm has the best performance among the four algorithms, and it can provide higher prediction accuracy than other algorithms. In terms of variable combination, the modeling performance of variables after variable analysis is better than that of original variables.
4. Discussion
4.1. Comparison of Different Variable Combination Models
In this study, the DJI P4M UAV is selected, which was equipped with a multispectral camera and has five multispectral channels (B, G, R, RE, NIR), and the gray values of five spectral band images are used as the independent variables. Through curve estimation and significance analysis, eight variables were obtained. The eight variables and the original variables were used as independent variables for modeling to analyze the correlation between the data of different bands and the concentration of cyanobacteria, and to improve the model performance. Compared with the original variable model, the model established after variable analysis improved the R2 of all algorithm models, especially the MLR algorithm. However, the accuracy of MLR was slightly lower than that of SVR and ELM, which indicated that the relationship between cyanobacterial concentrations and multispectral data was not only a simple linear relationship but also a more complex structure. Through variable analysis, eight variables are obtained, many of which are related to the RE and NIR bands, as shown in Table 4. This was also consistent with the remote sensing inversion of the phytoplankton pigment concentration to express the degree of cyanobacteria outbreak, which focuses on the NIR band [59,60], but this study involves more bands, which is also different from the past. This showed that the reflection of light by cyanobacteria mainly comes from the pigment in chl-a [61], but there are other reflection sources that together constitute the spectral characteristics of cyanobacteria. This is also consistent with the conclusion that other pigments are used to represent the cyanobacteria blooms [62].
4.2. Adaptability of the Algorithm
In this study, we used four algorithms (MLR, SVR, LSTM, ELM) to predict the concentration of cyanobacteria. The adaptability of the four algorithms to multispectral data prediction of cyanobacteria mode is different. When the variables after variable analysis were used for modeling, the ELM effect of deep learning was the best (R2 = 0.7609, RMSE = 4197), the SVR effect of machine learning was the second (R2 = 0.759, RMSE = 4797), followed by MLR (R2 = 0.6779, RMSE = 5226), and the LSTM effect of deep learning is the worst (R2 = 0.5844, RMSE = 7524), as shown in Table 6. MLR was used to find the functional relationship between multiple independent variables and a dependent variable, and it can only analyze the linear relationship, but it cannot automatically explore the nonlinear relationship between independent variables and dependent variables. Therefore, the nonlinear relationship of variables after adding variable analysis makes the effect significantly improved. The MLR algorithm was suitable for simple linear models [63]. SVR can analyze and select support vectors, which has certain robustness, but it cannot automatically adjust parameters [64]. It is difficult to achieve the best effect by manually adjusting the parameters. The LSTM algorithm needs a large amount of data to learn, and it was easy to overfit when the data were insufficient, which leads to high training accuracy and low testing accuracy. Moreover, the prediction effect is good for long time series data [65]. ELM was more suitable for the prediction of cyanobacterial concentrations under complex conditions [56].
4.3. Comparison with Traditional Algorithms
Currently, the data source of cyanobacteria remote sensing monitoring is mainly satellite remote sensing, and a small part is UAV remote sensing. Among them, there are few long-term monitoring methods [66]. Most long-term monitoring only involves the analysis of remote sensing images at different times and rarely involves long-term sampling analysis [67,68]. Additionally, the remote sensing monitoring of cyanobacteria mainly involved the spatial characteristics of harmful cyanobacteria and remote sensing inversion of the phytoplankton pigment concentration. It is difficult to analyze the specific concentration of cyanobacteria. Therefore, we monitored the cyanobacteria in Erhai Lake for two months, obtained multispectral data and the corresponding cyanobacterial concentrations, and established cyanobacterial concentrations prediction models using the experimental data.
4.4. Deficiency and Prospects
The data collection site of this experiment is Erhai Lake in Dali, which is a plateau lake. There is sufficient light and good air transmittance, which is very suitable for the collection of experimental data. However, whether there are differences between the water quality data of high-altitude lakes and low-altitude lakes should be further studied. Compared with satellite remote sensing, UAV remote sensing images have a higher resolution, accurate positioning, are more convenient and efficient but have a smaller monitoring range. Data are also collected in some areas of Erhai Lake, and the amount of data is not large enough. More data should be added in the future to obtain more range and more data for analysis. During this data collection, cyanobacteria were the dominant group in the water, but there were also a few diatoms in the water. As diatoms contain chl-a and carotene, the reflection of light is similar to that of cyanobacteria, which leads to error in cyanobacteria prediction. In the future, we should try more image and data processing methods to improve the accuracy.
5. Conclusions
In this study, MLR, SVR, LSTM, and ELM algorithms were used to establish the prediction model of cyanobacterial concentrations by original variables and variables from variable analysis, which realized the prediction of cyanobacterial concentrations by multispectral data. We used R2, RMSE, and MRE as evaluation indices to evaluate the performance of the models. The major findings of this study are the following:
- (1)
- We used variable analysis to transform multispectral data, and then predicted cyanobacterial concentrations by machine learning algorithm, and found that it was feasible. Although it contains some errors, which are mainly affected by other phytoplankton and impurities in water, it has certain guiding significance in the rapid monitoring of cyanobacteria. This provides a new idea for the prediction of cyanobacterial concentrations.
- (2)
- Through variable analysis, the prediction effect of cyanobacterial concentrations was improved. The variables obtained from curve estimation and significance analysis are compared with the original variables, and the performance of all algorithm models is improved. These results are consistent with the input variables of chlorophyll remote sensing inversion. However, there are more variables involved, and the relationship between variables and models was more complicated.
- (3)
- By comprehensively comparing R2, RMSE, and MRE of different algorithms, it is found that the prediction model of cyanobacterial concentrations established by the ELM algorithm (R2 = 0.7609, RMSE = 4197 cells/mL, MRE = 0.0440) are better than other algorithms. The model was effective in predicting the concentration of cyanobacteria.
Author Contributions
X.Z., Y.L. and Y.C. designed the experiments and collected data. X.Z. coded the workflow on MATLAB and analyzed the data. X.Z. and X.Q. drafted and revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
The work in this paper was supported by the National Key Research and Development Program of China (2021YFD1400100 and 2021YFD1400101) and the Guangxi Ba-Gui Scholars Program of China (2019A33).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Codd, G.A.; Morrison, L.F.; Metcalf, J.S. Cyanobacterial toxins: Risk management for health protection. Toxicol. Appl. Pharmacol. 2005, 203, 264–272. [Google Scholar] [CrossRef] [PubMed]
- Pal, M.; Yesankar, P.J.; Dwivedi, A.; Qureshi, A. Biotic control of harmful algal blooms (HABs): A brief review. J. Environ. Manag. 2020, 268, 110687. [Google Scholar] [CrossRef] [PubMed]
- Jose Huertas, M.; Mallen-Ponce, M.J. Dark side of cyanobacteria: Searching for strategies to blooms control. Microb. Biotechnol. 2022, 15, 1321–1323. [Google Scholar] [CrossRef] [PubMed]
- Hu, C.M.; Muller-Karger, F.E.; Taylor, C.; Carder, K.L.; Kelble, C.; Johns, E.; Heil, C.A. Red tide detection and tracing using MODIS fluorescence data: A regional example in SW Florida coastal waters. Remote Sens. Environ. 2005, 97, 311–321. [Google Scholar] [CrossRef]
- Paerl, H.W.; Xu, H.; McCarthy, M.J.; Zhu, G.; Qin, B.; Li, Y.; Gardner, W.S. Controlling harmful cyanobacterial blooms in a hyper-eutrophic lake (Lake Taihu, China): The need for a dual nutrient (N & P) management strategy. Water Res. 2011, 45, 1973–1983. [Google Scholar]
- Shi, K.; Zhang, Y.; Zhu, G.; Liu, X.; Zhou, Y.; Xu, H.; Qin, B.; Liu, G.; Li, Y. Long-term remote monitoring of total suspended matter concentration in Lake Taihu using 250 m MODIS-Aqua data. Remote Sens. Environ. 2015, 164, 43–56. [Google Scholar] [CrossRef]
- Gower, J.F.R. Red Tide Monitoring Using Avhrr Hrpt Imagery from a Local Receiver. Remote Sens. Environ. 1994, 48, 309–318. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Tomlinson, M.C. Remote Sensing of Harmful Algal Blooms. In Remote Sensing of Coastal Aquatic Environments: Technologies, Techniques and Applications; Miller, R.L., Del Castillo, C.E., McKee, B.A., Eds.; Springer: Dordrecht, The Netherlands, 2005; pp. 277–296. [Google Scholar]
- Zhou, Y.; He, B.; Fu, C.; Xiao, F.; Feng, Q.; Liu, H.; Zhou, X.; Yang, X.; Yun, D. An improved Forel-Ule index method for trophic state assessments of inland waters using Landsat 8 and sentinel archives. Giscience Remote Sens. 2021, 58, 1316–1334. [Google Scholar] [CrossRef]
- Viso-Vazquez, M.; Acuna-Alonso, C.; Luis Rodriguez, J.; Alvarez, X. Remote Detection of Cyanobacterial Blooms and Chlorophyll-a Analysis in a Eutrophic Reservoir Using Sentinel-2. Sustainability 2021, 13, 8570. [Google Scholar] [CrossRef]
- Hu, C. A novel ocean color index to detect floating algae in the global oceans. Remote Sens. Environ. 2009, 113, 2118–2129. [Google Scholar] [CrossRef]
- Obata, K.; Miura, T.; Yoshioka, H.; Huete, A.R. Derivation of a MODIS-compatible enhanced vegetation index from visible infrared imaging radiometer suite spectral reflectances using vegetation isoline equations. J. Appl. Remote Sens. 2013, 7, 073467. [Google Scholar] [CrossRef]
- Hu, C.; Lee, Z.; Ma, R.; Yu, K.; Li, D.; Shang, S. Moderate Resolution Imaging Spectroradiometer (MODIS) observations of cyanobacteria blooms in Taihu Lake, China. J. Geophys. Res. Ocean. 2010, 115, C04002. [Google Scholar] [CrossRef]
- Xing, Q.; Hu, C. Mapping macroalgal blooms in the Yellow Sea and East China Sea using HJ-1 and Landsat data: Application of a virtual baseline reflectance height technique. Remote Sens. Environ. 2016, 178, 113–126. [Google Scholar] [CrossRef]
- Matthews, M.W. Eutrophication and cyanobacterial blooms in South African inland waters: 10 years of MERIS observations. Remote Sens. Environ. 2014, 155, 161–177. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Borstad, G.; Brown, L. Detection of intense plankton blooms using the 709 nm band of the MERIS imaging spectrometer. Int. J. Remote Sens. 2005, 26, 2005–2012. [Google Scholar] [CrossRef]
- Wang, M.; Shi, W.; Tang, J. Water property monitoring and assessment for China’s inland Lake Taihu from MODIS-Aqua measurements. Remote Sens. Environ. 2011, 115, 841–854. [Google Scholar] [CrossRef]
- Mouw, C.B.; Greb, S.; Aurin, D.; DiGiacomo, P.M.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moore, T.; et al. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recommendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Allee, R.J.; Johnson, J.E. Use of satellite imagery to estimate surface chlorophyll and Secchi disc depth of Bull Shoals Reservoir, Arkansas, USA. Int. J. Remote Sens. 1999, 20, 1057–1072. [Google Scholar] [CrossRef]
- Binding, C.E.; Greenberg, T.A.; Bukata, R.P. Time series analysis of algal blooms in Lake of the Woods using the MERIS maximum chlorophyll index. J. Plankton Res. 2011, 33, 1847–1852. [Google Scholar] [CrossRef]
- Duan, H.; Ma, R.; Hu, C. Evaluation of remote sensing algorithms for cyanobacterial pigment retrievals during spring bloom formation in several lakes of East China. Remote Sens. Environ. 2012, 126, 126–135. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, L.; Li, J.; Luo, L.; Yin, Y.; Liu, M.; Li, Y. Seasonal-spatial variation and remote sensing of phytoplankton absorption in Lake Taihu, a large eutrophic and shallow lake in China. J. Plankton Res. 2010, 32, 1023–1037. [Google Scholar] [CrossRef]
- Tao, M.; Duan, H.; Qi, L.; Zhang, Y.; Ma, R. An operational algorithm to estimate chlorophyll-a concentrations in Lake Chaohu from MODIS imagery. J. Lake Sci. 2015, 27, 1140–1150. [Google Scholar]
- Yang, H.; Du, Y.; Zhao, H.; Chen, F. Water Quality Chl-a Inversion Based on Spatio-Temporal Fusion and Convolutional Neural Network. Remote Sens. 2022, 14, 1267. [Google Scholar] [CrossRef]
- Keiner, L.E.; Brown, C.W. Estimating oceanic chlorophyll concentrations with neural networks. Int. J. Remote Sens. 1999, 20, 189–194. [Google Scholar] [CrossRef]
- Hunter, P.D.; Tyler, A.N.; Willby, N.J.; Gilvear, D.J. The spatial dynamics of vertical migration by Microcystis aeruginosa in a eutrophic shallow lake: A case study using high spatial resolution time-series airborne remote sensing. Limnol. Oceanogr. 2008, 53, 2391–2406. [Google Scholar] [CrossRef]
- Qi, L.; Hu, C.; Duan, H.; Barnes, B.B.; Ma, R. An EOF-Based Algorithm to Estimate Chlorophyll a Concentrations in Taihu Lake from MODIS Land-Band Measurements: Implications for Near Real-Time Applications and Forecasting Models. Remote Sens. 2014, 6, 10694–10715. [Google Scholar] [CrossRef]
- O’Shea, R.E.; Pahlevan, N.; Smith, B.; Bresciani, M.; Egerton, T.; Giardino, C.; Li, L.; Moore, T.; Ruiz-Verdu, A.; Ruberg, S.; et al. Advancing cyanobacteria biomass estimation from hyperspectral observations: Demonstrations with HICO and PRISMA imagery. Remote Sens. Environ. 2021, 266, 112693. [Google Scholar] [CrossRef]
- Becker, R.H.; Sultan, M.I.; Boyer, G.L.; Twiss, M.R.; Konopko, E. Mapping cyanobacterial blooms in the Great Lakes using MODIS. J. Great Lakes Res. 2009, 35, 447–453. [Google Scholar] [CrossRef]
- Flores-Anderson, A.I.; Griffin, R.; Dix, M.; Romero-Oliva, C.S.; Ochaeta, G.; Skinner-Alvarado, J.; Ramirez Moran, M.V.; Hernandez, B.; Cherrington, E.; Page, B.; et al. Hyperspectral Satellite Remote Sensing of Water Quality in Lake Atitlan, Guatemala. Front. Environ. Sci. 2020, 8, 1–8. [Google Scholar] [CrossRef]
- Chen, X.; Feng, L. Remote Sensing of Lakes’ Water Environment. In Comprehensive Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2018; pp. 249–277. [Google Scholar]
- Hassan, N.; Woo, C.S. Machine Learning Application in Water Quality Using Satellite Data. IOP Conf. Ser. Earth Environ. Sci. 2021, 842, 012018. [Google Scholar] [CrossRef]
- Li, S.; Song, K.; Wang, S.; Liu, G.; Wen, Z.; Shang, Y.; Lyu, L.; Chen, F.; Xu, S.; Tao, H.; et al. Quantification of chlorophyll-a in typical lakes across China using Sentinel-2 MSI imagery with machine learning algorithm. Sci. Total Environ. 2021, 778, 146271. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Huang, H.; Chen, B.; Zheng, B.; Wang, Y. Application of Extreme Learning Machine for Predicting Chlorophyll-a Concentration Inartificial Upwelling Processes. Math. Probl. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Sonobe, R.; Yamashita, H.; Mihara, H.; Morita, A.; Ikka, T. Estimation of Leaf Chlorophyll a, b and Carotenoid Contents and Their Ratios Using Hyperspectral Reflectance. Remote Sens. 2020, 12, 3265. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, J.-J.; Alam, M.A.; An, K.-G. Prediction of Algal Chlorophyll-a and Water Clarity in Monsoon-Region Reservoir Using Machine Learning Approaches. Water 2019, 12, 30. [Google Scholar] [CrossRef]
- Zhang, T.; Huang, M.; Wang, Z. Estimation of chlorophyll-a Concentration of lakes based on SVM algorithm and Landsat 8 OLI images. Environ. Sci Pollut. Res. Int. 2020, 27, 14977–14990. [Google Scholar] [CrossRef]
- Hu, C.; Feng, L.; Guan, Q. A Machine Learning Approach to Estimate Surface Chlorophyll a Concentrations in Global Oceans From Satellite Measurements. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4590–4607. [Google Scholar] [CrossRef]
- Guan, Q.; Feng, L.; Hou, X.; Schurgers, G.; Zheng, Y.; Tang, J. Eutrophication changes in fifty large lakes on the Yangtze Plain of China derived from MERIS and OLCI observations. Remote Sens. Environ. 2020, 246, 111890. [Google Scholar] [CrossRef]
- Ansari, M.; Akhoondzadeh, M. Mapping water salinity using Landsat-8 OLI satellite images (Case study: Karun basin located in Iran). Adv. Space Res. 2020, 65, 1490–1502. [Google Scholar] [CrossRef]
- Ali, M.M. Estimation of ocean subsurface thermal structure from surface parameters: A neural network approach. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Chang, N.B.; Imen, S. Improving the control of water treatment plant with remote sensing-based water quality forecasting model. In Proceedings of the 12th International Conference on Networking, Sensing and Control, Taipei, Taiwan, 9–11 April 2015; Volume 12, pp. 51–57. [Google Scholar]
- Bangira, T.; Alfieri, S.M.; Menenti, M.; van Niekerk, A. Comparing Thresholding with Machine Learning Classifiers for Mapping Complex Water. Remote Sens. 2019, 11, 1351. [Google Scholar] [CrossRef]
- Govedarica, M.; Jakovljević, G. Monitoring spatial and temporal variation of water quality parameters using time series of open multispectral data. SPIE Proc. 2019, 11174, 298–307. [Google Scholar]
- Zhang, Y.N.; Zheng, X.S. An improved algorithm for retrieval of aerosol optical properties over the Yellow Sea from Geostationary Ocean Color Imager. Int. Geosci. Remote Sens. Symp. 2016, 10, 4077–4079. [Google Scholar]
- Lim, J.; Choi, M. Assessment of water quality based on Landsat 8 operational land imager associated with human activities in Korea. Environ. Monit. Assess. 2015, 187, 384. [Google Scholar] [CrossRef]
- Karki, S.; Sultan, M.; Elkadiri, R.; Elbayoumi, T. Mapping and Forecasting Onsets of Harmful Algal Blooms Using MODIS Data over Coastal Waters Surrounding Charlotte County, Florida. Remote Sens. 2018, 10, 1656. [Google Scholar] [CrossRef]
- Green, R.E.; Gould, R.W.; Ko, D.S. Statistical models for sediment/detritus and dissolved absorption coefficients in coastal waters of the northern Gulf of Mexico. Cont. Shelf Res. 2008, 28, 1273–1285. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, H.; Liu, C.; Zhang, S.; Ding, A.; Xie, E.; Li, J.; Wang, S. Prediction of harmful algal blooms in large water bodies using the combined EFDC and LSTM models. J. Environ. Manag. 2021, 295, 113060. [Google Scholar] [CrossRef]
- Mohebzadeh, H.; Lee, T. Spatial downscaling of MODIS Chlorophyll-a with machine learning techniques over the west coast of the Yellow Sea in South Korea. J. Oceanogr. 2020, 77, 103–122. [Google Scholar] [CrossRef]
- He, J.; Chen, Y.; Wu, J.; Stow, D.A.; Christakos, G. Space-time chlorophyll-a retrieval in optically complex waters that accounts for remote sensing and modeling uncertainties and improves remote estimation accuracy. Water Res. 2020, 171, 115403. [Google Scholar] [CrossRef]
- Peppa, M.; Vasilakos, C.; Kavroudakis, D. Eutrophication Monitoring for Lake Pamvotis, Greece, Using Sentinel-2 Data. ISPRS Int. J. Geo-Inf. 2020, 9, 143. [Google Scholar] [CrossRef]
- Korkmaz, M. A study over the Formulation of the Parameters 5 or Less Independent Variables of Multiple Linear Regression. J. Funct. Spaces 2019, 2019, 1526920. [Google Scholar] [CrossRef]
- Ding, S.; Zhang, N.; Zhang, X.; Wu, F. Twin support vector machine: Theory, algorithm and applications. Neural Comput. Appl. 2017, 28, 3119–3130. [Google Scholar] [CrossRef]
- Pei, S.; Qin, H.; Yao, L.; Liu, Y.; Wang, C.; Zhou, J. Multi-Step Ahead Short-Term Load Forecasting Using Hybrid Feature Selection and Improved Long Short-Term Memory Network. Energies 2020, 13, 4121. [Google Scholar] [CrossRef]
- Mao, L.; Zhang, L.; Liu, X.; Li, C.; Yang, H. Improved Extreme Learning Machine and Its Application in Image Quality Assessment. Math. Probl. Eng. 2014, 2014, 426152. [Google Scholar] [CrossRef]
- Huang, G.B.; Siew, C.K. Extreme Learning Machine with Randomly Assigned RBF Kernels. Int. J. Inf. Technol. 2005, 11, 16–24. [Google Scholar]
- Huang, G.; Huang, G.-B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef]
- Ouma, Y.O.; Noor, K.; Herbert, K. Modelling Reservoir Chlorophyll-a, TSS, and Turbidity Using Sentinel-2A MSI and Landsat-8 OLI Satellite Sensors with Empirical Multivariate Regression. J. Sens. 2020, 2020, 1–21. [Google Scholar] [CrossRef]
- Fernandez-Figueroa, E.G.; Wilson, A.E.; Rogers, S.R. Commercially available unoccupied aerial systems for monitoring harmful algal blooms: A comparative study. Limnol. Oceanogr. Methods 2021, 20, 146–158. [Google Scholar] [CrossRef]
- Zhai, Z.K.; Lu, S.L.; Wang, P.; Wang, C.; Tang, H.L.; Liu, D.Y.; Han, Q.Y.; Guo, J.; Liu, X.H.; Wei, T.L. Ocean Chlorophyll-a retrieval using GF1-WFV data-a case study of the central Bohai Sea. IOP Conf. Ser. Earth Environ. Sci. 2021, 626, 012021. [Google Scholar] [CrossRef]
- Ogashawara, I.; Li, L. Removal of Chlorophyll-a Spectral Interference for Improved Phycocyanin Estimation from Remote Sensing Reflectance. Remote Sens. 2019, 11, 1764. [Google Scholar] [CrossRef]
- Hoaglin, D.C. Regressions are commonly misinterpreted. Stata J. 2016, 16, 5–22. [Google Scholar] [CrossRef]
- Li, M.-W.; Geng, J.; Hong, W.-C.; Zhang, Y. Hybridizing Chaotic and Quantum Mechanisms and Fruit Fly Optimization Algorithm with Least Squares Support Vector Regression Model in Electric Load Forecasting. Energies 2018, 11, 2226. [Google Scholar] [CrossRef]
- Jones, G.; Macken, B. Long-term associative learning predicts verbal short-term memory performance. Mem. Cognit. 2018, 46, 216–229. [Google Scholar] [CrossRef] [PubMed]
- Jia, T.; Zhang, X.; Dong, R. Long-Term Spatial and Temporal Monitoring of Cyanobacteria Blooms Using MODIS on Google Earth Engine: A Case Study in Taihu Lake. Remote Sens. 2019, 11, 2269. [Google Scholar] [CrossRef]
- Wang, X.; Xu, L. Unsteady Multi-Element Time Series Analysis and Prediction Based on Spatial-Temporal Attention and Error Forecast Fusion. Future Internet 2020, 12, 34. [Google Scholar] [CrossRef]
- Yussof, F.N.; Maan, N.; Md Reba, M.N. LSTM Networks to Improve the Prediction of Harmful Algal Blooms in the West Coast of Sabah. Int. J. Environ. Res. Public Health 2021, 18, 7650. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).