Study on the Calculation Method of Water Inflow Velocity of Loose Rock Landslide

Abstract

Landslide surges pose a serious threat to the ecological environment and human life safety. Based on rock structure mechanics and water sediment dynamics, considering the additional resistance caused by the interference of loose landslide particles on flow structure, this paper deduces the resistance calculation formula of loose-rock landslide particles when entering water. It modifies the landslide velocity formula (ASCE) recommended by the American Society of Civil Engineers. The acceleration calculation formula and velocity calculation formula of bulk-rock landslides entering water are obtained, and the determination method of the main parameters in the formula is given. Based on the data of the Xintan Landslide into the Yangtze River, the rationality of the calculation results of this formula and the ASCE formula are compared and analyzed. It shows that the ASCE formula calculates the average velocity of landslide movement on land, and there will be a noticeable deviation from the actual situation when it is used to calculate the water entry velocity of a loose-rock landslide. The formula given in this paper is more practical and can be used to calculate the velocity of loose-rock landslides entering water.

1. Introduction

Landslides occur in rivers, reservoirs, lakes or coastal areas with a certain depth of water. When sliding into the water at high speed, the water body will be disturbed and squeezed by the landslide mass, which will produce huge water waves propagating along the coast, causing serious impact on engineering facilities and the ecological environment, and threatening the lives and property safety of upstream and downstream residents. In the case of serious landslide, the whole river will be cut off to form a barrier lake, which will cause the rapid disappearance of the original river ecosystem. The degree of damage caused by a landslide surge to the ecological environment is directly related to its initial surge height, which is determined by such key factors as landslide mass scale, sliding speed, and water depth, etc. Generally, the scale of a landslide mass and river water depth are easy to determine, and the reasonable determination of landslide inflow velocity is always worth discussing. At present, it is a common method to study the generation, propagation and climbing process of a landslide surge based on an indoor physical simulation test [1]. Edward Noda established the relationship between the initial surge height and water depth, and the horizontal or vertical water entry velocity of landslide mass [2]; Davidson and Mccartney [3] analyzed the surge characteristics caused by a landslide in the Kootenal River according to investigation data, and established the relationship between landslide surge height and landslide mass velocity; based on the theory of energy conservation, Hao et al. [4] deduced the failure form of the landslide structural plane on the basis of the critical thickness of the landslide, clarified the value of the parameters, and predicted the final velocity of the landslide. Wieczorek et al. [5] collected, sorted and analyzed the common empirical calculation formulas of landslide surge height, and expounded the applicability of relevant formulas; Risio et al. [6] discussed the surge height generated during the movement of a landslide along the linear reservoir bank; Evers and Hager [7] take the attenuation rate of head wave height as the research object, specifically analyze the main factors affecting the attenuation rate of the head wave height, and establish the corresponding empirical relationship, based on Edward Noda’s research. Wang and Yin [8] applied the slice method to determine the relevant parameters of sliding slope velocity, acceleration and head wave height, and selected the Xintan Landslide for example analysis. Li et al. [9] analyzed the influence of landslide shape, volume, sliding height and reservoir water depth on surge height based on the generalized model experiment of the surge tank of a block landslide in a near-dam reservoir area; Wang et al. [10] studied the effects of landslide width, landslide thickness and sliding surface inclination on surge height by using the landslide surge test model of the Three Gorges Reservoir. Pudasaini and Krautblatter [11] derived a general landslide velocity model applicable to different types of landslide motions and solved it analytically to obtain several exact solutions as a function of space and time for landslide motion.

At present, the common calculation methods of landslide velocity mainly include the method recommended by the American Society of Civil Engineers [12], the kinetic energy theorem method (ibid), the slice method [13] and the time increment step method [14]. Xue et al. [15] calculated the velocity of the landslide based on the improved slice method of the viscous resistance of the landslide into water and evaluated the landslide disaster level. When the landslide enters water, it will be affected by the water resistance, and the acceleration and velocity will decrease. Strictly speaking, the movement velocity of a landslide on land cannot be directly used to calculate the surge formed by its water inflow impact. Based on the study of water wave dynamics, Huang et al. [16] pointed out that for the existing landslide velocity research, the calculation results are too conservative; the main reason for this is the influence of water resistance and friction after the landslide meets water is ignored. However, various calculation formulas consider different forms. Based on Pan Jiazheng’s procedure, Huang [17] comprehensively considered the influence of water resistance and friction coefficient and claimed that the underwater-friction coefficient of a landslide is much smaller than one onshore. Based on 30 groups of physical tests, Wang et al. [18] discussed the variation law of plane-sliding and curved-sliding wading resistance on sliding block speed. The results showed that water resistance significantly impacts underwater landslide speed. However, these studies regard the landslide mass as a single rigid block entering water and do not consider the collision between loose landslide particles. The results can only be used to calculate the velocity of a single block landslide entering water.

Natural-rock landslide mass is mainly composed of rock structure, fissure, fault, weak interlayer, and void, etc. In the process of movement and sliding, most of the rock landslide mass may be cracked and cut into blocks of different sizes and numerous fragments due to extrusion, collision and scraping. With the acceleration of the decline rate, the degree of dispersion will also intensify. Therefore, to determine the surge height value formed by the water inflow impact of loose-rock landslide more realistically, it is necessary to consider the additional resistance to the flow structure caused by the spatial distribution of loose-landslide particles and explore the calculation method of the velocity of a loose-rock landslide entering the water. In this paper, the model test landslide is mainly to simulate the rock landslide. In order to better simulate the geometric shape and physical indexes of the landslide mass, this paper collected and counted the characteristic parameters of typical rocky landslides in the mainstream and tributaries before and after the impoundment of the Three Gorges Project, including the characteristic parameters of the Xintan Landslide.

2. Derivation of Calculation Formula

The study of particle motion and force in fluid began with the flow field condition of prolonged flow. Stokes was the first to analyze particle motion using viscous fluid theory and first studied the linear harmonic motion of a single sphere, cylinder, and infinite plate in a viscous fluid. He deduced the resistance of the creeping viscous liquid to particles by using the N-S formula, which contains two terms related to particle acceleration and velocity, respectively. The drag term for speed is $F=6\pi \alpha {\mu }_{f}V$, the drag coefficient is $C_d=24/R_{es}$, and $R_{es}$ is the particle Reynolds number.

Generally, the Reynolds number used in the flow around a single sphere is:

$$R_e=VD/\nu$$

(1)

where $D$ is the sphere diameter (m), $V$ is the viscosity coefficient of water flow movement (m²/s), and $\nu$ is the relative velocity of particles and water flow (m/s).

Unlike the underwater movement of single-block landslide particles, due to pores in the sliding block particle group of bulk landslide and the mutual collision and diffusion deformation in entering the water, complex water relative flow is generated in the sliding block particle group. If the porosity in the particle group of the loose landslide is $\epsilon$ and the average velocity of the water flow is $u$, according to the basic law of solid particle flow in fluid mechanics the relative speed between the particle group and the water flow is:

$$v=u/\epsilon$$

(2)

Therefore, replacing $V$ in Formula (1) with $v$ in Formula (2) to obtain the flow Reynolds number of particle group of loose landslide:

$$R_e^{/}=uD/(\epsilon \nu )$$

(3)

In fluid mechanics, the resistance of solid particles moving in liquid, that is, the fluid resistance, can be expressed as [19]:

$$F_w=C_D\rho A{v}^2/2$$

(4)

where $F_w$ is the fluid resistance, $\rho$ is the density of fluid (g/m³), $C_D$ is the resistance coefficient, $A$ is the orthographic projection area relative to the fluid, and $v$ is the movement speed of sliding block (m/s).

According to the investigation of the landslide movement process of wading examples and the physical model test of a landslide surge, for bulk landslides, when the landslide moves to the water surface, it is not a single block particle, but a group of bulk particles of different sizes entering the water at the same time. The resistance coefficient of the particle group in the deformation stage is more significant than that of the single block particles. In addition to the flow resistance caused by general relative movement, there is also additional resistance caused by the interference effect on the flow structure caused by the collision between particles. Assuming that the extra resistance caused by the crash between slider particles and the interference with the flow structure leads to a change in resistance coefficient, according to Formula (4), the resistance of each sliding block particle in the particle group of a bulk landslide can be written as:

$$F_w^{/}=C_D^{/}\rho A\frac{u^2}{2{\epsilon }^2}$$

(5)

In the formula, $C_D^{/}$ is the resistance coefficient, including additional resistance.

The number of particles per unit slider particle group volume is:

$$n=\frac{6(1-\epsilon )}{\pi D^3}$$

(6)

The particle number of the whole landslide particle group is:

$$N=n\cdot A\cdot s=\frac{6(1-\epsilon )}{\pi D^3}As$$

(7)

In this formula, $s$ is the thickness of the landslide mass (m).

Therefore, it can be obtained that the resistance of the sliding block particle group of a loose landslide when entering the water is:

$$F=N\cdot F_w^{/}=C_D^{/}\rho A\frac{u^2}{2{\epsilon }^2}\cdot \frac{6(1-\epsilon )}{\pi D^3}As=3C_D^{/}\rho A^{2}s\frac{(1-\epsilon )}{{\epsilon }^2}\frac{u^2}{\pi D^3}$$

(8)

For a landslide particle group composed of spherical blocks, the resistance of water flow acting on the whole particle group is:

$$F=N\cdot F_w^{/}=C_D^{/}\frac{3}{4}\frac{1-\epsilon }{D}As\frac{\rho u^2}{{\epsilon }^2}=\frac{3\pi }{16}{C}_D^{/}\rho Ds{u}^2\frac{(1-\epsilon )}{{\epsilon }^2}$$

(9)

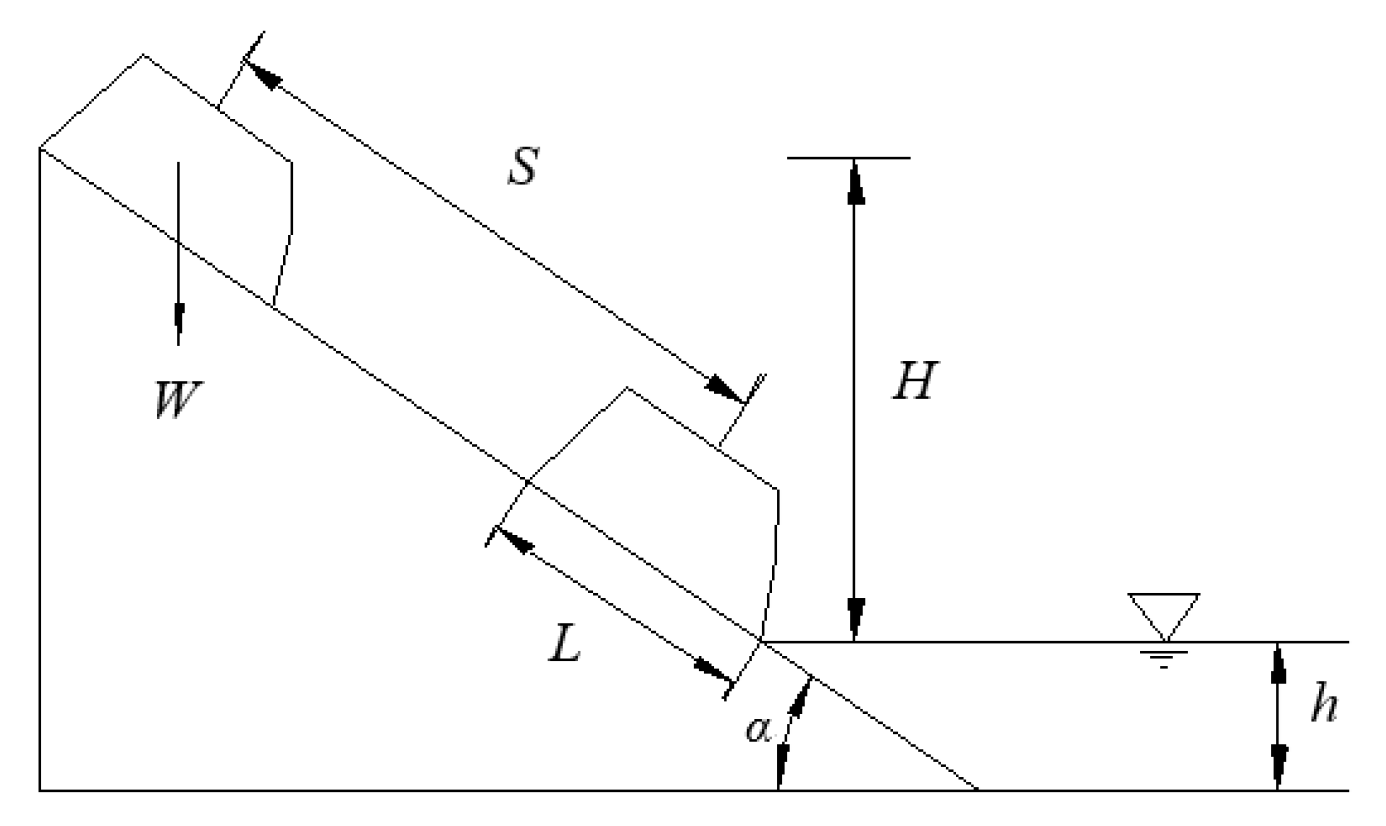
According to Formula (8) or Formula (9), the commonly used calculation formula of landslide velocity recommended by the American Society of Civil Engineers (from now on referred to as “ASCE formula”) can be modified to obtain the calculation formula of the acceleration and speed of a loose-rock landslide when entering water. The ASCE formula regards the sliding body as a whole and establishes particle motion with the center of gravity. The motion speed of the sliding body is deduced according to Newton’s second law and kinematics formula. The method is that the force of the sliding body along the sliding surface is equal to the difference between the sliding force and the anti-sliding force, as shown in Figure 1:

$$F=W\sin \alpha -(W\cos \alpha \tan \phi +cL)$$

(10)

According to $F=ma$, then:

$$a=g(\sin \alpha -\cos \alpha \tan \phi )-\frac{cL}{m}$$

(11)

$$V=\sqrt{[(1-\cot \alpha \tan \phi )-\frac{cL}{mg\sin \alpha }]}\cdot \sqrt{2gH}$$

(12)

where $a$ is the acceleration of the sliding body (m/s²); $V$ is the sliding speed of the sliding body (m/s); $\alpha$ is the inclination of the sliding surface (°); $W$ is the weight per unit width of the sliding body (kg); $m$ is the mass per unit width of the sliding body (kg); $g$ is the gravitational acceleration (m/s²); $c$ is the cohesion of the sliding surface (kPa), generally taken as 0; $\phi$ is the internal friction angle of the sliding surface (°), which is generally 0.7~0.95 times that of the static state; $H$ is the height of the barycenter of the sliding body from the water surface (m); $S$ is the sliding distance (m); and $L$ is the contact surface length between the sliding body and sliding surface (m).

According to Formula (9), Formulas (11) and (12) are modified to obtain the calculation formula of the acceleration and velocity of a loose-rock landslide when entering the water as follows:

$$a=g(\sin \alpha -\cos \alpha \tan \phi )-\frac{cL}{m}-\frac{3\pi }{16m}{C}_D^{/}\rho Ds{u}^2\frac{(1-\epsilon )}{{\epsilon }^2}$$

(13)

$$V=\sqrt{(1-\cot \alpha \tan \phi )-\frac{cL}{mg\sin \alpha }-\frac{3\pi }{16mg\sin \alpha }{C}_D^{/}\rho Ds{u}^2\frac{(1-\epsilon )}{{\epsilon }^2}}\cdot \sqrt{2gH}$$

(14)

3. Determination Method of Main Parameters

When using Formulas (13) and (14), it is necessary to determine the resistance coefficient $C_D^{/}$, particle group’s porosity, and particle size $D$, etc.

➀

Determination of resistance coefficient $C_D^{/}$:

According to Formula (3), the flow Reynolds number of loose particles $R_e^{/}$ can be calculated. Generally, when the landslide enters the water, the relative water flow velocity is tremendous. The turbulence of water flow is enhanced and $R_e^{/}$ will be much greater than 1000. According to Stokes’s theory, the inertia term caused by the acceleration of water particles is substantial. Particles will separate when moving in water flow, and the viscous force can be ignored. At this time, the resistance coefficient $C_D^{/}$ is a constant, that is:

$$C_D^{/}=0.45$$

(15)

➁

Determination of porosity $\epsilon$:

The pore volume per unit volume in the slider particle group to the volume of the whole slider particle group is called porosity. If the porosity of the slider particle group is ${\epsilon }_z$ and the thickness of the particle group is $s_z$ in the natural accumulation state, then the number of slider particles with size $D$ in the slider particle group is:

$$N_1=\frac{s_{z}A(1-{\epsilon }_z)}{\frac{1}{6}\pi D^3}$$

(16)

After the sliding block particle group enters the water, the particle group will collide and diffuse under the action of water flow resistance. When the thickness increases to $s$ and the porosity becomes $\epsilon$, the number of particles can be written as follows:

$$N_2=\frac{sA(1-\epsilon )}{\frac{1}{6}\pi D^3}$$

(17)

During the deformation of the particle group of the loose landslide, the number of particles in the sliding block does not change, that is, $N_1=N_2$. Therefore, the porosity of the particle group after the deformation of the loose landslide is:

$$\epsilon =1-\frac{s_z}{s}(1-{\epsilon }_z)$$

(18)

In the physical model test, the porosity under natural accumulation and the porosity of accumulation after the landslide mass enters the water can be measured directly according to the prepared loose-rock landslide sliding block particles. For the actual landslide mass, the natural accumulation state and the porosity and thickness after deformation can be obtained according to field sampling tests and analysis.

➂

Determination of particle size D of the particle group

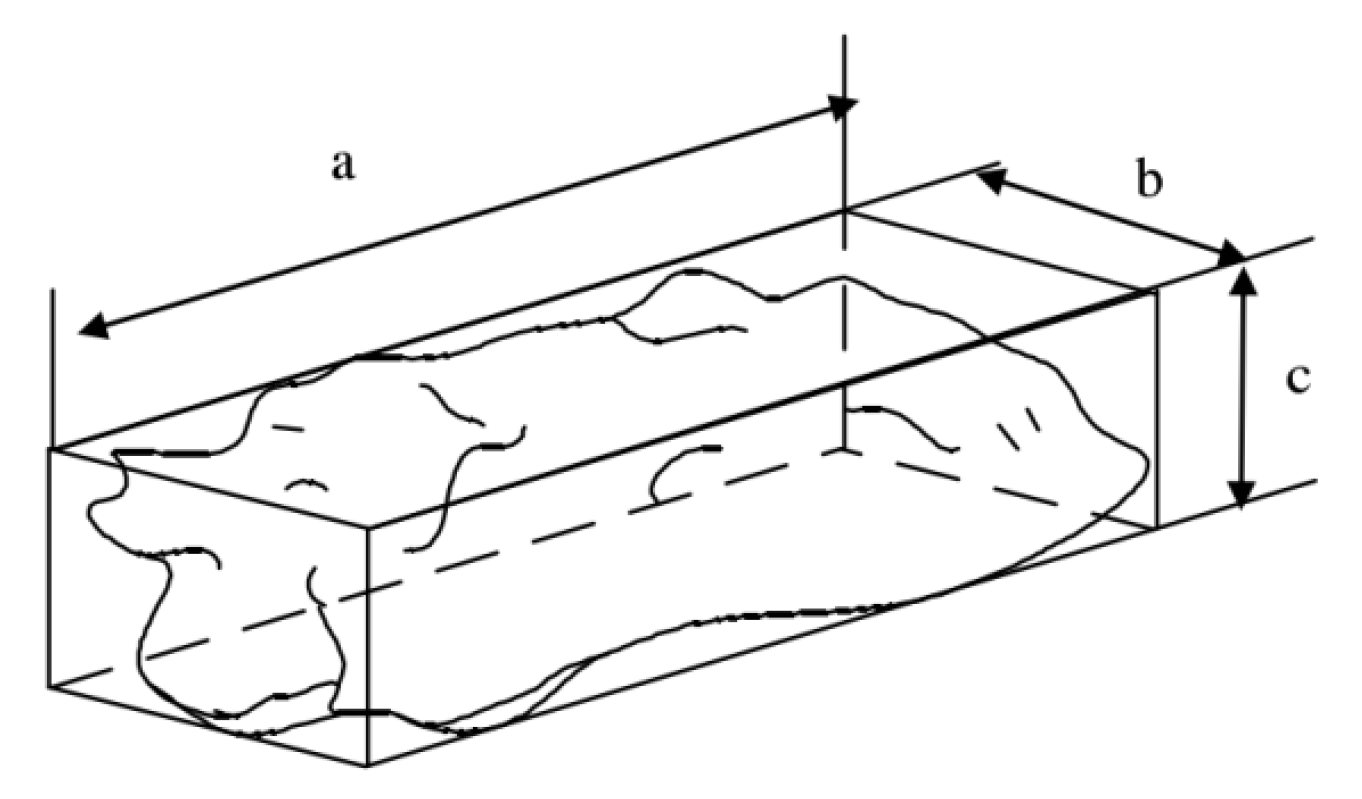
For objects with a regular shape, such as spheres, cubes, columns, and disks, the particle size can be characterized by diameter or side length. However, for the sliding block particles of a bulk landslide, the shape of each sliding block is highly complex and has unique appearance characteristics. Therefore, the concept of equivalent diameter or average particle size in sediment mechanics can be used to accurately characterize the particle size of an irregular sliding body. For single particle or loose-landslide particles with a uniform particle-size distribution, the particle size is generally expressed by ball equivalent diameter, triaxial particle size, projected particle size, screening average particle size, hydraulic diameter, and other methods. In practice, the particle size of most bulk rocks can be counted on site, and the triaxial length of particles, as shown in Figure 2 [20], can be given. The average particle size can be calculated by the following formula.

$$D=\sqrt[3]{\mathrm{a}\mathrm{b}\mathrm{c}}$$

(19)

In the formula, a, b and c are the lengths of the long, medium, and short axes of rock debris particles, respectively.

For the particle group of loose landslides with an uneven particle-size distribution, the above representation method is not accurate enough. According to the basic principle of sediment movement mechanics, the gradation curve of a particle group can be drawn., as shown in Figure 3 [21]; several characterization methods such as weighted average particle size, geometric average particle size, and median particle size are used to give the average particle size of the particle group.

a.

Weighted average particle size

$$D_m=\frac{{\displaystyle \sum \Delta P_i{D}_i}}{100}=\frac{\Delta P_1{D}_1+\Delta P_2{D}_2+\dots +\Delta P_n{D}_n}{100}$$

(20)

In the formula, $\Delta P_i$ represents the percentage of particles with size $D_i$ in the weight, volume, or number of the whole landslide mass.

b.

Geometric average particle size

$$D_g={\left(D_1^{\Delta P_1}•D_2^{\Delta P_2}•\dots D_n^{\Delta P_n}\right)}^{\frac{1}{100}}$$

(21)

$$\mathrm{or} \lg D_g=\frac{{\displaystyle \sum \Delta P_i\lg D_i}}{100}$$

(22)

When the frequency curve of particles conforms to Gaussian normal distribution:

$$\lg D_g=\frac{1}{2}\left(\lg D_{15.9}+\lg D_{84.1}\right)$$

(23)

$$\mathrm{or} D_g=\sqrt{D_{15.9}{D}_{84.1}}$$

(24)

In the formula, $D_{15.9}$ and $D_{84.1}$ are the particle sizes corresponding to $\Delta P=15.9\%$ and $\Delta P=84.1\%$ on the grading curve, respectively.

c.

Median particle size

On the grading curve, the particle size corresponding to $\Delta P=50\%$ is called the median particle size, which is represented by $D_{50}$.

4. Comparative Calculation with ASCE Formula

4.1. Comparison and Calculation of Model Test Data

According to the complex water environment of the main stream of the Three Gorges Reservoir Area and the fissure structure of the rock landslide mass in the reservoir area, the author made a three-dimensional physical model of the swell of a rock landslide in the main stream of the Three Gorges Reservoir Area under hydrodynamic conditions. In addition, a representative model test of a working condition (model water depth of 0.25 m, flow velocity of 0.24 m/s, landslide volume of 0.4 m³, and slip surface inclination of 40°) was carried out as an example of a comparative calculation, as shown in Figure 4. See

Table 1. Proportioning of landslide mass model (length 100 cm × width 100 cm × thickness 40 cm).

Small Block Model	Length (cm)	Width (cm)	Thickness (cm)	Single Volume (cm3)	Matching Number
Vmax	21	14	6	1764	91
V60	18	12	5	1080	74
V40	15	10	4	600	133
V20	12	8	3	288	139
V10	9	6	2	108	370

for the proportioning data of the loose-rock landslide model used in the test. Using the triaxial length of particles and Formula (19), the average particle sizes of five small blocks can be calculated as 12.08 cm, 10.26 cm, 8.43 cm, 6.60 cm, and 4.76 cm, respectively. According to the proportion percentage of each small block in Table 1 and Formula (20), the average particle size of the landslide particle group can be calculated as 9.71 cm. According to the test, the porosity of the natural accumulation of the landslide mass is 0.39, the porosity of the accumulation mass after the landslide mass enters the water is 0.46, the internal friction angle of the sliding surface is 18°, and the cohesion of the sliding surface is 10 kPa. The distance between the gravity center of the landslide and the water surface is 0.7 m, so the height between the gravity center and the water surface is 0.45 m. The movement process of the test landslide was photographed with a high-definition camera (a SONY DSC-RX10M4 camera, which is able to shoot up to 1000 frames per second (fps), with a resolution of 3840 × 2160 pixels), and the water inflow velocity of the landslide was determined to be 1.90 m/s through image-processing calculations, which was converted to 15.90 m/s for the prototype.

In general, Formula (12) is the average velocity formula of the landslide mass on the landslide surface, and Equation (14) is the velocity formula of the water entry point of the landslide mass. Using ASCE Formula (12), the average speed of the model landslide mass is 2.44 m/s, which is converted to the average speed of the prototype landslide mass as 20.41 m/s. The water inflow velocity of the model landslide mass calculated by Formula (14) in this paper is 1.95 m/s, which is converted to 16.31 m/s of the prototype landslide mass. The comparison of the water inflow velocity of the landslide observed by the test shows that the calculated result of the ASCE formula is obviously larger than that of the formula given in this paper.

4.2. Comparative Calculation of Xintan Landslide in the Yangtze River

The Xintan Landslide is located on the North Bank of the exit of the Bingshu Baojian Gorge in the upper section of Xiling Gorge of the Yangtze River. It faces the Lianziya dangerous rock mass across the river and is about 26 km away from the sanding dam site of the Three Gorges Project. The Xintan Landslide has experienced many large-scale landslides, a large-scale slide occurred at 3:00 on 12 June 1985, which lasted 4 min and 7 s, and the whole of Xintan town was destroyed instantly. The entire terrain of the Xintan Landslide is high in the north and low in the south, and the trailing edge of the landslide is steep. The plane shape is irregular quadrilateral, the rear-edge elevation is about 900 m, the front-edge elevation is about 60 m, the length is nearly 2000 m, and the area is approximately 0.75 × 106 m², with an overall volume of 3 × 107 m³, the relative height difference between the rear wall of the landslide. The riverbed is about 800 m, the average longitudinal gradient is 23°, and the local steepness and slowness are different. The rear edge of the landslide is narrow, about 300 m, the front edge is wide, about 500~1000 m, and the average width is 450 m.

The Xintan Landslide is an accumulation landslide. The thickness of deposits is generally between 30~40 m and 86 m in local sections. According to the particle size and grading composition of landslide block stone measured by the Xintan Landform investigation team of Nanjing University (see

Table 2. Composition of block stone particles of the Xintan Landslide.

Serial Number	Particle Size (m)	Number of Measurement Blocks	Proportion in Total Blocks (%)
1	≥5	26	3.17
2	2~5	75	9.15
3	1~2	345	42.07
4	≤1	374	45.61

), the average particle size of Xintan-Landslide block stone is calculated to be 1.47 m. The porosity of the landslide mass is 0.45, the internal friction angle of the sliding surface is 17.5°, the friction coefficient is 0.277, and the cohesion of the sliding surface is 21.0 kPa. The density of the landslide mass is 2.3 × 10³ kg/m³, and the viscous resistance coefficient is 0.18. When the landslide is unstable, the water level is about 62 m, and the height from the weight center of the landslide to the water surface is about 220 m.

When the Xintan Landslide occurs, the Yangtze River is a natural channel with a maximum water depth of about 40 m, an average water depth of about 30 m, a water surface width of about 380 m, and an average flow velocity of about 3.0 m/s. As the thickness of the deposit is generally between 30~40 m, the thickness of the landslide mass is close to the water depth of the river. After the landslide is unstable, it slides into the Yangtze River with a total volume of about 3 million cubic metres, blocking about half of the river course; the landslide speed is about 10~30 m/s, the average rate when entering the water is about 20 m/s, and the maximum head wave height is approximately 34.24 m. The slope angle of the opposite bank slope is 19.71°, the wave height in front of the opposite bank slope is 16.33 m, and the climbing wave on the opposite bank is about 54 m; ships within 8 km are overturned, which affects the range of 16 km upstream and 26 km downstream.

According to the above relevant parameters, the average Xintan Landslide mass calculated by ASCE Formula (12) is 54.34 m/s, 171.7% higher than the actual average velocity of 20 m/s, and 81.1% higher than the actual maximum sliding velocity of 30 m/s. The water inflow velocity of the Xintan Landslide mass calculated by Formula (14) in this paper is 22.56 m/s, which is 12.8% higher than the average velocity of actual water inflow. Thus, it is close to the actual value. Therefore, it can be shown that the calculation result of the ASCE formula is significantly larger than the reality, and the calculation result of this formula is more in-line with reality.

5. Conclusions

(1)

At present, the landslide motion velocity method recommended by the American Society of Civil Engineers is based on the rigid sliding body as a particle and analyzing the position and the velocity of particle motion. As its characteristic parameters neither consider the volume of the slider and the characteristics of the landslide shape, nor the change in velocity and the influence of water resistance in the process of landslide movement, it can only calculate the average velocity of the landslide on the land. Therefore, there will be a noticeable deviation from the actual situation when used to calculate the surge height formed by the water inflow impact of a bulk landslide.

(2)

Based on rock structure mechanics and water sediment dynamics, and considering the additional resistance caused by the interference of loose landslide particles on the flow structure, this paper deduces the calculation formula of resistance when the loose-rock landslide particles enter the water, and then modifies the ASCE formula to obtain the acceleration and velocity calculation formula of a loose-rock landslide when entering the water. At the same time, the determination method of main parameters such as resistance coefficient, the porosity of particle group, and particle size of particle group in the formula has also been established.

(3)

Based on the data of the Xintan Landslide into the Yangtze River, the ASCE formula and the modified formula in this paper are used to calculate the water entry velocity of the landslide. The calculation results show that the calculation results of the ASCE formula are larger than those given by the author. The calculation results of the formula in this paper are in good agreement with the reality, and can be used to calculate the velocity of loose-rock landslides when they enter water, so that the height of landslide surge and its damage to the ecological environment can be reasonably determined.