Low-Carbon Product Family Planning for Manufacturing as a Service (MaaS): Bilevel Optimization with Linear Physical Programming
Abstract
1. Introduction
2. Literature Review and Contributions
2.1. Future Manufacturing Trends towards MaaS
2.2. Low-Carbon Product Design
2.3. PFP for Manfacturing
2.4. Contributions
- Coordinated decision making of low-carbon PFP and MLB for MaaS is proposed and described as a joint optimization problem.
- A leader–follower interactive decision-making mechanism is proposed, and we formulate the joint optimization of low-carbon PFP and MLB as a bilevel optimization model with linear physical programming (both upper level and lower level have multiple objectives).
- A NBGA algorithm embedded linear physical programming method is designed to solve the proposed bilevel model and obtain the near-equilibrium points between the upper-level PFP and the lower-level MLB, which can be used to effectively solve similar bilevel multi-objective optimization problems that consider the goal preferences of decision makers.
- A case study of low-carbon PFP and MaaS operational planning for the WS Company is presented and corresponding management insights are given.
3. Problem Formulation
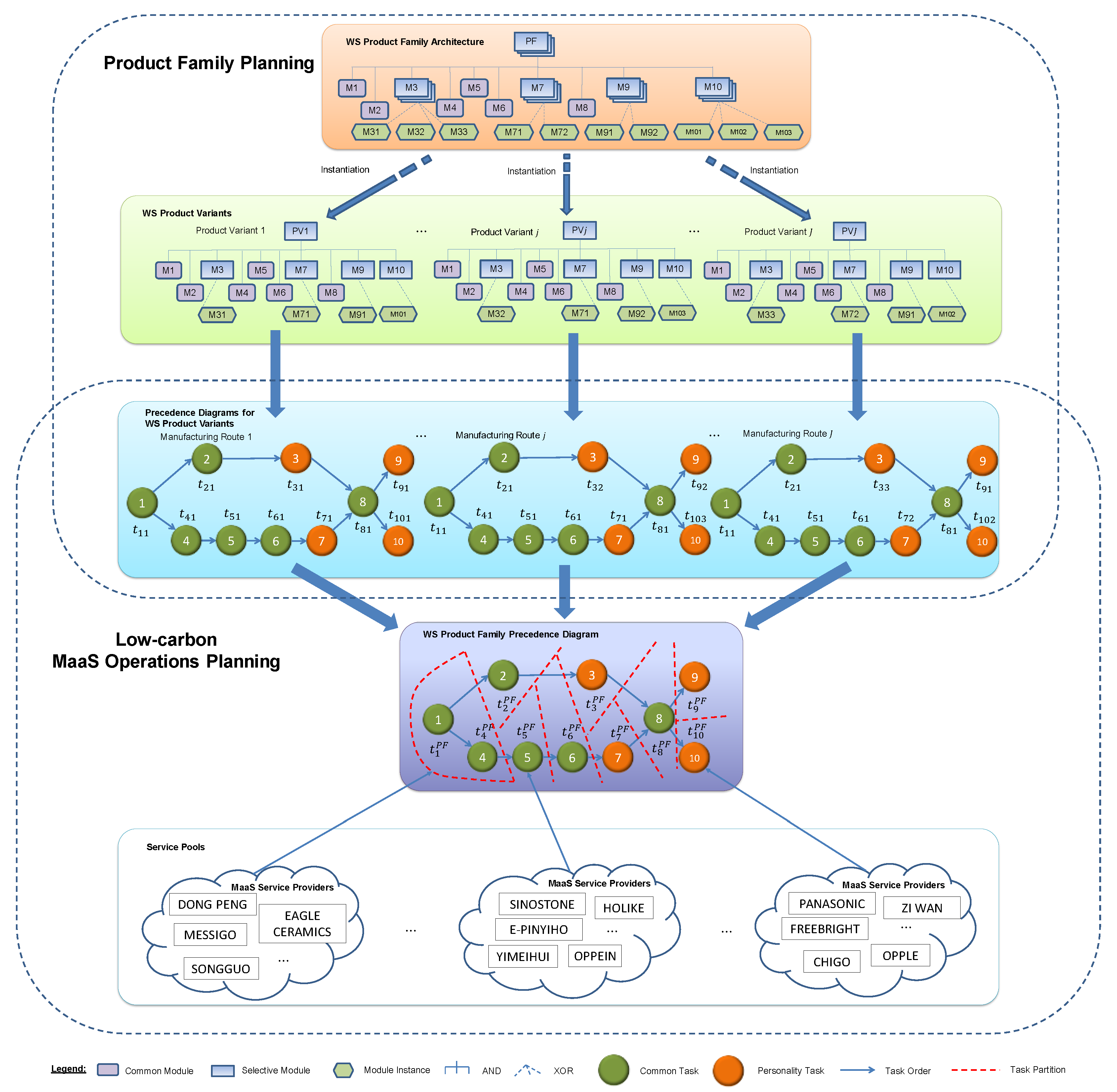
3.1. A Motivating Example
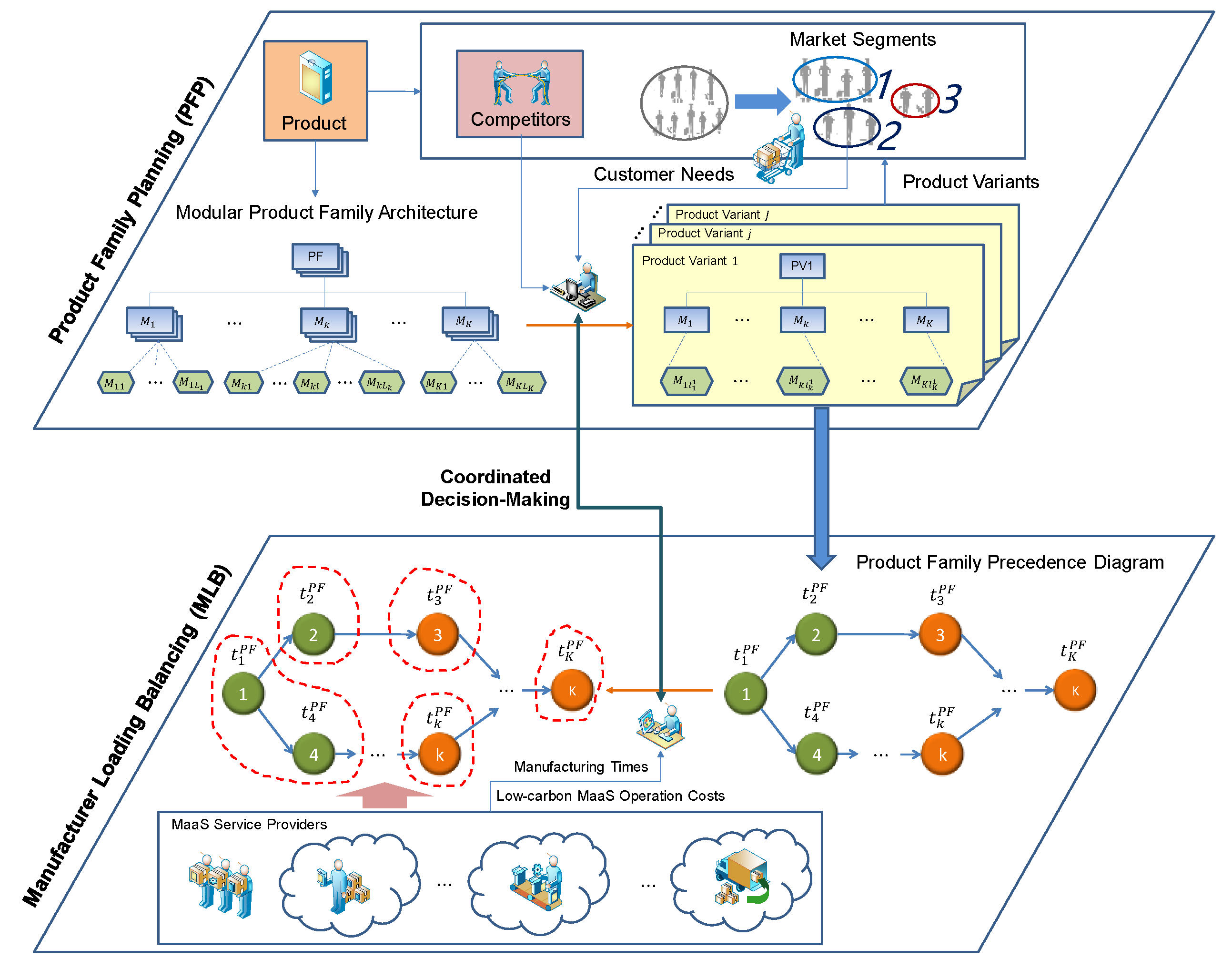
3.2. Problem Description
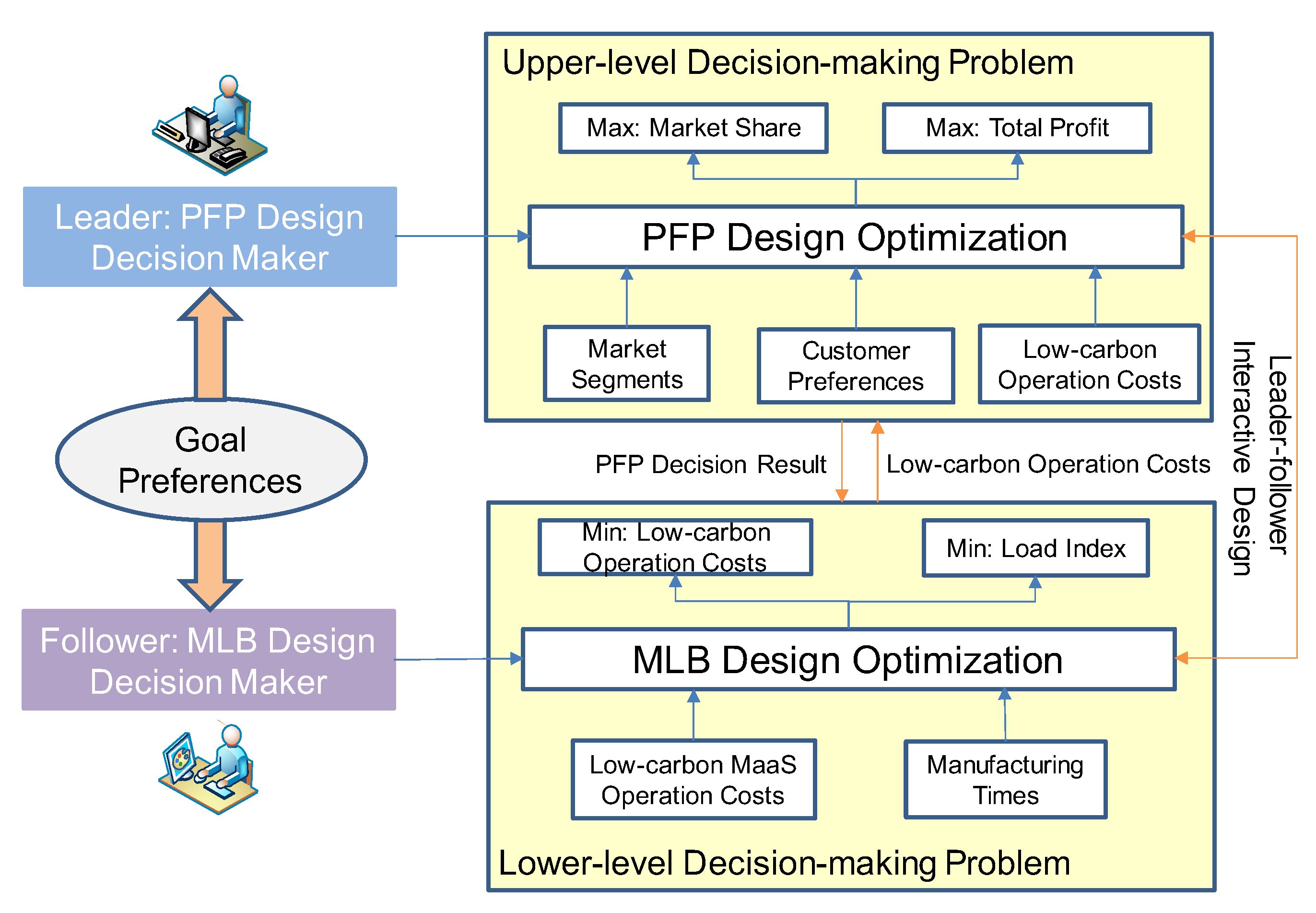
3.3. Leader–Follower Interactive Mechanism
4. Joint Optimization of Low-Carbon PFP and MLB
4.1. Upper-Level PFP
4.2. Lower-Level MLB
4.3. Bilevel Optimization Model
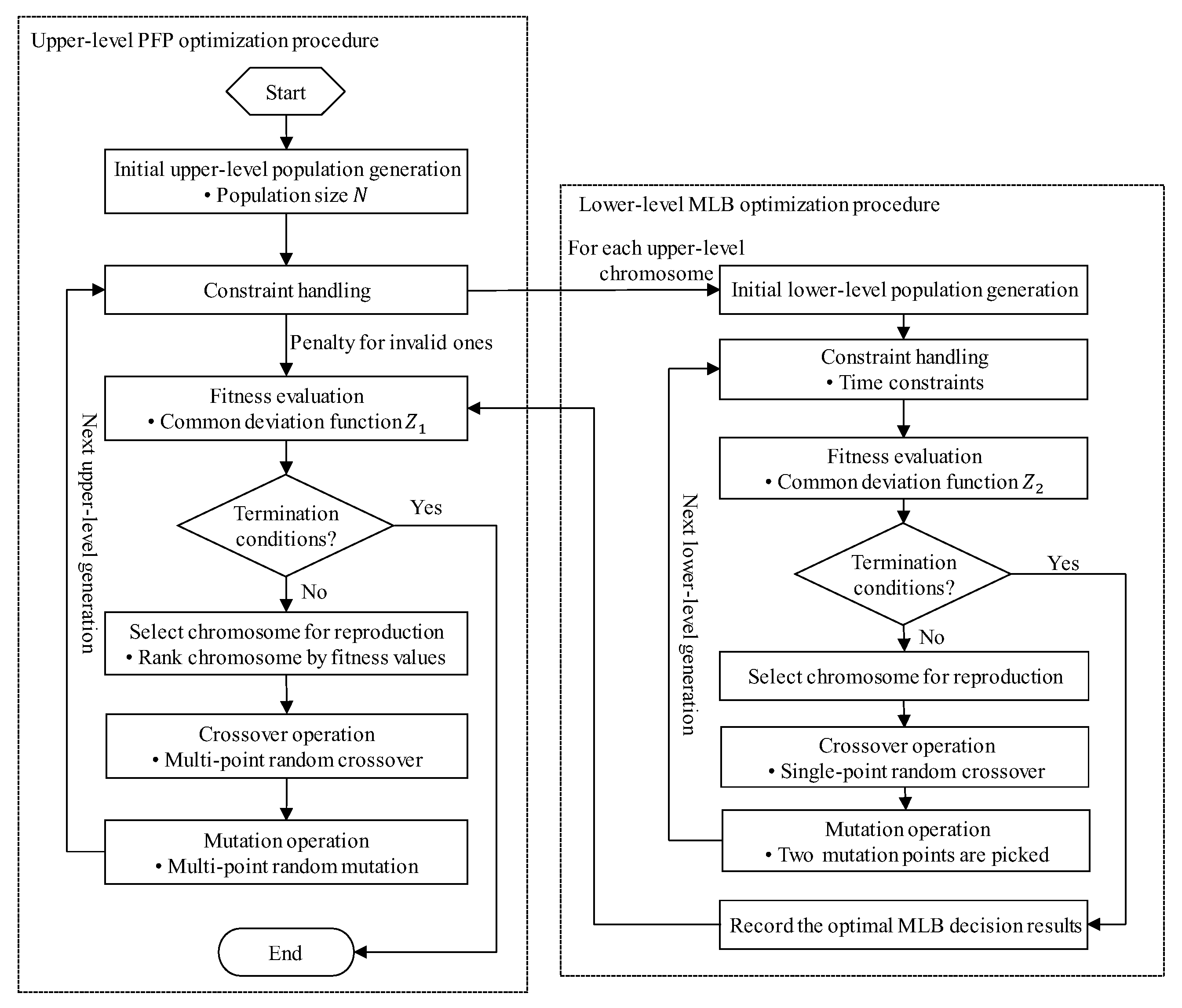
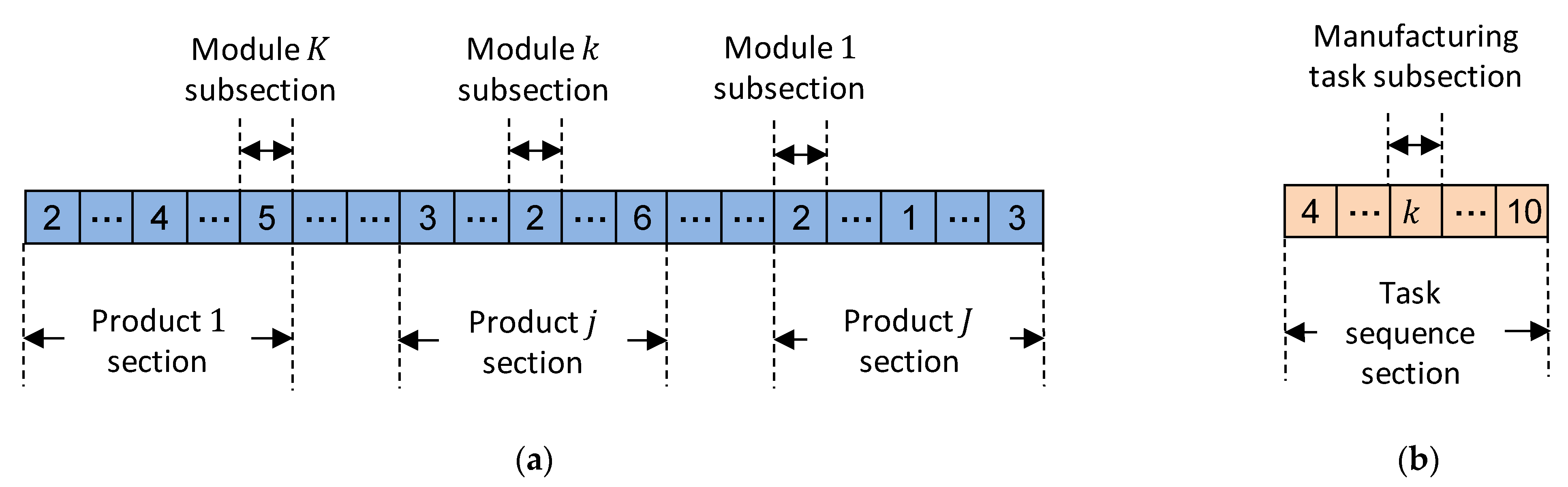
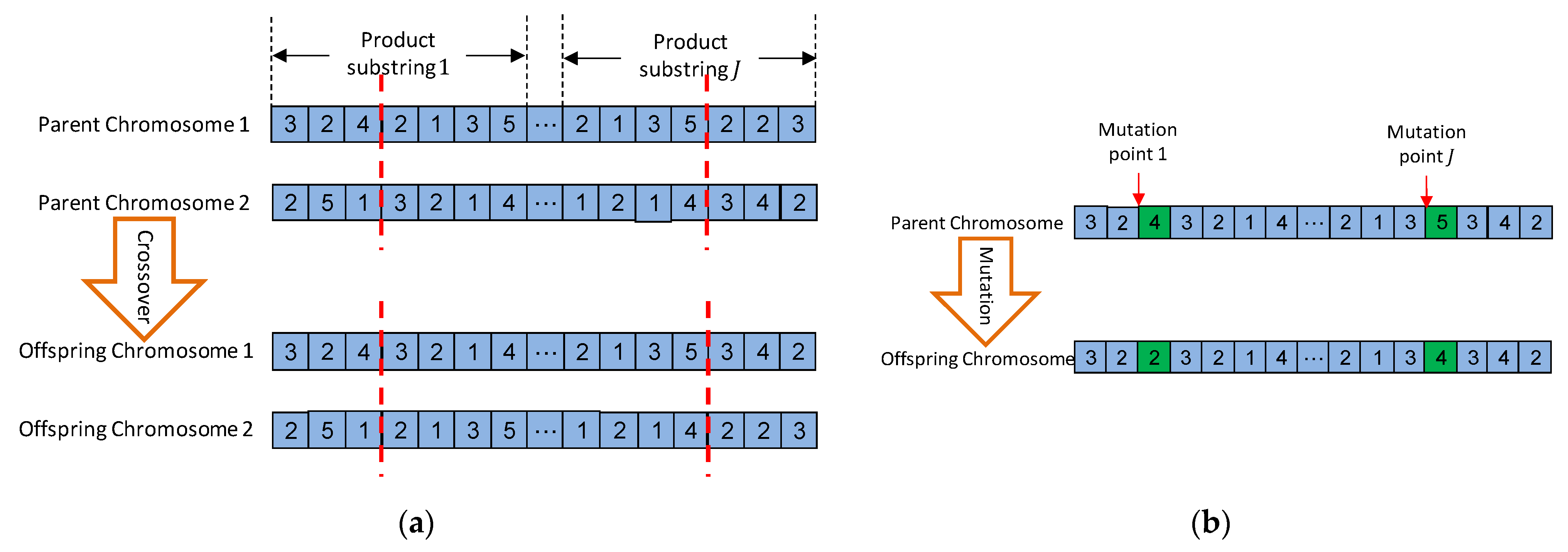
5. Design of NBGA
5.1. Flow Chart of NBGA
5.2. Upper-Level GA
5.3. Lower-Level GA
6. Case Study
6.1. Case Description
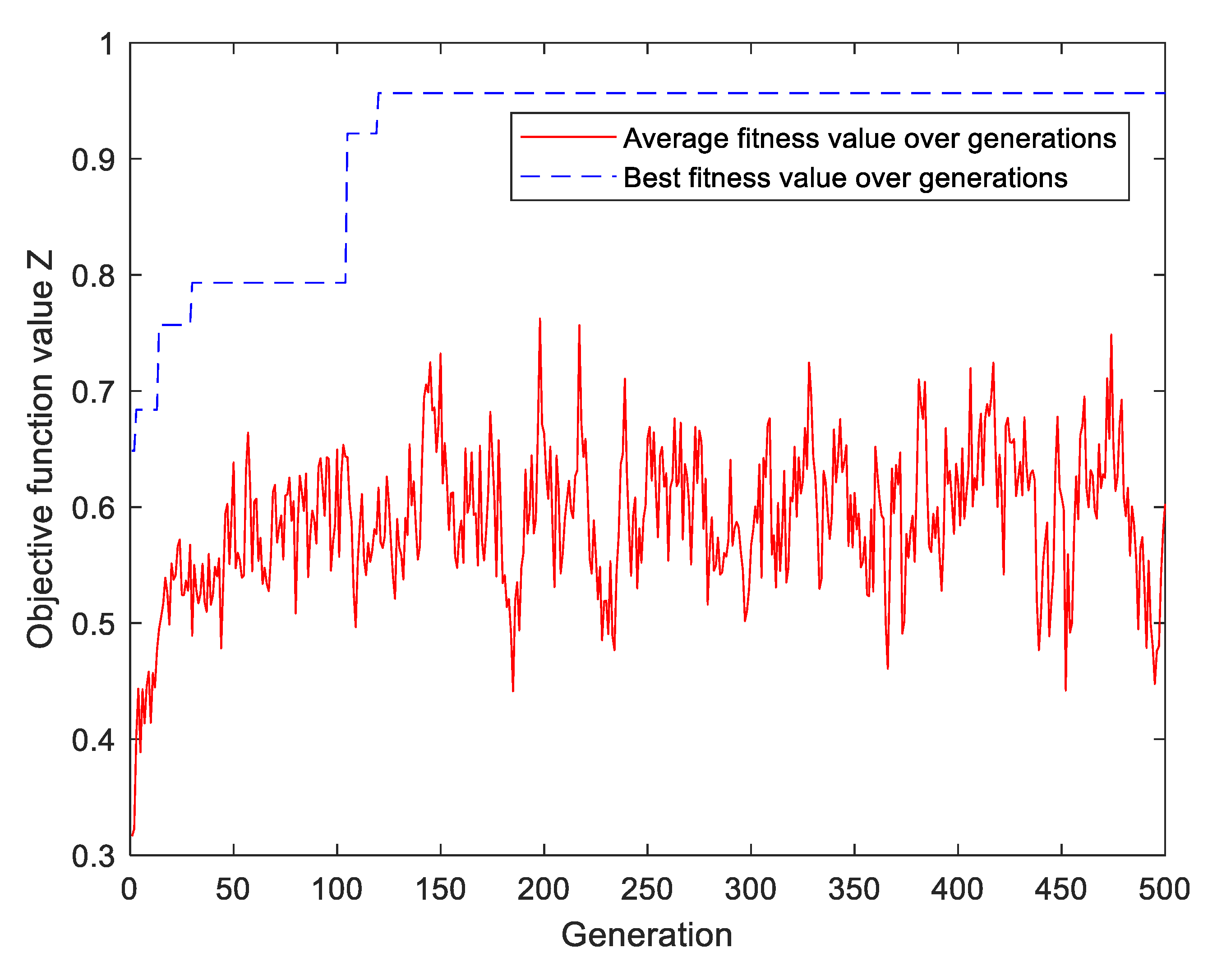
6.2. Implementation Results
6.3. Comparison with Other Approaches
6.4. Sensitivity Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brettel, M.; Friederichsen, N.; Keller, M.; Rosenberg, M. How Virtualization, Decentralization and Network Building Change the Manufacturing Landscape: An Industry 4.0 Perspective. World Acad. Sci. Eng. Technol. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2014, 8, 37–44. [Google Scholar]
- Chesbrough, H.W.; Appleyard, M.M. Open Innovation and Strategy. Calif. Manag. Rev. 2007, 50, 57–76. [Google Scholar] [CrossRef]
- Freitag, M.; Becker, T.; Duffie, N.A. Dynamics of resource sharing in production networks. CIRP Ann.-Manuf. Technol. 2015, 64, 435–438. [Google Scholar] [CrossRef]
- Kortmann, S.; Piller, F.T. Open Business Models and Closed-Loop Value Chains: Redefining the Firm-Consumer Relationship. Calif. Manag. Rev. 2016, 58, 88–108. [Google Scholar] [CrossRef]
- Kusiak, A. Service manufacturing = process-as-a-service + manufacturing operations-as-a-service. J. Intell. Manuf. 2020, 31, 1–2. [Google Scholar] [CrossRef]
- Kusiak, A. Service manufacturing: Basic concepts and technologies. J. Manuf. Syst. 2019, 52, 198–204. [Google Scholar] [CrossRef]
- Park, J.; Simpson, T.W. Toward an activity-based costing system for product families and product platforms in the early stages of development. Int. J. Prod. Res. 2008, 46, 99–130. [Google Scholar] [CrossRef]
- Jiao, J.R.; Simpson, T.W.; Siddique, Z. Product family design and platform-based product development: A state-of-the-art review. J. Intell. Manuf. 2007, 18, 5–29. [Google Scholar] [CrossRef]
- Pirmoradi, Z.; Wang, G.G.; Simpson, T.W. A review of recent literature in product family design and platform-based product development. In Advances in Product Family and Product Platform Design; Springer: New York, NY, USA, 2014; pp. 1–46. [Google Scholar]
- Jiao, J.; Zhang, Y. Product portfolio planning with customer-engineering interaction. IIE Trans. 2005, 37, 801–814. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, D.; Yin, L.; Salido, M.A.; Giret, A.; Xu, Y. Bi-objective optimization for low-carbon product family design. Robot. Comput.-Integr. Manuf. 2016, 41, 53–65. [Google Scholar] [CrossRef][Green Version]
- Wang, Q.; Tang, D.; Yin, L.; Ullah, I.; Salido, M.A.; Giret, A. An Optimization Method for Coordinating Supplier Selection and Low-Carbon Design of Product Family. Int. J. Precis. Eng. Manuf. 2018, 19, 1715–1726. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, D.; Yin, L.; Ullah, I.; Tan, L.; Zhang, T. An optimization model for low carbon oriented modular product platform planning (MP 3). Int. J. Precis. Eng. Manuf.-Green Technol. 2018, 5, 121–132. [Google Scholar] [CrossRef]
- Wang, Q.; Tang, D.; Li, S.; Yang, J.; Salido, M.A.; Giret, A.; Zhu, H. An Optimization Approach for the Coordinated Low-Carbon Design of Product Family and Remanufactured Products. Sustainability 2019, 11, 460. [Google Scholar] [CrossRef]
- Yang, D.; Li, J.; Wang, B.; Jia, Y.J. Module-based product configuration decisions considering both economical and carbon emission-related environmental factors. Sustainability 2020, 12, 1145. [Google Scholar] [CrossRef]
- Liu, D.; Li, Z.; He, C.; Wang, S. Risk-Averse Co-Decision for Lower-Carbon Product Family Configuration and Resilient Supplier Selection. Sustainability 2021, 14, 384. [Google Scholar] [CrossRef]
- Monostori, L.; Kádár, B.; Bauernhansl, T.; Kondoh, S.; Kumara, S.; Reinhart, G.; Sauer, O.; Schuh, G.; Sihn, W.; Ueda, K. Cyber-physical systems in manufacturing. CIRP Ann. -Manuf. Technol. 2016, 65, 621–641. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.M.; Liu, G.; Liu, L.; He, J.; Huang, G.Q. Toward open manufacturing: A cross-enterprises knowledge and services exchange framework based on blockchain and edge computing. Ind. Manag. Data Syst. 2018, 118, 303–320. [Google Scholar] [CrossRef]
- Du, G.; Zhang, Y.; Liu, X.; Jiao, R.J.; Xia, Y.; Li, Y. A review of leader-follower joint optimization problems and mathematical models for product design and development. Int. J. Adv. Manuf. Technol. 2019, 103, 3405–3424. [Google Scholar] [CrossRef]
- Medeiros, G.H.A.; Cao, Q.; Zanni-Merk, C.; Samet, A. Manufacturing as a Service in Industry 4.0: A Multi-Objective Optimization Approach. In International Conference on Intelligent Decision Technologies; Springer: Singapore, 2020; pp. 37–47. [Google Scholar]
- Gong, X.; Jiao, R.; Jariwala, A.; Morkos, B. Crowdsourced manufacturing cyber platform and intelligent cognitive assistants for delivery of manufacturing as a service: Fundamental issues and outlook. Int. J. Adv. Manuf. Technol. 2021, 117, 1997–2007. [Google Scholar] [CrossRef]
- Kwong, C.K.; Luo, X.G.; Tang, J.F. A multiobjective optimization approach for product line design. IEEE Trans. Eng. Manag. 2011, 58, 97–108. [Google Scholar] [CrossRef]
- Hernandez, G.; Allen, J.K.; Mistree, F. The compromise decision support problem: Modeling the deviation function as in physical programming. Eng. Optim. 2001, 33, 445–471. [Google Scholar] [CrossRef]
- Ilgin, M.A.; Akçay, H.; Araz, C. Disassembly line balancing using linear physical programming. Int. J. Prod. Res. 2017, 55, 6108–6119. [Google Scholar] [CrossRef]
- Schwab, K. The Fourth Industrial Revolution; Currency: New York, NY, USA, 2017. [Google Scholar]
- Hasan, M.; Starly, B. Decentralized cloud manufacturing-as-a-service (CMaaS) platform architecture with configurable digital assets. J. Manuf. Syst. 2020, 56, 157–174. [Google Scholar] [CrossRef]
- Pahwa, D.; Starly, B.; Cohen, P. Reverse auction mechanism design for the acquisition of prototyping services in a manufacturing-as-a-service marketplace. J. Manuf. Syst. 2018, 48, 134–143. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Datta, P.P.; Fernandes, K.J.; Xiong, Y. Optimal pricing strategies for manufacturing-as-a service platforms to ensure business sustainability. Int. J. Prod. Econ. 2021, 234, 108065. [Google Scholar] [CrossRef]
- Pahwa, D.; Starly, B. Dynamic matching with deep reinforcement learning for a two-sided Manufacturing-as-a-Service (MaaS) marketplace. Manuf. Lett. 2021, 29, 11–14. [Google Scholar] [CrossRef]
- Gong, X.; Jiao, R.; Jariwala, A.; Morkos, B. Crowdsourced Manufacturing for Delivery of Manufacturing as a Service. In Proceedings of the 2021 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 13–16 December 2021; pp. 1617–1621. [Google Scholar]
- Kaihara, T.; Katsumura, Y.; Suginishi, Y.; Kadar, B. Simulation model study for manufacturing effectiveness evaluation in crowdsourced manufacturing. CIRP Ann. 2017, 66, 445–448. [Google Scholar] [CrossRef]
- Wu, J.; Du, G.; Jiao, R.J. Optimal postponement contracting decisions in crowdsourced manufacturing: A three-level game-theoretic model for product family architecting considering subcontracting. Eur. J. Oper. Res. 2021, 291, 722–737. [Google Scholar] [CrossRef]
- Zhou, K.; Du, G.; Jiao, R.J. Personalized service product family design optimization considering crowdsourced service operations. Comput. Ind. Eng. 2022, 166, 107973. [Google Scholar] [CrossRef]
- Kuo, T.C.; Chen, H.M.; Liu, C.Y.; Tu, J.C.; Yeh, T.C. Applying multi-objective planning in low-carbon product design. Int. J. Precis. Eng. Manuf. 2014, 15, 241–249. [Google Scholar] [CrossRef]
- Xu, Z.Z.; Wang, Y.S.; Teng, Z.R.; Zhong, C.Q.; Teng, H.F. Low-carbon product multi-objective optimization design for meeting requirements of enterprise, user and government. J. Clean. Prod. 2015, 103, 747–758. [Google Scholar] [CrossRef]
- Chiang, T.A.; Che, Z.H. A decision-making methodology for low-carbon electronic product design. Decis. Support Syst. 2015, 71, 1–13. [Google Scholar] [CrossRef]
- He, B.; Huang, S.; Wang, J. Product low-carbon design using dynamic programming algorithm. Int. J. Precis. Eng. Manuf. -Green Technol. 2015, 2, 37–42. [Google Scholar] [CrossRef]
- He, B.; Wang, J.; Deng, Z. Cost-constrained low-carbon product design. Int. J. Adv. Manuf. Technol. 2015, 79, 1821–1828. [Google Scholar] [CrossRef]
- He, B.; Wang, J.; Huang, S.; Wang, Y. Low-carbon product design for product life cycle. J. Eng. Des. 2015, 26, 321–339. [Google Scholar] [CrossRef]
- Baud-Lavigne, B.; Agard, B.; Penz, B. Environmental constraints in joint product and supply chain design optimization. Comput. Ind. Eng. 2014, 76, 16–22. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, K.; Zhang, T.; Pang, C. Green supply chain coordination with greenhouse gases emissions management: A game-theoretic approach. J. Clean. Prod. 2016, 112, 2004–2014. [Google Scholar] [CrossRef]
- Ma, S.; Chen, S.; Cai, X. An Incentive-based Bi-level optimization Model for Collaborative Green Product Line Design. In Proceedings of the 2018 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Bangkok, Thailand, 16–19 December 2018; pp. 981–985. [Google Scholar]
- Xiao, W.; Du, G.; Zhang, Y.; Liu, X. Coordinated optimization of low-carbon product family and its manufacturing process design by a bilevel game-theoretic model. J. Clean. Prod. 2018, 184, 754–773. [Google Scholar] [CrossRef]
- Abdi, M.R.; Labib, A.W. Grouping and selecting products: The design key of reconfigurable manufacturing systems (RMSs). Int. J. Prod. Res. 2004, 42, 521–546. [Google Scholar] [CrossRef]
- Raman, N.; Chhajed, D. Simultaneous determination of product attributes and prices, and production processes in product-line design. J. Oper. Manag. 1995, 12, 187–204. [Google Scholar] [CrossRef]
- Hernandez, G.; Allen, J.K.; Woodruff, G.W.; Simpson, T.W.; Bascaran, E.; Avila, L.F.; Salinas, F. Robust design of families of products with production modeling and evaluation. J. Mech. Des. 2001, 123, 183–190. [Google Scholar] [CrossRef]
- Michalek, J.J.; Ceryan, O.; Papalambros, P.Y.; Koren, Y. Balancing marketing and manufacturing objectives in product line design. J. Mech. Des. 2006, 128, 1196–1204. [Google Scholar] [CrossRef][Green Version]
- Michalek, J.J.; Ebbes, P.; Adigüzel, F.; Feinberg, F.M.; Papalambros, P.Y. Enhancing marketing with engineering: Optimal product line design for heterogeneous markets. Int. J. Res. Mark. 2011, 28, 1–12. [Google Scholar] [CrossRef]
- Luo, L. Product line design for consumer durables: An integrated marketing and engineering approach. J. Mark. Res. 2011, 48, 128–139. [Google Scholar] [CrossRef]
- Xu, Z.; Liang, M. Integrated planning for product module selection and assembly line design/reconfiguration. Int. J. Prod. Res. 2006, 44, 2091–2117. [Google Scholar] [CrossRef]
- Xu, Z.; Liang, M. Concurrent optimization of product module selection and assembly line configuration: A multi-objective approach. J. Manuf. Sci. Eng. 2005, 127, 875–884. [Google Scholar] [CrossRef]
- Bryan, A.; Hu, S.J.; Koren, Y. Concurrent product portfolio planning and mixed product assembly line balancing. Chin. J. Mech. Eng. 2007, 20, 96–99. [Google Scholar] [CrossRef]
- Bryan, A.; Wang, H.; Abell, J. Concurrent design of product families and reconfigurable assembly systems. J. Mech. Des. 2013, 135, 051001. [Google Scholar] [CrossRef]
- Bryan, A.; Ko, J.; Hu, S.J.; Koren, Y. Co-evolution of product families and assembly systems. CIRP Ann. -Manuf. Technol. 2007, 56, 41–44. [Google Scholar] [CrossRef]
- Cao, Y.; Luo, X.G.; Kwong, C.K.; Tang, J.F.; Zhou, W. Joint optimization of product family design and supplier selection under multinomial logit consumer choice rule. Concurr. Eng. 2012, 20, 335–347. [Google Scholar] [CrossRef]
- Liu, X.; Xia, Y.; Chen, M.; Li, A.D. Integrating Assembly Line Balancing in Product Family Planning Design under the Multinomial Logit Choice Model. In Proceedings of the 2019 International Conference on Industrial Engineering and Systems Management (IESM), Shanghai, China, 25–27 September 2019; pp. 1–6. [Google Scholar]
- Hanafy, M.; ElMaraghy, H. Modular product platform configuration and co-planning of assembly lines using assembly and disassembly. J. Manuf. Syst. 2017, 42, 289–305. [Google Scholar] [CrossRef]
- Abbas, M.; ElMaraghy, H. Co-platforming of products and assembly systems. Omega-Int. J. Manag. Sci. 2018, 78, 5–20. [Google Scholar] [CrossRef]
- Jiao, J.; Xu, Q.; Wu, Z.; Ng, N. Coordinating product, process, and supply chain decisions: A constraint satisfaction approach. Eng. Appl. Artif. Intell. 2009, 22, 992–1004. [Google Scholar] [CrossRef]
- Valilai, O.F.; Houshmand, M. A platform for optimisation in distributed manufacturing enterprises based on cloud manufacturing paradigm. Int. J. Comput. Integr. Manuf. 2014, 27, 1031–1054. [Google Scholar] [CrossRef]
- Messac, A.; Gupta, S.M.; Akbulut, B. Linear physical programming: A new approach to multiple objective optimization. Trans. Oper. Res. 1996, 8, 39–59. [Google Scholar]
- Hernandez, G.; Seepersad, C.C.; Mistree, F. Designing for maintenance: A game theoretic approach. Eng. Optim. 2002, 34, 561–577. [Google Scholar] [CrossRef]
- Maria, A.; Mattson, C.; Ismail-Yahaya, A.; Messac, A. Linear physical programming for production planning optimization. Eng. Optim. 2003, 35, 19–37. [Google Scholar] [CrossRef]
- McAllister, C.D.; Simpson, T.W.; Hacker, K.; Lewis, K.; Messac, A. Integrating linear physical programming within collaborative optimization for multiobjective multidisciplinary design optimization. Struct. Multidiscip. Optim. 2005, 29, 178–189. [Google Scholar] [CrossRef]
- Lai, X.; Xie, M.; Tan, K.C. QFD optimization using linear physical programming. Eng. Optim. 2006, 38, 593–607. [Google Scholar] [CrossRef]
- Kongar, E.; Gupta, S.M. Solving the disassembly-to-order problem using linear physical programming. Int. J. Math. Oper. Res. 2009, 1, 504–531. [Google Scholar] [CrossRef]
- Ilgin, M.A.; Gupta, S.M. Physical programming: A review of the state of the art. Stud. Inform. Control 2012, 21, 349–366. [Google Scholar] [CrossRef][Green Version]
- Dhingra, A.K.; Rao, S.S. A cooperative fuzzy game theoretic approach to multiple objective design optimization. Eur. J. Oper. Res. 1995, 83, 547–567. [Google Scholar] [CrossRef]


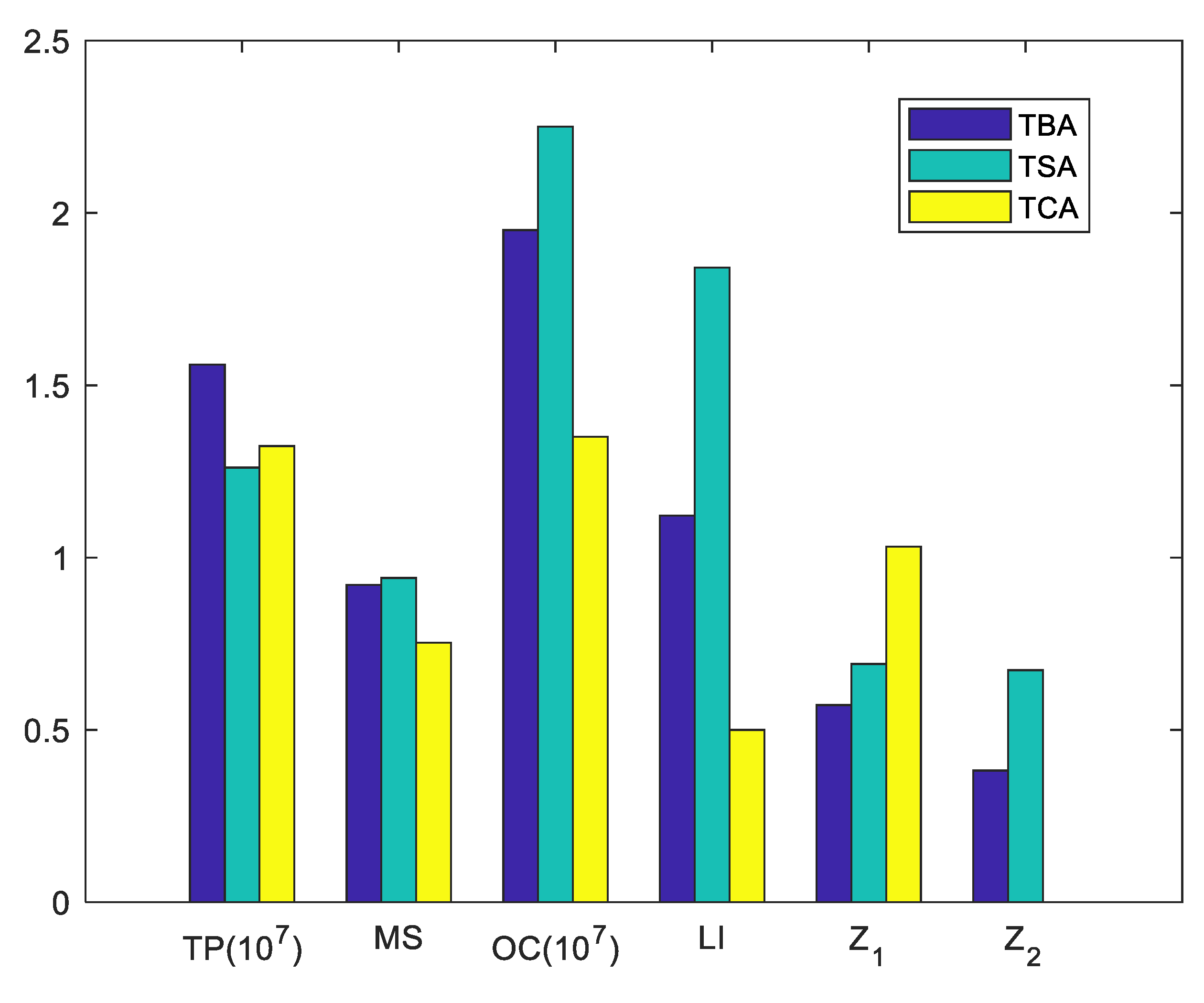
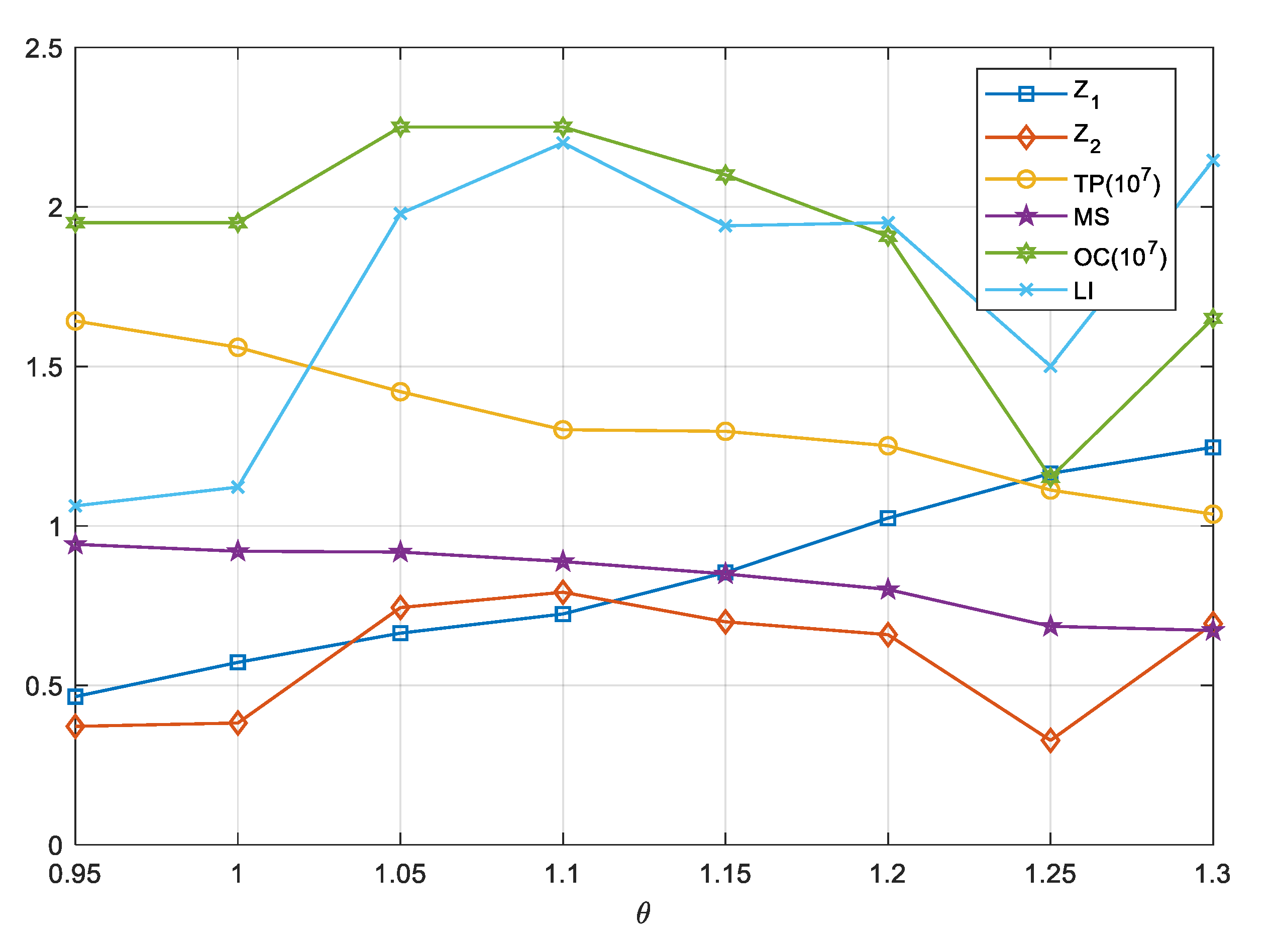
| Segment 1 | Segment 2 | Segment 3 | |
|---|---|---|---|
| Utility surplus of one competitive product | 10.5 | 8.5 | 9.6 |
| Utility surplus of one existing product | 8.7 | 9.4 | 8.3 |
| Estimated sizes of market segments | 250,000 | 350,000 | 150,000 |
| Part-Worth Utilities | Manufacturing Times | Module Costs | ||||
|---|---|---|---|---|---|---|
| Segment 1 | Segment 2 | Segment 3 | ||||
| M1 | 8.9 | 8.5 | 8.2 | 0 | 7.8 | |
| M2 | 9.2 | 9.7 | 9.9 | 6 | 8.5 | |
| M3 | M31 | 0 | 0 | 0 | 0 | 0 |
| M32 | 6.8 | 6.6 | 6.3 | 5 | 5.3 | |
| M33 | 8.3 | 8.9 | 8.5 | 8 | 7.6 | |
| M4 | 4.5 | 4.7 | 4.9 | 7 | 3.5 | |
| M5 | 6.5 | 6.9 | 6.2 | 5 | 5.7 | |
| M6 | 6.5 | 7.2 | 7.9 | 5 | 5.2 | |
| M7 | M71 | 0 | 0 | 0 | 0 | 0 |
| M72 | 5.9 | 4.8 | 5.2 | 8 | 3.9 | |
| M8 | 5.8 | 5.6 | 5.3 | 10 | 4.8 | |
| M9 | M91 | 0 | 0 | 0 | 0 | 0 |
| M92 | 5.8 | 3.8 | 6.8 | 4 | 2.8 | |
| M10 | M101 | 0 | 0 | 0 | 0 | 0 |
| M102 | 4.1 | 4.5 | 4.8 | 6 | 3.6 | |
| M103 | 6.8 | 6.6 | 6.2 | 9 | 4.8 | |
| Upper-Level PFP Decision Maker | ||
|---|---|---|
| 1 | 2 | 90 |
| 2 | 1.5 | 80 |
| 3 | 1 | 70 |
| 4 | 0.7 | 60 |
| 5 | 0.5 | 50 |
| Lower-Level MLB Decision Maker | ||
| ) | ||
| 1 | 1.5 | 0.5 |
| 2 | 2 | 1 |
| 3 | 2.3 | 1.5 |
| 4 | 2.5 | 2 |
| 5 | 3 | 3 |
| Upper-Level PFP Decision Maker | ||
|---|---|---|
| 1 | 0/2.6 | 0/3 |
| 2 | 0/0.26 | 0/0.3 |
| 3 | 0/7.15 | 0/3.63 |
| 4 | 0/21.522 | 0/7.623 |
| Lower-Level MLB Decision Maker | ||
| ) | ) | |
| 1 | 0.2/0 | 0.3/0 |
| 2 | 0.3333/0 | 0.18/0 |
| 3 | 1.5467/0 | 0.768/0 |
| 4 | 0.0832/0 | 0.3744/0 |
| The Bilevel Approach | The Sequential Approach | The Cooperative Approach | ||
|---|---|---|---|---|
| Upper-level PFP decisions | Configuration of product variant 1 | [1 1 2 1 1 1 2 1 2 3] | [1 1 3 1 1 1 2 1 2 3] | [1 1 2 1 1 1 2 1 1 3] |
| Configuration of product variant 2 | [1 1 1 1 1 1 2 1 2 3] | [1 1 2 1 1 1 2 1 2 3] | [1 1 2 1 1 1 1 1 2 1] | |
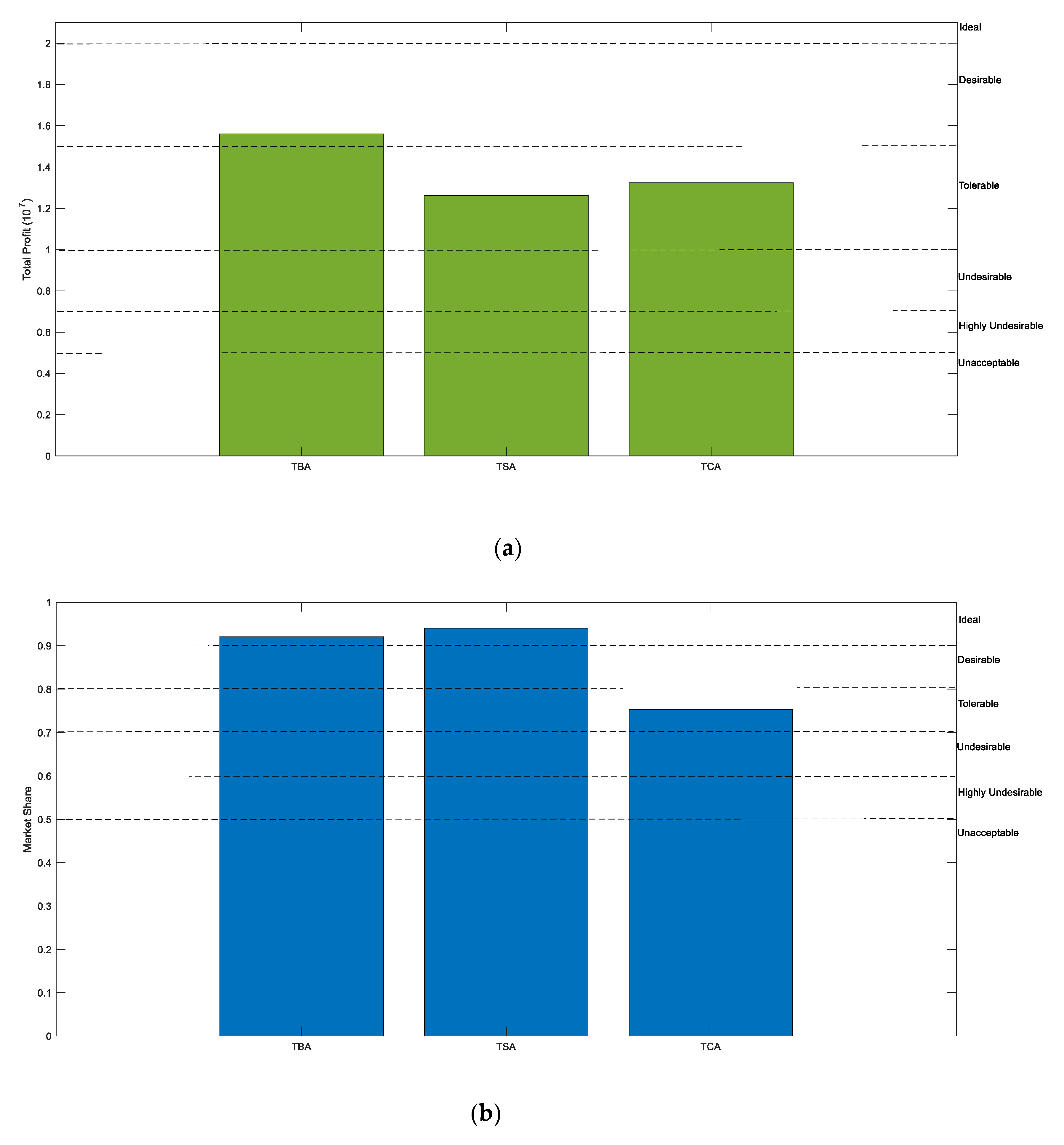
| Upper-level objective values | 1.5600 | 1.2615 | 1.3234 | |
| Market share | 0.9205 | 0.9405 | 0.7530 | |
| 0.5721 | 0.6913 | 1.0316 | ||
| Lower-level MLB decisions | Manufacturing task partition solution | 1 4 | 5 | 6 | 2 | 3 | 7 | 8 | 9 | 10 | 1 4 |2 | 5 | 6 | 3 | 7 | 8 | 9 | 10 | 1 2 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Number of MaaS service providers for each manufacturer | 2 2 2 2 1 2 3 1 2 | 2 2 2 2 2 2 3 1 2 | 2 2 1 1 1 2 1 1 | |
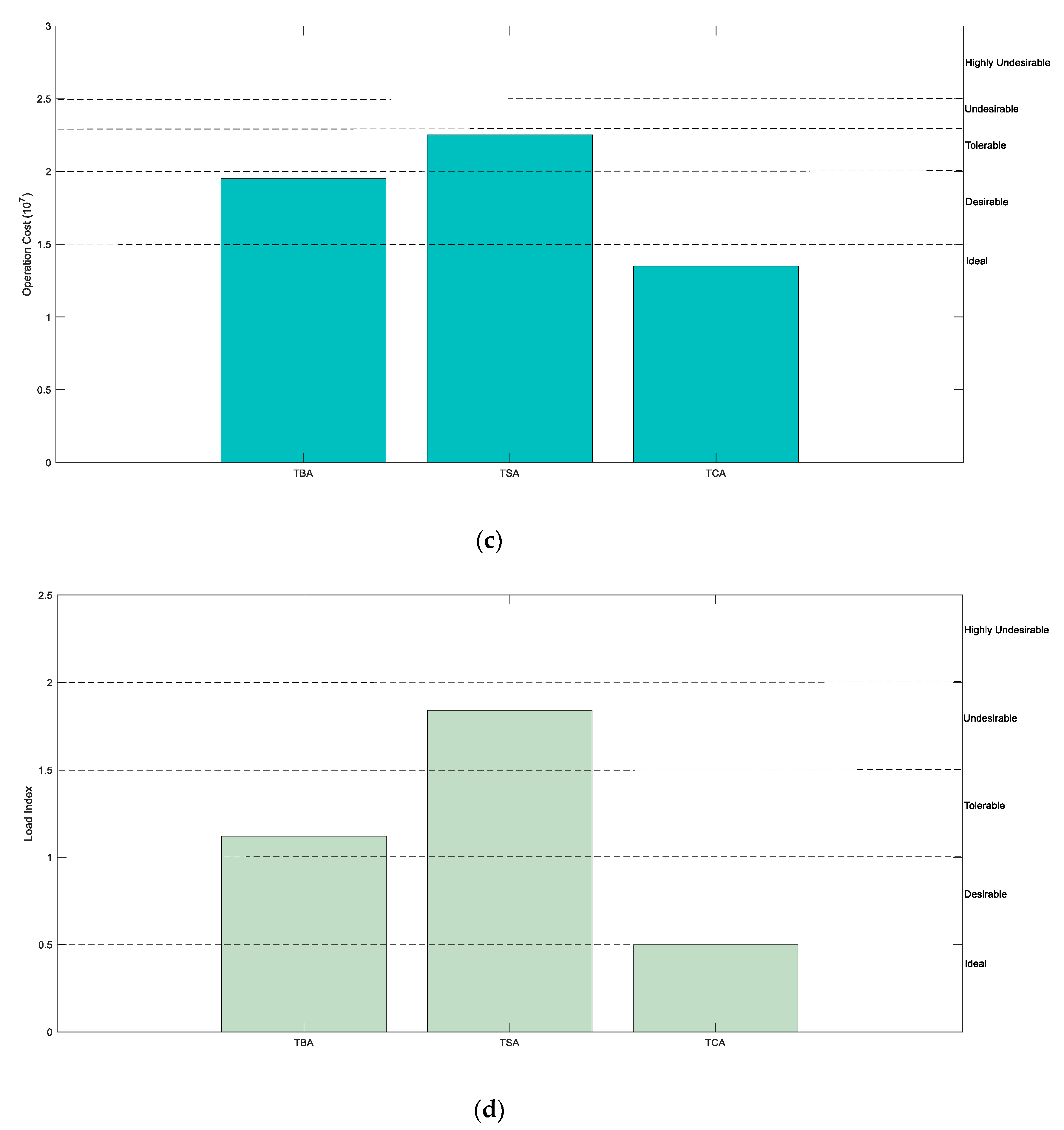
| Lower-level objective values | 1.9507 | 2.2508 | 1.3505 | |
| Load index | 1.1217 | 1.8413 | 0.5000 | |
| 0.3820 | 0.6732 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Gong, X.; Jiao, R.J. Low-Carbon Product Family Planning for Manufacturing as a Service (MaaS): Bilevel Optimization with Linear Physical Programming. Sustainability 2022, 14, 12566. https://doi.org/10.3390/su141912566
Liu X, Gong X, Jiao RJ. Low-Carbon Product Family Planning for Manufacturing as a Service (MaaS): Bilevel Optimization with Linear Physical Programming. Sustainability. 2022; 14(19):12566. https://doi.org/10.3390/su141912566
Chicago/Turabian StyleLiu, Xiaojie, Xuejian Gong, and Roger J. Jiao. 2022. "Low-Carbon Product Family Planning for Manufacturing as a Service (MaaS): Bilevel Optimization with Linear Physical Programming" Sustainability 14, no. 19: 12566. https://doi.org/10.3390/su141912566
APA StyleLiu, X., Gong, X., & Jiao, R. J. (2022). Low-Carbon Product Family Planning for Manufacturing as a Service (MaaS): Bilevel Optimization with Linear Physical Programming. Sustainability, 14(19), 12566. https://doi.org/10.3390/su141912566






