A Markov Chain Approach to Multicriteria Decision Analysis with an Application to Offshore Decommissioning
Abstract
1. Introduction
2. Literature Review
2.1. Multicriteria Decision Analysis
2.2. Uncertainty Analysis
2.3. Probabilistic MCDA Approaches
3. Mathematical Formulation
4. Numerical Experiments
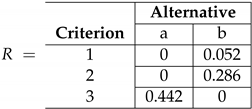
4.1. An Example with Uncertain Performance Functions
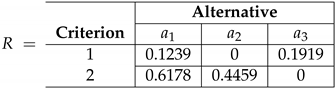
4.2. Application to Decommissioning of Oil and Gas Fields
4.3. Analysis of the Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chakhar, S.; Mousseau, V. GIS-based multicriteria spatial modeling generic framework. Int. J. Geogr. Inf. Sci. 2008, 22, 1159–1196. [Google Scholar] [CrossRef]
- Mardani, A.; Jusoh, A.; Nor, K.; Khalifah, Z.; Zakwan, N.; Valipour, A. Multiple criteria decision-making techniques and their applications—A review of the literature from 2000 to 2014. Econ. Res.-Ekon. Istraž. 2015, 28, 516–571. [Google Scholar] [CrossRef]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R.C. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Vieira, A.C.L.; Oliveira, M.D.; Bana e Costa, C.A. Enhancing knowledge construction processes within multicriteria decision analysis: The collaborative value modelling framework. Omega 2019, 94, 102047. [Google Scholar] [CrossRef]
- Garg, H. New exponential operational laws and their aggregation operators for interval-valued Pythagorean fuzzy multicriteria decision-making. Int. J. Intell. Syst. 2018, 33, 653–683. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, J.; Zhang, H. Stochastic multicriteria decision-making approach based on SMAA-ELECTRE with extended gray numbers. Int. Trans. Oper. Res. 2019, 26, 2032–2052. [Google Scholar] [CrossRef]
- Saaty, T.L. How to make a decision: The analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
- Brans, J.; Vincke, P. Note—A Preference Ranking Organisation Method: (The PROMETHEE Method for Multiple Criteria Decision-Making). Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Roy, B. The outranking approach and the foundations of ELECTRE methods. In Readings in Multiple Criteria Decision Aid; Springer: Berlin/Heidelberg, Germany, 1990; pp. 155–183. [Google Scholar]
- Edwards, W.; Newman, J.R. Multiattribute Evaluation; Cambridge University Press: Cambridge, UK, 1986. [Google Scholar]
- Fishburn, P.C. Letter to the editor—Additive utilities with incomplete product sets: Application to priorities and assignments. Oper. Res. 1967, 15, 537–542. [Google Scholar] [CrossRef]
- Dias, L.C.; Clímaco, J.N. Additive aggregation with variable interdependent parameters: The VIP analysis software. J. Oper. Res. Soc. 2000, 51, 1070–1082. [Google Scholar] [CrossRef]
- Hwang, C.; Yoon, K. Methods for multiple attribute decision making. In Multiple Attribute Decision Making; Springer: Berlin/Heidelberg, Germany, 1981; pp. 58–191. [Google Scholar]
- Figueira, J.; Greco, S.; Ehrgott, M. Decision Rule Approach. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: Berlin/Heidelberg, Germany, 2005; pp. 507–555. [Google Scholar]
- Bana e Costa, C.A. A multicriteria decision aid methodology to deal with conflicting situations on the weights. Eur. J. Oper. Res. 1986, 26, 22–34. [Google Scholar] [CrossRef]
- Montibeller, G.; Patel, P.; Victor, J. A critical analysis of multi-criteria models for the prioritisation of health threats. Eur. J. Oper. Res. 2020, 281, 87–99. [Google Scholar] [CrossRef]
- Eum, Y.S.; Park, K.S.; Kim, S.H. Establishing dominance and potential optimality in multi-criteria analysis with imprecise weight and value. Comput. Oper. Res. 2001, 28, 397–409. [Google Scholar] [CrossRef]
- Choo, E.U.; Schoner, B.; Wedley, W.C. Interpretation of criteria weights in multicriteria decision making. Comput. Ind. Eng. 1999, 37, 527–541. [Google Scholar] [CrossRef]
- Mareschal, M. Weight stability intervals in multicriteria decision aid. Eur. J. Oper. Res. 1988, 33, 54–64. [Google Scholar] [CrossRef]
- Macharis, C.; Bernardini, A. Reviewing the use of Multi-Criteria Decision Analysis for the evaluation of transport projects: Time for a multi-actor approach. Transp. Policy 2015, 37, 177–186. [Google Scholar] [CrossRef]
- Martins, I.D.; Bahiense, L.; Infante, C.E.D.; Arruda, E.F. Dimensionality reduction for multi-criteria problems: An application to the decommissioning of oil and gas installations. Expert Syst. Appl. 2020, 148, 113236. [Google Scholar] [CrossRef]
- Javid, N.; Khalili-Damghani, K.; Makui, A.; Abdi, F. Multi-objective flexibility-complexity trade-off problem in batch production systems using fuzzy goal programming. Expert Syst. Appl. 2020, 148, 113266. [Google Scholar] [CrossRef]
- Lahtinen, T.; Hämäläinen, R.P.; Jenytin, C. On preference elicitation processes which mitigate the accumulation of biases in multi-criteria decision analysis. Eur. J. Oper. Res. 2020, 282, 201–210. [Google Scholar] [CrossRef]
- Mosadeghi, R.; Warnken, J.; Tomlinson, R.; Mirfenderesk, H. Uncertainty analysis in the application of multi-criteria decision-making methods in Australian strategic environmental decisions. J. Environ. Plan. Manag. 2013, 56, 1097–1124. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, J.; Shahbaz, K.; Xevi, E. A GIS-based sensitivity analysis of multi-criteria weights. In Proceedings of the 18th World IMACS/MODSIM Congress, Cairns, Australia, 13–17 July 2009; pp. 13–17. [Google Scholar]
- Madani, K.; Lund, J.R. A Monte-Carlo game theoretic approach for multi-criteria decision making under uncertainty. Adv. Water Resour. 2011, 34, 607–616. [Google Scholar] [CrossRef]
- Lyu, H.; Zhou, W.; Shen, S.; Zhou, A. Inundation risk assessment of metro system using AHP and TFN-AHP in Shenzhen. Sustain. Cities Soc. 2020, 56, 102103. [Google Scholar] [CrossRef]
- Tervonen, T.; Lahdelma, R. Implementing stochastic multicriteria acceptability analysis. Eur. J. Oper. Res. 2007, 178, 500–513. [Google Scholar] [CrossRef]
- Brémaud, P. Gibbs Fields, Monte Carlo Simulation, and Queues; Springer: New York, NY, USA, 1999. [Google Scholar]
- Ching, W.; Ng, M.K. Markov Chains: Models, Algorithms and Applications; Springer: New York, NY, USA, 2006. [Google Scholar]
- Martins, I.D.; Moraes, F.F.; Távora, G.; Soares, H.L.F.; Infante, C.E.; Arruda, E.F.; Bahiense, L.; Caprace, J.; Lourenço, M.I. A review of the multicriteria decision analysis applied to oil and gas decommissioning problems. Ocean. Coast. Manag. 2020, 184, 105000. [Google Scholar] [CrossRef]
- Vincke, P. Multicriteria Decision-Aid; John Wiley & Sons: Bruxelles, Belgium, 1992. [Google Scholar]
- Emmerich, M.T.M.; Deutz, A.H. A tutorial on multiobjective optimization: Fundamentals and evolutionary methods. Nat. Comput. 2018, 17, 585–609. [Google Scholar] [CrossRef]
- Roy, B. Méthodologie Multicritère D’aide à la Décision; Economica: Paris, France, 1985. [Google Scholar]
- Tian, C.; Zhang, W.Y.; Zhang, S.; Peng, J. An extended single-valued neutrosophic projection-based qualitative flexible multi-criteria decision-making method. Mathematics 2019, 7, 39. [Google Scholar] [CrossRef]
- Keeney, R.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Trade-Offs; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Berger, J.O. Prior information and subjective probability. In Statistical Decision Theory and Bayesian Analysis; Springer: Berlin/Heidelberg, Germany, 1985; pp. 74–117. [Google Scholar]
- Stewart, T.J. Dealing with uncertainties in MCDA. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: Berlin/Heidelberg, Germany, 2005; pp. 445–466. [Google Scholar]
- Roszkowska, E. Multi-criteria decision making models by applying the TOPSIS method to crisp and interval data. Mult. Criteria Decis. Mak. Univ. Econ. Katow. 2011, 6, 200–230. [Google Scholar]
- Brans, J.; Mareschal, B. Prométhée-Gaia: Une Méthodologie D’aide à la Décision en Présence de Critères Multiples; Éditions de l’Université de Bruxelles: Brussels, Belgium, 2002. [Google Scholar]
- Hyde, K.; Maier, H.R.; Colby, C. Incorporating uncertainty in the PROMETHEE MCDA method. J. Multi-Criteria Decis. Anal. 2003, 12, 245–259. [Google Scholar] [CrossRef]
- Benítez, J.; Carpitella, S.; Certa, A.; Izquierdo, J. Management of uncertain pairwise comparisons in AHP through probabilistic concepts. Appl. Soft Comput. 2019, 78, 274–285. [Google Scholar] [CrossRef]
- Pelegrina, G.D.; Duarte, L.T.; Grabisch, M.; Romano, J.M.T. The multilinear model in multicriteria decision making: The case of 2-additive capacities and contributions to parameter identification. Eur. J. Oper. Res. 2020, 282, 945–956. [Google Scholar] [CrossRef]
- Durbach, I.N.; Stewart, T.J. Modeling uncertainty in multi-criteria decision analysis. Eur. J. Oper. Res. 2012, 223, 1–14. [Google Scholar] [CrossRef]
- Mosalam, K.M.; Alibrandi, U.; Lee, H.; Armengou, J. Performance-based engineering and multi-criteria decision analysis for sustainable and resilient building design. Struct. Saf. 2018, 74, 1–13. [Google Scholar] [CrossRef]
- Lahdelma, R.; Salminen, P. Stochastic multicriteria acceptability analysis (SMAA). In Trends in Multiple Criteria Decision Analysis; Springer: Berlin/Heidelberg, Germany, 2010; pp. 285–315. [Google Scholar]
- Hodgett, R.E.; Siraj, S. SURE: A method for decision-making under uncertainty. Expert Syst. Appl. 2019, 115, 684–694. [Google Scholar] [CrossRef]
- Beynon, M. DS/AHP method: A mathematical analysis, including an understanding of uncertainty. Eur. J. Oper. Res. 2002, 140, 148–164. [Google Scholar] [CrossRef]
- Sadiq, R.; Tesfamariam, S. Environmental decision-making under uncertainty using intuitionistic fuzzy analytic hierarchy process (IF-AHP). Stoch. Environ. Res. Risk Assess. 2009, 23, 75–91. [Google Scholar] [CrossRef]
- Yang, X.; Yan, L.; Zeng, L. How to handle uncertainties in AHP: The Cloud Delphi hierarchical analysis. Inf. Sci. 2013, 222, 384–404. [Google Scholar] [CrossRef]
- Jahanshahloo, G.R.; Lotfi, F.H.; Izadikhah, M. Extension of the TOPSIS method for decision-making problems with fuzzy data. Appl. Math. Comput. 2006, 181, 1544–1551. [Google Scholar] [CrossRef]
- Engau, A.; Sigler, D. Pareto solutions in multicriteria optimization under uncertainty. Eur. J. Oper. Res. 2020, 281, 357–368. [Google Scholar] [CrossRef]
- Hahn, E.D. Decision making with uncertain judgments: A stochastic formulation of the analytic hierarchy process. Decis. Sci. 2003, 34, 443–466. [Google Scholar] [CrossRef]
- Carnero, M.C.; Gómez, A. A multicriteria decision making approach applied to improving maintenance policies in healthcare organizations. BMC Med. Inform. Decis. Mak. 2016, 16, 47. [Google Scholar] [CrossRef] [PubMed]
- Carnero, M.C.; Gómez, A. Optimization of Maintenance in Production and Storage Systems for Domestic Water. Water Resour. Manag. 2018, 32, 359–380. [Google Scholar] [CrossRef]
- Hemam, S.M.; Hioual, Q. Load balancing issue in cloud services selection by using MCDA and Markov Chain Model approaches. In Proceedings of the 2016 2nd International Conference on Cloud Computing Technologies and Applications (CloudTech), Marrakesh, Morocco, 24–26 May 2016; pp. 163–169. [Google Scholar]
- Nawaz, F.; Asadabadi, M.R.; Janjua, N.K.; Hussain, O.K.; Chang, E.; Saberi, M. An MCDM method for cloud service selection using a Markov chain and the best-worst method. Knowl.-Based Syst. 2018, 159, 120–131. [Google Scholar] [CrossRef]
- Kirytopoulos, K.; Voulgaridou, D.; Platis, A.; Leopoulos, V. An effective Markov based approach for calculating the Limit Matrix in the analytic network process. Eur. J. Oper. Res. 2011, 214, 85–90. [Google Scholar] [CrossRef]
- Brans, J.; Mareschal, B. Promethee Methods. In Multiple Criteria Decision Analysis: State of the Art Surveys; Springer: New York, NY, USA, 2005; pp. 163–186. [Google Scholar] [CrossRef]
- Shell. Brent Field Decommissioning: Comparative Assessment Procedure; Technical Report; Shell U. K. Limited: London, UK, 2017. [Google Scholar]
| Area | Label | Unit | Criterion |
|---|---|---|---|
| Safety | 1 | PLL | Safety risk to offshore project personnel |
| 2 | PLL | Safety risk to other users of the sea | |
| 3 | PLL | Safety risk to onshore project personnel | |
| Environmental | 4 | Score | Operational environmental impacts |
| 5 | Score | Legacy environmental impacts | |
| 6 | GJ | Energy use | |
| 7 | tons of CO2 | Emissions | |
| Technical | 8 | Score | Technical feasibility |
| Social | 9 | £ | Effects on commercial fisheries |
| 10 | Employees Year | Employment | |
| 11 | Score | Communities | |
| Economic | 12 | £ | Cost |
| Alternatives | Description |
|---|---|
| Leave tied-in at platform; remote and trenched | |
| Leave tied-in at platform; remote and rock-dumped | |
| Disconnect from the installation; trench and backfill whole length | |
| Disconnect from the installation; rock-dump whole length | |
| Recover whole length by cutting and lifting | |
| Recover whole length with a reverse S-lay |
| Criterion | Alternatives | |||||
|---|---|---|---|---|---|---|
| 1 | 625.00 | 625.00 | 416.67 | 500.00 | 357.14 | 232.56 |
| 2 | 12.50 | 10.66 | 625.00 | 625.00 | 833.33 | 833.33 |
| 3 | 833.33 | 833.33 | 833.33 | 833.33 | 833.33 | 833.33 |
| 4 | 0.99 | 0.98 | 0.91 | 0.85 | 0.91 | 0.95 |
| 5 | 0.95 | 0.95 | 1 | 0.90 | 1 | 1 |
| 6 | ||||||
| 7 | ||||||
| 8 | 0.92 | 1 | 0.80 | 1 | 0.84 | 0.35 |
| 9 | 0.00 | 0.00 | 228,344.2 | 183,367.3 | 228,344.2 | 228,344.2 |
| 10 | 6.35 | 3.17 | 9.53 | 6.35 | 19.05 | 31.76 |
| 11 | 1 | 1 | 1 | 1 | 0.95 | 0.95 |
| 12 | 0.75 | 0.93 | 0.47 | 0.53 | 0.20 | 0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moraes, F.F.; Filho, V.J.M.F.; Infante, C.E.D.d.C.; Santos, L.; Arruda, E.F. A Markov Chain Approach to Multicriteria Decision Analysis with an Application to Offshore Decommissioning. Sustainability 2022, 14, 12019. https://doi.org/10.3390/su141912019
Moraes FF, Filho VJMF, Infante CEDdC, Santos L, Arruda EF. A Markov Chain Approach to Multicriteria Decision Analysis with an Application to Offshore Decommissioning. Sustainability. 2022; 14(19):12019. https://doi.org/10.3390/su141912019
Chicago/Turabian StyleMoraes, Fernanda F., Virgílio José M. Ferreira Filho, Carlos Eduardo Durange de C. Infante, Luan Santos, and Edilson F. Arruda. 2022. "A Markov Chain Approach to Multicriteria Decision Analysis with an Application to Offshore Decommissioning" Sustainability 14, no. 19: 12019. https://doi.org/10.3390/su141912019
APA StyleMoraes, F. F., Filho, V. J. M. F., Infante, C. E. D. d. C., Santos, L., & Arruda, E. F. (2022). A Markov Chain Approach to Multicriteria Decision Analysis with an Application to Offshore Decommissioning. Sustainability, 14(19), 12019. https://doi.org/10.3390/su141912019






