Soil Liquefaction Prediction Based on Bayesian Optimization and Support Vector Machines
Abstract
:1. Introduction
2. Process of Soil Liquefaction
3. Method
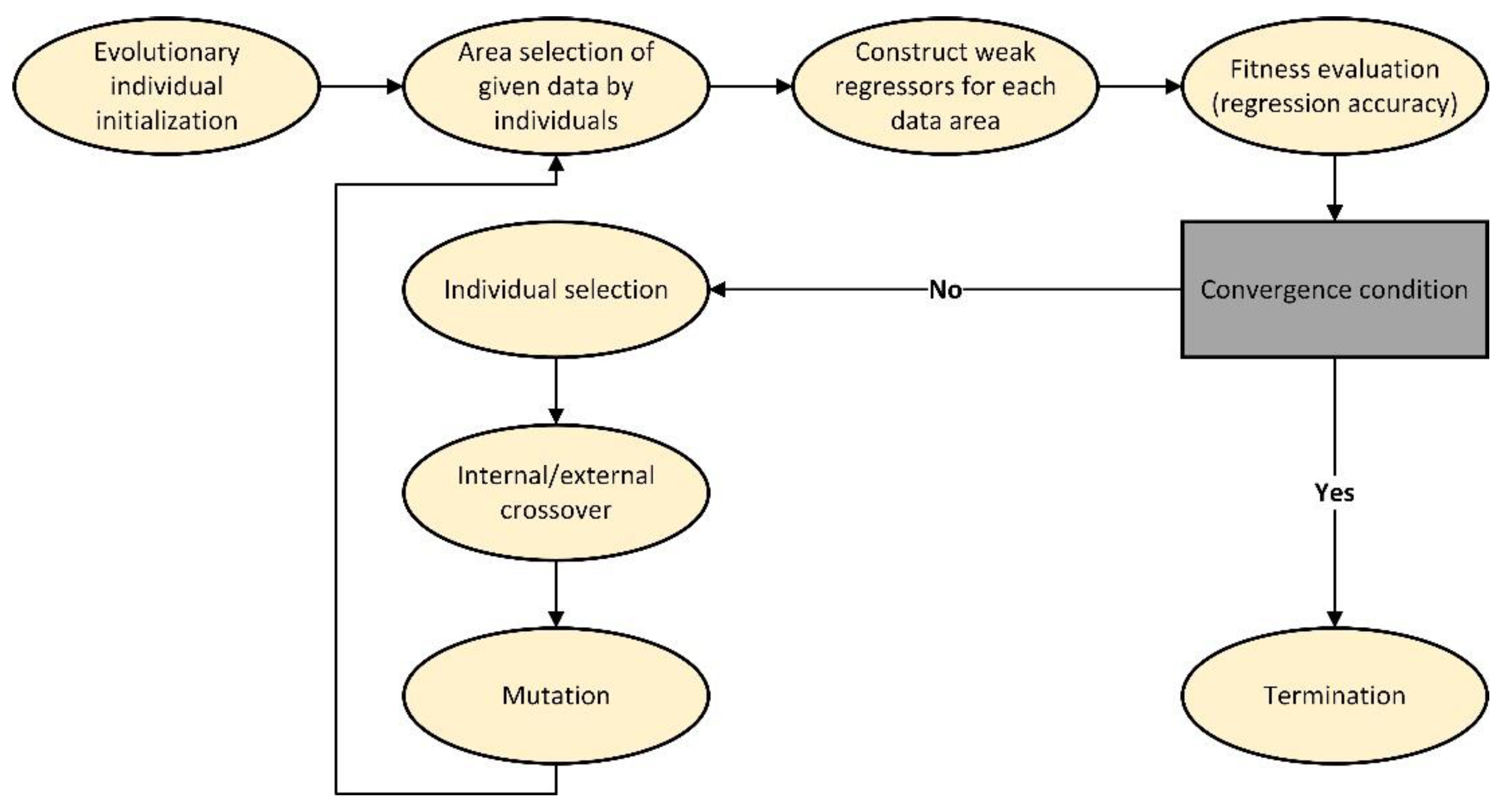
3.1. Evolutionary Random Forest (ERF)
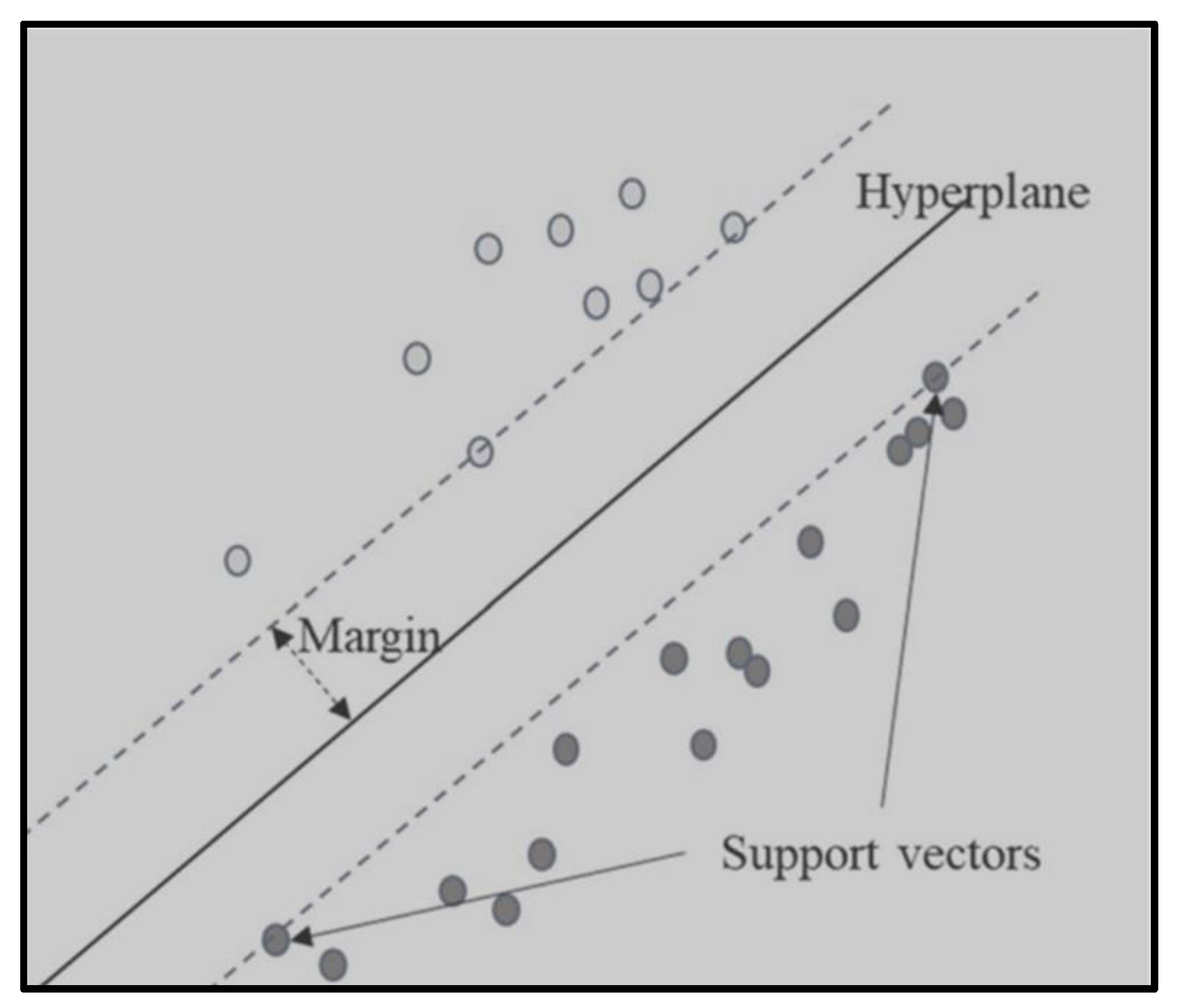
3.2. Support Vector Machines
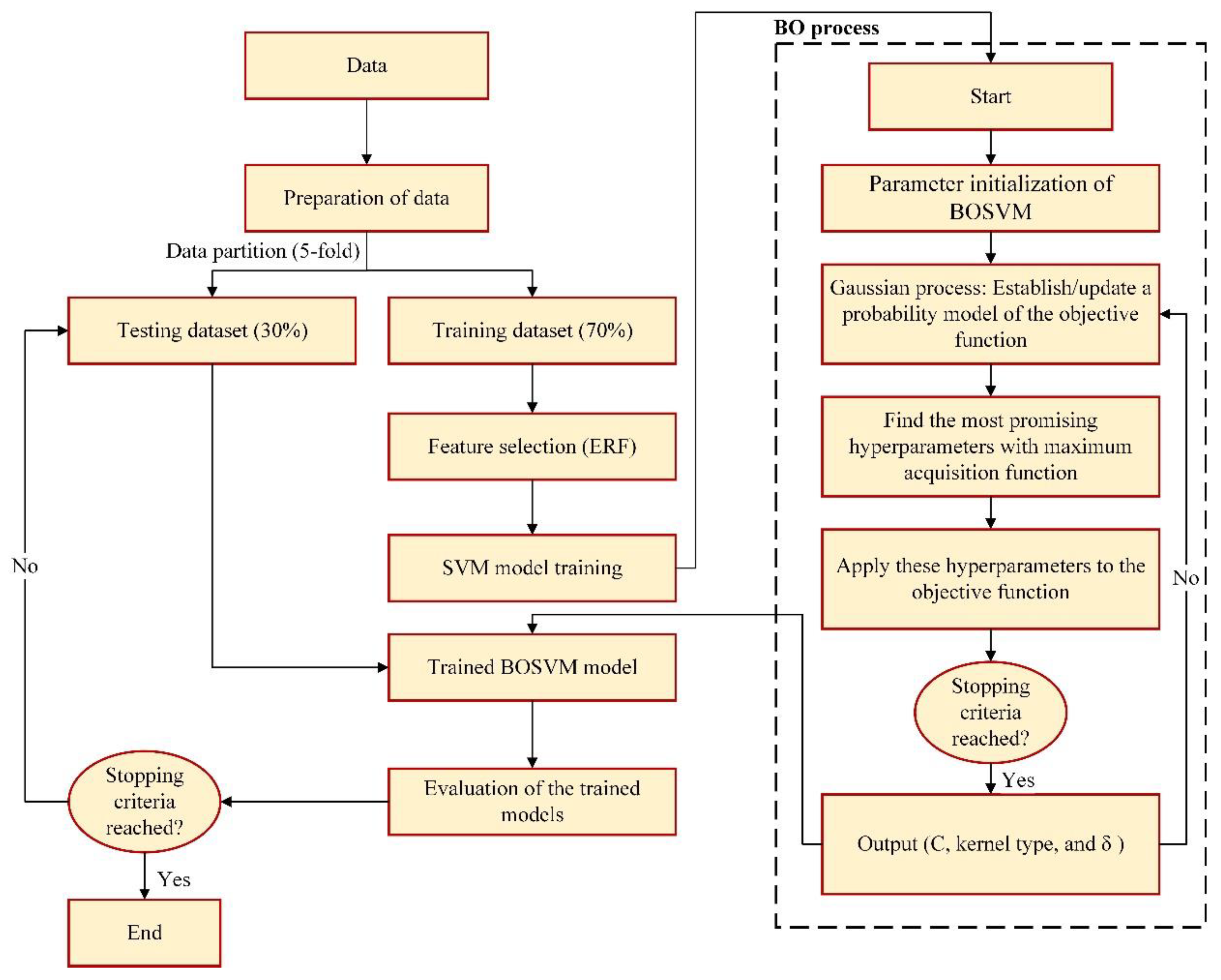
3.3. Bayesian Optimization Algorithm
3.4. Performance Criteria
3.5. Data for Modeling
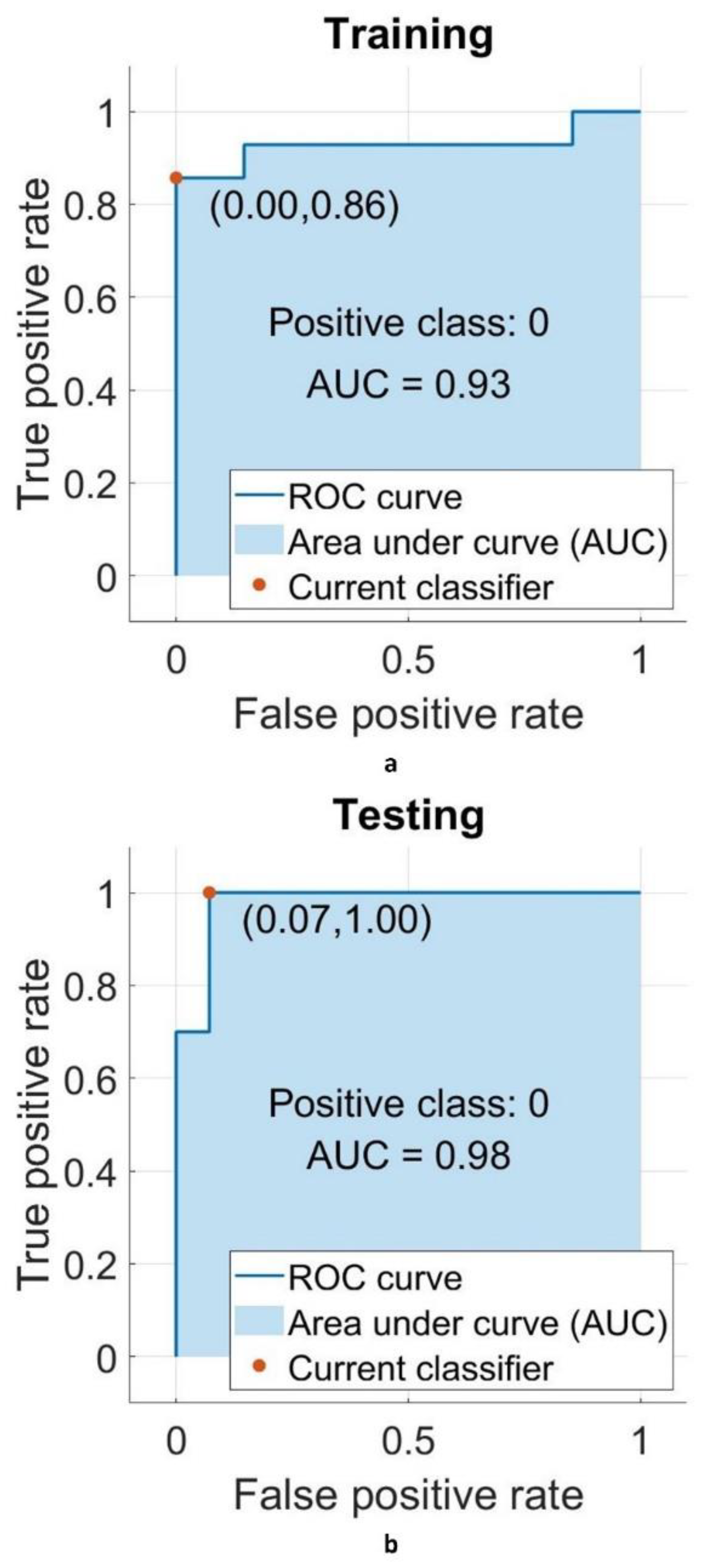
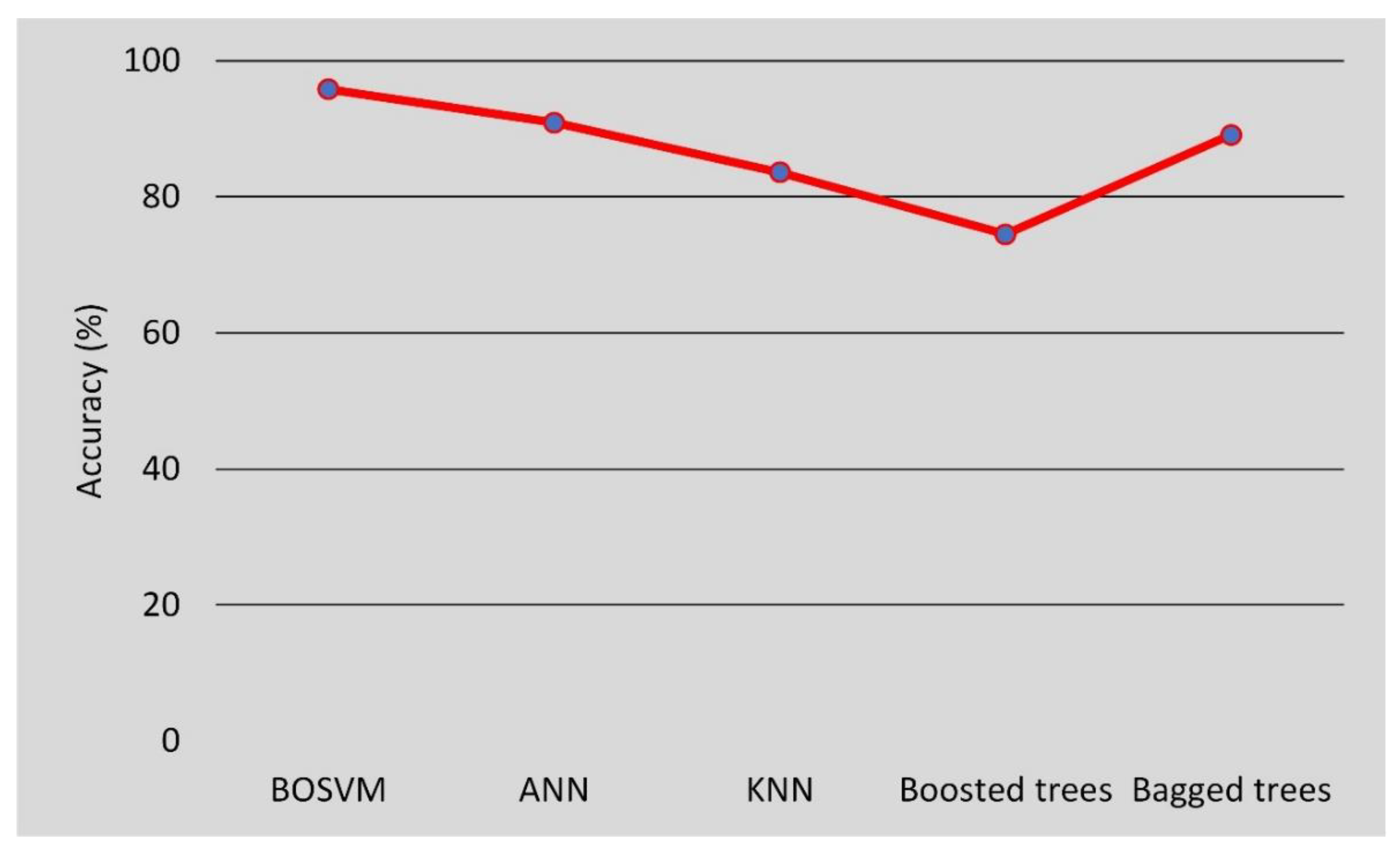
4. Results and Discussion
4.1. Input Selection
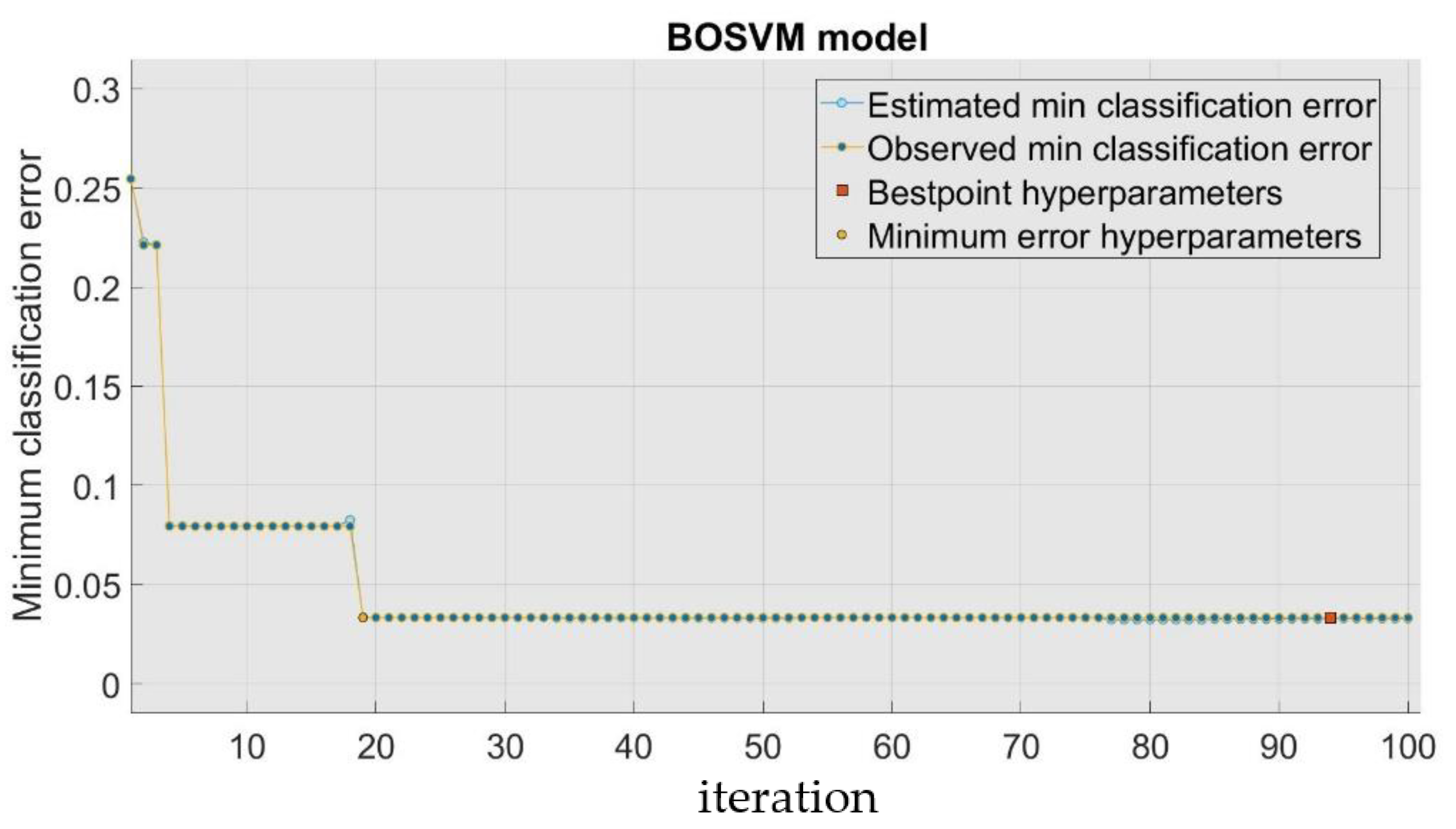
4.2. BOSVM Model Development
- Examination of fitness: The fitness function is computed and assessed before optimizing the target parameter value. The fitness function in this study is classification error.
- Adjusting the settings: hyperparameter optimization criteria may be adjusted according to the outcomes of each iteration, if desired.
- Stop checking for conditions: Optimization stops once the best parameters have been found.
5. Limitations and Future Works
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Term |
| AUC | Area Under the ROC Curve |
| ANN | Artificial Neural Network |
| BO | Bayesian Optimization |
| CPT | Cone Penetration Test |
| CSR | Cyclic Stress Ratio |
| DT | Decision Tree |
| DE | Differential Evolution |
| EGMDH | Ensemble Group Method of Data Handling |
| ERF | Evolutionary Random Forest |
| DMT | Flat Dilatometer Test |
| FSVM | Fuzzy Support Vector Machine |
| GA | Genetic Algorithm |
| GWO | Grey Wolf Optimization |
| KELM | Kernel Extreme Learning Machine |
| KFDA | Kernel Fisher Discriminant Analysis |
| LSSVM | Least Squares Support Vector Machine |
| ML | Machine Learning |
| MGGP | Multi-Gene Genetic Programming |
| ANFIS | Neuro Fuzzy Inference System |
| PSO | Particle Swarm Optimization |
| RBFNN | Radial Basis Function Neural Network |
| RF | Random Forest |
| ROC | Receiver Operating Characteristic Curve |
| Vs | Shear Wave Velocity |
| SPT | Standard Penetration Test |
| SVM | Support Vector Machine |
Appendix A
References
- Xue, X.; Yang, X. Application of the adaptive neuro-fuzzy inference system for prediction of soil liquefaction. Nat. Hazards 2013, 67, 901–917. [Google Scholar] [CrossRef]
- Xue, X.; Yang, X. Seismic liquefaction potential assessed by support vector machines approaches. Bull. Eng. Geol. Environ. 2016, 75, 153–162. [Google Scholar] [CrossRef]
- Sami, M.; de Patrick, B. Minimum principle and related numerical scheme for simulating initial flow and subsequent propagation of liquefied ground. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 1065–1086. [Google Scholar]
- Huang, Y.; Yu, M. Review of soil liquefaction characteristics during major earthquakes of the twenty-first century. Nat. Hazards 2013, 65, 2375–2384. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T.; Zhang, Y.; Chen, Y.; Xiao, Y. Assessment of soil liquefaction based on capacity energy concept and multivariate adaptive regression splines. Eng. Geol. 2015, 188, 29–37. [Google Scholar] [CrossRef]
- Chen, G.; Xu, L.; Kong, M.; Li, X. Calibration of a CRR model based on an expanded SPT-based database for assessing soil liquefaction potential. Eng. Geol. 2015, 196, 305–312. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, L.; Sun, R.; Chen, Y.; Wang, W. A depth-consistent SPT-based empirical equation for evaluating sand liquefaction. Eng. Geol. 2017, 221, 41–49. [Google Scholar] [CrossRef]
- Pei, X.; Zhang, X.; Guo, B.; Wang, G.; Zhang, F. Experimental case study of seismically induced loess liquefaction and landslide. Eng. Geol. 2017, 223, 23–30. [Google Scholar] [CrossRef]
- Kayabasi, A.; Gokceoglu, C. Liquefaction potential assessment of a region using different techniques (Tepebasi, Eskişehir, Turkey). Eng. Geol. 2018, 246, 139–161. [Google Scholar] [CrossRef]
- Chen, J.; Hideyuki, O.; Takeyama, T.; Oishi, S.; Hori, M. Toward a numerical-simulation-based liquefaction hazard assessment for urban regions using high-performance computing. Eng. Geol. 2019, 258, 105153. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, X. Field-observed phenomena of seismic liquefaction and subsidence during the 2008 Wenchuan earthquake in China. Nat. Hazards 2010, 54, 839–850. [Google Scholar] [CrossRef]
- Juang, C.H.; Yuan, H.; Lee, D.-H.; Lin, P.-S. Simplified cone penetration test-based method for evaluating liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2003, 129, 66–80. [Google Scholar] [CrossRef]
- Duan, W.; Zhao, Z.; Cai, G.; Pu, S.; Liu, S.; Dong, X. Evaluating model uncertainty of an in situ state parameter-based simplified method for reliability analysis of liquefaction potential. Comput. Geotech. 2022, 151, 104957. [Google Scholar] [CrossRef]
- Pal, M. Support vector machines-based modelling of seismic liquefaction potential. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 983–996. [Google Scholar] [CrossRef]
- Sulewska, M.J. Applying artificial neural networks for analysis of geotechnical problems. Comput. Assist. Methods Eng. Sci. 2017, 18, 231–241. [Google Scholar]
- Samui, P.; Sitharam, T. Machine learning modelling for predicting soil liquefaction susceptibility. Nat. Hazards Earth Syst. Sci. 2011, 11, 1–9. [Google Scholar] [CrossRef]
- Tolon, M. A comparative study on computer aided liquefaction analysis methods. Int. J. Hous. Sci. 2013, 37, 121–135. [Google Scholar]
- Erzin, Y.; Ecemis, N. The use of neural networks for CPT-based liquefaction screening. Bull. Eng. Geol. Environ. 2015, 74, 103–116. [Google Scholar] [CrossRef]
- Duan, W.; Congress, S.S.C.; Cai, G.; Liu, S.; Dong, X.; Chen, R.; Liu, X. A hybrid GMDH neural network and logistic regression framework for state parameter–based liquefaction evaluation. Can. Geotech. J. 2021, 99, 1801–1811. [Google Scholar] [CrossRef]
- Muduli, P.K.; Das, S.K. CPT-based seismic liquefaction potential evaluation using multi-gene genetic programming approach. Indian Geotech. J. 2014, 44, 86–93. [Google Scholar] [CrossRef]
- Muduli, P.K.; Das, S.K. Evaluation of liquefaction potential of soil based on standard penetration test using multi-gene genetic programming model. Acta Geophys. 2014, 62, 529–543. [Google Scholar] [CrossRef]
- Javdanian, H.; Heidari, A.; Kamgar, R. Energy-based estimation of soil liquefaction potential using GMDH algorithm. Iran. J. Sci. Technol. Trans. Civ. Eng. 2017, 41, 283–295. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, W.; Cai, G. A novel PSO-KELM based soil liquefaction potential evaluation system using CPT and vs. measurements. Soil Dyn. Earthq. Eng. 2021, 150, 106930. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Bui, D.T. Predicting earthquake-induced soil liquefaction based on a hybridization of kernel Fisher discriminant analysis and a least squares support vector machine: A multi-dataset study. Bull. Eng. Geol. Environ. 2018, 77, 191–204. [Google Scholar] [CrossRef]
- Kurnaz, T.F.; Kaya, Y. A novel ensemble model based on GMDH-type neural network for the prediction of CPT-based soil liquefaction. Environ. Earth Sci. 2019, 78, 339. [Google Scholar] [CrossRef]
- Rahbarzare, A.; Azadi, M. Improving prediction of soil liquefaction using hybrid optimization algorithms and a fuzzy support vector machine. Bull. Eng. Geol. Environ. 2019, 78, 4977–4987. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Monjezi, M.; Shahnazar, A.; Armaghani, D.J.; Farazmand, A. Feasibility of indirect determination of blast induced ground vibration based on support vector machine. Measurement 2015, 75, 289–297. [Google Scholar] [CrossRef]
- Parsajoo, M.; Armaghani, D.J.; Mohammed, A.S.; Khari, M.; Jahandari, S. Tensile strength prediction of rock material using non-destructive tests: A comparative intelligent study. Transp. Geotech. 2021, 31, 100652. [Google Scholar] [CrossRef]
- Asteris, P.G.; Mamou, A.; Hajihassani, M.; Hasanipanah, M.; Koopialipoor, M.; Le, T.-T.; Kardani, N.; Armaghani, D.J. Soft computing based closed form equations correlating L and N-type Schmidt hammer rebound numbers of rocks. Transp. Geotech. 2021, 29, 100588. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen, M.D.; Nguyen-Thoi, T.; Ho, L.S.; Koopialipoor, M.; Quoc, N.K.; Armaghani, D.J.; Van Le, H. A novel approach for classification of soils based on laboratory tests using Adaboost, Tree and ANN modeling. Transp. Geotech. 2021, 27, 100508. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Zhu, S.; Armaghani, D.J.; Khandelwal, M.; Mohamad, E.T. Estimation of the TBM advance rate under hard rock conditions using XGBoost and Bayesian optimization. Undergr. Space 2021, 6, 506–515. [Google Scholar] [CrossRef]
- Harandizadeh, H.; Armaghani, D.J.; Hasanipanah, M.; Jahandari, S. A novel TS Fuzzy-GMDH model optimized by PSO to determine the deformation values of rock material. Neural Comput. Appl. 2022, 34, 15755–15779. [Google Scholar] [CrossRef]
- Asteris, P.G.; Rizal, F.I.M.; Koopialipoor, M.; Roussis, P.C.; Ferentinou, M.; Armaghani, D.J.; Gordan, B. Slope stability classification under seismic conditions using several tree-based intelligent techniques. Appl. Sci. 2022, 12, 1753. [Google Scholar] [CrossRef]
- Momeni, E.; Nazir, R.; Armaghani, D.J.; Maizir, H. Prediction of pile bearing capacity using a hybrid genetic algorithm-based ANN. Measurement 2014, 57, 122–131. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mohamad, E.T.; Narayanasamy, M.S.; Narita, N.; Yagiz, S. Development of hybrid intelligent models for predicting TBM penetration rate in hard rock condition. Tunn. Undergr. Space Technol. 2017, 63, 29–43. [Google Scholar] [CrossRef]
- Asteris, P.G.; Lourenço, P.B.; Roussis, P.C.; Adami, C.E.; Armaghani, D.J.; Cavaleri, L.; Chalioris, C.E.; Hajihassani, M.; Lemonis, M.E.; Mohammed, A.S. Revealing the nature of metakaolin-based concrete materials using artificial intelligence techniques. Constr. Build. Mater. 2022, 322, 126500. [Google Scholar] [CrossRef]
- Zhou, J.; Huang, S.; Zhou, T.; Armaghani, D.J.; Qiu, Y. Employing a genetic algorithm and grey wolf optimizer for optimizing RF models to evaluate soil liquefaction potential. Artif. Intell. Rev. 2022, 55, 5673–5705. [Google Scholar]
- Zeng, J.; Mohammed, A.S.; Mirzaei, F.; Moosavi, S.M.H.; Armaghani, D.J.; Samui, P. A parametric study of ground vibration induced by quarry blasting: An application of group method of data handling. Environ. Earth Sci. 2022, 81, 127. [Google Scholar] [CrossRef]
- Barkhordari, M.S.; Armaghani, D.J.; Mohammed, A.S.; Ulrikh, D.V. Data-Driven Compressive Strength Prediction of Fly Ash Concrete Using Ensemble Learner Algorithms. Buildings 2022, 12, 132. [Google Scholar] [CrossRef]
- Li, D.; Liu, Z.; Armaghani, D.J.; Xiao, P.; Zhou, J. Novel ensemble intelligence methodologies for rockburst assessment in complex and variable environments. Sci. Rep. 2022, 12, 1844. [Google Scholar]
- He, B.; Armaghani, D.J.; Lai, S.H. A Short Overview of Soft Computing Techniques in Tunnel Construction. Open Constr. Build. Technol. J. 2022, 16. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Asteris, P.G.; Mohammed, A.S.; Alexakis, D.E.; Mamou, A.; Armaghani, D.J. Introducing stacking machine learning approaches for the prediction of rock deformation. Transp. Geotech. 2022, 34, 100756. [Google Scholar] [CrossRef]
- Liu, Z.; Armaghani, D.-J.; Fakharian, P.; Li, D.; Ulrikh, D.-V.; Orekhova, N.-N.; Khedher, K.-M. Rock Strength Estimation Using Several Tree-Based ML Techniques. Comput. Modeling Eng. Sci. 2022, 133, 799–824. [Google Scholar] [CrossRef]
- Barkhordari, M.S.; Armaghani, D.J.; Asteris, P.G. Structural Damage Identification Using Ensemble Deep Convolutional Neural Network Models. Comput. Model. Eng. Sci. 2022, 134, 835–855. [Google Scholar] [CrossRef]
- Yang, H.; Li, Z.; Jie, T.; Zhang, Z. Effects of joints on the cutting behavior of disc cutter running on the jointed rock mass. Tunn. Undergr. Space Technol. 2018, 81, 112–120. [Google Scholar] [CrossRef]
- Liu, B.; Yang, H.; Karekal, S. Effect of water content on argillization of mudstone during the tunnelling process. Rock Mech. Rock Eng. 2020, 53, 799–813. [Google Scholar] [CrossRef]
- Yang, H.; Xing, S.; Wang, Q.; Li, Z. Model test on the entrainment phenomenon and energy conversion mechanism of flow-like landslides. Eng. Geol. 2018, 239, 119–125. [Google Scholar] [CrossRef]
- Yang, H.; Zeng, Y.; Lan, Y.; Zhou, X. Analysis of the excavation damaged zone around a tunnel accounting for geostress and unloading. Int. J. Rock Mech. Min. Sci. 2014, 69, 59–66. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Song, K. A new hybrid grey wolf optimizer-feature weighted-multiple kernel-support vector regression technique to predict TBM performance. Eng. Comput. 2020, 38, 2469–2485. [Google Scholar] [CrossRef]
- Schmidt, J.; Moss, R. Bayesian hierarchical and measurement uncertainty model building for liquefaction triggering assessment. Comput. Geotech. 2021, 132, 103963. [Google Scholar] [CrossRef]
- Zhao, Z.; Congress, S.S.C.; Cai, G.; Duan, W. Bayesian probabilistic characterization of consolidation behavior of clays using CPTU data. Acta Geotech. 2022, 17, 931–948. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, W.; Cai, G.; Wu, M.; Liu, S. CPT-based fully probabilistic seismic liquefaction potential assessment to reduce uncertainty: Integrating XGBoost algorithm with Bayesian theorem. Comput. Geotech. 2022, 149, 104868. [Google Scholar] [CrossRef]
- Cai, M.; Hocine, O.; Mohammed, A.S.; Chen, X.; Amar, M.N.; Hasanipanah, M. Integrating the LSSVM and RBFNN models with three optimization algorithms to predict the soil liquefaction potential. Eng. Comput. 2022, 38, 3611–3623. [Google Scholar] [CrossRef]
- Sladen, J.; D’hollander, R.; Krahn, J. The liquefaction of sands, a collapse surface approach. Can. Geotech. J. 1985, 22, 564–578. [Google Scholar] [CrossRef]
- Castro, G. On the Behavior of Soils during Earthquakes–Liquefaction. In Developments in Geotechnical Engineering; Elsevier: Amsterdam, The Netherlands, 1987; Volume 42, pp. 169–204. [Google Scholar]
- Fogel, D.B. Evolutionary Computation: Toward a New Philosophy of Machine Intelligence; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 1. [Google Scholar]
- Lee, J.-H.; Ahn, C.W. An Evolutionary Approach to Driving Tendency Recognition for Advanced Driver Assistance Systems. In Proceedings of the MATEC Web of Conferences, Amsterdam, The Netherlands, 23–25 March 2016; p. 02012. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, J.; Zhang, Y.; Xie, Y. The adoption of a support vector machine optimized by GWO to the prediction of soil liquefaction. Environ. Earth Sci. 2021, 80, 360. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical bayesian optimization of machine learning algorithms. Adv. Neural Inf. Processing Syst. 2012, 25. [Google Scholar] [CrossRef]
- Greenhill, S.; Rana, S.; Gupta, S.; Vellanki, P.; Venkatesh, S. Bayesian optimization for adaptive experimental design: A review. IEEE Access 2020, 8, 13937–13948. [Google Scholar] [CrossRef]
- Kobliha, M.; Schwarz, J.; Očenášek, J. Bayesian optimization algorithms for dynamic problems. In Proceedings of the Workshops on Applications of Evolutionary Computation, Budapest, Hungry, 10–12 April 2006; pp. 800–804. [Google Scholar]
- Shibata, T.; Teparaksa, W. Evaluation of liquefaction potentials of soils using cone penetration tests. Soils Found. 1988, 28, 49–60. [Google Scholar] [CrossRef]
- Zhou, J.; Shen, X.; Qiu, Y.; Li, E.; Rao, D.; Shi, X. Improving the efficiency of microseismic source locating using a heuristic algorithm-based virtual field optimization method. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 89. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, C.; Wang, M.; Khandelwal, M. Proposing a novel comprehensive evaluation model for the coal burst liability in underground coal mines considering uncertainty factors. Int. J. Min. Sci. Technol. 2021, 31, 799–812. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Khandelwal, M.; Zhu, S.; Zhang, X. Developing a hybrid model of Jaya algorithm-based extreme gradient boosting machine to estimate blast-induced ground vibrations. Int. J. Rock Mech. Min. Sci. 2021, 145, 104856. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.; Mitri, H.S. Classification of rockburst in underground projects: Comparison of ten supervised learning methods. J. Comput. Civ. Eng. 2016, 30, 04016003. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A gravitational search algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Shawky, L.A. Flower pollination algorithm: A comprehensive review. Artif. Intell. Rev. 2019, 52, 2533–2557. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]

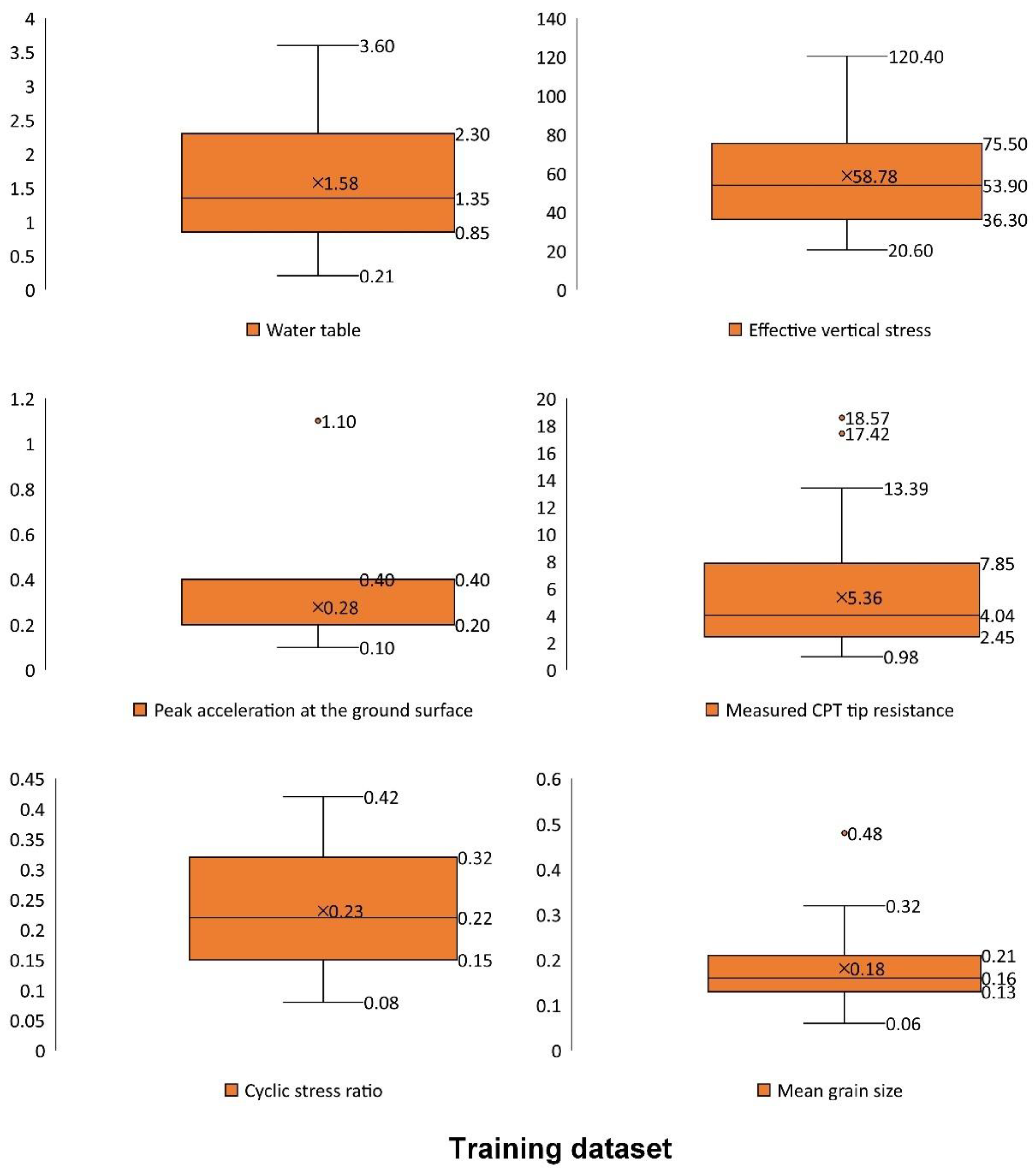
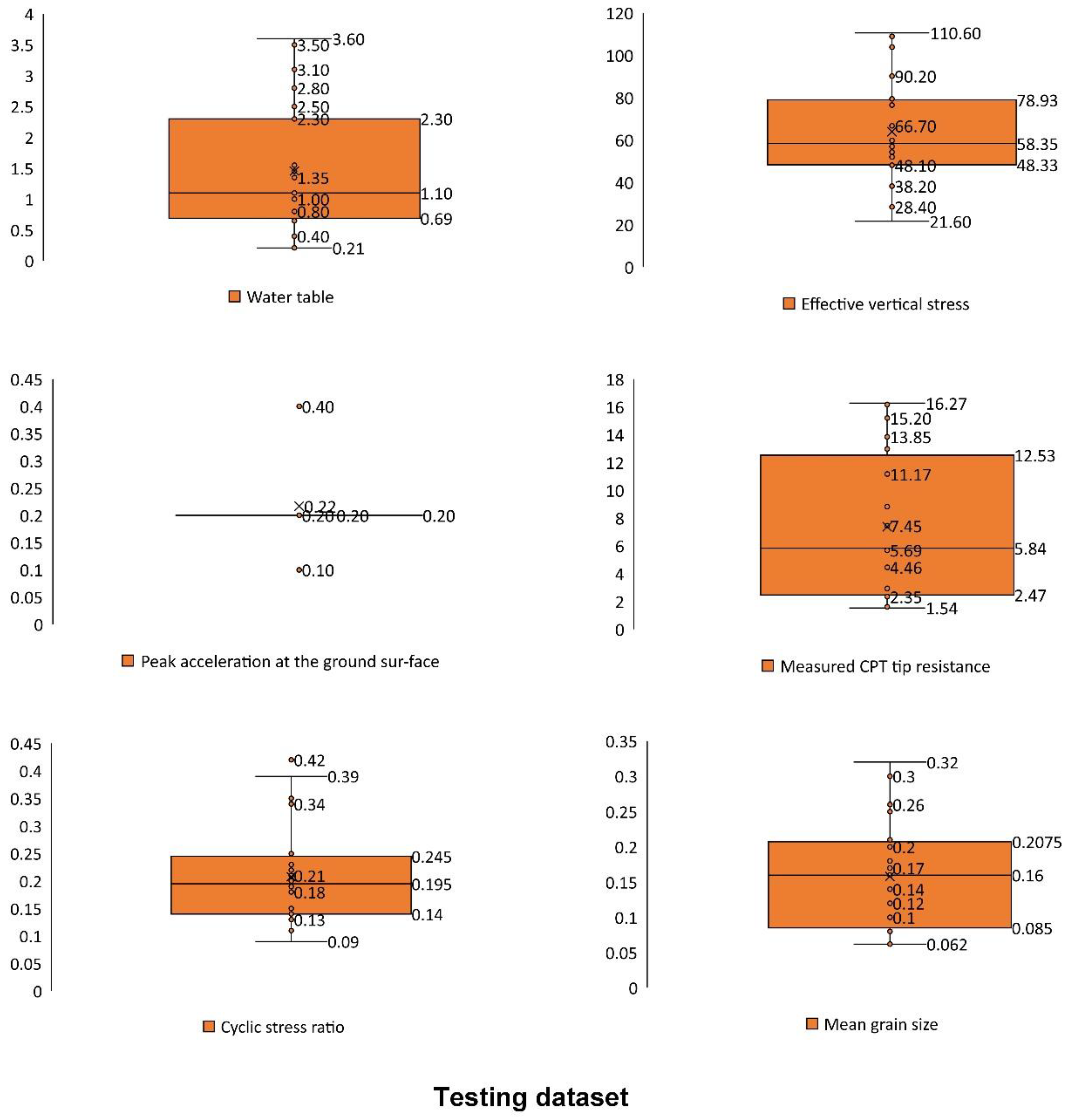
| Variable | Symbol | Unit | Min | Max |
|---|---|---|---|---|
| Earthquake magnitude | M | - | 7.8 | 7.8 |
| Effective vertical stress | kPa | 20.6 | 120.4 | |
| Total vertical stress | kPa | 16.7 | 244.2 | |
| Mean grain size | mm | 0.06 | 0.48 | |
| Water table | m | 0.21 | 3.6 | |
| Peak acceleration at the ground surface | g | 0.1 | 1.1 | |
| Depth | m | 0.9 | 13.1 | |
| Measured CPT tip resistance | MPa | 0.98 | 18.57 | |
| CSR | - | 0.08 | 0.42 | |
| Liquefaction observed * | - | - | 0 | 1 |
| Model | Train | Test | |||||
|---|---|---|---|---|---|---|---|
| Actual | Prediction | Prediction | |||||
| 0 | 1 | Accuracy (%) | 0 | 1 | Accuracy (%) | ||
| SVM | 0 | 9 | 5 | 90.9 | 9 | 1 | 91.7 |
| 1 | 0 | 41 | 1 | 13 | |||
| BOSVM | 0 | 12 | 2 | 96.4 | 10 | 0 | 95.8 |
| 1 | 0 | 41 | 1 | 13 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; He, B.; Sabri, M.M.S.; Al-Bahrani, M.; Ulrikh, D.V. Soil Liquefaction Prediction Based on Bayesian Optimization and Support Vector Machines. Sustainability 2022, 14, 11944. https://doi.org/10.3390/su141911944
Zhang X, He B, Sabri MMS, Al-Bahrani M, Ulrikh DV. Soil Liquefaction Prediction Based on Bayesian Optimization and Support Vector Machines. Sustainability. 2022; 14(19):11944. https://doi.org/10.3390/su141911944
Chicago/Turabian StyleZhang, Xuesong, Biao He, Mohanad Muayad Sabri Sabri, Mohammed Al-Bahrani, and Dmitrii Vladimirovich Ulrikh. 2022. "Soil Liquefaction Prediction Based on Bayesian Optimization and Support Vector Machines" Sustainability 14, no. 19: 11944. https://doi.org/10.3390/su141911944
APA StyleZhang, X., He, B., Sabri, M. M. S., Al-Bahrani, M., & Ulrikh, D. V. (2022). Soil Liquefaction Prediction Based on Bayesian Optimization and Support Vector Machines. Sustainability, 14(19), 11944. https://doi.org/10.3390/su141911944










