Water Quality Index Prediction for Improvement of Treatment Processes on Drinking Water Treatment Plant
Abstract
:1. Introduction
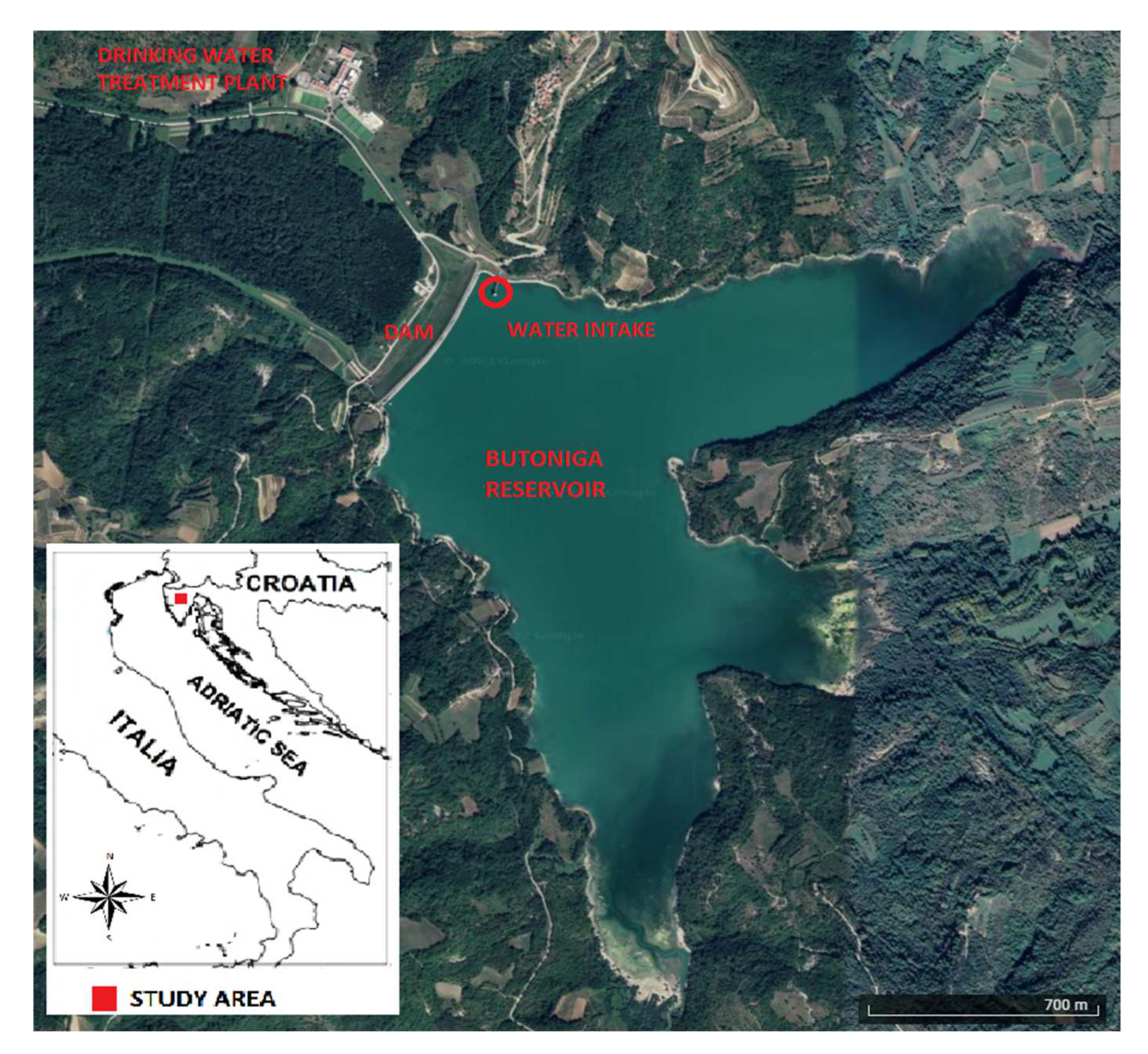
2. Study Area and Data Description
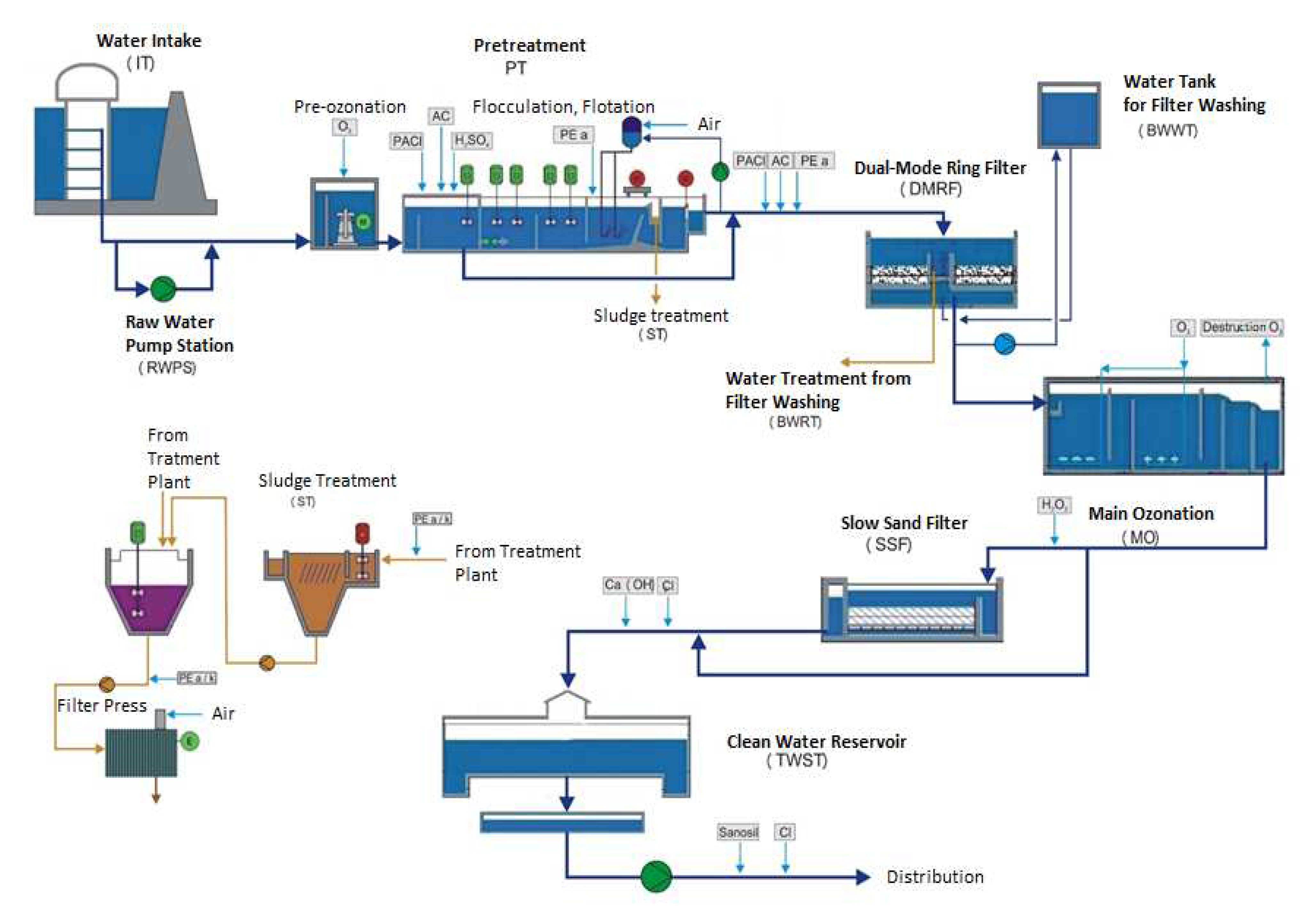
3. Materials and Methods
3.1. Modelling Methods; Rule-Based Models
3.2. Water Quality Index
3.3. Description of the Modelling Experiment
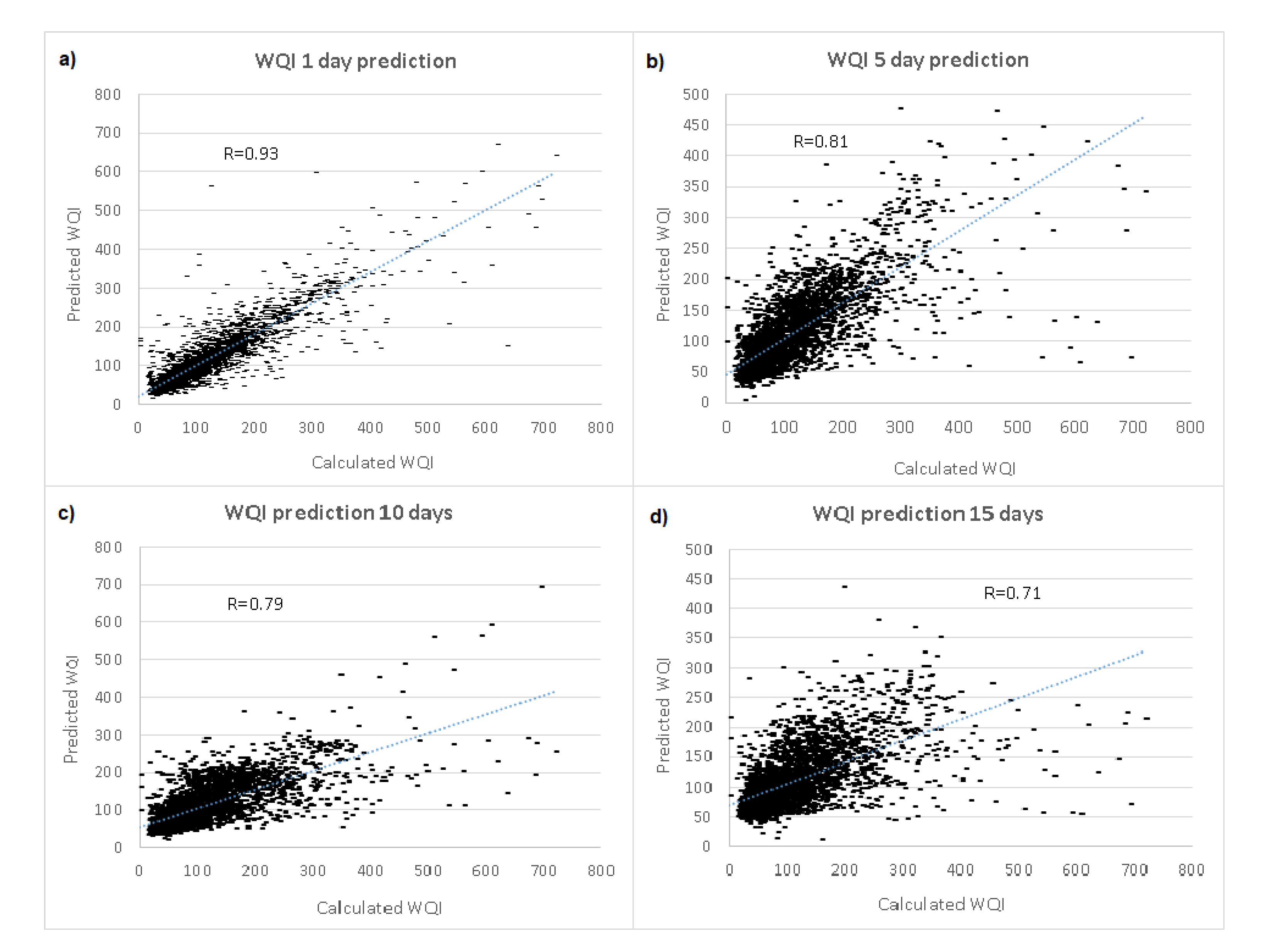
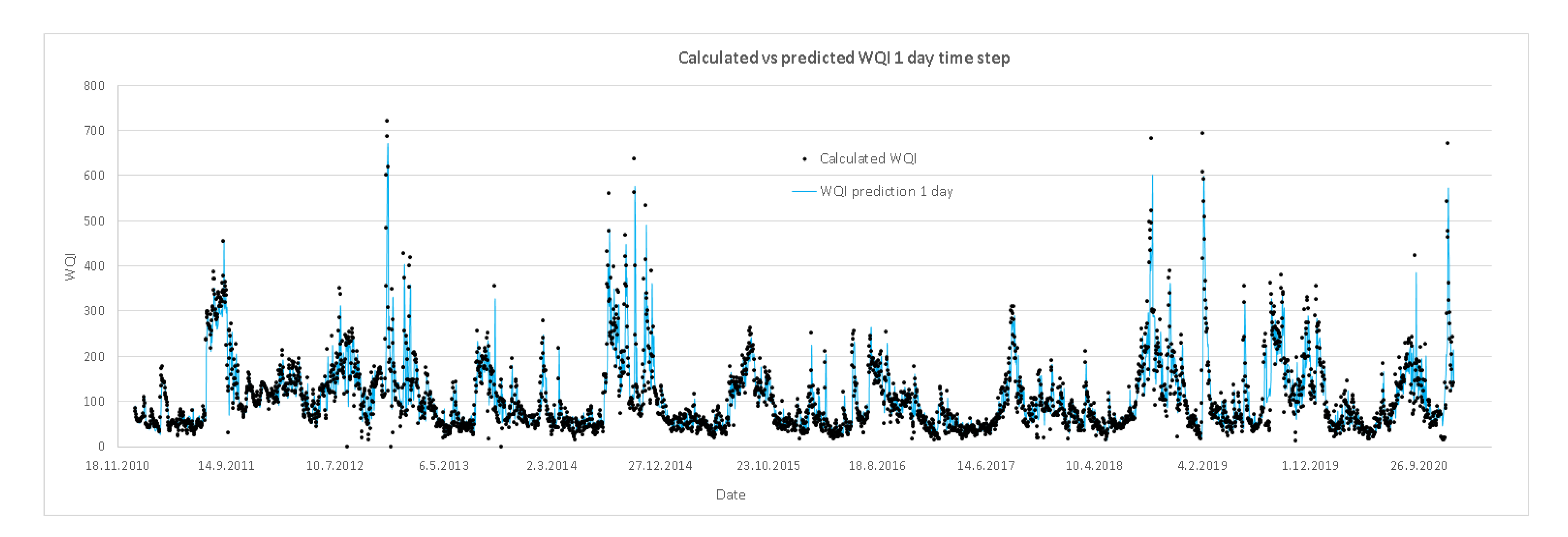
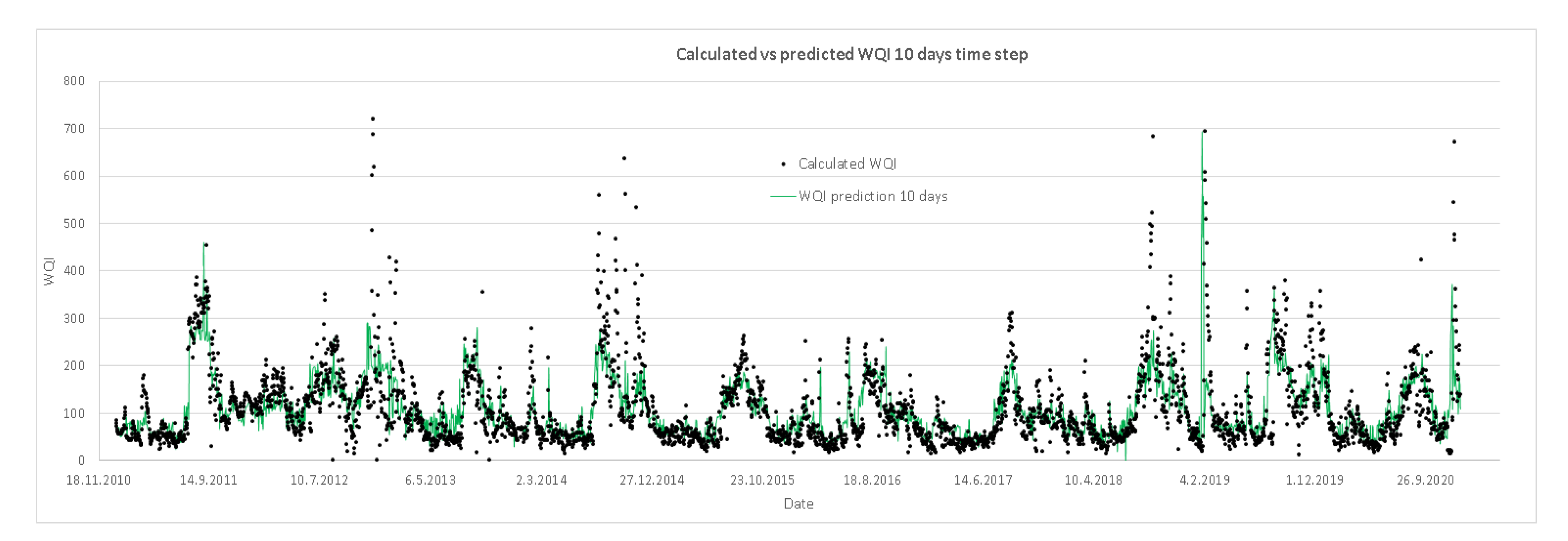
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| AR | Additive Regression |
| BC | Bagging Classifier |
| BTM | Bagged Tree Models |
| CNN | Convolutional Neural Network |
| DT | Decision Tree |
| DWTP | Drinking Water Treatment Plant |
| GBC | Gradient Boosting Classifier |
| GNB | Guassian Naïve Bayes |
| HRA | Health Risk Assessment |
| KNN | k-Nearest Neighbors |
| LSTM | Long Short-Term Memory |
| LWLR | Locally Weighted Linear Regression |
| MAC | Maximum Allowable Concentration |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MLR | Multinomial Logistic Regression |
| NARNET | Nonlinear Autoregressive Neural Network |
| NN | Neural Network |
| PCA | Principal Component Analysis |
| R | Correlation Coefficient |
| RF | Random Forest |
| RLR | Ridge and Lasso Regression |
| RSS | Random Subspace |
| SGD | Stochastic Gradient Descent |
| SLR | Simple Linear Regression |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| WQI | Water Quality Index |
References
- Aalipour Erdi, M.; Gasempour Niari, H.; Meshkini, S.R.M.; Foroug, S. Surveying drinking water quality (Balikhlou River, Ardabil Province, Iran). Appl. Water Sci. 2018, 8, 34. [Google Scholar] [CrossRef]
- Kumar, A.; Sharma, M.P.; Rai, S.P. A novel approach for river health assessment of Chambal using fuzzy modeling, India. Desalination Water Treat. 2017, 58, 72–79. [Google Scholar] [CrossRef]
- Kumar, A.; Taxak, A.K.; Mishra, S.; Pandey, R. Long term trend analysis and suitability of water quality of River Ganga at Himalayan hills of Uttarakhand, India. Environ. Technol. Inno. 2021, 22, 101405. [Google Scholar] [CrossRef]
- Tiri, A.; Belkhiri, L.; Mouni, L. Evaluation of surface water quality for drinking purposes using fuzzy inference system. Groundw. Sustain. Dev. 2018, 6, 235–244. [Google Scholar] [CrossRef]
- Braga, F.H.R.; Dutra, M.L.S.; Lima, N.S.; Silva, G.M.; Miranda, R.C.M.; Firmo, W.C.A.; Moura, A.R.L.; Monteiro, A.S.; Silva, L.C.N.; Silva, D.F.; et al. Study of the Influence of Physicochemical Parameters on the Water Quality Index (WQI) in the Maranhão Amazon, Brazil. Water 2022, 14, 1546. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, L.; Deng, L.; Jin, Z. Characteristics, sources, water quality and health risk assessment of trace elements in river water and well water in the Chinese Loess Plateau. Sci. Total Environ. 2019, 650, 2004–2012. [Google Scholar] [CrossRef] [PubMed]
- Alver, A. Evaluation of conventional drinking water treatment plant efficiency according to water quality index and health risk assessment. Environ. Sci. Pollut. Res. 2019, 26, 27225–27238. [Google Scholar] [CrossRef] [PubMed]
- Mbavarira, T.M.; Grimm, C. A Systemic View on Circular Economy in the Water Industry: Learnings from a Belgian and Dutch Case. Sustainability 2021, 13, 3313. [Google Scholar] [CrossRef]
- Aldhyani, T.H.H.; Al-Yaari, M.; Alkahtani, H.; Maashi, M. Water Quality Prediction Using Artificial Intelligence Algorithms. Appl. Bionics Biomech. 2020, 2020, 6659314. [Google Scholar] [CrossRef] [PubMed]
- Sheikh Khozani, Z.; Iranmehr, M.; Wan Mohtar, W.H.M. Improving Water Quality Index prediction for water resources management plans in Malaysia: Application of machine learning techniques. Geocarto Int. 2022, 1–18. [Google Scholar] [CrossRef]
- Hassan, M.; Hassan, M.; Akter, L.; Rahman, M.; Zaman, S.; Hasib, K.; Jahan, N.; Smrity, R.N.; Farhana, J.; Raihan, M.; et al. Efficient Prediction of Water Quality Index (WQI) Using Machine Learning Algorithms. Hum. Cent. Intell. Syst. 2021, 1, 86–97. [Google Scholar] [CrossRef]
- Kouadri, S.; Elbeltagi, A.; Islam, A.R.M.T.; Kateb, S. Performance of machine learning methods in predicting water quality index based on irregular data set: Application on Illizi region (Algerian southeast). Appl. Water. Sci. 2021, 11, 190. [Google Scholar] [CrossRef]
- Ahmed, U.; Mumatz, R.; Anwar, H.; Shah, A.A.; Irfan, R.; Garcia-Nieto, J. Efficient Water Quality Prediction Using Supervised Machine Learning. Water 2019, 11, 2210. [Google Scholar] [CrossRef]
- Khoi, D.N.; Quan, N.T.; Linh, D.Q.; Nhi, P.T.T.; Thuy, N.T.D. Using Machine Learning Models for Predicting the Water Quality Index in the La Buong River, Vietnam. Water 2022, 14, 1552. [Google Scholar] [CrossRef]
- Aalipour, M.; Št’astný, B.; Horký, F.; Jabbarian Amiri, B. Scaling an Artificial Neural Network-Based Water Quality Index Model from Small to Large Catchments. Water 2022, 14, 920. [Google Scholar] [CrossRef]
- Fernández del Castillo, A.; Yebra-Montes, C.; Verduzco Garibay, M.; de Anda, J.; Garcia-Gonzalez, A.; Gradilla-Hernández, M.S. Simple Prediction of an Ecosystem-Specific Water Quality Index and the Water Quality Classification of a Highly Polluted River through Supervised Machine Learning. Water 2022, 14, 1235. [Google Scholar] [CrossRef]
- Hajduk Černeha, B. Akumulacija Butoniga u Istri—Prva iskustva u korištenju za vodoopskrbu. In Proceedings of the Vodni dnevi 2021, Rimske Toplice, Slovenia, 7–8 October 2021. [Google Scholar]
- Zorko, S. Akumulacija Butoniga—pritisci u slijevu i zaštita voda. In Proceedings of the Zbornik radova—Upravljanje jezerima i akumulacijama u Hrvatskoj i Okrugli stol o aktualnoj problematici Vranskog jezera kod Biograda na Moru, Biograd na Moru, Croatia, 4–6 May 2017. [Google Scholar]
- Republic of Croatia regulations, Act on water intended for human consumption. 2020. In Cro., Zakon o Vodi za Ljudsku Potrošnju; NN 56/13, 64/15, 104/17, 115/18, 16/20; Effective from 20 February 2020. Available online: https://narodne-novine.nn.hr/clanci/sluzbeni/2013_05_56_1138.html (accessed on 9 March 2022).
- Volf, G.; Atanasova, N.; Kompare, B.; Precali, R.; Ožanić, N. Descriptive and prediction models of phytoplankton in the northern Adriatic. Ecol. Model. 2011, 222, 2502–2511. [Google Scholar] [CrossRef]
- Technical Committees, ISO/TC 147, Water Quality. Available online: https://www.iso.org/committee/52834/x/catalogue (accessed on 4 February 2022).
- Baird, R.B.; Eaton, A.D.; Rice, E.W. Standard Methods for the Examination of Water and Wastewater, 23rd ed.; AWWA: Washington, DC, USA, 2017. [Google Scholar]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Yisa, J.; Jimoh, T. Analytical Studies on Water Quality Index of River Landzu. Am. J. Appl. Sci. 2010, 7, 453–458. [Google Scholar] [CrossRef] [Green Version]


| Parameter | Limit Values [19] | Water Quality Index (WQI) | |
|---|---|---|---|
| wi | Wi | ||
| Temperature | 25 °C | 1 | 0.034 |
| pH | 8 | 3 | 0.103 |
| Turbidity | 4 NTU | 2 | 0.069 |
| KMnO4 | 5 mg/L | 4 | 0.138 |
| NH4 | 0.5 mg/L | 4 | 0.138 |
| Mn | 0.05 mg/L | 5 | 0.172 |
| Al | 0.2 mg/L | 5 | 0.172 |
| Fe | 0.2 mg/L | 5 | 0.172 |
| WQI | Water Quality |
|---|---|
| <50 | Excellent |
| 50–100 | Good |
| 100–200 | Bad |
| 200–300 | Very bad |
| >300 | Unfit for drinking |
| Symbol | Interpretation | Unit |
|---|---|---|
| Temp | Water temperature | - |
| pH | pH | - |
| Turb | Turbidity | NTU |
| KMnO4 | Potassium permanganate | mg/L |
| NH4 | Ammonium | mg/L |
| Mn | Manganese | mg/L |
| Al | Aluminum | mg/L |
| Fe | Iron | mg/L |
| O2 | Oxygen concentration | mg/L |
| O2p | Oxygen saturation | % |
| TOC | Total organic carbon | mg/L |
| UV254 | Organic matter in water | 1/cm |
| WQI | Calculated water quality index | - |
| WQI_1_day_pred | WQI 1 day prediction | - |
| WQI_5_day_pred | WQI 5 days prediction | - |
| WQI_10_day_pred | WQI 10 days prediction | - |
| WQI_15_day_pred | WQI 15 days prediction | - |
| Rule No. | Rule | Equation |
|---|---|---|
| 1. | - | WQI_1_day_pred = −2.1437 × O2 − 6.613 × pH − 0.6083 × Tur + 78.459 × UV254 + 20.5083 × NH4 + 72.6239 × Mn + 168.8286 × Al + 74.7368 × Fe + 0.5695 × WQI + 76.5001 |
| Rule No. | Rule | Equation |
|---|---|---|
| 1. | Mn ≤ 0.178 UV254 > 0.05 O2p ≤ 91.263 WQI ≤ 67.5 Temp ≤ 14.647 | WQI_5_day_pred = 0.0492 × Temp − 0.1442 × O2 + 0.0116 × O2p + 18.4678 × pH + 0.1147 × Tur + 0.1954 × TOC − 0.0833 × KMnO4 + 1.0771 × UV254 + 0.359 × NH4 + 3.4449 × Mn + 1.4357 × Al + 194.1906 × Fe + 0.0154 × WQI − 117.4061 |
| 2. | Mn ≤ 0.178 UV254 > 0.05 NH4 > 0.116 NH4 ≤ 0.217 | WQI_5_day_pred = −0.0314 × Temp − 4.0616 × O2 + 0.4277 × O2p − 30.9666 × pH + 0.0146 × Tur + 0.409 × TOC - 0.1268 × KMnO4 + 1.9415 × UV254 + 0.4537 × NH4 + 5.6159 × Mn + 8.273 × Al + 218.0231 × Fe + 0.2294 × WQI + 271.4172 |
| 3. | Mn ≤ 0.238 UV254 > 0.05 | WQI_5_day_pred = −1.3998 × Temp − 3.7955 × O2 + 0.2478 × O2p − 73.5681 × pH + 0.0134 × Tur − 0.0776 × TOC − 13.3644 × KMnO4 − 234.667 × UV254 + 0.4444 × NH4 + 1.6204 × Mn + 1.9645 × Al + 132.2723 × Fe − 0.2347 × WQI + 717.3281 |
| 4. | Mn > 0.154 Mn ≤ 0.556 pH > 7.514 Mn > 0.273 NH4 ≤ 0.444 NH4 > 0.168 | WQI_5_day_pred = 2.3592 × Temp − 0.344 × O2 − 0.0068 × O2p − 1.3764 × pH + 0.2721 × Tur − 1.6152 × TOC − 19.6394 × KMnO4 − 13.095 × UV254 + 6.8627 × NH4 + 4.9796 × Mn + 45.1687 × Al + 69.3252 × Fe + 0.0377 × WQI + 137.004 |
| 5. | Mn > 0.154 Mn ≤ 0.625 WQI > 145.5 O2 > 4.29 TOC > 2.144 | WQI_5_day_pred = −2.2601 × Temp + 1.0762 × O2 − 0.5878 × O2p − 51.0854 × pH + 4.2073 × Tur + 0.4781 × TOC − 442.8518 × UV254 + 53.2808 × NH4 + 83.5576 × Mn − 462.669 × Al − 14.6656 × Fe + 0.0126 × WQI + 598.894 |
| 6. | Mn > 0.154 WQI ≤ 145.5 | WQI_5_day_pred = −0.1431 × Temp − 15.6738 × O2 + 0.9714 × O2p − 2.2167 × pH + 1.5839 × Tur + 29.7531 × TOC + 3.9299 × NH4 + 119.515 × Mn + 41.3706 × Al + 146.8431 × Fe + 0.4928 × WQI − 18.3667 |
| 7. | Mn > 0.196 NH4 ≤ 0.656 Temp > 14.521 | WQI_5_day_pred = −0.2457 × Temp + 16.8424 × O2 - 2.17 × O2p - 1.9383 × pH + 4.5045 × Tur + 1.5087 × TOC + 36.4246 × UV254 + 4.2032 × NH4 + 466.3063 × Mn + 68.4722 × Al − 11.5351 × Fe − 1.1276 × WQI + 250.7915 |
| 8. | UV254 ≤ 0.051 Tur > 1.77 O2 > 6.671 | WQI_5_day_pred = −0.1311 × Temp − 0.8676 × O2 + 0.0209 × O2p − 4.7746 × pH + 0.2683 × Tur − 11.8676 × TOC + 12.0203 × KMnO4 − 1084.1325 × UV254 + 0.9434 × NH4 - 197.3272 × Mn + 28.2832 × Al - 11.6473 × Fe + 0.4091 × WQI + 149.8425 |
| 9. | UV254 ≤ 0.051 O2 > 6.685 | WQI_5_day_pred = −2.1766 × Temp − 12.4999 × O2 + 1.0932 × O2p − 30.7421 × pH + 6.042 × Tur − 9.7481 × TOC + 0.5713 × KMnO4 + 60.3924 × UV254 − 44.7147 × NH4 + 7.7437 × Mn + 55.508 × Al + 69.3385 × Fe + 345.6699 |
| 10. | UV254 > 0.051 O2 ≤ 1.646 | WQI_5_day_pred = −5.4435 × Temp + 1.8677 × O2 − 0.6007 × O2p − 5.9718 × pH − 0.8719 × Tur + 37.473 × TOC + 12.2012 × KMnO4 − 2209.8031 × UV254 − 45.2861 × NH4 + 171.9741 × Mn − 12.49 × Fe + 416.9164 |
| 11. | UV254 > 0.051 Temp ≤ 14.146 NH4 > 0.243 | WQI_5_day_pred = 7.2088 × O2 − 0.3865 × O2p − 10.7903 × pH + 6.4896 × Tur + 4.3084 × TOC + 7.6783 × KMnO4 + 68.6909 × UV254 − 22.0766 × NH4 − 78.7705 × Mn − 16.5265 × Fe + 173.4252 |
| 12. | - | WQI_5_day_pred = −12.6524 × Temp − 51.1841 × O2 + 4.544 × O2p − 169.1456 × pH + 43.3802 × KMnO4 + 723.3245 × UV254 + 36.264 × NH4 + 99.2001 × Mn + 1428.6758 × Al + 1506.6314 |
| Rule No. | Rule | Equation |
|---|---|---|
| 1. | Mn ≤ 0.161 UV254 > 0.049 Fe > 0.08 pH > 7.903 UV254 ≤ 0.07 | WQI_10_day_pred = 1.5616 × Temp − 0.1592 × O2 + 0.2154 × O2p + 31.8486 × pH − 0.1474 × Tur + 16.4278 × TOC + 0.0481 × KMnO4 − 6.5069 × UV254 + 0.3496 × NH4 − 0.7361 × Mn + 2.4 × Al + 246.8828 × Fe + 0.0231 × WQI − 292.6473 |
| 2. | Mn ≤ 0.228 UV254 > 0.049 O2 > 6.037 TOC > 2.068 | WQI_10_day_pred = −1.3609 × Temp − 10.3742 × O2 + 1.3011 × O2p − 33.9897 × pH − 3.2088 × Tur + 0.0438 × TOC − 565.14 × UV254 + 0.3834 × NH4 + 65.7253 × Mn − 221.5725 × Al + 188.8055 × Fe + 0.1485 × WQI + 360.0167 |
| 3. | Mn > 0.131 pH > 7.63 Mn ≤ 0.42 | WQI_10_day_pred = 1.5174 × Temp − 0.4902 × O2 + 0.0296 × O2p − 1.0916 × pH − 2.1281 × Tur + 0.0978 × TOC − 362.8943 × UV254 + 58.198 × NH4 + 11.7774 × Mn + 436.819 × Al + 110.5269 × Fe + 0.1953 × WQI + 70.6604 |
| 4. | Mn > 0.147 | WQI_10_day_pred = −4.7909 × Temp − 29.3983 × O2 + 1.9398 × O2p + 27.2021 × pH − 3.6554 × Tur + 0.4596 × TOC + 36.9032 × NH4 + 176.6099 × Mn + 556.3115 × Al + 56.7678 × Fe − 0.3055 × WQI + 79.0885 |
| 5. | UV254 ≤ 0.05 Tur ≤ 1.349 Temp > 13.085 | WQI_10_day_pred = −1.1396 × Temp − 6.1336 × O2 + 0.4967 × O2p − 31.8387 × pH + 0.4681 × Tur − 13.8161 × TOC + 5.2705 × KMnO4 + 90.5952 × UV254 − 4.0772 × NH4 − 234.7263 × Mn − 22.4896 × Al + 8.6443 × Fe + 0.041 × WQI + 349.673 |
| 6. | UV254 > 0.05 Al ≤ 0.002 Temp ≤ 19.35 | WQI_10_day_pred = 0.0935 × Temp + 12.3922 × O2 − 1.4555 × O2p − 21.8854 × pH + 4.3067 × Tur + 31.5541 × TOC − 28.5229 × KMnO4 − 107.7914 × UV254 + 15.9927 × NH4 + 21.5347 × Al + 131.9561 × Fe - 0.7713 × WQI + 263.7697 |
| 7. | UV254 > 0.05 UV254 > 0.052 | WQI_10_day_pred = 9.6063 × Temp + 36.7844 × O2 - 3.7629 × O2p - 29.6123 × pH + 14.0689 × Tur + 7.3178 × TOC - 66.8263 × UV254 + 439.762 × Mn - 692.8787 × Al - 313.2304 × Fe + 0.0563 × WQI + 146.4862 |
| 8. | UV254 ≤ 0.048 O2 ≤ 7.389 pH > 7.755 | WQI_10_day_pred = −0.3282 × Temp − 8.0303 × O2 + 0.5504 × O2p + 37.8754 × pH + 18.7798 × Tur + 3.8309 × TOC + 339.0088 × UV254 − 62.2836 × NH4 − 173.1733 × Mn − 83.2919 × Al + 21.4339 × Fe + 0.0471 × WQI - 263.5586 |
| 9. | UV254 ≤ 0.049 pH > 7.785 Tur ≤ 1.468 | WQI_10_day_pred = −0.2551 × Temp − 0.1407 × O2 − 11.9135 × pH + 9.0883 × Tur − 5.6761 × TOC + 7.0392 × KMnO4 + 406.0863 × UV254 − 29.4935 × Mn − 60.929 × Al + 69.954 × Fe + 109.2525 |
| 10. | Tur > 1.504 pH > 7.762 pH ≤ 8.157 | WQI_10_day_pred = 0.6663 × Temp + 0.2275 × O2 − 11.1661 × pH + 4.3653 × Tur − 8.2495 × TOC + 5.6081 × KMnO4 + 564.6441 × UV254 − 10.1607 × NH4 − 92.4626 × Mn + 216.0347 × Fe − 0.4035 × WQI + 109.4049 |
| 11. | WQI > 38.5 O2 > 6.874 Tur ≤ 2.111 O2 > 8.921 | WQI_10_day_pred = −3.2172 × Temp − 0.7486 × O2 − 59.4558 × pH − 0.6238 × Tur + 6.9855 × TOC + 8.644 × KMnO4 + 1134.6654 × UV254 − 174.1622 × Al − 55.1062 × Fe + 0.2754 × WQI + 496.4482 |
| 12. | UV254 ≤ 0.049 pH > 7.673 | WQI_10_day_pred = −1.5223 × Temp + 9.0823 × O2 − 0.84 × O2p − 43.5423 × pH + 8.2979 × Tur + 13.9948 × KMnO4 + 2670.0583 × UV254 + 272.8255 |
| 13. | Temp > 9.654 | WQI_10_day_pred = −7.5086 × Temp − 112.8856 × pH + 69.6063 × TOC + 967.9153 |
| 14. | - | WQI_10_day_pred = −61.5182 × O2 − 751.5462 × Tur + 1847.615 |
| Rule No. | Rule | Equation |
|---|---|---|
| 1. | pH > 7.722 Mn ≤ 0.182 Tur > 1.675 Temp ≤ 15.32 | WQI_15_day_pred = −2.308 × Temp − 7.9764 × O2 + 1.0935 × O2p + 28.5839 × pH + 3.8658 × Tur + 0.2701 × TOC + 0.183 × KMnO4 − 12.663 × UV254 + 1.2919 × NH4 + 2.8251 × Mn − 224.3635 × Al + 119.207 × Fe + 0.0008 × WQI − 184.4439 |
| 2. | pH > 7.703 Mn > 0.134 pH > 7.948 | WQI_15_day_pred = −1.1171 × Temp − 9.6787 × O2 + 0.7265 × O2p − 47.8948 × pH − 1.7395 × Tur + 10.9147 × TOC − 16.9889 × KMnO4 − 571.2309 × UV254 + 2.2305 × NH4 + 6.0254 × Mn + 431.2766 × Al + 209.4744 × Fe + 0.0623 × WQI + 518.4762 |
| 3. | Mn > 0.134 Mn ≤ 0.52 Temp ≤ 21.01 pH > 7.63 WQI > 114.5 | WQI_15_day_pred = −2.3239 × Temp − 4.9107 × O2 + 0.1752 × O2p − 5.5331 × pH − 5.4288 × Tur − 1.1149 × TOC + 7.5097 × NH4 + 145.6845 × Mn + 676.501 × Al + 5.0832 × Fe − 0.0928 × WQI + 201.3688 |
| 4. | Mn > 0.134 Temp ≤ 21.065 Tur > 3.084 UV254 ≤ 0.071 | WQI_15_day_pred = −0.2501 × Temp + 5.9114 × O2 + 0.2627 × O2p − 73.2176 × pH − 6.2534 × Tur + 1.7585 × TOC − 1.2392 × KMnO4 + 1308.1435 × UV254 + 117.9952 × NH4 + 11.2328 × Mn + 1364.4201 × Al + 1.451 × Fe − 0.0057 × WQI + 584.6712 |
| 5. | - | WQI_15_day_pred = −3.1871 × Temp − 11.7564 × O2 + 0.7338 × O2p − 101.7279 × pH − 1628 × Tur + 24.9861 × TOC − 245.935 × UV254 + 48.1042 × NH4 + 151.9509 × Mn + 417.6806 × Al + 108.3222 × Fe − 0.1082 × WQI + 918.6201 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volf, G.; Sušanj Čule, I.; Žic, E.; Zorko, S. Water Quality Index Prediction for Improvement of Treatment Processes on Drinking Water Treatment Plant. Sustainability 2022, 14, 11481. https://doi.org/10.3390/su141811481
Volf G, Sušanj Čule I, Žic E, Zorko S. Water Quality Index Prediction for Improvement of Treatment Processes on Drinking Water Treatment Plant. Sustainability. 2022; 14(18):11481. https://doi.org/10.3390/su141811481
Chicago/Turabian StyleVolf, Goran, Ivana Sušanj Čule, Elvis Žic, and Sonja Zorko. 2022. "Water Quality Index Prediction for Improvement of Treatment Processes on Drinking Water Treatment Plant" Sustainability 14, no. 18: 11481. https://doi.org/10.3390/su141811481
APA StyleVolf, G., Sušanj Čule, I., Žic, E., & Zorko, S. (2022). Water Quality Index Prediction for Improvement of Treatment Processes on Drinking Water Treatment Plant. Sustainability, 14(18), 11481. https://doi.org/10.3390/su141811481







