Modeling and Feature Analysis of Air Traffic Complexity Propagation
Abstract
:1. Introduction
2. Propagation Models
2.1. Definition of Air Traffic Complexity Propagation Behavior
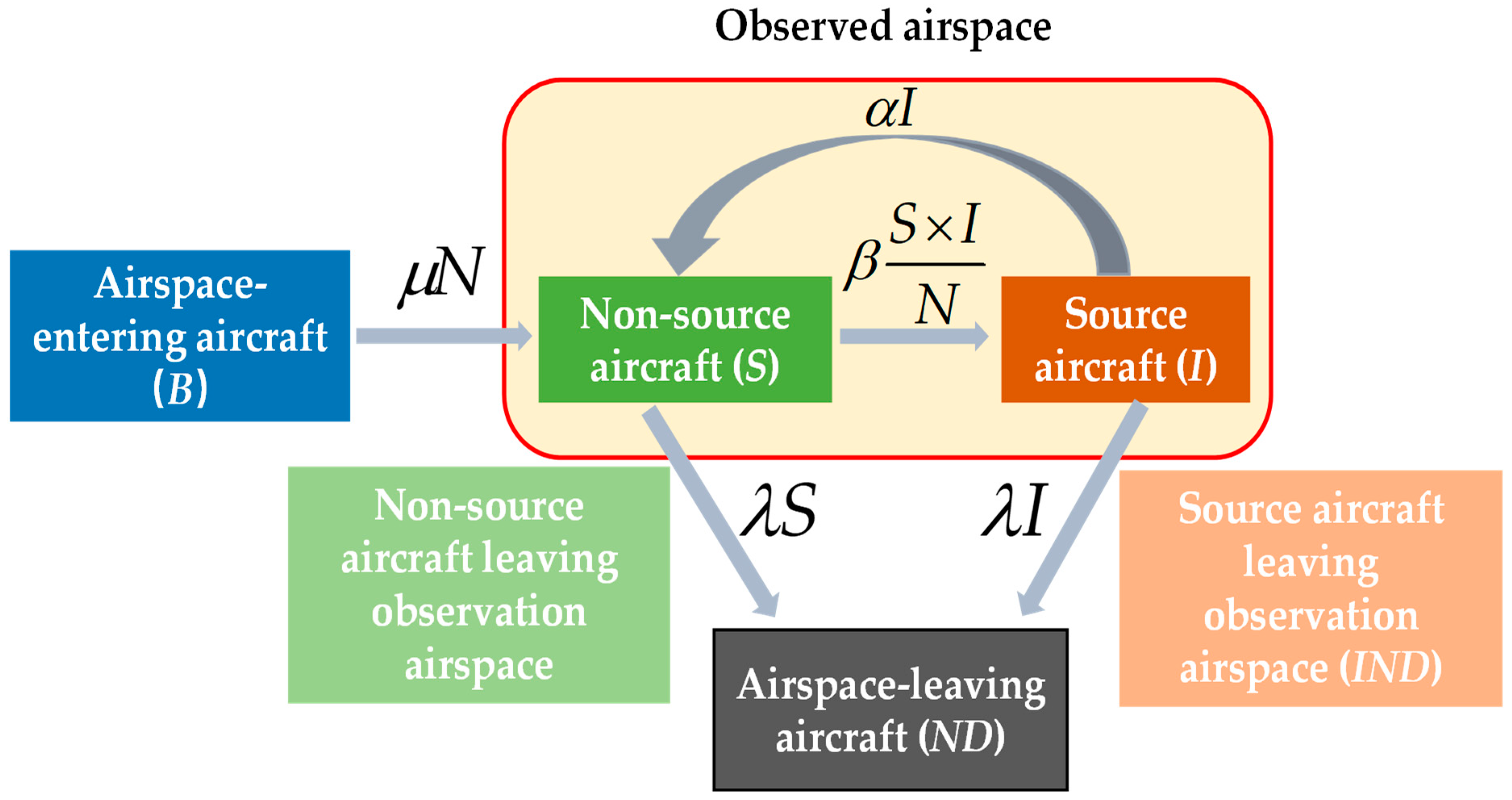
2.2. Modeling of Air Traffic Complexity Propagation
3. Influence Factors of the Propagation Model
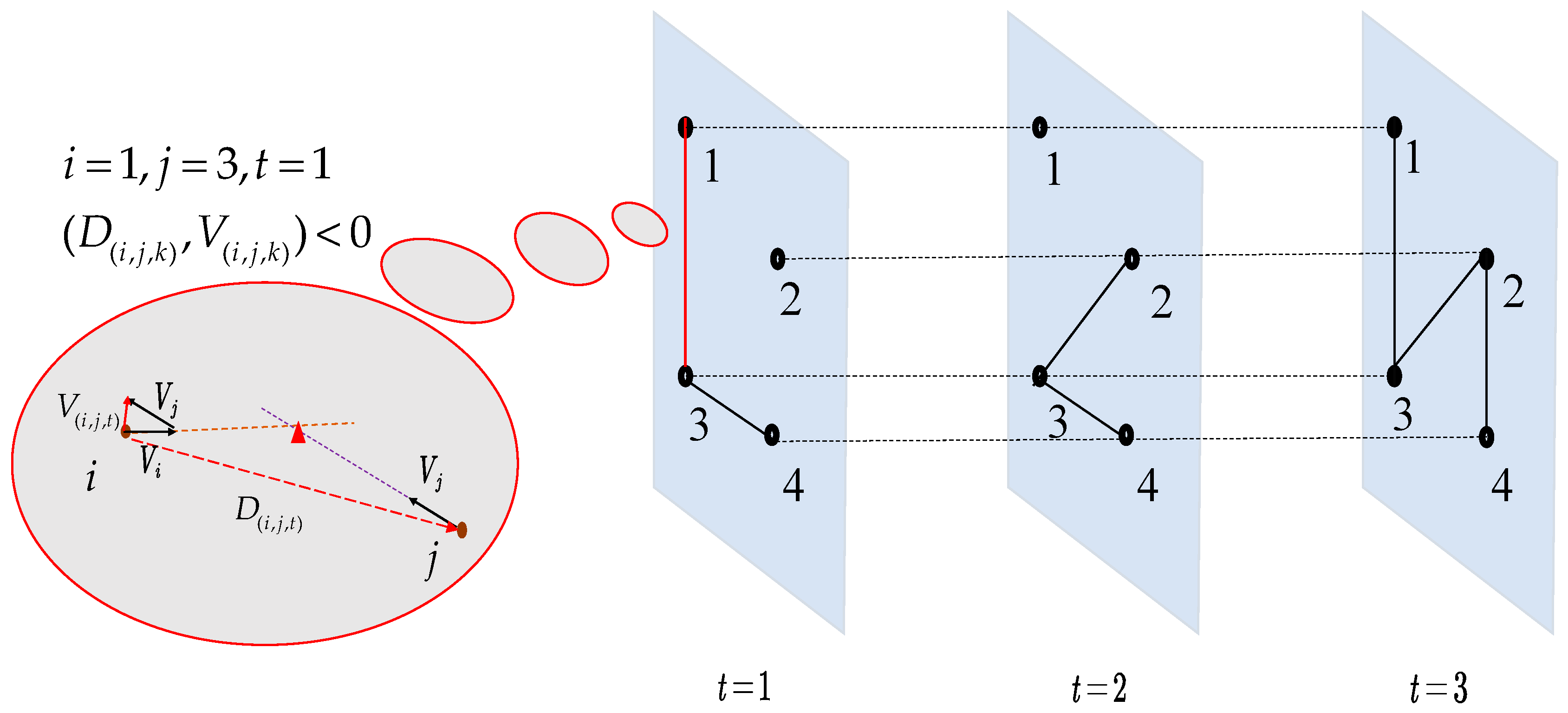
3.1. Relative Velocity and Duration
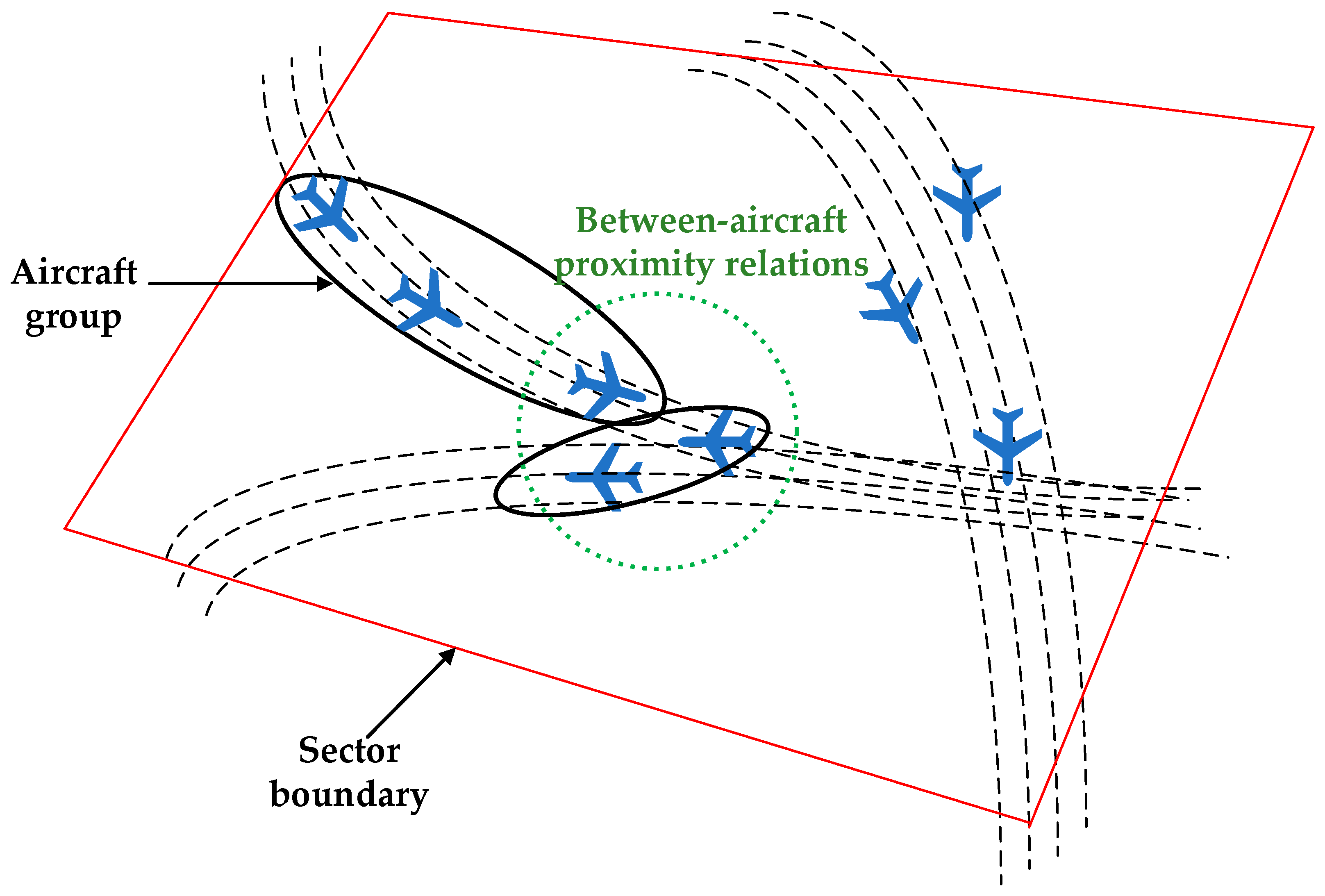
3.2. Clustering Degree
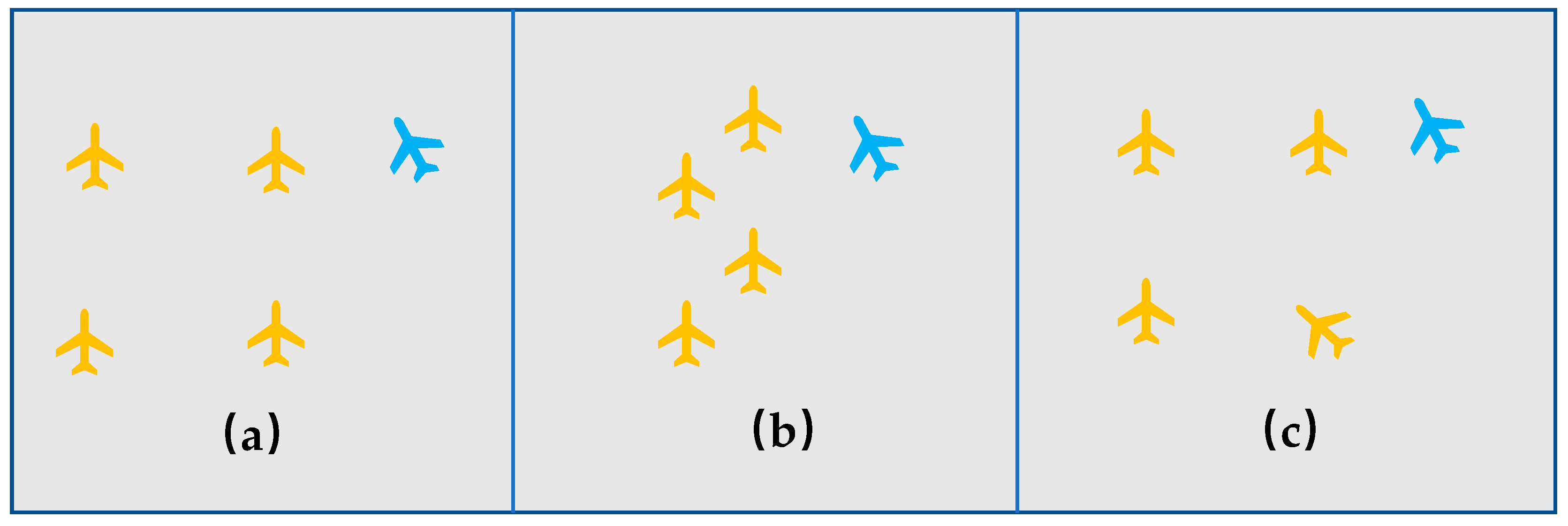
3.2.1. Aircraft Group Division
- Preprocessing of trajectory data
- 2.
- Clustering algorithm
- 3.
- Determination of clustering result.
3.2.2. Computation of Clustering Degree
3.3. Nodes and Network Evolution Features
4. Propagation Model Solving and Propagation Ability Division
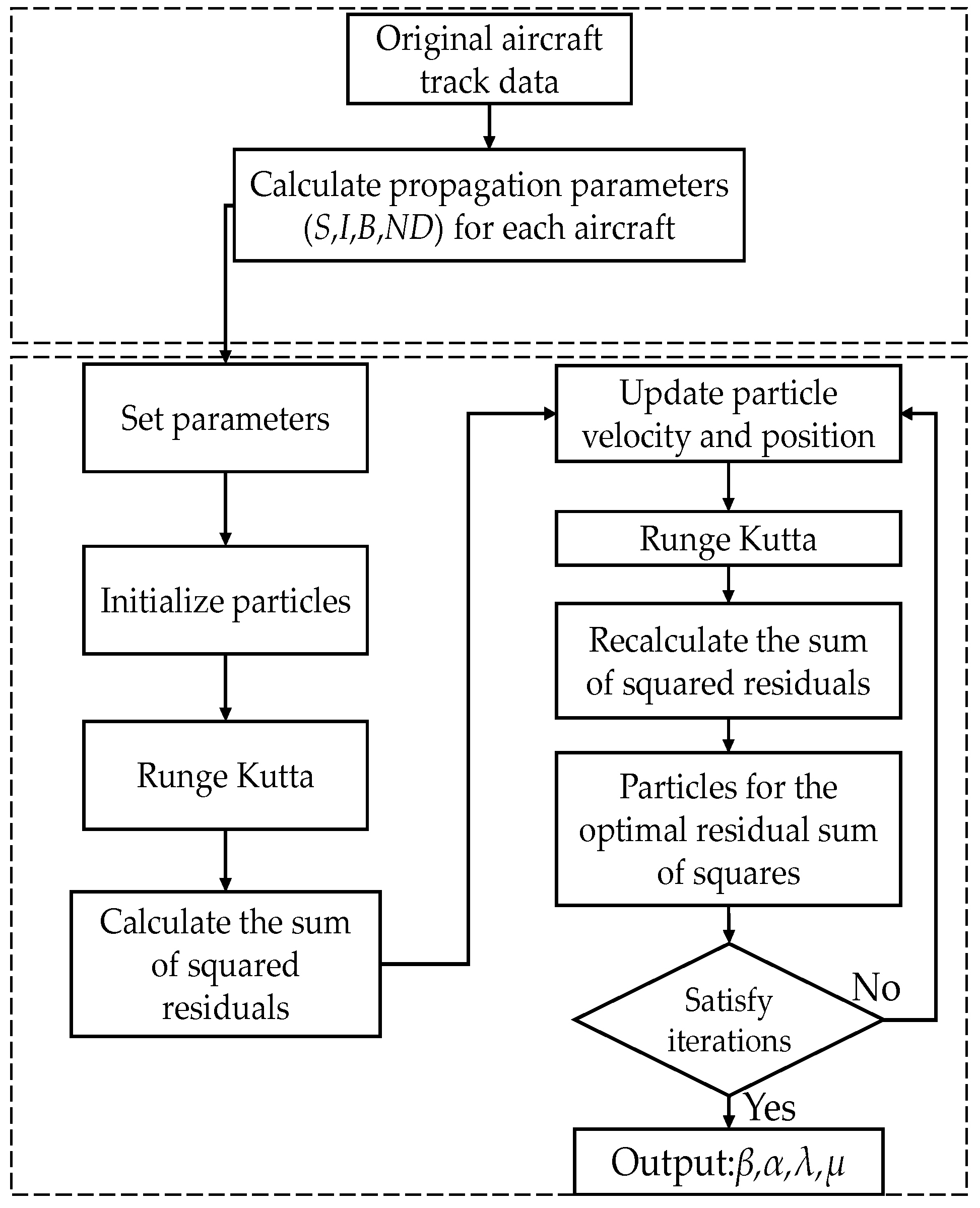
4.1. Solving the Differential Equation of the Propagation Model
4.2. Optimization of Differential Equation Parameters
4.3. Division of Propagation Ability
5. Case Validation
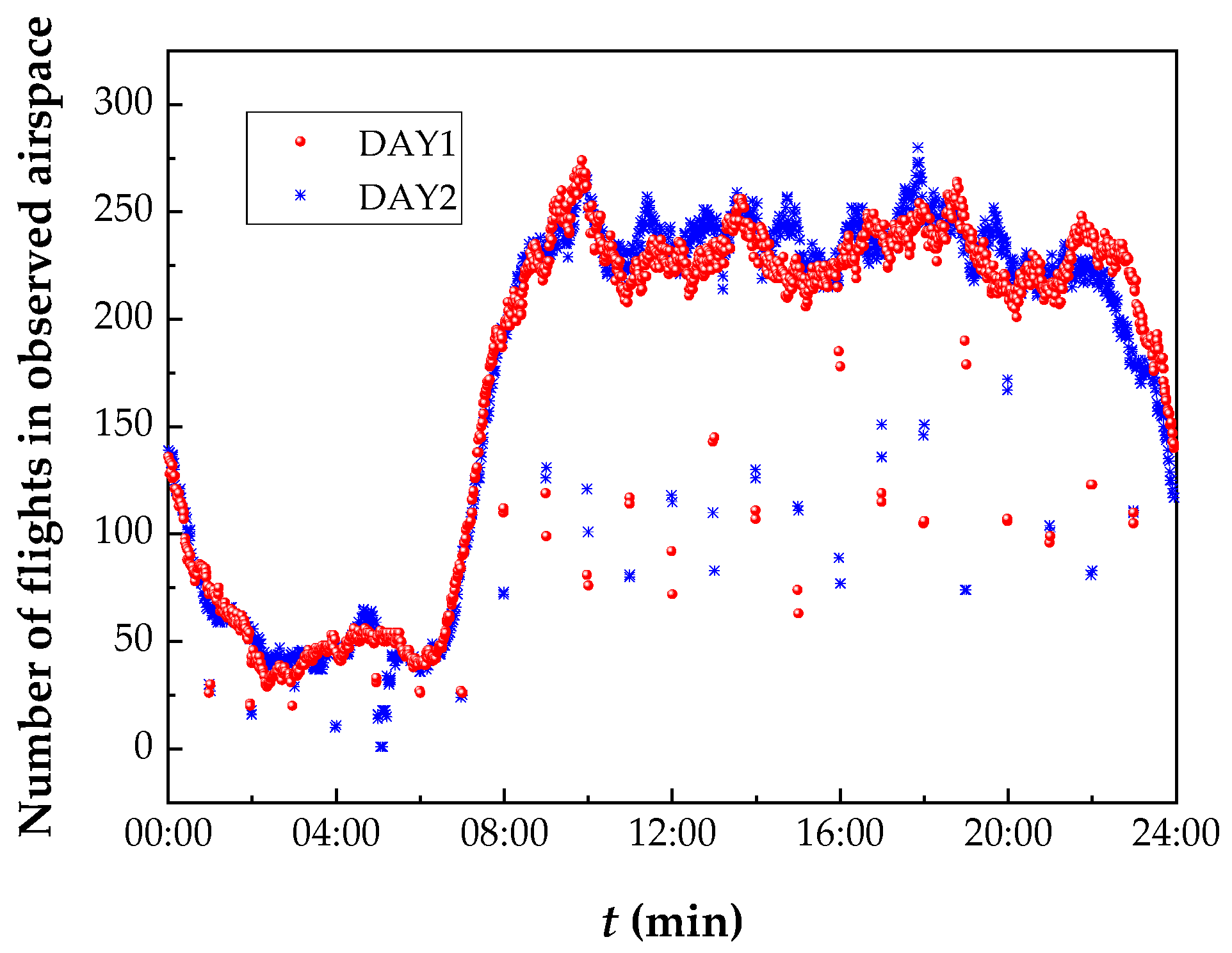
5.1. Description of Real Data
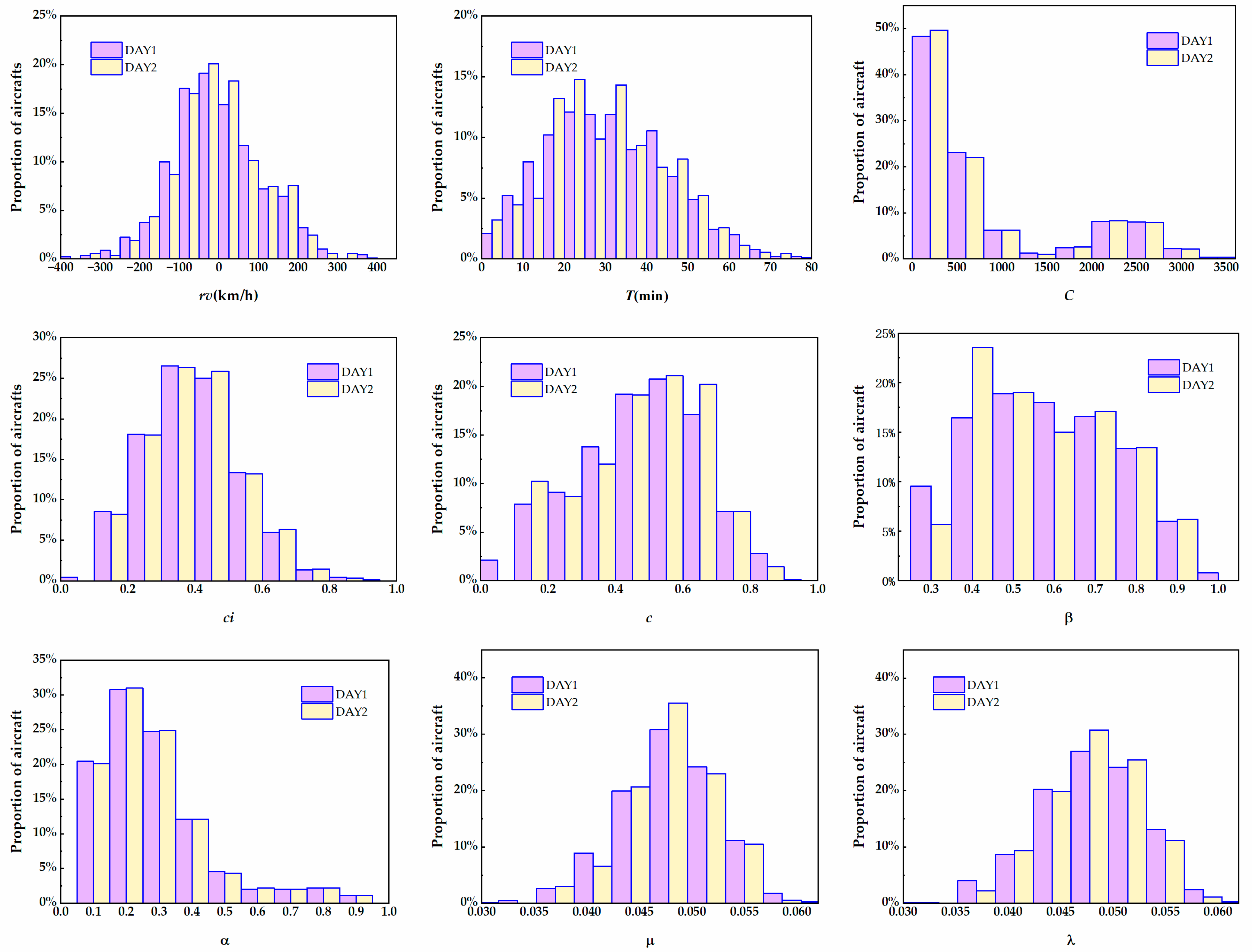
5.2. Calculated Results of Propagation Model Parameters
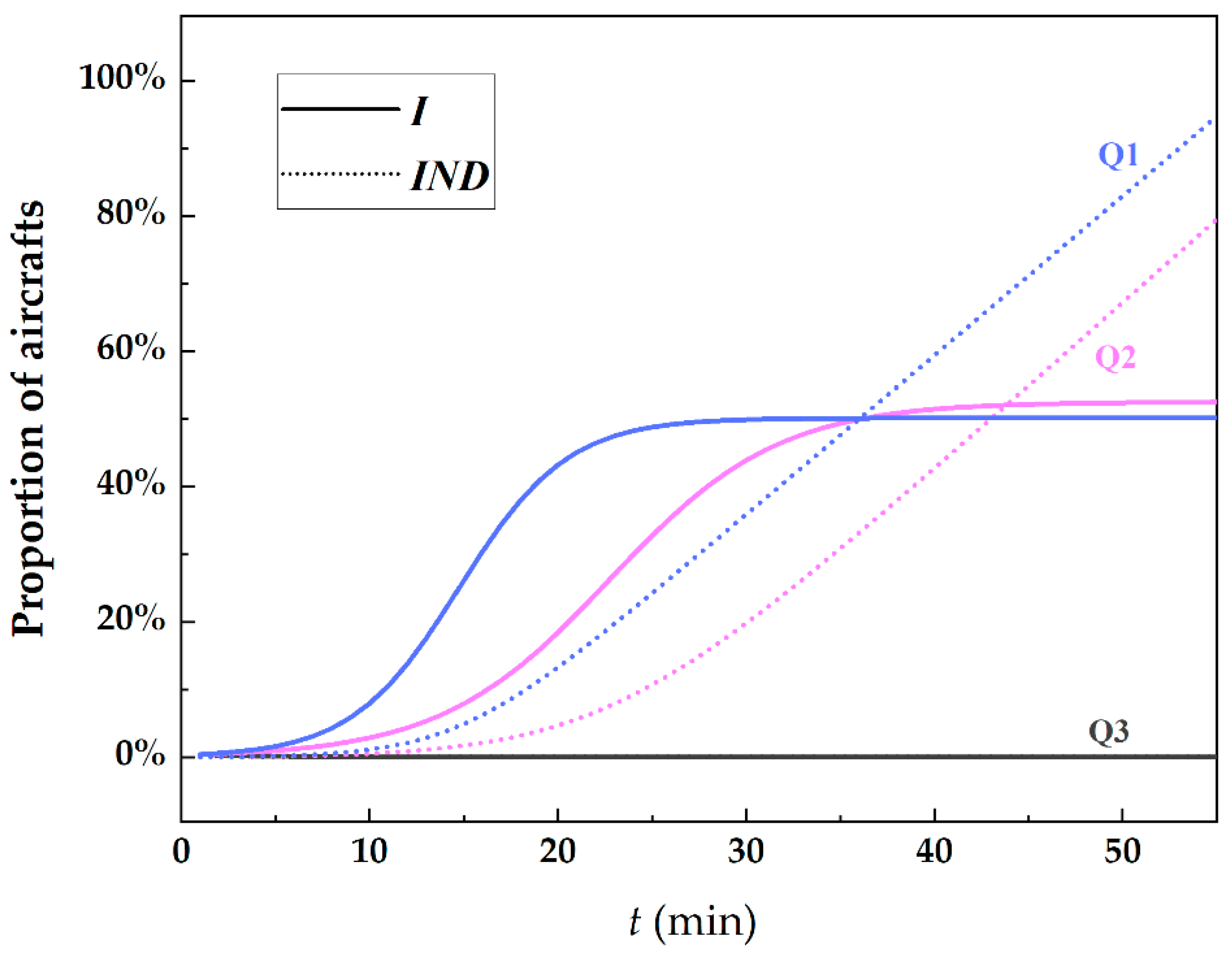
5.3. Results of Propagation Ability Division
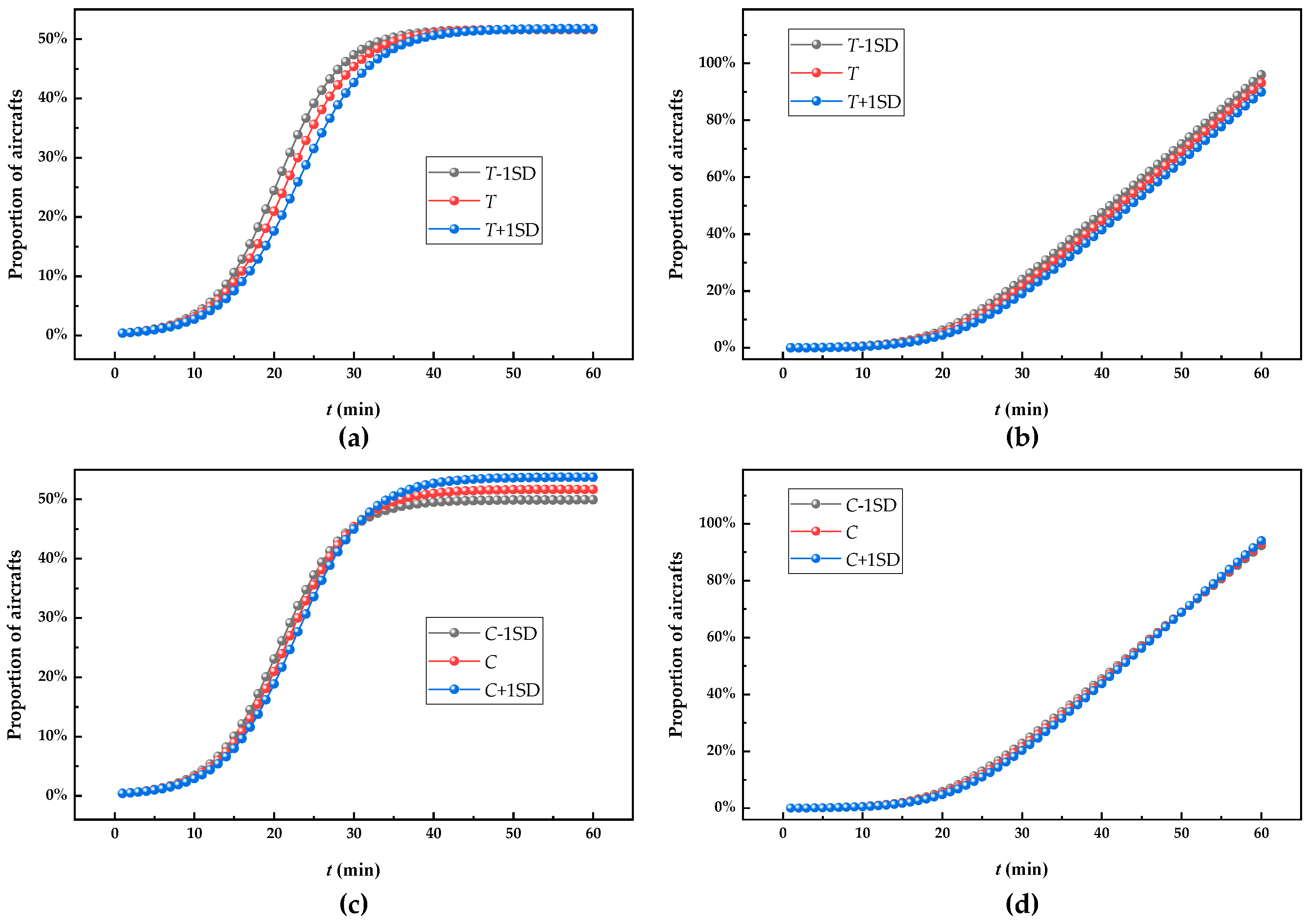
5.4. Analytical Results of Influence Factors
- Aircraft with high propagation capability (Q1)
- 2.
- Aircraft with medium propagation capability (Q2)
- 3.
- Aircraft with low propagation capability (Q3)
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Schmidt, D.K. On modeling ATC workload and sector capacity. J. Aircr. 1976, 13, 531–537. [Google Scholar] [CrossRef]
- Hurst, M.W.; Rose, R.M. Objective job difficulty, behavioral response, and sector characteristics in air route traffic control centers. Ergonomics 1978, 21, 697–708. [Google Scholar] [CrossRef]
- Netjasov, F.; Janic, M.; Tosic, V. Developing a generic metric of terminal airspace traffic complexity. Transportmetrica 2011, 7, 369–394. [Google Scholar] [CrossRef]
- Prevot, T.; Lee, P.U. Trajectory-based complexity (TBX): A modified aircraft count to predict sector complexity during trajectory-based operations. In Proceedings of the IEEE/AIAA 30th Digital Avionics Systems Conference, Seattle, WA, USA, 16–20 October 2011. [Google Scholar]
- Lee, K.; Feron, E.; Pritchett, A. Describing airspace complexity: Airspace response to disturbances. J. Guid. Control Dyn. 2009, 32, 210–222. [Google Scholar] [CrossRef]
- Lee, K.; Feron, E.; Pritchett, A. Air traffic complexity: An input-output approach. In Proceedings of the 2007 American Control Conference, New York, NY, USA, 9–13 July 2007. [Google Scholar]
- Lyons, R. Complexity analysis of the next gen air traffic management system: Trajectory based operations. Work 2012, 41, 4514–4522. [Google Scholar] [CrossRef]
- Prandini, M.; Piroddi, L.; Puechmorel, S. Toward air traffic complexity assessment in new generation air traffic management systems. IEEE Trans. Intell. Transp. Syst. 2011, 12, 809–818. [Google Scholar] [CrossRef]
- Prandini, M.; Putta, V.; Hu, J. Air traffic complexity in future Air Traffic Management systems. J. Aerosp. Oper. 2012, 1, 281–299. [Google Scholar] [CrossRef]
- Rocha, E.C. Dynamics of air transport networks: A review from a complex systems perspective. Chin. J. Aeronaut. 2017, 2, 7–16. [Google Scholar] [CrossRef]
- Sun, X.Q.; Wandelt, S. Robustness of air transportation as complex networks: Systematic review of 15 years of research and outlook into the future. Sustainability 2021, 13, 6446. [Google Scholar] [CrossRef]
- Hossain, M.M.; Alam, S.; Symon, F.; Blom, H. A Complex Network Approach to Analyze the Effect of Intermediate Waypoints on Collision Risk Assessment. Air Traffic Control Q. 2014, 22, 87–114. [Google Scholar] [CrossRef]
- Hossain, M.M.; Alam, S. A complex network approach towards modeling and analysis of the Australian Airport Network. J. Air Transp. Manag. 2017, 60, 1–9. [Google Scholar]
- Complexity Metrics for ANSP Benchmarking Analysis. Available online: https://www.eurocontrol.int/publication/complexity-metrics-air-navigation-service-providers (accessed on 1 April 2006).
- Wang, H.Y.; Xu, X.H.; Zhao, Y.F. Empirical analysis of aircraft clusters in air traffic situation networks. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 231, 1718–1731. [Google Scholar] [CrossRef]
- Wang, H.Y.; Song, Z.Q.; Wen, R.Y. Modeling air traffic situation complexity with a dynamic weighted network approach. J. Adv. Transp. 2018, 1, 1–15. [Google Scholar] [CrossRef]
- Holme, P.; Saramäki, J. Temporal networks. Phys. Rep. 2012, 519, 97–125. [Google Scholar] [CrossRef]
- Holme, P. Modern temporal network theory: A colloquium. Eur. Phys. J. B 2015, 88, 1–30. [Google Scholar] [CrossRef]
- Rebollo, J.J.; Balakrishnan, H. Characterization and prediction of air traffic delays. Transp. Res. Part C Emerg. Technol. 2014, 44, 231–241. [Google Scholar] [CrossRef]
- Sismanidou, A.; Tarradellas, J.; Suau-Sanchez, P. The uneven geography of us air traffic delays: Quantifying the impact of connecting passengers on delay propagation. J. Transp. Geogr. 2022, 98, 103260. [Google Scholar]
- Balcan, D.; Colizza, V.; Goncalves, B.; Hu, H.; Ramasco, J.J.; Vespignani, A. Multiscale mobility networks and the large scale spreading of infectious diseases. Proc. Natl. Acad. Sci. USA 2009, 106, 21484–21489. [Google Scholar] [CrossRef]
- Balcan, D.; Hu, H.; Goncalves, B.; Bajarid, P.; Poletto, C.; Ramasco, J.J.; Paolotti, D.; Perra, N.; Tizzoni, M.; Broeck, W.V.D.; et al. Seasonal transmission potential and activity peaks of the new influenza A (H1N1): A Monte Carlo Likelihood analysis based on human mobility. BMC Med. 2009, 7, 45. [Google Scholar] [CrossRef]
- Fleurquin, P.; Ramasco, J.J.; Eguiluz, V.M. Systemic delay propagation in the US airport network. Sci. Rep. 2013, 3, 1159. [Google Scholar] [CrossRef]
- Pyrgiotis, N.; Malone, K.M.; Odoni, A. Modelling delay propagation within an airport network. Transp. Res. 2013, 27C, 60–75. [Google Scholar] [CrossRef]
- Li, Q.; Jing, R. Characterization of delay propagation in the air traffic network. J. Air Transp. Manag. 2021, 94, 102075. [Google Scholar] [CrossRef]
- Zanin, M.; Belkoura, S.; Zhu, Y. Network analysis of chinese air transport delay propagation. Chin. J. Aeronaut. 2017, 30, 491–499. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, H.; Wu, F.; Chen, J.; Hansen, M. A Comparative Study on Flight Delay Networks of the USA and China. J. Adv. Transp. 2020, 8, 1–11. [Google Scholar] [CrossRef]
- Li, S.M.; Xie, D.F.; Zhang, X.; Zhang, Z.Y.; Bai, W. Data-Driven Modeling of Systemic Air Traffic Delay Propagation: An Epidemic Model Approach. J. Adv. Transp. 2020, 2020, 1–12. [Google Scholar] [CrossRef]
- Cai, Q.; Alam, S.; Duong, V.N. A Spatial-Temporal Network Perspective for the Propagation Dynamics of Air Traffic Delays. Engineering 2021, 7, 452–464. [Google Scholar] [CrossRef]
- Shao, W.; Prabowo, A.; Zhao, S.; Koniusz, P.; Salim, F.D. Predicting flight delay with spatio-temporal trajectory convolutional network and airport situational awareness map. Neurocomputing 2022, 472, 280–293. [Google Scholar] [CrossRef]
- Jiang, J.L.; Fang, H.; Li, S.Q.; Li, W.M. Identifying important nodes for temporal networks based on the ASAM model. Phys. A: Stat. Mech. Its Appl. 2022, 586, 126455. [Google Scholar] [CrossRef]
- Maulud, D.; Abdulazeez, A.M. A review on linear regression comprehensive in machine learning. J. Appl. Sci. Technol. Trends 2020, 1, 140–147. [Google Scholar] [CrossRef]

| Q1 | Q2 | Q3 | ||||
|---|---|---|---|---|---|---|
| DAY1 | DAY2 | DAY1 | DAY2 | DAY1 | DAY2 | |
| Clustering center of infection rate | 0.6891 | 0.7016 | 0.4312 | 0.428 | 0.4622 | 0.4867 |
| Clustering center of recovery rate | 0.2933 | 0.3042 | 0.1687 | 0.1571 | 0.6901 | 0.7092 |
| Aircraft number | 1231 | 1126 | 2317 | 1926 | 278 | 242 |
| Proportion of aircraft number | 32% | 34% | 61% | 58% | 7% | 8% |
| Model | Influence Factor | Unstandardized Coefficients | Standardized Coefficients | Sig. | |||
|---|---|---|---|---|---|---|---|
| DAY1 | DAY2 | DAY1 | DAY2 | DAY1 | DAY2 | ||
| Infection rate of Q1 | (constant) | 0.731 | 0.730 | 0.000 | 0.000 | ||
| Velocity | 1.96 × 10−6 | 6.62 × 10−6 | 0.002 | 0.008 | 0.964 | 0.877 | |
| Duration | −0.001 | −0.001 | −0.177 | −0.185 | 0.001 | 0.001 | |
| Clustering degree | −9.71 × 10−6 | −9.89 × 10−6 | −0.072 | −0.073 | 0.181 | 0.175 | |
| ci | 0.008 | 0.007 | 0.138 | 0.125 | 0.013 | 0.023 | |
| c | 0.015 | 0.024 | 0.033 | 0.050 | 0.540 | 0.350 | |
| R2 (DAY1) = 0.267 R2 (DAY2) = 0.251 | |||||||
| Model | Influence Factor | Unstandardized Coefficients | Standardized Coefficients | Sig. | |||
|---|---|---|---|---|---|---|---|
| DAY1 | DAY2 | DAY1 | DAY2 | DAY1 | DAY2 | ||
| Recovery rate of Q1 | (constant) | 0.346 | 0.344 | 0.000 | 0.000 | ||
| Velocity | 5.73 × 10−5 | 6.50 × 10−5 | 0.084 | 0.092 | 0.094 | 0.065 | |
| Duration | −0.002 | −0.002 | −0.422 | −0.424 | 0.000 | 0.000 | |
| Clustering degree | −4.21 × 10−7 | −6.70 × 10−7 | −0.004 | −0.006 | 0.942 | 0.911 | |
| ci | 0.006 | 0.005 | 0.116 | 0.088 | 0.023 | 0.041 | |
| c | −0.022 | −0.009 | −0.054 | −0.021 | 0.281 | 0.666 | |
| R2 (DAY1) = 0.282 R2 (DAY2) = 0.293 | |||||||
| Model | Influence Factor | Unstandardized Coefficients | Standardized Coefficients | Sig. | |||
|---|---|---|---|---|---|---|---|
| DAY1 | DAY2 | DAY1 | DAY2 | DAY1 | DAY2 | ||
| Infection rate of Q2 | (constant) | 0.487 | 0.484 | 0.000 | 0.000 | ||
| Velocity | 9.40 × 10−6 | 1.30 × 10−5 | 0.013 | 0.018 | 0.793 | 0.714 | |
| Duration | −0.001 | −0.001 | −0.140 | −0.143 | 0.003 | 0.002 | |
| Clustering degree | −1.90 × 10−5 | −1.86 × 10−5 | −0.241 | −0.235 | 0.000 | 0.000 | |
| ci | 0.002 | 0.002 | 0.041 | 0.038 | 0.386 | 0.412 | |
| c | −0.002 | −0.001 | −0.004 | −0.002 | 0.924 | 0.964 | |
| R2 (DAY1) = 0.277 R2 (DAY2) = 0.285 | |||||||
| Model | Influence Factor | Unstandardized Coefficients | Standardized Coefficients | Sig. | |||
|---|---|---|---|---|---|---|---|
| DAY1 | DAY2 | DAY1 | DAY2 | DAY1 | DAY2 | ||
| Recovery rate of Q2 | (constant) | 0.216 | 0.216 | 0.000 | 0.000 | ||
| Velocity | 1.41 × 10−5 | 1.44 × 10−5 | 0.026 | 0.027 | 0.586 | 0.574 | |
| Duration | −0.001 | −4.97 × 10−4 | −0.131 | −0.127 | 0.004 | 0.006 | |
| Clustering degree | −1.38 × 10−5 | −1.34 × 10−5 | −0.239 | −0.233 | 0.000 | 0.000 | |
| ci | −0.003 | −0.004 | −0.083 | −0.088 | 0.074 | 0.057 | |
| c | −0.013 | −0.014 | −0.038 | −0.041 | 0.401 | 0.361 | |
| R2 (DAY1) = 0.254 R2 (DAY2) = 0.232 | |||||||
| Model | Influence Factor | Unstandardized Coefficients | Standardized Coefficients | Sig. | |||
|---|---|---|---|---|---|---|---|
| DAY1 | DAY2 | DAY1 | DAY2 | DAY1 | DAY2 | ||
| Infection rate of Q3 | (constant) | 1.032 | 1.058 | 0.000 | 0.000 | ||
| Velocity | −1.00 × 10−3 | −0.001 | −0.340 | −0.374 | 0.014 | 0.005 | |
| Duration | −0.002 | −0.002 | −0.147 | −0.125 | 0.328 | 0.364 | |
| Clustering degree | −1.28 × 10−6 | −2.11 × 10−5 | 0.002 | −0.040 | 0.987 | 0.765 | |
| ci | 0.009 | 0.006 | 0.053 | 0.037 | 0.694 | 0.774 | |
| c | 0.043 | 0.079 | 0.046 | 0.086 | 0.714 | 0.464 | |
| R2 (DAY1) = 0.155 R2 (DAY2) = 0.149 | |||||||
| Model | Influence Factor | Unstandardized Coefficients | Standardized Coefficients | Sig. | |||
|---|---|---|---|---|---|---|---|
| DAY1 | DAY2 | DAY1 | DAY2 | DAY1 | DAY2 | ||
| Recovery rate of Q3 | (constant) | 0.746 | 0.786 | 0.000 | 0.000 | ||
| Velocity | −1.93 × 10−5 | −7.41 × 10−5 | −0.021 | −0.085 | 0.878 | 0.532 | |
| Duration | 0.001 | 0.001 | 0.153 | 0.146 | 0.327 | 0.319 | |
| Clustering degree | −2.99 × 10−5 | −3.19 × 10−5 | −0.095 | −0.102 | 0.533 | 0.473 | |
| ci | 0.004 | 0.002 | 0.041 | 0.018 | 0.769 | 0.893 | |
| c | −0.109 | −0.072 | −0.198 | −0.132 | 0.133 | 0.291 | |
| R2 (DAY1) = 0.094 R2 (DAY2) = 0.047 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Xu, P.; Zhong, F. Modeling and Feature Analysis of Air Traffic Complexity Propagation. Sustainability 2022, 14, 11157. https://doi.org/10.3390/su141811157
Wang H, Xu P, Zhong F. Modeling and Feature Analysis of Air Traffic Complexity Propagation. Sustainability. 2022; 14(18):11157. https://doi.org/10.3390/su141811157
Chicago/Turabian StyleWang, Hongyong, Ping Xu, and Fengwei Zhong. 2022. "Modeling and Feature Analysis of Air Traffic Complexity Propagation" Sustainability 14, no. 18: 11157. https://doi.org/10.3390/su141811157
APA StyleWang, H., Xu, P., & Zhong, F. (2022). Modeling and Feature Analysis of Air Traffic Complexity Propagation. Sustainability, 14(18), 11157. https://doi.org/10.3390/su141811157







