A Hybrid Framework for Multivariate Time Series Forecasting of Daily Urban Water Demand Using Attention-Based Convolutional Neural Network and Long Short-Term Memory Network
Abstract
:1. Introduction
- (1)
- We propose a novel attention-based CNN-LSTM hybrid model consisting of multiple deep learning technologies to predict daily urban water demand that is transformed into multivariate time series by the correlation analysis and max-min method.
- (2)
- Deep LSTM networks are used as the building blocks of the encoder-decoder network to capture the historical and future information among multiple time series affecting water demand.
- (3)
- The CNN layers and AM are introduced to improve the performance of the encoder-decoder network for water demand forecasting. The CNN layers can consider the correlation between multivariate time series, while AM highlights important temporal features and ignores irrelevant data points of water demand sequences.
2. Methodology
2.1. Problem Description
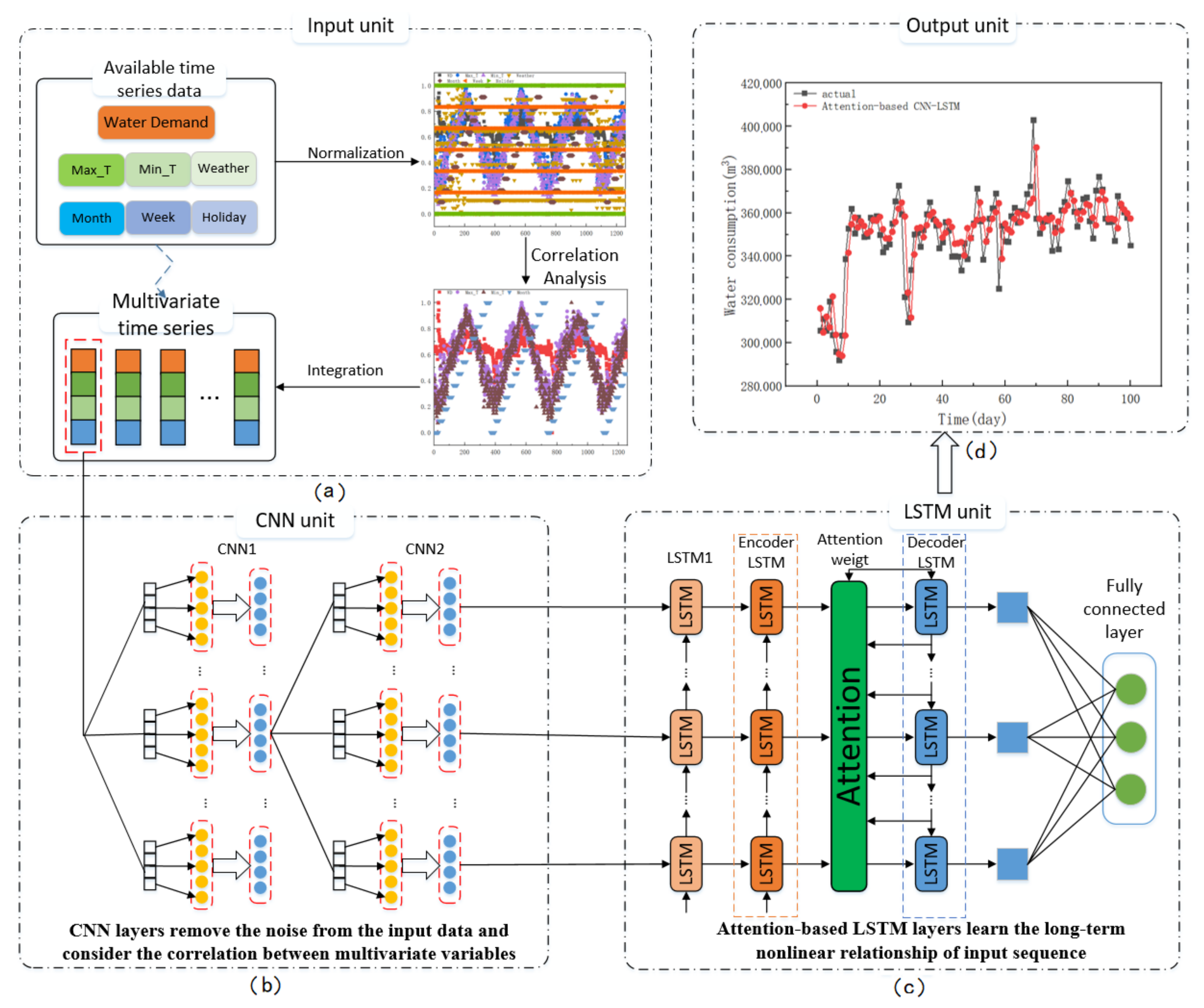
2.2. Forecasting Framework
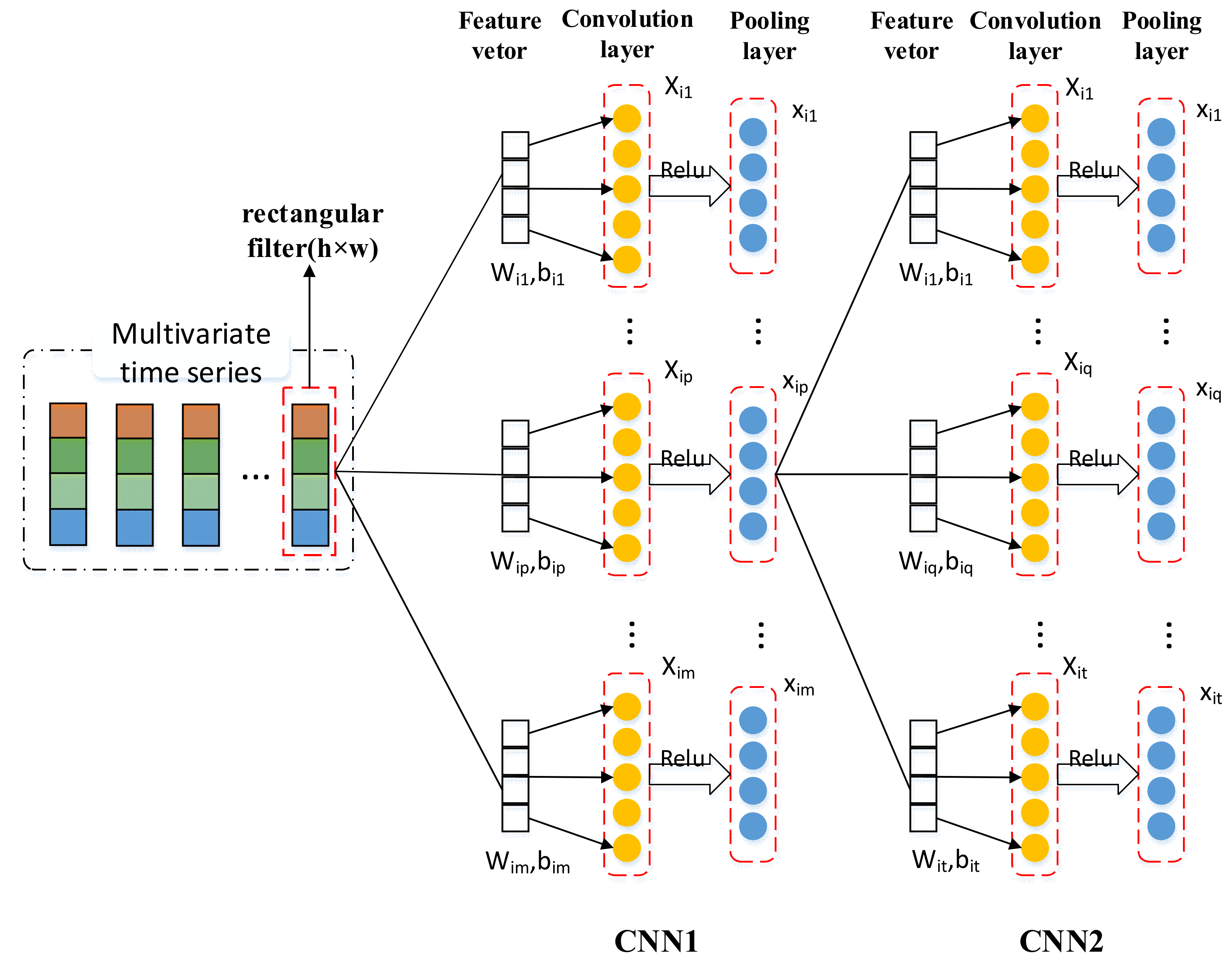
2.3. 1D-CNN as the Multivariable Feature Extraction Module
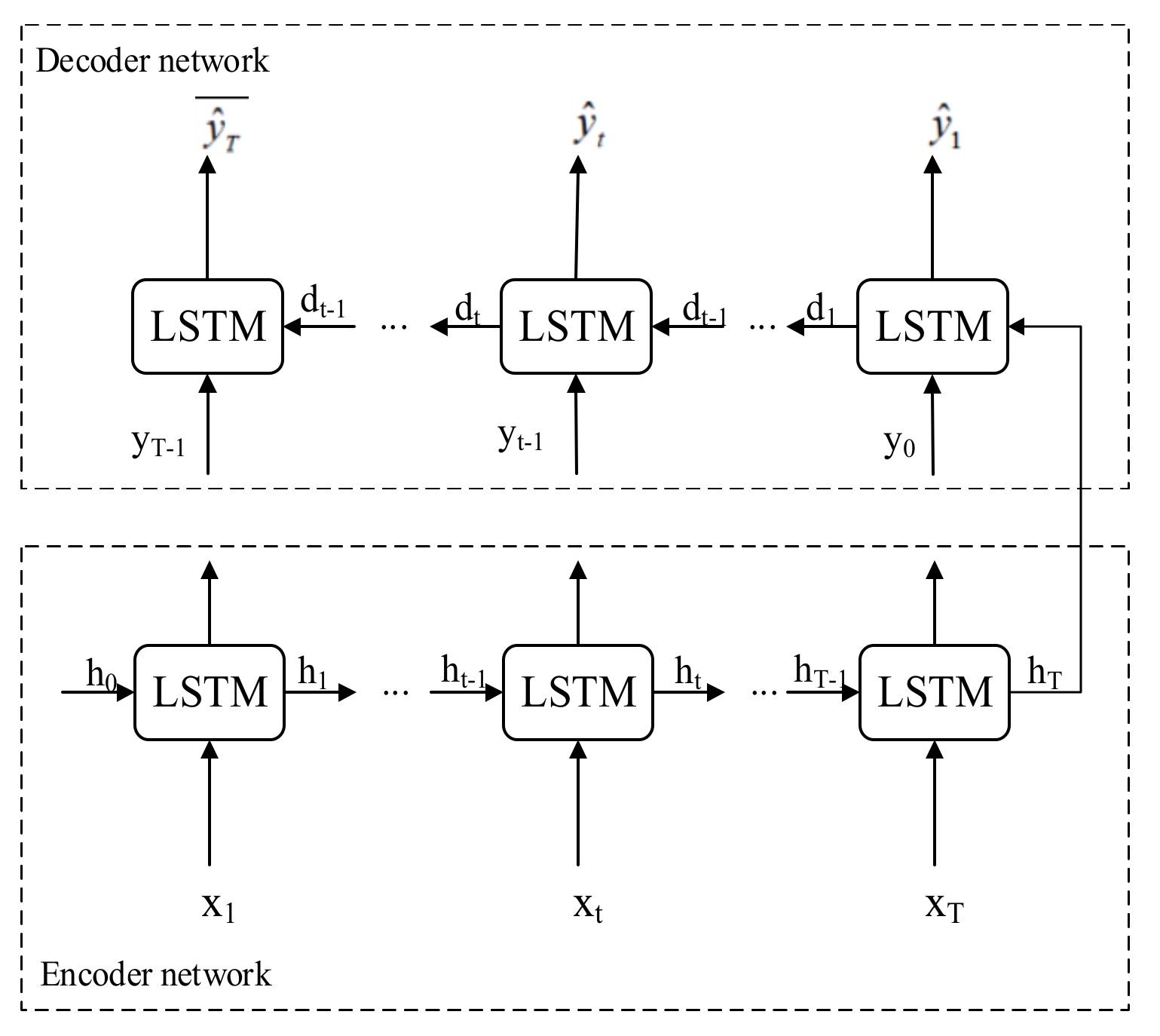
2.4. LSTM as the Temporal Characteristic Extraction Block
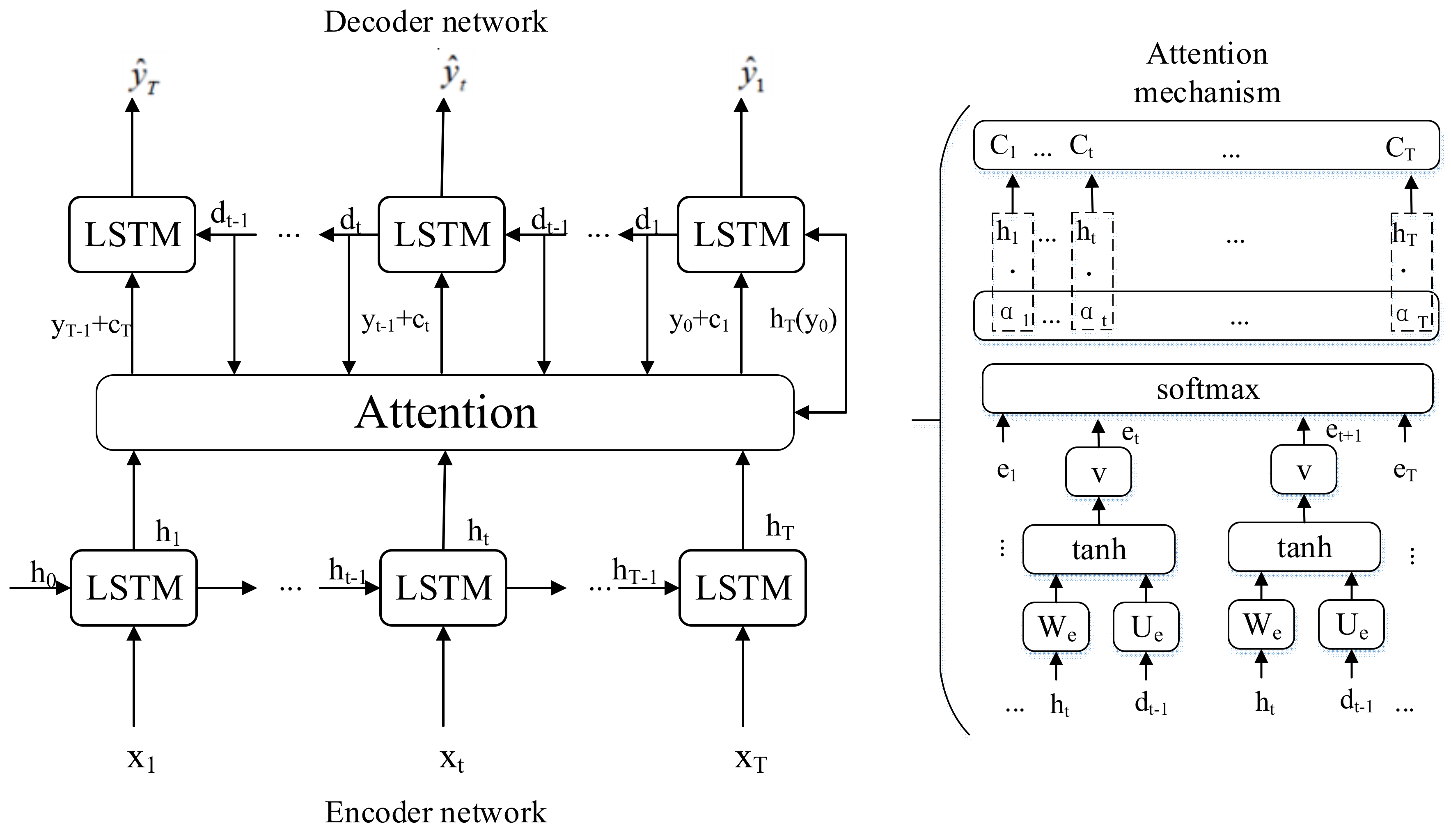
2.5. Attention-Based Encoder-Decoder Network of Feature Learning Module
3. Application Example
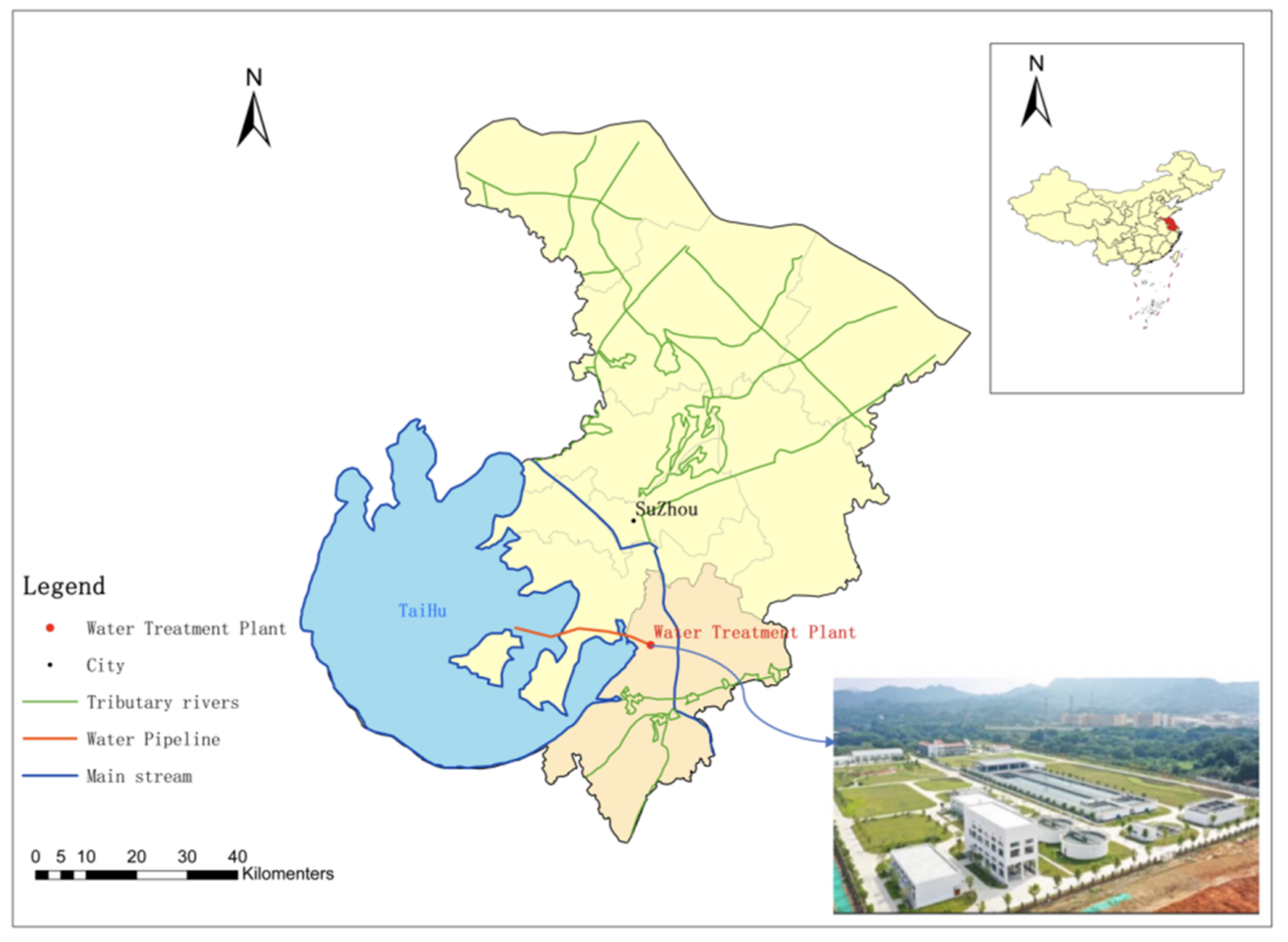
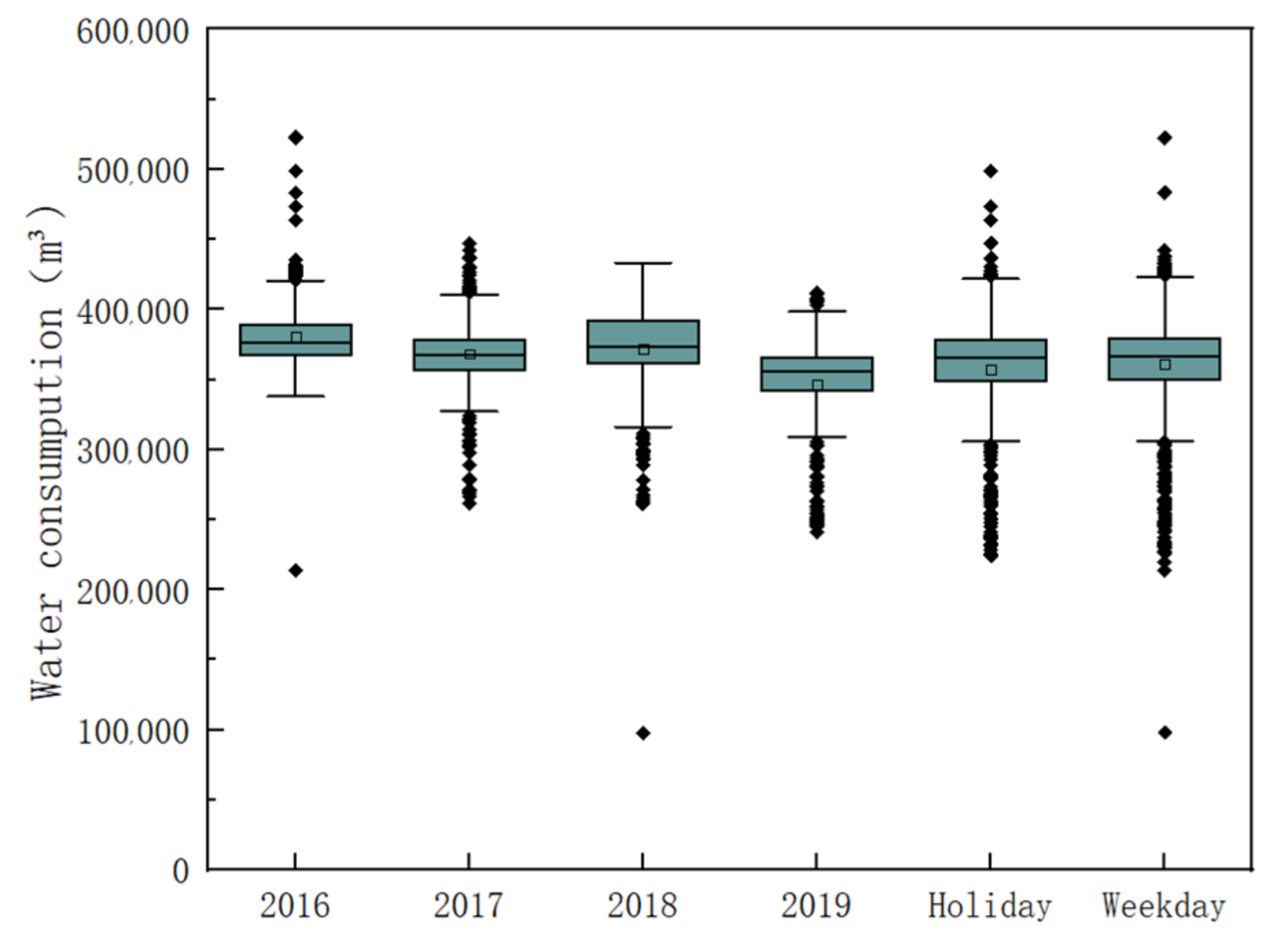
3.1. Data Description
3.2. Preprocessing Techniques
- (1)
- Normalization
- (2)
- Selection of explanatory variables
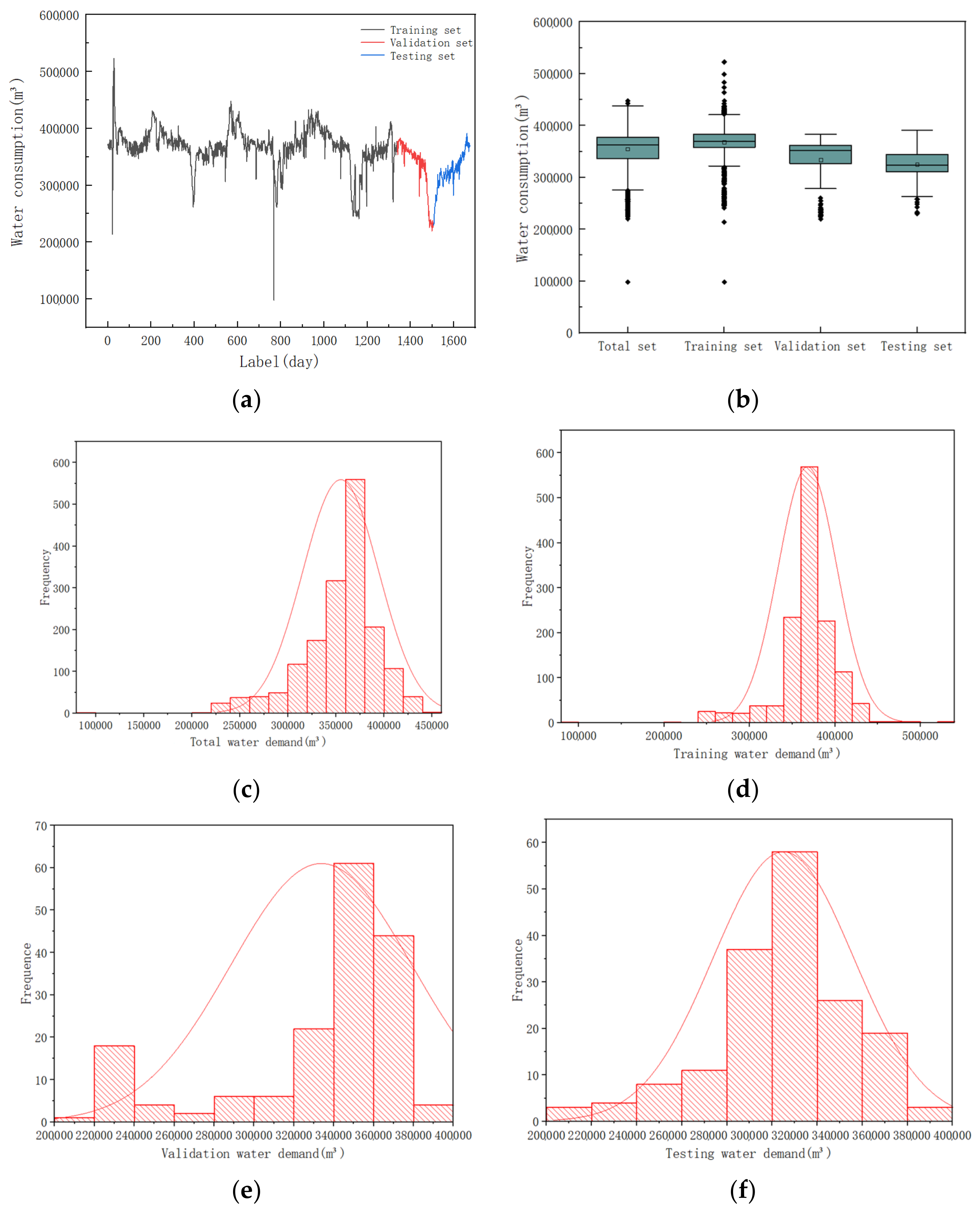
3.3. Experimental Setup
3.4. Evaluate Criterions
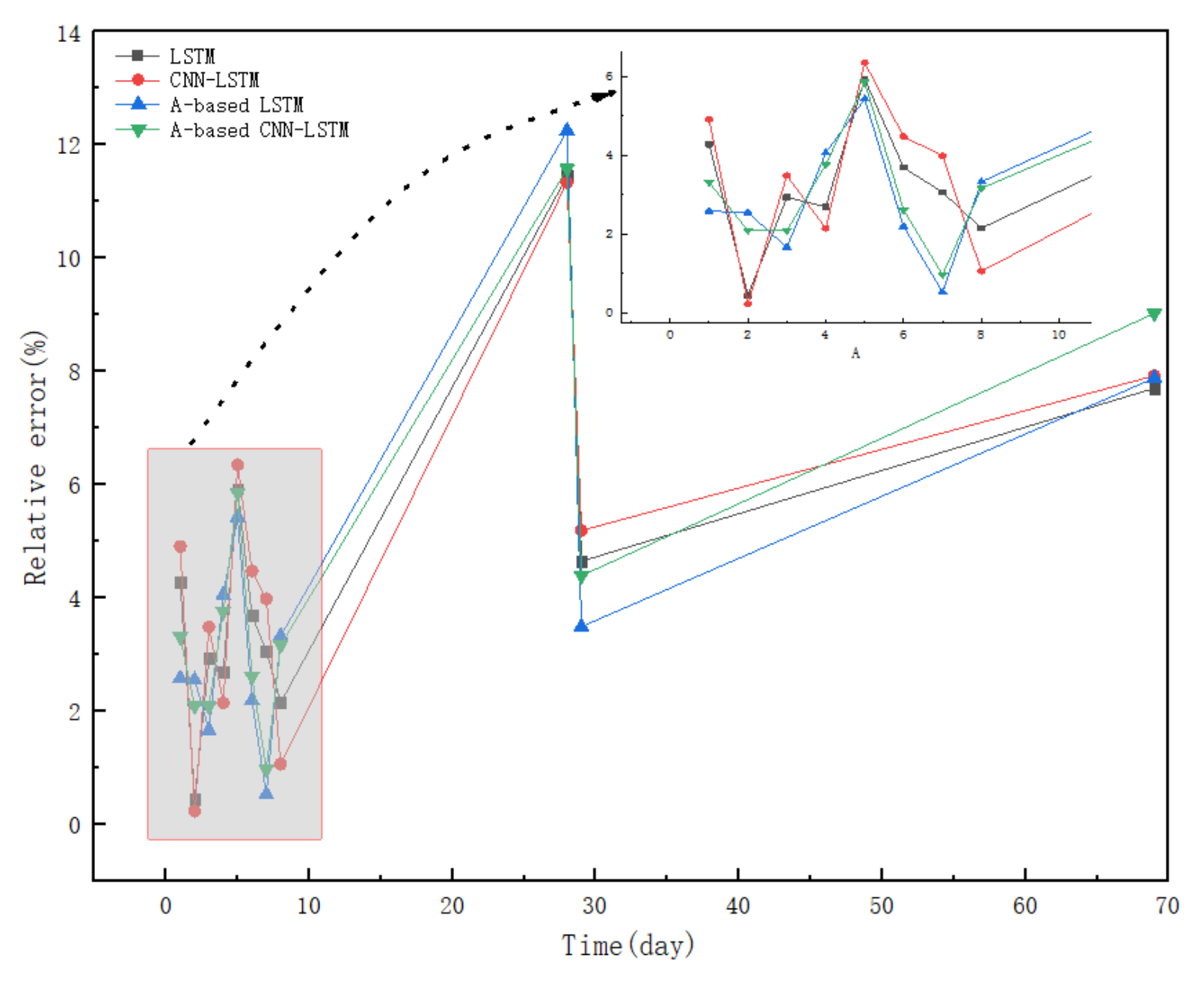
4. Results and Discussions
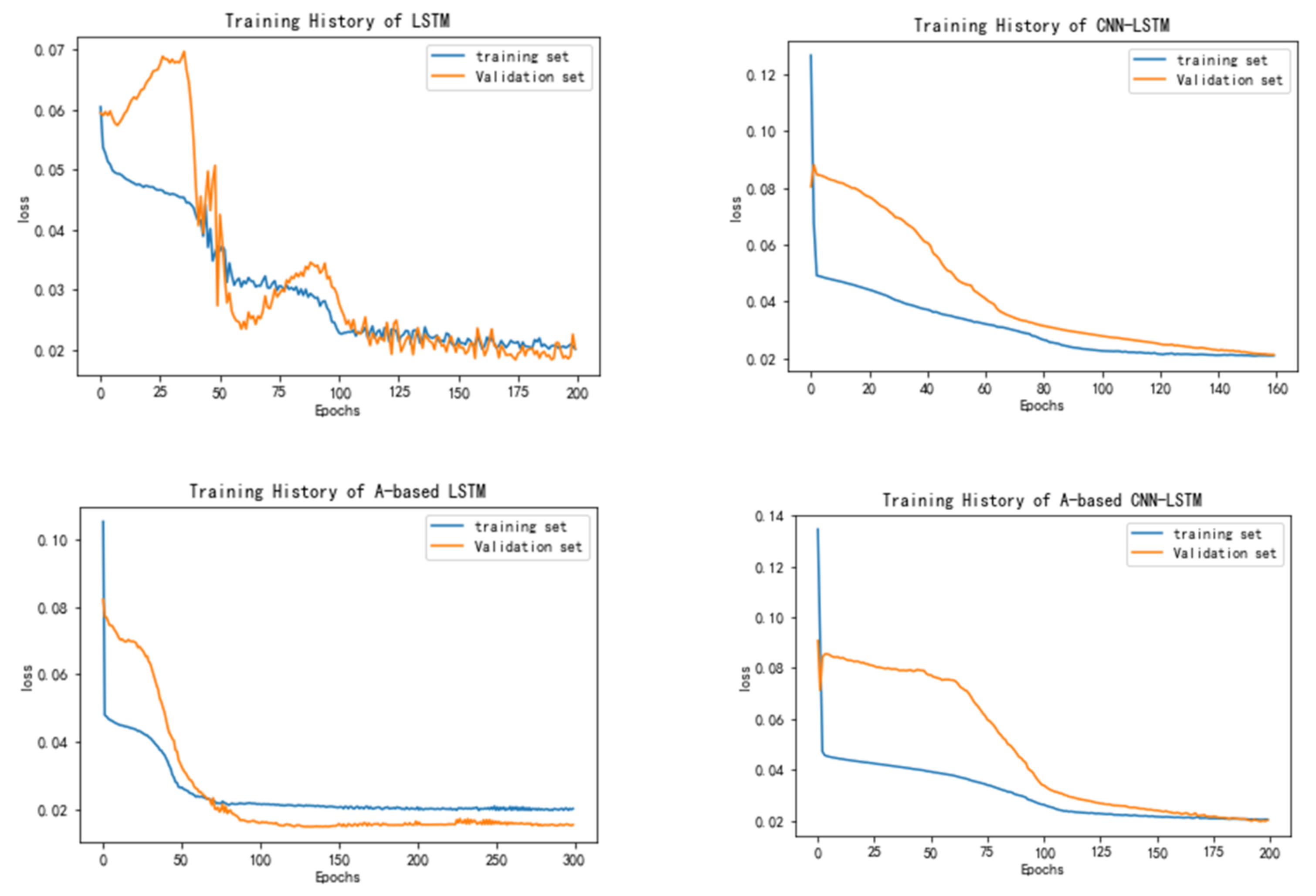
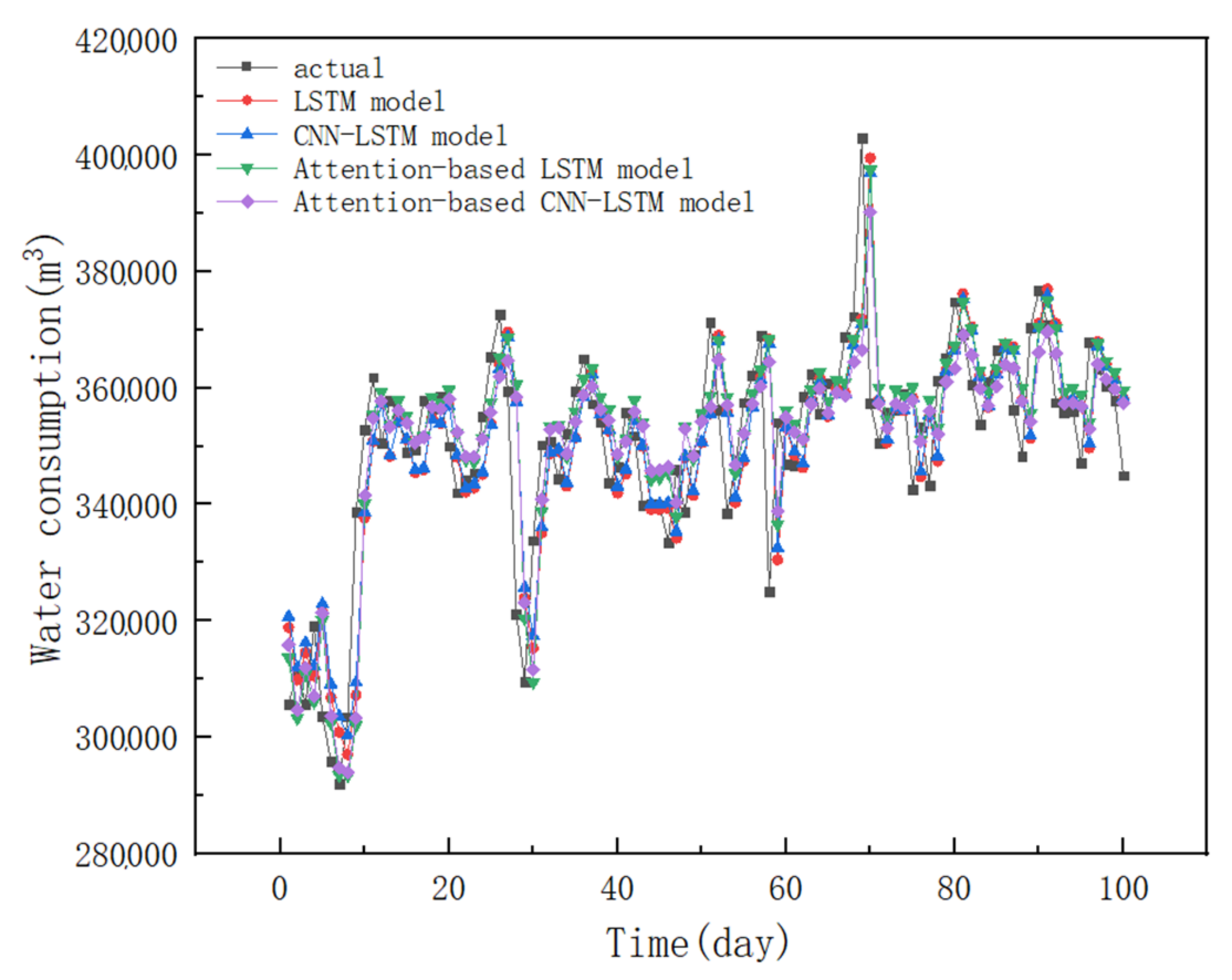
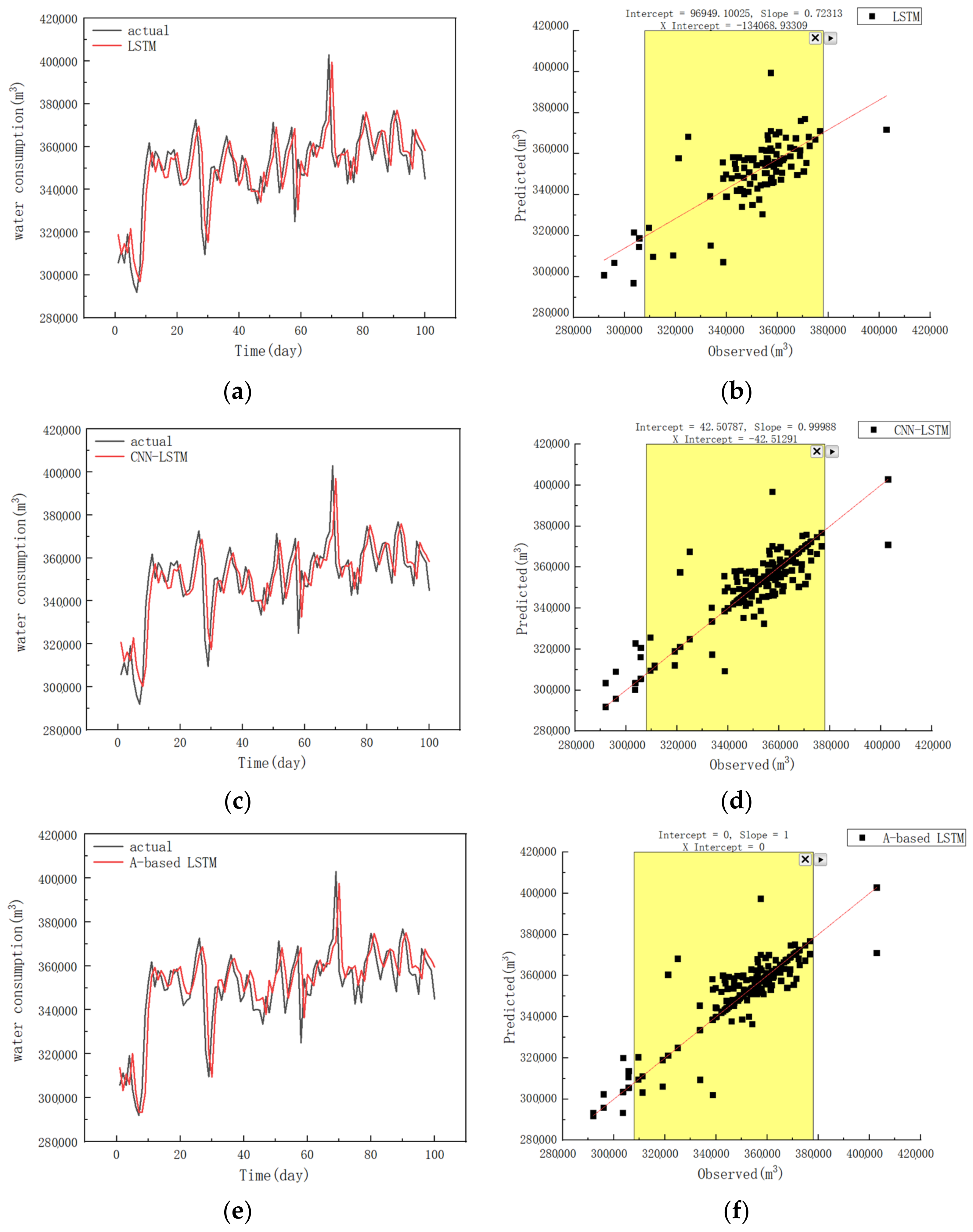
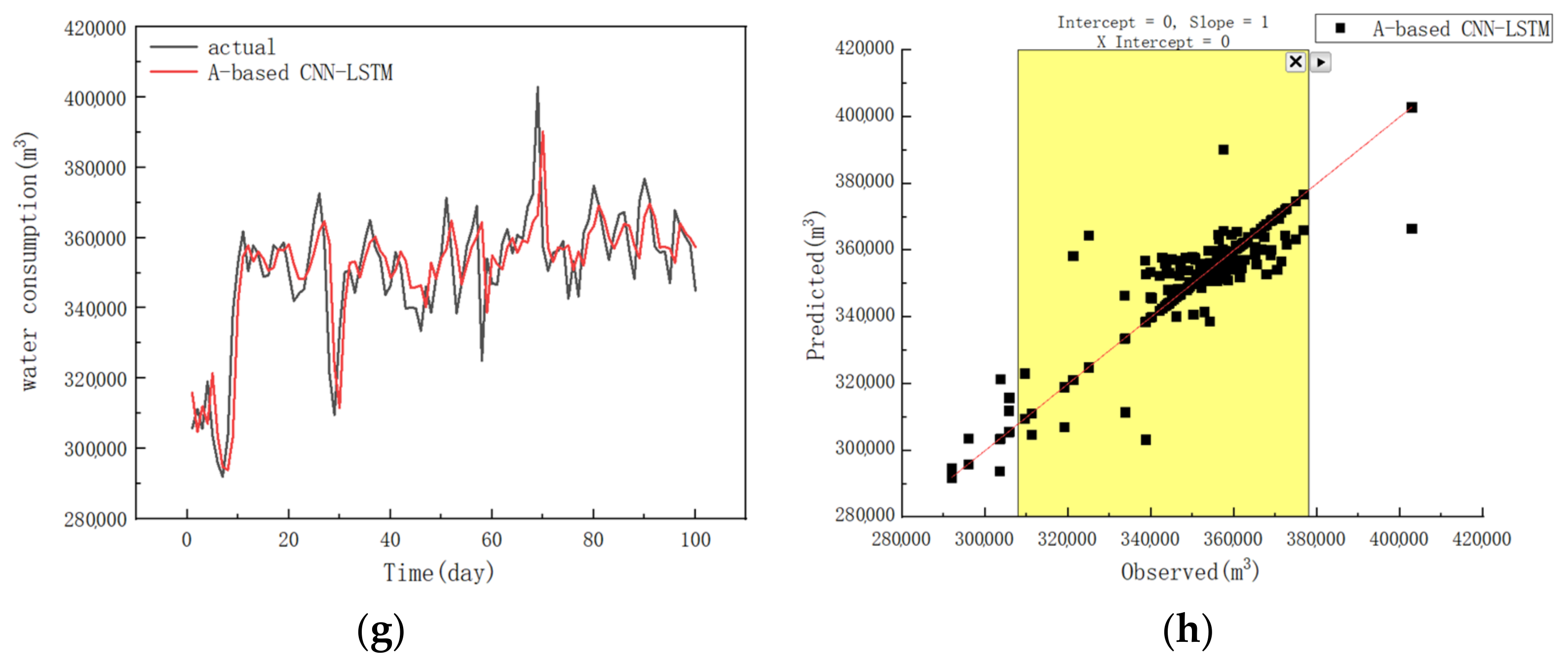
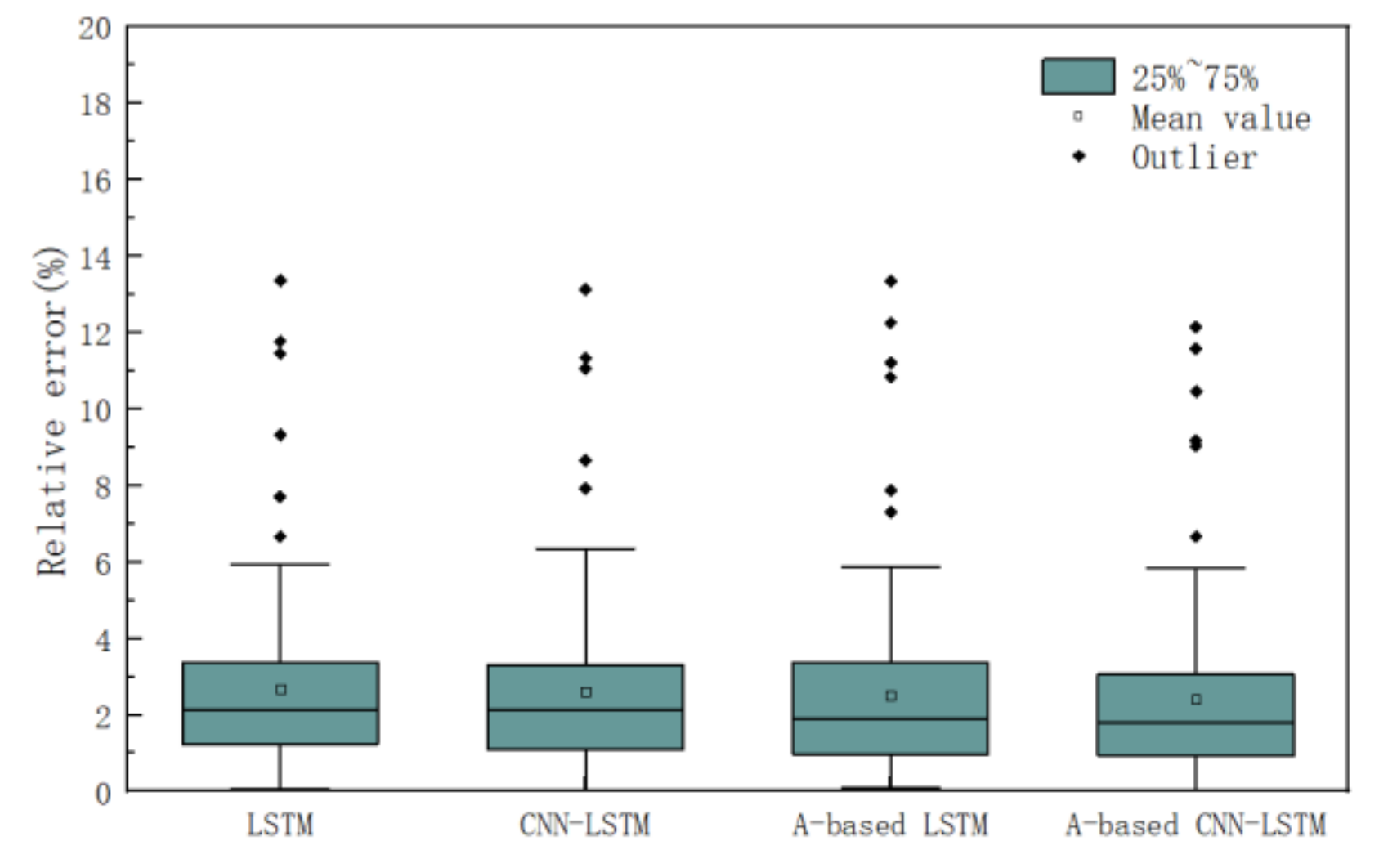
4.1. The Prediction Results of Different Models
4.2. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, W.; Liu, T.; Dai, F.; Xu, P. An improved whale optimization algorithm for forecasting water resources demand. Appl. Soft Comput. 2020, 86, 105925. [Google Scholar] [CrossRef]
- Niva, V.; Cai, J.; Taka, M.; Kummu, M.; Varis, O. China’s sustainable water-energy-food nexus by 2030: Impacts of urbanization on sectoral water demand. J. Clean. Prod. 2020, 251, 119755. [Google Scholar] [CrossRef]
- Niknam, A.; Zare, H.K.; Hosseininasab, H.; Mostafaeipour, A.; Herrera, M. A Critical Review of Short-Term Water Demand Forecasting Tools—What Method Should I Use? Sustainability 2022, 14, 5412. [Google Scholar] [CrossRef]
- Abdalla, G.; Özyurt, F. Sentiment Analysis of Fast Food Companies With Deep Learning Models. Comput. J. 2021, 64, 383–390. [Google Scholar] [CrossRef]
- Yalçıntaş, M.; Bulu, M.; Küçükvar, M.; Samadi, H. A framework for sustainable urban water management through demand and supply forecasting: The case of Istanbul. Sustainability 2015, 7, 11050–11067. [Google Scholar] [CrossRef]
- Haque, M.; Rahman, A.; Hagare, D.; Chowdhury, R.K. A Comparative Assessment of Variable Selection Methods in Urban Water Demand Forecasting. Water 2018, 10, 419. [Google Scholar] [CrossRef]
- Granata, F.; Papirio, S.; Esposito, G.; Gargano, R.; De Marinis, G. Machine Learning Algorithms for the Forecasting of Wastewater Quality Indicators. Water 2017, 9, 105. [Google Scholar] [CrossRef]
- Smolak, K.; Kasieczka, B.; Fialkiewicz, W.; Rohm, W.; Sila-Nowicka, K.; Kopanczyk, K. Applying human mobility and water consumption data for short-term water demand forecasting using classical and machine learning models. Urban Water J. 2020, 17, 32–42. [Google Scholar] [CrossRef]
- Koo, K.-M.; Han, K.-H.; Jun, K.-S.; Lee, G.; Kim, J.-S.; Yum, K.-T. Performance Assessment for Short-Term Water Demand Forecasting Models on Distinctive Water Uses in Korea. Sustainability 2021, 13, 6056. [Google Scholar] [CrossRef]
- Pesantez, J.E.; Berglund, E.Z.; Kaza, N. Smart meters data for modeling and forecasting water demand at the user-level. Environ. Model. Softw. 2020, 125, 104633. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Long, Z.; Lv, M. Daily Urban Water Demand Forecasting Based on Chaotic Theory and Continuous Deep Belief Neural Network. Neural Process. Lett. 2019, 50, 1173–1189. [Google Scholar] [CrossRef]
- Du, B.; Zhou, Q.; Guo, J.; Guo, S.; Wang, L. Deep learning with long short-term memory neural networks combining wavelet transform and principal component analysis for daily urban water demand forecasting. Expert Syst. Appl. 2021, 171, 114571. [Google Scholar] [CrossRef]
- Ebtehaj, I.; Bonakdari, H.; Gharabaghi, B. A reliable linear method for modeling lake level fluctuations. J. Hydrol. 2019, 570, 236–250. [Google Scholar] [CrossRef]
- Shen, Z.P.; Zhang, Y.M.; Lu, J.W.; Xu, J.; Xiao, G. A novel time series forecasting model with deep learning. Neurocomputing 2020, 396, 302–313. [Google Scholar] [CrossRef]
- Abbasimehr, H.; Shabani, M.; Yousefi, M. An optimized model using LSTM network for demand forecasting. Comput. Ind. Eng. 2020, 143, 13. [Google Scholar] [CrossRef]
- Hajiabotorabi, Z.; Kazemi, A.; Samavati, F.F.; Ghaini, F.M.M. Improving DWT-RNN model via B-spline wavelet multiresolution to forecast a high-frequency time series. Expert Syst. Appl. 2019, 138, 9. [Google Scholar] [CrossRef]
- Fekri, M.N.; Patel, H.; Grolinger, K.; Sharma, V. Deep learning for load forecasting with smart meter data: Online Adaptive Recurrent Neural Network. Appl. Energy 2020, 282, 116177. [Google Scholar] [CrossRef]
- Sagheer, A.; Kotb, M. Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing 2019, 323, 203–213. [Google Scholar] [CrossRef]
- Liu, Y. Novel volatility forecasting using deep learning-Long Short Term Memory Recurrent Neural Networks. Expert Syst. Appl. 2019, 132, 99–109. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Yu, Y.; Hu, C.H.; Si, X.S.; Zheng, J.F.; Zhang, J.X. Averaged Bi-LSTM networks for RUL prognostics with non-life-cycle labeled dataset. Neurocomputing 2020, 402, 134–147. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Multi-Sequence LSTM-RNN Deep Learning and Metaheuristics for Electric Load Forecasting. Energies 2020, 13, 391. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. Predictions for COVID-19 with deep learning models of LSTM, GRU and Bi-LSTM. Chaos Solitons Fractals 2020, 140, 110212. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.-Y.; Cho, S.-B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Wang, K.; Li, K.L.; Zhou, L.Q.; Hu, Y.K.; Cheng, Z.Y.; Liu, J.; Chen, C. Multiple convolutional neural networks for multivariate time series prediction. Neurocomputing 2019, 360, 107–119. [Google Scholar] [CrossRef]
- Khaki, S.; Wang, L.; Archontoulis, S.V. A CNN-RNN Framework for Crop Yield Prediction. Front. Plant Sci. 2020, 10, 1750. [Google Scholar] [CrossRef] [PubMed]
- Li, T.Y.; Hua, M.; Wu, X. A Hybrid CNN-LSTM Model for Forecasting Particulate Matter (PM2.5). IEEE Access 2020, 8, 26933–26940. [Google Scholar] [CrossRef]
- Essien, A.; Giannetti, C. A Deep Learning Model for Smart Manufacturing Using Convolutional LSTM Neural Network Autoencoders. IEEE Trans. Industr. Inform. 2020, 16, 6069–6078. [Google Scholar] [CrossRef]
- Taieb, S.B.; Atiya, A.F. A Bias and Variance Analysis for Multistep-Ahead Time Series Forecasting. IEEE Trans. Neural Networks Learn. Syst. 2016, 27, 62–76. [Google Scholar] [CrossRef]
- Xiao, Y.; Yin, H.; Zhang, Y.; Qi, H.; Zhang, Y.; Liu, Z. A dual-stage attention-based Conv-LSTM network for spatio-temporal correlation and multivariate time series prediction. Int. J. Intell. Syst. 2021, 36, 2036–2057. [Google Scholar] [CrossRef]
- Du, S.; Li, T.; Yang, Y.; Horng, S.-J. Multivariate time series forecasting via attention-based encoder-decoder framework. Neurocomputing 2020, 388, 269–279. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, B.; Zhu, Y. Short-Term Traffic Speed Forecasting Based on Attention Convolutional Neural Network for Arterials. Comput. Civ. Infrastruct. Eng. 2018, 33, 999–1016. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, Y.; Feng, J.; Zhang, P.; Cheng, Z. Interpretable spatio-temporal attention LSTM model for flood forecasting. Neurocomputing 2020, 403, 348–359. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, C.; Yang, L.; Chen, Y. DSTP-RNN: A dual-stage two-phase attention-based recurrent neural network for long-term and multivariate time series prediction. Expert Syst. Appl. 2020, 143, 113082. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Wang, S.; Wang, D. Bi-directional long short-term memory method based on attention mechanism and rolling update for short-term load forecasting. Int. J. Electr. Power Energy Syst. 2019, 109, 470–479. [Google Scholar] [CrossRef]
- Li, Y.; Zou, L.; Jiang, L.; Zhou, X. Fault Diagnosis of Rotating Machinery Based on Combination of Deep Belief Network and One-dimensional Convolutional Neural Network. IEEE Access 2019, 7, 165710–165723. [Google Scholar] [CrossRef]
- Fang, X.; Yuan, Z. Performance enhancing techniques for deep learning models in time series forecasting. Eng. Appl. Artif. Intell. 2019, 85, 533–542. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Zhao, B. Real-time reservoir operation using recurrent neural networks and inflow forecast from a distributed hydrological model. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.-C.; Chang, F.-J. Exploring a Long Short-Term Memory based Encoder-Decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Zubaidi, S.L.; Gharghan, S.K.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M. Short-Term Urban Water Demand Prediction Considering Weather Factors. Water Resour. Manag. 2018, 32, 4527–4542. [Google Scholar] [CrossRef]



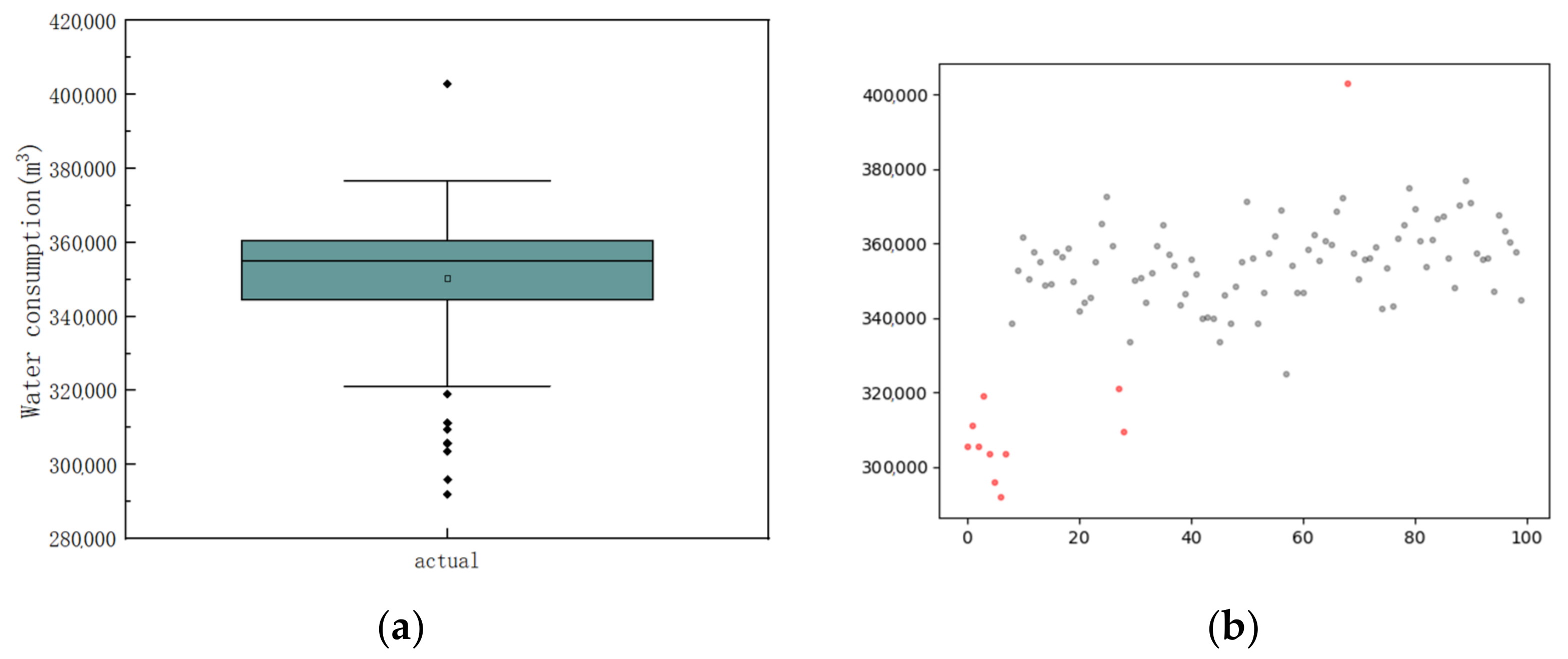

| Historical Data | Feature | Characterization |
|---|---|---|
| Consumption data | L(d − 1), L(d − 2), …, L(d − n) | Historical water demand series in the previous n days |
| Meteorological data | Max-T | Daily maximum temperature |
| Min-T | Daily minimum temperature | |
| W-data | Encode weather with different weather types according to local weather forecast, such as cloudy, rainy, sunny, snowy, windy, foggy days, etc. | |
| Date data | M-label | 1 to 12 represent January to December, respectively |
| W-label | 1 to 7 denote Monday to Sunday, respectively | |
| H-label | 1 label holidays, 0 label work days |
| Consumption | L(d) | L(d − 1) | L(d − 2) | L(d − 3) | L(d − 4) | L(d − 5) | L(d − 6) |
|---|---|---|---|---|---|---|---|
| L(d) | 1 | 0.920 ** | 0.879 ** | 0.857 ** | 0.831 ** | 0.802 ** | 0.782 ** |
| L(d − 1) | 0.920 ** | 1 | 0.920 ** | 0.879 ** | 0.857 ** | 0.831 ** | 0.802 ** |
| L(d − 2) | 0.879 ** | 0.920 ** | 1 | 0.920 ** | 0.879 ** | 0.857 ** | 0.831 ** |
| L(d − 3) | 0.857 ** | 0.879 ** | 0.920 ** | 1 | 0.920 ** | 0.879 ** | 0.857 ** |
| L(d − 4) | 0.831 ** | 0.857 ** | 0.879 ** | 0.920 ** | 1 | 0.920 ** | 0.879 ** |
| L(d − 5) | 0.802 ** | 0.831 ** | 0.857 ** | 0.879 ** | 0.920 ** | 1 | 0.920 ** |
| L(d − 6) | 0.782 ** | 0.802 ** | 0.831 ** | 0.857 ** | 0.879 ** | 0.920 ** | 1 |
| Factors | L | Max-T | Min-T | W-Data | M-label | W-Label | H-Label |
|---|---|---|---|---|---|---|---|
| L | 1.000 | 0.473 ** | 0.444 ** | −0.025 | 0.395 ** | 0.020 | −0.031 |
| Max-T | 0.473 ** | 1.000 | 0.963 ** | 0.007 | 0.335 ** | 0.000 | −0.022 |
| Min-T | 0.444 ** | 0.963 ** | 1.000 | 0.034 | 0.358 ** | −0.005 | −0.024 |
| W-data | −0.025 | 0.007 | 0.034 | 1.000 | −0.007 | 0.016 | 0.013 |
| M-label | 0.395 ** | 0.335 ** | 0.358 ** | −0.007 | 1.000 | 0.003 | −0.026 |
| W-label | 0.020 | 0.000 | −0.005 | 0.016 | 0.003 | 1.000 | 0.686 ** |
| H-label | −0.031 | −0.022 | −0.024 | 0.013 | −0.026 | 0.686 ** | 1.000 |
| Model | Batch Size | Learning Rate | Epochs | Layers | Hidden Layers Size |
|---|---|---|---|---|---|
| LSTM | 20 | 0.002 | 200 | 4 | LSTM (48,16) |
| CNN-LSTM | 20 | 0.001 | 160 | 6 | CNN (6,3), LSTM (24,4) |
| A-based LSTM | 30 | 0.001 | 300 | 7 | LSTM (24,24), AM (24) |
| A-based CNN-LSTM | 30 | 0.001 | 250 | 8 | CNN (6,3), LSTM (24,24,24), AM (24) |
| Models | MAE/m3 | RMSE/m3 | MAPE/% | R2 |
|---|---|---|---|---|
| LSTM | 7528.95 | 10,074.99 | 2.34 | 0.854 |
| CNN-LSTM | 6550.08 | 9131.56 | 2.03 | 0.880 |
| Attention-based LSTM | 6269.18 | 8727.57 | 1.94 | 0.890 |
| Attention-based CNN-LSTM | 5773.90 | 7251.52 | 1.77 | 0.924 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Guo, S.; Du, B.; Huang, S.; Guo, J. A Hybrid Framework for Multivariate Time Series Forecasting of Daily Urban Water Demand Using Attention-Based Convolutional Neural Network and Long Short-Term Memory Network. Sustainability 2022, 14, 11086. https://doi.org/10.3390/su141711086
Zhou S, Guo S, Du B, Huang S, Guo J. A Hybrid Framework for Multivariate Time Series Forecasting of Daily Urban Water Demand Using Attention-Based Convolutional Neural Network and Long Short-Term Memory Network. Sustainability. 2022; 14(17):11086. https://doi.org/10.3390/su141711086
Chicago/Turabian StyleZhou, Shengwen, Shunsheng Guo, Baigang Du, Shuo Huang, and Jun Guo. 2022. "A Hybrid Framework for Multivariate Time Series Forecasting of Daily Urban Water Demand Using Attention-Based Convolutional Neural Network and Long Short-Term Memory Network" Sustainability 14, no. 17: 11086. https://doi.org/10.3390/su141711086
APA StyleZhou, S., Guo, S., Du, B., Huang, S., & Guo, J. (2022). A Hybrid Framework for Multivariate Time Series Forecasting of Daily Urban Water Demand Using Attention-Based Convolutional Neural Network and Long Short-Term Memory Network. Sustainability, 14(17), 11086. https://doi.org/10.3390/su141711086







