Forecasting Photovoltaic Power Generation with a Stacking Ensemble Model
Abstract
:1. Introduction
- An ensemble stacking model (Stack-ETR) was developed that can be utilized as a baseline model for one-day-ahead PV power output forecasts, utilizing metrological data without heavy hyperparameter tuning.
- A performance evaluation of the proposed Stack-ETR was conducted on three different actual Malaysian PV systems over four years (2018 to 2021).
- In addition, the proposed model was compared with existing models and works to highlight the superiority of the proposed model.
2. Methodology
2.1. The Machine Learning Models
2.1.1. Bagging Ensemble Model
Random Forest Regressor (RFR)
Extra Trees Regressor (ETR)
2.1.2. Boosting Ensemble Model
Extreme Gradient Boosting (XGBoost)
Adaptive Boosting (AdaBoost)
2.1.3. Stack Generalization
| Model Name | Base Learners | Meta-Learner |
|---|---|---|
| Stack-RFR | ETR, XGBoost, AdaBoost | RFR |
| Stack-ETR | RFR, XGBoost, AdaBoost | ETR |
| Stack-XGBoost | RFR, ETR, AdaBoost | XGBoost |
| Stack-AdaBoost | RFR, ETR, XGBoost | AdaBoost |

2.2. Performance Metrics Utilized to Assess the Model’s Effectiveness
2.3. Data Preparation and Partitioning
2.4. A Summary of the Grid-Connected PV Systems Utilized for Forecasting
3. Results and Discussions
3.1. Evaluation of Stack-ETR for Forecasting Thin-Film PV System Output Power
3.2. Evaluation of Stack-ETR for Forecasting Monocrystalline PV System Output Power
3.3. Evaluation of Stack-ETR for Forecasting Polycrystalline PV System Output Power
3.4. Discussion
3.5. Comparative Studies
4. Conclusions
- For all investigated PV systems, the proposed Stack-ETR model consistently outperformed earlier models in varied climates, showing that the proposed model is superior and acceptable. Consequently, extending the model’s predictions to other regions is simple.
- Due to its efficacy in forecasting daily PV output power, Stack-ETR could potentially be applied to other studies, such as global horizontal irradiance, electricity consumption, and wind speed and power.
- A real-time evaluation of the proposed model’s performance and practical applicability to building energy management systems would also be interesting.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | |
| PV | Photovoltaic |
| RFR | Random Forest Regressor |
| XGBoost | Extreme Gradient Boosting |
| AdaBoost | Adaptive Boosting |
| ETR | Extra Trees Regressor |
| TF | Thin-Film |
| MC | Monocrystalline |
| PC | Polycrystalline |
| CO2 | Carbon Dioxide |
| ML | Machine learning |
| AR | Auto-Regression |
| ARMA | Auto-Regressive Moving Average |
| ARMAX | Autoregressive Moving Average with Exogenous Variable |
| LR | Linear Regression |
| RF | Random Forest |
| GBRT | Gradient Boosting Regression Trees |
| RNN | Recurrent Neural Network |
| ANN | Artificial Neural Network |
| PEARL | Power Electronics and Renewable Energy Research Laboratory |
| LSTM | Long Short-Term Memory |
| DT | Decision Trees |
| DTR | Decision Trees Regression |
| OOB | Out-of-Bag |
| CART | Classification and Regression Trees |
| ELM | Extreme Learning Machine |
| RMSE | Root Mean Square Error |
| MSE | Mean Square Error |
| R2 | Coefficient of Determination |
| MAE | Mean Absolute Error |
| SEDA | Sustainable Energy Development Authority |
| Nomenclature | |
| Actual Values | |
| Forecasted Values | |
| Average of the Actual | |
| The Collected Data | |
| The Normalized Collected Data | |
| μ | The Mean Value |
| σ | Standard Deviation |
| H | Dataset’s Size |
| Value of Each Datapoint in the Dataset | |
| Actual Data Forecasted | |
References
- Yu, J.; Tang, Y.M.; Chau, K.Y.; Nazar, R.; Ali, S.; Iqbal, W. Role of solar-based renewable energy in mitigating CO2 emissions: Evidence from quantile-on-quantile estimation. Renew. Energy 2022, 182, 216–226. [Google Scholar] [CrossRef]
- Kanwal, S.; Mehran, M.T.; Hassan, M.; Anwar, M.; Naqvi, S.R.; Khoja, A.H. An integrated future approach for the energy security of Pakistan: Replacement of fossil fuels with syngas for better environment and socio-economic development. Renew. Sustain. Energy Rev. 2022, 156, 111978. [Google Scholar] [CrossRef]
- Zahoor, Z.; Khan, I.; Hou, F. Clean energy investment and financial development as determinants of environment and sustainable economic growth: Evidence from China. Environ. Sci. Pollut. Res. 2022, 29, 16006–16016. [Google Scholar] [CrossRef] [PubMed]
- Couto, A.; Estanqueiro, A. Assessment of wind and solar PV local complementarity for the hybridization of the wind power plants installed in Portugal. J. Clean. Prod. 2021, 319, 128728. [Google Scholar] [CrossRef]
- Mlilo, N.; Brown, J.; Ahfock, T. Impact of intermittent renewable energy generation penetration on the power system networks–A review. Technol. Econ. Smart Grids Sustain. Energy 2021, 6, 25. [Google Scholar] [CrossRef]
- Zandrazavi, S.F.; Guzman, C.P.; Pozos, A.T.; Quiros-Tortos, J.; Franco, J.F. Stochastic multi-objective optimal energy management of grid-connected unbalanced microgrids with renewable energy generation and plug-in electric vehicles. Energy 2022, 241, 122884. [Google Scholar] [CrossRef]
- Zhu, Y.; Xu, X.; Yan, Z.; Lu, J. Data acquisition, power forecasting and coordinated dispatch of power systems with distributed PV power generation. Electr. J. 2022, 35, 107133. [Google Scholar] [CrossRef]
- Mubarak, H.; Muhammad, M.A.; Mansor, N.N.; Mokhlis, H.; Ahmad, S.; Ahmed, T.; Sufyan, M. Operational Cost Minimization of Electrical Distribution Network during Switching for Sustainable Operation. Sustainability 2022, 14, 4196. [Google Scholar] [CrossRef]
- Mubarak, H.; Mansor, N.N.; Mokhlis, H.; Mohamad, M.; Mohamad, H.; Muhammad, M.A.; Al Samman, M.; Afzal, S. Optimum Distribution System Expansion Planning Incorporating DG Based on N-1 Criterion for Sustainable System. Sustainability 2021, 13, 6708. [Google Scholar] [CrossRef]
- Mubarak, H.; Mokhlis, H.; Mansor, N.N.; Mohamad, M.; Khairuddin, A.S.M.; Afzal, S. Optimal Distribution Networks Expansion Planning with DG for Power Losses Reduction. In Proceedings of the 2021 Innovations in Power and Advanced Computing Technologies (i-PACT), Kuala Lumpur, Malaysia, 27–29 November 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Zhang, Z.; Mishra, Y.; Yue, D.; Dou, C.; Zhang, B.; Tian, Y.-C. Delay-tolerant predictive power compensation control for photovoltaic voltage regulation. IEEE Trans. Ind. Inform. 2021, 17, 4545–4554. [Google Scholar] [CrossRef]
- Zhang, Z.; Dou, C.; Yue, D.; Zhang, B. Predictive voltage hierarchical controller design for islanded microgrids under limited communication. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 933–945. [Google Scholar] [CrossRef]
- Samu, R.; Calais, M.; Shafiullah, G.M.; Moghbel, M.; Shoeb, M.A.; Nouri, B.; Blum, N. Applications for solar irradiance nowcasting in the control of microgrids: A review. Renew. Sustain. Energy Rev. 2021, 147, 111187. [Google Scholar] [CrossRef]
- Dimd, D.; Völler, S.; Cali, U.; Midtgård, O.-M. A Review of Machine Learning-Based photovoltaic Output Power Forecasting: Nordic Context. IEEE Access 2022, 10, 26404–26425. [Google Scholar] [CrossRef]
- Chu, Y.; Urquhart, B.; Gohari, S.M.; Pedro, H.T.; Kleissl, J.; Coimbra, C.F. Short-term reforecasting of power output from a 48 MWe solar PV plant. Sol. Energy 2015, 112, 68–77. [Google Scholar] [CrossRef]
- Li, Y.; Su, Y.; Shu, L. An ARMAX model for forecasting the power output of a grid connected photovoltaic system. Renew. Energy 2014, 66, 78–89. [Google Scholar] [CrossRef]
- Bessa, R.J.; Trindade, A.; Silva, C.S.; Miranda, V. Probabilistic solar power forecasting in smart grids using distributed information. Int. J. Electr. Power Energy Syst. 2015, 72, 16–23. [Google Scholar] [CrossRef]
- Koster, D.; Minette, F.; Braun, C.; O’Nagy, O. Short-term and regionalized photovoltaic power forecasting, enhanced by reference systems, on the example of Luxembourg. Renew. Energy 2019, 132, 455–470. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Ahmed, R.; Sreeram, V.; Mishra, Y.; Arif, M. A review and evaluation of the state-of-the-art in PV solar power forecasting: Techniques and optimization. Renew. Sustain. Energy Rev. 2020, 124, 109792. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, H.; Yan, B. A review on renewable energy and electricity requirement forecasting models for smart grid and buildings. Sustain. Cities Soc. 2020, 55, 102052. [Google Scholar] [CrossRef]
- Demolli, H.; Dokuz, A.S.; Ecemis, A.; Gokcek, M. Wind power forecasting based on daily wind speed data using machine learning algorithms. Energy Convers. Manag. 2019, 198, 111823. [Google Scholar] [CrossRef]
- Persson, C.; Bacher, P.; Shiga, T.; Madsen, H. Multi-site solar power forecasting using gradient boosted regression trees. Sol. Energy 2017, 150, 423–436. [Google Scholar] [CrossRef]
- Wang, J.; Li, P.; Ran, R.; Che, Y.; Zhou, Y. A short-term photovoltaic power prediction model based on the gradient boost decision tree. Appl. Sci. 2018, 8, 689. [Google Scholar] [CrossRef]
- Guo, X.; Gao, Y.; Zheng, D.; Ning, Y.; Zhao, Q. Study on short-term photovoltaic power prediction model based on the Stacking ensemble learning. Energy Rep. 2020, 6, 1424–1431. [Google Scholar] [CrossRef]
- Munawar, U.; Wang, Z. A framework of using machine learning approaches for short-term solar power forecasting. J. Electr. Eng. Technol. 2020, 15, 561–569. [Google Scholar] [CrossRef]
- Liu, D.; Sun, K. Random forest solar power forecast based on classification optimization. Energy 2019, 187, 115940. [Google Scholar] [CrossRef]
- Niu, D.; Wang, K.; Sun, L.; Wu, J.; Xu, X. Short-term photovoltaic power generation forecasting based on random forest feature selection and CEEMD: A case study. Appl. Soft Comput. 2020, 93, 106389. [Google Scholar] [CrossRef]
- Zhang, H.; Zhu, T. Stacking Model for Photovoltaic-Power-Generation Prediction. Sustainability 2022, 14, 5669. [Google Scholar] [CrossRef]
- Lateko, A.A.; Yang, H.-T.; Huang, C.-M.; Aprillia, H.; Hsu, C.-Y.; Zhong, J.-L.; Phương, N.H. Stacking Ensemble Method with the RNN Meta-Learner for Short-Term PV Power Forecasting. Energies 2021, 14, 4733. [Google Scholar] [CrossRef]
- Abdel-Nasser, M.; Mahmoud, K. Accurate photovoltaic power forecasting models using deep LSTM-RNN. Neural Comput. Appl. 2019, 31, 2727–2740. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Extreme gradient boosting and deep neural network based ensemble learning approach to forecast hourly solar irradiance. J. Clean. Prod. 2021, 279, 123285. [Google Scholar] [CrossRef]
- Akhter, M.N.; Mekhilef, S.; Mokhlis, H.; Almohaimeed, Z.M.; Muhammad, M.A.; Khairuddin, A.S.M.; Akram, R.; Hussain, M.M. An Hour-Ahead PV Power Forecasting Method Based on an RNN-LSTM Model for Three Different PV Plants. Energies 2022, 15, 2243. [Google Scholar] [CrossRef]
- Hossain, M.; Mekhilef, S.; Danesh, M.; Olatomiwa, L.; Shamshirband, S. Application of extreme learning machine for short term output power forecasting of three grid-connected PV systems. J. Clean. Prod. 2017, 167, 395–405. [Google Scholar] [CrossRef]
- Zhang, J.; Verschae, R.; Nobuhara, S.; Lalonde, J.-F. Deep photovoltaic nowcasting. Sol. Energy 2018, 176, 267–276. [Google Scholar] [CrossRef]
- Zjavka, L. PV power intra-day predictions using PDE models of polynomial networks based on operational calculus. IET Renew. Power Gener. 2020, 14, 1405–1412. [Google Scholar] [CrossRef]
- Khan, W.; Walker, S.; Zeiler, W. Improved solar photovoltaic energy generation forecast using deep learning-based ensemble stacking approach. Energy 2022, 240, 122812. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Reynolds, J.; Rezgui, Y. Predictive modelling for solar thermal energy systems: A comparison of support vector regression, random forest, extra trees and regression trees. J. Clean. Prod. 2018, 203, 810–821. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Barrow, D.K.; Crone, S.F. A comparison of AdaBoost algorithms for time series forecast combination. Int. J. Forecast. 2016, 32, 1103–1119. [Google Scholar] [CrossRef]
- Kim, S.-G.; Jung, J.-Y.; Sim, M.K. A two-step approach to solar power generation prediction based on weather data using machine learning. Sustainability 2019, 11, 1501. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Breiman, L. Stacked regressions. Mach. Learn. 1996, 24, 49–64. [Google Scholar] [CrossRef]
- SEDA Malaysia. SEDA Malaysia Grid-Connected PV System Course Design; SEDA Malaysia: Putrajaya, Malaysia, 2016. [Google Scholar]
- Anang, N.; Azman, S.S.N.; Muda, W.; Dagang, A.; Daud, M.Z. Performance analysis of a grid-connected rooftop solar PV system in Kuala Terengganu, Malaysia. Energy Build. 2021, 248, 111182. [Google Scholar] [CrossRef]
- Farhoodnea, M.; Mohamed, A.; Khatib, T.; Elmenreich, W. Performance evaluation and characterization of a 3-kWp grid-connected photovoltaic system based on tropical field experimental results: New results and comparative study. Renew. Sustain. Energy Rev. 2015, 42, 1047–1054. [Google Scholar] [CrossRef]
- Saadatian, O.; Sopian, K.; Elhab, B.; Ruslan, M.; Asim, N. Optimal solar panels’ tilt angles and orientations in Kuala Lumpur, Malaysia. In Proceedings of the 1st WSEAS International Conference on Energy and Environment Technologies and Equipment (EEETE’ 12), Zlin, Czech Republic, 20–22 September 2012. [Google Scholar]
- Ahmed, T.; Mekhilef, S.; Shah, R.; Mithulananthan, N. An assessment of the solar photovoltaic generation yield in Malaysia using satellite derived datasets. Int. Energy J. 2019, 19, 61–76. [Google Scholar]
- Zhen, Z.; Liu, J.; Zhang, Z.; Wang, F.; Chai, H.; Yu, Y.; Lu, X.; Wang, T.; Lin, Y. Deep learning based surface irradiance mapping model for solar PV power forecasting using sky image. IEEE Trans. Ind. Appl. 2020, 56, 3385–3396. [Google Scholar] [CrossRef]









| Ref | Model | Input Variables | Horizon | PV Module | Dataset Duration | Target | ||
|---|---|---|---|---|---|---|---|---|
| MC | PC | TF | ||||||
| [29] | Stacking-GBDT | Light intensity, wind speed and direction, weather temperature, PV module temperature, transfer efficiency | Ultra-short-term (5 min ahead) | Not mentioned | 4 years | PV power output | ||
| [32] | XGBoost-DNN | Temperature, pressure, wind speed and direction, relative humidity, month number, clear sky index, time | Short-term (1 h ahead) | Not included | 10 years | Solar irradiance | ||
| [33] | RNN-LSTM | Time, solar irradiance, wind speed, ambient temperature, PV module temperature, actual output power | Short-term (1 h ahead) | ✓ | ✓ | ✓ | 4 years | PV power output |
| [34] | ELM | Solar irradiance, wind speed, ambient temperature, PV module temperature, actual output power | Short-term (1 day ahead and 1 h ahead) | ✓ | ✓ | ✓ | 1 year | PV power output |
| [31] | LSTM-RNN | Actual output power | Short-term (1 h ahead) | Not mentioned | 1 year | PV power output | ||
| [35] | LSTM | Actual output power and sky images | Ultra-short-term (1, 2, 5, 10 min ahead) | Not mentioned | Not mentioned | PV power output | ||
| [36] | DPNN | Temperature, wind speed and direction, relative humidity, sky condition, time, solar irradiance, sea level pressure | Short-term (1-9 h ahead) | ✓ | ✕ | ✕ | 2 weeks | PV power output |
| [37] | DSE-XGB | Hour, day, month, previous day, same-time historical PV generation, previous 15 min, previous hour, solar irradiance, relative humidity, temperature | Ultra-short and short-term (15 min and 1 h ahead) | ✓ | ✕ | ✕ | 3 years | PV power output |
| Proposed Research | Stacking-ETR | Time, solar irradiance, wind speed, ambient temperature, PV module temperature, actual output power | Short-term (1 day ahead) | ✓ | ✓ | ✓ | 4 years | PV power output |
| Model | Thin-Film | |||
|---|---|---|---|---|
| MSE (Wh/m2) | RMSE (Wh/m2) | MAE (Wh/m2) | R2 | |
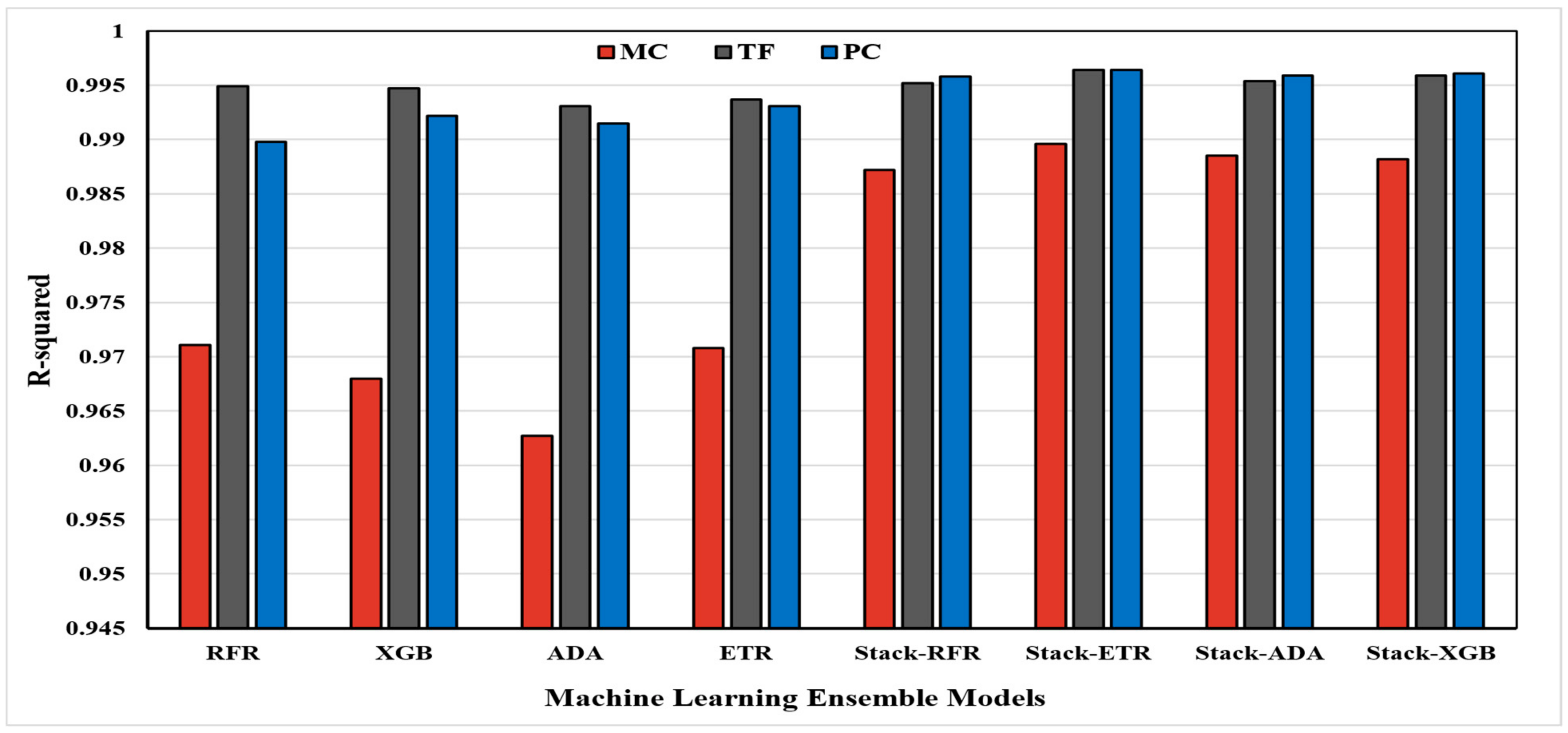
| RFR | 1967.3 | 44.35 | 33.26 | 0.9949 |
| XGB | 2013.01 | 44.87 | 33.64 | 0.9947 |
| DTR | 3038.29 | 55.12 | 41.01 | 0.9921 |
| ADA | 2622.19 | 51.21 | 38.33 | 0.9931 |
| ETR | 2395.43 | 48.94 | 36.38 | 0.9937 |
| Stack-RFR | 1826.15 | 42.73 | 31.63 | 0.9952 |
| Stack-ETR | 1365.16 | 36.95 | 25.87 | 0.9964 |
| Stack-ADA | 1755.79 | 41.9 | 30.88 | 0.9954 |
| Stack-XGB | 1575.48 | 39.69 | 28.8 | 0.9959 |
| Model | Monocrystalline | |||
|---|---|---|---|---|
| MSE (Wh/m2) | RMSE (Wh/m2) | MAE (Wh/m2) | R2 | |
| RFR | 939.12 | 30.65 | 23.68 | 0.9711 |
| XGB | 1038.73 | 32.23 | 25.09 | 0.968 |
| DTR | 1933.63 | 43.97 | 33.04 | 0.9405 |
| ADA | 1213.94 | 34.84 | 30.1 | 0.9627 |
| ETR | 950.04 | 30.82 | 24.93 | 0.9708 |
| Stack-RFR | 414.43 | 20.36 | 14.38 | 0.9872 |
| Stack-ETR | 339.6 | 18.43 | 13.16 | 0.9896 |
| Stack-ADA | 375.01 | 19.37 | 13.74 | 0.9885 |
| Stack-XGB | 383.74 | 19.59 | 13.91 | 0.9882 |
| Model | Polycrystalline | |||
|---|---|---|---|---|
| MSE (Wh/m2) | RSME (Wh/m2) | MAE (Wh/m2) | R2 | |
| RFR | 1518.1 | 38.96 | 27.57 | 0.9898 |
| XGB | 1163.5 | 34.11 | 23.37 | 0.9922 |
| DTR | 1340.41 | 36.61 | 27.85 | 0.991 |
| ADA | 1261.89 | 35.52 | 27.05 | 0.9915 |
| ETR | 1027.2 | 32.05 | 24.53 | 0.9931 |
| Stack-RFR | 619.92 | 24.9 | 17.39 | 0.9958 |
| Stack-ETR | 533.33 | 23.09 | 14.5 | 0.9964 |
| Stack-ADA | 604.05 | 24.58 | 16.76 | 0.9959 |
| Stack-XGB | 574.4 | 23.97 | 15.8 | 0.9961 |
| Predicting Method | Year | Ref. | RMSE (Wh/m2) | MAE (Wh/m2) |
|---|---|---|---|---|
| Stack-ETR (TF) | - | Present Study | 37.37 | 23.36 |
| Stack-ETR (MC) | 13.95 | 8.79 | ||
| Stack-ETR (PC) | 20.41 | 12.24 | ||
| Stack-GBDT | 2022 | [29] | 47.7826 | 106.0726 |
| RNN-LSTM (TF) | 2022 | [33] | 39.2 | - |
| RNN-LSTM (MC) | 19.78 | - | ||
| RNN-LSTM (PC) | 26.85 | - | ||
| XGBoost-DNN | 2021 | [32] | 51.35 | - |
| DPNN | 2020 | [36] | 52.8 | - |
| Kmeans-AE-CNN-LSTM | 2020 | [52] | 45.11 | - |
| LSTM-RNN | 2019 | [31] | 82.15 | - |
| LSTM | 2018 | [35] | 139.3 | - |
| ELM (TF) | 2018 | [34] | 90.41 | - |
| ELM (MC) | 59.93 | - | ||
| ELM (PC) | 54.96 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdellatif, A.; Mubarak, H.; Ahmad, S.; Ahmed, T.; Shafiullah, G.M.; Hammoudeh, A.; Abdellatef, H.; Rahman, M.M.; Gheni, H.M. Forecasting Photovoltaic Power Generation with a Stacking Ensemble Model. Sustainability 2022, 14, 11083. https://doi.org/10.3390/su141711083
Abdellatif A, Mubarak H, Ahmad S, Ahmed T, Shafiullah GM, Hammoudeh A, Abdellatef H, Rahman MM, Gheni HM. Forecasting Photovoltaic Power Generation with a Stacking Ensemble Model. Sustainability. 2022; 14(17):11083. https://doi.org/10.3390/su141711083
Chicago/Turabian StyleAbdellatif, Abdallah, Hamza Mubarak, Shameem Ahmad, Tofael Ahmed, G. M. Shafiullah, Ahmad Hammoudeh, Hamdan Abdellatef, M. M. Rahman, and Hassan Muwafaq Gheni. 2022. "Forecasting Photovoltaic Power Generation with a Stacking Ensemble Model" Sustainability 14, no. 17: 11083. https://doi.org/10.3390/su141711083
APA StyleAbdellatif, A., Mubarak, H., Ahmad, S., Ahmed, T., Shafiullah, G. M., Hammoudeh, A., Abdellatef, H., Rahman, M. M., & Gheni, H. M. (2022). Forecasting Photovoltaic Power Generation with a Stacking Ensemble Model. Sustainability, 14(17), 11083. https://doi.org/10.3390/su141711083









