Evaluation of Urban Green Building Design Schemes to Achieve Sustainability Based on the Projection Pursuit Model Optimized by the Atomic Orbital Search
Abstract
:1. Introduction
2. Related Research
3. The Evaluation Index System of Green Building Design Schemes
3.1. Analysis of the Evaluation Factors
3.2. Evaluation Index System
3.3. Definition and Data Acquisition Methods of Secondary Indicators
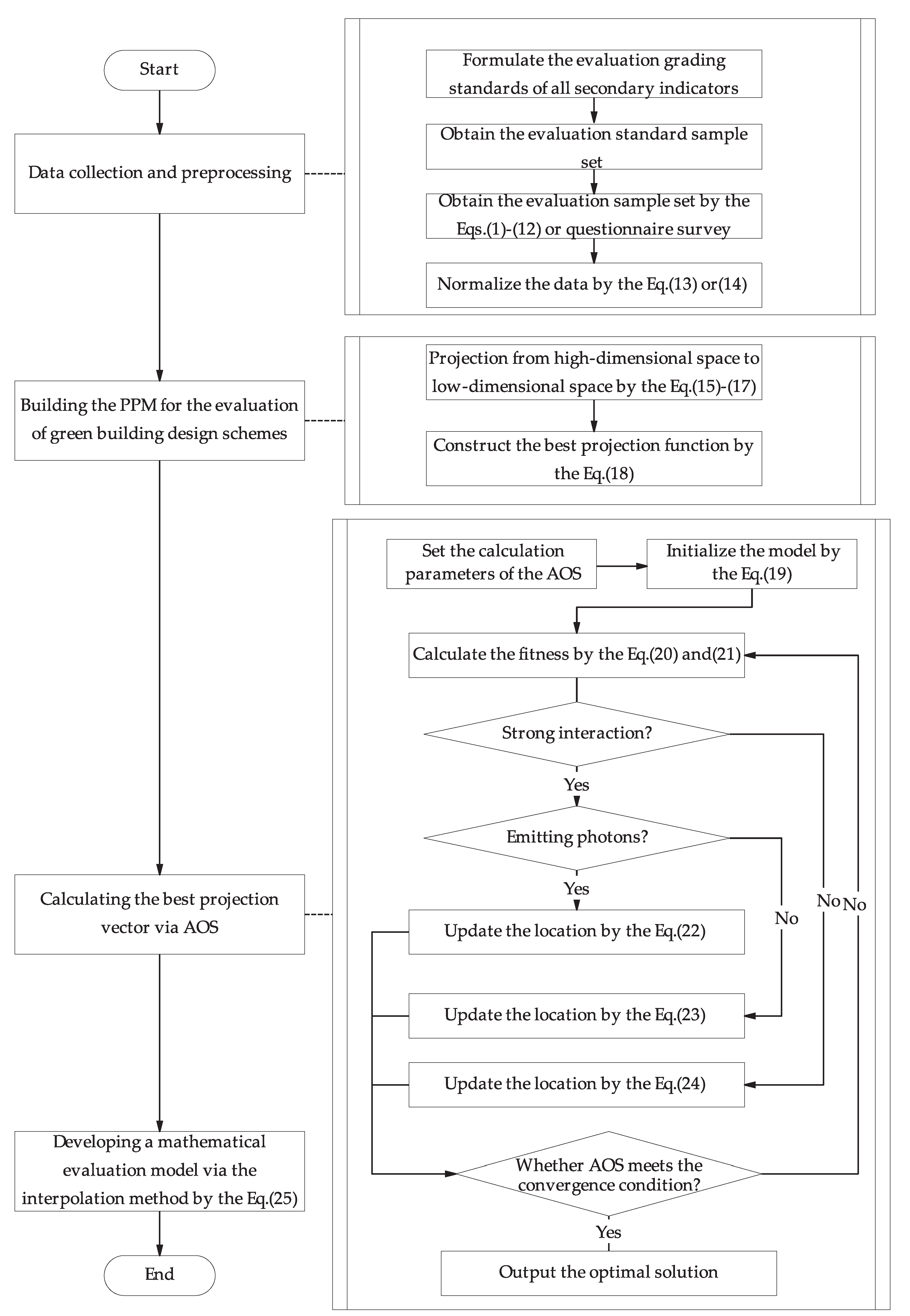
4. The Proposed Evaluation Model of Green Building Design Schemes
4.1. Data Collection and Preprocessing
4.2. Building the PPM for the Evaluation of Green Building Design Schemes
4.3. Title
4.4. Developing a Mathematical Evaluation Model via the Interpolation Method
4.5. The Implementation of the Proposed Model
5. Case Study
5.1. Engineering Background
5.2. Data Collection and Preprocessing
5.3. Building the PPM for the Evaluation of Green Building Design Schemes
5.4. Developing a Mathematical Evaluation Model via the Interpolation Method
6. Discussion
6.1. Computational Performance of Different Optimization Algorithms
6.2. Computational Performance of Different Evaluation Methods
6.3. Impact of the Evaluation Index System on the Evaluation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, W.; Li, W.; Xu, S.; Wang, W.; An, X. Time, Cost, and Energy Consumption Analysis on Construction Optimization in High-Rise Buildings. J. Constr. Eng. Manag. 2021, 147, 04021128. [Google Scholar] [CrossRef]
- Jiang, T.; Li, S.; Yu, Y.; Peng, Y. Energy-related carbon emissions and structural emissions reduction of China’s construction industry: Tthe perspective of input-output analysis. Environ. Sci. Pollut. Res. 2022, 29, 39515–39527. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Sui, Y.; Zhao, J. Research on sustainable development of green building. J. Environ. Prot. Ecol. 2020, 21, 561–570. [Google Scholar]
- Chen, L.; Chan, A.P.; Darko, A.; Gao, X. Spatial-temporal investigation of green building promotion efficiency: The case of China. J. Clean. Prod. 2022, 362, 132299. [Google Scholar] [CrossRef]
- Qian, Q.K.; Chan, E.H.W.; Visscher, H.; Lehmann, S. Modeling the green building (GB) investment decisions of developers and end-users with transaction costs (TCs) considerations. J. Clean. Prod. 2015, 109, 315–325. [Google Scholar] [CrossRef]
- Chen, X.; Yang, H.X.; Wang, T. Developing a robust assessment system for the passive design approach in the green building rating scheme of Hong Kong. J. Clean. Prod. 2017, 153, 176–194. [Google Scholar] [CrossRef]
- Bo, L.; Cheng, S.; Li, D. Establishment and application of fuzzy comprehensive evaluation of green building design based on data mining. J. Intell. Fuzzy Syst. 2020, 38, 6815–6823. [Google Scholar] [CrossRef]
- Chen, X.; Yang, H.; Lu, L. A comprehensive review on passive design approaches in green building rating tools. Renew. Sustain. Energy Rev. 2015, 50, 1425–1436. [Google Scholar] [CrossRef]
- Xu, S.; Sun, Y. Research on Evaluation of Green Smart Building Based on Improved AHP-FCE Method. Comput. Intell. Neurosci. 2021, 2021, 5485671. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Zhou, J.; Qiao, Y.; Zhang, Y.; Liu, D.; Zhu, H. BIM-VE-Based Optimization of Green Building Envelope from the Perspective of both Energy Saving and Life Cycle Cost. Sustainability 2020, 12, 7862. [Google Scholar] [CrossRef]
- Li, M.; Xu, K.; Huang, S. Evaluation of green and sustainable building project based on extension matter-element theory in smart city application. Comput. Intell. 2020, 12286, 1–19. [Google Scholar] [CrossRef]
- Celikbilek, Y.; Tuysuz, F. An in-depth review of theory of the TOPSIS method: An experimental analysis. J. Manag. Anal. 2020, 7, 281–300. [Google Scholar] [CrossRef]
- Kuo, C.F.J.; Lin, C.H.; Hsu, M.-W.; Li, M.-H. Evaluation of of intelligent green building policies in Taiwan-Using fuzzy analytic hierarchical process and fuzzy transformation matrix. Energy Build. 2017, 139, 146–159. [Google Scholar] [CrossRef]
- Zhang, X.L.; Yu, Y.; He, W.T.; Chen, Y. Bidding Decision-Support Model for Construction Projects Based on Projection Pursuit Learning Method. J. Constr. Eng. Manag. 2021, 147, 04021054. [Google Scholar] [CrossRef]
- Yu, X.; Xie, J.C.; Jiang, R.G.; Zuo, G.G.; Liang, J. Assessment of water resource carrying capacity based on the chicken swarm optimization-projection pursuit model. Arab. J. Geosci. 2020, 13, 39. [Google Scholar] [CrossRef]
- Wu, H.; Wang, J.W. Assessment of Waterlogging Risk in the Deep Foundation Pit Projects Based on Projection Pursuit Model. Adv. Civ. Eng. 2020, 2020, 2569531. [Google Scholar] [CrossRef]
- Lan, Z.G.; Huang, M. Safety assessment for seawall based on constrained maximum entropy projection pursuit model. Nat. Hazards 2018, 91, 1165–1178. [Google Scholar] [CrossRef]
- Azizi, M. Atomic orbital search: A novel metaheuristic algorithm. Appl. Math. Model. 2021, 93, 657–683. [Google Scholar] [CrossRef]
- Meng, C.; Wang, Q.; Li, B.; Guo, C.; Zhao, N. Development and Application of Evaluation Index System and Model for Existing Building Green-Retrofitting. J. Therm. Sci. 2019, 28, 1252–1261. [Google Scholar] [CrossRef]
- Omar, M.S.; Quinn, M.M.; Buchholz, B.; Geiser, K. Are green building features safe for preventive maintenance workers? Examining the evidence. Am. J. Ind. Med. 2013, 56, 410–423. [Google Scholar] [CrossRef]
- Akomea-Frimpong, I.; Kukah, A.S.; Jin, X.H.; Osei-Kyei, R.; Pariafsai, F. Green finance for green buildings: A systematic review and conceptual foundation. J. Clean. Prod. 2022, 356, 131869. [Google Scholar] [CrossRef]
- Huang, M.; Wang, B. Evaluating Green Performance of Building Products Based on Gray Relational Analysis and Analytic Hierarchy Process. Environ. Prog. Sustain. Energy 2014, 33, 1389–1395. [Google Scholar] [CrossRef]
- Shao, Q.G.; Liou, J.J.H.; Weng, S.S.; Chuang, Y.C. Improving the Green Building Evaluation System in China Based on the DANP Method. Sustainability 2018, 10, 1173. [Google Scholar] [CrossRef]
- Celadyn, M. Integrative Design Classes for Environmental Sustainability of Interior Architectural Design. Sustainability 2020, 12, 7383. [Google Scholar] [CrossRef]
- Wu, Z.; Ma, G. Incremental cost-benefit quantitative assessment of green building: A case study in China. Energy Build. 2022, 269, 112251. [Google Scholar] [CrossRef]
- Huo, X.; Yu, A.T.W.; Wu, Z. A comparative analysis of site planning and design among green building rating tools. J. Clean. Prod. 2017, 47, 352–359. [Google Scholar] [CrossRef]
- Mirkatouli, J.; Samadi, R. An analysis on the role of urban land market in spatial development of cities: A case study of mashhad, iran. Int. J. Strateg. Prop. Manag. 2017, 21, 371–383. [Google Scholar] [CrossRef]
- Saharkhiz, M.A.; Pradhan, B.; Rizeei, H.M.; Jung, H.-S. Land Use Feature Extraction and Sprawl Development Prediction from Quickbird Satellite Imagery Using Dempster-Shafer and Land Transformation Model. Korean J. Remote Sens. 2020, 36, 15–27. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Lin, M.-D.; Tsai, K.-T.; Deng, M.-J.; Ishii, H. Multi-objective optimization design of green building envelopes and air conditioning systems for energy conservation and CO2 emission reduction. Sustain. Cities Soc. 2021, 64, 102555. [Google Scholar] [CrossRef]
- Niu, R.; Fan, Y.; Geng, L. Adaptability of a temperature and humidity independent control air- conditioning system in green office buildings. J. Build. Eng. 2021, 42, 102432. [Google Scholar] [CrossRef]
- Spacek, A.D.; Neto, J.M.; Bilessimo, L.D.; Ando Junior, O.H.; De Freitas Neto, G.P.; Giansella, R.D.S.; Ferreira De Santana, M.V.; Malfatti, C.D.F. Proposal for an Experimental Methodology for Evaluation of Natural Lighting Systems Applied in Buildings. Energies 2017, 10, 1014. [Google Scholar] [CrossRef] [Green Version]
- He, Q.; Zhang, C.; Chai, H.-X.; Fan, M.-Y. Orthogonal experiment on reclaimed water treatment and economic optimization model in green building. J. Cent. South Univ. Technol. 2009, 16, 322–328. [Google Scholar] [CrossRef]
- Wang, H.-C.; Cui, D.; Han, J.-L.; Cheng, H.-Y.; Liu, W.-Z.; Peng, Y.-Z.; Chen, Z.-B.; Wang, A.-J. A(2)O-MBR as an efficient and profitable unconventional water treatment and reuse technology: A practical study in a green building residential community. Resour. Conserv. Recycl. 2019, 150, 104418. [Google Scholar] [CrossRef]
- Stratigea, D.; Makropoulos, C. Balancing water demand reduction and rainfall runoff minimisation: Modelling green roofs, rainwater harvesting and greywater reuse systems. Water Sci. -Technol.-Water Supply 2015, 15, 248–255. [Google Scholar] [CrossRef]
- Chang, Y.-H.; Huang, P.-H.; Chuang, T.-F.; Chang, S.-W. A pilot study of the color performance of recycling green building materials. J. Build. Eng. 2016, 7, 114–120. [Google Scholar] [CrossRef]
- Ottele, M.; Perini, K. Comparative experimental approach to investigate the thermal behaviour of vertical greened facades of buildings. Ecol. Eng. 2017, 108, 152–161. [Google Scholar] [CrossRef]
- Ibrahim, M.I.M. Estimating the sustainability returns of recycling construction waste from building projects. Sustain. Cities Soc. 2016, 23, 78–93. [Google Scholar] [CrossRef]
- Vilventhan, A.; Ram, V.G.; Sugumaran, S. Value stream mapping for identification and assessment of material waste in construction: A case study. Waste Manag. Res. 2019, 37, 815–825. [Google Scholar] [CrossRef]
- Yu, A.T.W.; Wong, I.; Wu, Z.; Poon, C.-S. Strategies for Effective Waste Reduction and Management of Building Construction Projects in Highly Urbanized Cities-A Case Study of Hong Kong. Buildings 2021, 11, 214. [Google Scholar] [CrossRef]
- Guo, H.-f.; Ge, J.; Yue, M.; Zhou, X.; Jin, W. Landscape design method for a green community based on green building design theory. J. Zhejiang-Univ.-Sci. 2010, 11, 691–700. [Google Scholar] [CrossRef]
- Wu, I.C.; Chang, S. Visual Req calculation tool for green building evaluation in Taiwan. Autom. Constr. 2013, 35, 608–617. [Google Scholar] [CrossRef]
- Hassouneh, K.; Al-Salaymeh, A.; Qoussous, J. Energy audit, an approach to apply the concept of green building for a building in Jordan. Sustain. Cities Soc. 2015, 14, 456–462. [Google Scholar] [CrossRef]
- Li, C.; Tang, H. Evaluation on year-round performance of double-circulation waterflow window. Renew. Energy 2020, 150, 176–190. [Google Scholar] [CrossRef]
- Azkorra, Z.; Perez, G.; Coma, J.; Cabeza, L.F.; Bures, S.; Alvaro, J.E.; Erkoreka, A.; Urrestarazu, M. Evaluation of green walls as a passive acoustic insulation system for buildings. Appl. Acoust. 2015, 89, 46–56. [Google Scholar] [CrossRef]
- Tang, V.T.; Rene, E.R.; Hu, L.; Behera, S.K.; Phong, N.T.; Thi Da, C. Vertical green walls for noise and temperature reduction - An experimental investigation. Sci. Technol. Built Environ. 2021, 27, 806–818. [Google Scholar] [CrossRef]
- Chang, A.S.; Tsai, C.Y. Difficulty and reasons for sustainable roadway design-the case from Taiwan. J. Civ. Eng. Manag. 2015, 21, 395–406. [Google Scholar] [CrossRef]
- Simion, C.-P.; Nicolescu, C.; Vrincut, M. Green Procurement in Romanian Construction Projects. A Cluster Analysis of the Barriers and Enablers to Green Procurement in Construction Projects from the Bucharest-Ilfov Region of Romania. Sustainability 2019, 11, 6231. [Google Scholar] [CrossRef]
- Li, L.; Chen, K. Quantitative assessment of carbon dioxide emissions in construction projects: A case study in Shenzhen. J. Clean. Prod. 2017, 141, 394–408. [Google Scholar] [CrossRef]
- Liu, H.; Lin, B. Ecological indicators for green building construction. Ecol. Indic. 2016, 67, 68–77. [Google Scholar] [CrossRef]
- Ahuja, R.; Sawhney, A.; Arif, M. Developing organizational capabilities to deliver lean and green project outcomes using BIM. Eng. Constr. Archit. Manag. 2018, 25, 1255–1276. [Google Scholar] [CrossRef]
- Sang, P.; Liu, J.; Zhang, L.; Zheng, L.; Yao, H.; Wang, Y. Effects of Project Manager Competency on Green Construction Performance: The Chinese Context. Sustainability 2018, 10, 3406. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Wu, Y.; Shen, L. Embedding “green” in project-based organizations: The way ahead in the construction industry? J. Clean. Prod. 2015, 107, 420–427. [Google Scholar] [CrossRef]
- He, H.; Jim, C.Y. Coupling model of energy consumption with changes in environmental utility. Energy Policy 2012, 43, 235–243. [Google Scholar] [CrossRef]
- Pak, W.; Kim, I.; Choi, J. Proposal of the energy consumption analysis process for the residential houses using big data analytics technique. J. Comput. Des. Eng. 2021, 8, 1591–1604. [Google Scholar] [CrossRef]
- Wu, S.R.; Fan, P.; Chen, J. Incorporating Culture Into Sustainable Development: A Cultural Sustainability Index Framework for Green Buildings. Sustain. Dev. 2016, 24, 64–76. [Google Scholar] [CrossRef]
- Cui, Y.; Jiang, S.M.; Jin, J.L.; Feng, P.; Ning, S.W. Decision-Making of Irrigation Scheme for Soybeans in the Huaibei Plain Based on Grey Entropy Weight and Grey Relation-Projection Pursuit. Entropy 2019, 21, 877. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Yang, Z.; Ding, J.; Shen, Z. Projection pursuit cluster model based on genetic algorithm and its application in Karstic water pollution evaluation. Int. J. Environ. Pollut. 2006, 28, 253–260. [Google Scholar] [CrossRef]
- Onuoha, I.J.; Aliagha, G.U.; Rahman, M.S.A. Modelling the effects of green building incentives and green building skills on supply factors affecting green commercial property investment. Renew. Sustain. Energy Rev. 2018, 90, 814–823. [Google Scholar] [CrossRef]
- Peng, B.; Zou, H.M.; Bai, P.F.; Feng, Y.Y. Building energy consumption prediction and energy control of large-scale shopping malls based on a noncentralized self-adaptive energy management control system. Energy Explor. Exploit. 2021, 39, 1381–1393. [Google Scholar] [CrossRef]
- Alghoul, S.K.; Rijabo, H.G.; Mashena, M.E. Energy consumption in buildings: A correlation for the influence of window to wall ratio and window orientation in Tripoli, Libya. J. Build. Eng. 2017, 11, 82–86. [Google Scholar] [CrossRef]
- Fathi, S.; Kavoosi, A. Effect of electrochromic windows on energy consumption of high-rise office buildings in different climate regions of Iran. Sol. Energy 2021, 223, 132–149. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.N.; Tan, D.Z. Set-based discrete particle swarm optimization and its applications: A survey. Front. Comput. Sci. 2018, 12, 203–216. [Google Scholar] [CrossRef]
- Engelbrecht, A.P. Particle swarm optimization with crossover: A review and empirical analysis. Artif. Intell. Rev. 2016, 45, 131–165. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef] [Green Version]
- Jiao, R.; Shang, Q.; Hu, R.; Yin, X.; Zhao, L.; Gong, L.; Jiang, Z. Evaluation Model for Layout Rationality of Power Grid Business Halls Based on Analytic Hierarchy Process. In Proceedings of the 5th IEEE International Conference on Cloud Computing and Intelligence Systems (CCIS), Nanjing, China, 23–25 November 2018; pp. 1008–1012. [Google Scholar]
- Xu, W.; Cheng, Y. Study on the method and index of rationality evaluation for energy utilization process. In Proceedings of the International Conference on Green Building, Materials and Civil Engineering (GBMCE 2011), Shangri La, China, 22–23 August 2011; pp. 2509–2512. [Google Scholar]
| Primary Indicator | Secondary Indicator | Type | Refs |
|---|---|---|---|
| : Economic Index | : Project cost | Cost | [5] |
| : Incremental NPV of investment | Benefit | [5,6] | |
| : Incremental payback period | Cost | [6,25] | |
| : Resource Utilization Index | : Rate of land use | Benefit | [26,27,28] |
| : Energy consumption of the air conditioning system | Cost | [29,30] | |
| : Energy consumption of the lighting system | Cost | [31] | |
| : Utilization rate of reclaimed water | Benefit | [32,33] | |
| : Utilization rate of rainwater | Benefit | [32,34] | |
| : Utilization rate of new wall materials | Benefit | [35,36] | |
| : Recovery rate of construction waste | Benefit | [37,38,39] | |
| : Environmental Impact Index | : Indoor sunshine | Benefit | [40,41] |
| : Ratio of the window area to the indoor area | Benefit | [42,43] | |
| : Effect of sound insulation and noise reduction | Benefit | [44,45] | |
| : Technical Management Index | : Technical difficulty of construction | Benefit | [46,47] |
| : Reduction of the construction period | Benefit | [48,49] | |
| : Difficulty of project management organization | Benefit | [50,51,52] | |
| : Social Impact Index | : Ratio of the energy consumption of the building area to the GDP | Cost | [53,54] |
| : Coordination between architectural modeling and regional planning | Benefit | [55] | |
| : Effect of protecting the human environment | Benefit | [55] |
| Secondary Indicator | Unit | I | II | III | IV |
|---|---|---|---|---|---|
| Million CNY | [100, 200] | [75, 100) | [50, 75) | [0, 50) | |
| Million CNY | [0, 5) | [5, 10) | [10, 20) | [20, 50] | |
| Year | [20, 50] | [10, 20) | [5, 10) | [0, 5) | |
| % | [75, 100] | [50, 75) | [25, 50) | [0, 25) | |
| [65, 85] | [45, 65) | [25, 45) | [0, 25) | ||
| [8, 10] | [5, 8) | [3, 5) | [0, 3) | ||
| % | [0, 10) | [10, 20) | [20, 30) | [30, 50] | |
| % | [0, 10) | [10, 20) | [20, 30) | [30, 50] | |
| % | [0, 5) | [5, 10) | [10, 20) | [20, 30] | |
| % | [0, 10) | [10, 20) | [20, 30) | [30, 50] | |
| - | [0, 5) | [5, 10) | [10, 15) | [15, 20] | |
| % | [0, 25) | [25, 50) | [50, 75) | [75, 100] | |
| - | Difficult [0, 25) | Simple [25, 50) | Very simple [50, 75) | Simplest [75, 100] | |
| % | [0, 10) | [10, 15) | [15, 20) | [20, 30] | |
| - | Difficult [0, 25) | Simple [25, 50) | Very simple [50, 75) | Simplest [75, 100] | |
| Ton of standard coal/ten thousand CNY | [1, 1.5] | [0.75, 1) | [0.5, 0.75) | [0, 0.5) | |
| - | Average [0, 25) | Harmonious [25, 50) | Very harmonious [50, 75) | Most harmonious [75, 100] | |
| - | Partially effective [0, 25) | Effective [25, 50) | Very effective [50, 75) | Most effective [75, 100] |
| Secondary Indicator | Original Data | Normalized Data | Secondary Indicator | Original Data | Normalized Data |
|---|---|---|---|---|---|
| 128 | 0.640 | 8 | 0.400 | ||
| 7.25 | 0.145 | 30.43 | 0.304 | ||
| 9.33 | 0.187 | 45.5 | 0.455 | ||
| 70 | 0.700 | 72 | 0.720 | ||
| 57.5 | 0.676 | 12 | 0.400 | ||
| 4.12 | 0.412 | 65 | 0.650 | ||
| 18.76 | 0.375 | 0.661 | 0.441 | ||
| 12.57 | 0.251 | 45 | 0.450 | ||
| 28.02 | 0.934 | 55.5 | 0.555 | ||
| 13.47 | 0.269 | - | - | - |
| Typical Technology | I | II | III | IV | Score |
|---|---|---|---|---|---|
| Difficult [0, 25) | Simple [25, 50) | Very Simple [50, 75) | Simplest [75, 100] | ||
| The supporting system is very complicated, construction amount is very large. | Supporting system is complex, construction amount is large. | Supporting system is simple, construction amount is general. | The supporting system is very simple, construction amount is small. | 30 | |
| Concrete pouring and curing are very difficult, quality is difficult to control. | Concrete pouring and curing are difficult, quality is difficult to control. | Concrete pouring and curing are not difficult, quality is easy to control. | Concrete pouring and curing are easy, there are almost no quality problems. | 75 | |
| Many kinds of steel bars and complicated connections. | Many kinds of steel bars, connections are not too complicated. | A few kinds of steel bars, connections are simple | Few kinds of steel bars, connections are very simple. | 85 | |
| The template system is too large and the security risk is high. | The template system is huge and the security risk is high. | The template system is simple and the security risks are controllable. | The template is very simple and the security risks are completely controllable. | 75 | |
| The construction is very difficult, quality is very difficult to control. | The construction is difficult, quality is difficult to control. | The construction is simple, quality is simple to control. | The construction is very simple, quality is very simple to control. | 60 | |
| Waterproof and pipe network structures are very complex. | Waterproof and pipe network structures are complex. | Waterproof and pipe network structures are simple. | Waterproof and pipe network structures are very simple. | 20 | |
| Many kinds of steel members, and the connection is very complicated. | Many kinds of steel members, and the connection is complicated. | A few kinds of steel members, and the connection is simple. | Few kinds of steel members, and the connection is very simple. | 25 | |
| Too many high-altitude hoisting operations. | High-altitude hoisting operations. | High-altitude hoisting operations. | Few high-altitude hoisting operations. | 45 | |
| Building information modeling (BIM) is not applied. | BIM technology is initially applied. | BIM technology is acceptably applied. | BIM technology is deeply applied. | 80 |
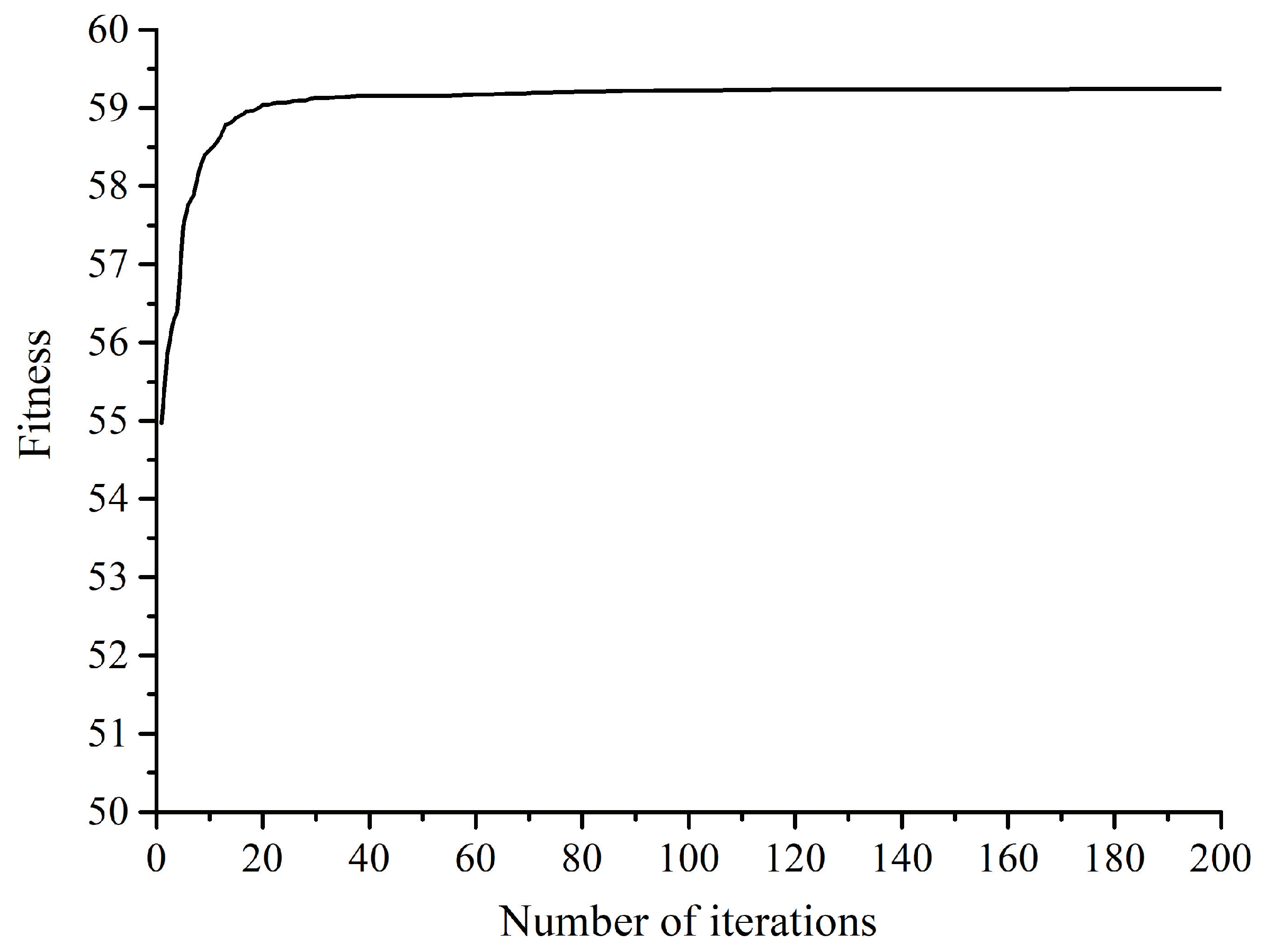
| Iteration (n) | Fitness (n − 1) | Fitness (n) | Fitness (n)–Fitness (n − 1) | Result |
|---|---|---|---|---|
| 126 | 59.23787871 | 59.23787871 | 0 < 0.00001 | Continue |
| 127 | 59.23787871 | 59.23800214 | 0.00012343 > 0.0001 | Continue |
| 128 | 59.23800214 | 59.23800214 | 0 < 0.0001 | Continue |
| 1000 | 59.23800214 | 59.23800214 | 0 < 0.0001 | Stop |
| Secondary Indicator | Corresponding Element | Weight | Ranking | Secondary Indicator | Corresponding Element | Weight | Ranking |
|---|---|---|---|---|---|---|---|
| 0.2610 | 0.0681 | 6 | 0.1747 | 0.0305 | 17 | ||
| 0.3207 | 0.1029 | 1 | 0.2764 | 0.0764 | 3 | ||
| 0.2175 | 0.0473 | 11 | 0.1713 | 0.0293 | 18 | ||
| 0.2138 | 0.0457 | 12 | 0.2652 | 0.0703 | 5 | ||
| 0.2800 | 0.0784 | 2 | 0.2204 | 0.0486 | 9 | ||
| 0.2702 | 0.0730 | 4 | 0.2411 | 0.0581 | 7 | ||
| 0.1372 | 0.0188 | 19 | 0.1931 | 0.0373 | 15 | ||
| 0.2346 | 0.0550 | 8 | 0.1990 | 0.0396 | 14 | ||
| 0.1778 | 0.0316 | 16 | 0.2034 | 0.0414 | 13 | ||
| 0.2181 | 0.0476 | 10 | - | - | - | - |
| Computational Performance | AOS | PSO | GA | |
|---|---|---|---|---|
| Computation speed | Best result | 107th | 132th | 174th |
| Average result | 131.54th | 197.39th | 284.08th | |
| Worst result | 154th | 274th | 402th | |
| Stability | Variance of the fitness | 0.0000074 | 0.0000684 | 0.0001974 |
| Variance of maximum projection value | 0.0000120 | 0.0000769 | 0.0001026 | |
| Variance of optimal projection vector | 0.0000032 | 0.0000107 | 0.0000184 | |
| Secondary Indicator | Group 1 | Group 2 | Group 3 | Group 4 | ||||
|---|---|---|---|---|---|---|---|---|
| Weights | Rankings | Weights | Rankings | Weights | Rankings | Weights | Rankings | |
| 0.0522 | 9 | 0.0580 | 9 | 0.0193 | 16 | 0.0407 | 11 | |
| 0.0821 | 3 | 0.1100 | 1 | 0.0852 | 3 | 0.1222 | 2 | |
| 0.0431 | 13 | 0.0854 | 4 | 0.0338 | 13 | 0.0832 | 4 | |
| 0.0364 | 16 | 0.0530 | 11 | 0.0449 | 11 | 0.0317 | 13 | |
| 0.0919 | 1 | 0.1040 | 2 | 0.1080 | 1 | 0.1279 | 1 | |
| 0.0372 | 14 | 0.0547 | 10 | 0.0470 | 10 | 0.0925 | 3 | |
| 0.0541 | 8 | 0.0505 | 12 | 0.0285 | 15 | 0.0342 | 12 | |
| 0.0899 | 2 | 0.0643 | 6 | 0.0323 | 14 | 0.0279 | 15 | |
| 0.0745 | 4 | 0.0324 | 13 | 0.0562 | 9 | 0.0311 | 14 | |
| 0.0665 | 6 | 0.0706 | 5 | 0.0870 | 2 | 0.0228 | 17 | |
| 0.0498 | 10 | 0.0992 | 3 | 0.0625 | 8 | 0.0448 | 9 | |
| 0.0659 | 7 | 0.0151 | 17 | 0.0175 | 17 | 0.0200 | 18 | |
| 0.0258 | 18 | 0.0180 | 15 | 0.0705 | 7 | 0.0439 | 10 | |
| 0.0445 | 12 | 0.0588 | 8 | 0.0375 | 12 | 0.0574 | 7 | |
| 0.0671 | 5 | 0.0592 | 7 | 0.0754 | 6 | 0.0276 | 16 | |
| 0.0490 | 11 | 0.0173 | 16 | 0.0794 | 5 | 0.0158 | 19 | |
| 0.0283 | 17 | 0.0261 | 14 | 0.0817 | 4 | 0.0597 | 6 | |
| 0.0367 | 15 | 0.0133 | 18 | 0.0167 | 19 | 0.0686 | 5 | |
| 0.0049 | 19 | 0.0100 | 19 | 0.0168 | 18 | 0.0480 | 8 | |
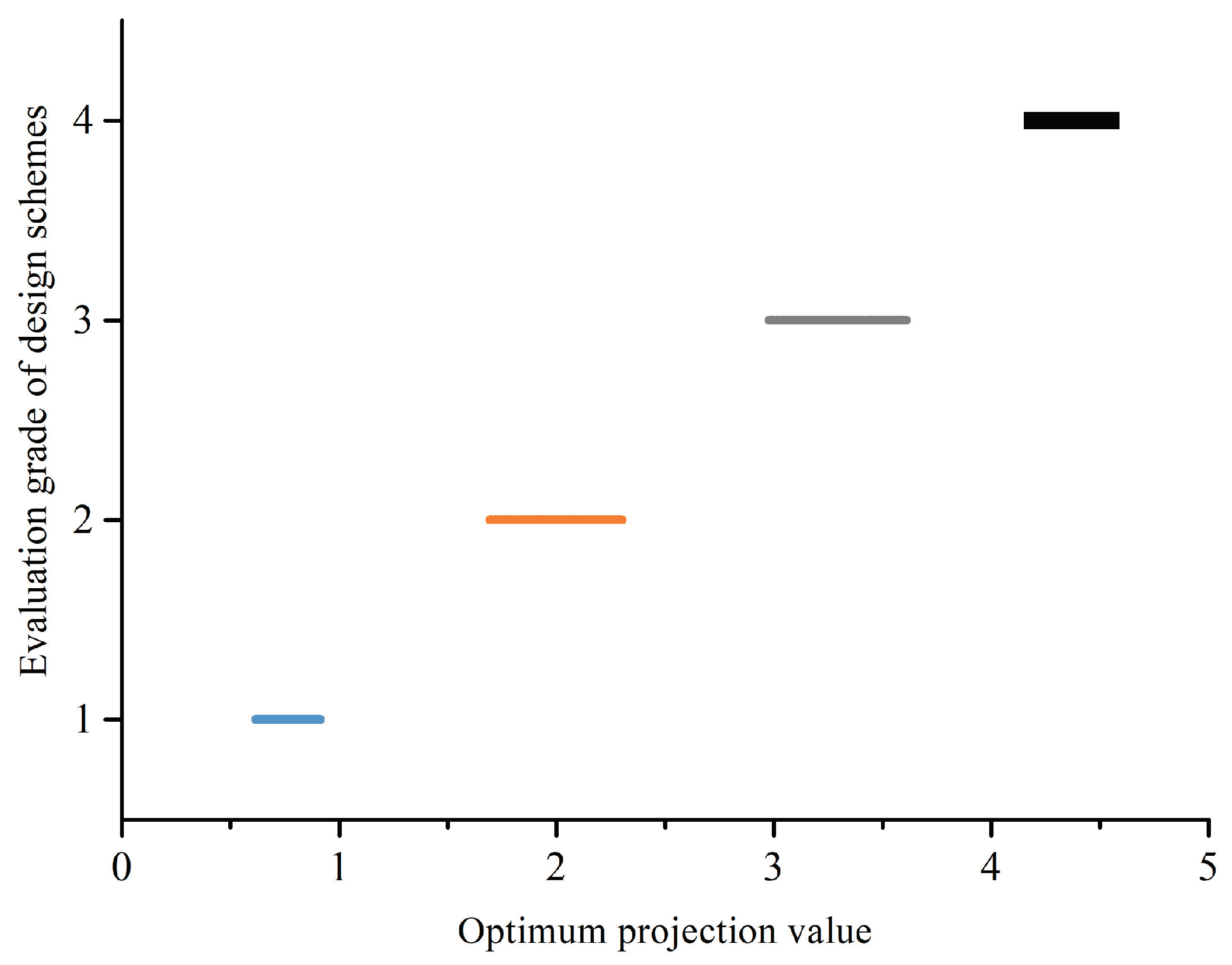
| Deleted Indicators | Optimum Projection Value | Evaluation Grade | The Minimum Index Set or Not? |
|---|---|---|---|
| 3.471 | 2.104 | No | |
| , | 3.832 | 2.433 | No |
| , , | 4.541 | 2.680 | No |
| , , , | 5.048 | 3.157 | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Zhao, T.; Yan, H.; Wu, H.; Wang, F. Evaluation of Urban Green Building Design Schemes to Achieve Sustainability Based on the Projection Pursuit Model Optimized by the Atomic Orbital Search. Sustainability 2022, 14, 11007. https://doi.org/10.3390/su141711007
Liu G, Zhao T, Yan H, Wu H, Wang F. Evaluation of Urban Green Building Design Schemes to Achieve Sustainability Based on the Projection Pursuit Model Optimized by the Atomic Orbital Search. Sustainability. 2022; 14(17):11007. https://doi.org/10.3390/su141711007
Chicago/Turabian StyleLiu, Genbao, Tengfei Zhao, Hong Yan, Han Wu, and Fuming Wang. 2022. "Evaluation of Urban Green Building Design Schemes to Achieve Sustainability Based on the Projection Pursuit Model Optimized by the Atomic Orbital Search" Sustainability 14, no. 17: 11007. https://doi.org/10.3390/su141711007
APA StyleLiu, G., Zhao, T., Yan, H., Wu, H., & Wang, F. (2022). Evaluation of Urban Green Building Design Schemes to Achieve Sustainability Based on the Projection Pursuit Model Optimized by the Atomic Orbital Search. Sustainability, 14(17), 11007. https://doi.org/10.3390/su141711007







