Abstract
Water abandonment risk caused by inflow uncertainties is a major problem in cascade hydropower generation operation and water resources management. In this study, we propose a theoretical estimation method (TEM) to calculate water abandonment risk probability (WARP) utilizing sample inflow data and historical forecast errors. The method analyzes the differences in risk quantification between the head hydropower station and downstream stations, and the corresponding probability formula is provided. Then, a short-term optimal operation model of cascade hydropower stations considering the additional WARP water level constraints is constructed to dynamically control water level risk. The Dahuashui (DHS)-Geliqiao (GLQ) cascade hydropower stations in the Wujiang River Basin of China is investigated as a case study. The results show that compared with the historical scheme, the total amount of water abandonment of DHS, GLQ and DHS-GLQ in the WARP optimal scheme decreases by 11.69%, 47.69% and 28.27%, respectively, and the flood peak of GLQ is reduced by 21.6%. In conclusion, compared with the traditional control approach and actual operation processes, the proposed risk control in optimization of cascade hydropower considering WARP can improve the comprehensive utilization efficiency of cascade hydropower systems by reducing the occurrence of water abandonment and thereby increase generation profits.
1. Introduction
With the shortage of fossil energy and the increasing demand for clean production, hydropower generation, as a renewable energy, plays an increasingly important role in sustainable development [1,2]. Although hydropower generation operation optimization theory has been rapidly developed [3,4,5,6,7], it remains difficult to make full use of hydropower resources due to complex uncertainties from different sources [8,9,10] both in long-term and short-term operation [11,12]. For example, when there is a large deviation between the actual inflow process and the forecasts, cascade hydropower stations operating based on forecasts may have insufficient reservoir storage capacity to utilize over-forecast inflow and need to abandon water to ensure safety. The discharge may exceed the maximum generating capacity of the hydropower station units. The non-power-generating portion of the flow is called abandoned water or water abandonment. A lack of consideration of potential water abandonment risk may result in a large hydropower losses and even make the hydropower system unsafe and unreliable [13,14]. Therefore, to facilitate the hydropower generation management level, it is vital to estimate the water abandonment risk under uncertainties and control the risk through the optimization of cascade hydropower operations [15,16,17,18,19,20,21].
In China, water abandonment is becoming an important parameter for the operation of cascade hydropower generation for the power grid, and also an important aspect of water resources management. Scholars have paid increasing attention to the initial study of the water abandonment problem and relevant research can be divided into two categories.
One focus of study is analysis of the various factors causing the water abandonment problem to determine the influence of uncertainties in the hydropower system [22]. For example, a strong negative correlation between water abandonment and forecast accuracy has been demonstrated, that is, the higher the forecast accuracy, the lower the spillage [11]. The present research focuses on WARP due to the same cause as Tan [11]. The unreasonable electricity price mechanism and the lack of overall planning and reallocation of power transmission channels [23] are also considered to be the main reasons for water abandonment by the Central China Power Net [24] and southwest China hydropower system [25]. Water abandonment related to the compensation for wind and photovoltaic power forecasting is analyzed both in the flood season and the dry season and in relation to the complementary operation of the wind-photovoltaic-hydropower system [26].
A second research area is concerned with how to take factors causing water abandonment into consideration through hydropower operation optimization. In order to fully utilize the head efficiency of hydropower, operating at a high water level may, in theory, result in the maximum power generation profits. However, the lack of consideration of potential water abandonment risk under high water levels may make the operation unsafe and unreliable. Thus, it is of great significance to consider water abandonment risk in different runoff processes, and to coordinate the power generation benefit and water abandonment risk in the actual operations [27,28]. In particular, a concept for evaluating water abandonment risk by its probability is proposed in the actual operation of Wujiang River Cascade in China [29]. In the relevant research, it is assumed that the runoff error follows a specific distribution and a large number of runoff series are simulated by the Monte Carlo method for constant output simulation to realize the description of the main risk factors (runoff uncertainty). Many indexes such as maximum probability spillage water quantity, expected spillage water quantity and up limit spillage water quantity are calculated and corresponding probability distributions are built to reflect the resulting risk faced by different generation plans [30,31]. The reasonable range of control indexes (such as the beginning regulation water level and the operation mode) for formulating cascade reservoir operation plans is determined through typical frequent flood process simulation under proposed operation strategies [32]. These studies and their applications pay much attention to the response relationship between runoff, water level and the resulting statistical probability of water abandonment, and to the determination of risk control indexes in operation plan formulation. However, there are few studies introducing the quantified WARP factor into the optimal operation model directly to realize the dynamic water level risk control of hydropower stations.
In fact, under the condition that the forecast flow is known, the WARP of a hydropower station in a certain period is related not only to the control water level at the beginning but also to the level at the end of the period. In the reservoir operation, the control water level at the end of the period will become the starting level for the next period which will affect the WARP calculation in that period. The water levels upstream and downstream are also linked. Therefore, the WARP in the cascade hydropower system is not independent and unrelated. It should be considered an integral and dynamic process to reduce the WARP by controlling the water level of each station in each period.
On the basis of previous studies, the present research attempts to quantify WARP and dynamically control the water level under risk in the cascade hydropower optimal operation model. Specifically, a TEM is first proposed and applied to calculate WARP using sample inflow data and historical forecast errors. Second, based on this method, the short-term cascade hydropower optimal operation model for dynamic risk control with the additional WARP-water level constraints is constructed and the cuckoo algorithm (CA) is applied to solve the model. Additionally, the performance of the model with the additional WARP-water level constraints is explored regarding the decrease in the dynamic risk of water abandonment and the increase in cascade power generation profits.
The remainder of this paper is organized as follows. Section 2 introduces the methodology by which the TEM is used to calculate WARP using sample inflow data and historical forecast errors. The differences in risk quantification between the head hydropower station and downstream stations are also determined. The corresponding probability formulas and the short-term cascade hydropower optimal operation model considering WARP are described in detail. Subsequently, the case study and results are presented and discussed in Section 3. Section 4 is devoted to drawing conclusions.
2. Methodology
2.1. Description of WARP
Generally, the probability of water abandonment risk refers to the possibility of water abandonment at the end of the operation period without considering some uncertainties under a certain combination of control water level and hydropower generation operation plan [32]. There is currently no unified standard method for calculating WARP.
For the head hydropower station, the larger the over-forecast runoff and the higher the initial water level of the reservoir, the greater the WARP; for downstream stations, the WARP is not only related to the interval forecast runoff and the initial water level, but also to the upstream reservoir release. The differences in risk quantification between the head hydropower station and downstream stations and the corresponding probability formulas are described in detail in Section 2.2. The short-term cascade hydropower optimal operation model considering WARP is established in Section 2.3, in which the expressions of WARP are translated to certain water level constraints.
2.2. TEM of WARP Based on Runoff Forecasting Error
2.2.1. WARP of the Head Hydropower Station
The head hydropower station is not affected by an upstream release, and its inflow is only related to the natural runoff. According to the regulations of reservoir operation, when it is necessary to abandon water, the water level must be equal to or greater than the control water level. If the unit overflows with the maximum generating capacity during a certain period, and the inflow still results in the reservoir water level at the end of the period equal to or greater than the control water level, water abandonment events will occur. The TEM of WARP of the primary reservoir can be established by calculating the water balance equation as follows:
where is the average inflow during the period in m3/s; and are the maximum generation discharge and the average water abandonment discharge, respectively, during the period, with the units m3/s; and are the water storage of the reservoir at time and , m3, respectively; and is the length of the period.
Given that , the occurring condition of the water abandonment events can be expressed as:
Then, the critical value of the average inflow during the period can be expressed using as:
The probability of water abandonment events during the period can be expressed and calculated as:
where is the forecast runoff of inflow in m3/s; is the runoff forecasting error between and the actual inflow value in m3/s; and is the CDF of the runoff forecasting error.
2.2.2. WARP of the Downstream Hydropower Station
For the downstream hydropower station, the influence of the upstream reservoir release on the WARP should be considered. For this reason, the expected release of each cascade reservoir should be calculated reservoir by reservoir and constitute a fixed part of the downstream reservoir inflow. The fixed part should then be added with the interval inflow random variables to be considered as the whole inflow of the downstream reservoir. Based on the achieved inflow, the WARP of the downstream hydropower station can be calculated using a similar method to that used for the head stations.
- (1)
- The expected release of each cascade reservoir
The release of the upstream reservoir is a function of its inflow, and the inflow is a random variable varying with the runoff forecasting error. Therefore, the release is also a random variable. According to the water balance Equation (1), the release can be calculated as:
In general, for a random variable function , the mathematical expectation can be calculated as:
where is the mathematical expectation; and is the probability density function (PDF) of random variable .
According to Equations (5) and (6), the key to calculating the expected release is the PDF of the actual inflow . It can be calculated through the CDF of as:
where and are the CDF and PDF, respectively, of the actual inflow ; and is the PDF of the runoff forecasting error.
According to Equations (5), (6) and (8), the expected release of the upstream reservoir can be calculated as:
- (2)
- WARP calculation based on the expected release of the upstream reservoir
The expected release of the upstream reservoir is taken as a fixed part of the downstream reservoir inflow and only the randomness of the interval inflow is considered (without considering the correlation between the upper release and the interval inflow) when calculating the WARP of the downstream hydropower station. According to the principle of water balance and Equation (1), the relevant equations can be expressed as follows:
where is the actual inflow of the i-th reservoir in m3/s; is the expected release of the (i−1)-th reservoir in m3/s; is the interval inflow between the i-th reservoir and the (i−1)-th reservoir in m3/s; and are the maximum generation discharge and the average water abandonment discharge, respectively, of the i-th hydropower station during the period, with the units m3/s; and and are the water storage of the i-th reservoir at time and , respectively, with the unit m3.
Given that , the occurring condition of the water abandonment events can be expressed as:
Then, the critical value of the average inflow during the period can be expressed using as:
The probability of water abandonment events during the period can be expressed and calculated as:
where is the forecast interval inflow between the i-th reservoir and the (i−1)-th reservoir in m3/s; is the runoff forecasting error between and the actual interval inflow value in m3/s; and is the CDF of the runoff forecasting error.
According to the proposed TEM and Equations (4) and (14), the CDF of the runoff forecasting error is necessary as a foundation for the WARP quantification.
2.3. Cascade Hydropower Optimal Operation Model under WARP
2.3.1. Objective Function
In the cascade hydropower station system, the main objective is to maximize the power generation efficiency. The aim of controlling the WARP in the optimal operation is also to improve the cascade hydropower system power generation profits during the whole period. Thus, the maximum total power generation objective function is considered in the proposed cascade hydropower optimal operation model under WARP, as shown in Equation (15):
where is the total power generation in kW·h; is the efficiency coefficient of the i-th hydropower station; and is the effective head of the i-th hydropower station at period t.
2.3.2. Constraints
- (1)
- General constraints
There are hydraulic connections between the cascade stations. The hydraulic connections can be shown in Equation (10).
Other general constraints mainly include water balance constraints, reservoir capacity (water level) constraints, power station overflow constraints, output constraints, etc., as shown in Equations (16)–(19):
where and are the inflow and outflow, respectively, of the i-th reservoir at period t in m3/s; and are the water storage of the i-th reservoir at period t + 1 and period t, respectively, with the unit m3; and are the minimum and maximum water levels, respectively, of the i-th reservoir at period t, with the unit m; and are the minimum and maximum outflow, respectively, of the i-th reservoir at period t; and and are the minimum power output and the installed capacity, respectively, of the i-th hydroelectric plant at period t.
Restrictions arising from different uses, such as water supply to populations, use of water lines for leisure activities and the possible need to maintain ecological flows, should be considered and translated to the constraints mentioned above. Therefore, in this study, WARP is translated into water level constraints to be considered in the model.
- (2)
- WARP water level constraints
To reduce WARP caused by runoff forecast errors, different upper limits of WARP are adopted according to the risk preference of decision-makers, as shown in Equation (20):
where is the TEM function of the WARP in the i-th reservoir at period t when the initial and final water levels are and the forecast inflow is ; and is the upper limit of the allowable WARP in the i-th reservoir at period t.
Combined with the TEM of WARP mentioned in Section 2.2, the risk control demand of WARP in each period can be transformed into the corresponding constraint of reservoir water level in the order from upstream to downstream for each hydropower station. First, the threshold or feasible range of WARP is obtained. Then, based on the corresponding forecast error from the probability distribution curve, a critical flow of the reservoir is determined. According to the principle of water balance, the water level constraints are defined, and all the hydropower stations are traversed in turn.
For the head hydropower station, the water level constraint transformed by the WARP can be calculated, as shown in Equation (21):
where is a function of the storage capacity and water level; and is the corresponding inverse function.
For the downstream hydropower station, when calculating the constraint according to the water balance equation, the influence of the upstream outflow should be taken into account, as shown in Equation (22):
2.3.3. Solution
Compared with the traditional algorithm, it has been demonstrated that the cuckoo search algorithm has a higher convergence accuracy and stability in the solution of the cascade hydropower optimal operation model [33]. In this study, the cuckoo search algorithm is applied, combined with the initial solution generation and search step dynamics based on dynamic corridor constraints.
2.4. Entire Solution Process
The entire solution process for the risk control study of the optimization of cascade hydropower considering water abandonment risk probability consists of the following four steps:
Step 1 builds the runoff forecasting error cumulative distribution function (CDF): According to the statistical analysis of historical runoff and forecast data, the appropriate probability distribution curve is selected and calibrated to fit the runoff forecasting error statistical characteristics. It is recommended to use the latest available data for modeling and analysis of short-term models to reduce the influence of long-term climate change. The common error CDFs include normal distributions, uniform distributions, triangular distributions, Rayleigh distributions and others.
Step 2 determines different expressions of WARP: Based on the achieved runoff forecasting error CDF, the corresponding probability formulas for the WARP of the head hydropower station and downstream stations can be determined in detail by using different quantification methods.
Step 3 translates WARP to WARP water level constraints: According to the upper limit values of WARP in a certain period under the decision maker’s risk preference, the expressions of WARP can be translated to certain water level constraints, which will be considered in the cascade hydropower optimal operation model under WARP.
Step 4 constructs and solves the optimal operation model: the short-term cascade hydropower optimal operation model is constructed considering the additional WARP water level constraints and can be solved by the cuckoo algorithm. The water level risk control scheme and hydropower operation strategy will be determined.
3. Case Study
3.1. Study Area and Data
We analyzed the water abandonment problem in the operation of cascade hydropower stations in Wujiang River Basin, located in the Guizhou Province of southern China. As shown in Figure 1, Wujiang River is an upstream tributary of the Yangtze River, with a basin area of 87,900 km2. The main purpose of Wujiang River hydropower system is not only to maximize the total cascade power generation but also to ensure the safety of the downstream area during the flood season. In actual operation, the flood season for Wujiang River is from June to September every year, when due to multiple reasons, most of the water abandonment occurs.
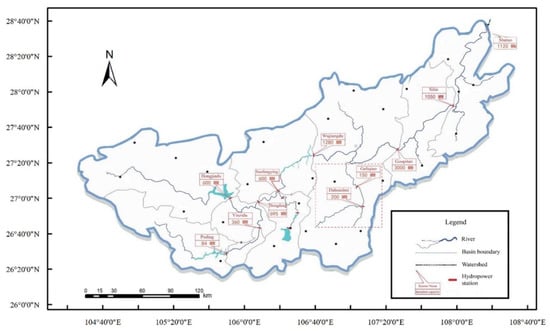
Figure 1.
Locations of cascade hydropower stations in Wujiang River Basin.
The water abandonment problem in Wujiang River Basin is concentrated in the downstream areas, especially for the stations with small reservoir capacity. Thus, the DHS-GLQ cascade hydropower stations, which are in the downstream reaches of Wujiang River, are considered in the case study. The main parameters of the DHS-GLQ cascade hydropower stations are shown in Table 1.

Table 1.
Characteristic parameters of cascade hydropower stations in DHS-GLQ.
The data source is the hydropower operation database of Wujiang River Basin remote centralized control center of the Wujiang Hydropower Development Co., Ltd., Guizhou, China. The data includes forecast runoff, observed runoff, water level, inflow, and outflow etc. The maximum historical WARP for each specific period is used as the upper limit value of WARP.
3.2. Results and Discussion
3.2.1. The Probability Distribution of Runoff Forecast Errors
The historical observed and forecast runoff series of DHS-GLQ for the flood season in 2018, which were collected hourly, were used to calculate the runoff forecasting error and corresponding statistical parameters. Several common error distribution curves were selected to fit the runoff forecasting error to determine an appropriate probability distribution, including a normal distribution, uniform distribution, triangular distribution, Rayleigh distribution and others.
Taking DHS as an example, the frequency distribution histograms of runoff forecasting relative error of various forecast periods were plotted, as shown in Figure 2.
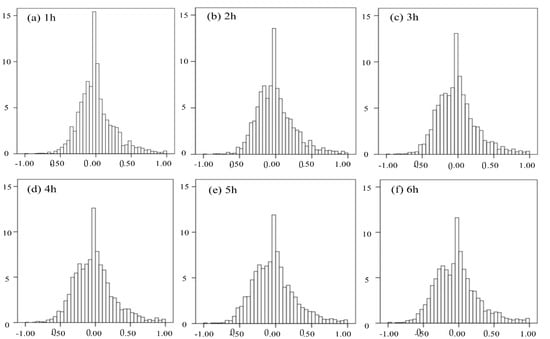
Figure 2.
The frequency distribution histograms of runoff forecasting relative error of various forecast periods (a) 1h. (b) 2h. (c) 3h. (d) 4h. (e) 5h. (f) 6h.
Figure 2 shows a bell-shaped distribution with Y-axis symmetry. It can be assumed that the runoff forecasting relative error of forecast period t follows the normal distribution of location parameter and scale parameter . In addition, the forecast accuracy decreases with the increase in forecast periods, and the relative error increases. It is assumed that the standard deviation of the relative error in the next 1 h forecast period is , and it then increases linearly with the extension of the forecast period. To simplify the calculation, the linear increment is calculated according to the average increment of the standard deviation of various forecast periods in the first 6 h. Thus, the hourly runoff forecast relative error distribution curve of the DHS can be obtained. The relative error distribution function obtained above is multiplied by the forecasted runoff value in the corresponding period as the distribution function of the absolute error of the forecast runoff. The same process was applied to the data for Geliqiao.
3.2.2. Hydropower Optimal Operation Strategy
In this hydropower optimal operation case study, the typical daily operation from 00:00 12 June 2018 to 24:00 15 June 2018 of DHS-GLQ was selected for calculation and analysis. Taking 1 h as the operation scale, the WARP control scheme and the hydropower optimal operation strategy is obtained through solving the cascade hydropower optimal operation model under WARP, as shown in Figure 3.
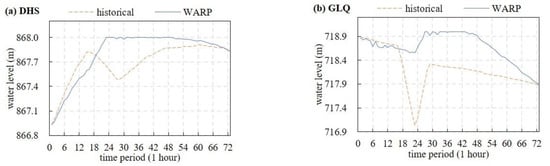
Figure 3.
The water level scheme of DHS (a) and GLQ (b) in the historical and WARP optimal models.
According to Figure 3a, during the actual historical operation of the DHS water level scheme, the reservoir performed pre-release during the hours 16–28. As a result, the water level decreased significantly, and gradually from the normal storage level of 868 m. The lowest water level (867.48 m) occurred at hour 28. After that, the reservoir gradually impounded, but until the end of the operation period, the highest water level was 867.91 m, which was below the normal water level. The possible reason is that the operation scheme for flood control and pre-release is greatly affected by subjective decisions. The risk preferences of decision-makers result in longer pre-release times and larger quantities of pre-release water to prevent flood risk as far as possible. On the other hand, the decision-makers and flood forecasting data cannot accurately predict future runoff, and the actual late flood is not as expected, which is also one of the possible reasons for the low water level condition.
During the WARP optimal operation of the DHS water level scheme, the water level continued to rise during the hours 1–24 and reached the normal water level of 868 m. After that, the reservoir maintained high head operation near the normal water level, and slowly decreased to 867.83 m after hour 49, which was consistent with the initial and final water levels of the historical scheme. The higher water level condition in the optimal scheme more fully utilizes the water head power generation and hydropower storage (or water supply) in the later period. The reason is that the TEM is used to objectively quantify the WARP resulting from the uncertainty of the inflow forecast. This can avoid the subjective limitations of decision-makers and realize a reservoir regulation scheme that fully utilizes flood resources.
It can be seen from Figure 3b that in the actual historical operation of the GLQ water level scheme, the water level presents an overall downward trend. The pre-discharge capacity of the reservoir occurred during the hours 17–23, which was mainly considered as the corresponding measures affected by the upstream DHS pre-discharge scheme. After the pre-release, the water level of the reservoir rose rapidly to 718.31 m and then slowly decreased to 717.88 m.
In the WARP optimal operation of the GLQ water level scheme, the water level rose from 718.55 m to 719 m after 20 h of decline and maintained operation until hour 46 before dropping to 717.9 m. Similar to DHS, the GLQ optimal scheme ensures an invariable water level at the beginning and end of the operation period, while the water level is higher than the historical scheme during most of the operation period.
3.2.3. Water Abandonment
The flow process of water abandonment under the two schemes is shown in Figure 4. Compared with the historical scheme, the total amount of water abandonment in DHS, GLQ and DHS-GLQ decreases by 11.69%, 47.69% and 28.27% respectively. It can be seen that the WARP optimal model established in this paper plays a significant role in solving the water abandonment problem of the cascade hydropower system in the basin, especially for downstream stations with poor regulation capacity for which the water abandonment can be reduced by nearly half.
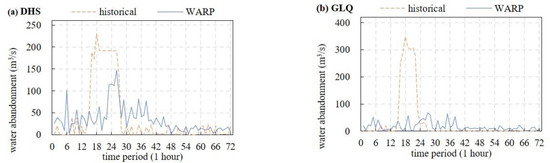
Figure 4.
Water abandonment of DHS (a) and GLQ (b) in the historical and WARP optimal models.
3.2.4. WARP
Accordingly, the distribution process of WARP is shown in Figure 5. As shown in Figure 5a, the optimal model proposed in this paper can effectively reduce the WARP of DHS, especially the peak. The peak value is greater than 0.9 in the DHS historical scheme and remains near the peak value during the hours 16–26, while in the optimal scheme, the peak value is greater than 0.8 twice at hours 6 and 26, respectively, and the maximum value is 0.852. However, for small reservoirs with poor regulation capacity, WARP is greatly affected by upstream release and outflow. As shown in Figure 5b, the WARP peak relief is not significant in the GLQ optimal scheme. It can be seen that the flood process caused by upstream abandoned water readily causes a large amount of water abandonment in downstream reservoirs with poor regulation capacity. Therefore, it is necessary to avoid the occurrence of abandoned water events in large reservoirs as much as possible, that is, to reduce the WARP of upstream stations so as to relieve the overall abandoned water pressure of the cascade system.
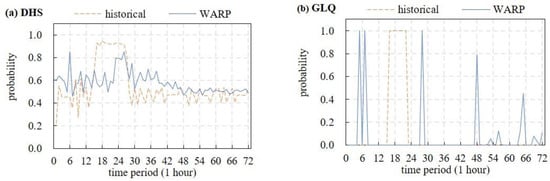
Figure 5.
WARP of DHS (a) and GLQ (b) in the historical and WARP optimal models.
Considering Figure 3 and Figure 5, it can be observed that the water level in the optimal operation for the WARP relieved period is significantly higher than that of the historical operation. For the same period, the more the water level increases, the lower the WARP. This phenomenon can be explained using Equations (21) and (22), which means WARP level constraints can be regarded as water climbing constraints for a certain period.
3.2.5. Efficient Utilization of Medium and Small Flood Resources
The purpose of this paper is to improve the utilization efficiency of small and medium flood resources in the basin and improve the economic benefits of power generation while ensuring flood control safety. The runoff and output processes in this case study are shown in Figure 6 and Figure 7.
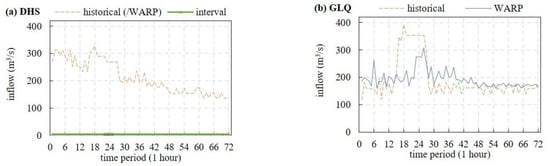
Figure 6.
Inflow processes of DHS (a) and GLQ (b) in the historical and WARP optimal models.
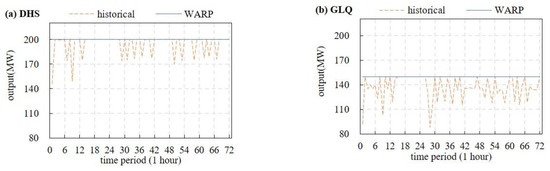
Figure 7.
Output processes of DHS (a) and GLQ (b) in the historical and WARP optimal models.
Figure 6a can be used to analyze the causes of downstream flood peaks. The overall DHS inflow process showed a downward trend, and the interval inflow was always small, while the flood peak of the downstream inflow process occurred in the period when DHS abandoned water was large, so it can be seen that the downstream flood peak was mainly caused by the upstream abandoned water (outflow runoff). The proposed optimal model fully considers the influence of upstream potential releasees when quantifying the downstream WARP. Setting the upper limit of the downstream WARP can limit both the upstream release and the downstream risk, which meets the actual operation requirements.
Figure 6b can be used to analyze the beneficial effects of peak-cutting and flood detention of the proposed optimal model. The inflow process of GLQ is similar to the water abandonment process of DHS in Figure 4a. The flood peak in the GLQ optimal scheme is reduced by 21.6% compared with that in the historical scheme and is delayed by 8 h.
Figure 7 shows the beneficial effect of the proposed optimal model on increasing output. Although WARP water climbing constraints may lead to a decrease in the upstream outflow in a certain period, the resulting optimal operation scheme can still achieve full output and continuously show the hydraulic head benefits in the later period.
4. Conclusions
An integrated development framework for risk control in the optimization of cascade hydropower considering water abandonment risk probability is introduced in this paper. Two innovations are proposed and included in the study. On the one hand, we propose a novel TEM of WARP to avoid the subjective limitations of decision-makers in risk quantification. On the other hand, we introduce the quantified WARP factor into the water level constraints in the optimal operation model directly to realize dynamic risk control.
The results show that:
- (1)
- The optimal scheme ensures an invariable water level at the beginning and end of the operation period, while the water level is higher than the historical scheme during most of the operation period due to the addition of WARP water level constraints (water climbing constraints for a certain period);
- (2)
- Water abandonment, especially in the downstream hydropower stations with small reservoir capacity caused by runoff uncertainties and forecast errors, can be flexibly alleviated and controlled to efficiently utilize flood resources. In the case study, compared with the historical scheme, the total amount of water abandonment in DHS, GLQ and DHS-GLQ decreases by 11.69%, 47.69% and 28.27%, respectively;
- (3)
- Adopting the appropriate WARP water level constraints can effectively guide the head hydropower station with a large reservoir capacity to function as a flood storage at the early stage to stagger the downstream flood peak. In the case study, the flood peak in the GLQ optimal scheme is reduced by 21.6% compared with that in the historical scheme;
- (4)
- The output may be reduced appropriately to meet the requirement to increase the water level at the early stage but improved with greater head efficiency at the later stage, and thereby the system generation profits of the whole operation period can be improved.
In conclusion, compared with the traditional risk control strategy and actual operation process, risk control in optimization of cascade hydropower considering WARP can improve the comprehensive utilization efficiency of cascade hydropower systems by reducing the occurrence of water abandonment and increasing cascade power generation profits.
Author Contributions
Conceptualization, X.Z. and G.F.; methodology, X.Z. and J.L.; software, X.Z. and J.Y.; validation, C.W. and X.W.; resources, G.F. and X.W.; data curation, X.Z.; writing—original draft preparation, X.Z.; writing—review and editing, X.Z.; visualization, X.Z.; funding acquisition, G.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52179012 and National Key R & D Program of China, grant number 2019YFE0105200.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ren, D. Outlook for renewable energy development of 13th Five Year Plan. Sci. Technol. Rev. 2016, 34, 133–138. [Google Scholar]
- China Renewable Energy Engineering Institute. China Renewable Energy Development Report; China Renewable Energy Engineering Institute: Beijing, China, 2021. [Google Scholar]
- Hall, W.A.; Butcher, W.S.; Esogbue, A. Optimization of the operation of a multiple-purpose reservoir by dynamic programming. Water Resour. Res. 1968, 4, 471–477. [Google Scholar] [CrossRef]
- Keckler, W.G.; Larson, R.E. Dynamic programming applications to water resource system operation and planning. J. Math. Anal. Appl. 1968, 24, 80–109. [Google Scholar] [CrossRef]
- Mizyed, N.R.; Loftis, J.C.; Fontane, D.G. Operation of large multireservoir systems using optimal-control theory. J. Water Resour. Plan. Manag. 1992, 118, 371–387. [Google Scholar] [CrossRef]
- Russell, S.O.; Campbell, P.F. Reservoir operating rules with fuzzy programming. J. Water Resour. Plan. Manag. 1996, 122, 165–170. [Google Scholar] [CrossRef]
- Alcamo, J.; Flörke, M.; Märker, M. Future long-term changes in global water resources driven by socio-economic and climatic changes. Hydrol. Sci. J. 2007, 52, 247–275. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Burn, D.H. An improved methodology for short-term operation of a single multipurpose reservoir. Water Resour. Res. 1989, 25, 1–8. [Google Scholar] [CrossRef]
- Xie, M.; Zhou, J.; Li, C.; Zhu, S. Long-term generation scheduling of Xiluodu and Xiangjiaba cascade hydro plants considering monthly streamflow forecasting error. Energy Convers. Manag. 2015, 105, 368–376. [Google Scholar] [CrossRef]
- Zhao, T.; Yang, D.; Cai, X.; Zhao, J.; Wang, H. Identifying effective forecast horizon for real-time reservoir operation under a limited inflow forecast. Water Resour. Res. 2012, 48, 1–15. [Google Scholar] [CrossRef]
- Tan, Q.; Fang, G.; Wen, X.; Lei, X.; Wang, X.; Wang, C.; Ji, Y. Bayesian stochastic dynamic programming for hydropower generation operation based on copula functions. Water Resour. Manag. 2020, 34, 1589–1607. [Google Scholar] [CrossRef]
- Yuan, L.; Zhou, J. Self-optimization system dynamics simulation of real-time short term cascade hydropower system considering uncertainties. Water Resour. Manag. 2017, 31, 2127–2140. [Google Scholar] [CrossRef]
- Schultz, G.A.; Plate, E.J. Developing optimal operating rules for flood protection reservoirs. J. Hydrol. 1976, 28, 245–264. [Google Scholar] [CrossRef]
- Sigvaldson, O. A simulation model for operating a multipurpose multireservoir system. Water Resour. Res. 1976, 12, 263–278. [Google Scholar] [CrossRef]
- Karamouz, M.; Vasiliadis, H.V. Bayesian stochastic optimization of reservoir operation using uncertain forecasts. Water Resour. Res. 1992, 28, 1221–1232. [Google Scholar] [CrossRef]
- Ahmed, I. On the Determination of Multi-Reservoir Operating Policy under Uncertainty. Ph.D. Thesis, The University of Arizona, Tucson, AZ, USA, 2001. [Google Scholar]
- Yamout, G.M.; Hatfield, K.; Romeijn, H.E. Comparison of new conditional value-at-risk-based management models for optimal allocation of uncertain water supplies. Water Resour. Res. 2007, 43, 1–13. [Google Scholar] [CrossRef]
- You, J.; Cai, X. Hedging rule for reservoir operations: 1. A theoretical analysis. Water Resour. Res. 2008, 44, 1–9. [Google Scholar] [CrossRef]
- You, J.; Cai, X. Hedging rule for reservoir operations: 2. A numerical model. Water Resour. Res. 2008, 44, 1–11. [Google Scholar] [CrossRef]
- Piantadosi, J.; Metcalfe, A.; Howlett, P. Stochastic dynamic programming (SDP) with a conditional value-at-risk (CVaR) criterion for management of storm-water. J. Hydrol. 2008, 348, 320–329. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, C.; Peng, Y.; Fu, G.; Zhou, H. A two stage Bayesian stochastic optimization model for cascaded hydropower systems considering varying uncertainty of flow forecasts. Water Resour. Res. 2014, 50, 9267–9286. [Google Scholar] [CrossRef]
- Datta, B.; Houck, M.H. A stochastic optimization model for real-time operation of reservoirs using uncertain forecasts. Water Resour. Res. 1984, 20, 1039–1046. [Google Scholar] [CrossRef]
- Ji, C.; Li, R.; Tian, K.; Zhang, Y.; Li, C. A coupling model of load adjustment for cascade hydropower stations based on inflow uncertainty: A case study of Jinping-guandi cascade hydropower stations. J. Hydraul. Eng. 2017, 48, 1–12. [Google Scholar]
- Wen, Q.; Xue, N. Study on the spill electricity price of central china power net. Autom. Electr. Power Syst. 2001, 25, 48–51. [Google Scholar]
- Shuai, W. The problems and countermeasures about abandoned water in China southwest hydropower station. Electr. Power 2017, 50, 171–175. [Google Scholar]
- Tan, Q.; Wen, X.; Sun, Y.; Lei, X.; Wang, Z.; Qin, G. Evaluation of the risk and benefit of the complementary operation of the large wind-photovoltaic-hydropower system considering forecast uncertainty. Appl. Energy 2021, 285, 116442. [Google Scholar] [CrossRef]
- Windsor, J.S. Optimization model for the operation of flood control systems. Water Resour. Res. 1973, 9, 1219–1226. [Google Scholar] [CrossRef]
- Wu, Z.; Hu, C.; Wang, B.; Liu, H. Risk analysis on limited water level of reservoirs in flood season and flood control system in midstream and downstream of Yellow River. J. Hydraul Eng. 2006, 37, 641–648. [Google Scholar]
- Xiao, Y. Research on optimal scheduling based on abandoned water probability. Express Water Resour. Hydropower 2015, 36, 22–24. [Google Scholar]
- Zhang, C. Research on Risk Analysis and Control method of Spillage for Cascade Reservoirs in Wujiang River Basin. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Sun, X.; Dong, S.; Xu, X. The Minimum Abandoned Water Optimization Model of Reservoir and Its Application. In Proceedings of the 2009 Fifth International Conference on Natural Computation, Tianjin, China, 14–16 August 2009; pp. 131–135. [Google Scholar]
- He, Y. Research on the cascade reservoirs surplus water risk control methods for frequent flood. China Rural. Water Hydropower 2019, 9, 162–170, 180. [Google Scholar]
- Yang, X.S. Cuckoo search and firefly algorithm: Overview and analysis. In Cuckoo Search and Firefly Algorithm; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–26. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).