Study on Peak Travel Avoidance Behavior of Car Travelers during Holidays
Abstract
1. Introduction
2. Literature Review
3. Methodology
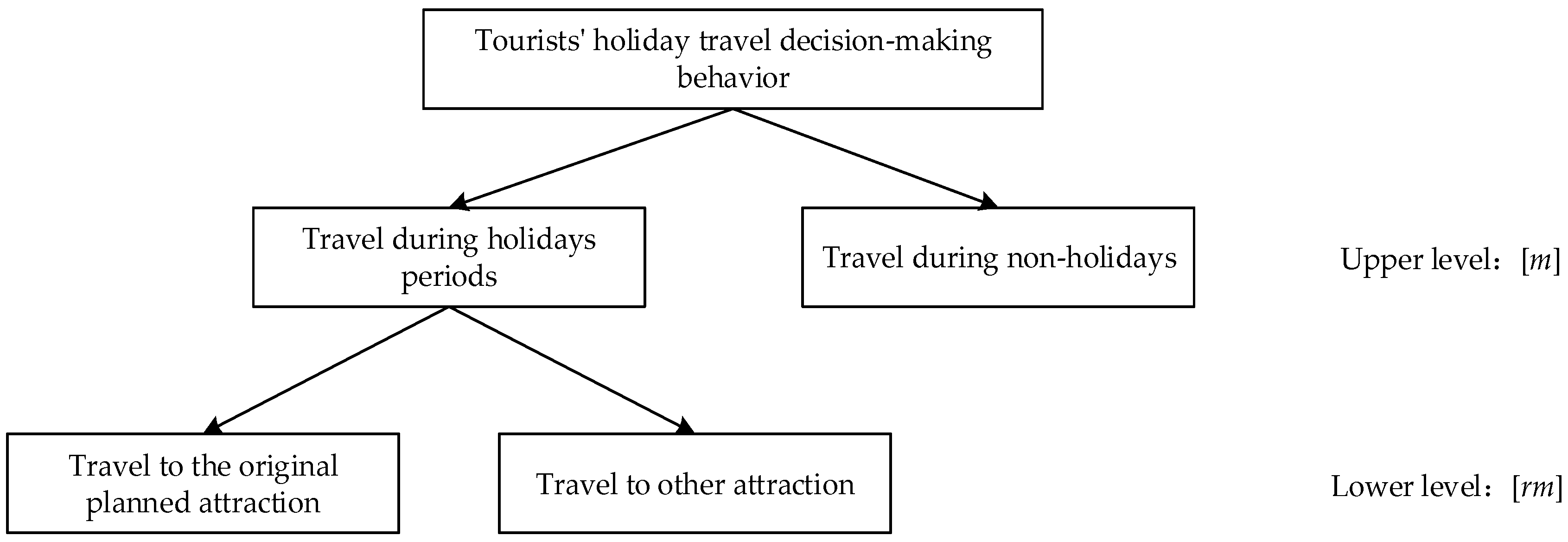
3.1. Framework of NL Model
3.2. Estimation Method of NL Model
4. Data and Modeling
4.1. Sample Description
4.2. Model Specification
5. Results and Discussion
5.1. Estimation Results of NL Model
- (1)
- Decision-making behavior analysis of travel destination of the lower model
- (2)
- Decision-making behavior analysis of travel time of upper model
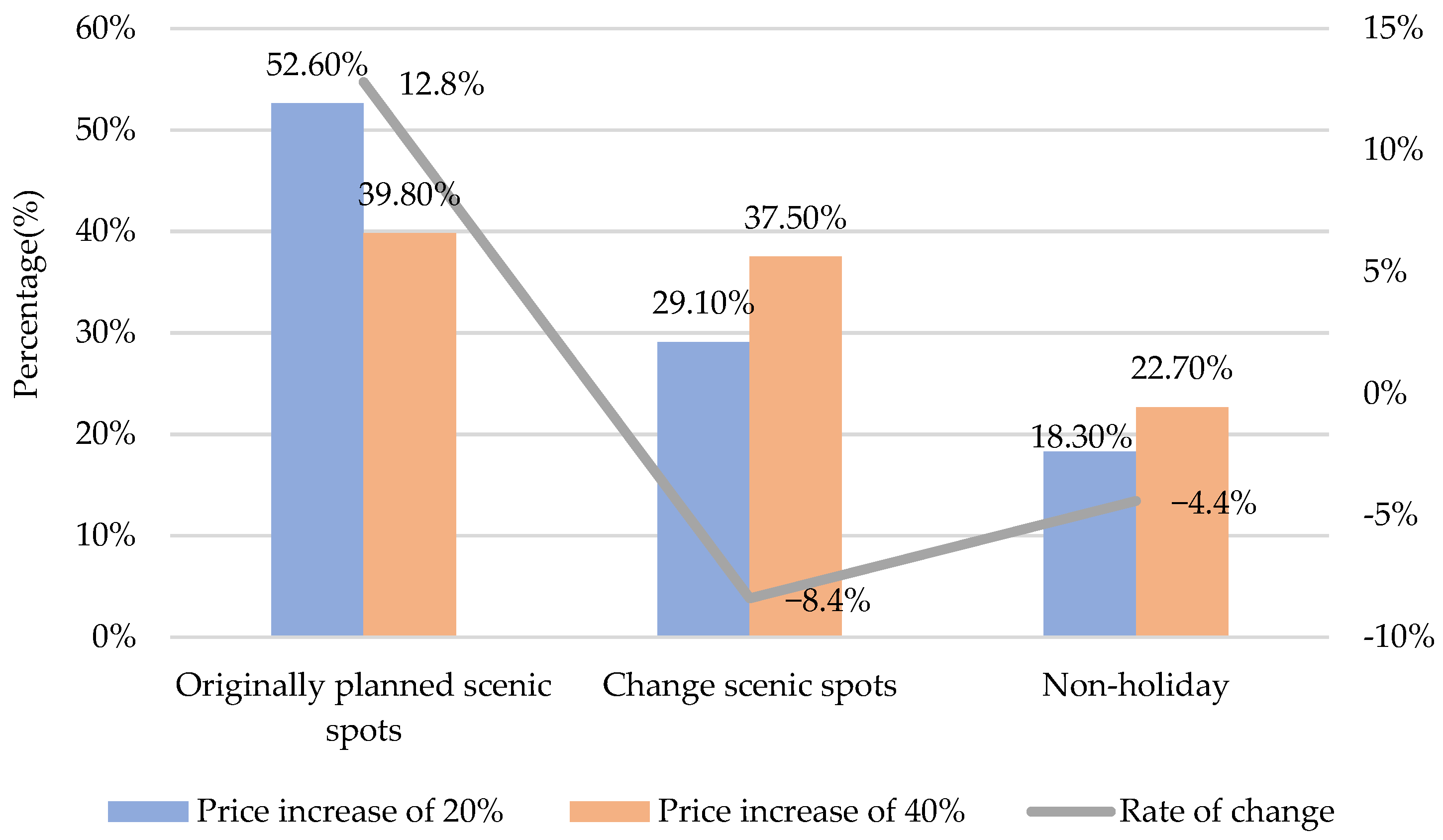
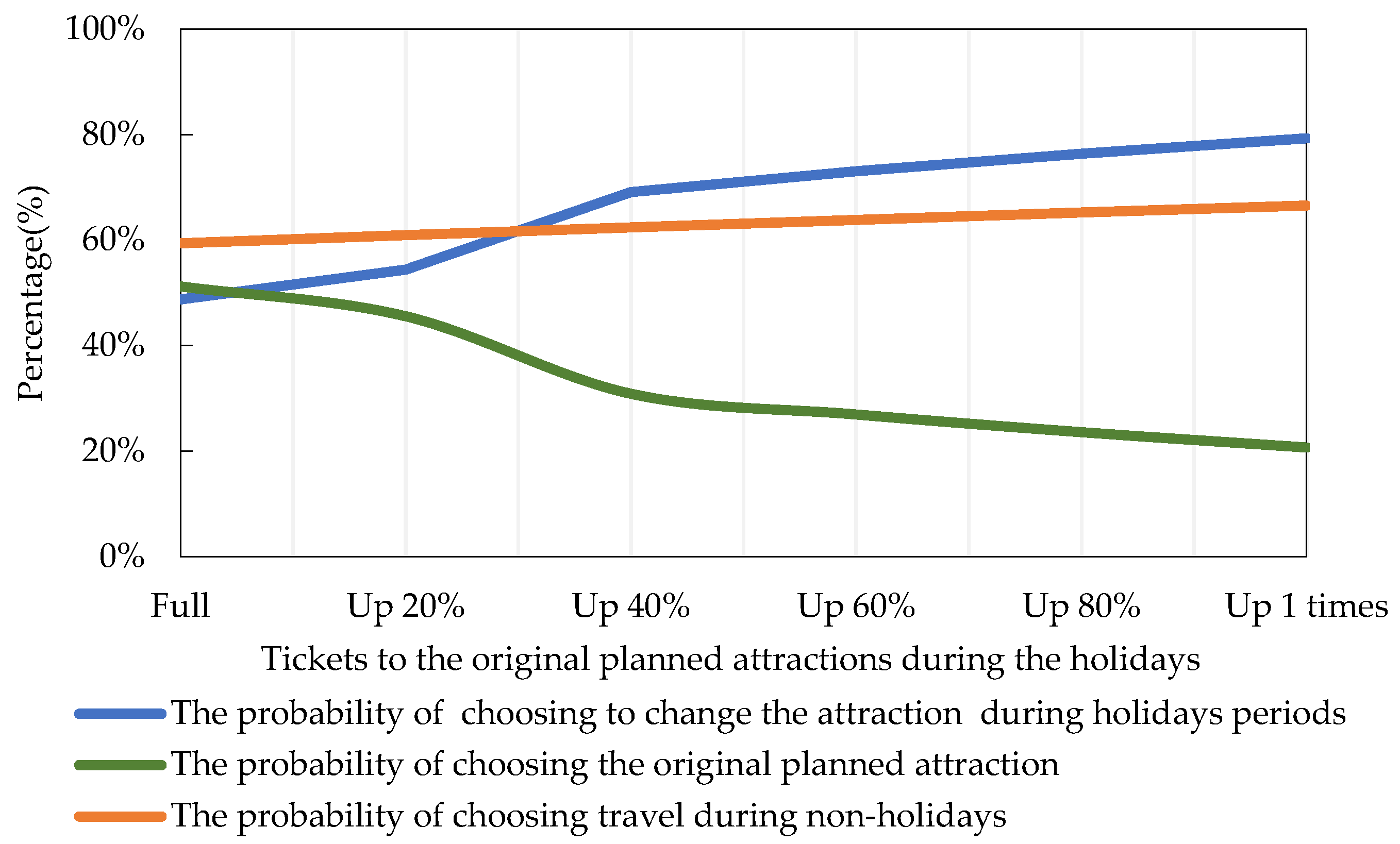
5.2. Sensitivity Analysis of Variables
6. Conclusions
- (1)
- According to the calibration results of the NL model, occupation, age, family resident population, the size of the tourist group and the relationship with the group, tour duration time, number of visits, tourism motivation, travel range, tourist attraction type, tourist attraction grade, crowding degree, traffic congestion around tourist attractions, holiday admission ticket prices, and non-holiday admission ticket prices significantly impact tourists’ travel time and destination decisions.
- (2)
- The results of the elasticity analysis show that travel time and destination decision behavior are elastic to the number of visits, the degree of road congestion around the original tourist attraction, and holiday admission ticket prices.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, Y.; Zhang, T.; Wang, M. Holiday travel behavior analysis and empirical study with Integrated Travel Reservation Information usage. Transp. Res. Part A Policy Pract. 2020, 134, 130–151. [Google Scholar] [CrossRef]
- Lin, X.; Susilo, Y.; Shao, C.; Liu, C. The Implication of Road Toll Discount for Mode Choice: Intercity Travel during the Chinese Spring Festival Holiday. Sustainability 2018, 10, 2700. [Google Scholar] [CrossRef]
- Bao, Y.; Xiao, F.; Gao, Z.; Gao, Z. Investigation of the traffic congestion during public holiday and the impact of the toll-exemption policy. Transp. Res. Part B Methodol. 2017, 104, 58–81. [Google Scholar] [CrossRef]
- Jin, Q.; Hu, H.; Kavan, P. Factors Influencing Perceived Crowding of Tourists and Sustainable Tourism Destination Management. Sustainability 2016, 8, 976. [Google Scholar] [CrossRef]
- Yang, G.; Han, Y.; Gong, H.; Zhang, T. Spatial-Temporal Response Patterns of Tourist Flow under Real-Time Tourist Flow Diversion Scheme. Sustainability 2020, 12, 3478. [Google Scholar] [CrossRef]
- Wu, J.; Zhou, X.; Peng, Y.; Zhao, X. Recurrence analysis of urban traffic congestion index on multi-scale. Phys. A Stat. Mech. Its Appl. 2022, 585, 126439. [Google Scholar] [CrossRef]
- Hammami, F. The impact of optimizing delivery areas on urban traffic congestion. Res. Transp. Bus. Manag. 2020, 37, 100569. [Google Scholar] [CrossRef]
- Rahman, M.M.; Najaf, P.; Fields, M.G.; Thill, J.C. Traffic congestion and its urban scale factors: Empirical evidence from American urban areas. Int. J. Sustain. Transp. 2022, 16, 406–421. [Google Scholar] [CrossRef]
- Brög, W.; Erl, E.; Ker, I.; Ryle, J.; Wall, R. Evaluation of voluntary travel behaviour change: Experiences from three continents. Transp. Policy 2009, 16, 281–292. [Google Scholar] [CrossRef]
- Eriksson, L.; Nordlund, A.M.; Garvill, J. Expected car use reduction in response to structural travel demand management measures. Transp. Res. Part F Traffic Psychol. Behav. 2010, 13, 329–342. [Google Scholar] [CrossRef]
- Habibian, M.; Kermanshah, M. Coping with congestion: Understanding the role of simultaneous transportation demand management policies on commuters. Transp. Policy 2013, 30, 229–237. [Google Scholar] [CrossRef]
- Salomon, I.; Mokhtarian, P.L. Coping with Congestion: Understanding the Gap between Policy Assumptions and Behavior. Transp. Res. Part D Trans. Environ. 1997, 2, 107–123. [Google Scholar] [CrossRef]
- Choo, S.; Mokhtarian, P.L. Individual responses to congestion policies: Modeling the consideration of factor-based travel-related strategy bundles. KSCE J. Civ. Eng. 2012, 16, 822–834. [Google Scholar] [CrossRef]
- Zhu, H.; Guan, H.; Han, Y.; Li, W. A study of tourists’ holiday rush-hour avoidance travel behavior considering psychographic segmentation. Sustainability 2019, 11, 3755. [Google Scholar] [CrossRef]
- Zhu, H.; Guan, H.; Han, Y.; Li, W. Can Road Toll Convince Car Travelers to Adjust Their Departure Times? Accounting for the Effect of Choice Behavior under Long and Short Holidays. Sustainability 2020, 12, 10470. [Google Scholar] [CrossRef]
- Lim, X.; Shao, C.; Dong, C. The behavior characteristics of inter-city travel under the implication of expressway toll-free policy during holiday. J. Transp. Sys. Eng. Inf. Technol. 2019, 19, 247–254. [Google Scholar]
- Chung, J.Y.; Kyle, G.T.; Petrick, J.F.; Absher, J.D. Fairness of prices, user fee policy and willingness to pay among visitors to a national forest. Tour. Manag. 2011, 32, 1038–1046. [Google Scholar] [CrossRef]
- Han, Y.; Yang, G.; Zhang, T. Spatial-temporal response patterns of tourist flow under entrance tourist flow control scheme. Tour. Manag. 2021, 83, 104246. [Google Scholar] [CrossRef]
- Wang, B.; Shao, C.; Li, J.; Weng, J.; Ji, X. Holiday travel behavior analysis and empirical study under integrated multimodal travel information service. Transp. Policy 2015, 39, 21–36. [Google Scholar] [CrossRef]
- Kaplan, S.; Manca, F.; Nielsen, T.A.S.; Prato, C.G. Intentions to use bike-sharing for holiday cycling: An application of the Theory of Planned Behavior. Tour. Manag. 2015, 47, 34–46. [Google Scholar] [CrossRef]
- Yang, L.; Shen, Q.; Li, Z. Comparing travel mode and trip chain choices between holidays and weekdays. Transp. Res. Part A Policy Pract. 2016, 91, 273–285. [Google Scholar] [CrossRef]
- Lia, J.; Wenga, J.; Shaoa, C.; Guo, H. Cluster-Based Logistic Regression Model for Holiday Travel Mode Choice. Proc. Eng. 2016, 137, 729–737. [Google Scholar] [CrossRef]
- Cools, M.A.W. Assessing the Impact of Public Holidays on Travel Time Expenditure: Differentiation by Trip Motive. Transp. Res. Rec. J. Transp. Res. Board 2010, 2157, 29–37. [Google Scholar] [CrossRef]
- Huybers, T. Domestic tourism destination choices—A choice modelling analysis. Int. J. Tour. Res. 2003, 5, 445–459. [Google Scholar] [CrossRef]
- Wen, C.; Yeh, Y. Modeling air travelers’ choice of flight departure and return dates on long holiday weekends. J. Air Transp. Manag. 2017, 65, 220–225. [Google Scholar] [CrossRef]
- Wang, B.; Shao, C.; Li, J.; Zhao, D.; Meng, M. Investigating the interaction between the parking choice and holiday travel behavior. Adv. Mech. Eng. 2015, 7, 1687814015589499. [Google Scholar] [CrossRef]
- Yang, L.; Zheng, G.; Zhu, X. Cross-nested logit model for the joint choice of residential location, travel mode, and departure time. Habitat Int. 2013, 38, 157–166. [Google Scholar] [CrossRef]
- Dargay, J.M.; Clark, S. The determinants of long distance travel in Great Britain. Transp. Res. Part A Policy Pract. 2012, 46, 576–587. [Google Scholar] [CrossRef]
- Wang, B.; Shao, C.; Ji, X. Dynamic analysis of holiday travel behaviour with integrated multimodal travel information usage: A life-oriented approach. Transp. Res. Part A Policy Pract. 2017, 104, 255–280. [Google Scholar] [CrossRef]
- Ben-Akiva, M.; Lerman, S.R. Discrete Choice Analysis: Theory and Application to Travel Demand; MIT Press: Cambridge, UK, 1985. [Google Scholar]
- Morley, C. Experimental destination choice analysis. Ann. Tour. Res. 1994, 21, 780–791. [Google Scholar] [CrossRef]
- Yang, X.; Chu, H. Study on Macro-Travel Impact Analysis of Staggered Shifts. J. Tongji Univ. 2006, 34, 899–903. [Google Scholar]
- Zhu, H.R.; Yang, X.G. Effect Mechanism of Stagger Shifts and Its Traffic Feasibility—A Case Study of Shanghai. J. Transp. Syst. Eng. Inf. Technol. 2005, 5, 77–81. [Google Scholar]
- Henderson, J.V. The economics of staggered work hours. J. Urban Econ. 1981, 9, 349–364. [Google Scholar] [CrossRef]
- Wilson, P.W. Residential location and scheduling of work hours. J. Urban Econ. 1992, 31, 325–336. [Google Scholar] [CrossRef]
- Arnott, R.; Palma, A.D.; Lindsey, R. A Structural Model of Peak-Period Congestion: A Traffic Bottleneck with Elastic Demand. Amer. Econ. Rev. 1993, 83, 161–179. [Google Scholar]
- Jansson, J.O.; Ljungberg, A. Staggered school hours to spread Peak demand for public transport–Benefits and costs. Int. J. Transp. Econ. 2009, 36, 141–160. [Google Scholar]
- Li, S. Determination of optimal work start time. Transport 2007, 22, 45–49. [Google Scholar] [CrossRef]
- Lin, C.X. Behavioral Economic Analysis of avoid peak Travel Policy. Integr. Transp. 2013, 5, 27–31. [Google Scholar]
- Chen, D.; Zhang, N.; Liu, L. Bottleneck Model for dual objective time-The principle of traffic staggered peak. J. Manag. Sci. 2015, 18, 52–60. [Google Scholar]
- Ben-Elia, E.; Ettema, D. Carrots versus sticks: Rewarding commuters for avoiding the rush-hour—A study of willingness to participate. Transp. Policy 2009, 16, 68–76. [Google Scholar] [CrossRef]
- Ben-Elia, E.; Ettema, D. Changing commuters’ behavior using rewards: A study of rush-hour avoidance. Transp. Res. Part F Traffic Psychol. Behav. 2011, 14, 354–368. [Google Scholar] [CrossRef]
- Ben-Elia, E.; Ettema, D. Rewarding rush-hour avoidance: A study of commuters’ travel behavior. Transp. Res. Part A Policy Pract. 2011, 45, 567–582. [Google Scholar] [CrossRef]
- Tillema, T.; Ben-Elia, E.; Ettema, D.; van Delden, J. Charging versus rewarding: A comparison of road-pricing and rewarding peak avoidance in the Netherlands. Transp. Policy 2013, 26, 4–14. [Google Scholar] [CrossRef]
- Zhang, Z.; Fujii, H.; Managi, S. How does commuting behavior change due to incentives? An empirical study of the Beijing Subway System. Transp. Res. Part F Traffic Psychol. Behav. 2014, 24, 17–26. [Google Scholar] [CrossRef]
- Thorhauge, M.; Cherchi, E.; Rich, J. How flexible is flexible? Accounting for the effect of rescheduling possibilities in choice of departure time for work trips. Transp. Res. Part A Policy Pract. 2016, 86, 177–193. [Google Scholar] [CrossRef]
- Wang, C.C. Feasibility of subway fare guiding peak travel avoidance based on tourist flow survey. Urban Rapid Rail Transit. 2014, 5, 52–54. [Google Scholar]
- Qin, H.M.; Gao, J.Q. Car Commuters’ Travel Behavior Based on Rewarding and Punishments Strategies. J. Transp. Sys. Eng. Inf. Technol. 2018, 18, 115–120. [Google Scholar]
- Lancaster, K.J. A New Approach to Consumer Theory. J. Political Econ. 1966, 74, 132–157. [Google Scholar] [CrossRef]
- Thurstone, L.L. A law of comparative judgement. Psychol. Rev. 1994, 101, 266. [Google Scholar] [CrossRef]
- Mcfadden, D. Conditional logit analysis of qualitative choice behavior. In Frontiers in Econometrics; Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- McFadden, D. Econometric models of probabilistic choice. In Structural Analysis of Discrete Data with Econometric Applications; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Pan, L.; Zhang, M.; Gursoy, D.; Lu, L. Development and validation of a destination personality scale for mainland Chinese travelers. Tour. Manag. 2017, 59, 338–348. [Google Scholar] [CrossRef]
- Williams, H.C.W.L. On the formation of travel demand models and economic evaluation measures of user benefit. Environ. Plan. A 1977, 9, 285–344. [Google Scholar] [CrossRef]
- Train, K.E. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Louviere, J.J.; Hensher, D.A.; Swait, J.D. Swait Stated Choice Methods: Analysis and Applications; Cambridge University Press: Cambridge, UK, 2000; pp. 34–82. [Google Scholar]
- Guan, H. The theoretical foundation of disaggregate model. In Disaggregate Model-A Tool for Traffic Behavior Analysis; China Communication Press: Beijing, China, 2004. [Google Scholar]
- Hess, S.; Daly, A.; Rohr, C.; Hyman, G. On the development of time period and mode choice models for use in large scale modelling forecasting systems. Transp. Res. Part A Policy Pract. 2007, 41, 802–826. [Google Scholar] [CrossRef][Green Version]
- Asakura, Y.; Iryo, T. Analysis of tourist behaviour based on the tracking data collected using a mobile communication instrument. Transp. Res. Part A Policy Pract. 2007, 41, 684–690. [Google Scholar] [CrossRef]
- Jones, S.; Hensher, D.A. Modelling corporate failure: A multinomial nested logit analysis for unordered outcomes. Br. Account. Rev. 2007, 39, 89–107. [Google Scholar] [CrossRef]
- Koppelman, F.S.; Wen, C. The paired combinatorial logit model: Properties, estimation and application. Transp. Res. Part B Methodol. 2000, 34, 75–89. [Google Scholar] [CrossRef]







| Variable Category | Variable | Parameter Setting and Definition |
|---|---|---|
| Socioeconomic characteristics | Occupation | 1 = staff and worker; 0 = teacher, student, retired/unemployed, freelance |
| Age (year) | 1 = 18–44; 0 = 45–65 | |
| Family resident population | 1 = 1 and 2 people; 0 = 3 and more | |
| Travel characteristics | Travel range | 1 = in the city and suburbs; 0 = cross-city |
| Last trip time | 1 = during holidays; 0 = before holidays | |
| Tourism characteristics | Tour duration time | divided into 1–7 days and above, value is 1–7, taking the actual value |
| Tourist group | divided into 1–7 persons and above, value is 1–7, taking the actual value | |
| Travel companion | 1 = family, friends/colleagues/classmates; 0 = alone and other | |
| Tourism motivation | 1 = leisure, relaxation, and sightseeing attractions 0 = expand knowledge, enjoy delicious food and shopping, spend time with family | |
| Tourist attraction characteristics | The number of visits | taking the actual value, 1 = the first tour, 2 = 1–2, 3 = 3–4, 4 = 5 times and more |
| Tourist attraction tour time | 1 = within 4 h; 0 = 4 h or more | |
| Original tourist attraction type | 1 = culture and nature; 0 = outdoor and entertainment | |
| Original tourist attraction grade | 1 = 3A and above; 0 = 2A and below and no grades | |
| Original attractions ticket price | 1 = RMB 100 or less; 0 = more than 100 yuan | |
| Crowding degree of the original tourist attraction | divided into 1–5 grades, the crowding degree increases step by step, and the value is 1–5 | |
| External conditions | Road congestion around the tourist attractions | divided into 0.5 h and 1 h, with values of 1 and 2 |
| Holiday attraction ticket price | divided into 20% increase and 40% increase, with values of 1 and 2 | |
| Non-holiday attraction ticket price | divided into 40% off and free, with values of 1 and 2 |
| Upper Level (Travel Time Choice) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Alternative sets | Select results | Age | Family resident population | Tour duration time | Travel range | Last trip time | Crowding degree | |
| Upper level | Lower level | Xm1 | Xm2 | Xm3 | Xm4 | Xm5 | Xm6 | |
| Holiday | Original tourist attraction | M11n | 1 | 0 | 0 | 1 | 1 | 1 |
| Change tourist attraction | M21n | |||||||
| Non-holiday | M2n | 0 | 1 | 1 | 0 | 0 | 0 | |
| Unknown parameter | λ2 | θ1 | θ2 | θ3 | θ4 | θ5 | θ6 | |
| Upper Level (Travel Time Choice) | Lower Level (Destination Choice) | |||||||
| Road congestion | Holiday attractions ticket price | Non-holiday attractions ticket price | Occupation | Tourist group | Relationship | Tour duration time | The number of visits | |
| Xm7 | Xm8 | Xm9 | X(r|m)1 | X(r|m)2 | X(r|m)3 | X(r|m)4 | X(r|m)5 | |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 0 | ||||
| 1 | 0 | 1 | ||||||
| θ7 | θ8 | θ9 | β1 | β2 | β3 | β4 | β5 | |
| Lower Level (Destination Choice) | ||||||||
| Tourism motivation | Tourist attraction tour time | Tourist attraction type | Tourist attraction grade | Attractions ticket price | Crowding degree | Road congestion | Holiday attractions ticket price | |
| X(r|m)6 | X(r|m)7 | X(r|m)8 | X(r|m)9 | X(r|m)10 | X(r|m)11 | X(r|m)12 | X(r|m)13 | |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | |
| β6 | β7 | β8 | β9 | β10 | β11 | β12 | β13 | |
| Level | Variable | Estimate | Std. Err. | t Test | |
|---|---|---|---|---|---|
| Lower Level | Inherent dummy | ASC | 2.09 | 0.591 | 3.54 *** |
| Occupation | X(r|m)1 | 0.449 | 0.159 | 2.83 *** | |
| Tourist group | X(r|m)2 | 0.106 | 0.0484 | 2.19 ** | |
| Relationship with tourist group | X(r|m)3 | −1.47 | 0.321 | −4.59 *** | |
| Tour duration time | X(r|m)4 | 0.895 | 0.162 | 5.53 *** | |
| The number of visits | X(r|m)5 | −1.64 | 0.224 | −7.35 *** | |
| Tourism motivation | X(r|m)6 | 0.782 | 0.188 | 4.17 *** | |
| Tourist attraction tour time | X(r|m)7 | 0.344 | 0.162 | 2.13 ** | |
| Tourist attraction type | X(r|m)8 | 0.599 | 0.203 | 2.95 *** | |
| Tourist attraction grade | X(r|m)9 | 0.343 | 0.177 | 1.94 ** | |
| Attractions ticket price | X(r|m)10 | 0.422 | 0.185 | 2.28 ** | |
| Crowding degree of spot | X(r|m)11 | −0.47 | 0.0809 | −5.82 *** | |
| Road congestion | X(r|m)12 | 0.828 | 0.136 | 6.08 *** | |
| Holiday attractions ticket price | X(r|m)13 | 0.556 | 0.135 | 4.11 *** | |
| Model statistics: L(0): −813.755; L(): −652.612; −2(L(0) − L()): 322.286; : 0.213; : 0.202 | |||||
| Level | Variable | Estimate | Std. Err. | t Test | |
| Upper Level | Inherent dummy | ASC | 2.85 | 0.595 | 4.79 *** |
| Age | X(m)1 | 0.246 | 0.142 | 1.73 * | |
| Family resident population | X(m)2 | 0.571 | 0.131 | 4.37 *** | |
| Tour duration time | X(m)3 | 0.139 | 0.0675 | 2.06 ** | |
| Travel range | X(m)4 | 0.354 | 0.145 | 3.24 *** | |
| Last trip time | X(m)5 | 0.53 | 0.185 | 2.86 *** | |
| Crowding degree of spot | X(m)6 | −0.131 | 0.0606 | −2.16 ** | |
| Road congestion | X(m)7 | 0.241 | 0.12 | 2.01 ** | |
| Holiday attractions ticket price | X(m)8 | −0.267 | 0.122 | −2.2 ** | |
| Non-holiday attractions ticket price | X(m)9 | 0.449 | 0.122 | 3.68 *** | |
| Inclusive coefficients | X(m)10 | 0.273 | 0.069 | 3.96 *** | |
| Model statistics: L(0): −966.940; L(): −699.437; −2(L(0) − L()): 535.007; : 0.277; : 0.263 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Guan, H.; Han, Y.; Li, W. Study on Peak Travel Avoidance Behavior of Car Travelers during Holidays. Sustainability 2022, 14, 10744. https://doi.org/10.3390/su141710744
Zhu H, Guan H, Han Y, Li W. Study on Peak Travel Avoidance Behavior of Car Travelers during Holidays. Sustainability. 2022; 14(17):10744. https://doi.org/10.3390/su141710744
Chicago/Turabian StyleZhu, Haiyan, Hongzhi Guan, Yan Han, and Wanying Li. 2022. "Study on Peak Travel Avoidance Behavior of Car Travelers during Holidays" Sustainability 14, no. 17: 10744. https://doi.org/10.3390/su141710744
APA StyleZhu, H., Guan, H., Han, Y., & Li, W. (2022). Study on Peak Travel Avoidance Behavior of Car Travelers during Holidays. Sustainability, 14(17), 10744. https://doi.org/10.3390/su141710744






