Abstract
This study develops a data-driven, comprehensive evaluation method to improve the science and technology innovative efficiency of industrial enterprises above designated size (hereinafter “industrial enterprises”). Based on an innovation value chain perspective, a two-stage evaluation index system is constructed. Thereafter, the Pearson correlation coefficient method was used to analyze correlations in the constructed index system. A two-stage network data envelopment analysis model with additional intermediate input was constructed to measure and evaluate industrial enterprises’ science and technology innovative efficiency from three aspects—research and development (R&D), commercialization, and comprehensive efficiencies—to reveal the temporal and spatial evolution. The feasibility and effectiveness of the method was verified using the statistical data of industrial enterprises in 16 cities in Anhui Province, China, from 2011 to 2020. The results show that the comprehensive efficiency of the scientific and technological innovation of industrial enterprises in these cities is at a medium level, and the efficiency development of the two stages is uncoordinated; the two-stage efficiency distribution tends to be “high R&D–high commercialization” and “low R&D–low commercialization”, and targeted countermeasures and suggestions are proffered. This study provides a reference for the sustainable development of industrial enterprises in relevant regions.
1. Introduction
With the global energy crisis and increasingly serious environmental pollution [1], scientific and technological innovation has become the main driving force to support the development of countries [2]. Industrial enterprises above a designated scale are the backbone of national economic development and the most important carrier of technological innovation activities [3,4]. Thus, it is necessary to base industrial enterprise development on innovation and rely on innovation to promote quality [5], efficiency, and dynamic change [6,7] toward realizing a high-quality and sustainable development of regional economies [8]. Innovation-driven development is an urgent requirement for achieving high-quality and sustainable global economic development. Industrial enterprises are the leading enterprises in the national economy. The historical processes of developed countries show that the national industrial level is synchronized with the national scientific, technological, and economic development levels [9]. However, China’s industrial enterprises still encounter some problems, such as weak independent innovation capabilities, lack of core technologies, and redundant innovation resources [10,11]. In particular, with the proposal of the “Industry 5.0” development strategy [12,13], China faces increasingly significant challenges in industrial technology innovation [14,15]. Therefore, conceptualizing approaches to improve the scientific and technological innovation efficiency levels of industrial enterprises [16] is exigent to promote the sustainable development of regional economies.
This study aims to construct a data-driven, comprehensive evaluation method to quantitatively measure and evaluate the scientific and technological innovation efficiency of industrial enterprises, reveal its temporal and spatial evolution law, and clarify the bottleneck restricting its improvement. This can facilitate the realization of the goal of optimizing/improving the scientific and technological innovation path and efficiency of industrial enterprises. Scholars have been widely concerned with research on science and technology innovation for industrial enterprises. In our literature review, the primary focus is the research on industrial enterprises’ science and technology innovative efficiency from three aspects: influencing factors [17], evaluation indicators [18], and evaluation methods [19,20].
At present, the influencing factors of industrial enterprises’ science and technology innovative efficiency are concentrated on macro policies and industrial enterprises. In terms of macro policies, scholars have revealed the importance of industry—university research cooperation [21], tax subsidies [22,23], policy mix [24], government support [25], and environmental regulation [26,27] to improve industrial enterprises’ science and technology innovative efficiency. Zhu et al. [28] discussed the impact of environmental regulations on the technological innovation efficiency of Chinese industrial enterprises from a spatial analysis perspective. Tang et al. [29] explored the impact of command-and-control regulation on the basic innovation efficiency of Chinese industrial enterprises. For industrial enterprises themselves, focus should be placed on green investment [30], organizational structure optimization [31], and corporate governance [32] to accelerate science and technology innovation efficiency improvement. Hou et al. [33] used a stochastic frontier model to explore the impact of industry–university cooperation and government funding on industrial enterprises’ innovation efficiency. Miao et al. [34] noted that reducing energy consumption and increasing investment in pollution control have significant roles in promoting industrial enterprises’ technological innovation efficiency.
Regarding evaluation indicators, most existing studies have created single-stage [35] and two-stage [36] evaluation index systems from an input-output perspective [37,38]. Full-time equivalent of research and development (R&D) personnel [39] and internal R&D expenditure [40] are common input indicators, whereas the number of invention patents [41,42] and new product sales revenue [43,44] are common output indicators. Guan and Zuo [45] constructed a science and technology innovation evaluation index system from two stages: knowledge production process and knowledge commercialization process. Lin et al. [46] developed three input indicators—R&D personnel, investment in technical renovation and internal R&D investment, and full-time equivalent of R&D personnel—and three output indicators: number of invention patent applications, number of new product development projects, and new product sales revenue—and used the data envelopment analysis (DEA) window analysis method to evaluate the technological innovation efficiency of seven categories of industrial enterprises in China from 2006 to 2015. Miao et al. [47] constructed a two-stage green technology innovation evaluation index system, including energy and bad output. In addition, Chen et al. [48] divided the science and technology innovation of industrial enterprises into three stages—technology development, achievement transformation, and industrialization—and built a three-stage evaluation index system.
Many methods are available for evaluating science and technology innovative efficiency, including subjective evaluation methods such as the analytic hierarchy process [49,50] and fuzzy comprehensive evaluation [51], and objective evaluation methods such as factor analysis [52], ordinary least squares regression analysis [53], and stochastic frontier analysis [54,55,56]. Further, several studies have been conducted from the input-output perspective [57,58]; thus, the DEA method [59,60] has been widely used. Zhang and Liu [61] adopted BC2-DEA and Malmquist-DEA models to measure the overall technological innovation efficiency of industrial enterprises above designated size in China. In addition, scholars have gradually adopted efficiency stage theory to break the “black box” of efficiency research [62]. Relational network DEA models [63,64] have been constructed, and two-stage [65] and three-stage DEA models [66] have gradually become widely used. Xiao et al. [67] applied a DEA model of a factor correlation network to measure the overall and stage efficiency of technological innovation in industrial enterprises. Wang et al. [68] divided innovation into R&D and marketing stages and used the non-radial DEA method to measure innovation efficiency in China’s new energy enterprises. Du et al. [69] used a two-stage network DEA of shared investment to measure the technological innovation efficiency of regional industrial enterprises. Chen et al. [48] used a three-stage chain network DEA model to evaluate the green innovation efficiency of Chinese industrial enterprises. Miao et al. [47] used a two-stage SBM-DEA model to measure the green innovation efficiency of industrial enterprises in China’s provinces. Zeng et al. [70] used the five-stage DEA model to evaluate the technological innovation efficiency of China’s strategic emerging industries. Popelo et al. [71] used the dialectics of scientific cognition to identify the contradictions and interrelations of the innovation and development of the main bodies in the regional economic system
According to our literature review, scholars have conducted extensive research on industrial enterprises’ science and technology innovative efficiency, which provides a reference for the work conducted in the present study. However, there are still some limitations and expandable areas. First, in relation to research trends, scholars have increasingly studied industrial enterprises’ science and technology innovative efficiency from a multi-stage perspective, but the evolution of its spatial and temporal pattern and its influencing factors have not been comprehensively explored. Second, from a research perspective, most extant studies have focused on the national, regional, and industrial levels, and relatively few studies have combined regions with industrial enterprises above designated size. Third, in terms of research methods, different evaluation index systems or DEA models will lead to different results, which also presents opportunities for further research on science and technology innovative efficiency. To meet the abovementioned challenges, this study used industrial enterprises above the regional scale (hereinafter “industrial enterprises”) as the research object and constructed a two-stage network DEA model with additional intermediate input to measure and assess industrial enterprises’ science and technology innovative efficiency, reveal its space–time evolution law, clarify the key factors affecting efficiency improvement, and then put forward targeted optimization suggestions.
This research has strong theoretical value and practical significance. Regarding the theoretical value, first, taking regional industrial enterprises as the research object, the comparative study of science and technology innovative efficiency plays a representative role and provides a new research vision. Second, this study builds a two-stage network DEA model with additional intermediate input to enrich the research methodology. Third, this study constructs a data-driven, comprehensive evaluation mechanism for the science and technology innovation of industrial enterprises that is “measurable, evaluable, and optimizable” to establish a theoretical path. In terms of practical significance, first, at the enterprise level, this study can facilitate the optimization of innovation resource allocation and the establishment of a phased dynamic development system and mechanism of science and technology innovation. Second, at the government level, this study is conducive to the rational investment of government innovation funds and can guide regional industrial enterprises to change their innovative development modes. Third, at a practical level, this study not only expands the theory of science and technology innovation but also provides an important reference for measuring and improving the science and technology innovative efficiency of industrial enterprises in the same type of urban agglomeration.
The remainder of this paper is organized as follows. Section 2 describes the study’s method. Section 3 presents a case study using 16 cities in Anhui Province as an example, to examine the method’s effectiveness and feasibility, and then puts forward countermeasures and suggestions. Finally, Section 4 is the conclusion.
2. Method
This section provides a comprehensive introduction to the methods used to measure and evaluate the regional industrial enterprises’ science and technology innovative efficiency, including method flow, data collection and processing, and data modeling.
2.1. Method Flow
This study examines the efficiency and temporal and spatial evolution of science and technology innovation in data-driven industrial enterprises from an innovation value chain perspective. The classic DEA model [72] regards the industrial enterprises’ science and technology innovation as a “black box”, ignoring the intermediate links and relationship between links of the science and technology innovation systems, as well as the science and technology innovation process and transmission mechanism of industrial enterprises. In fact, the process of science and technology innovation in industrial enterprises has obvious two-stage characteristics [73]. Thus, the two-stage network DEA model [74,75] is an effective method for considering difficulties in this regard. The two-stage network DEA model divides the “black box” into two stages for research. Specifically, it can analyze and evaluate the system’s internal structure [76] and evaluate the performance of the two-stage multi-input and multi-output unit. Therefore, this study proposes a two-stage network DEA evaluation model with additional intermediate input to measure, assess, and improve the stage efficiency and comprehensive efficiency of science and technology innovation in regional industrial enterprises, to promote the high-quality development of regional industrial enterprises. The method flowchart is shown in Figure 1.
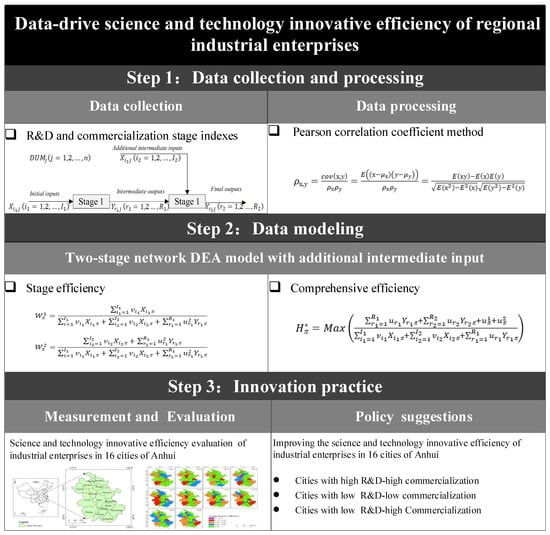
Figure 1.
Data-driven flowchart of the evaluation method.
Step 1: Data collection and processing. The data of science and technology innovation research and development and commercialization of regional industrial enterprises are collected, involving two-stage input and output indicators. The Pearson correlation coefficient method is used to process the index data and test the correlation of the index.
Step 2: Data modeling. A two-stage network DEA evaluation model with additional intermediate input is built. The model is applied to measure the stage efficiency and comprehensive efficiency of regional industrial enterprises’ science and technology innovation.
Step 3: Innovative practice. The model is applied to 16 cities in Anhui Province to reveal the temporal and spatial evolution law of their industrial enterprises’ science and technology innovative efficiency, to test the model’s effectiveness. Finally, targeted countermeasures and suggestions are put forward according to the evaluation results.
2.2. Data Collection and Processing
Drawing on the views of relevant scholars [77], this study divided industrial enterprises’ science and technology innovation into two stages: R&D stage and commercialization stage. Combined with the characteristics of industrial enterprises’ science and technology innovation, and following the principles of scientificity, systematization, operability, dynamics, and comparability, this study comprehensively collected the relevant input and output indicator data of regional industrial enterprises’ science and technology innovation in two stages. R&D performed is to acquire new knowledge and technology, and the R&D investment stage includes personnel investment and financial resources. Based on the views of Yang et al. [35] and Su et al. [78], this study selects the full-time equivalent of R&D personnel and internal expenditure of R&D funds as human and financial inputs at the R&D stage, whereat outputs include patents and knowledge. Patents are naturally related to science and technology innovation. Owing to the low (high) conversion rate (cost) of papers, monographs, and other achievements, this study only used the number of invention patent applications and that of utility model and design applications as the R&D stage output based on the views of Miao et al. [47] and Du et al. [69]. At the commercialization stage, science and technology achievements are transformed from virtual technology into specific commercial products, and enterprises realize economic benefits. In the commercialization stage, in addition to the output from the R&D stage as the input, there is also capital investment. Part of the capital is used to introduce technology, while another part is used for technological transformation and upgrades. Referring to the views of relevant scholars [79,80], the selected evaluation indicators were the technological transformation expenditure and the technology introduction and absorption expenditure. The output indicator in the commercialization stage was the new product sales revenue based on the views of scholars [35,36]. Table 1 shows the evaluation index system and reference basis.

Table 1.
Evaluation index system.
Based on the determination of the index system, the index data are collected, and the data are obtained from the statistical data in the statistical yearbook of the research area. We conducted basic analysis on the collected index data, including descriptive statistical analysis and Pearson correlation analysis, and analyzed the characteristics of the collected data and correlations between the indicators, to better perform the empirical analysis of the following models. To obtain reliable empirical results, it is necessary for the selected input indicators and output indicators to have a strong correlation. This study used the Pearson correlation coefficient method [81] to test the correlation coefficient of the input and output indices. Suppose there are two variables, and , and the relevant formula is as follows:
where the value range of correlation coefficient is [−1, 1]. The greater the absolute value of correlation coefficient , the stronger the correlation.
2.3. Data Modeling
For the two-stage DEA model proposed by Kao et al. [82], it must be ensured that the output of substage 1 is completely consistent with the input of substage 2, and the scope of application is small. The two-stage network DEA of sharing investment constructed by Khoveyni and Eslami [83] focuses on two-stage investment sharing, while it ignores the difference in characteristics of the two stages and the heterogeneity of resource demand. Wang et al. [84] constructed a two-stage network DEA model with shared input, additional intermediate input, and free intermediate output. Chen et al. [85] also proposed a two-stage network DEA model, which considers additional intermediate input and shared input but does not consider free intermediate output. These models have laid a solid foundation for this study, but the selection and construction of models still need to be carried out in combination with the actual situation. Herein, considering the actual situation of the scientific and technological innovation process of regional industrial enterprises, we fully understand the structural subordination between each stage, consider the heterogeneity of stage inputs, and propose a two-stage network DEA model with additional intermediate inputs. This is essentially a special network DEA model that can reflect stronger substage efficiency discrimination ability and better efficiency measure adjustment ability, as well as help the government and enterprise managers identify ineffective sources and efficiency improvement directions for the science and technology innovation process. Figure 2 shows the modeling diagram of the two-stage network DEA model with additional intermediate inputs.
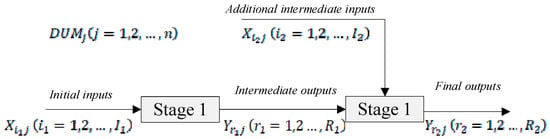
Figure 2.
Modeling concept diagram of a two-stage network DEA model with additional intermediate inputs.
According to the conceptual model shown in Figure 2, it is assumed that there are decision-making units in the model, which are expressed as . In the first stage, the input index is expressed by vector , and the output index is expressed by vector . The output index of the first stage, as an intermediate output, becomes part of the input in the second stage. In the second stage, under the joint action of intermediate output in the first stage and additional intermediate input , the output of the second stage is also the final output .
Regarding the efficiency decomposition method, Chen et al. [86] advocated for weighting each stage differently to calculate the overall efficiency through the weighting method, which was also adopted as follows:
where represents the weight of stage 1, represents the weight of the second stage and should meet . The weight of efficiency measures the impact of the efficiency of each substage on the overall efficiency. For a specific decision-making unit , a set of reasonable weights can be defined as the proportion of the input in each stage to the total input, as follows:
where the numerator represents the weighted value of each substage input, and the denominator is the weighted value of all inputs. To avoid the extreme values of 0 or 1 in the weight, we also set some constraints for the weight, namely and . , , and represent, respectively, the weight of , , and and , where represents the stage corresponding to the weight. Charnes, Cooper, and Rhodes [65] provided the infinitesimal with non-Archimedes . In this study, we set the lower limit for the weight values of these variables, that is, the non-Archimedes infinitesimal.
Referring to Kao and Hwang [82], this study assumed that the weight of intermediate output in each stage would be equal , because they essentially serve the role of variables of the same nature in different stages, and have the same status as a whole.
Assumption is the free variable of the first stage; is the free variable of the second stage. Drawing on the hypothesis of relevant scholars [2,80] regarding variable return on scale, in each substage, the efficiency of can be expressed as follows:
The efficiency value range of the substage is clearly [0, 1]. Under the variable return on scale assumption, the overall efficiency of can be obtained using the following formula:
3. Case Study
We used industrial enterprises above designated size as the research object, and selected relevant statistical data on the science and technology innovation of industrial enterprises in 16 cities in Anhui Province from 2011 to 2020 to verify this method. The main data was obtained from the Anhui Statistical Yearbook.
3.1. Background
Anhui is located in the eastern region of the Chinese Mainland and is part of East China. It governs 16 prefecture-level cities (Figure 3). Under the background of Anhui undertaking the transfer of high-quality industries in the Yangtze River Delta, the 16 cities in Anhui, driven by science and technology innovation and focusing on improving the industrial chain, have accelerated the high-quality leap forward of industrial development, while the overall strength of the industrial economy has been continuously enhanced, and the quality and efficiency steadily improved. In December 2020, the added value of industries above designated size in Anhui Province increased by 12.0% year-to-year, and the product sales rate for industrial enterprises was 98.1%, representing an increase of 0.8 percentage points year-to-year. The supporting and leading roles of industrial enterprises’ science and technology innovation have been further highlighted in the construction of a new development pattern. However, innovation-driven industrial development also includes many problems, such as weak independent innovation ability, lack of core technology, and redundancy of innovation resources, which affect science and technology innovative efficiency. However, questions remain regarding the science and technology innovative efficiency of industrial enterprises in the 16 cities of Anhui, including what problems have been encountered and how improvements can be made. This issue urgently needs to be addressed. Thus, this study measured, evaluated, and optimized the science and technology innovative efficiency of industrial enterprises in 16 cities of Anhui, to provide a decision-making reference for relevant departments.
Figure 3.
Administrative districts of 16 cities in Anhui Province.
3.2. Results
3.2.1. Data Acquisition and Processing Results
To ensure the accuracy of index data selection and the reliability of empirical analysis, SPSS software was used to obtain descriptive statistics of the samples, as shown in Table 2. Pearson correlation analysis was used to verify the correlation matrix between input and output variables, as shown in Figure 4.

Table 2.
Samples descriptive statistical analysis of related variables.
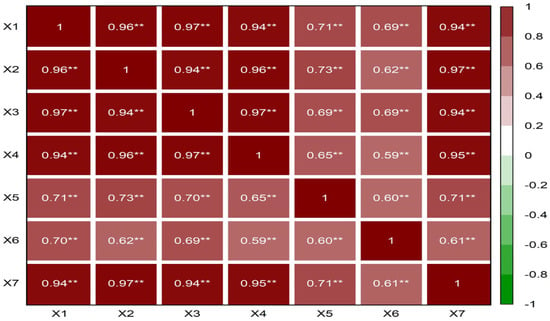
Figure 4.
Correlation matrix of related variables. ** p < 0.01.
In using a two-stage network DEA model to measure and evaluate regional industrial enterprises’ science and technology innovative efficiency, input and output indicator selection was very important. As Figure 3 shows, the input and output indicators selected in this study were significantly correlated at the 0.01 level, meeting the preconditions for using the two-stage DEA model for analysis.
3.2.2. Two-Stage Network DEA Measurement Results
In this study, we used MaxDEA 8 Ultra software and a two-stage network DEA model with additional intermediate input to process the input-output data on the science and technology innovation of industrial enterprises in 16 cities in Anhui Province. We obtained the two-stage dynamic evaluation results, including R&D efficiency (Table 3), commercialization efficiency (Table 4), and comprehensive efficiency (Table 5).

Table 3.
R&D efficiency from 2011 to 2020.

Table 4.
Commercialization efficiency from 2011 to 2020.

Table 5.
Comprehensive efficiency from 2011 to 2020.
3.3. Results Analysis
3.3.1. Analysis of Temporal and Spatial Evolution
To comprehensively analyze the science and technology innovative efficiency of industrial enterprises in 16 cities of Anhui, and assess the differences between cities, we clustered the results on R&D efficiency, commercialization efficiency, and comprehensive efficiency. Efficiency values between 0.85–1 were regarded as “high efficiency”, 0.65–0.85 was “good efficiency”, 0.45–0.65 was “medium efficiency”, and below 0.45 was “low efficiency”. On this basis, the temporal and spatial differences in the science and technology innovative efficiency in the 16 cities are shown in Figure 5, Figure 6 and Figure 7.
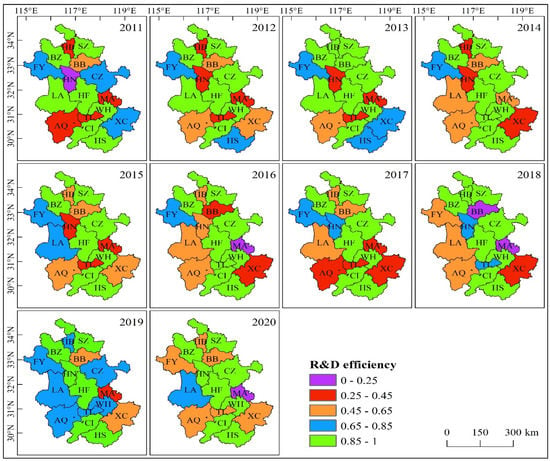
Figure 5.
Spatial and temporal evolution of the R&D efficiency for industrial enterprises in Anhui Province.
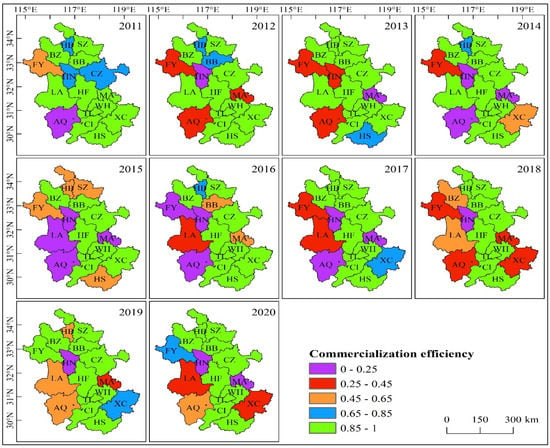
Figure 6.
Spatial and temporal evolution of the commercialization efficiency for industrial enterprises in Anhui Province.
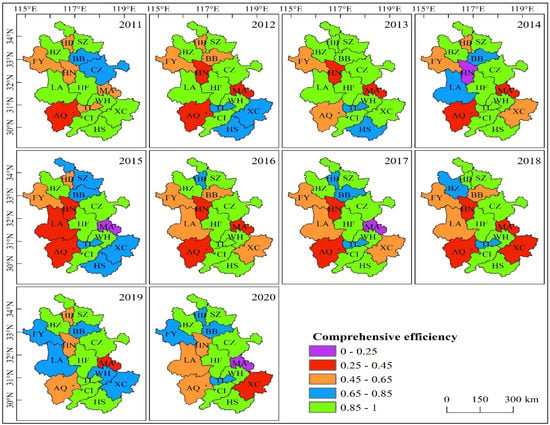
Figure 7.
Spatial and temporal evolution of the comprehensive efficiency for industrial enterprises in Anhui Province.
As Figure 5 shows, the largest number of cities with high R&D efficiency was nine in 2013, and the smallest was six in 2019. R&D efficiency in Suzhou, Bozhou, Hefei, and Chizhou was always at the high efficiency level, and the R&D efficiency value was relatively high. The R&D efficiency of Huaibei, Bengbu, Lu’an, Anqing, Tongling, and Xuancheng fluctuated greatly during the study period. Huainan fluctuated in an upward trend overall, moving from low efficiency to medium efficiency, to good efficiency, to high efficiency. Chuzhou and Huangshan showed good R&D efficiency for two years and high efficiency for eight years. Fuyang’s R&D efficiency was at the medium efficiency level in 2018 and 2019, and at the good efficiency level for the other years in the study period. Wuhu showed good R&D efficiency in 2019, and high efficiency in all other years. In 2014, Ma’anshan had medium R&D, but low efficiency in the other years.
As Figure 6 shows, the number of cities with commercial efficiency at the high efficiency level was the largest in 2011, and the smallest was eight in 2015. The commercialization efficiency in Hefei, Wuhu, Tongling, and Chizhou remained high throughout the study period, and the commercialization efficiency value was relatively high. The commercialization efficiency of Huaibei, Fuyang, and Xuancheng fluctuated greatly during the study period. Suzhou, Chuzhou, and Bozhou showed high efficiency for 9 of the 10 years. Bengbu and Huangshan were at the high efficiency level for 8 of the 10 years. Lu’an’s commercialization efficiency was at a high from 2011 to 2014, but decreased significantly over the following six years, remaining at or below the medium efficiency level. The commercialization efficiency of Anqing was always low from 2011 to 2018, but then rose to medium efficiency 2019 to 2020. Ma’anshan showed high commercialization efficiency in 2011, medium efficiency in 2016, and low efficiency in the other years. Huainan showed good efficiency in 2011, but low efficiency in the other years.
As Figure 7 shows, the largest number of cities at the high comprehensive efficiency level was ten in 2013, and the smallest was five in 2015. The comprehensive efficiency of the science and technology innovation for industrial enterprises in Hefei and Chizhou remained at a high throughout the study period, and the commercialization efficiency value was relatively high. The comprehensive efficiency of Huaibei, Bengbu, Lu’an, Tongling, Xuancheng, Anqing, and Huangshan fluctuated between 2011 and 2020. Suzhou, Chuzhou, Bozhou, and Wuhu showed good efficiency for one year and high efficiency for nine years. Fuyang’s comprehensive efficiency remained at the medium level for eight consecutive years, and then increased to high efficiency from 2019 to 2020. Huainan’s comprehensive efficiency was at the medium level in 2011, and remained at the low level from 2012 to 2018, before increasing to the medium level from 2019 to 2020. Ma’anshan showed medium comprehensive efficiency in 2011, and low efficiency in other years.
3.3.2. Two-Dimensional Distribution Analysis
Based on the temporal-spatial evolution analysis results, we further analyzed the relationship between R&D and commercialization for industrial enterprises in 16 cities of Anhui Province, and comprehensively analyzed the differences between these two dimensions. Taking the two-stage efficiency of 0.850 in each city as the cutoff point, we divided 16 cities into four combination modes: high R&D–high commercialization, low R&D–high commercialization, high R&D–low commercialization, and low R&D–low commercialization. The two-dimensional distribution results of R&D efficiency and commercialization efficiency are shown in Figure 8.
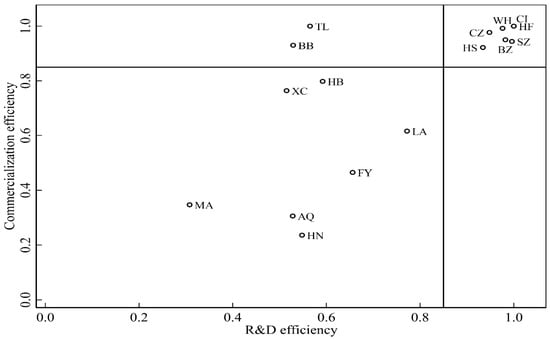
Figure 8.
Comparison of two-dimensional distribution.
The high R&D–high commercialization category included Huangshan, Chuzhou, Wuhu, Chizhou, Hefei, Bozhou, and Suzhou, accounting for approximately 44% of the total number of cities. The science and technology innovation of industrial enterprises in these cities showed high R&D efficiency and commercialization efficiency. The high R&D–low commercialization category included Bengbu and Tongling. The remaining seven cities, Lu’an, Huaibei, Xuancheng, Fuyang, Huainan, Anqing, and Ma’anshan, were in the low R&D–low commercialization category, accounting for approximately 44% of the total number of cities. The technological innovation of these urban industrial enterprises was characterized by low R&D efficiency and low commercialization efficiency. No cities met the requirements for the low R&D–high commercialization category. The two-stage distribution indicated that the science and technology innovative efficiency for Anhui industrial enterprises tended to be either high R&D–high commercialization or low R&D–low commercialization. From this, we can also conclude that the two stages of R&D and commercialization are closely linked and jointly affect overall science and technology innovation.
Based on the above-stated analysis results, we conducted an overall summary. The average comprehensive efficiency of the scientific and technological innovation of Anhui’s industrial enterprises was 0.753, which was at a medium level. The efficiency development of the two stages was uncoordinated, and the development of scientific and technological innovation efficiency was uneven among regions. During the study period, the science and technology innovative efficiency remained relatively stable in Hefei and Chizhou, but fluctuated greatly in Huaibei, Bengbu, Lu’an, Tongling, and Xuancheng, showing an alternating phenomenon of rising and declining. The scientific and technological innovation efficiency of Huainan, Ma’anshan, and Anqing was below the average value. Other cities fluctuated slightly in individual years, but remained basically stable. In addition, through the comparative distribution of R&D efficiency and commercialization efficiency, it is evident that the two-stage efficiency distribution is mostly concentrated in the two modes of “high R&D–high commercialization” and “low R&D–low commercialization”.
3.4. Policy Suggestions
Based on the results of the above empirical analysis, we propose the following policy recommendations to improve the science and technology innovative efficiency of industrial enterprises in Anhui Province.
3.4.1. Cities with High R&D–High Commercialization
Huangshan, Chuzhou, Wuhu, Chizhou, Hefei, Bozhou, and Suzhou were in a state of high R&D and high commercialization. The two-stage efficiency of these cities was above 0.850. Thus, we put forward the following suggestions: To improve the independent innovation ability of industrial enterprises, we propose the establishment of a technological innovation system with enterprises as the main body, that is market-oriented, and combines industry and university research, so that industrial enterprises can truly become the main body of R&D investment, technological innovation activities, and commercialization and application of innovative achievements. Finally, we suggest comprehensive improvements to the ability of high-level management, high-quality creation, high-efficiency transformation, high commercialization, and high standard protection of intellectual property rights, to form the comprehensive advantages of intellectual property rights for industrial enterprises.
3.4.2. Cities with Low R&D–Low Commercialization
Lu’an, Fuyang, Huaibei, Xuancheng, Anqing, Huainan, and Ma’anshan were in a state of the low R&D–low commercialization. The two-stage efficiency of these cities is below 0.850. Accordingly, we proffer the following suggestions: Industrial enterprises should enhance their understanding of the importance of R&D; establish a diversified investment mechanism [87] with enterprises as the main body, government as the guide, and wide participation from all sectors of society; and expand the scale of R&D investment. When enhancing R&D input capacity, we suggest providing attention to the effectiveness of new product development and R&D output capacity of industrial enterprises and striving to produce effective patents and other science and technology achievements. Further, we suggest establishing an incentive mechanism for intellectual property creation, actively promoting the implementation and industrialization of patented technology, and increasing the proportion of products with independent intellectual property rights. It will be necessary to optimize the ecosystem for the transformation of science and technology achievements, improve the transformation and application ability of industrial enterprises’ science and technology achievements, and truly transform more science and technology achievements into real productive forces.
3.4.3. Cities with Low R&D–High Commercialization
Bengbu and Tongling are in a state of low R&D and high commercialization. Their commercialization efficiency is above 0.900, but the R&D efficiency is still below 0.600. Therefore, we present the following suggestions: To improve the quality of R&D and innovation for industrial enterprises, we recommend paying close attention to the output of major science and technology achievements, striving to create more high-tech intellectual property rights, fostering the ability to maintain the progressiveness of technology, and building key technologies and well-known brands with international competitiveness [88]. Consequently, we suggest strengthening the patent protection of science and technology achievements, actively applying for patents for inventions and creations, and realizing the intellectual property rights of science and technology achievements. We further suggest guiding the cultivation of leading science and technology innovation enterprises, gathering and incubating several industrial chain enterprises, and creating a cluster area for science and technology innovation and transformation of industrial enterprises. Finally, it will be necessary to accelerate the cultivation of high-quality intermediaries, provide accurate and comprehensive guidance services for the transfer and transformation of science and technology achievements [89], speed up the implementation of science and technology achievements, and do a good job as a “guide” for the transformation of science and technology achievements.
3.5. Discussion and Managerial Implications
Using the science and technology innovation of regional industrial enterprises as the research object, this study primarily analyzed science and technology innovative efficiency and influencing factors. Compared with extant research [46,47,48], this study has several advantages. First, from the innovation value chain perspective, science and technology innovation was divided into R&D and commercialization stages to build a two-stage evaluation index system. Second, constructing a two-stage network DEA model with additional intermediate input allowed us to not only compare the differences in comprehensive efficiency of industrial enterprises in various cities but also the differences across stages. Third, according to the two-dimensional distribution characteristics of R&D efficiency and commercialization efficiency, the real reasons for the differences in science and technology innovative efficiency of industrial enterprises between cities were identified, and targeted countermeasures and suggestions were put forward based on classification.
Promoting the science and technology innovative efficiency is an internal requirement for the sustainable [90] and high-quality development of regional industrial enterprises, and has important practical significance for developing strategies to strengthen the province through industry. Thus, combined with the above, we identified three management implications. First, innovation is the initial driving force that leads development. Regional industrial enterprises’ science and technology innovative efficiency is related to the innovation and competitiveness of regional economic development. Thus, there is an urgent need to measure, assess, and improve industrial enterprises’ science and technology innovative efficiency. Second, based on the value chain theory, we suggest breaking the “black box” system of science and technology innovation for regional industrial enterprises, reveal the process and transmission mechanism of science and technology innovation, and construct a theoretical framework for the process as a whole and as multiple stages. Third, innovation-driven technological transformation and optimization, and upgrading regional industrial enterprises, is of great significance to consolidating the high-quality development of the regional economy. Therefore, it is necessary to strengthen reforms of the innovation system and mechanism and promote the transformation of science and technology innovation achievements.
4. Conclusions
To improve national comprehensive competitiveness, countries worldwide have raised science and technology innovation and technological progress as national development strategies. Industrial enterprises play important roles in regional economic growth and innovation development. Science and technology innovation drive is an important force to promote the industrialization process of industrial enterprises. This study proposes a data-driven, comprehensive evaluation method for the efficiency of the scientific and technological innovation of regional industrial enterprises. The method is applied to measure, evaluate, and optimize the efficiency of the scientific and technological innovation of industrial enterprises in 16 cities of Anhui Province. The following research results are obtained: (1) The comprehensive efficiencies of the scientific and technological innovation of industrial enterprises in 16 cities in Anhui Province apparently differ. The comprehensive efficiency of Hefei and Chizhou has always been 1, both at the “high-efficiency” level. (2) The difference in the comprehensive efficiency is caused by several reasons. Some cities, such as Bengbu and Huaibei, have low R&D efficiency. The average R&D efficiency of Bengbu was 0.530, and the average commercialization efficiency was 0.930. In some cities, such as Huainan and Tongling, the difference was caused by low commercialization efficiency. The average value of R&D efficiency in Huainan is 0.548, whereas the average value of commercialization efficiency is 0.236. (3) From the two-dimensional distribution of the average value, the industrial enterprises in 16 cities in Anhui were mostly in the state of “high R&D–high commercialization” and “low R&D–low commercialization”. Only Tongling and Bengbu were in the state of “low R&D–high commercialization”. Thus, we propose policy suggestions from these three states.
The Innovations of this study are as follows: (1) From the perspective of research, considering the innovation process and innovation value chain, a scientific and reasonable evaluation index system of science and technology for regional industrial enterprises was constructed. (2) In terms of research methods, considering the relationship between the two stages and the integrity of innovation, a two-stage network DEA model with additional intermediate input was constructed to measure and evaluate regional industrial enterprises’ science and technology innovative efficiency. (3) In terms of strategy formulation, this study can provide theoretical support for constructing a periodic dynamic development system and a science and technology innovation mechanism in regional industrial enterprises.
However, the science and technology innovation of regional industrial enterprises is a complex system engineering. In view of the complexity of indicators and data availability, the integrity of the evaluation index system still needs further discussion. In this study, a two-stage DEA model was constructed, taking into account the operation mode of the whole system. However, in the process of calculating industrial enterprises’ science and technology innovative efficiency, the time lag of science and technology innovation itself was not considered. In this regard, further research can be conducted in the future.
Author Contributions
Conceptualization, Y.Y. and Y.W.; methodology, Y.Y.; software, Y.W.; validation, Y.Y., Y.W. and C.W.; formal analysis, C.Z.; investigation, C.W.; resources, C.Z.; data curation, C.W.; writing—original draft preparation, Y.Y.; writing—review and editing, Y.W.; visualization, Y.Z.; supervision, Y.Z.; project administration, Y.Z.; funding acquisition, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by 2021 Anhui Social Sciences Innovation and Development Research Project, grant number 2021CX069, 2021CX064.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the funding given by 2021 Anhui Social Sciences Innovation and Development Research Project, grant number 2021CX069, 2021CX064.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, C.; Cai, W.; Zhai, M.; Zhu, G.; Zhang, C.; Jiang, Z. Decoupling of wastewater eco-environmental damage and China’s economic development. Sci. Total Environ. 2021, 789, 147980. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wang, Y.; Zhang, Y.; Liu, C. Data-driven coupling coordination development of regional innovation EROB composite system: An integrated model perspective. Mathematics 2022, 10, 2246. [Google Scholar] [CrossRef]
- Liu, C.; Gao, M.; Zhu, G.; Zhang, C.; Zhang, P.; Chen, J.; Cai, W. Data driven eco-efficiency evaluation and optimization in industrial production. Energy 2021, 224, 120170. [Google Scholar] [CrossRef]
- Potashnik, Y.S.; Artemyeva, M.V.; Kuznetsova, S.N.; Garin, A.P.; Letyagina, E.N. The status and trends in innovative activity of industrial enterprises of Nizhny Novgorod Region. In Growth Poles of the Global Economy: Emergence, Changes and Future Perspectives. Lecture Notes in Networks and Systems; Popkova, E., Ed.; Springer: Cham, Switzerland, 2020; Volume 73, pp. 525–534. [Google Scholar]
- Marhasova, V.; Garafonova, O.; Popelo, O.; Tulchynska, S.; Pohrebniak, A.; Tkachenko, T. Environmentalization of Production as a direction of ensuring the sustainability of production activities of enterprises and increasing their economic security. Int. J. Safe. Secur. Eng. 2022, 12, 159–166. [Google Scholar] [CrossRef]
- Liu, C.; Chen, J.; Cai, W. Data-driven remanufacturability evaluation method of waste parts. IEEE Trans. Indust Inform. 2022, 18, 4587–4595. [Google Scholar] [CrossRef]
- Xu, L.; Zhao, X.; Chen, J. Exploring the governance dilemma of nuclear wastewater in Fukushima: A tripartite evolutionary game model. Ocean. Coast. Manag. 2022, 225, 106220. [Google Scholar] [CrossRef]
- Geng, Y.; Sarkis, J.; Bleischwitz, R. How to globalize the circular economy. Nature 2019, 565, 153–155. [Google Scholar] [CrossRef]
- Ma, T.; Liu, C. Identification of driving factors of scientific and technological innovation in the new material industry based on the theory of complex adaptive system: Taking the construction of green innovation system as an example. Complexity 2021, 2021, 5537789. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, Y.; Wang, K.; Xu, H.; Yi, X. An analysis on the spatial effect of absorptive capacity on regional innovation ability based on empirical research in China. Sustainability 2020, 12, 3021. [Google Scholar] [CrossRef]
- Wang, Y. How is innovation performance under the restriction of industry cluster: Evidence from a survey on high-tech firms. Converter 2021, 2021, 11–20. [Google Scholar] [CrossRef]
- Alvarez-Aros, E.L.; Bernal-Torres, C.A. Technological competitiveness and emerging technologies in Industry 4.0 and Industry 5.0. An. Acad Bras. Ciênc 2021, 93. [Google Scholar] [CrossRef] [PubMed]
- Akundi, A.; Euresti, D.; Luna, S.; Ankobiah, W.; Lopes, A.; Edinbarough, I. State of Industry 5.0—Analysis and identification of current research trends. Appl. Syst. Innov. 2022, 5, 27. [Google Scholar] [CrossRef]
- Wanke, P.; Tan, Y.; Antunes, J.; Hadi-Vencheh, A. Business environment drivers and technical efficiency in the Chinese energy industry: A robust Bayesian stochastic frontier analysis. Comput. Ind. Eng. 2020, 144, 106487. [Google Scholar] [CrossRef]
- Gu, W.; Saaty, T.L.; Wei, L. Evaluating and optimizing technological innovation efficiency of industrial enterprises based on both data and judgments. Int. J. Inf. Technol. Decis Mak. 2018, 17, 9–43. [Google Scholar] [CrossRef]
- Bezin, E. The economics of green consumption, cultural transmission and sustainable technological change. J. Econ. Theory 2019, 181, 497–546. [Google Scholar] [CrossRef]
- Ziyuan, X.; Lijuan, W. Industrial agglomeration level and innovation efficiency of industrial enterprises—an empirical study based on the panel data of 20 industries from the year 2000 to 2012. Sci. Res. Manag. 2017, 38, 91. [Google Scholar]
- Nizar, B.; Rejean, L.; Asmara, N. Lessons from innovation empirical studies in the manufacturing sector a systematic review of the literature from 1993-2003. Technovation 2006, 26, 64–78. [Google Scholar]
- Grigoryevich, C.A. Methodological approach to determination of innovations efficiency at industrial enterprises. Russ. J. Educ. Psychol. 2013, 7, 55. [Google Scholar]
- Zhang, J.; Kang, L.; Li, H.; Ballesteros-Pérez, P.; Skitmore, M.; Zuo, J. The impact of environmental regulations on urban green innovation efficiency: The case of Xi’an. Sustain. Cities Soc. 2020, 57, 102123. [Google Scholar] [CrossRef]
- Bartlett, D.; Trifilova, A. Green technology and eco-innovation: Seven case-studies from a Russian manufacturing context. J. Manuf. Technol. Manag. 2010, 21, 910–929. [Google Scholar] [CrossRef]
- Meltzer, J. A carbon tax as a driver of green technology innovation and the implications for international trade. Energy LJ 2014, 35, 45. [Google Scholar]
- Shi, H.; Shen, C. Tax competition, capital flow, and the innovation efficiency of industrial enterprises. Sustainability 2022, 14, 4645. [Google Scholar] [CrossRef]
- Costantini, V.; Crespi, F.; Palma, A. Characterizing the policy mix and its impact on eco-innovation: A patent analysis of energy-efficient technologies. Res. Policy 2017, 46, 799–819. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, Y. Research on the impact of environmental regulations on the green innovation efficiency of Chinese industrial enterprises. Pol. J. Environ. Stud. 2021, 30, 1433–1445. [Google Scholar] [CrossRef]
- Lian, G.; Xu, A.; Zhu, Y. Substantive green innovation or symbolic green innovation? The impact of ER on enterprise green innovation based on the dual moderating effects. J. Innov. Knowl. 2022, 7, 100203. [Google Scholar] [CrossRef]
- Jin, W.; Zhang, H.Q.; Liu, S.; Zhang, H.B. Technological innovation, environmental regulation, and green total factor efficiency of industrial water resources. J. Clean. Prod. 2019, 211, 61–69. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Z.; Qiu, S.; Zhu, L. Effects of environmental regulations on technological innovation efficiency in China’s industrial enterprises: A spatial analysis. Sustainability 2019, 11, 2186. [Google Scholar] [CrossRef]
- Tang, K.; Qiu, Y.; Zhou, D. Does command-and-control regulation promote green innovation performance? Evidence from China’s industrial enterprises. Sci. Total Environ. 2020, 712, 136362. [Google Scholar] [CrossRef]
- Zhang, H.; Shao, Y.; Han, X.; Chang, H.L. A road towards ecological development in China: The nexus between green investment, natural resources, green technology innovation, and economic growth. Resour. Policy 2022, 77, 102746. [Google Scholar] [CrossRef]
- Shinkevich, A.I.; Ershova, I.G.; Galimulina, F.F.; Yarlychenko, A.A. Innovative Mesosystems Algorithm for Sustainable Development Priority Areas Identification in Industry Based on Decision Trees Construction. Mathematics 2021, 9, 3055. [Google Scholar] [CrossRef]
- Amore, M.D.; Bennedsen, M. Corporate governance and green innovation. J. Environ. Econ. Manag. 2016, 75, 54–72. [Google Scholar] [CrossRef]
- Hou, B.; Hong, J.; Wang, H.; Zhou, C. Academia-industry collaboration, government funding and innovation efficiency in Chinese industrial enterprises. Technol Anal. Strateg Manag. 2019, 31, 692–706. [Google Scholar] [CrossRef]
- Miao, C.; Meng, X.; Duan, M.; Wu, X.Y. Energy consumption, environmental pollution, and technological innovation efficiency: Taking industrial enterprises in China as empirical analysis object. Environ. Sci. Pollut. Res. 2020, 27, 34147–34157. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wu, X.; Liu, F.; Zhang, Y.; Liu, C. Promoting the efficiency of scientific and technological innovation in regional industrial enterprises: Data-driven DEA-Malmquist evaluation model. J. Intell Fuzzy Syst. 2022, 43, 4911–4928. [Google Scholar] [CrossRef]
- Chen, H.; Lin, H.; Zou, W. Research on the regional differences and influencing factors of the innovation efficiency of China’s high-tech industries: Based on a shared inputs two-stage network DEA. Sustainability 2020, 12, 3284. [Google Scholar] [CrossRef]
- Asheim, B.T.; Isaksen, A. Regional innovation systems: The integration of local ‘sticky’ and global ‘ubiquitous’ knowledge. J. Technol. Transf. 2002, 27, 77–86. [Google Scholar] [CrossRef]
- Luo, Q. Research on the dynamic evolution of scientific and technological innovation efficiency in universities and identification of influencing factors—based on Markov chain estimation and GMM model. Math. Probl. Eng. 2021, 2021, 9831124. [Google Scholar] [CrossRef]
- Guan, J.; Chen, K. Measuring the innovation production process: A cross-region empirical study of China’s high-tech innovations. Technovation 2010, 30, 348–358. [Google Scholar] [CrossRef]
- Hong, J.; Feng, B.; Wu, Y.; Wang, L. Do government grants promote innovation efficiency in China’s high-tech industries? Technovation 2016, 57, 4–13. [Google Scholar] [CrossRef]
- Revilla, E.; Sarkis, J.; Modrego, A. Evaluating performance of public–private research collaborations: A DEA analysis. J. Oper. Res. Soc. 2003, 54, 165–174. [Google Scholar] [CrossRef]
- Park, H.; Anderson, T.R.; Seo, W. Regional innovation capability from a technology-oriented perspective: An analysis at industry level. Comput. Ind. 2021, 129. [Google Scholar] [CrossRef]
- Lin, S.; Lin, R.; Sun, J.; Wang, E.; Wu, W. Dynamically evaluating technological innovation efficiency of high-tech industry in China: Provincial, regional and industrial perspective. Socioeco. Plann. Sci. 2021, 74, 100939. [Google Scholar] [CrossRef]
- Shen, W.; Shi, J.; Meng, Q.; Chen, X.; Liu, Y.; Cheng, K.; Liu, W. Influences of environmental regulations on industrial green technology innovation efficiency in China. Sustainability 2022, 14, 4717. [Google Scholar] [CrossRef]
- Guan, J.; Zuo, K. A cross-country comparison of innovation efficiency. Scientometr. 2014, 100, 541–575. [Google Scholar] [CrossRef]
- Lin, S.; Sun, J.; Wang, S. Dynamic evaluation of the technological innovation efficiency of China’s industrial enterprises. Sci. Public Policy 2018, 46, 232–243. [Google Scholar] [CrossRef]
- Miao, C.; Duan, M.; Zuo, Y.; Wu, X.Y. Spatial heterogeneity and evolution trend of regional green innovation efficiency—an empirical study based on panel data of industrial enterprises in China’s provinces. Energy Policy 2021, 156, 112370. [Google Scholar] [CrossRef]
- Chen, W.; Wang, X.; Peng, N.; Wei, X.; Lin, C. Evaluation of the green innovation efficiency of Chinese industrial enterprises: Research based on the three-stage chain network SBM model. Math. Prob. Eng. 2020, 2020, 3143651. [Google Scholar] [CrossRef]
- Wang, H.; An, L.; Zhang, X. Evaluation of regional innovation ability based on green and low-carbon perspective. Bulg. Chem. Commun. 2017, 49, 55–58. [Google Scholar]
- Heindl, A.B.; Liefner, I. The analytic hierarchy process as a methodological contribution to improve regional innovation system research: Explored through comparative research in China. Technol. Soc. 2019, 59, 101197. [Google Scholar] [CrossRef]
- Li, L.; Wang, R.; Li, X. Grey fuzzy comprehensive evaluation of regional financial innovation ability based on two types weights. Grey Syst. Theory Appl. 2016, 6, 187–202. [Google Scholar] [CrossRef]
- Krndzija, L. Public sector innovation performance in Federation of Bosnia and Herzegovina: An exploratory factor analysis. Croat. Rev. Econ. Bus. Soc. Stat. 2021, 7, 13–30. [Google Scholar] [CrossRef]
- Ke, H.; Dai, S.; Yu, H. Effect of green innovation efficiency on ecological footprint in 283 Chinese Cities from 2008 to 2018. Environ. Dev. Sustain. 2022, 24, 2841–2860. [Google Scholar] [CrossRef]
- Huang, Q.; Jiang, M.S.; Miao, J. Effect of government subsidization on Chinese industrial firms’ technological innovation efficiency: A stochastic frontier analysis. J. Bus. Econ. Manag. 2016, 17, 187–200. [Google Scholar] [CrossRef]
- Haider, S.; Mishra, P. Does innovative capability enhance the energy efficiency of Indian Iron and Steel firms? A Bayesian stochastic frontier analysis. Energ. Econ. 2021, 95, 105128. [Google Scholar] [CrossRef]
- Li, T.; Liang, L.; Han, D. Research on the efficiency of green technology innovation in China’s provincial high-end manufacturing industry based on the RAGA-PP-SFA model. Math. Prob. Eng. 2018, 2018, 9463707. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wang, Y.; Lan, Y. Measuring the bias of technical change of industrial energy and environment productivity in China: A global DEA-Malmquist productivity approach. Environ. Sci. Pollut. Res. 2021, 28, 41896–41911. [Google Scholar] [CrossRef]
- Xin-gang, Z.; Zhen, W. The technical efficiency of China’s wind power list enterprises: An estimation based on DEA method and micro-data. Renew. Energy 2019, 133, 470–479. [Google Scholar] [CrossRef]
- Saeedi, H.; Behdani, B.; Wiegmans, B.; Zuidwijk, R. Assessing the technical efficiency of intermodal freight transport chains using a modified network DEA approach. Transp. Res. Part. E Logist. Transp. Rev. 2019, 126, 66–86. [Google Scholar] [CrossRef]
- Jin, F.; Garg, H.; Pei, L.; Liu, J.; Chen, H. Multiplicative consistency adjustment model and data envelopment analysis-driven decision-making process with probabilistic hesitant fuzzy preference relations. Int. J. Fuzzy Syst. 2020, 22, 2319–2332. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, L. Research on the Evaluation of Technological Innovation Efficiency of Different Industrial Enterprises in China. In Proceedings of the 2020 International Conference on Social Sciences and Big Data Application (ICSSBDA 2020), Xi’an, China, 17–18 October 2020; Atlantis Press: Amsterdam, The Netherlands, 2020; pp. 277–283. [Google Scholar]
- Ma, J.; Qi, L.; Deng, L. Efficiency measurement and decomposition in hybrid two-stage DEA with additional inputs. Expert Syst. Appl. 2017, 79, 348–357. [Google Scholar] [CrossRef]
- Tone, K.; Tsutsui, M. Dynamic DEA with network structure: A slacks-based measure approach. Omega 2014, 42, 124–131. [Google Scholar] [CrossRef]
- Kao, C. Efficiency decomposition in network data envelopment analysis: A relational model. Eur. J. Oper. Res. 2009, 192, 949–962. [Google Scholar] [CrossRef]
- Lin, B.; Luan, R. Do government subsidies promote efficiency in technological innovation of China’s photovoltaic enterprises? J. Clean. Prod. 2020, 254, 120108. [Google Scholar] [CrossRef]
- Li, H.; Zhang, J.; Wang, C.; Wang, Y.; Coffey, V. An evaluation of the impact of environmental regulation on the efficiency of technology innovation using the combined DEA model: A case study of Xi’an, China. Sustain. Cities Soc. 2018, 42, 355–369. [Google Scholar] [CrossRef]
- Xiao, R.Q.; Wang, Z.J.; Qian, L. Research on technology innovation efficiency of Chinese inter-provincial industrial enterprises under environmental constraints. Manage. Rev. 2014, 26, 56–65. [Google Scholar] [CrossRef]
- Wang, Q.; Hang, Y.; Sun, L.; Zhao, Z. Two-stage innovation efficiency of new energy enterprises in China: A non-radial DEA approach. Technol. Forecast. Soc. Change 2016, 112, 254–261. [Google Scholar] [CrossRef]
- Du, J.; Liu, Y.; Diao, W. Assessing regional differences in green innovation efficiency of industrial enterprises in China. Int. J. Environ. Res. Public Health 2019, 16, 940. [Google Scholar] [CrossRef]
- Zeng, G.; Guo, H.; Geng, C. A Five-stage DEA model for technological innovation efficiency of China’s strategic emerging industries, considering environmental factors and statistical errors. Pol. J. Environ. Stud. 2021, 30, 927–941. [Google Scholar] [CrossRef]
- Popelo, O.; Tulchynska, S.; Revko, A.; Butko, M.; Derhaliuk, M. Methodological approaches to the evaluation of innovation in Polish and Ukrainian regions, taking into account digitalization. Comp. Econ. Res. Cent. East. Eur. 2022, 25, 55–74. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Liu, H.; Yang, G.; Liu, X.; Song, Y. R&D performance assessment of industrial enterprises in China: A two-stage DEA approach. Socioecon. Plan. Sci. 2020, 71, 100753. [Google Scholar]
- Lim, S.; Zhu, J. A note on two-stage network DEA model: Frontier projection and duality. Eur. J. Oper. Res. 2016, 248, 342–346. [Google Scholar] [CrossRef]
- Jiang, B.; Chen, H.; Li, J.; Lio, W. The uncertain two-stage network DEA models. Soft Comput. 2021, 25, 421–429. [Google Scholar] [CrossRef]
- Kao, C. Efficiency decomposition and aggregation in network data envelopment analysis. Eur. J. Oper. Res. 2016, 255, 778–786. [Google Scholar] [CrossRef]
- Furman, J.L.; Porter, M.E.; Stern, S. The determinants of national innovative capacity. Res. Policy 2002, 31, 899–933. [Google Scholar] [CrossRef]
- Su, Y.; Liang, D.; Guo, W. Application of multiattribute decision-making for evaluating regional innovation capacity. Math. Prob. Eng. 2020, 2020, 2851840. [Google Scholar] [CrossRef]
- Luo, Q.; Miao, C.; Sun, L.; Meng, X.; Duan, M. Efficiency evaluation of green technology innovation of China’s strategic emerging industries: An empirical analysis based on Malmquist-data envelopment analysis index. J. Clean. Prod. 2019, 238, 117782. [Google Scholar] [CrossRef]
- Zhou, S.; Deng, Q.; Peng, F. Effect of International Technology Transfer on the Technical Efficiency of High-Tech Manufacturing in China: A RAGA-PP-SFA Analysis. Complexity 2021, 2021, 6633484. [Google Scholar] [CrossRef]
- Boiarynova, K.; Popelo, O.; Tulchynska, S.; Gritsenko, S.; Prikhno, I. Conceptual foundations of evaluation and forecasting of innovative development of regions. Period. Polytech Soc. Manag Sci. 2022, 30, 167–174. [Google Scholar] [CrossRef]
- Kao, C.; Hwang, S.N. Efficiency decomposition in two-stage data envelopment analysis: An application to non-life insurance companies in Taiwan. Eur. J. Oper. Res. 2008, 185, 418–429. [Google Scholar] [CrossRef]
- Khoveyni, M.; Eslami, R. Two-stage network DEA with shared resources: Illustrating the drawbacks and measuring the overall efficiency. Knowl. Based. Syst. 2022, 250, 108725. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, J.; Pei, R.; Yi, B.; Yang, G. Assessing the technological innovation efficiency of China’s high-tech industries with a two-stage network DEA approach. Socio-Econ. Plan. Sci. 2020, 71, 100810. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Zhu, Q. Performance evaluation of China’s high-tech innovation process: Analysis based on the innovation value chain. Technovation 2018, 74, 42–53. [Google Scholar] [CrossRef]
- Chen, Y.; Du, J.; David Sherman, H.; Zhu, J. DEA model with shared resources and efficiency decomposition. Eur. J. Oper. Res. 2010, 207, 339–349. [Google Scholar] [CrossRef]
- Jin, F.; Cao, M.; Liu, J.; Martínez, L.; Chen, H. Consistency and trust relationship-driven social network group decision-making method with probabilistic linguistic information. Appl. Soft Comput. 2021, 103, 107170. [Google Scholar] [CrossRef]
- Liu, Z.; Li, K.W.; Tang, J.; Gong, B.; Huang, J. Optimal operations of a closed-loop supply chain under a dual regulation. Int. J. Prod. Econ. 2021, 233, 107991. [Google Scholar] [CrossRef]
- Hohberger, J.; Almeida, P.; Parada, P. The direction of firm innovation:the contrasting roles of strategic alliances and individual scientific collaborations. Res. Policy 2015, 44, 1473–1478. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, X.-X.; Li, D.-F.; Liao, C.-N.; Sheu, J.-B. A novel cooperative game-based method to coordinate a sustainable supply chain under psychological uncertainty in fairness concerns. Transport. Res. E-Log. 2021, 147, 102237. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).