Analytic Network Process-Based Sustainability Life Cycle Assessment of Concrete Bridges in Coastal Regions
Abstract
:1. Introduction
2. Materials and Methods
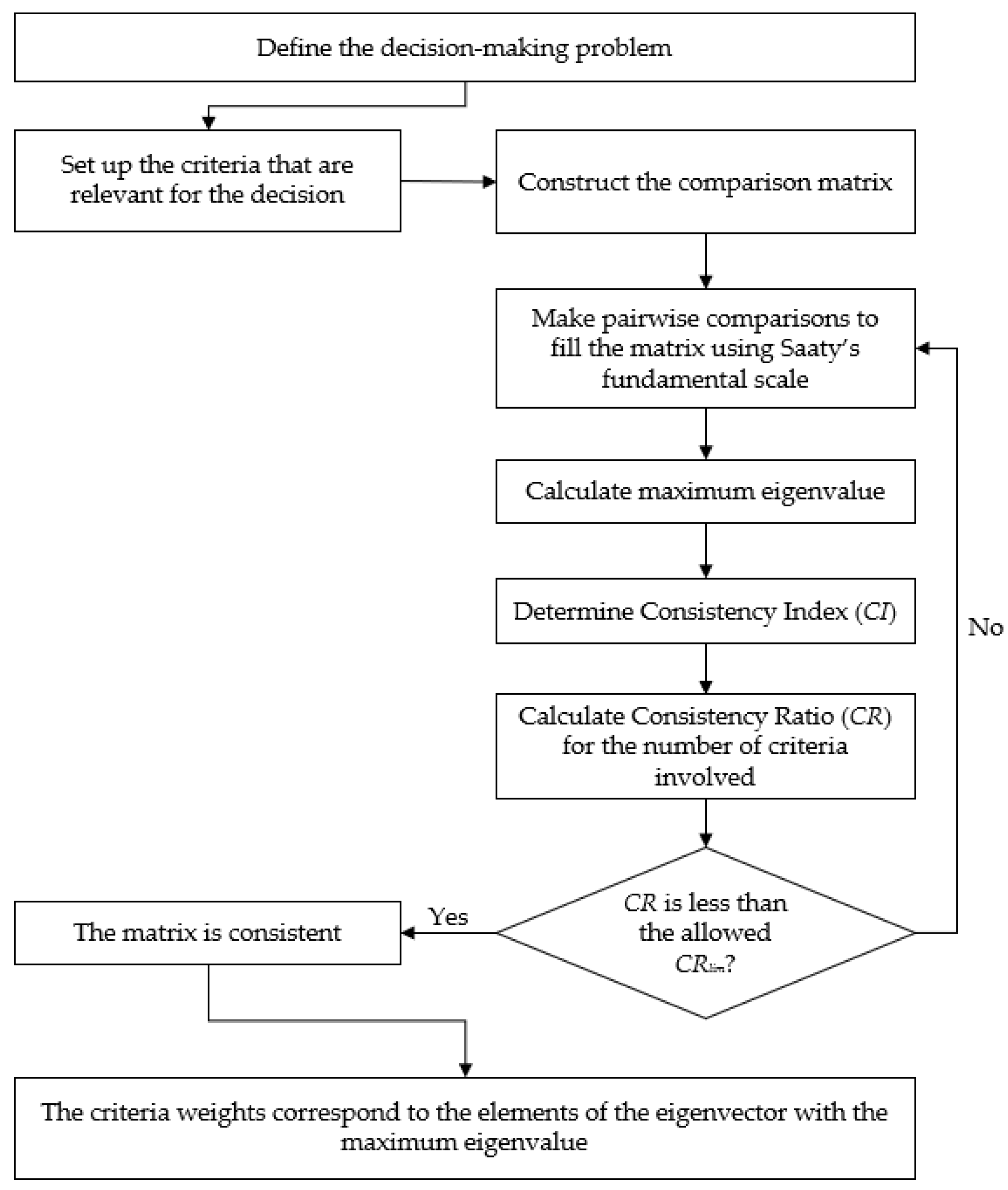
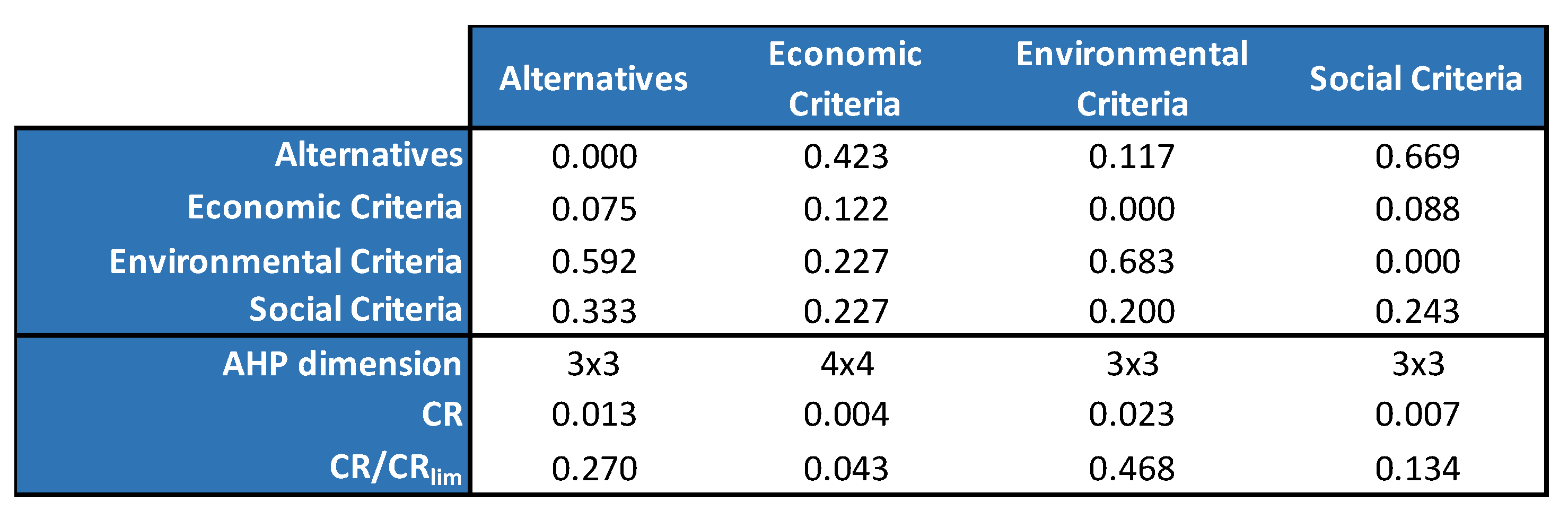
2.1. The Analytic Hierarchy Process and the Consistency Measure
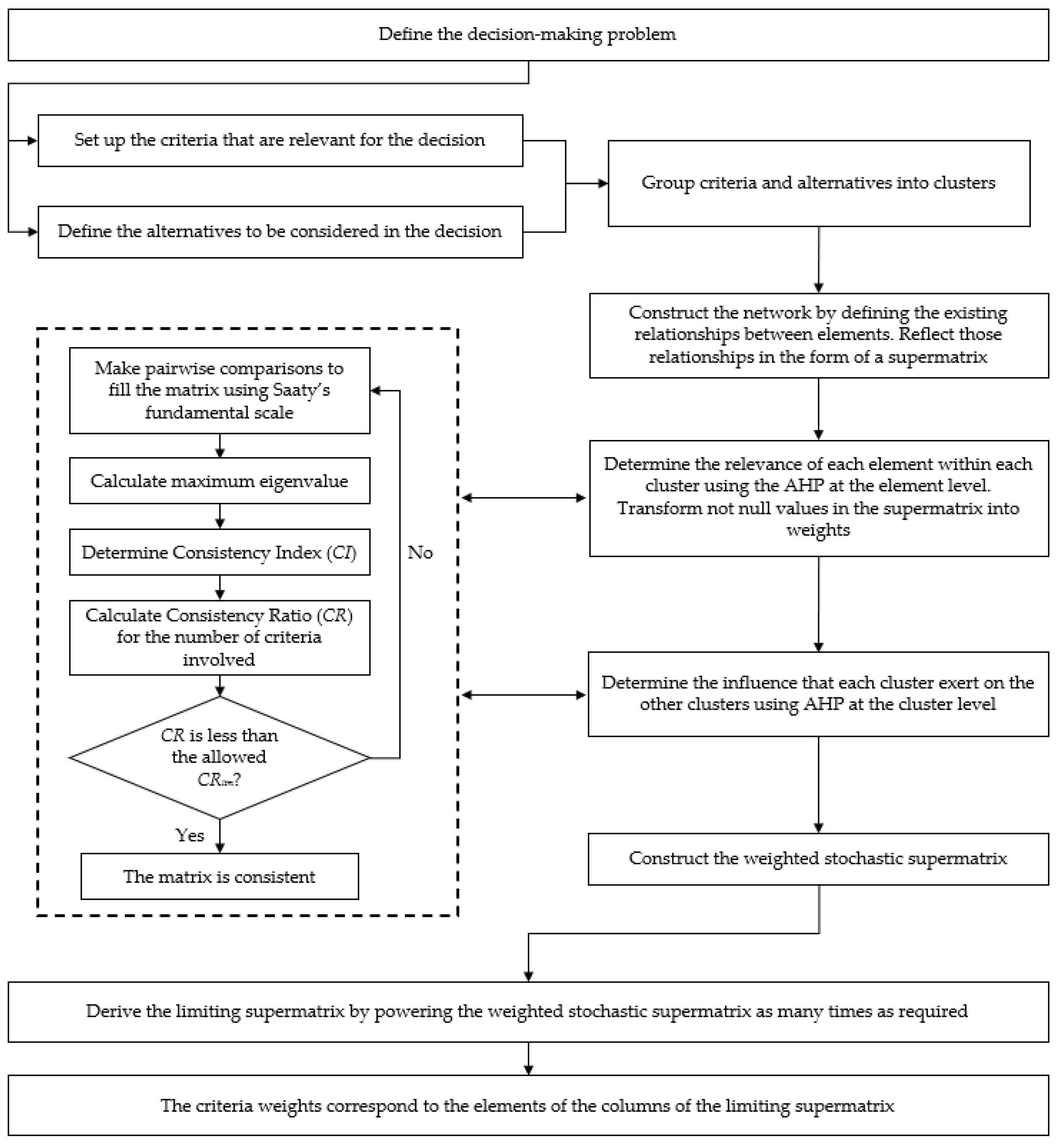
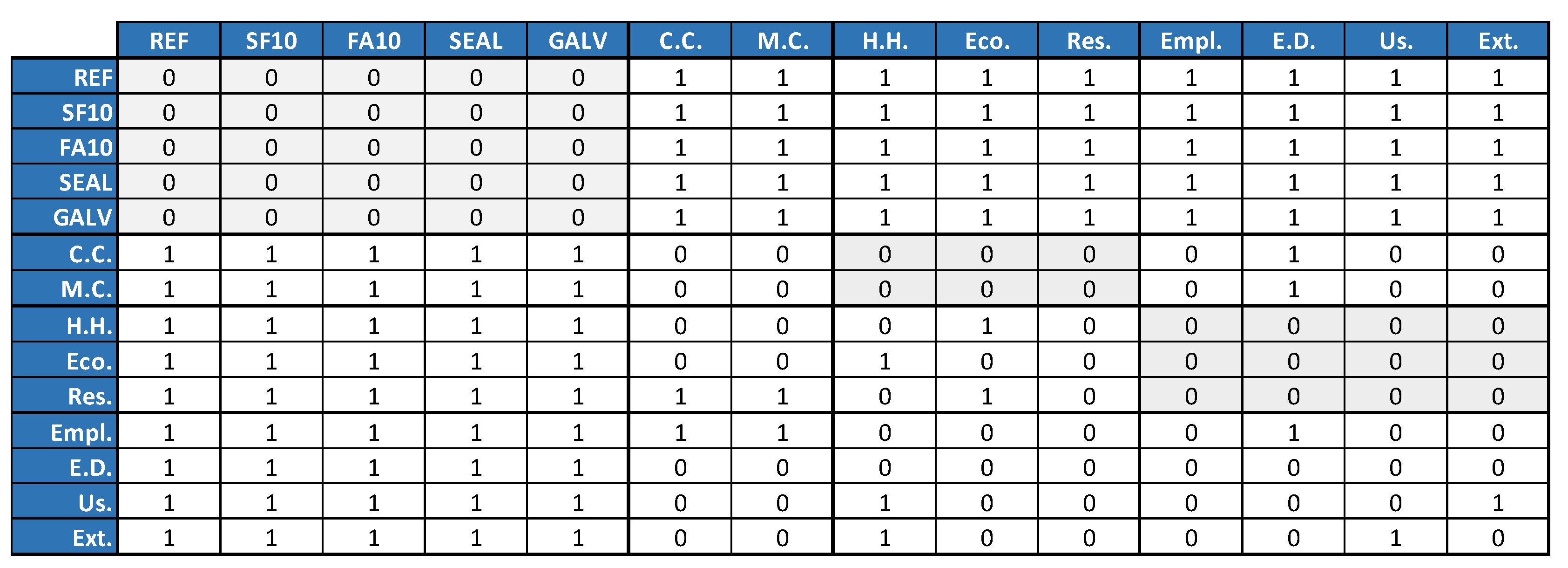
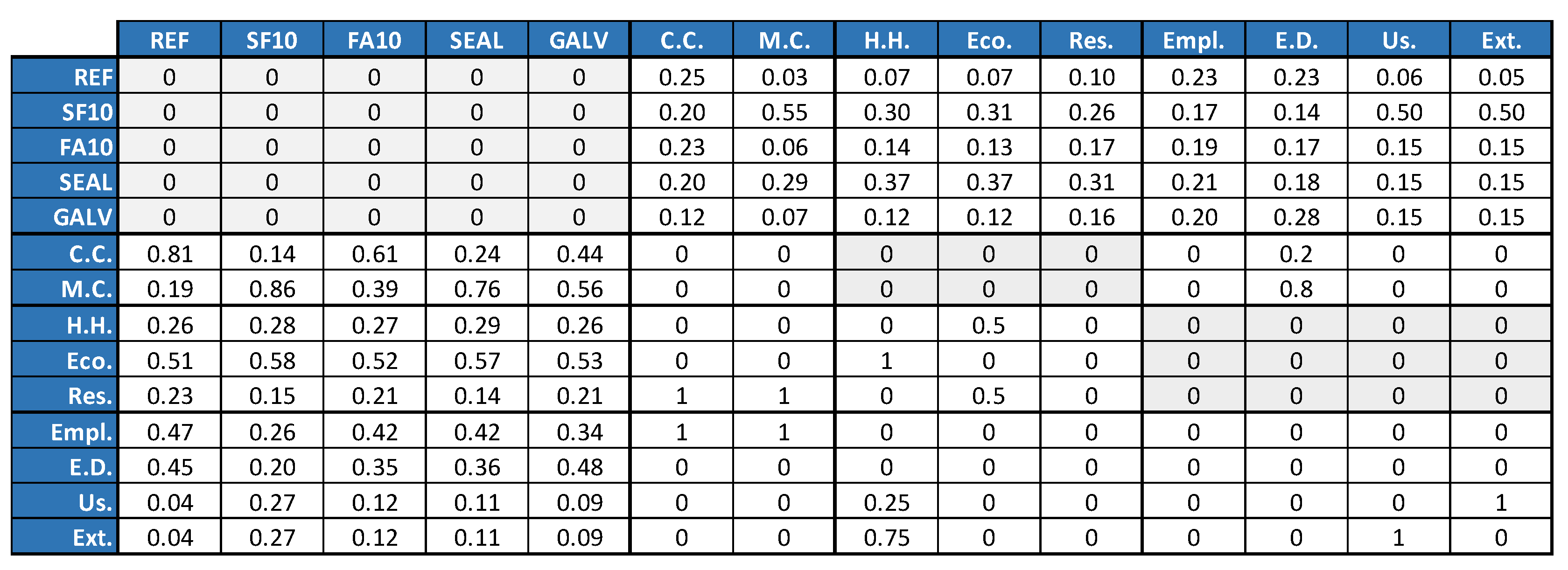
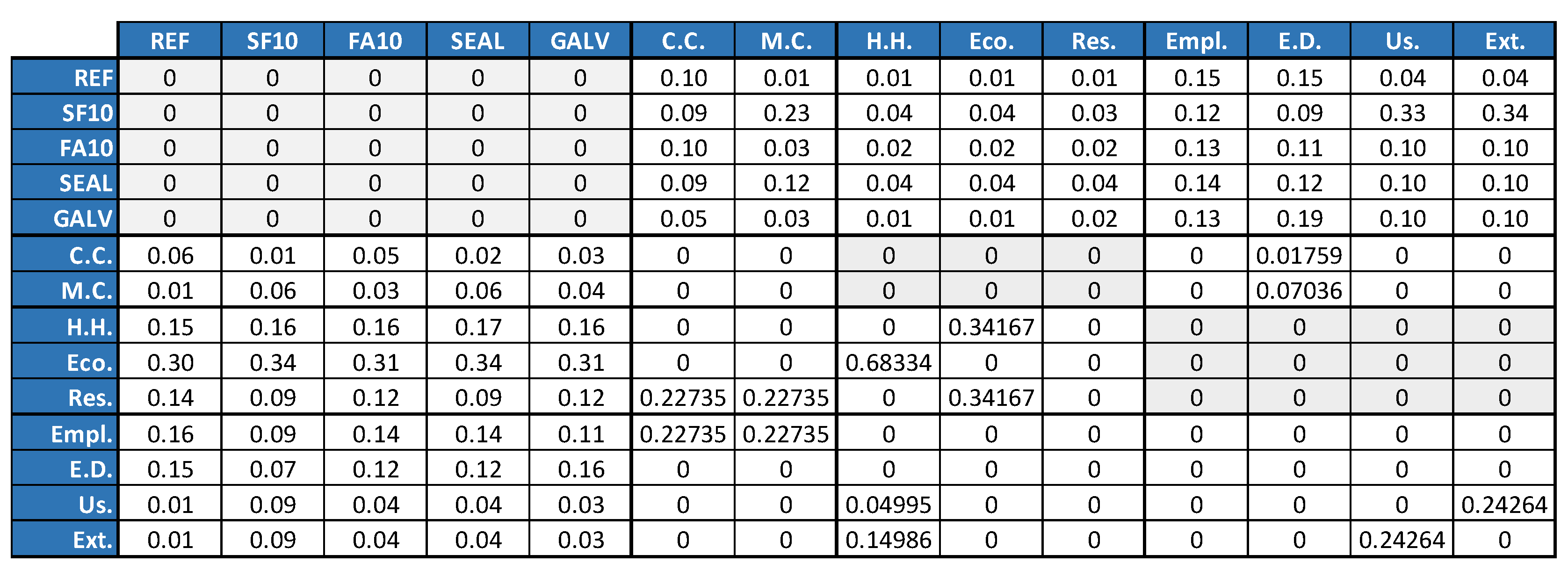
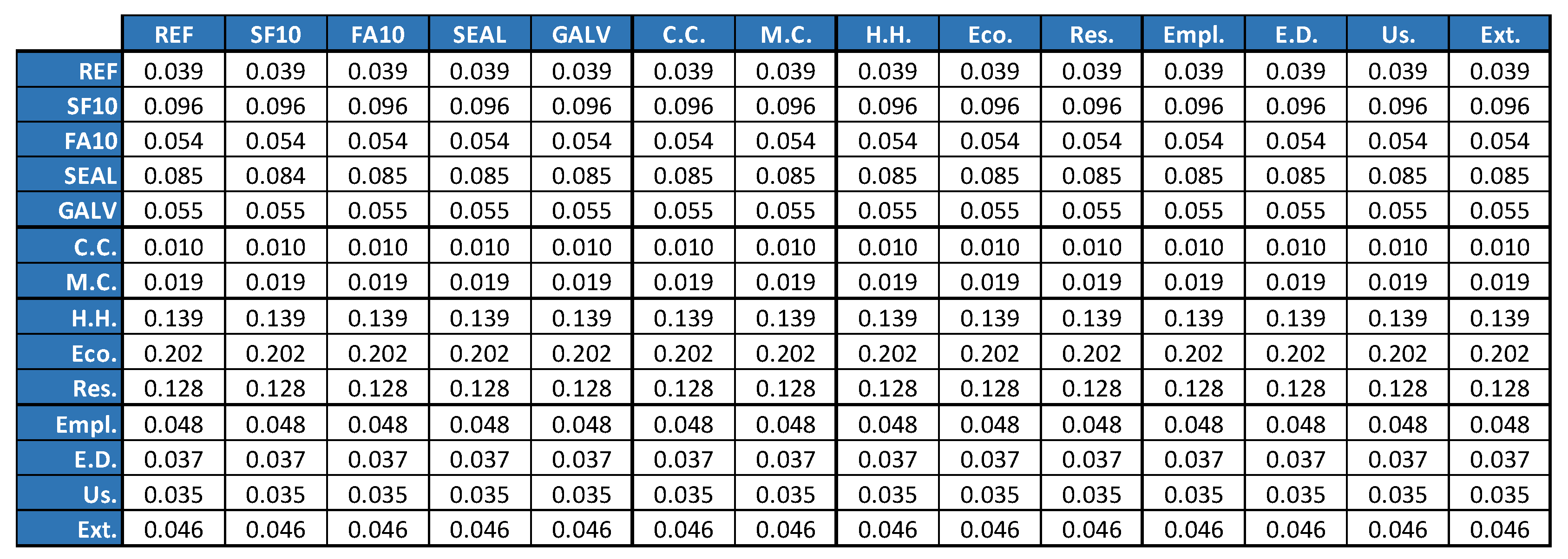
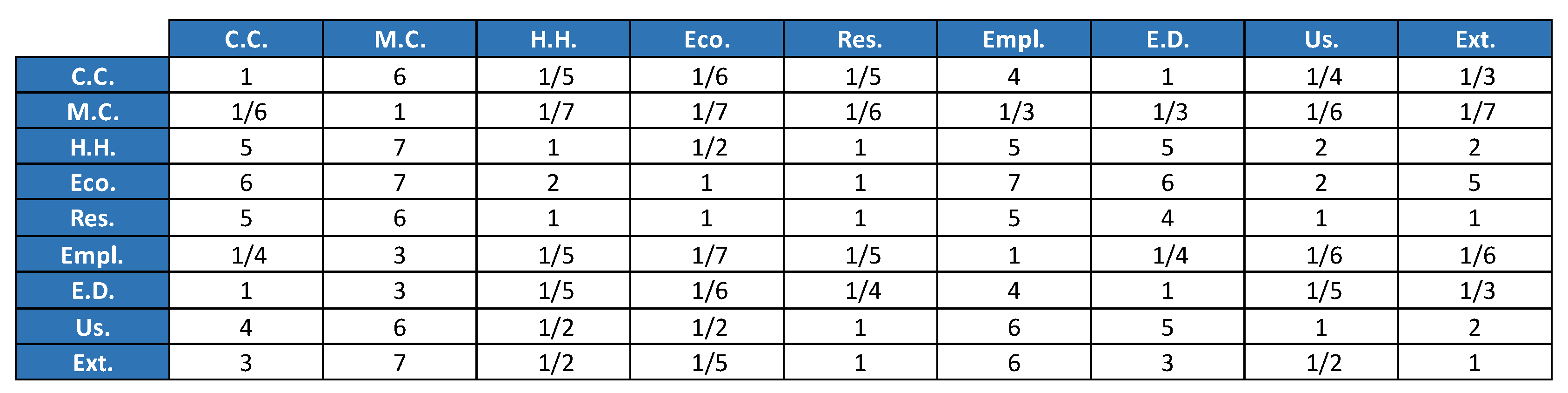
2.2. The Analytic Network Process
2.3. TOPSIS Technique
3. Case Study
4. Results and Discussion
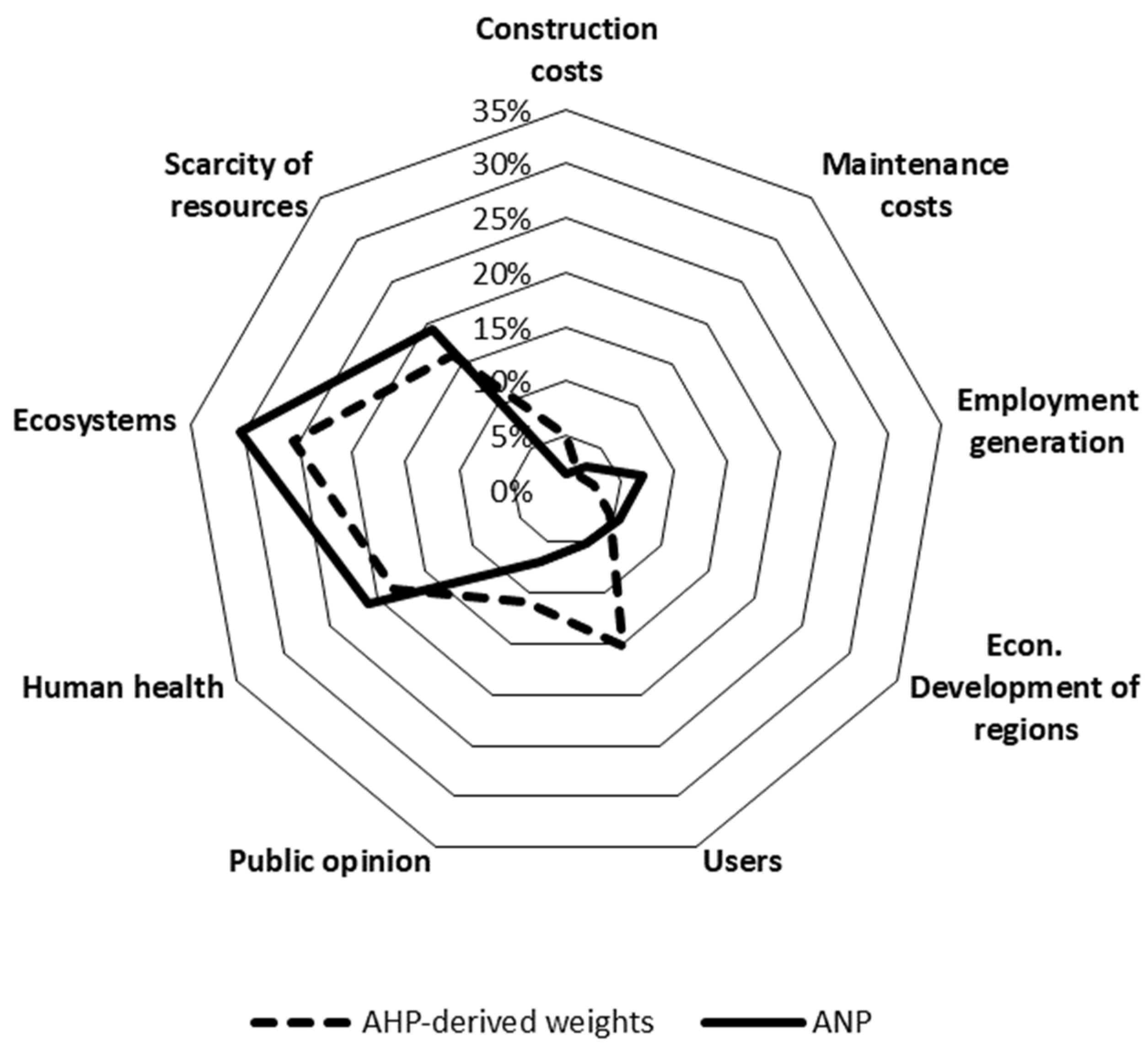
4.1. Analytic Network Process Results
4.2. AHP-TOPSIS
4.3. ANP vs. AHP-TOPSIS Results
5. Conclusions
- The use of concrete with silica fume additions was shown to offer the best response throughout its life cycle when the structure is exposed to chloride environments. This is due to its high durability and to the fact that this alternative replaces part of the cement of a conventional design with silica fume, allowing it to reduce part of the environmental impact associated with cement production and also allowing the reuse of residual by-products of the metallurgical industry, namely the silica fume.
- The least preferred solution in terms of its life cycle sustainability performance corresponded to the design based on conventional materials. The highly aggressive environment associated with coastal spaces and the reduced durability of such designs results in excessively high maintenance needs. This leads to equally high economic and environmental costs in the maintenance phase, making this solution the least successful.
- Conventional designs, although associated with the lowest construction costs and greatest employment generation, lead to maintenance costs that are two to twenty times greater than those corresponding to durable materials.
- The use of corrosion-resistant materials, such as the ones considered in the present research, leads to environmental impacts along their life cycle that can be up to 20% of those corresponding to conventional designs.
- Compared to the AHP approach, the ANP technique further models the complex relationships between the different criteria, making it possible for the expert to reflect his/her vision of the problem more flexibly and accurately.
- The use of this technique to address decision-making problems involving quantitative criteria has proven useful in reducing the inconsistencies associated with conventional methods (AHP), thus increasing the reliability of the final decision. As shown in the discussion of the results obtained, using a quantitative ANP made it possible, when faced with the same decision problem, to make judgments with an average consistency more than three times higher than that obtained by the conventional AHP technique.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- UN General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015. Available online: https://www.refworld.org/docid/57b6e3e44.html (accessed on 15 August 2022).
- Ozturk, O.; Ozyurt, N. Sustainability and cost-effectiveness of steel and polypropylene fiber reinforced concrete pavement mixtures. J. Clean. Prod. 2022, 363, 132582. [Google Scholar] [CrossRef]
- Torres-Machí, C.; Chamorro, A.; Pellicer, E.; Yepes, V.; Videla, C. Sustainable pavement management: Integrating economic, technical, and environmental aspects in decision making. Transp. Res. Record. 2015, 2523, 56–63. [Google Scholar] [CrossRef]
- Gilani, G.; Hosseini, S.M.A.; Pons-Valladares, O.; de la Fuente, A. An enhanced multi-criteria decision-making approach oriented to sustainability analysis of building facades: A case study of Barcelona. J. Build. Eng. 2022, 54, 104630. [Google Scholar] [CrossRef]
- Sánchez-Garrido, A.J.; Navarro, I.J.; Yepes, V. Multi-criteria decision-making applied to the sustainability of building structures based on Modern Methods of Construction. J. Clean. Prod. 2022, 330, 129724. [Google Scholar] [CrossRef]
- Adhikari, P.; Mahmoud, H.; Xie, A.; Simonen, K.; Ellingwood, B. Life-cycle cost and carbon footprint analysis for light-framed residential buildings subjected to tornado hazard. J. Build. Eng. 2020, 32, 101657. [Google Scholar] [CrossRef]
- Speranza, G.; Ferrari, A.; Lassalle, P.L. Life cycle environmental assessment of retaining walls in unsaturated soils. Geomech. Energy Environ. 2022, 30, 100241. [Google Scholar] [CrossRef]
- Molina-Moreno, F.; García-Segura, T.; Martí, J.V.; Yepes, V. Optimization of Buttressed Earth-Retaining Walls using Hybrid Harmony Search Algorithms. Eng. Struct. 2017, 134, 205–216. [Google Scholar] [CrossRef]
- Pons, J.J.; Penadés-Plà, V.; Yepes, V.; Martí, J.V. Life cycle assess-ment of earth-retaining walls: An environmental comparison. J. Clean. Prod. 2018, 192, 411–420. [Google Scholar] [CrossRef]
- Martínez Fernández, P.; Villalba Sanchis, I.; Insa Franco, R.; Yepes, V. Slab track optimisation using metamodels to improve rail construction sustainability. J. Constr. Eng. Manag. ASCE 2022, 148, 04022053. [Google Scholar] [CrossRef]
- Zamarrón-Mieza, I.; Yepes, V.; Moreno-Jiménez, J.M. A systematic review of application of multi-criteria decision analysis for aging-dam management. J. Clean. Prod. 2017, 147, 217–230. [Google Scholar] [CrossRef] [Green Version]
- Frangopol, D.M.; Dong, Y.; Sabatino, S. Bridge life-cycle performance and cost: Analysis, prediction, optimization, and decision-making. Struct. Infrastruct. Eng. 2017, 13, 1239–1257. [Google Scholar] [CrossRef]
- Sajedi, S.; Huang, Q. Reliability-based life-cycle-cost comparison of different corrosion management strategies. Eng. Struct. 2019, 186, 52–63. [Google Scholar] [CrossRef]
- Hatami, A.; Morcous, G. Deterministic and Probabilistic Lifecycle Cost Assessment: Applications to Nebraska Bridges. J. Perform. Constr. Fac. 2016, 30, 04015025. [Google Scholar] [CrossRef]
- Hammervold, J.; Reenaas, M.; Brattebø, H. Environmental life cycle assessment of bridges. J. Bridge Eng. 2013, 18, 153–161. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Wu, W.J.; Wang, Y.F. Bridge life cycle assessment with da-ta uncertainty. Int. J. Life Cycle Ass. 2016, 21, 569–576. [Google Scholar] [CrossRef]
- Navarro, I.J.; Yepes, V.; Martí, J.V.; González-Vidosa, F. Life cycle impact assessment of corrosion preventive designs applied to prestressed concrete bridge decks. J. Clean. Prod. 2018, 196, 698–713. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Eng. Struct. 2019, 179, 556–565. [Google Scholar] [CrossRef]
- Wang, A.; Yang, D.Y.; Frangopol, D.M.; Jin, W. Inclusion of environmental impacts in life-cycle cost analysis of bridge structures. Sustain. Resilient Infrastruct. 2020, 5, 252–267. [Google Scholar] [CrossRef]
- García-Segura, T.; Penadés-Plà, V.; Yepes, V. Sustainable bridge design by metamodel-assisted multi-objective optimization and decision-making under uncertainty. J. Clean. Prod. 2018, 202, 904–915. [Google Scholar] [CrossRef]
- Penadés-Plà, V.; Martínez-Muñoz, D.; García-Segura, T.; Navarro, I.J.; Yepes, V. Environmental and social impact assessment of optimized post-tensioned concrete road bridges. Sustainability 2020, 12, 4265. [Google Scholar] [CrossRef]
- Gervásio, H.; da Silva, L.S. Life-cycle social analysis of motorway bridges. Struct. Infrastruct. Eng. 2013, 9, 1019–1039. [Google Scholar] [CrossRef]
- Saaty, T.L. The analytic hierarchy process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Yannis, G.; Kopsacheili, A.; Dragomanovits, A.; Petraki, V. State-of-the-art review on multi-criteria decision-making in the transport sector. J. Traffic Transp. Eng. 2020, 7, 413–431. [Google Scholar] [CrossRef]
- Nazim, M.; Mohammad, C.W.; Sadiq, M. A comparison between fuzzy AHP and fuzzy TOPSIS methods to software requirements selection. Alex. Eng. J. 2022, 61, 10851–10870. [Google Scholar] [CrossRef]
- Ha-Mim, N.M.; Rahman, M.A.; Hossain, M.Z.; Fariha, J.N.; Rahaman, K.R. Employing multi-criteria decision analysis and geospatial techniques to assess flood risks: A study of Barguna district in Bangladesh. Int. J. Disast. Risk Reduct. 2022, 77, 103081. [Google Scholar] [CrossRef]
- Bagherigorji, R.; Nourtaghani, A.; Farrokhzad, M. Multicriteria Decision-Making Model for the Selection of an Affordable Prefabricated Housing System Using Delphi-AHP Method. J. Archit. Eng. 2022, 28. [Google Scholar] [CrossRef]
- Alao, M.A.; Popoola, O.M.; Ayodele, T.R. A novel fuzzy integrated MCDM model for optimal selection of waste-to-energy-based-distributed generation under uncertainty: A case of the City of Cape Town, South Africa. J. Clean. Prod. 2022, 343, 130824. [Google Scholar] [CrossRef]
- Balali, A.; Valipour, A. Identification and selection of building façade’s smart materials according to sustainable development goals. Sustain. Mater. Technol. 2020, 26, e00213. [Google Scholar] [CrossRef]
- Alkharabsheh, A.; Moslem, S.; Oubahman, L.; Duleba, S. An Integrated Approach of Multi-Criteria Decision-Making and Grey Theory for Evaluating Urban Public Transportation Systems. Sustainability 2021, 13, 2740. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process; RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Liu, K.; Liu, Y.; Qin, J. An integrated ANP-VIKOR methodology for sustainable supplier selection with interval type-2 fuzzy sets. Granul. Comput. 2018, 3, 193–208. [Google Scholar] [CrossRef]
- Radwan, N.; Senousy, M.; Riad, A. Neutrosophic AHP multi-criteria decision-making method applied on the selection of learning management system. Int. J. Adv. Comput. Technol. 2016, 8, 95–105. [Google Scholar]
- Navarro, I.J.; Penadés-Plà, V.; Martínez-Muñoz, D.; Rempling, R.; Yepes, V. Life cycle sustainability assessment for multi-criteria decision making in bridge design: A review. J. Civ. Eng. Manag. 2020, 26, 690–704. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Springer-Verlag: New York, NY, USA, 1981. [Google Scholar]
- Yuan, W.; Cai, Z.; Guo, A. Rapid determination method of the seismic failure modes of coastal bridge columns in the whole life cycle. Structures 2020, 28, 943–955. [Google Scholar] [CrossRef]
- Yuan, W.; Cai, Z.; Pan, X.; Lin, J. Time-dependent seismic performance of coastal bridges reinforced with hybrid FRP and steel bars. Materials 2022, 15, 5293. [Google Scholar] [CrossRef] [PubMed]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Sustainability assessment of concrete bridge deck designs in coastal environments using neutrosophic criteria weights. Struct. Infrastruct. Eng. 2020, 16, 949–967. [Google Scholar] [CrossRef]
- Nogueira, C.G.; Leonel, E.D.; Coda, H.B. Reliability algorithms applied to reinforced concrete structures durability assessment. Rev. IBRACON Estrut. Mater. 2012, 5, 440–450. [Google Scholar] [CrossRef]
- Fib. Fib Bulletin 34: Model Code for Service Life Design; Fib: Lausanne, Switzerland, 2006. [Google Scholar]
- Ministerio de Fomento. Obras de Paso de Nueva Construcción: Conceptos Generales; Ministerio de Fomento: Madrid, Spain, 2000. [Google Scholar]
- Navarro, I.J.; Yepes, V.; Martí, J.V. Social life cycle assessment of concrete bridge decks exposed to aggressive environments. Environ. Impact Asses. 2018, 72, 50–63. [Google Scholar] [CrossRef]
- OECD. Handbook on Constructing Composite Indicators: Methodology and User Guide; OECD Publications: Paris, France, 2008. [Google Scholar]
- European Institute for Gender Equality. Gender Equality Index 2015—Measuring Gender Equality in the European Union 2005–2012; EIGE: Vilnius, Lithuania, 2015. [Google Scholar]
- Ozturk, O.; Ozbay, K.; Yang, H.; Bartin, B. Crash Frequency Modeling for Highway Construction Zones. In Proceedings of the Transportation Research Board’s 92nd Annual Meeting, Washington, DC, USA, 14–16 January 2013. [Google Scholar]
- Dette, G.; Sigrist, V. Performance indicators for concrete bridges. In Proceedings of the Fib Symposium Proceedings, Prague, Czech Republic, 8–10 June 2011. [Google Scholar]
- Martínez-Cámara, E.; Santamaría, J.; Sanz-Adán, F.; Arancón, D. Digital Eco-Design and Life Cycle Assessment – Key elements in a circular economy: A case study of conventional desk. Appl. Sci. 2021, 11, 10439. [Google Scholar] [CrossRef]
- Decorte, Y.; Steeman, M.; Van den Bossche, N. Effect of a one-dimensional approach in LCA on the environmental life cycle impact of buildings: Multi-family case study in Flanders. Build. Environ. 2021, 206, 108381. [Google Scholar] [CrossRef]
| Number of Criteria n | Random Index (RI) | Maximum Acceptable CR |
|---|---|---|
| 2 | 0 | 0% |
| 3 | 0.58 | 5% |
| 4 | 0.90 | 9% |
| 5 | 1.12 | 10% |
| 6 | 1.24 | 10% |
| 7 | 1.32 | 10% |
| 8 | 1.41 | 10% |
| 9 | 1.45 | 10% |
| 10 | 1.49 | 10% |
| Component | Baseline (REF) | 10% Silica Fume (SF10) | 10% Fly Ash (FA10) | Sealant (SEAL) | Galvanized Steel (GALV) |
|---|---|---|---|---|---|
| Water (l/m³) | 140 | 140 | 140 | 140 | 140 |
| Cement (kg/m³) | 350 | 280 | 339.5 | 350 | 350 |
| Fine aggregates (kg/m³) | 1068 | 1129 | 1077 | 1068 | 1068 |
| Coarse aggregates (kg/m³) | 1017 | 1017 | 1017 | 1017 | 1017 |
| Silica fume (kg/m³) | - | 35 | - | - | - |
| Fly ash (kg/m³) | - | - | 35 | - | - |
| Plasticizer (kg/m³) | 5.3 | 4.2 | 5.1 | 5.3 | 5.3 |
| Parameter | Baseline (REF) | 10% Silica Fume (SF10) | 10% Fly Ash (FA10) | Sealant (SEAL) | Galvanized Steel (GALV) |
|---|---|---|---|---|---|
| D0 (m²/s) | 8.9 × 10−12 (0.9 × 10−12) | 1.2 × 10−12 (0.2 × 10−12) | 5.5 × 10−12 (0.4 × 10−12) | 4.3 × 10−12 (0.3 × 10−12) | 8.9 × 10−12 (0.9 × 10−12) |
| Ccr (%) | 0.6 (0.1) | 0.6 (0.03) | 0.6 (0.1) | 0.6 (0.1) | 1.2 (0.2) |
| Criterion | Baseline (REF) | 10% Silica Fume (SF10) | 10% Fly Ash (FA10) | Sealant (SEAL) | Galvanized Steel (GALV) | |
|---|---|---|---|---|---|---|
| Economic criteria | Construction costs | 1296.4 | 1566.6 | 1387.1 | 1557.9 | 2707.7 |
| Maintenance costs | 5511.3 | 258.2 | 2208.4 | 492.8 | 2121.3 | |
| Social criteria | Employment generation | 0.671 | 0.507 | 0.570 | 0.611 | 0.574 |
| Econ. development of regions | 0.637 | 0.395 | 0.471 | 0.519 | 0.801 | |
| Users | 0.060 | 0.526 | 0.160 | 0.156 | 0.157 | |
| Public opinion | 0.057 | 0.523 | 0.157 | 0.153 | 0.153 | |
| Environmental criteria | Human health | 270.6 | 62.8 | 138.4 | 50.7 | 151.8 |
| Ecosystems | 139.9 | 29.9 | 70.8 | 25.4 | 75.8 | |
| Scarcity of resources | 302.5 | 118.1 | 176.5 | 100.2 | 190.6 |
| Criterion | AHP-Derived Weights |
|---|---|
| Construction costs | 4.92% |
| Maintenance costs | 1.79% |
| Employment generation | 2.50% |
| Econ. development of regions | 4.56% |
| Users | 15.30% |
| Public opinion | 11.03% |
| Human health | 18.24% |
| Ecosystems | 25.46% |
| Scarcity of resources | 16.19% |
| Criterion | Baseline (REF) | 10% Silica Fume (SF10) | 10% Fly Ash (FA10) | Sealant (SEAL) | Galvanized Steel (GALV) |
|---|---|---|---|---|---|
| Distance to ideal positive Di+ | 0.2606 | 0.0187 | 0.1442 | 0.1180 | 0.1524 |
| Distance to ideal negative Di− | 0.0197 | 0.2522 | 0.1347 | 0.2170 | 0.1234 |
| TOPSIS Score Siw | 0.0702 | 0.9310 | 0.4829 | 0.6478 | 0.4474 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Navarro, I.J.; Martí, J.V.; Yepes, V. Analytic Network Process-Based Sustainability Life Cycle Assessment of Concrete Bridges in Coastal Regions. Sustainability 2022, 14, 10688. https://doi.org/10.3390/su141710688
Navarro IJ, Martí JV, Yepes V. Analytic Network Process-Based Sustainability Life Cycle Assessment of Concrete Bridges in Coastal Regions. Sustainability. 2022; 14(17):10688. https://doi.org/10.3390/su141710688
Chicago/Turabian StyleNavarro, Ignacio J., José V. Martí, and Víctor Yepes. 2022. "Analytic Network Process-Based Sustainability Life Cycle Assessment of Concrete Bridges in Coastal Regions" Sustainability 14, no. 17: 10688. https://doi.org/10.3390/su141710688
APA StyleNavarro, I. J., Martí, J. V., & Yepes, V. (2022). Analytic Network Process-Based Sustainability Life Cycle Assessment of Concrete Bridges in Coastal Regions. Sustainability, 14(17), 10688. https://doi.org/10.3390/su141710688







