The Whole Process CFD Numerical Simulation of Flow Field and Suspended Solids Distribution in a Full-Scale High-Rate Clarifier
Abstract
:1. Introduction
2. Materials and Methods
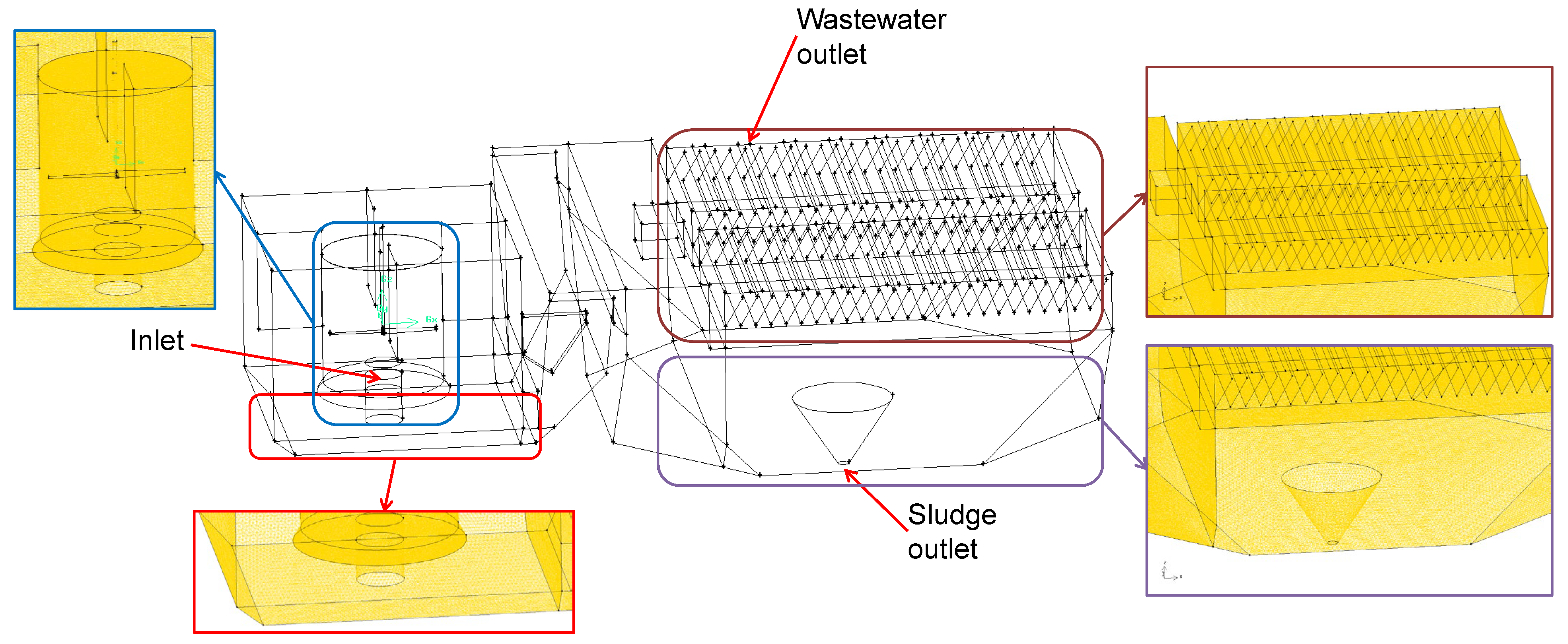
2.1. The Full-Scale High-Rate Clarifier Geometry
2.2. Mathematical Modeling
2.2.1. CFD Model
2.2.2. Governing Equations
2.2.3. Boundary Conditions
2.3. Experimental Measurements
2.3.1. Flow Field Measurements
2.3.2. Other Measurements
2.4. Statistical Analysis
3. Results and Discussion
3.1. Comparison of the Simulated and the Measured Flow Velocities
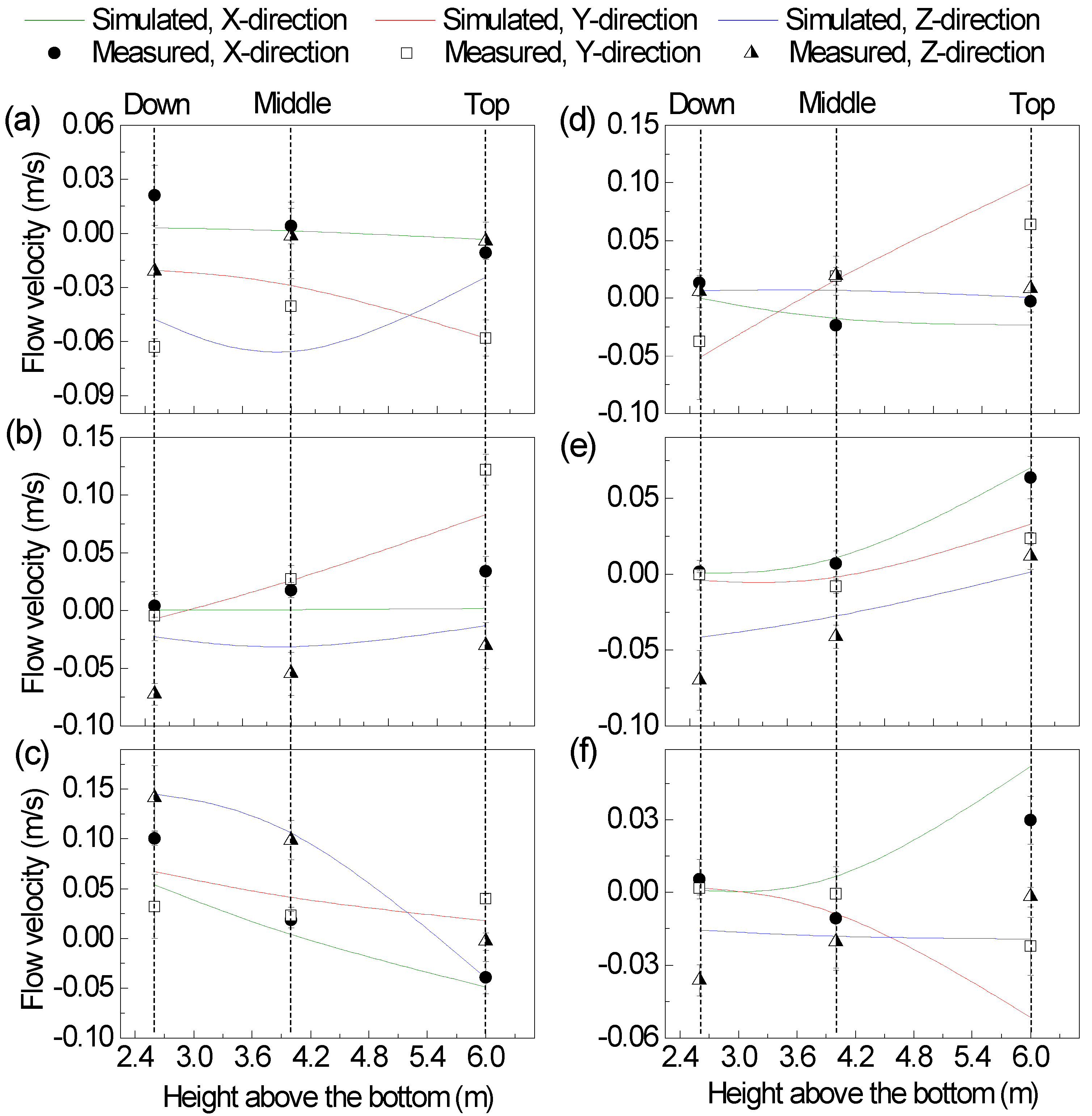
3.1.1. Comparison of the Simulated and the Measured Flow Velocities in the Reaction Tank
3.1.2. Comparison of the Simulated and the Measured Flow Velocities in the Settling Tank
3.2. Contour Profiles of Velocities and SS Concentrations of the High-Rate Clarifier
3.2.1. Contours of Velocity Profiles of the High-Rate Clarifier Simulated by the Two-Phase Model
3.2.2. Contours of SS Concentration Profiles of the High-Rate Clarifier Simulated by the Two-Phase Model
4. Conclusions
- (1)
- The simulated results of the developed CFD model were in good agreement with the experimental data obtained in the high-rate clarifier. The normalized standard error was less than 7.66%. The consistency between the simulated results and the measured data further proved that the flow field could be accurately simulated by the CFD model.
- (2)
- Through the analysis of the flow field distribution in the five typical sections, it was found that the overall flow velocities in the settling tank were much smaller than that in the reaction tank. After the fluid passed through the diversion effect of the overflow wall and the under-through channel, the overall kinetic energy loss was relatively large.
- (3)
- Through the analysis of the SS concentration distribution in the five typical sections, the sludge sedimentation happened at the edge of the settling tank due to the vertical angle between the plug-flow fluid and the outlet.
- (4)
- The successful construction of the CFD model demonstrated that hydraulic characteristics of the high-rate clarifier could be simulated and studied at a low cost and in a short time. This could be an insight into the sedimentation process and pollutant removal mechanism in-depth and lay the foundation for the next step of the high-rate clarifier optimization operation and research on pollutant removal.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.H.; Yang, W.; Ngo, H.H.; Guo, W.S.; Jin, P.K.; Dzakpasu, M.; Yang, S.; Wang, Q.; Wang, X.; Ao, D. Current Status of Urban Wastewater Treatment Plants in China. Environ. Int. 2016, 92, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Xiong, X.; Wu, C.; Elser, J.J.; Mei, Z.; Hao, Y. Occurrence and Fate of Microplastic Debris in Middle and Lower Reaches of the Yangtze River – From Inland to the Sea. Sci. Total Environ. 2019, 659, 66–73. [Google Scholar] [CrossRef] [PubMed]
- He, D.; Chen, X.; Zhao, W.; Zhu, Z.; Qi, X.; Zhou, L.; Chen, W.; Wan, C.; Li, D.; Zou, X.; et al. Microplastics Contamination in the Surface Water of the Yangtze River from Upstream to Estuary Based on Different Sampling Methods. Environ. Res. 2021, 196, 110908. [Google Scholar] [CrossRef] [PubMed]
- Feng, S.; Lu, H.; Yao, T.; Liu, Y.; Tian, P.; Lu, J. Microplastic Footprints in the Qinghai-tibet Plateau and Their Implications to the Yangtze River Basin. J. Hazard. Mater. 2021, 407, 124776. [Google Scholar] [CrossRef]
- Fan, J.; Zou, L.; Zhao, G. Microplastic Abundance, Distribution, and Composition in the Surface Water and Sediments of the Yangtze River Along Chongqing City, China. J. Soils Sediments. 2021, 21, 1840–1851. [Google Scholar] [CrossRef]
- Qu, J.H.; Wang, H.C.; Wang, K.J.; Yu, G.; Ke, B.; Yu, H.Q.; Ren, H.Q.; Zheng, X.C.; Li, J.; Li, W.W.; et al. Municipal Wastewater Treatment in China: Development History and Future Perspectives. Front. Env. Sci. Eng. 2019, 13, 7. [Google Scholar] [CrossRef]
- Luo, Y.; Yao, J.; Wang, X.; Zheng, M.; Guo, D.; Chen, Y. Efficient Municipal Wastewater Treatment by Oxidation Ditch Process at Low Temperature: Bacterial Community Structure in Activated Sludge. Sci. Total Environ. 2020, 703, 135031. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, K.; Wang, H.; Wu, Q.; Liang, S.; Yu, W.; Hou, H.; Liu, B.; Hu, J.; Yang, J. Insight into Effects of Organic and Inorganic Phosphorus Speciations on Phosphorus Removal Efficiency in Secondary Effluent. Environ. Sci. Pollut. Res. 2020, 27, 11736–11748. [Google Scholar] [CrossRef]
- Teh, C.Y.; Budiman, P.M.; Shak, K.P.Y.; Wu, T.Y. Recent Advancement of Coagulation–flocculation and Its Application in Wastewater Treatment. Ind. Eng. Chem. Res. 2016, 55, 4363–4389. [Google Scholar] [CrossRef]
- Fu, Y.; Wang, Y.Z. An Organic-inorganic Hybrid Coagulant Containing al, zn and fe (hoazf): Preparation, Efficiency and Mechanism of Removing Organic Phosphorus. J. Water Reuse Desalin. 2018, 8, 202–213. [Google Scholar] [CrossRef] [Green Version]
- Ma, B.; Xue, W.; Ding, Y.; Hu, C.; Liu, H.; Qu, J. Removal Characteristics of Microplastics by fe-Based Coagulants During Drinking Water Treatment. J. Environ. Sci. 2019, 78, 267–275. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.P.; Chen, Y.Z.; Wang, Y.; Yuan, S.J.; Yu, H.Q. Optimization of the Coagulation-flocculation Process for Pulp Mill Wastewater Treatment Using a Combination of Uniform Design and Response Surface Methodology. Water Res. 2011, 45, 5633–5640. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Zhang, W.J.; Yang, X.Y.; Xiao, P.; Wang, D.S.; Song, Y. Advanced Treatment of Effluent from Municipal wwtp with Different Metal Salt Coagulants: Contaminants Treatability and Floc Properties. Sep. Purif. Technol. 2013, 120, 123–128. [Google Scholar] [CrossRef]
- Ebeling, J.M.; Welsh, C.F.; Rishel, K.L. Performance Evaluation of an Inclined Belt Filter Using Coagulation/Flocculation Aids for the Removal of Suspended Solids and Phosphorus from Microscreen Backwash Effluent. Aquac. Eng. 2006, 35, 61–77. [Google Scholar] [CrossRef]
- Pavlova, S.; Dobrevsky, I. Modified Sirofloc Process for Natural Water Treatment. Desalination 2005, 173, 55–59. [Google Scholar] [CrossRef]
- Pukkella, A.K.; Vysyaraju, R.; Tammishetti, V.; Rai, B.; Subramanian, S. Improved Mixing of Solid Suspensions in Stirred Tanks with Interface Baffles: Cfd Simulation and Experimental Validation. Chem. Eng. J. 2019, 358, 621–633. [Google Scholar] [CrossRef]
- Wu, B. Cfd Simulation of Gas and Non-newtonian Fluid Two-phase Flow in Anaerobic Digesters. Water Res. 2010, 44, 3861–3874. [Google Scholar] [CrossRef]
- Goula, A.M.; Kostoglou, M.; Karapantsios, T.D.; Zouboulis, A.I. The Effect of Influent Temperature Variations in a Sedimentation Tank for Potable Water Treatment--a Computational Fluid Dynamics Study. Water Res. 2008, 42, 3405–3414. [Google Scholar] [CrossRef]
- Brannock, M.; Wang, Y.; Leslie, G. Mixing Characterisation of Full-scale Membrane Bioreactors: Cfd Modelling with Experimental Validation. Water Res. 2010, 44, 3181–3191. [Google Scholar] [CrossRef]
- Le Moullec, Y.; Gentric, C.; Potier, O.; Leclerc, J.P. Cfd Simulation of the Hydrodynamics and Reactions in an Activated Sludge Channel Reactor of Wastewater Treatment. Chem. Eng. Sci. 2010, 65, 492–498. [Google Scholar] [CrossRef]
- Guimet, V.; Savoye, P.; Audic, J.; Do-Quang, Z.; Van Loosdrecht, M.; Clement, J. Advanced cfd tool for wastewater: Today complex modelling and tomorrow easy-to-use interface. In Proceedings of the 2nd IWA Leading-Edge Conference on Water and Wastewater Treatment Technologies, Prague, Czech Republic, 1–4 June 2004; Guimet, V., Savoye, P., Audic, J., Do-Quang, Z., Van Loosdrecht, M., Clement, J., Eds.; IWA Publishing: London, UK, 2005; Volume 4, pp. 1–4. [Google Scholar]
- Zhang, J.; Chen, X.; Liu, J.; Huang, B.; Xu, M. Structural Characteristics of a Spiral Symmetry Stream Anaerobic Bioreactor Based on Cfd. Biochem. Eng. J. 2018, 137, 50–61. [Google Scholar] [CrossRef]
- Fayolle, Y.; Gillot, S.; Cockx, A.; Roustan, M.; Héduit, A. In Situ Local Parameter Measurements for Cfd Modeling to Optimize Aeration. Proc. Water Environ. Fed. 2006, 2006, 3314–3326. [Google Scholar] [CrossRef]
- Fayolle, Y.; Cockx, A.; Gillot, S.; Roustan, M.; Héduit, A. Oxygen Transfer Prediction in Aeration Tanks Using Cfd. Chem. Eng. Sci. 2007, 62, 7163–7171. [Google Scholar] [CrossRef]
- Lakghomi, B.; Lawryshyn, Y.; Hofmann, R. A Model of Particle Removal in a Dissolved Air Flotation Tank: Importance of Stratified Flow and Bubble Size. Water Res. 2014, 68, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, F.; Viedma, A.; Kaiser, A.S. Hydraulic Characterization of an Activated Sludge Reactor with Recycling System by Tracer Experiment and Analytical Models. Water Res. 2016, 101, 382–392. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, F.; Rey, H.; Viedma, A.; Nicolás-Pérez, F.; Kaiser, A.; Martínez, M. Cfd Simulation of Fluid Dynamic and Biokinetic Processes Within Activated Sludge Reactors Under Intermittent Aeration Regime. Water Res. 2018, 139, 47–57. [Google Scholar] [CrossRef] [PubMed]
- Littleton, H.X.; Daigger, G.T.; Strom, P.F. Application of Computational Fluid Dynamics to Closed-loop Bioreactors: Ii. Simulation of Biological Phosphorus Removal Using Computational Fluid Dynamics. Water Environ. Res. 2007, 79, 613–624. [Google Scholar] [CrossRef]
- Littleton, H.X.; Daigger, G.T.; Strom, P.F. Application of Computational Fluid Dynamics to Closed-loop Bioreactors: I. Characterization and Simulation of Fluid-flow Pattern and Oxygen Transfer. Water Environ. Res. 2007, 79, 600–612. [Google Scholar] [CrossRef]
- Li, Z.-l.; Guo, L.-s.; Zhang, D.-j.; Xu, D.-y. Simulation of Liquid-gas Flow in Full-scale Caroussel Oxidation Ditch with Surface aeration. J. Cent. South Univ. 2012, 19, 1615–1621. [Google Scholar] [CrossRef]
- Song, T.; Jiang, K.; Zhou, J.; Wang, D.; Xu, N.; Feng, Y. Cfd Modelling of gas–Liquid Flow in an Industrial Scale Gas-stirred Leaching Tank. Int. J. Miner. Process. 2015, 142, 63–72. [Google Scholar] [CrossRef]
- Aubin, J.; Xuereb, C. Design of Multiple Impeller Stirred Tanks for the Mixing of Highly Viscous Fluids Using Cfd. Chem. Eng. Sci. 2006, 61, 2913–2920. [Google Scholar] [CrossRef]
- Achouri, R.; Dhaouadi, H.; Mhiri, H.; Bournot, P. Numerical and Experimental Investigation of the Self-inducing Turbine Aeration Capacity. Energy Conv. Manag. 2014, 83, 188–196. [Google Scholar] [CrossRef]
- Patziger, M. Computational Fluid Dynamics Investigation of Shallow Circular Secondary Settling Tanks: Inlet Geometry and Performance Indicators. Chem. Eng. Res. Des. 2016, 112, 122–131. [Google Scholar] [CrossRef]
- Valle Medina, M.E.; Laurent, J. Incorporation of a Compression Term in a Cfd Model Based on the Mixture Approach to Simulate Activated Sludge Sedimentation. Appl. Math. Model. 2020, 77, 848–860. [Google Scholar] [CrossRef]
- Lei, L.; Ni, J. Three-dimensional Three-phase Model for Simulation of Hydrodynamics, Oxygen Mass Transfer, Carbon Oxidation, Nitrification and Denitrification in an Oxidation Ditch. Water Res. 2014, 53, 200–214. [Google Scholar] [CrossRef]
- Fan, L.; Xu, N.; Wang, Z.; Shi, H. Pda Experiments and Cfd Simulation of a Lab-scale Oxidation Ditch with Surface Aerators. Chem. Eng. Res. Des. 2010, 88, 23–33. [Google Scholar] [CrossRef]
- Hribersek, M.; Zajdela, B.; Hribernik, A.; Zadravec, M. Experimental and Numerical Investigations of Sedimentation of Porous Wastewater Sludge Flocs. Water Res. 2011, 45, 1729–1735. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Yang, J.; Hu, Y.; Zhang, H.; Yang, Y.; Zhang, K.; Zhu, X.; Li, Y.; Yang, C. Simulation of Flow Field and Sludge Settling in a Full-scale Oxidation Ditch by Using a Two-phase Flow Cfd Model. Chem. Eng. Sci. 2014, 109, 296–305. [Google Scholar] [CrossRef]
- Patziger, M.; Kainz, H.; Hunze, M.; Jozsa, J. Influence of Secondary Settling Tank Performance on Suspended Solids Mass Balance in Activated Sludge Systems. Water Res. 2012, 46, 2415–2424. [Google Scholar] [CrossRef]
- Xu, Q.; Xiao, K.; Wu, Q.; Wang, H.; Liang, S.; Yu, W.; Tao, S.; Hou, H.; Liu, B.; Hu, J. The Optimization on Distributions of Flow Field and Suspended Solids in a Full-scale High-rate Clarifier Using Computational Fluid Dynamics. Biochem. Eng. J. 2020, 155, 107489. [Google Scholar] [CrossRef]
- Lapointe, M.; Brosseau, C.; Comeau, Y.; Barbeau, B. Assessing Alternative Media for Ballasted Flocculation. J. Environ. Eng-ASCE. 2017, 143, 4017071. [Google Scholar] [CrossRef]
- Imasuen, E.; Judd, S.; Sauvignet, P. High-rate Clarification of Municipal Wastewaters: A Brief Appraisal. J. Chem. Technol. Biotechnol. 2004, 79, 914–917. [Google Scholar] [CrossRef]
- Bridgeman, J.; Jefferson, B.; Parsons, S.A. Computational Fluid Dynamics Modelling of Flocculation in Water Treatment: A Review. Eng. Appl. Comp. Fluid Mech. 2014, 3, 220–241. [Google Scholar] [CrossRef]
- Bridgeman, J.; Jefferson, B.; Parsons, S. Assessing Floc Strength Using Cfd to Improve Organics Removal. Chem. Eng. Res. Des. 2008, 86, 941–950. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, J.; Hou, H.; Hu, Y.; Liang, S.; Xiao, K.; Wu, X.; Liu, B.; Hu, J.; Hu, J. Simulation on Flow Field and Gas Hold-up of a Pilot-scale Oxidation Ditch by Using Liquid-gas Cfd Model. Water Sci. Technol. 2018, 78, 1956–1965. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Stenstrom, M.K. Evaluation of Three Turbulence Models in Predicting the Steady State Hydrodynamics of a Secondary Sedimentation Tank. Water Res. 2018, 143, 445–456. [Google Scholar] [CrossRef]
- Takács, I.; Patry, G.G.; Nolasco, D. A Dynamic Model of the Clarification-thickening Process. Water Res. 1991, 25, 1263–1271. [Google Scholar] [CrossRef]
- Xu, Q.; Wan, Y.; Wu, Q.; Xiao, K.; Yang, J. An Efficient Hydrodynamic-biokinetic Model for the Optimization of Operational Strategy Applied in a Full-scale Oxidation Ditch by Cfd Integrated with Asm2. Water Res. 2021, 193, 116888. [Google Scholar] [CrossRef]
- Kulkarni, A.L.; Patwardhan, A.W. Cfd Modeling of Gas Entrainment in Stirred Tank Systems. Chem. Eng. Res. Des. 2014, 92, 1227–1248. [Google Scholar] [CrossRef]
- Villiger, T.K.; Neunstoecklin, B.; Karst, D.J.; Lucas, E.; Stettler, M.; Broly, H.; Morbidelli, M.; Soos, M. Experimental and Cfd Physical Characterization of Animal Cell Bioreactors: From Micro- to Production Scale. Biochem. Eng. J. 2018, 131, 84–94. [Google Scholar] [CrossRef]
- Ding, J.; Wang, X.; Zhou, X.-F.; Ren, N.-Q.; Guo, W.-Q. Cfd Optimization of Continuous Stirred-tank (cstr) Reactor for Biohydrogen Production. Bioresour. Technol. 2010, 101, 7005–7013. [Google Scholar] [CrossRef] [PubMed]

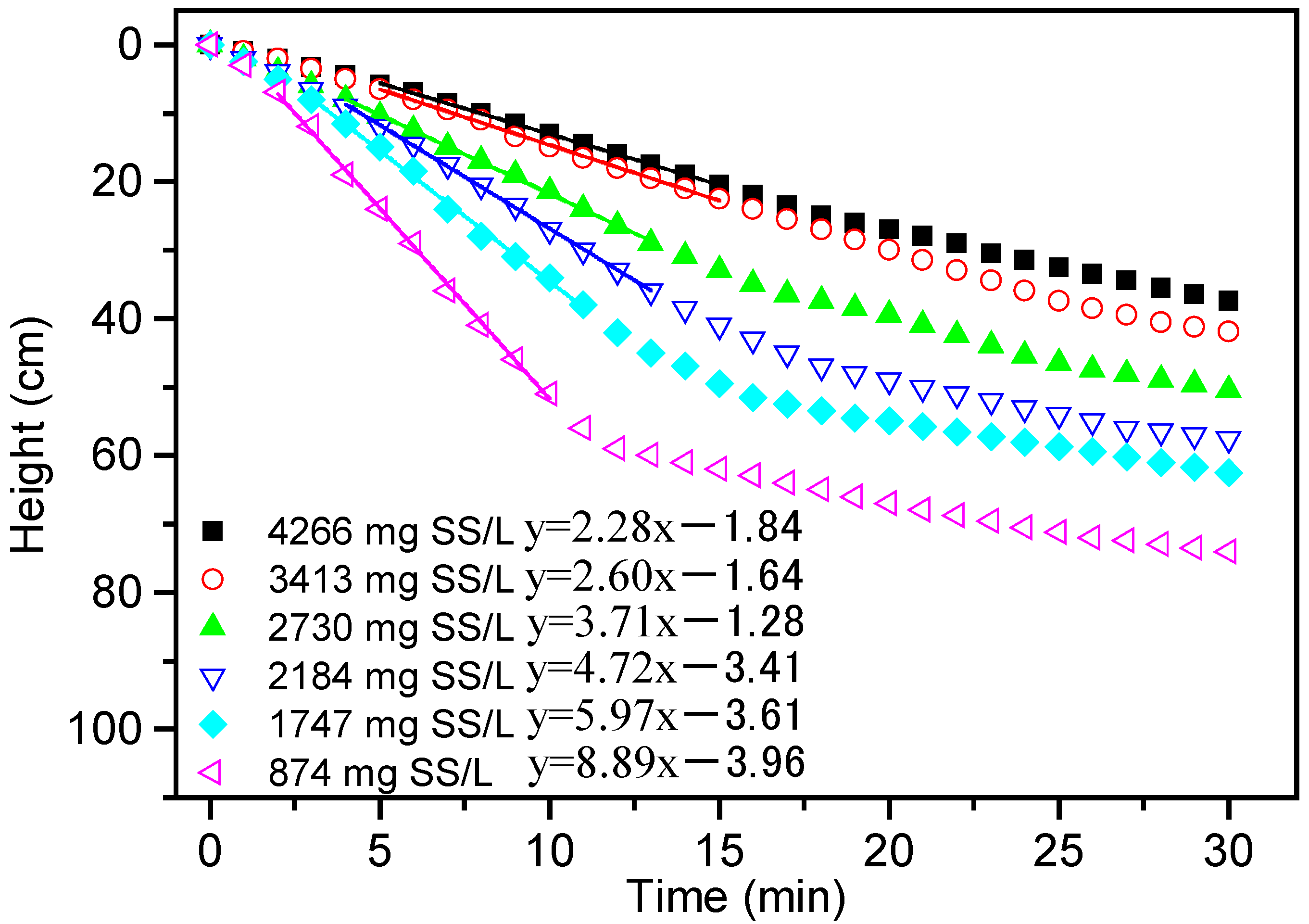







| SS (mg/L) | 874 | 1747 | 2184 | 2730 | 3413 | 4266 |
| Settling velocity (×10−4 m/s) | 8.89 | 5.97 | 4.72 | 3.71 | 2.60 | 2.28 |
| Regions | Sampling Sites * | Coordinates (mm) |
|---|---|---|
| Reaction tank | R1 | (−3000, −1080) |
| R2 | (−3000, 1080) | |
| R3 | (3000, −1080) | |
| R4 | (3000, 1310) | |
| R5 | (−1750, −4000) | |
| R6 | (−3800, −1080) | |
| R7 | (−3800, 1080) | |
| R8 | (3200, −3800) | |
| Settling tank | S1 | (4700, −3500) |
| S2 | (4700, 3500) | |
| S3 | (5600, −1100) | |
| S4 | (5600, 1330) | |
| S5 | (7300, −1100) | |
| S6 | (7300, 1330) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Luo, X.; Xu, C.; Wan, Y.; Xiong, G.; Chen, H.; Zhou, Q.; Yan, D.; Li, X.; Li, Y.; et al. The Whole Process CFD Numerical Simulation of Flow Field and Suspended Solids Distribution in a Full-Scale High-Rate Clarifier. Sustainability 2022, 14, 10624. https://doi.org/10.3390/su141710624
Xu Q, Luo X, Xu C, Wan Y, Xiong G, Chen H, Zhou Q, Yan D, Li X, Li Y, et al. The Whole Process CFD Numerical Simulation of Flow Field and Suspended Solids Distribution in a Full-Scale High-Rate Clarifier. Sustainability. 2022; 14(17):10624. https://doi.org/10.3390/su141710624
Chicago/Turabian StyleXu, Qi, Xi Luo, Chengjian Xu, Yanlei Wan, Guangcheng Xiong, Hao Chen, Qiuhong Zhou, Dan Yan, Xiang Li, Yingxi Li, and et al. 2022. "The Whole Process CFD Numerical Simulation of Flow Field and Suspended Solids Distribution in a Full-Scale High-Rate Clarifier" Sustainability 14, no. 17: 10624. https://doi.org/10.3390/su141710624
APA StyleXu, Q., Luo, X., Xu, C., Wan, Y., Xiong, G., Chen, H., Zhou, Q., Yan, D., Li, X., Li, Y., & Liu, H. (2022). The Whole Process CFD Numerical Simulation of Flow Field and Suspended Solids Distribution in a Full-Scale High-Rate Clarifier. Sustainability, 14(17), 10624. https://doi.org/10.3390/su141710624





