1. Introduction
In Peru, government expenditure—the nonfinancial expenditures of government in general (national government, regional governments, and local governments)—constitutes current expenditure accounts (periodic expenditures for the payment of salaries and pensions, the purchase and contracting of goods and services, as well as the transfer of resources to other public sector entities and/or to the private sector) and capital expenditure (gross capital formation and other capital expenditures) [
1]. In 2021, real government expenditure increased by 5.1% over the value in the previous year (its percentage variation in 2020 amounted to 12.8). This increase was due to higher expenditure on gross capital formation and purchases of goods and services to address the health crisis generated by COVID-19. However, as a fraction of GDP, government expenditure decreased by 4.4% owing to the high percentage variation in nominal GDP (21.5%). Similarly, real expenditure on transfers declined by 16.3%, and real expenditure on salaries dropped by 1.8% [
2].
During 2021, public expenditure—comprising government expenditure excluding compensation, pensions, transfers, and other capital expenditures—measured as the sum of public consumption and public investment increased at a rate of 14% owing to the growth rates of public consumption (10.6%) and public investment (24.9%). Public consumption increased the growth rate by 10.6% over the value in 2020 due to higher expenditures on the purchase of medical supplies, professional and technical services to address the health crisis, and road maintenance and upkeep (the percentage variation in public consumption was 7.8 in 2020). In addition, public investment increased by 24.9% with respect to the value in the previous year, contrasting with the −15.1 percentage variation registered in 2020. Regarding economic growth, during 2021, the percentage variation in Peruvian real GDP stood at 13.3% with respect to the value in the previous year (the percentage variation in real GDP was −11.0 in 2020 due to COVID-19) [
2]. In this study, we consider public expenditure in a similar way to the studies by Aparco and Flores [
3] and Peña [
4]; we define public expenditure as the sum of public consumption and gross fixed capital formation (GFCF).
Ansari [
5] documented that the relation between public expenditure and economic growth has been widely addressed by public finance [
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18], as well as by macroeconomic modeling (Some of these works include the following: [
19,
20,
21,
22]). Legrenzi and Milas [
23] empirically demonstrated that the omitted variables, bureaucracy and local expenditure, in an original bivariate model between GDP and public spending support the existence of a lung-run equilibrium relationship between these four variables, in Italy. Policymakers should have a proper understanding of the relation between these variables so that they may efficiently allocate public resources to achieve the desired economic growth and prosperity, according to Kirikkaleli and Ozbeser [
24]. Kumar et al. [
25] argued that governments should understand the dynamics of the relation between these variables to establish a proper macroeconomic policy. As Keynes [
26] had already stated, periods of recession (expansion) restrict (favor) the abilities of policymakers to stimulate the economy through fiscal measures unless the share of government expenditure to output increases (decreases). Kumar et al. [
25] further indicated that the long-term estimates of the relation between public expenditure and economic growth would identify a benchmark against which to ascertain the type of fiscal policy adopted by certain governments. Moreover, identifying this relation provides a theoretical framework to formulate and judge fiscal policy adjustment plans relative to medium-term budgetary objectives.
Two essential economic approaches that analyze the long-run relationship between public expenditure and economic growth include Wagner’s law and the Keynesian hypothesis (An alternative approach to those analyzed in this paper is the so-called displacement effect developed by Peacock and Wiseman [
27]) which establish a relationship between economic growth and public expenditure with opposite directions of causality; while the former considers that economic growth Granger causes public expenditure, the latter postulates the opposite [
28,
29]. However, as indicated below, some research results have demonstrated that economic growth and public expenditure cause each other, leading to the so-called feedback hypothesis. However, other studies have presented results of noncausality between these variables, leading to the neutrality hypothesis [
30].
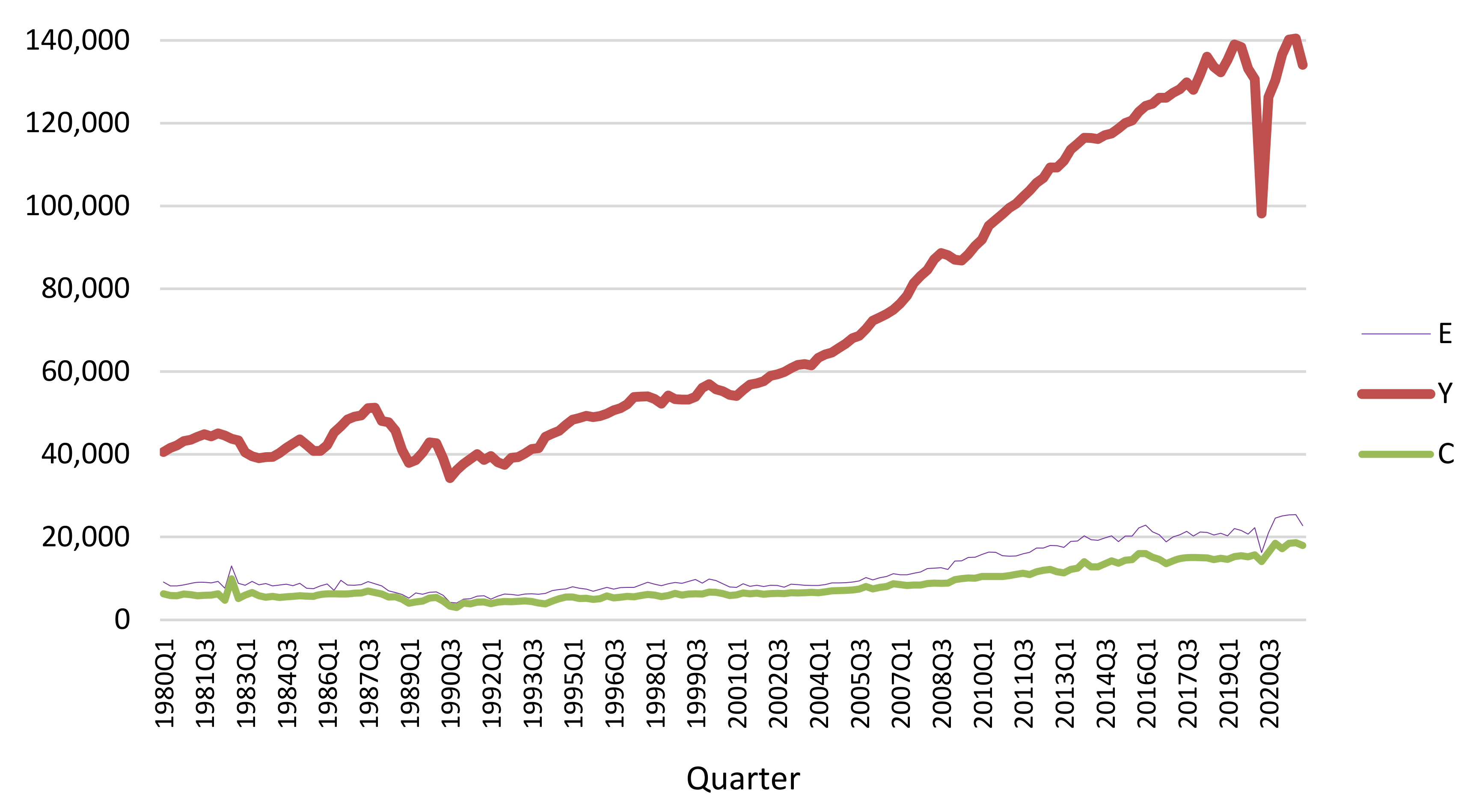
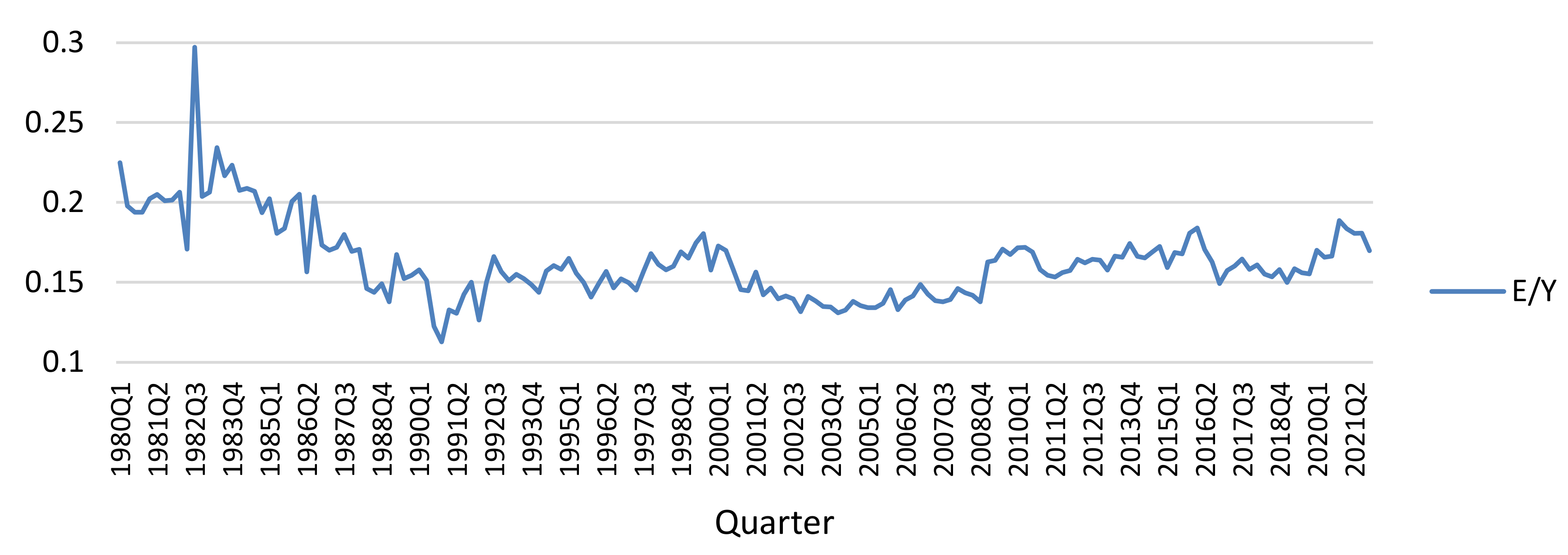
In this context, and considering evidence of an upward trend for the variables of real public consumption, real public expenditure, and real GDP since the third quarter of 1990 [
31], these conditions allow to analyze the dynamics of public expenditure and economic growth in the short and long terms in Peru. In this study we use three methodologies—Granger causality, Engle–Granger cointegration, and the autoregressive distributed lag (ARDL) model—to test Wagner’s law, the Keynesian hypothesis, the feedback hypothesis, or the neutrality hypothesis. In particular, our sample corresponds to the period 1980Q1–2021Q4, with quarterly frequency for the series real GDP, real public consumption expenditure, and real public expenditure. After analyzing stationarity, our findings are the cointegration between real GDP vs. real public expenditure, and real GDP vs. real public consumption, which affirms the Peacock and Wiseman [
27] and Pryor [
9] estimations supporting Wagner’s law. We also ran the autoregressive distributed lag (ARDL) model for Mann’s version [
16], estimating impacts that support Wagner’s law. However, taking the inverse functions for each type of model, we observe impacts that support the Keynesian hypothesis. Consequently, the purpose of this study enhances the national empirical evidence on the validity of the hypotheses concerning the relation between economic growth and public expenditure in an emerging economy.
This paper is divided into five sections. After the introduction,
Section 2 describes the materials and methods used in this research,
Section 3 and
Section 4 presents and discusses the results, respectively. Finally,
Section 5 outlines some conclusions.
Since Wagner [
6] postulated the law of increasing state activities, different interpretations and formulations have been made for its empirical testing. For instance, according to Mahar and Rezende [
12], and Pluta [
15], Wagner’s law posits that public expenditure increases in relation to aggregate output as per capita income increases. Furthermore, Nwude and Boloupremo [
32] argued that Wagner’s law analyzes the increase in the size of the public sector as a result of the economic growth of an economy. According to Arestis et al. [
29], Wagner’s law states that government activities and functions expand as an economy develops and that due to this, government expenditures grow at a higher rate than that of national income so that, over time, public expenditures grow as a share of national income. According to Peña [
4], Wagner’s law establishes that the public expenditure/GDP ratio is elastic with respect to GDP. According to Popescu and Diaconu (Maxim) [
33], Wagner’s law stipulates that economic growth implies an increase in public expenditure.
Nwude and Boloupremo [
32] sustain that “
according to Wagner [
6],
there are three reasons to expect the expansion of public activity: (i) When the countries achieve development, they expand its administrative and protectionist functions due to the greater complexity of legal relationships and communications. Thus, increased urbanization and population density will lead to greater public expenditure on law and order and other socioeconomic regulations. (ii) When income increases, societies demand more education, entertainment and generally more public services, achieve a more equitable distribution of wealth and income. Wagner believed that the income elasticity of demand for those public services exceeded unity. (iii) Finally, the technological needs of an industrialized society require greater amounts of capital infrastructure to private sector; hence, the government has to intervene to meet those needs”.
From the Wagnerian perspective, the growth of public expenditure is a consequence of the expansion of the state produced by the economic and social progress of a country, according to Pistoresi et al. [
34]. According this view, public expenditure is endogenous to economic development and national income growth Kónya and Abdullaev [
35].
Furthermore, the Keynesian hypothesis considers that public expenditure causes economic growth, and that public expenditure—autonomously determined and exogenously given—represents a macroeconomic policy instrument to reduce the cyclical fluctuations of the economy in the short term and boost economic growth in the long term. From Keynes [
26] perspective, an increase in public expenditure stimulates aggregate demand by generating an increase in national output. From this approach, public expenditure growth is seen as an engine that drives output growth through its multiplier effects on aggregate demand [
29].
Considering the measures of government size and economic growth, according to Granger causality results with time series data or panel data, Magazzino [
28], Barra et al. [
36], Irandoust [
37], and Nyasha and Odhiambo [
30] indicated the existence of four possible hypotheses:
Wagner’s law, in which unidirectional causality runs from economic growth to public expenditure [
3,
25,
38,
39,
40,
41,
42,
43,
44]; the
Keynesian hypothesis, in which unidirectional causality runs from public expenditure to economic growth [
4,
45];
feedback hypothesis, in which a bidirectional causality flow exists between economic growth and public expenditure [
33,
46,
47,
48,
49,
50,
51]; and
neutrality hypothesis, verified with variables that do not exhibit Granger causality in both directions [
3,
17,
52].
This diversity of interpretations, along with the multiplicity of variables, methodologies, periods analyzed, and proxy measures of government size (real or nominal total public expenditure, real or nominal total public expenditure per capita, real or nominal public consumption, or ratio between total public expenditure and aggregate GDP, among others) and economic growth (real or nominal gross national product, real or nominal aggregate GDP, real or nominal GDP per capita, or real or nominal gross national product per capita, among others) has produced different types of results.
The six original modeling versions of Wagner’s law were formulated by Peacock and Wiseman [
27], Gupta [
7] and Michas [
13], Pryor [
9], Goffman [
8], Musgrave [
10] and Mann [
16], whose models will be highlighted in this research. Mann [
16] argued that the Peacock and Wiseman’s version [
27] explains public expenditure as a function of gross domestic product. From Pryor [
9] perspective, public consumption expenditure is a function of national income. According to Goffman [
8] approach, public expenditure is a function of per capita gross domestic product. In addition, Musgrave [
10] version indicated that the per capita gross domestic product explains the share of public expenditure to gross domestic product. According to Gupta [
7] and Michas [
13], per capita public expenditure is a function of per capita gross domestic product. Finally, Mann [
16] formulated Wagner’s law by explaining the growth of public expenditure in terms of the growth of gross domestic product.
Wagner’s law has been empirically validated through econometric methods with cross-sectional, time series, and panel data. Gandhi [
11] provided empirical evidence with data from his past research on Wagner’s law, with cross-sectional data using various components of public expenditure as the dependent variable in simple linear regression models. The six original versions were present early [
53] and probably spurious econometric estimates [
18], as indicated in the methodology used by Abizadeh and Yousefi [
54] for current time series econometrics; this is even prior to the application of causality relationships by Granger [
55] of long-run time series equilibrium relationships [
56,
57,
58], and panel data [
59,
60,
61]. Ahsan et al. [
47] provided empirical evidence of Wagner’s law, confirming it in the direction of Granger causality between the macroeconomic variables under analysis. Oxley [
38], Iñiguez-Montiel [
39], Sarmiento [
41], and Aparco and Flores [
3] observed long-run time series equilibrium relations in Wagner’s law. Narayan et al. [
40] and Nirola and Sahu [
62] observed long-run equilibrium relations with panel data.
The literature review indicates that some cases of uniform results—validation of the same hypothesis—can be found with respect to the variables involved in the various versions of Wagner’s law.
Employing annual time series data of different measures of economic growth and public expenditure, both real and nominal, Abizadeh and Yousefi [
54] verified Wagner’s law in 10 US states during 1950–1984. To do so, they used the ordinary least squares (OLS) regression technique to estimate the elasticities of public expenditure with respect to economic growth for the six original versions of Wagner’s law, under the assumption that the error term of each version to be estimated is an autoregressive process of order one: AR (1). Their results with real variables were consistently similar to those obtained with nominal variables. Except for West Virginia, most elasticities calculated in the remaining 9 US states and the elasticity calculated with aggregate data from the 10 states analyzed was statistically significant and higher than or equal to unity, thereby validating Wagner’s law.
Iñiguez-Montiel [
39] estimated the versions of Peacock and Wiseman [
27], Gupta [
7] and Michas [
13], Musgrave [
10], and Mann [
16] using annual time series of real public expenditure and real national income during 1950–1999 to assess the validity of Wagner’s law and the Keynesian hypothesis in Mexico. He performed unit root tests only on the series expressed in logarithms and observed that they were not stationary; however, he did not apply unit root tests to the respective differenced series, making it impossible to know the order of integration of the series. The estimated versions constitute long-run equilibrium relations resulting from the Engle–Granger cointegration test. For the four estimated versions, he observed unidirectional Granger causality from GDP measures to the different measures of public expenditure, concluding that for the period analyzed, only Wagner’s law was valid in Mexico; however, this author did not state whether he applied the Granger causality test with stationary series.
Sarmiento [
41] empirically assessed the relation between the annual series of various measures of public expenditure and economic growth in Colombia between 1905 and 2010. To do so, he estimated all the original versions of Wagner’s law, except for Pryor [
9], performing unit root tests (the augmented Dickey–Fuller (ADF) test, Phillips–Perron (PP) test, or Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test), a cointegration test (Johansen and Juselius), and Granger causality in a vector error correction (VEC) model. For each of the five estimated versions, the author presented evidence (causality from economic growth to public expenditure, cointegration between the variables analyzed, and long-run equilibrium elasticity of public expenditure with respect to the measure of economic growth greater than unity and statistically significant) that Wagner’s law was verified in Colombia during the period analyzed. However, although causality and cointegration in Mann [
16] version supported Wagner’s law, the long-run equilibrium elasticity of public expenditure with respect to economic growth was greater than unity.
Peña [
4] estimated the versions of Peacock and Wiseman [
27], Gupta [
7] and Michas [
13], Goffman [
8], Musgrave [
10], and Mann [
16] using the real annual series of different measures of economic growth and public expenditure during 1950–2017 to analyze whether Wagner’s law or the Keynesian hypothesis may be validated in Venezuela. Thus, performing the unit root, Johansen cointegration, and Granger causality tests in a VEC model for each of the five estimated versions, the author observed cointegration and unidirectional causality from various public expenditure measures to economic growth measures, concluding that only the Keynesian hypothesis was valid in Venezuela for the period analyzed in the short and long run.
Paparas et al. [
50] assessed the validity of Wagner’s law in the UK using real annual series of various economic growth and public expenditure measures during 1850–2010. Estimating all the original versions of Wagner’s law, except for that of Pryor [
9], these researchers performed unit root tests (ADF and PP tests) and Chow tests for structural break on the variables under study. In addition, they performed cointegration (Engle–Granger and Johansen tests) and Granger causality tests for each of the five estimated versions, finding cointegration and verifying the feedback hypothesis between the various economic growth and public expenditure measures.
Popescu and Diaconu (Maxim) [
33] verified the validity of Wagner’s law and Keynes’ hypothesis in Romania using semiannual series of real GDP and real public expenditure during 1995–2018. The authors performed unit root tests (ADF, PP, Ng-Perron, and Toda–Yamamoto causality tests), Granger causality tests, and cointegration tests (Johansen). No long-run equilibrium relation was observed between real GDP and public expenditure. However, in the short run, their causality results validated the feedback hypothesis.
Afxentiou and Serletis [
17] statistically assessed the direction of Granger–Sims causality between various public expenditure and economic growth measures in Canada during 1947–1986. They assessed the six original versions of Wagner’s law using causality tests ranging from the independent variable (some measure of economic growth) to the dependent variable (some measure of public expenditure) according to Wagner’s law, and compared these with reverse causality test results in line with the Keynesian hypothesis. Their results validated the neutrality hypothesis.
The literature review indicates that it is possible to find mixed results—any of the four hypotheses validated—with respect to the variables involved in the various versions of Wagner’s law.
Kumar et al. [
25] analyzed the validity of Wagner’s law in New Zealand during 1960–2007, using various measures of public expenditure, real GDP, and real gross national product (GNP) as measures of economic growth. Using all the original versions of Wagner’s law except for [
9], these researchers detected cointegration in an ARDL model (Pesaran et al. [
58]) only for Musgrave’s version [
10]. For this version, estimating the short- and long-run equilibrium relations between the real public expenditure share and real GDP per capita, and the real public expenditure share and real GNP per capita, they found evidence in favor of Wagner’s law (long-run elasticities of the public expenditure share in real GDP with respect to GDP per capita, and public expenditure share in real GNP with respect to GNP per capita are positive values). Finally, in the short run, the authors found statistically significant evidence of a bidirectional causality relation between the variables analyzed. In the long run, the Granger causality direction allowed them to validate Wagner’s law.
Huang [
52] verified the original versions of Wagner’s law except for the version of Pryor [
9] in China and Taiwan, using annual series data for 1979–2002. Using various public expenditure and economic growth measures, the study did not detect Granger causality relations confirming the neutrality hypothesis in the versions of Wiseman [
27], Goffman [
8], Gupta [
7], and Michas [
13] in China, and in the versions of Musgrave [
10] and Mann [
16] in Taiwan. Wagner’s law holds true in China for the Musgrave [
10] and Mann [
16] versions, and holds true in Taiwan for the Wiseman [
27], Goffman [
8], Gupta [
7], and Michas [
13] versions.
In Peru, using annual series of real GDP, estimated population, government consumption, public gross fixed capital formation, and the versions of Wiseman [
27], Goffman [
8], Musgrave [
10], Gupta [
7], Michas [
13], and Mann [
16], Aparco and Flores [
3] tested Wagner’s law and the Keynesian hypothesis for the period 1950–2016. They performed unit root tests (ADF and PP tests), cointegration tests (Engle–Granger and Johansen tests), and causality tests (Granger) of the series under study based on VEC models. Their results revealed that for their five estimated versions, the research variables have a long-run equilibrium relation. These researchers observed that for the long run and for their five estimated versions, a unidirectional causality relation exists between economic growth and public expenditure; thus, the results validated Wagner’s law. Moreover, for the short run at the 10% significance level, and for the Peacock and Wiseman and Mann’s versions [
16,
27], a unidirectional causality relation runs from public expenditure to GDP, validating the Keynesian hypothesis. By contrast, for the versions of Goffman [
8], Musgrave [
10], Gupta [
7], and Michas [
13], the authors observed no evidence of causality in the Granger sense in the short run (neutrality hypothesis).
For the original versions of Wagner’s law, significant positive impacts may be required in their respective linear regression models, according to Inchauspe et al. [
44]. For the four hypotheses obtained using Granger causality for the relations between government size and economic growth measures, significant positive shocks may be required in the Wagner’s law models. Significant shocks will be assessed in the Keynesian hypothesis models based on the fiscal policy adopted for the relations between measures using time series data or panel data models.
1.1. Wagner’s Law Modeling
1.1.1. Peacock and Wiseman Version
Given that government expenditure
is a function of national income
, Wagner’s law states that public expenditure grows at a rate higher than the rate at which output grows [
27].
Comparing the instantaneous growth rates of the variables in Equation (1)
From Equation (2), we obtain the following
where
denotes the national income elasticity of public expenditure—equivalent to elasticity of public expenditure with respect to national income—whose value greater than unity indicates that public expenditure is elastic with respect to national income as a consequence of Wagner’s law.
Equation (3) is used as the slope of the line whose equation is based on the Peacock and Wiseman’s version [
27]
Wagner’s law has been empirically tested through the time series models-based Peacock and Wiseman’s version [
27] to estimate the national income elasticity of public expenditure. Using real variables, Abizadeh and Yousefi [
54] estimated an elasticity value of 0.76 (1.10 with nominal variables). These early results obviated the unit root test applied to the model variables. In Mexico (1950–1999), Iñiguez-Montiel [
39] estimated that national income presents a long-run equilibrium impact equal to 2.77 on public expenditure, indicating an elastic cointegrating regression line. Sarmiento [
41] used real variables to estimate the value of 1.51 for the long-run equilibrium elasticity in Colombia (1905–2010). In Peru (1950–2016), Aparco and Flores [
3] estimated the long-run equilibrium elasticity equal to 1.47 with real variables. In the UK (1850–2010), Paparas et al. [
50] obtained a long-run equilibrium elasticity equal to 1.18 with real variables. In Venezuela (1950–2017), Peña [
4] estimated the long-run equilibrium elasticity equal to 0.28 with real variables.
1.1.2. Pryor’s Version
The function for Pryor’s version [
9] is
, where
denotes public consumption expenditure and
denotes GDP, with their elasticities being greater than one. The equation for Pryor [
9] version is as follows
where
denotes the national income elasticity of public consumption expenditure—equivalent to elasticity of public consumption expenditure to national income.
Pryor’s version [
9] was applied by Abizadeh and Yousefi [
54] to the US case (1950–1984). They estimated an elasticity value of 0.79 with real variables (1.07 with nominal variables). These early results also obviated the unit root test applied to the model variables.
1.1.3. Mann’s Version
The function for Mann’s version [
16] is
, where
denotes the share of public expenditure to GDP and
is GDP; their elasticities must be greater than one. The equation for Mann’s version [
16] is as follows
where
denotes the national income elasticity of the share of public expenditure in GDP (Elasticity of the share of public expenditure in GDP with respect to national income).
Abizadeh and Yousefi [
54] observed the following relation between the elasticities corresponding to Peacock and Wiseman [
27] and Mann [
16] versions
Based on Equation (7), we can rename Mann’s version [
16] as the Peacock and Wiseman [
27] traditional version cited by [
17].
Henrekson [
18] indicated that to validate Wagner’s law, elasticity should be greater than zero rather than unity as stipulated by [
16].
Mann’s version [
16] was empirically tested using time series models and real variables [
16]. In Mexico (1950–1999), Iñiguez-Montiel [
39] estimated that national income presents a long-run equilibrium impact equal to 1.77 on real public expenditure as a fraction of real GDP, indicating an elastic cointegrating regression line. Sarmiento [
41] estimated a value of 0.51 for the long-run equilibrium elasticity in Colombia (1905–2010); Aparco and Flores [
3] estimated an elasticity equal to 0.46; Paparas et al. [
50] obtained a value of 0.18 for the long-run equilibrium elasticity in the UK (1850–2010); and Peña [
4] obtained a value of 0.09 for the long-run equilibrium elasticity in Venezuela (1950–2017).
1.1.4. Other Versions
Goffman
The function for Goffman’s version [
8] is
, where
denotes public expenditure and
denotes GDP per capita; their elasticities must be greater than one. The equation for Goffman’s version [
8] is as follows
where
denotes the per capita national income elasticity of public expenditure (Elasticity of public expenditure with respect to per capita national income).
Among the research papers that assessed Wagner’s law using models and time series techniques based on Goffman’s version [
8], Abizadeh and Yousefi [
54] estimated an elasticity equal to 0.83 (with nominal variables 1.48) for 10 US states (1950–1984). These early results obviated the unit root test applied to the variables of the models. Sarmiento [
41] estimated a value of 3.42 for the long-run equilibrium elasticity in Colombia (1905–2010). Aparco and Flores [
3] estimated a value of 4.00 for the long-run equilibrium elasticity in Peru (1950–2016).
Musgrave
The function for Musgrave’s version [
10] is
, where
denotes the share of public expenditure to GDP and
is GDP per capita; their elasticities must be greater than one. The equation for Musgrave’s version [
10] is as follows
where
denotes the per capita national income elasticity of the share of public expenditure in GDP (Elasticity of the share of public expenditure in GDP with respect to per capita national income).
Among the researchers who have empirically tested Wagner’s law using time series models and based on Musgrave’s version [
10], we can consider the following: In Mexico (1950–1999), Iñiguez-Montiel [
39] estimated that GDP per capita has a long-run equilibrium impact equal to 2.34 on real public expenditure as a fraction of real GDP, indicating an elastic cointegrating regression line; Sarmiento [
41] estimated a value of 1.11 for the long-run equilibrium elasticity in Colombia (1905–2010); For New Zealand (1960–2007), Kumar et al. [
25] estimated that the long-run equilibrium income elasticities (GDP and GNP as real per capita variables) for the real public expenditure share ranged between 0.56 and 0.84; In Peru (1950–2016), Aparco and Flores [
3] estimated the long-run equilibrium elasticity equal to 1.34; Paparas et al. [
50] estimated an elasticity equal to 0.19 in the UK (1850–2010); In Venezuela (1950–2017), Peña [
4] estimated an elasticity equal to 0.39.
Gupta and Michas
The function for the Gupta and Michas’ version [
7,
13] is
, where
denotes public expenditure per capita and
is GDP per capita; their elasticity must be greater than one.
The equation for the Gupta and Michas’ version [
7,
13] is as follows
where
denotes the per capita national income elasticity of per capita public expenditure (Elasticity of the share of per capita public expenditure to per capita national income).
From Equation (10), applying properties of logarithms, we can obtain the equation with variables used in Musgrave’s version [
10]
Considering Equations (9) and (11) as similar, we obtain the following property regarding the per capita national income elasticity of the share of public expenditure to GDP
Among the researchers who have tested Wagner’s law based on the Gupta and Michas’ version [
7,
13] with real variables, we can mention the following: Abizadeh and Yousefi [
54] estimated elasticity equal to 0.72 with real variables (with nominal variables 1.21) for 10 US states (1950–1984); these early results obviated the unit root test applied to the model variables. In Mexico (1950–1999), Iñiguez-Montiel [
39] estimated that GDP per capita presents a long-run equilibrium impact of 3.34 on real public expenditure per capita, indicating an elastic cointegrating regression line. Sarmiento [
41] estimated a value of 2.11 for the long-run equilibrium elasticity in Colombia (1905–2010). Using annual series for Japan during 1960–2010, Ono [
43] estimated a value of 0.84 for the long-run equilibrium elasticity. Aparco and Flores [
3] estimated the long-run equilibrium elasticity equal to 2.37 in Peru (1950–2016). Paparas et al. [
50] estimated a value of 1.19 for the long-run equilibrium elasticity in the UK (1850–2010). Using annual panel data for 81 provinces in Turkey (1992–2013), Sagdic et al. [
51] estimated a value of 0.58 for the long-run equilibrium elasticity. Peña [
4] estimated the long-run equilibrium elasticity equal to 0.10 in Venezuela (1950–2017).
According to Gandhi [
11] (Gandhi [
11] used GNP instead of GDP as a measure of economic growth) and Mann [
16], at least six different versions of Wagner’s law have been empirically used in the literature.
Table 1 presents these versions.
1.2. Keynesian Hypothesis Modeling
Following Dornbusch et al. [
63], we made the following assumptions on the components of Keynesian aggregate demand
: (i) that consumption
is a fraction
of the national income
(because we supposed that the public transfers and the taxes are nulls), and (ii) the investment
, the public expenditure
, and the net exports
are exogenous variables. Moreover, we assumed that
and
are autonomous.
In the equilibrium, the gross domestic product
equals aggregate demand
.That is,
Substituting (13) in (14), we were able to express the equilibrium level of national income
like a function
of the public expenditure
.
where
is the autonomous national income, and
is the Keynesian public expenditure multiplier.
Considering the modeling of Wagner’s law in the previous section, we modeled the Keynesian hypothesis represented in Equation (15) through the inverse functions of each of the versions studied; i.e., we modeled the public expenditure measures based on the economic growth measures.
Using Equation (1) in the version of Peacock and Wiseman [
27], we obtained its inverse function
whose equation
was derived from (4). Based on Pryor’s version [
9], we obtained its inverse function
whose equation
was derived from (5). In Mann’s version [
16], we obtained its inverse function
whose equation
was derived from (6). Based on Goffman’s version [
8], we obtained its inverse function
whose equation
was derived from (8). Using Musgrave’s version [
10], we obtained its inverse function
whose equation
was derived from (9). Based on the version of Gupta [
7] and Michas [
13], we obtained their inverse function
whose equation
was derived from (10).
Using annual series for Japan during 1960–2010, Ono [
43] estimated a value of 1.17 for the long-run equilibrium elasticity of real GDP per capita with respect to real public expenditure per capita, based on the version of Gupta [
7] and Michas [
13]. Using annual panel data for 81 provinces in Turkey (1992–2013), Sagdic et al. [
51] estimated the long-run equilibrium elasticity of real GDP per capita with respect to real public expenditure per capita equal to 0.26, according to Gupta [
7] and Michas [
13].
1.3. Theoretical Models
1.3.1. Wagner’s Law
In this study, we empirically tested Wagner’s law using the versions of Peacock and Wiseman [
27], Pryor [
9], and Mann [
16] to obtain the income elasticity of public expenditure.
1.3.2. Peacock and Wiseman
In our research, we developed the Peacock and Wiseman version [
27]; considering Equations (1) and (3), we formulated the following equation for an isoelastic function (Akitoby et al. [
64] used this type of function to analyze the dynamic relation between public expenditure and output in 51 developing countries from 1970 to 2002):
Log-linearizing Equation (17), we obtained the following:
where
denotes the national income elasticity of public expenditure.
1.3.3. Pryor
In our research, we developed Pryor’s version [
9]; then, we formulated the following equation for an isoelastic function
Log-linearizing Equation (19), we obtained the following
where
denotes the national income elasticity of public consumption expenditure.
1.3.4. Mann
In our research, we developed the Mann’s version [
16]; then, we formulated the following equation for an isoelastic function
Log-linearizing Equation (21), we obtained the following
where
denotes the national income elasticity of the share of government expenditure to GDP.
1.3.5. Keynesian Hypothesis
For this study, we assessed the Keynesian hypothesis using the variables of the Peacock and Wiseman version [
27]; thereafter, we formulated the following equation for an isoelastic function
Log-linearizing Equation (23), we obtained the following
where
denotes the elasticity of public expenditure to national income.
We tested the Keynesian hypothesis using the variables studied in Mann’s version [
16]; thereafter, we formulated the following equation for an isoelastic function
Log-linearizing Equation (25), we obtained the following:
where
denotes the elasticity of national income with respect to the share of public expenditure to real GDP.
Finally, we tested the Keynesian hypothesis using the variables analyzed in Pryor’s version [
9]; thereafter, we formulated the following equation for an isoelastic function:
Log-linearizing Equation (27), we obtained the following
where
denotes the elasticity of national income with respect to the share of public expenditure to real GDP.