An Optimal Scheduling Strategy of a Microgrid with V2G Based on Deep Q-Learning
Abstract
:1. Introduction
- (1)
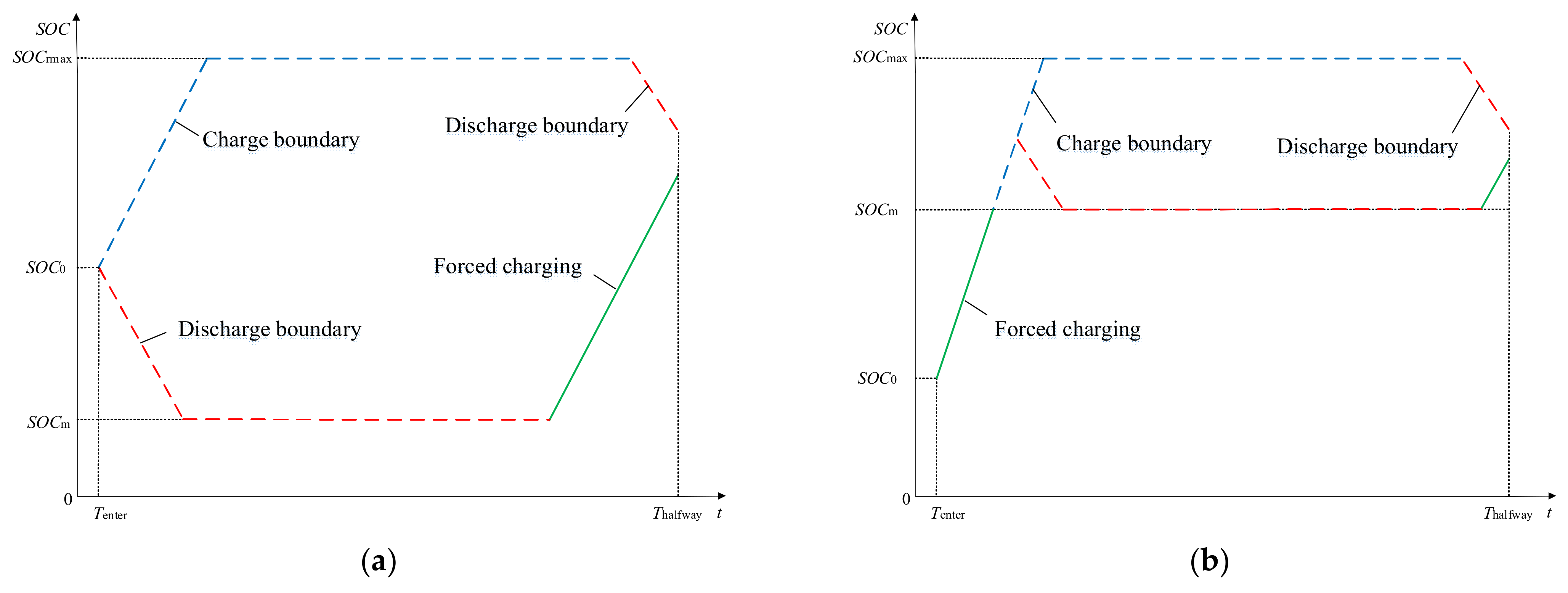
- A V2G mathematical model considering the mobility of EVs and the randomness of user charging behavior is proposed. The user charging time distribution model, charging demand model, EV state-of-charge (SOC) dynamic model and the model of travel location are comprehensively established, so that the agent can obtain the charging/discharging situation in an EV station to obtain the overall output power of the EV station.
- (2)
- A microgrid optimization scheduling strategy based on Deep Q-learning is proposed. The strategy has the ability of online learning and can cope with the randomness of renewable resources better. Meanwhile, the agent with experience replay ability can be trained to complete the evolution process, so as to adapt to the nonlinear influence caused by the mobility of EVs and the periodicity of user behavior, which is feasible and superior in the optimal scheduling of microgrids with renewable resources and EVs.
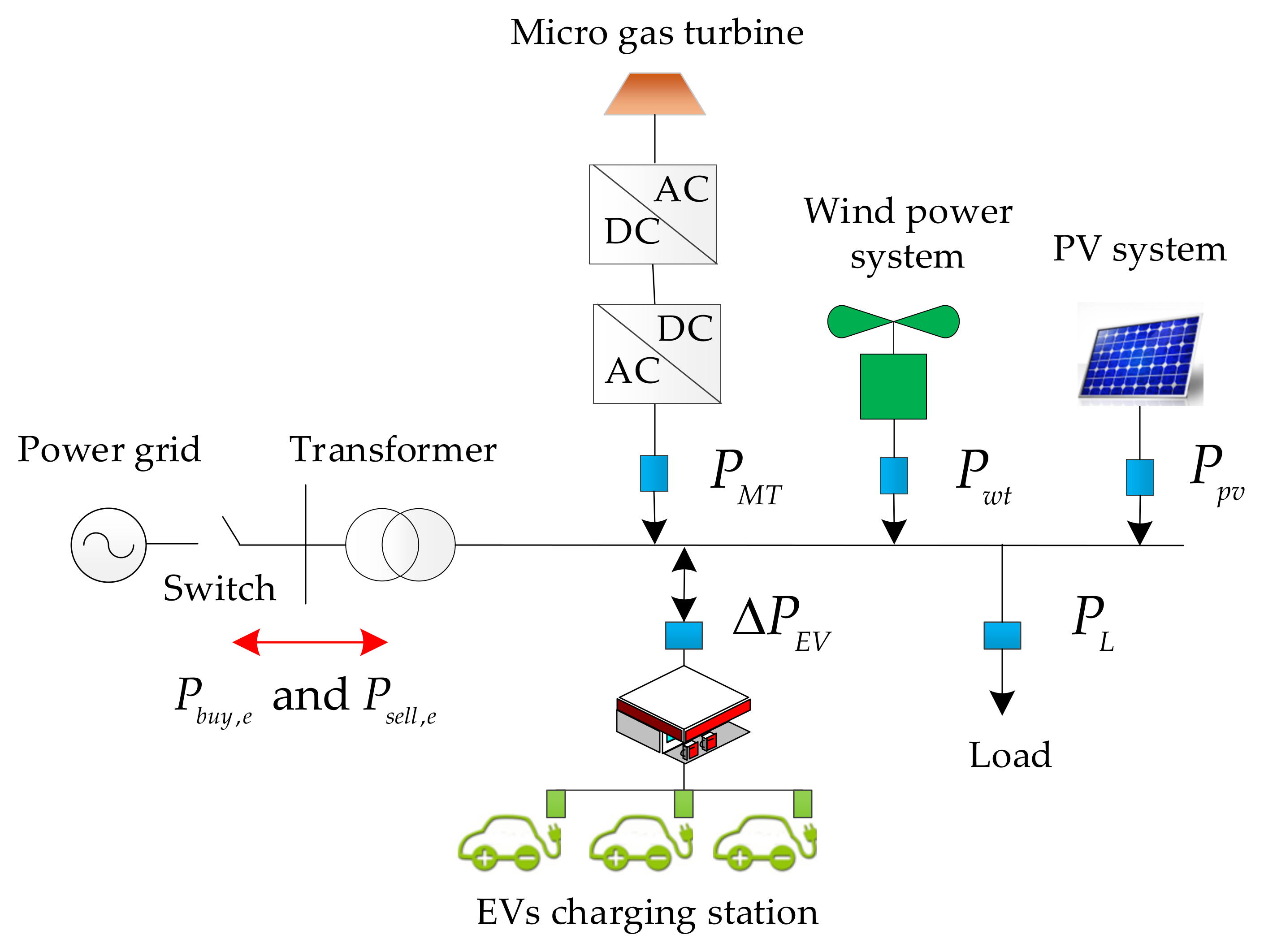
2. The Mathematical Model Construction of Microgrid with EVs
2.1. The V2G Model of EVs
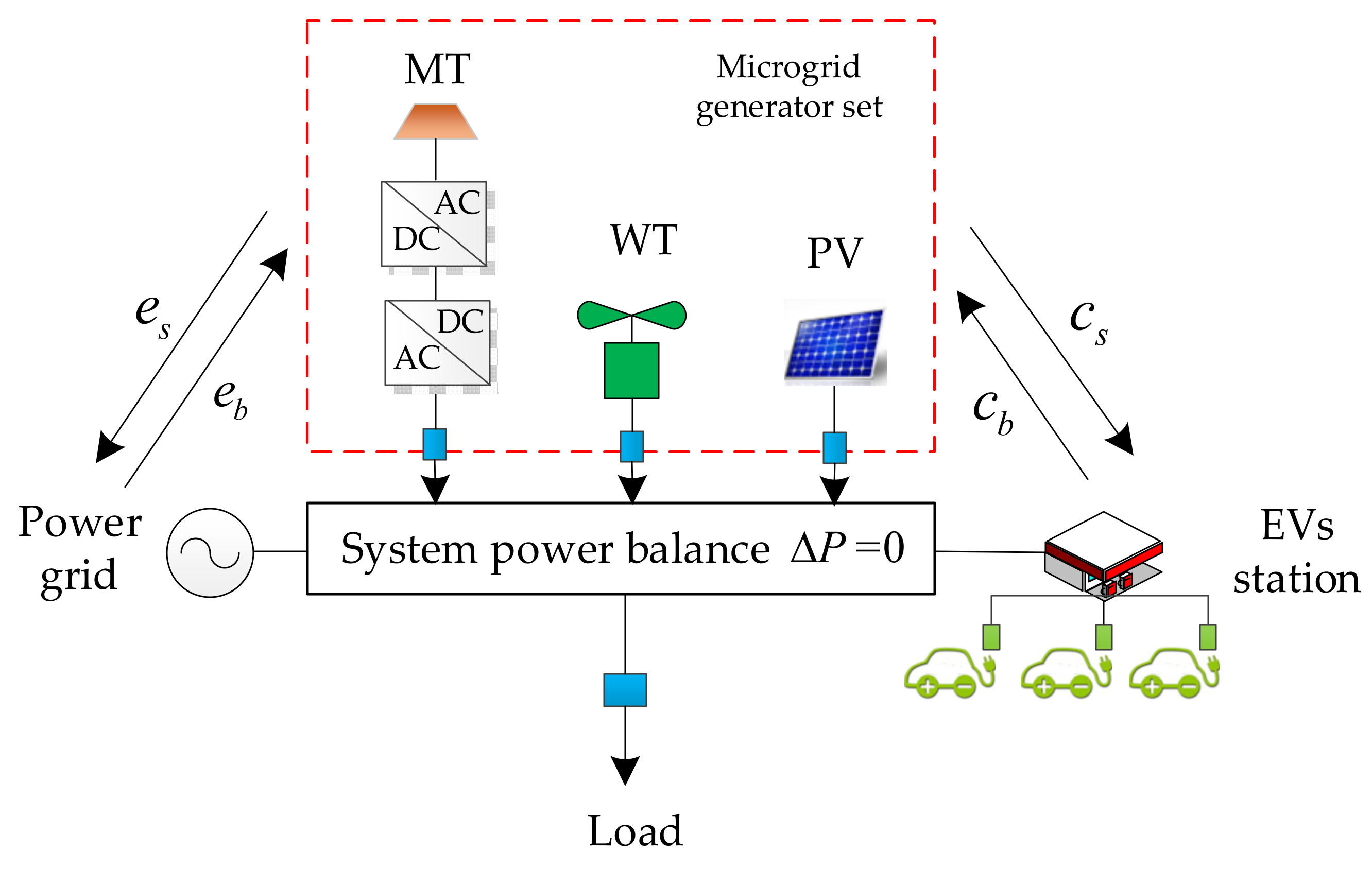
2.2. The Optimal Dispatching Model of Microgrid
2.2.1. Objective Function
2.2.2. Constraints
- (1)
- Power Balance Constraints:where Pwt(t), Ppv(t) represent the output power of winds and photovoltaics in the t period, and L(t) represents the load in the t period.
- (2)
- Micro gas turbine operating constraints:where PMT represents the output power of the micro-gas turbine, Rd and Ru represent the downward and upward ramp rates of the micro-gas turbine and PMT,min, PMT,max represent the lower and upper output limits of the micro-gas turbine.
- (3)
- Grid interaction power constraints:
- (4)
- EV station constraints:
3. A Microgrid Dispatch Model Based on Deep Reinforcement Learning
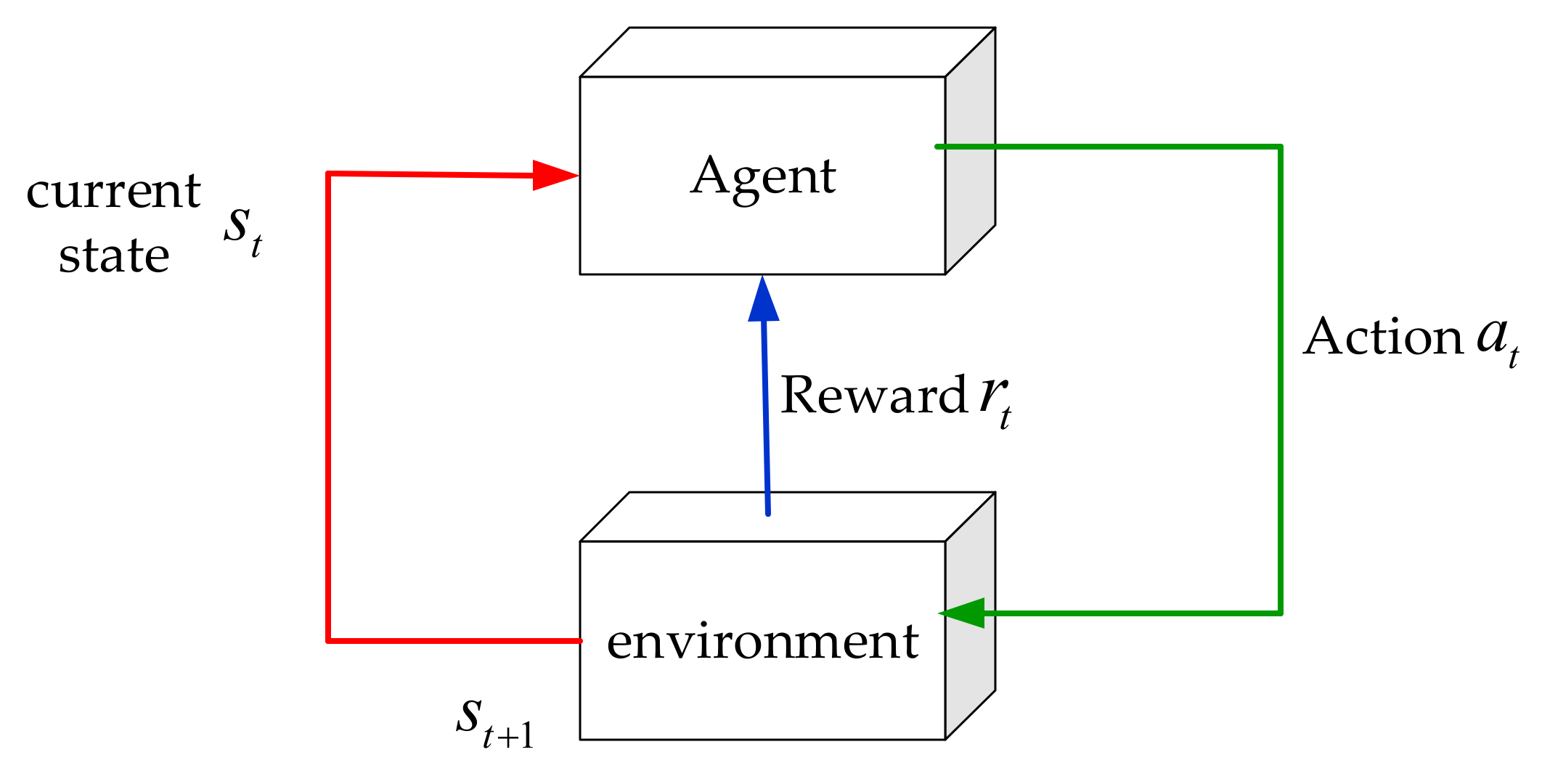
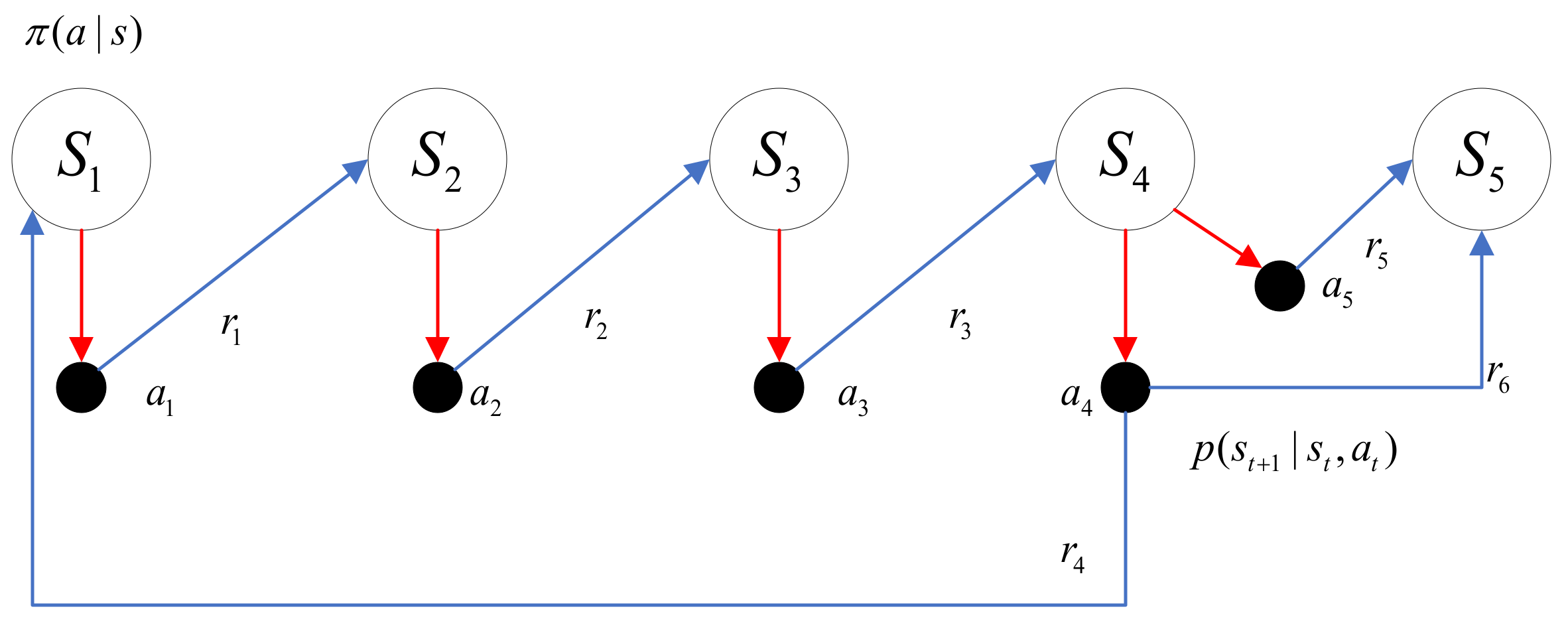
3.1. Theory of Reinforcement Learning Algorithms
3.2. Design of Optimal Scheduling Strategy for Microgrid Based on Deep Q-Learning
- (1)
- State space:
- (2)
- Action space:
- (3)
- Reward function:
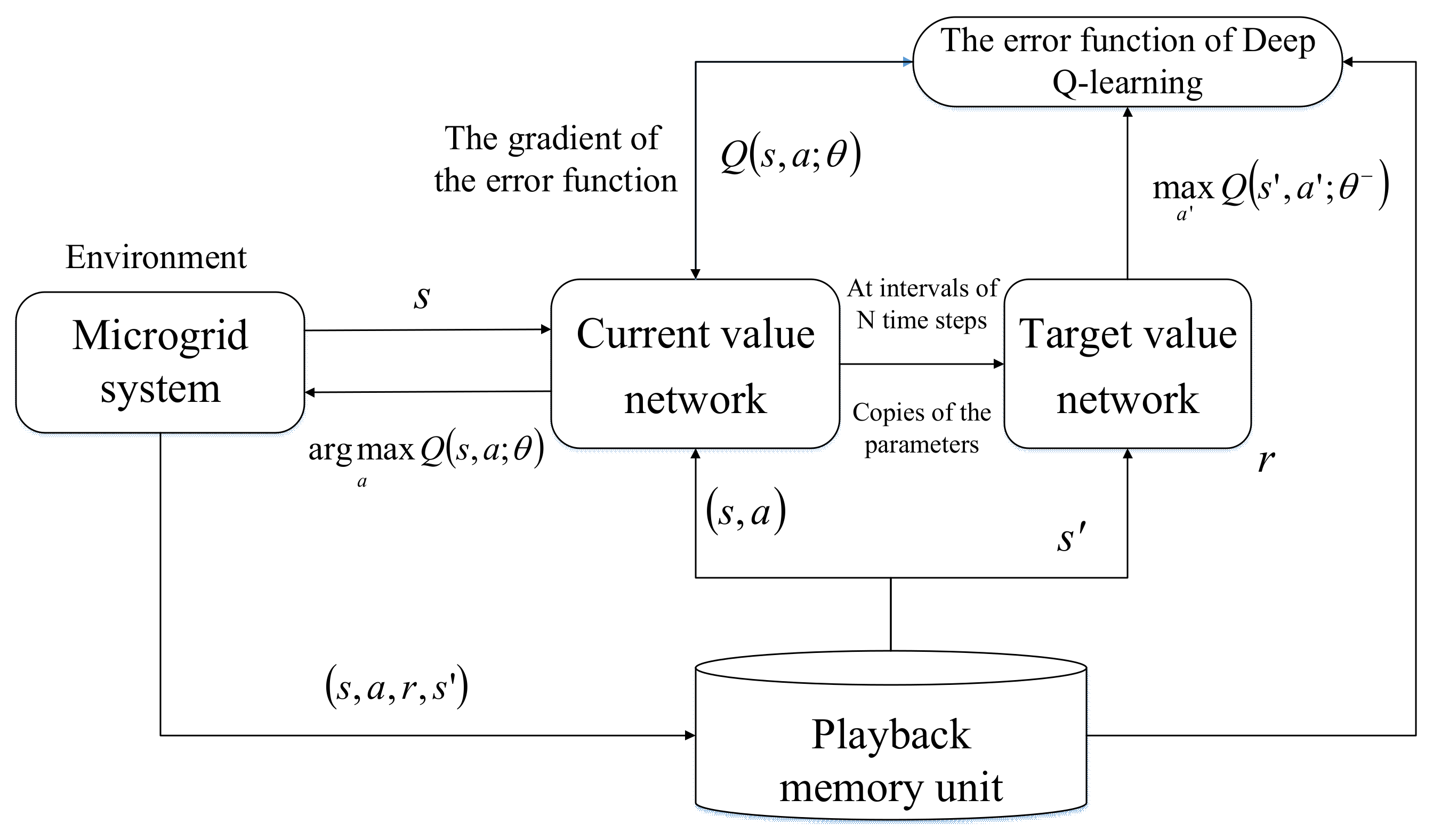
3.3. Neural Network Structure
3.4. The Flow Diagram of Deep Q-learning Algorithm
4. Simulation Results
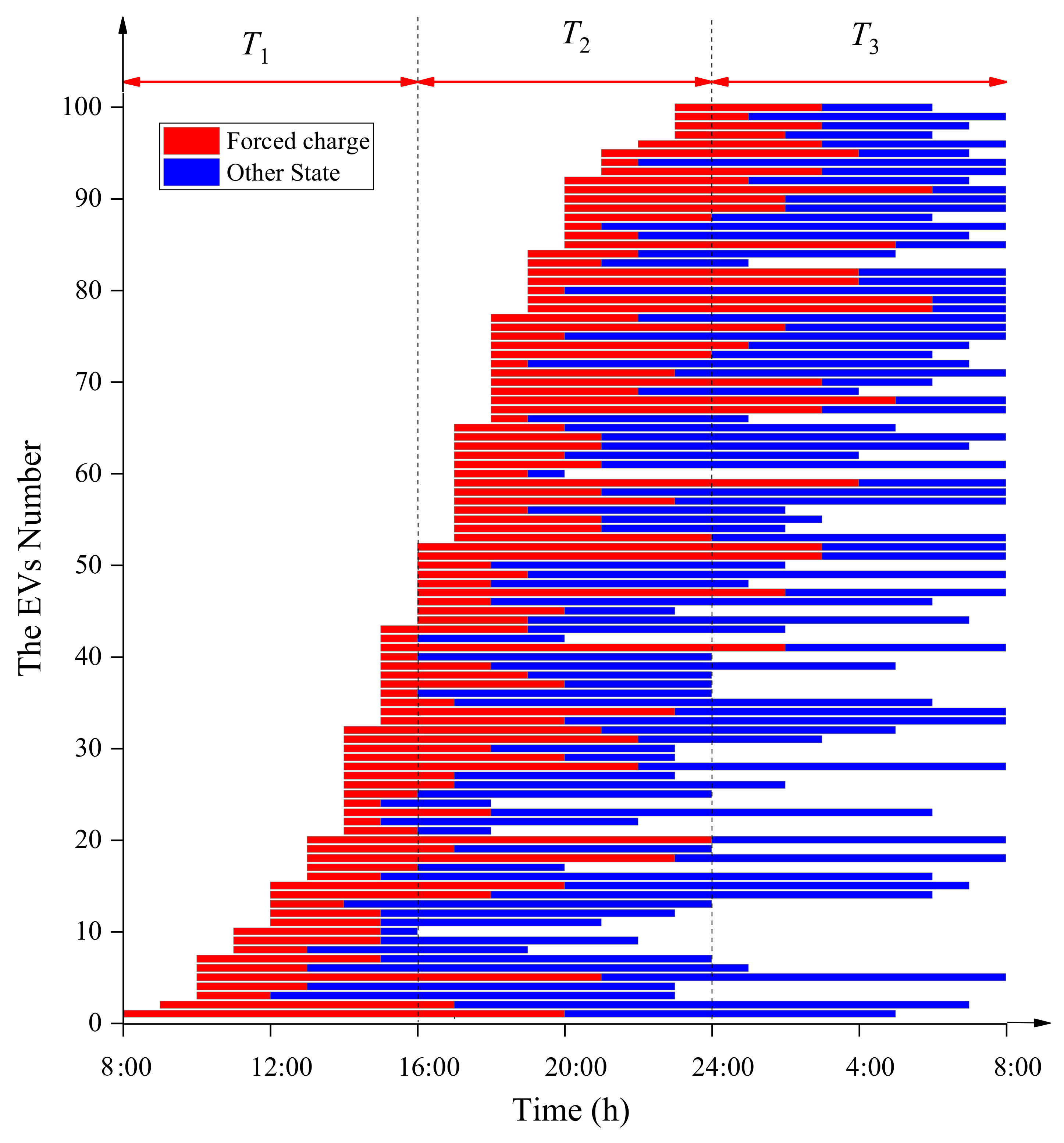
4.1. Case1: Analysis of Electric Vehicle Mobility and User Behavior Habits
4.2. Case2: Energy Dispatching Results of a Microgrid
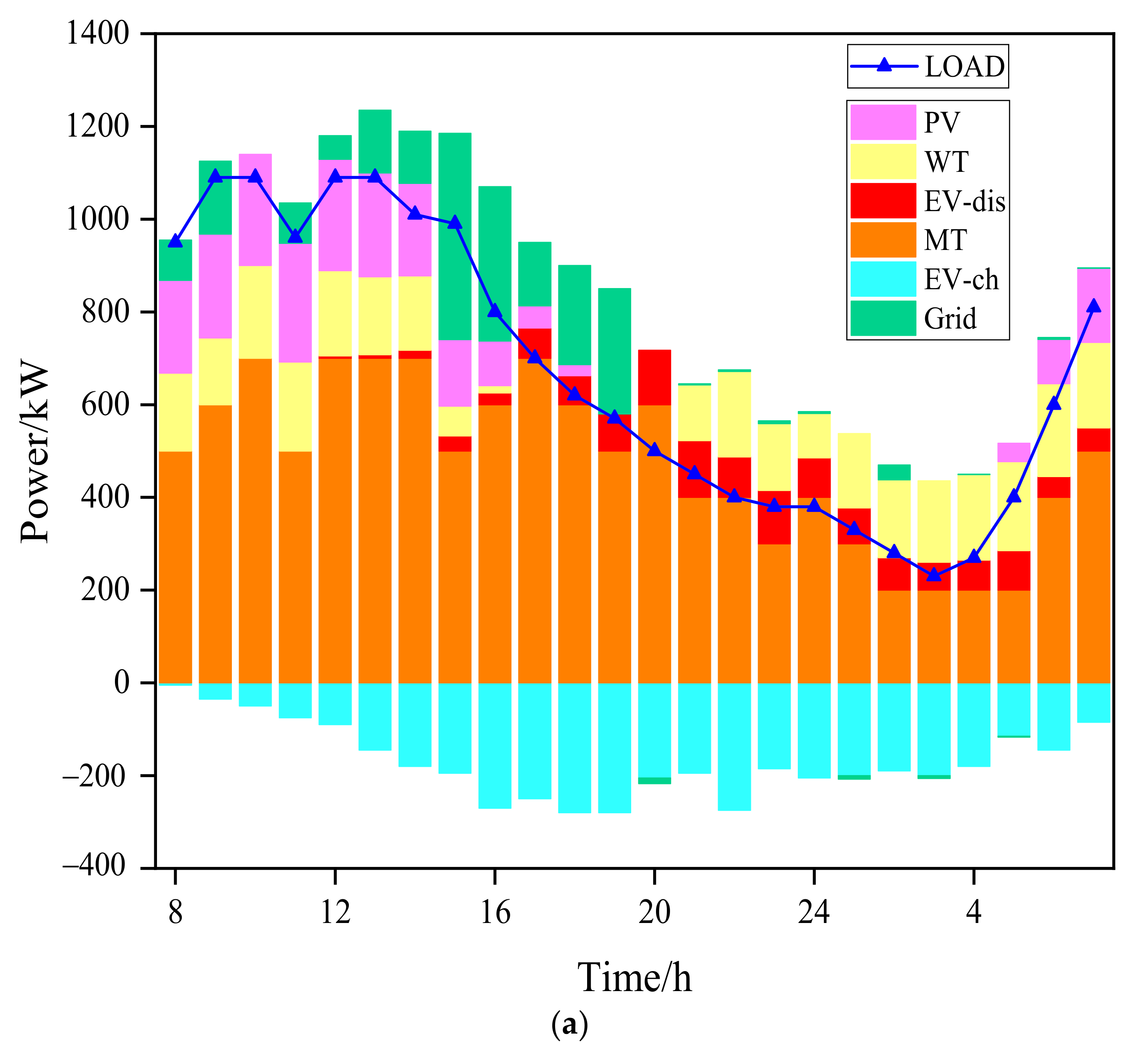
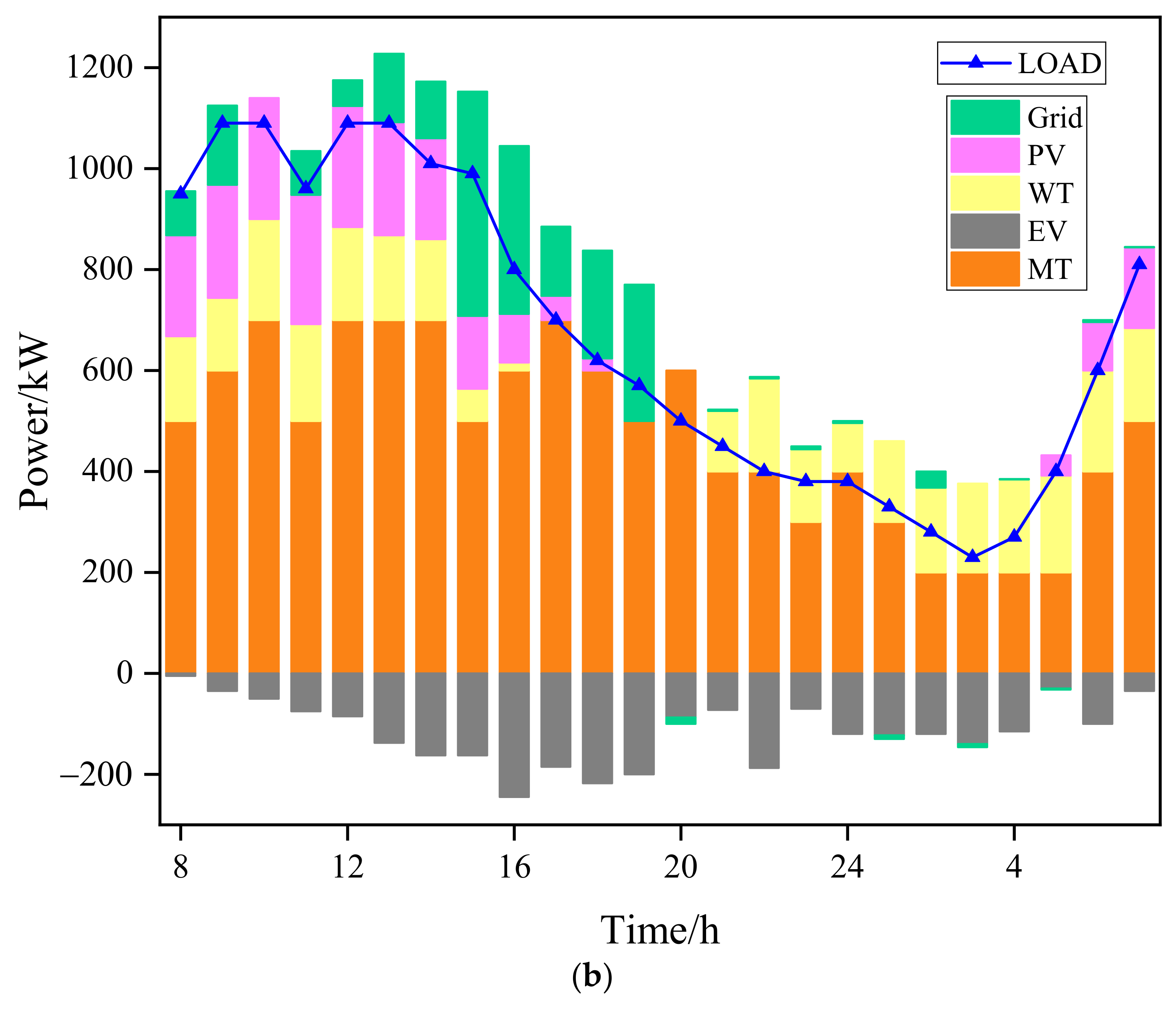
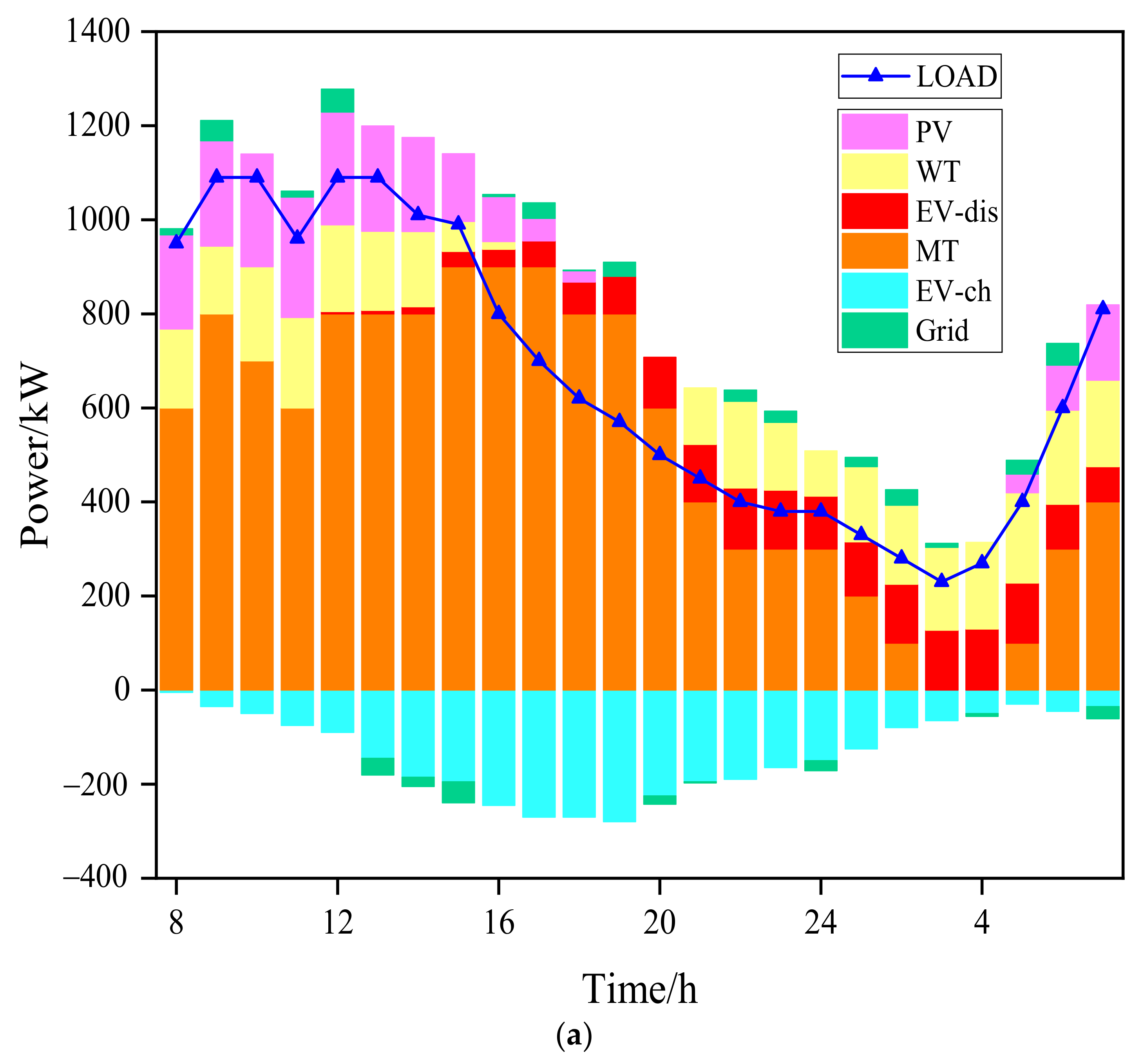
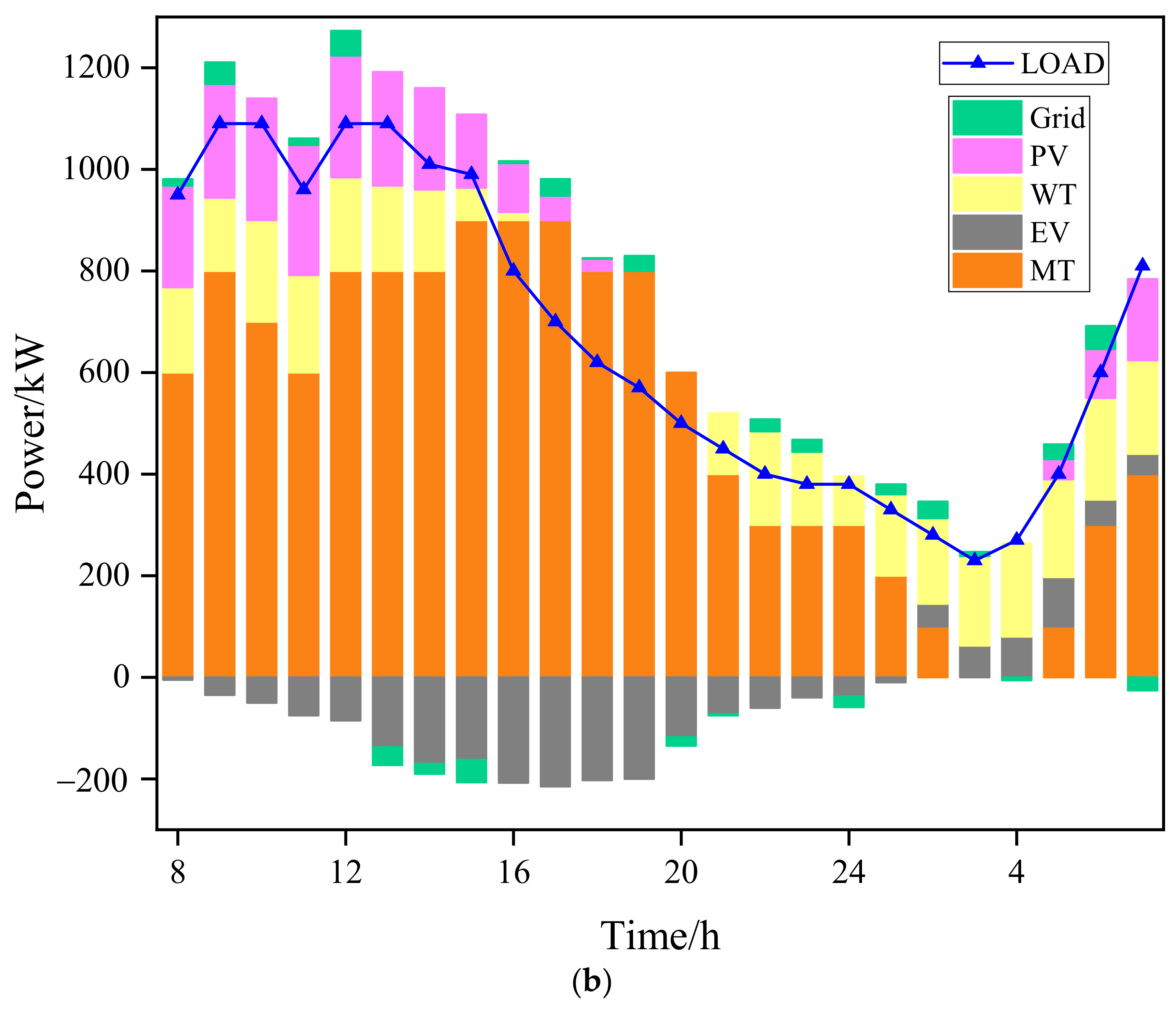
| Index | Operating Costs (USD) | Gas Costs (USD) | V2G Costs (USD) | Grid-Connected Costs (USD) | Calculation Time |
|---|---|---|---|---|---|
| PSO | 814.57 | 825.34 | −169.84 | 159.07 | 7 min 23 s |
| Deep Q-learning | 801.07 | 897.70 | −92.79 | −3.84 | 0.05 s |
5. Conclusions
- As a mobile energy storage component with V2 G capability, EVs can participate well in the dispatching control of the microgrid, providing a more flexible dispatching scheme for the stable operation of the microgrid.
- Compared with traditional algorithms, Deep Q-learning with online learning ability can better adapt to the strong nonlinear effects caused by the mobility of EVs, randomness of user behavior and renewable resources based on the experience accumulated in the training process. The cost of the microgrid under Deep Q-learning was 801.07 USD, and the calculation time was 0.05 s, while the total operating cost of the microgrid under the PSO algorithm was 814.57 USD, and the calculation time was 7 min 23 s. Therefore, Deep Q-learning was better than the PSO algorithm in all aspects, such as operating total costs, micro-turbine output, V2G interaction situation, grid-connected costs and operating time, which is explained in great detail in Section 4.2.
Author Contributions
Funding
Conflicts of Interest
References
- Lee, E.-K.; Shi, W.; Gadh, R.; Kim, W. Design and Implementation of a Microgrid Energy Management System. Sustainability 2016, 8, 1143. [Google Scholar] [CrossRef]
- Bevrani, H.; Feizi, M.R.; Ataee, S. Robust Frequency Control in an Islanded Microgrid: H∞ and μ-Synthesis Approaches. IEEE Trans. Smart Grid 2015, 99, 1527–1532. [Google Scholar] [CrossRef]
- Li, Q.; Gao, M.; Lin, H.; Chen, Z.; Chen, M. MAS-based distributed control method for multi-microgrids with high-penetration renewable energy. Energy 2019, 15, 284–295. [Google Scholar] [CrossRef]
- Chu, S.; Majumdar, A. Opportunities and challenges for a sustainable energy future. Nature 2012, 488, 294–303. [Google Scholar] [CrossRef]
- Ciftci, O.; Mehrtash, M.; Marvasti, A.K. Data-Driven Nonparametric Chance-Constrained Optimization for Microgrid Energy Management. IEEE Trans. Ind. Inform. 2019, 99, 2447–2457. [Google Scholar] [CrossRef]
- Askarzadeh, A. A memory-based genetic algorithm for optimization of power generation in a microgrid. IEEE Trans. Sustain. Energy 2017, 9, 1081–1089. [Google Scholar] [CrossRef]
- Anh, H.P.H.; Van Kien, C. Optimal energy management of microgrid using advanced multi-objective particle swarm optimization. Eng. Comput. 2020, 37, 2085–2110. [Google Scholar] [CrossRef]
- Liu, J.; Xu, F.; Lin, S.; Cai, H.; Yan, S. A Multi-Agent-Based Optimization Model for Microgrid Operation Using Dynamic Guiding Chaotic Search Particle Swarm Optimization. Energies 2018, 11, 3286. [Google Scholar] [CrossRef]
- Zhu, X.; Xia, M.; Chiang, H.D. Coordinated sectional droop charging control for EV aggregator enhancing frequency stability of microgrid with high penetration of renewable energy sources. Appl. Energy 2018, 210, 936–943. [Google Scholar] [CrossRef]
- Rahimi, F.; Ipakchi, A. Demand Response as a Market Resource Under the Smart Grid Paradigm. IEEE Trans. Smart Grid 2010, 1, 82–88. [Google Scholar] [CrossRef]
- Bremermann, L.E.; Matos, M.; Lopes, J.A.P.; Rosa, M. Electric vehicle models for evaluating the security of supply. Electr. Power Syst. Res. 2014, 111, 32–39. [Google Scholar] [CrossRef]
- Yang, J.; Zeng, Z.; Tang, Y.; Yan, J.; He, H.; Wu, Y. Load Frequency Control in Isolated Micro-Grids with Electrical Vehicles Based on Multivariable Generalized Predictive Theory. Energies 2015, 8, 2145–2164. [Google Scholar] [CrossRef]
- Fan, P.; Ke, S.; Kamel, S.; Yang, J.; Li, Y.; Xiao, J.; Xu, B.; Rashed, G.I. A Frequency and Voltage Coordinated Control Strategy of Island Microgrid including Electric Vehicles. Electronics 2022, 11, 17. [Google Scholar] [CrossRef]
- Tang, Y.; He, H.; Wen, J.; Liu, J. Power system stability control for a wind farm based on adaptive dynamic programming. IEEE Trans. Smart Grid 2015, 6, 166–177. [Google Scholar] [CrossRef]
- Ruelens, F.; Claessens, B.J.; Vandael, S.; De Schutter, B.; Babuška, R.; Belmans, R. Residential demand response of thermostatically controlled loads using batch Reinforcement Learning. IEEE Trans. Smart Grid 2017, 8, 2149–2159. [Google Scholar] [CrossRef]
- Foruzan, E.; Soh, L.K.; Asgarpoor, S. Reinforcement learning approach for optimal distributed energy management in a microgrid. IEEE Trans. Power Syst. 2018, 33, 5749–5758. [Google Scholar] [CrossRef]
- Kofinas, P.; Dounis, A.I.; Vouros, G.A. Fuzzy Q-Learning for multi-agent decentralized energy management in microgrids. Appl. Energy 2018, 210, 53–67. [Google Scholar] [CrossRef]
- Sun, J.Y.; Tang, J.M.; Chen, Z.R. Multi-agent Deep Reinforcement Learning for Distributed Energy Management and Strategy Optimization of Microgrid Market—Science Direct. Sustain. Cities Soc. 2021, 74, 103163. [Google Scholar]
- Li, P.; Hu, W.; Xu, X.; Huang, Q.; Liu, Z.; Chen, Z. A frequency control strategy of electric vehicles in microgrid using virtual synchronous generator control. Energy 2019, 189, 116389. [Google Scholar] [CrossRef]
- Zhong, W.; Xie, K.; Liu, Y.; Yang, C.; Xie, S. Topology-Aware Vehicle-to-Grid Energy Trading for Active Distribution Systems. IEEE Trans. Smart Grid 2018, 10, 2137–2147. [Google Scholar] [CrossRef]
- Rao, Y.; Yang, J.; Xiao, J.; Xu, B.; Liu, W.; Li, Y. A frequency control strategy for multimicrogrids with V2G based on the improved robust model predictive control. Energy 2021, 222, 119963. [Google Scholar] [CrossRef]
- Huang, L.; Fu, M.; Qu, H.; Wang, S.; Hu, S. A deep reinforcement learning-based method applied for solving multi-agent defense and attack problems. Expert Syst. Appl. 2021, 176, 114896. [Google Scholar] [CrossRef]
- Yang, Q.; Zhu, Y.; Zhang, J.; Qiao, S.; Liu, J. UAV Air Combat Autonomous Maneuver Decision Based on DDPG Algorithm. In Proceedings of the 2019 IEEE 15th International Conference on Control and Automation (ICCA) IEEE, Edinburgh, Scotland, 16–19 July 2019. [Google Scholar]
- Yu, T.; Zhou, B.; Chan, K.W.; Yuan, Y.; Yang, B.; Wu, Q.H. R(λ) imitation learning for automatic generation control of interconnected power grids. Automatica 2012, 48, 2130–2136. [Google Scholar] [CrossRef]



| The User Types | The Chain of Travel | The Proportion/% |
|---|---|---|
| 1 | R→C→R | 52.8 |
| 2 | R→P→R | 24.1 |
| 3 | R→C→P→R | 23.1 |
| Unit | Parameter | Meaning | Value |
|---|---|---|---|
| MT | η | generation efficiency | 0.85 |
| PMT | capacity of MT | 1000 kW | |
| EV | Pch | charge power for EV | 5 kW |
| Pdis | discharge power for EV | 2.5 kW |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, Y.; Fan, P.; Hu, J.; Ke, S.; Wu, F.; Zhu, X. An Optimal Scheduling Strategy of a Microgrid with V2G Based on Deep Q-Learning. Sustainability 2022, 14, 10351. https://doi.org/10.3390/su141610351
Wen Y, Fan P, Hu J, Ke S, Wu F, Zhu X. An Optimal Scheduling Strategy of a Microgrid with V2G Based on Deep Q-Learning. Sustainability. 2022; 14(16):10351. https://doi.org/10.3390/su141610351
Chicago/Turabian StyleWen, Yuxin, Peixiao Fan, Jia Hu, Song Ke, Fuzhang Wu, and Xu Zhu. 2022. "An Optimal Scheduling Strategy of a Microgrid with V2G Based on Deep Q-Learning" Sustainability 14, no. 16: 10351. https://doi.org/10.3390/su141610351
APA StyleWen, Y., Fan, P., Hu, J., Ke, S., Wu, F., & Zhu, X. (2022). An Optimal Scheduling Strategy of a Microgrid with V2G Based on Deep Q-Learning. Sustainability, 14(16), 10351. https://doi.org/10.3390/su141610351







