Optimization and Performance Analysis of Francis Turbine Runner Based on Super-Transfer Approximate Method under Multi-Energy Complementary Conditions
Abstract
:1. Introduction
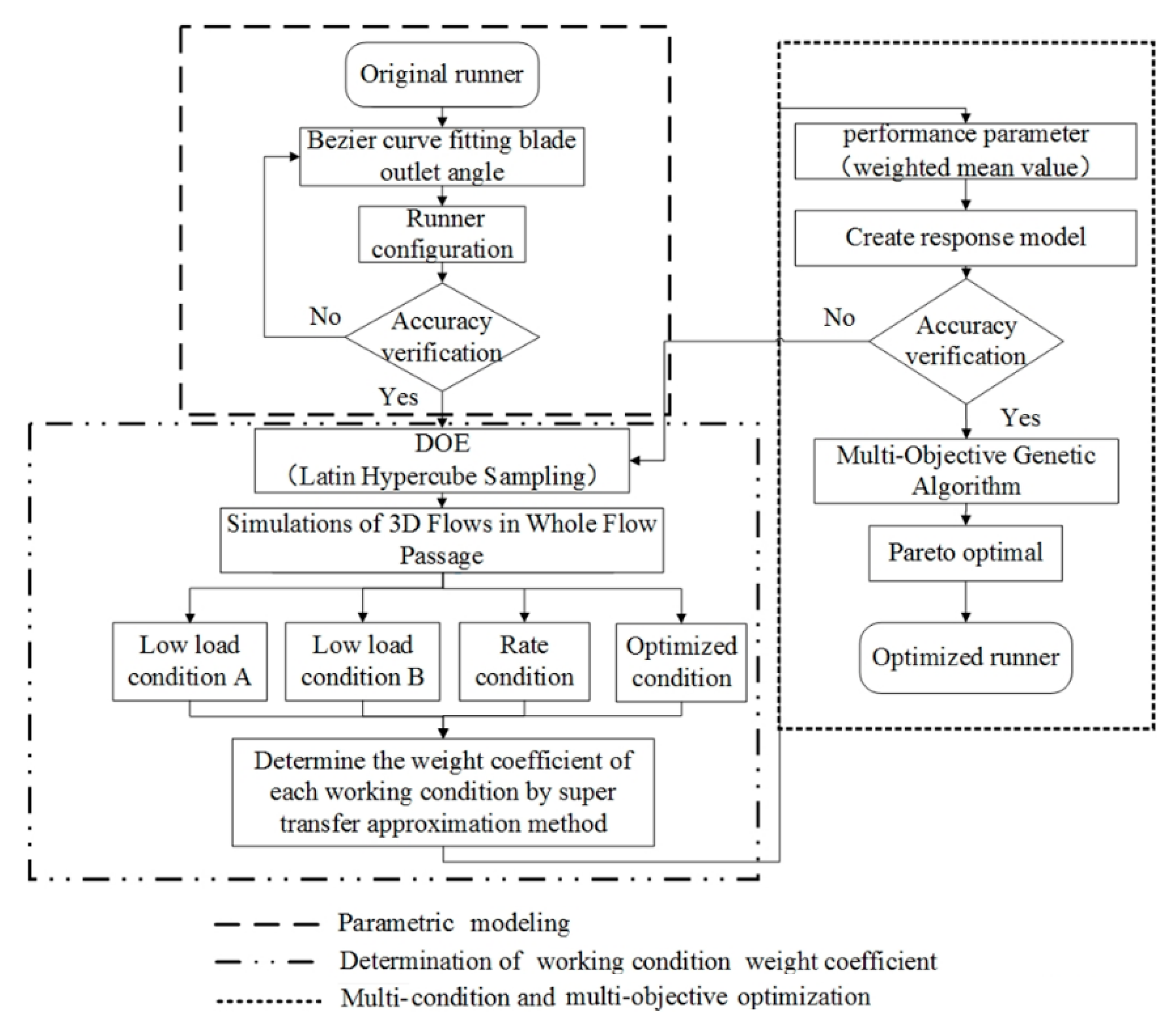
2. Establishment of Optimization Method
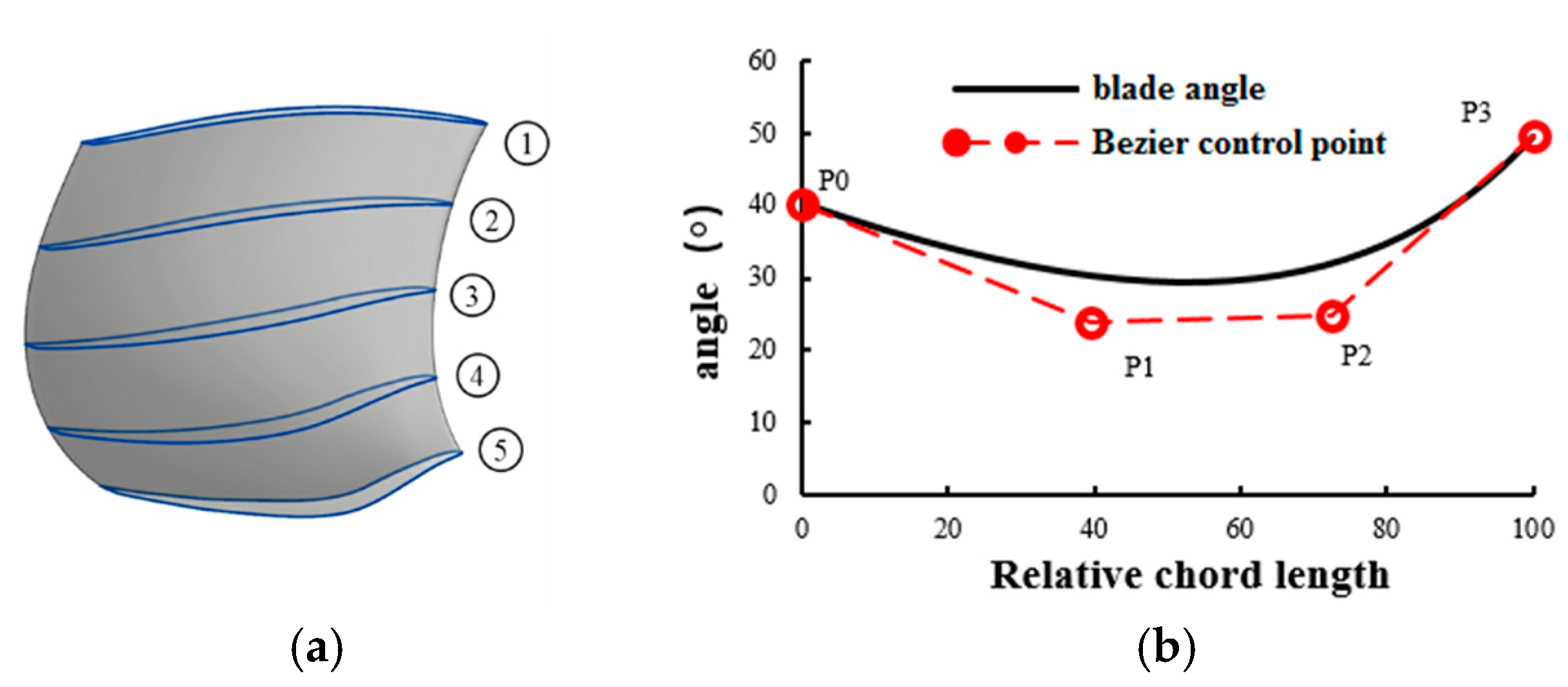
2.1. Blade Parameterization
2.2. Super-Transitive Approximate Method
2.3. Establishment of Optimization System
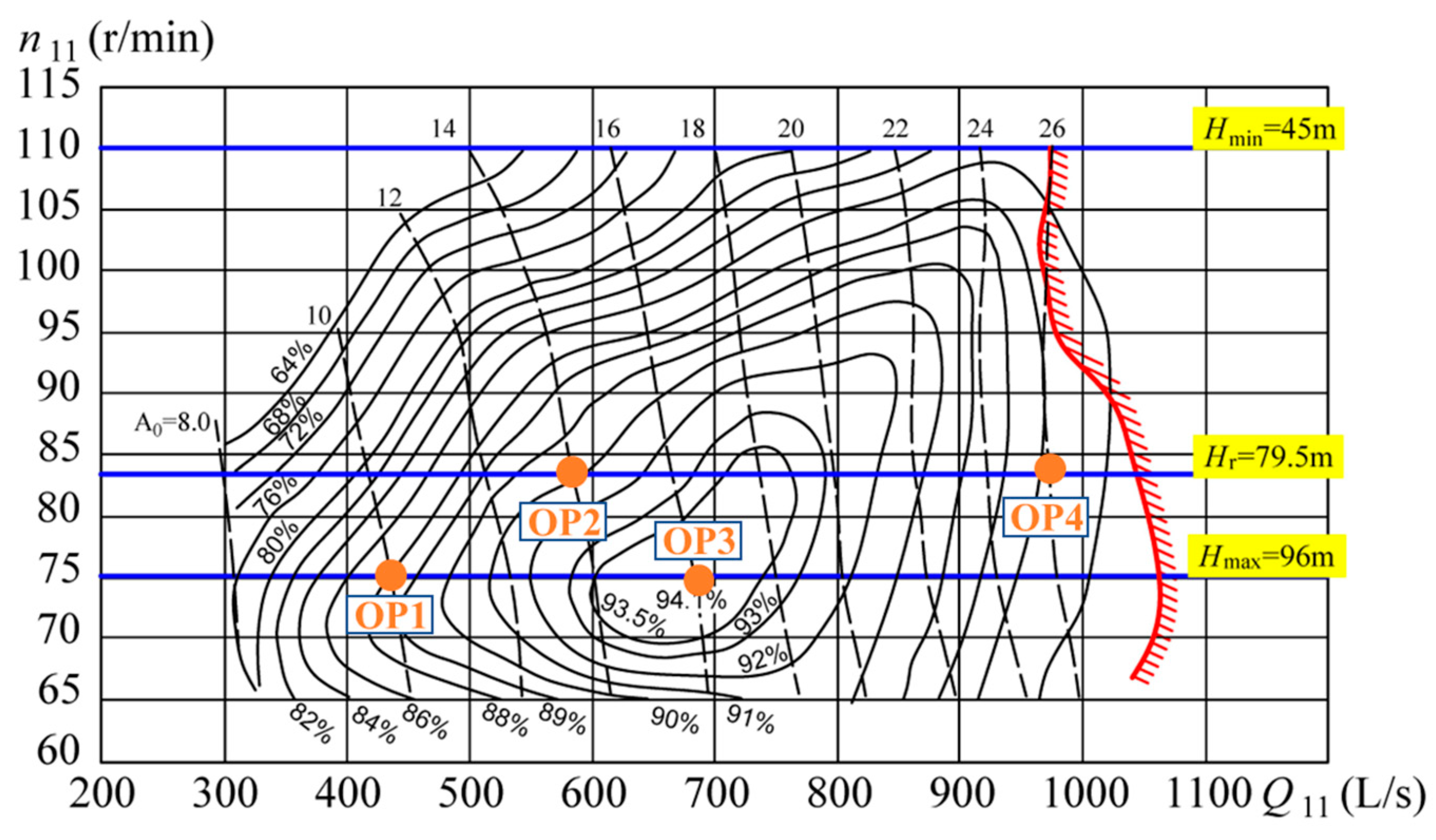
3. Numeric Calculation Method and Selection of Operating Point
Numerical Computation Model
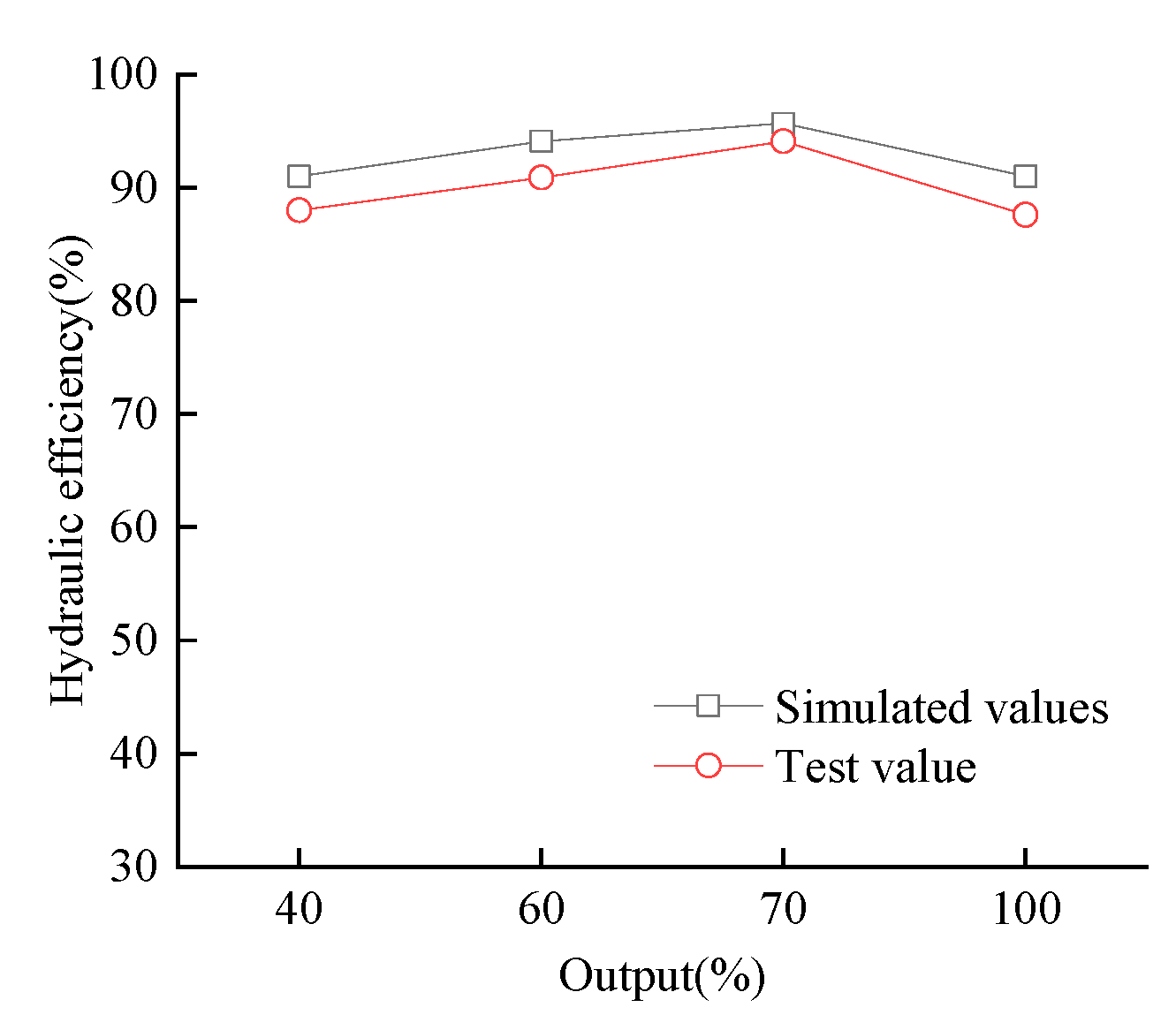
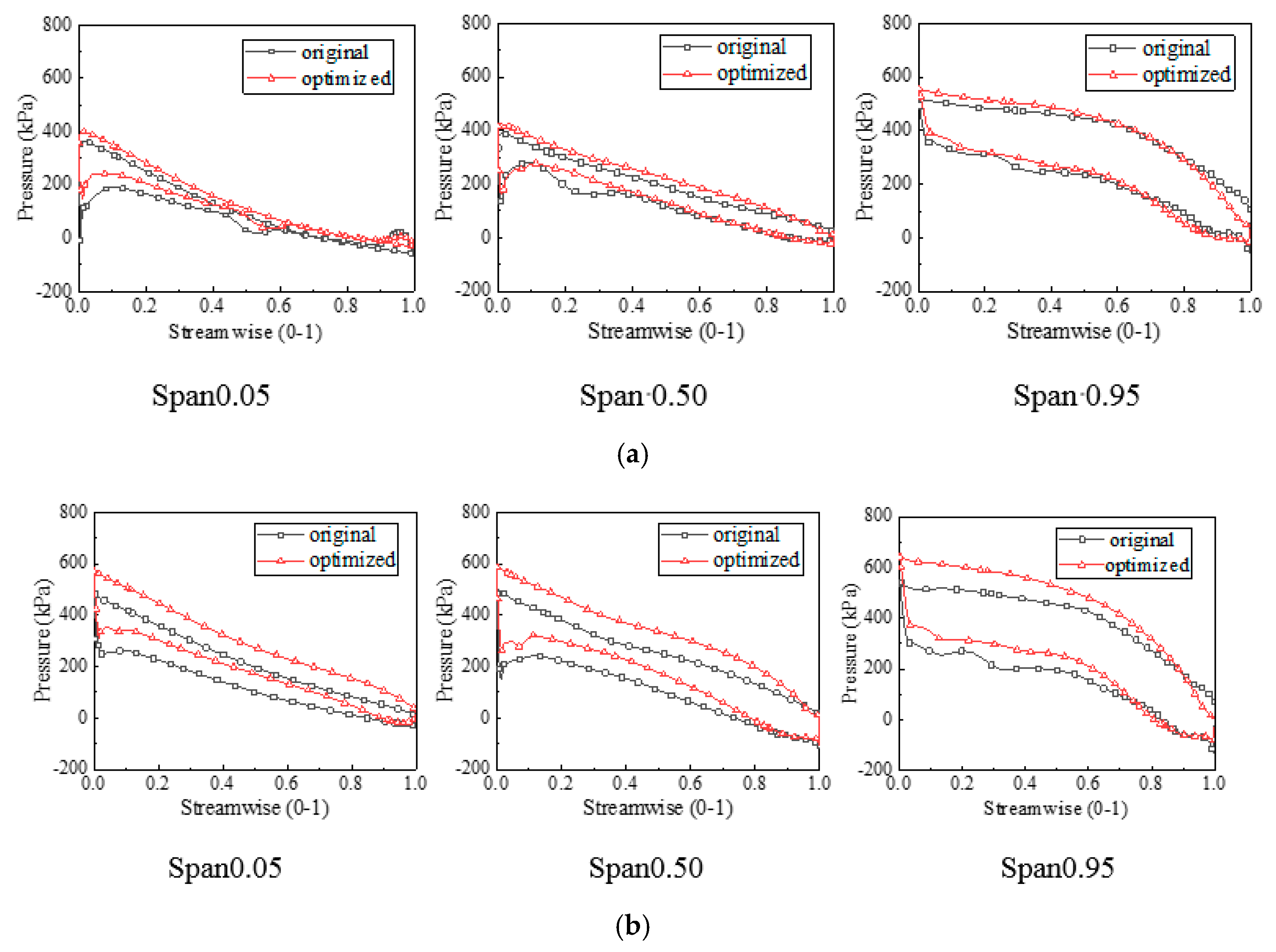
4. Results and Comparative Analysis
Optimization Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; He, Z.; Wang, Z.; Yuan, L.; Duan, H. Design for Stable and Economical Operation of Francis Turbine of Full—Load Range in Wind—PV—Hydro Complementary Power System. Northwest Hydropower 2021, 15–21. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=1v2y0gb0rq730gw06x5e0vq0wx569825&site=xueshu_se (accessed on 11 July 2022).
- Zhou, J. Realistic Conditions and Countermeasures Strategy of Double Carbon Goals in China. Shanghai Energy Conserv. 2022, 135–138. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=1x4b0cr0e54y0t801301089058166080&site=xueshu_se (accessed on 11 July 2022).
- Wang, Y.; Kang, L.; Zhang, J.; Zhao, W.; Zhu, Y.; Zhao, J. Development history, typical from and future trend of integrated energy system. Acta Energlae Sol. Sin. 2021, 42, 84–95. [Google Scholar]
- Yudong, L.; Luan, C.; Guozhou, Z.; Manman, R.; Weihao, H. Load Frequency Control Strategy of Hybrid Power Generation System: A Deep Reinforcement Learning—Based Approach. Trans. China Electrotech. Soc. 2022, 37, 1768–1779. [Google Scholar]
- Aponte, R.D.; Teran, L.A.; Grande, J.F.; Coronado, J.J.; Ladino, J.A.; Larrahondo, F.J.; Rodriguez, S.A. Minimizing erosive wear through a CFD multi-objective optimization methodology for different operating points of a Francis turbine. Renew. Energy 2020, 145, 2217–2232. [Google Scholar] [CrossRef]
- Li, D.; Qin, Y.; Wang, J.; Zhu, Y.; Wang, H.; Wei, X. Optimization of blade high-pressure edge to reduce pressure fluctuations in pump-turbine hump region. Renew. Energy 2022, 181, 24–38. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, J.; Wang, W.; Ye, T. Multi-condition optimization of cross-flow fan based on Bezier curve. Huazhong Univ. Sci. Technol. Nat. Sci. Ed. 2021, 49, 58–62. [Google Scholar]
- Wang, M.C.; Yuan, J.P.; Li, Y.J.; Zheng, Y. Multi-objective optimization of mixed-flow pump impeller based on 3-D inverse design. J. Harbin Eng. Univ. 2020, 41, 1854–1860. [Google Scholar]
- Shao, J.; Luo, C.; Zhou, Y.; Cao, H. Optimization design of splitter blade shape based on free from deformation technology. J. Aerosp. Power 2021, 36, 1315–1323. [Google Scholar]
- Teran, L.A.; Larrahondo, F.J.; Rodríguez, S.A. Performance improvement of a 500-kW Francis turbine based on CFD. Renew. Energy 2016, 96, 977–992. [Google Scholar] [CrossRef]
- Soares, L.M.V.; do Carmo Calijuri, M.; das Gracas Silva, T.F.; de Moraes Novo, E.M.L.; Cairo, C.T.; Barbosa, C.C.F. A parameterization strategy for hydrodynamic modelling of a cascade of poorly monitored reservoirs in Brazil. Environ. Model. Softw. 2020, 134, 104803. [Google Scholar] [CrossRef]
- Xiao, Q.; Wang, J.; Jiang, B.; Yang, W.; Yang, X. Parametric and Multi-objective Optimization of The Squirrel Cage Fan. J. Eng. Thermophys. 2020, 41, 2977–2981. [Google Scholar]
- Liu, H. The Optimization of Full Passage of Multistage Centrifugal Pump Based on CFD Analysis; Zhejiang University: Hangzhou, China, 2018. [Google Scholar]
- Qi, G. Parametric Design and Optimization of New Froward Type Mulit-Blade and Mix-Flow Impellers; Dalian University of Technology: Dalian, China, 2011. [Google Scholar]
- Xu, J.; Li, J. (Eds.) Theory and Method of Multiobjective Decision Making; Tsinghua University Press: Beijing, China, 2005. [Google Scholar]
- Mehr, G.; Durali, M.; Khakrand, M.H.; Hoghooghi, H. A novel design and performance optimization methodology for hydraulic Cross-Flow turbines using successive numerical simulations. Renew. Energy 2021, 169, 1402–1421. [Google Scholar] [CrossRef]
- Tsuzuki, M.S.G.; Vatanabe, S.L.; Castro, E.G.; Silva, E.C.; Martins, T.C.; Taniguchi, D.; Tiba, H. Development of a Complete Methodology to Reconstruct, Optimize, Analyze and Visualize Francis Turbine Runners. IFAC-PapersOnLine 2015, 48, 1900–1905. [Google Scholar] [CrossRef]
- Wang, J. Research on Multi-Objective Optimization Method Based on Kriging Surrogate Model; Dalian University of Technology: Dalian, China, 2019. [Google Scholar]
- Bahrami, S.; Tribes, C.; Devals, C.; Vu, T.C.; Guibault, F. Multi-fidelity shape optimization of hydraulic turbine runner blades using a multi-objective mesh adaptive direct search algorithm. Appl. Math. Model. 2016, 40, 1650–1668. [Google Scholar] [CrossRef]
- Li, Z. Research on Global Optimization of Multi-Wing Centrifugal Fan Based on Kriging-Model; Zhejiang University of Technology: Hangzhou, China, 2020. [Google Scholar]
- Qin, Y.; Li, D.; Wang, H.; Liu, Z.; Wei, X.; Wang, X. Multi-objective optimization design on high pressure side of a pump-turbine runner with high efficiency. Renew. Energy 2022, 190, 103–120. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, X.; Tan, L.; Zhou, D.; Zhao, Y.; Cao, S. Optimization design of a reversible pump–turbine runner with high efficiency and stability. Renew. Energy 2015, 81, 366–376. [Google Scholar] [CrossRef]
- Wang, W. Modified Particle Swarm Optimization Algorithm to Improve the Performance of a Centrifugal Pump and Investigation of Unsteady Flow; Jiangsu University: Zhenjiang, China, 2017. [Google Scholar]
- Li, Z. Multi-Objective Optimization of High Specific Speed Centrifugal Pump Based on Genetic Algorithm; Shandong University of Science and Technology: Qingdao, China, 2020. [Google Scholar]





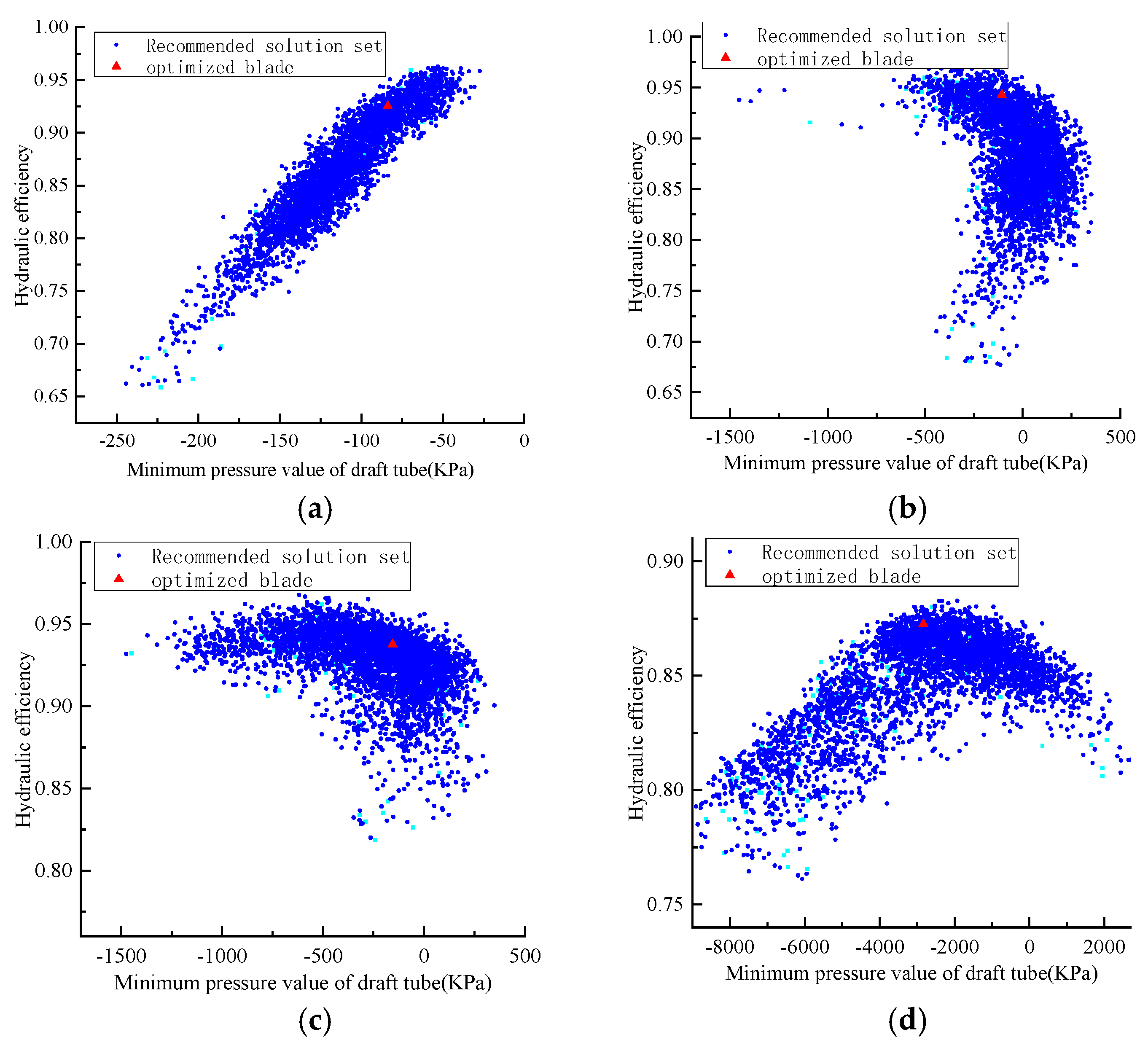
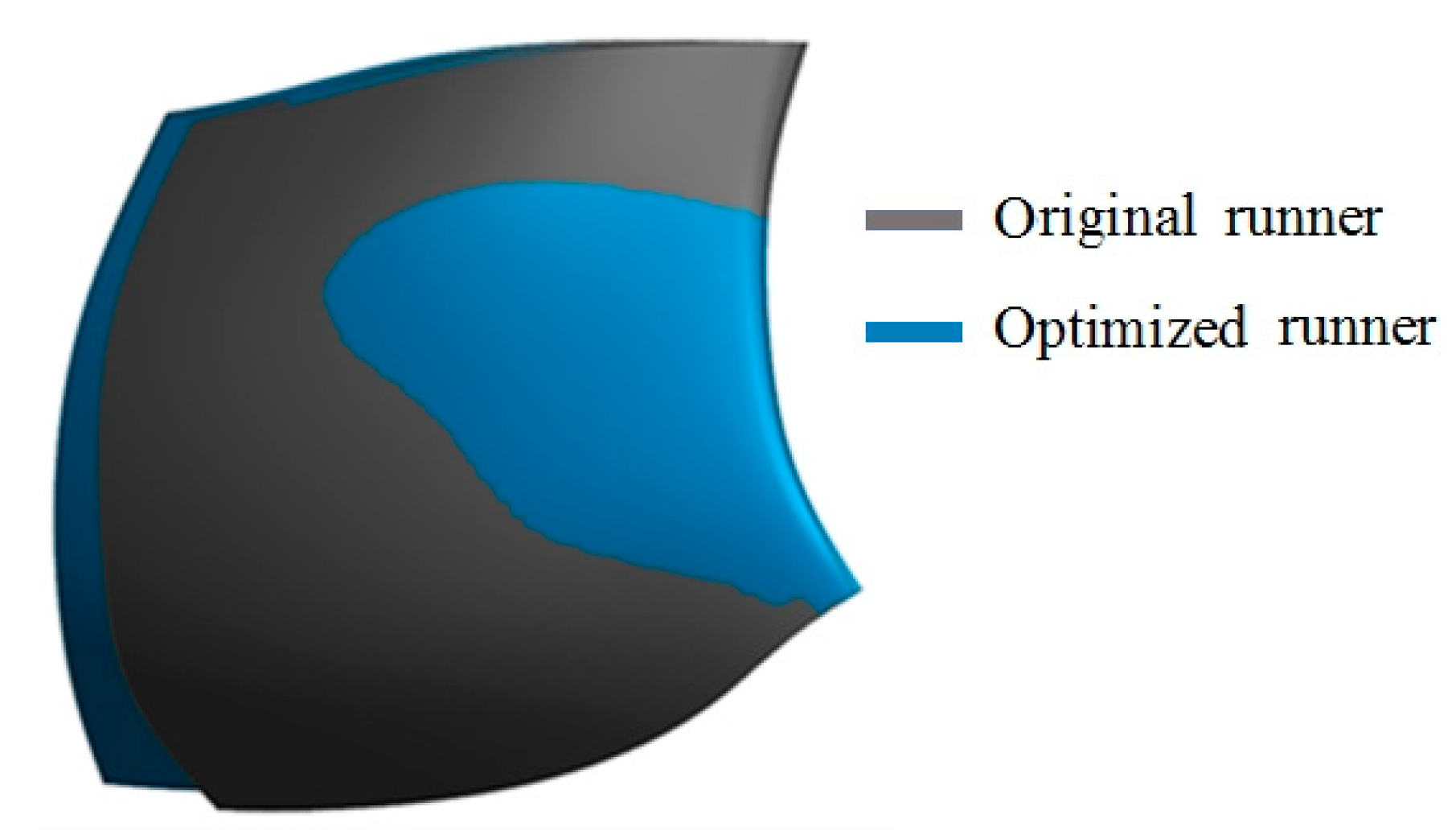
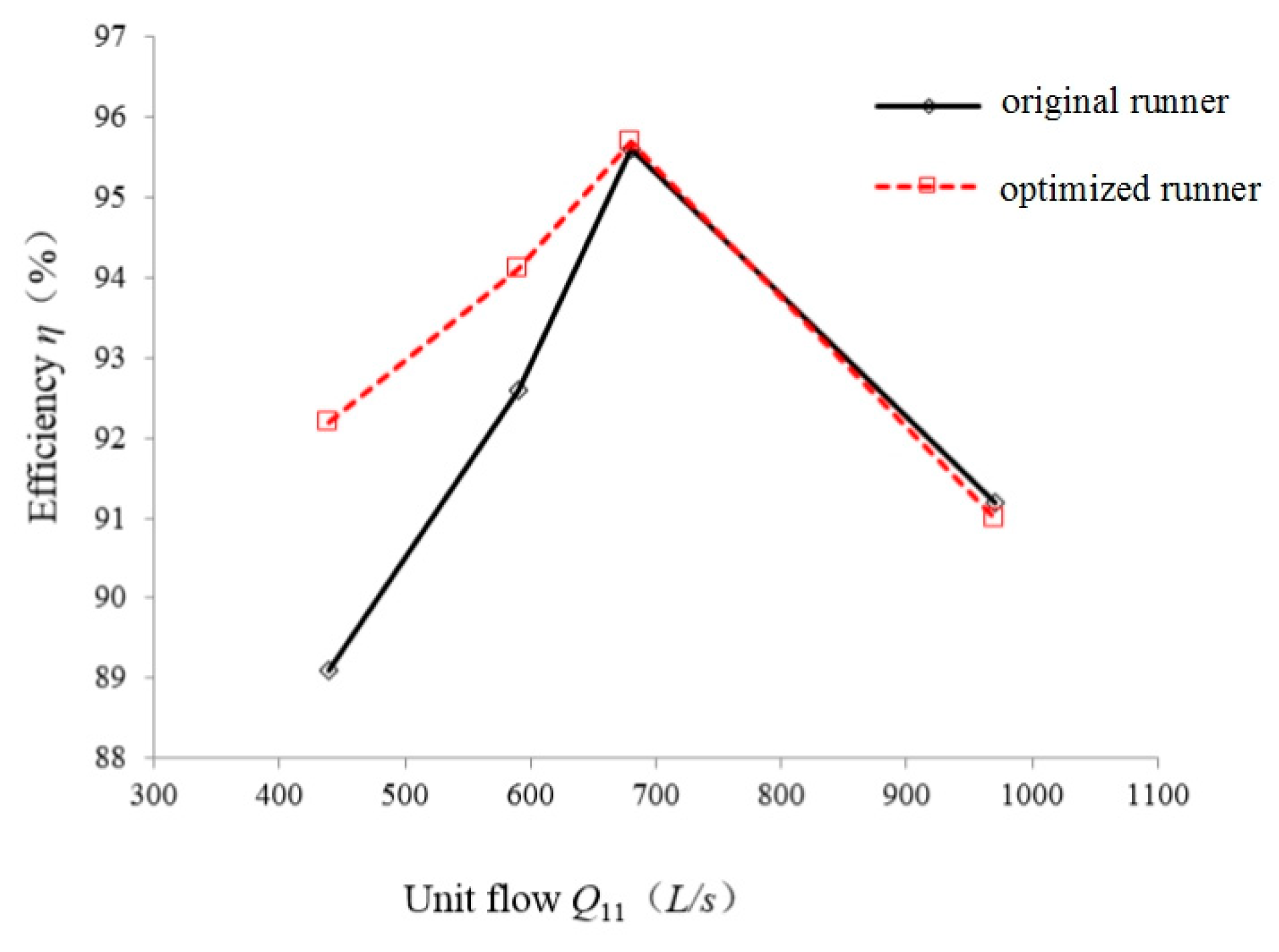
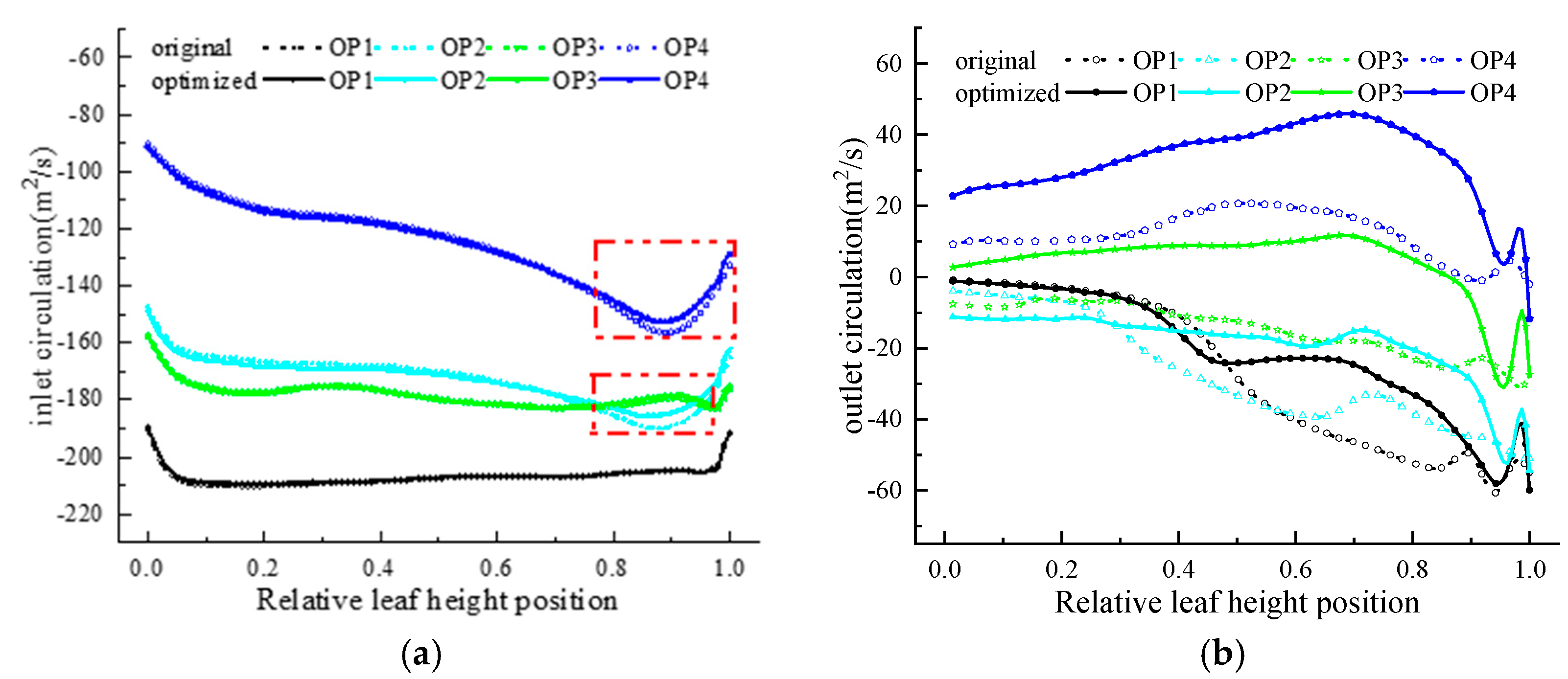



| Serial Number | x1 | x2 | x3 | x4 | … | x17 | x18 | x19 | x20 |
|---|---|---|---|---|---|---|---|---|---|
| Original blade | 40.35 | 18.08 | 25.86 | 49.71 | … | 49.02 | 40.36 | 68.60 | 77.55 |
| 1 | 37.10 | 17.63 | 24.24 | 54.21 | … | 49.02 | 40.36 | 68.60 | 77.55 |
| 2 | 42.38 | 16.37 | 23.31 | 45.56 | … | 51.20 | 43.05 | 67.60 | 75.42 |
| 3 | 42.75 | 16.64 | 27.06 | 51.18 | … | 44.83 | 38.73 | 73.09 | 78.36 |
| 4 | 42.79 | 19.08 | 27.40 | 46.65 | … | 49.83 | 42.00 | 63.07 | 85.26 |
| 5 | 42.83 | 19.75 | 26.67 | 51.92 | … | 53.90 | 41.55 | 65.20 | 80.30 |
| 6 | 42.87 | 17.16 | 27.89 | 53.86 | … | 45.61 | 41.96 | 71.51 | 75.96 |
| 7 | 42.91 | 16.68 | 25.85 | 47.40 | … | 53.36 | 38.81 | 74.87 | 73.71 |
| 8 | 42.95 | 19.82 | 24.79 | 50.13 | … | 53.75 | 44.30 | 74.74 | 70.53 |
| … | … | … | … | … | … | … | … | … | … |
| 194 | 44.36 | 16.63 | 23.81 | 54.53 | … | 49.27 | 36.61 | 75.11 | 77.21 |
| 195 | 44.31 | 16.75 | 28.07 | 54.19 | … | 49.61 | 44.10 | 74.77 | 75.57 |
| 196 | 44.36 | 16.63 | 23.81 | 54.61 | … | 49.27 | 37.55 | 75.23 | 78.10 |
| 197 | 44.33 | 19.87 | 28.04 | 54.55 | … | 48.57 | 44.35 | 74.99 | 77.26 |
| 198 | 44.15 | 18.43 | 28.30 | 54.33 | … | 48.96 | 42.07 | 75.41 | 79.10 |
| 199 | 44.32 | 18.58 | 28.26 | 54.43 | … | 50.46 | 43.30 | 73.47 | 76.29 |
| 200 | 44.15 | 18.43 | 27.99 | 54.40 | … | 47.88 | 42.18 | 75.44 | 79.19 |
| Algorithm Type | Parameter | Numerical Value |
|---|---|---|
| MOGA | Initial sample number | 10,000 |
| Number of iteration samples | 4000 | |
| Maximum Allowed Pareto Percentage | 95 | |
| Convergence Stable Ratio | 0.5 | |
| Maximum number of iterations | 1000 | |
| number of candidate points | 5 |
| Geometry Parameter Name | Parameter Value |
|---|---|
| Wheel diameter D1 (m) | 2.46 |
| Relative guide vane height | 0.29 |
| Rated speed nr (rpm) | 300 |
| Rated water head (m) | 79.5 |
| Number of runner blades | 14 |
| Number of active guide vanes | 24 |
| Number of fixed guide vanes | 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, X.; Zhao, Y.; Zhang, H.; Pu, Y.; Li, Z.; Guo, P. Optimization and Performance Analysis of Francis Turbine Runner Based on Super-Transfer Approximate Method under Multi-Energy Complementary Conditions. Sustainability 2022, 14, 10331. https://doi.org/10.3390/su141610331
Zheng X, Zhao Y, Zhang H, Pu Y, Li Z, Guo P. Optimization and Performance Analysis of Francis Turbine Runner Based on Super-Transfer Approximate Method under Multi-Energy Complementary Conditions. Sustainability. 2022; 14(16):10331. https://doi.org/10.3390/su141610331
Chicago/Turabian StyleZheng, Xiaobo, Yaping Zhao, Huan Zhang, Yongjian Pu, Zhihua Li, and Pengcheng Guo. 2022. "Optimization and Performance Analysis of Francis Turbine Runner Based on Super-Transfer Approximate Method under Multi-Energy Complementary Conditions" Sustainability 14, no. 16: 10331. https://doi.org/10.3390/su141610331
APA StyleZheng, X., Zhao, Y., Zhang, H., Pu, Y., Li, Z., & Guo, P. (2022). Optimization and Performance Analysis of Francis Turbine Runner Based on Super-Transfer Approximate Method under Multi-Energy Complementary Conditions. Sustainability, 14(16), 10331. https://doi.org/10.3390/su141610331





