Multi-Objective Optimization of Back-to-Back Starting for Pumped Storage Plants under Low Water Head Conditions Based on the Refined Model
Abstract
:1. Introduction
- (1)
- It is the first to establish a nonlinear PSP model combining the electrical subsystem with the fine hydraulic and mechanical subsystems for BTBS;
- (2)
- The effects of the hydraulic-mechanical-electrical parameters on the BTBS are comprehensively investigated on the basis of the model mentioned above;
- (3)
- An innovative multi-objective optimization scheme is proposed for the control strategy of BTBS at low water head conditions for the first time, which is proven to be suitable for a variety of working conditions.
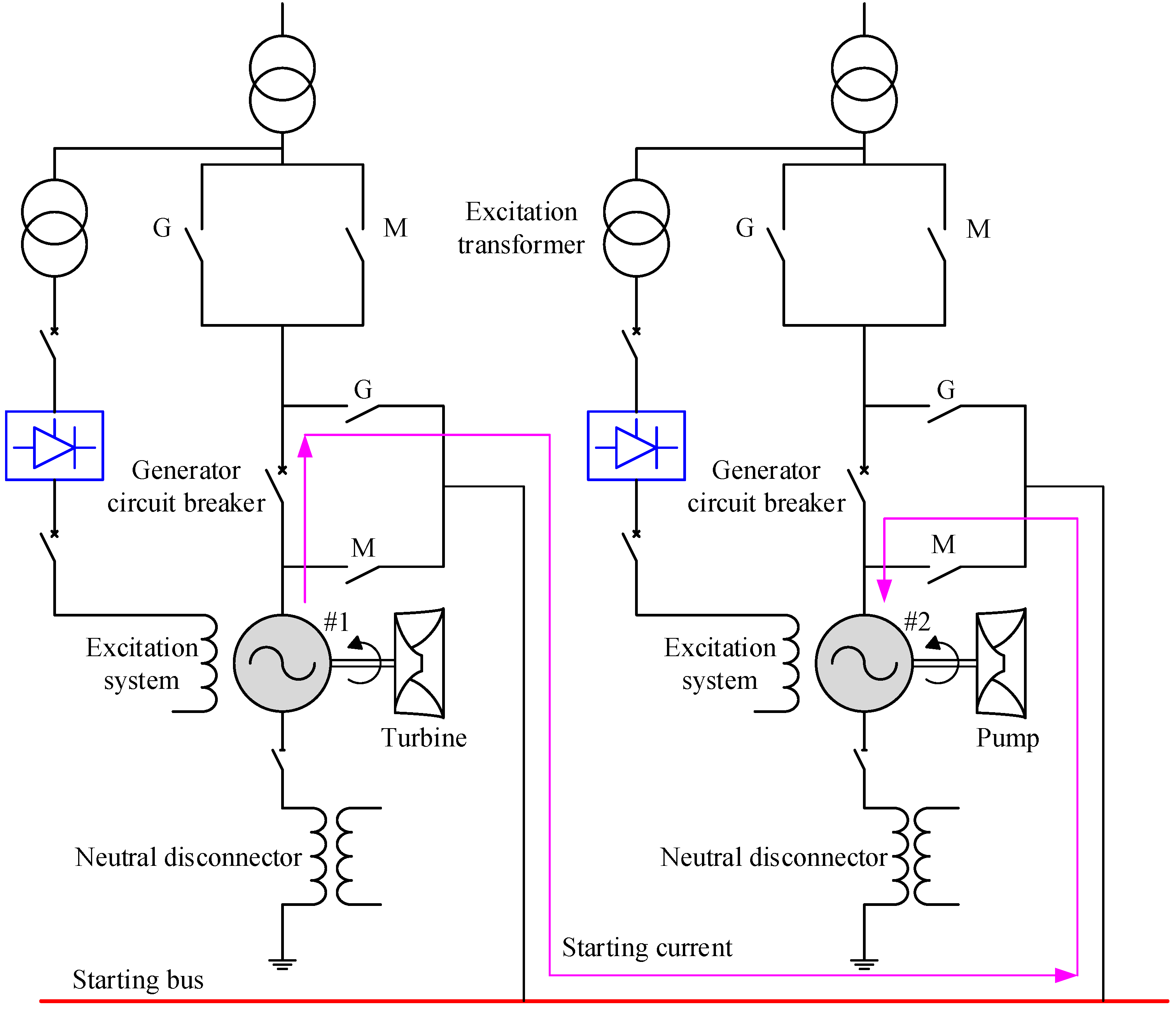
2. Refined Modelling of a Pumped Storage Plant for Back-to-Back Starting
2.1. The Hydraulic-Mechanical Subsystem
- (1)
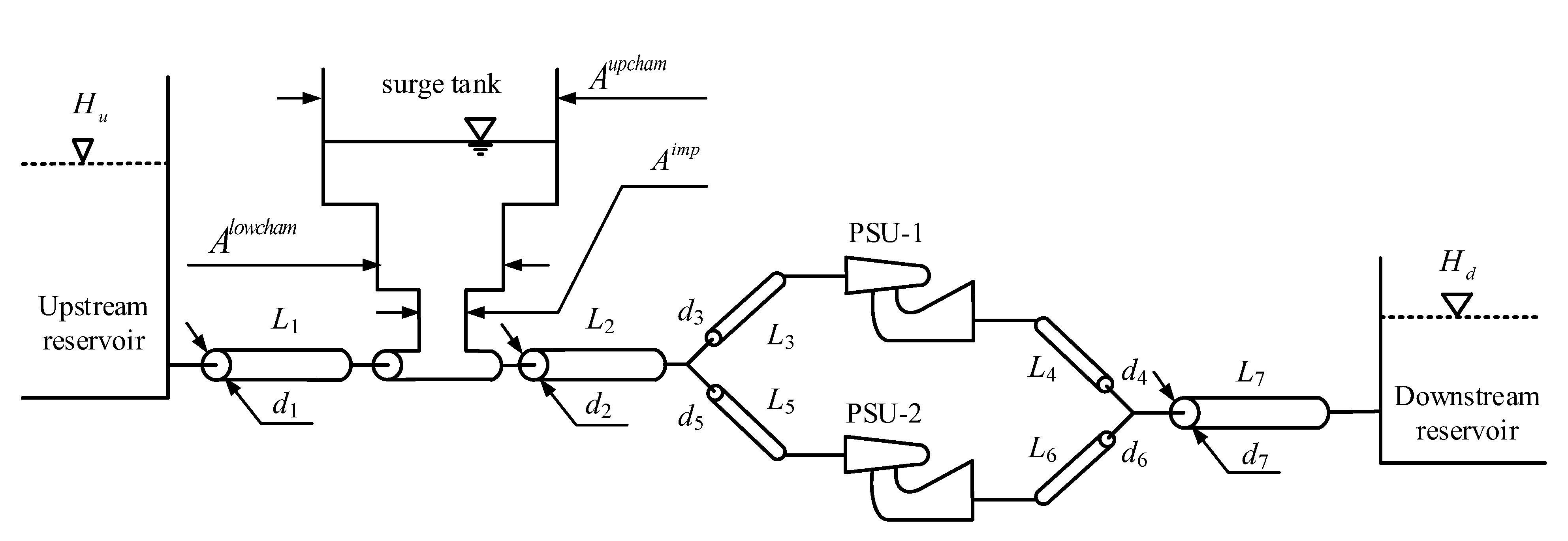
- Conduit System
- (2)
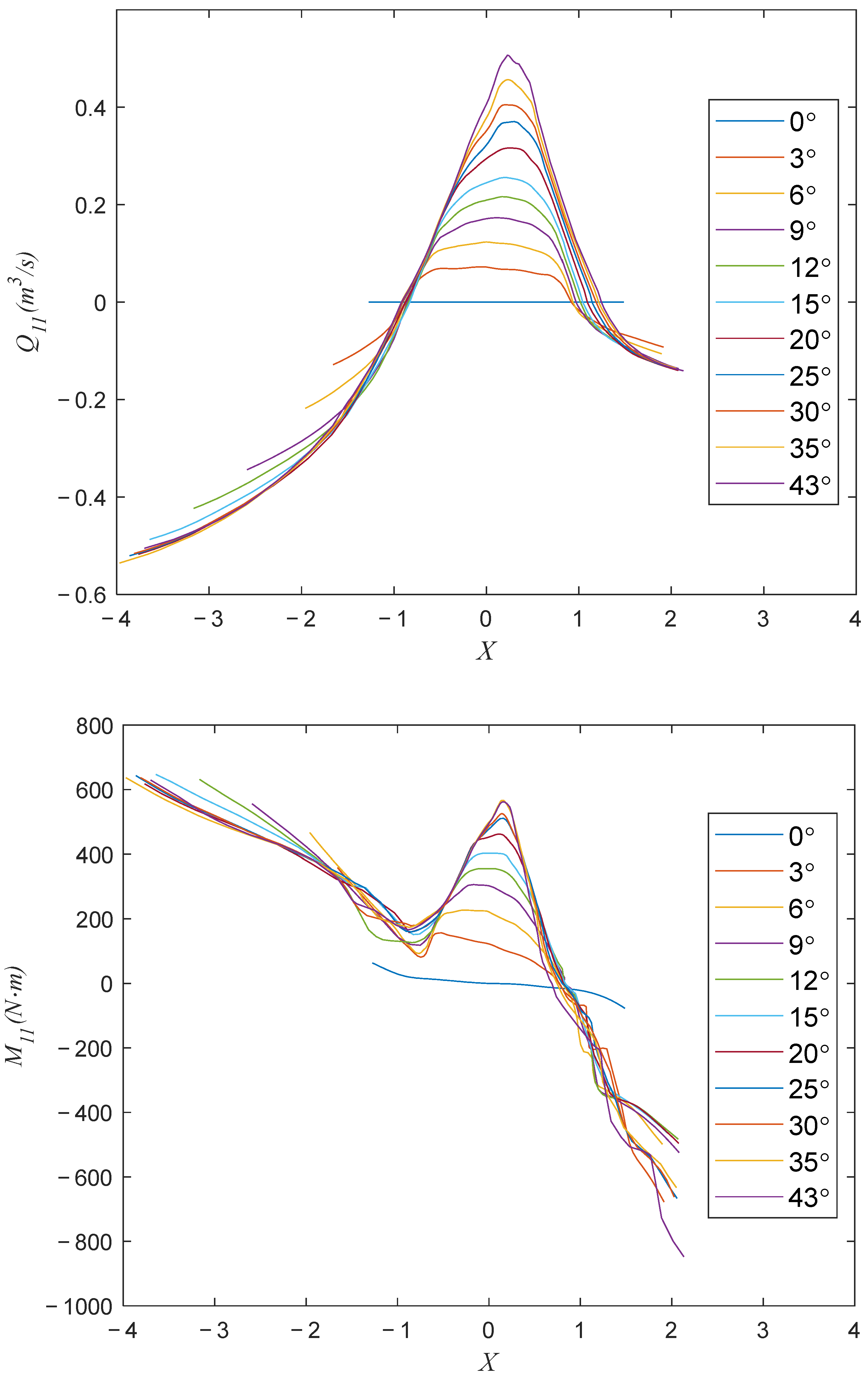
- The Pump turbine Model
- (3)
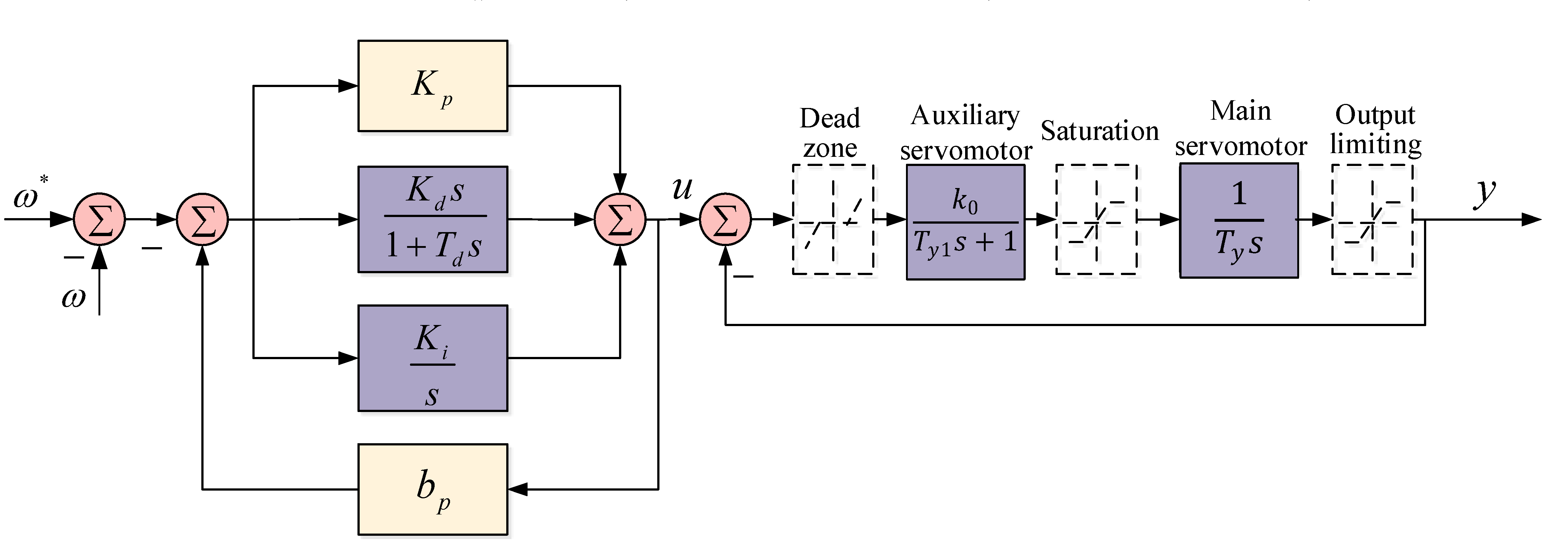
- The Turbine Governor System
2.2. The Electrical Subsystem
- (1)
- Synchronous Machine
- (2)
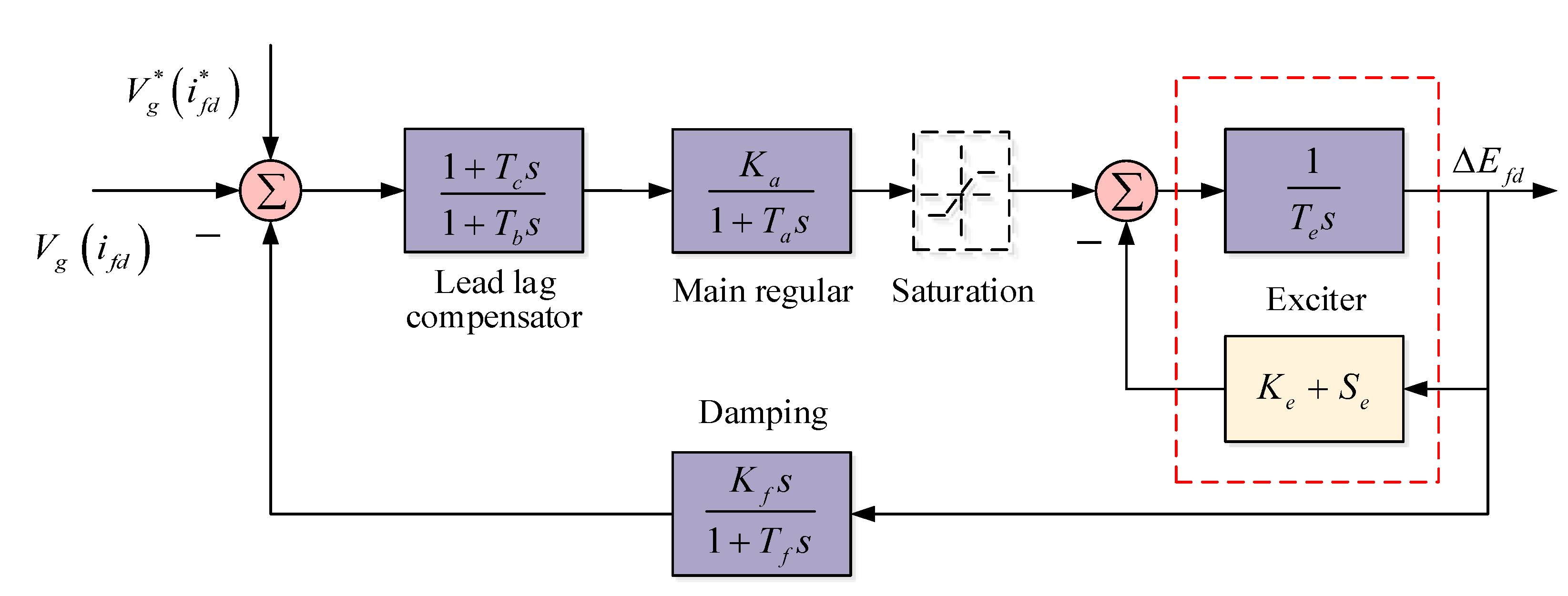
- The Excitation System
2.3. Model Validation with On-Site Measurement
3. Analysis of Factors Affecting Back-to-Back Starting
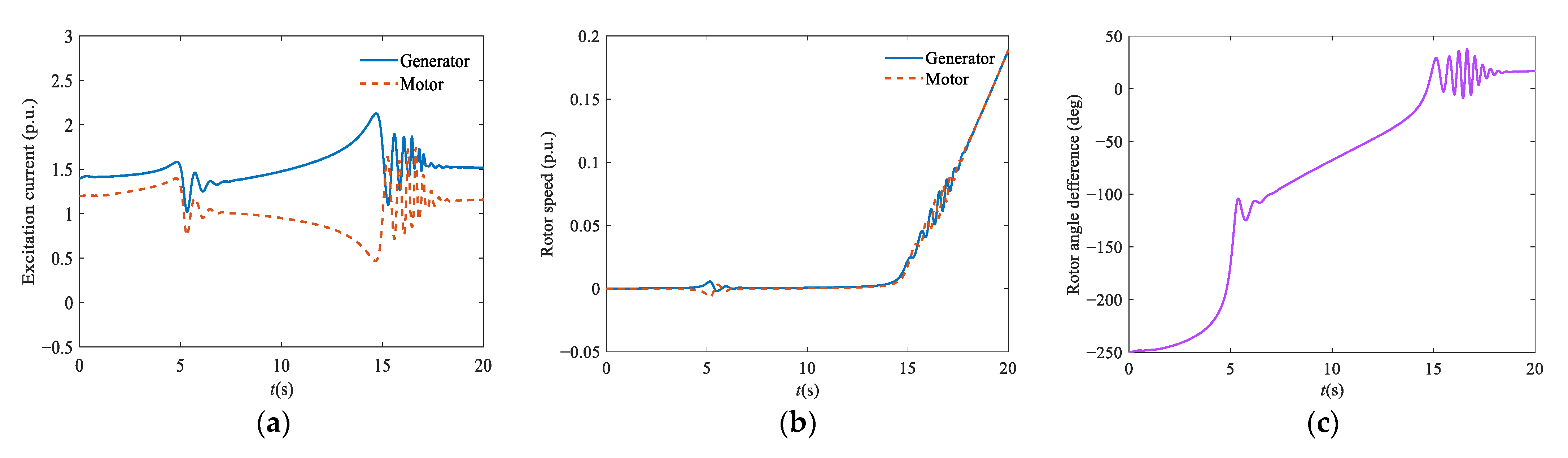
3.1. Excitation Current
3.2. Control Way of the Excitation System
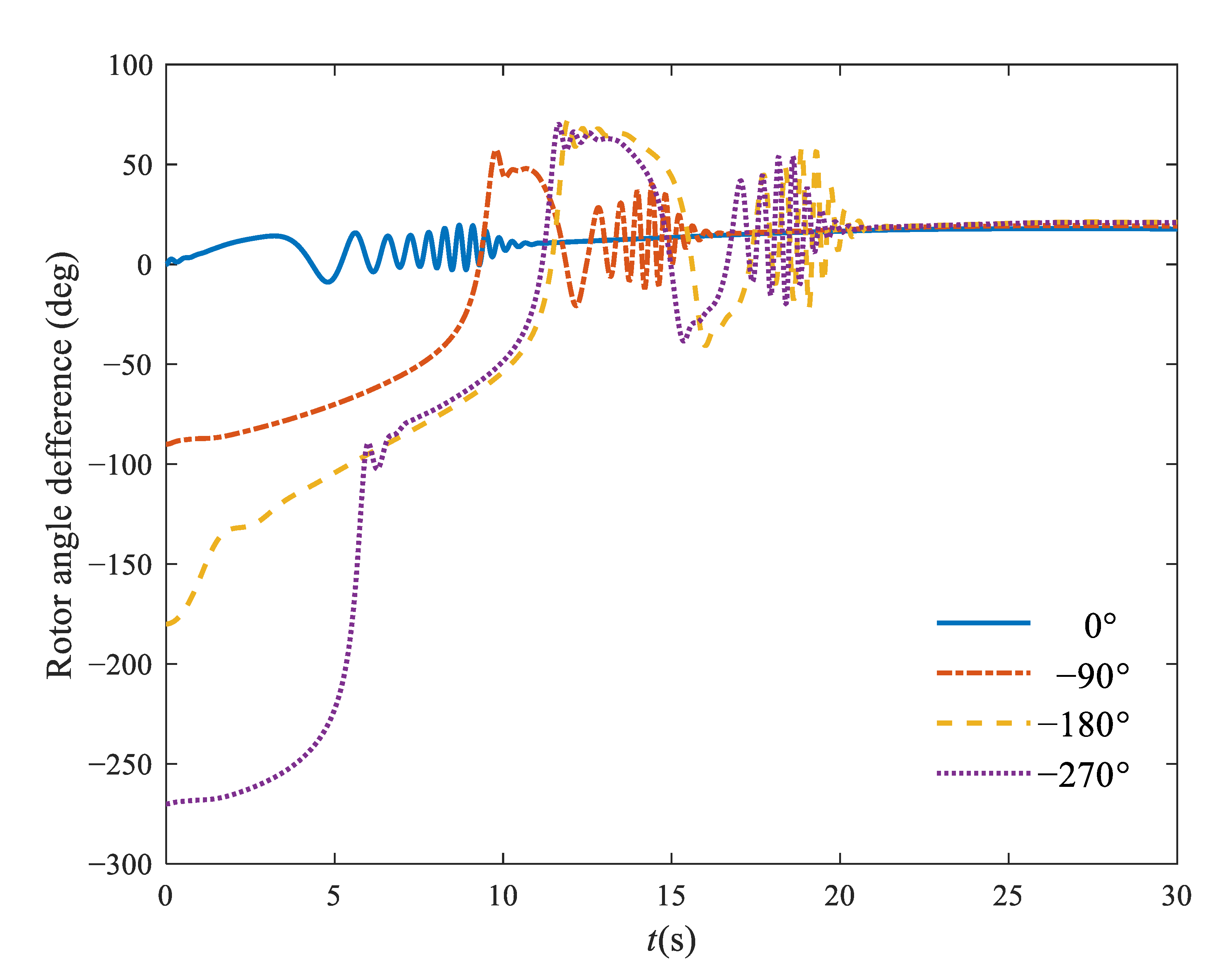
3.3. Initial Difference between Rotor Positions
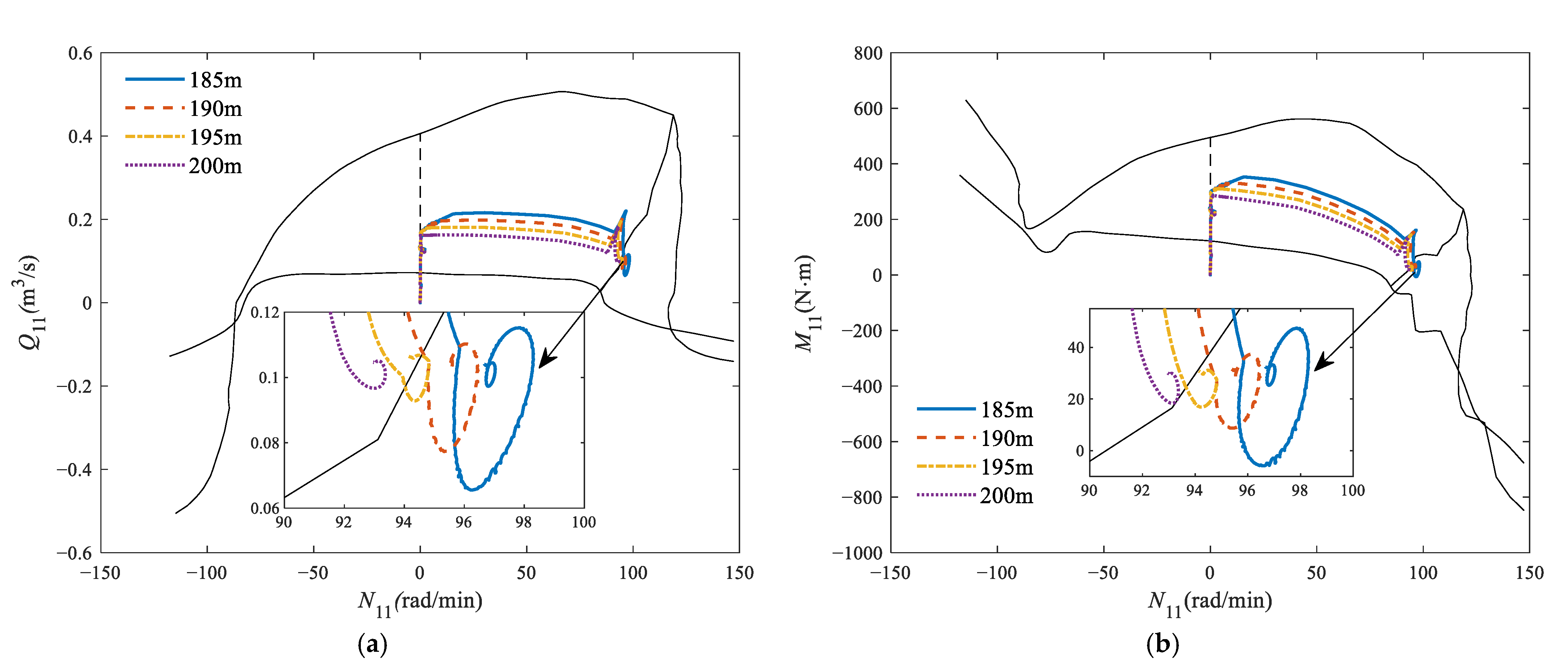
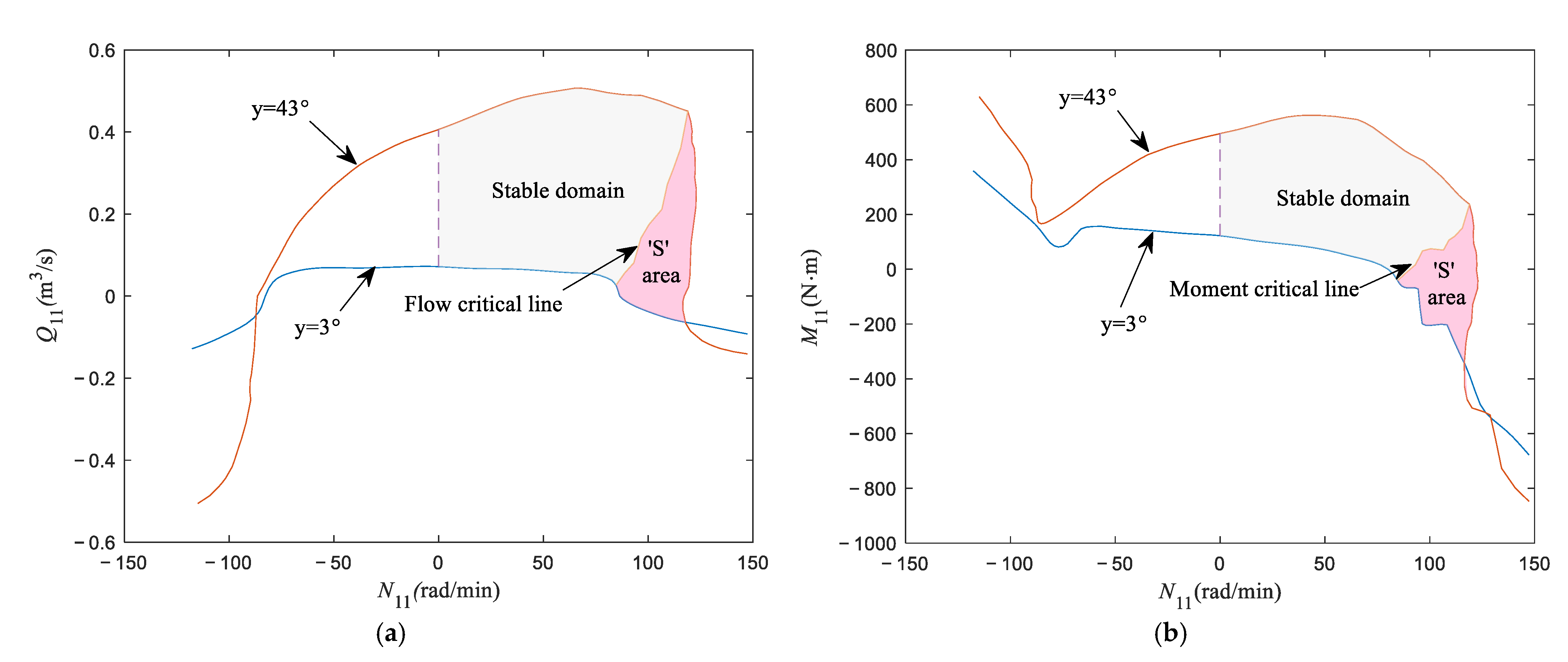
3.4. Water Head
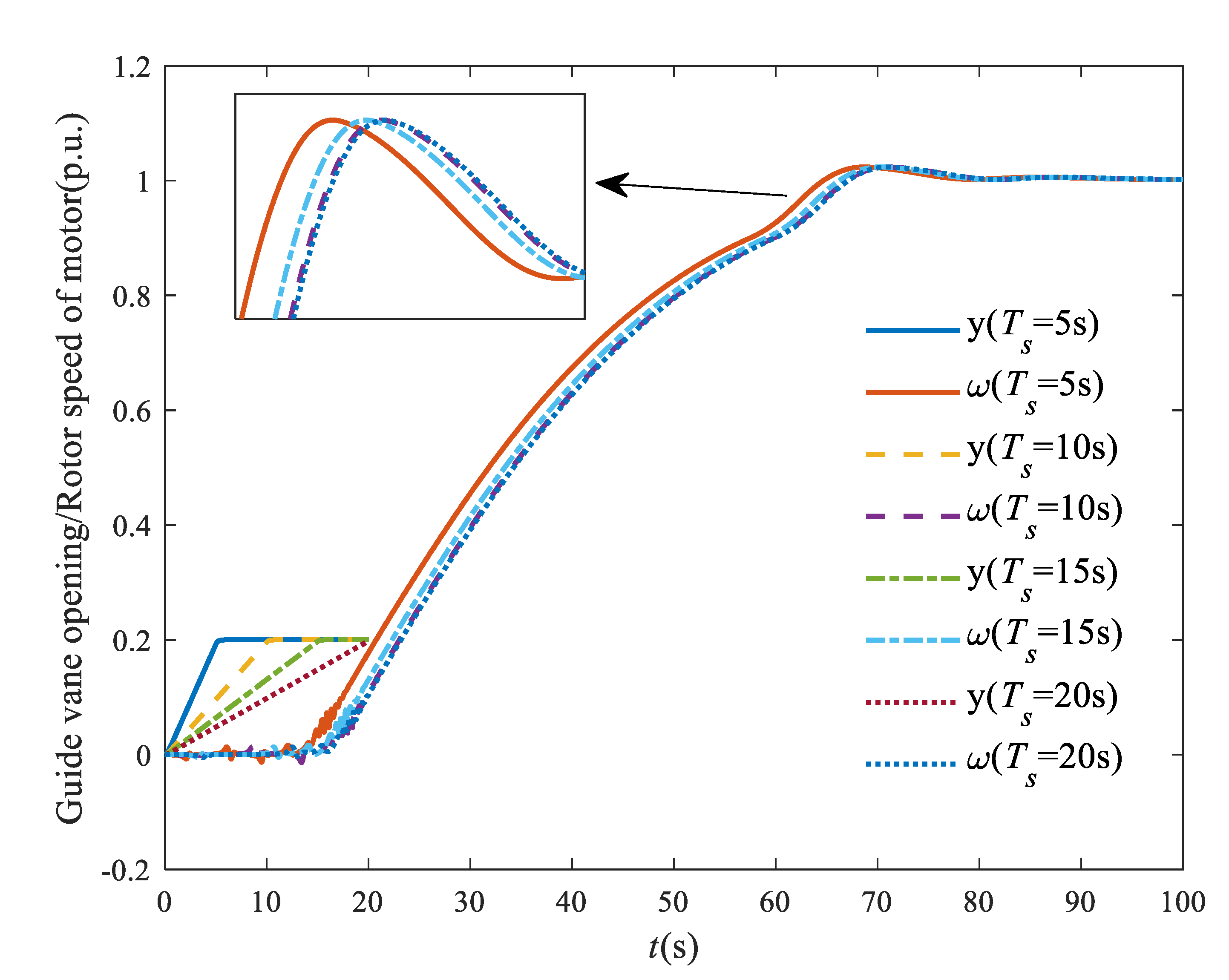
3.5. Control Scheme of the Governor
4. Optimization of BTBS Strategy Based on Multi-Objective Control
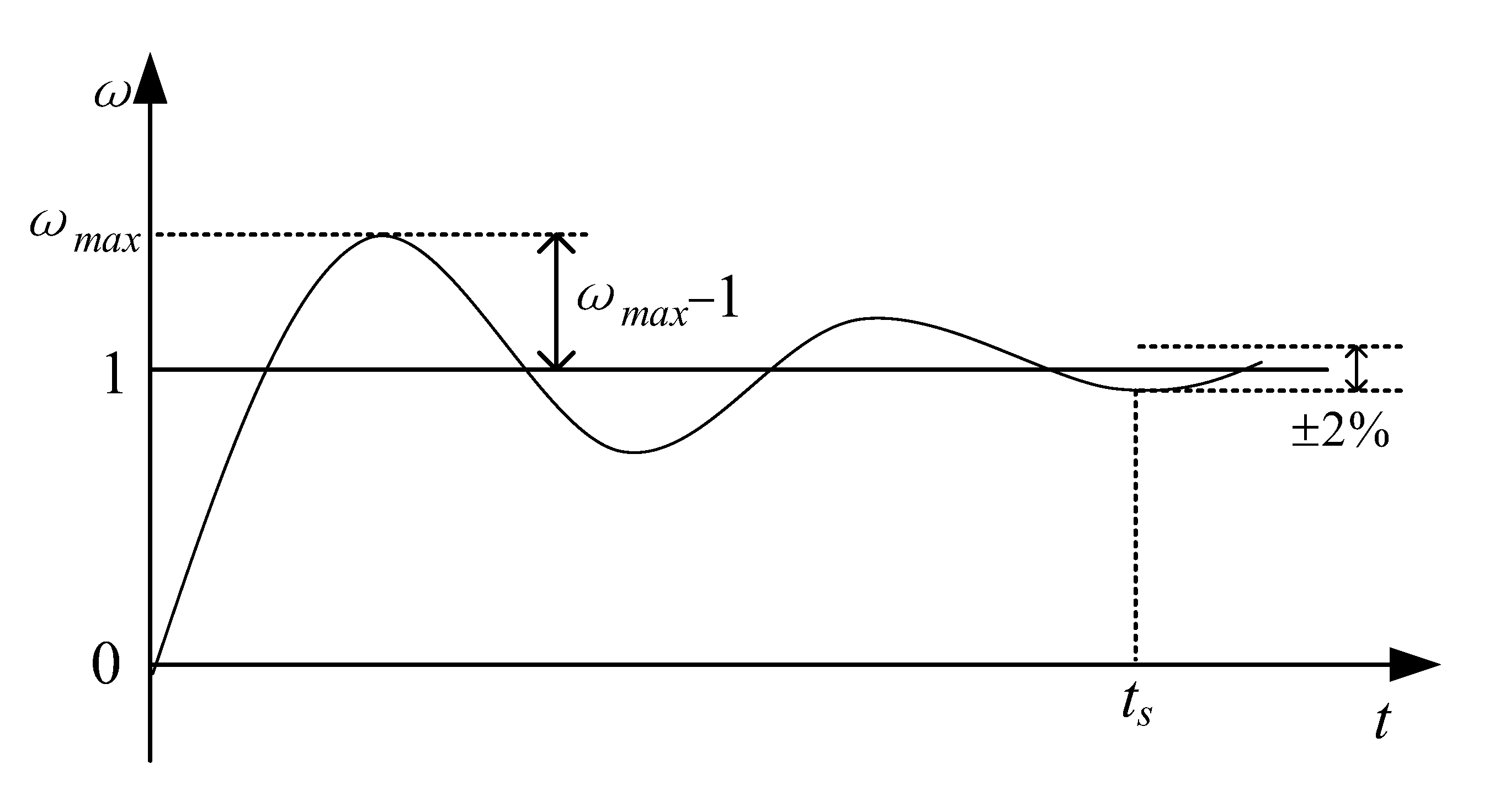
4.1. Objective Function
4.2. Decision Variables
- Scheme 1: The traditional CEC mode with one-stage DGVC+PID control. In one-stage DGVC, the guide vane of the driving machine is first opened at the rate kc, and remains unchanged when the guide vane opening reaches yc. When the speed reaches 90% of the rated speed, the PID controller will be put into operation. The excitation system of the two units shall first operate with the given excitation current, and switch to the constant terminal voltage mode when the speed reaches 90% of the rated speed. kc generally takes the maximum rate, which is a known parameter. Therefore, the given excitation current , and given opening yc are selected as the decision variables in the open-loop stage. Parameters of PID controller, Kp, Ki, and Kd, are adopted as the decision variables in the closed-loop stage.
- Scheme 2: The proposed CEV mode with one-stage DGVC+PID control. Similarly, the given excitation voltage, given opening yc, and the three parameters of PID controller, Kp, Ki, and Kd, are chosen as the decision variables.
4.3. Constraint Conditions
- (1)
- Operation Time Constraintwhere is the stability time of PSU-2. is the maximum operation time.
- (2)
- The Boundary of Decision Variableswhere is the decision variables of scheme; and indicate the lower limits and the upper limits of the boundary.
- (3)
- Rotor Speed Difference Between Two MachinesAccording to the requirements of the BTBS, the rotational speed difference between the two units shall not exceed a certain limit value; otherwise, it is considered a startup failure:where is the rotor speed of the driving machine and is the rotor speed of the driven machine. is the maximum allowable rotor speed difference between the two units.
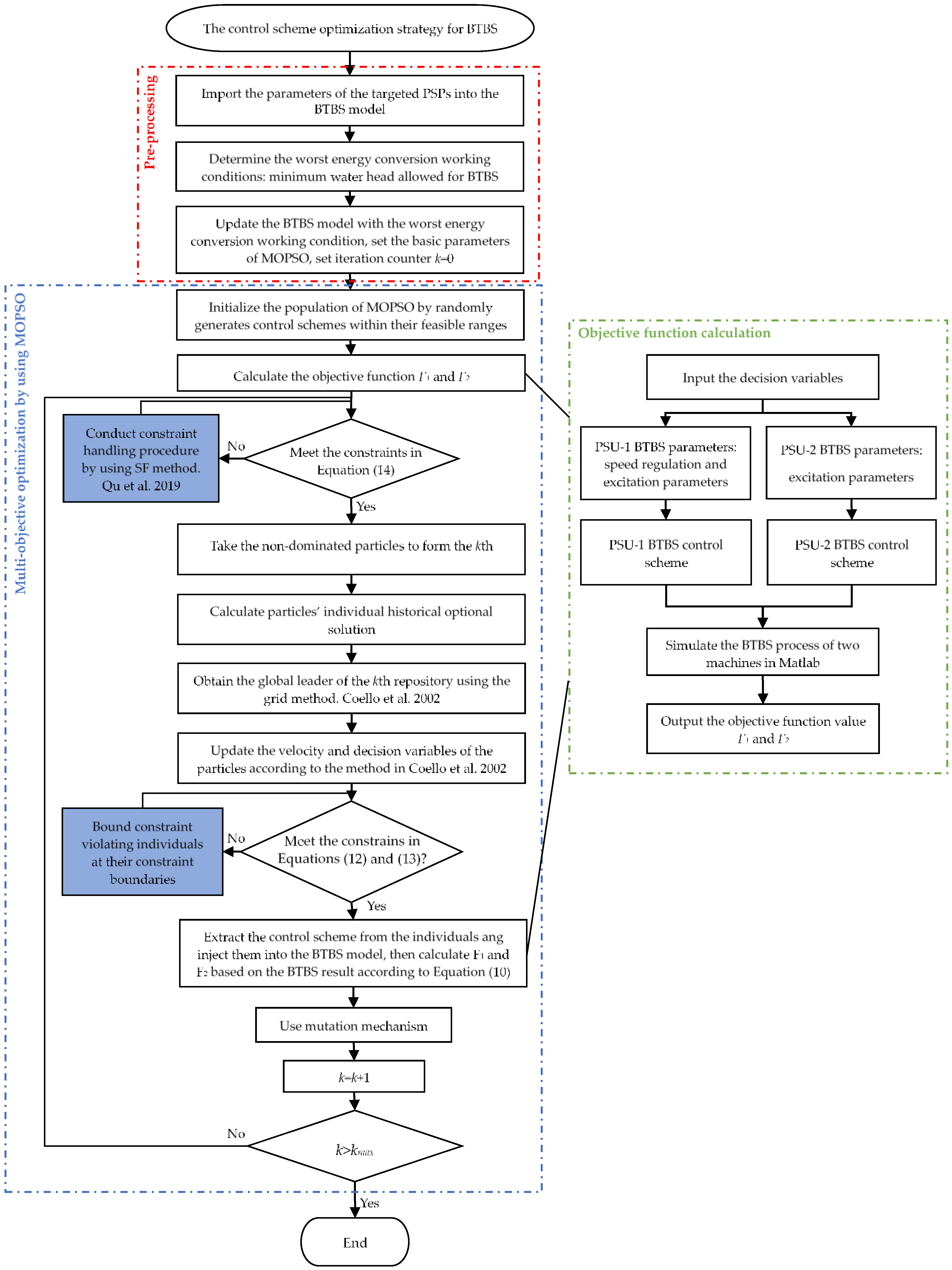
4.4. Optimization Procedures
5. Case Study and Analysis
5.1. Model Parameters Setting
5.2. Introduction to Comparative Experiments
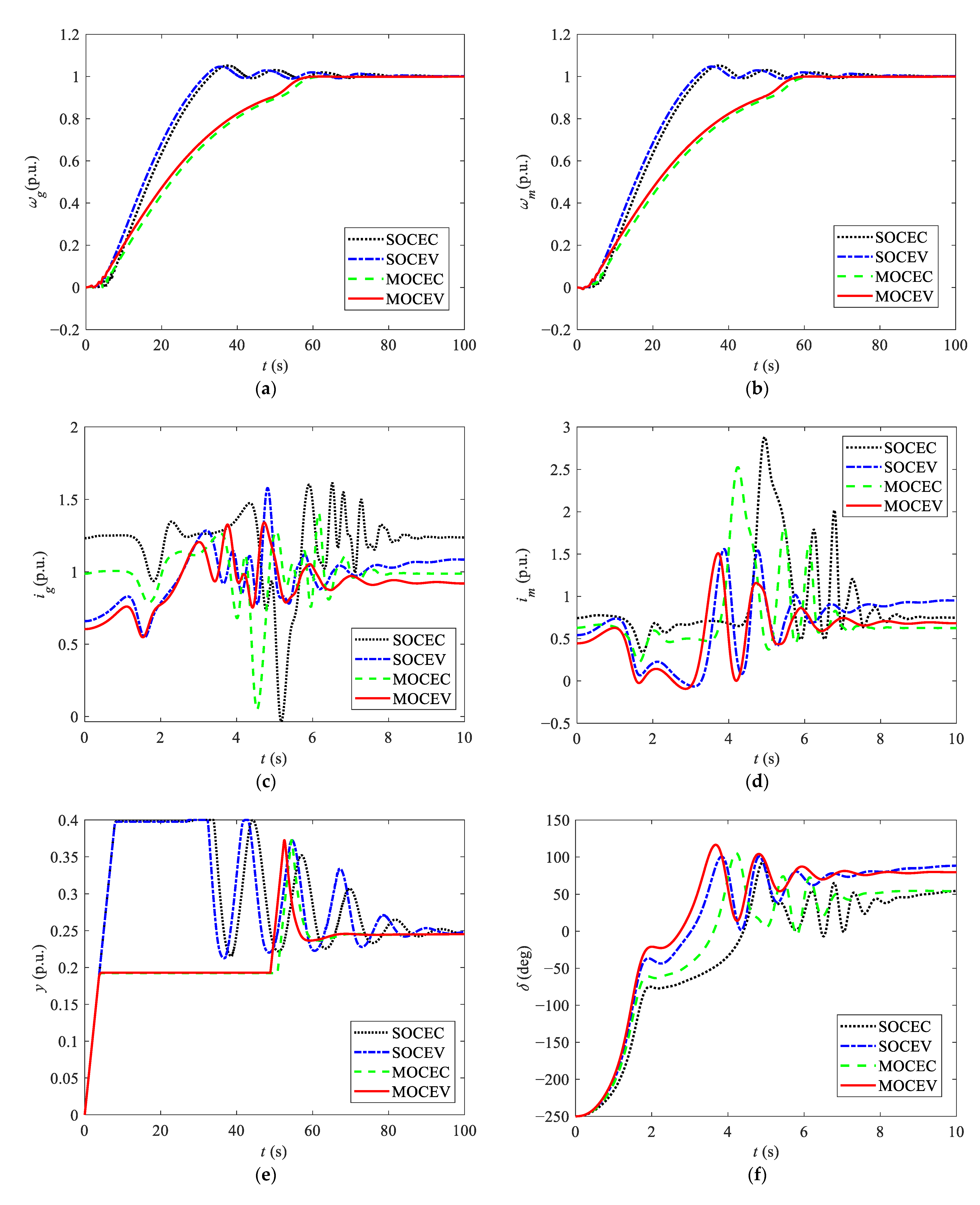
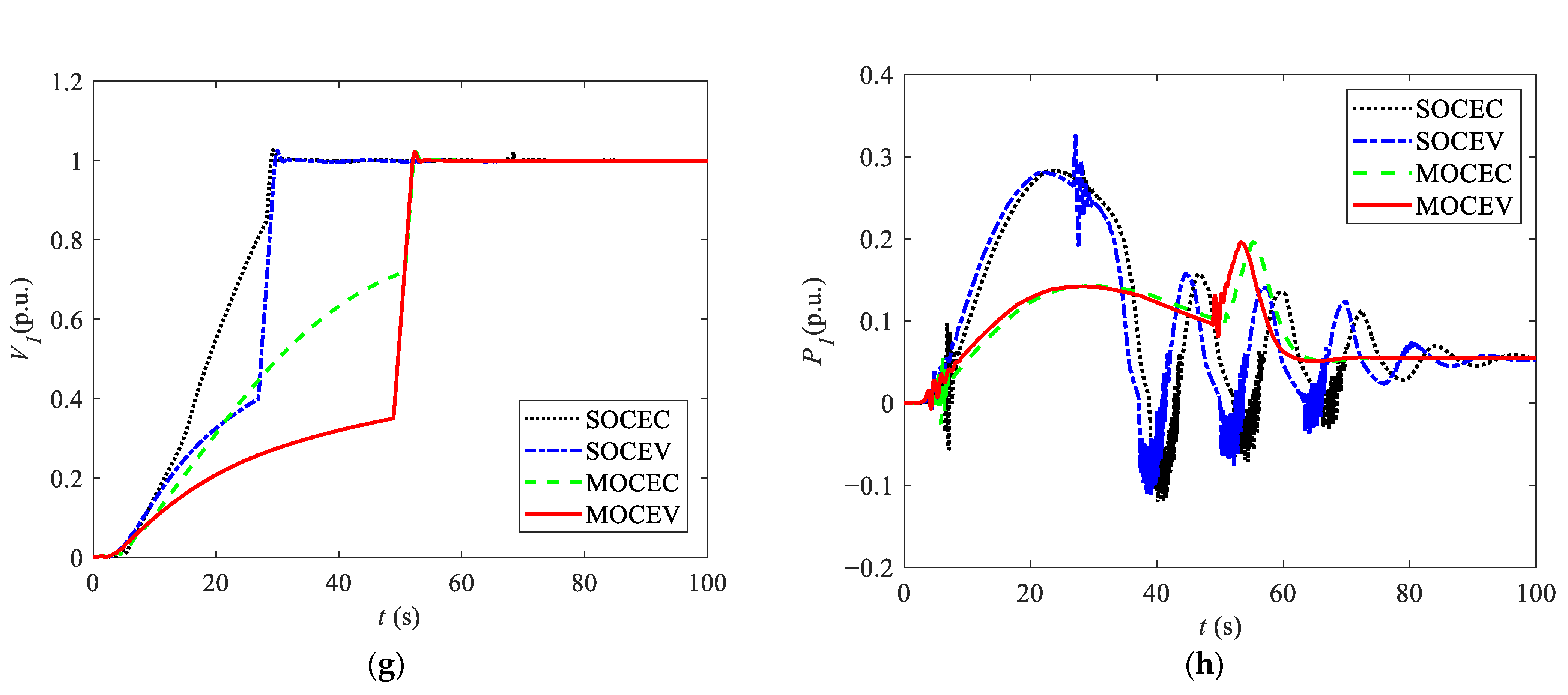
5.3. Effectiveness Analysis
5.4. Validation of the Proposed Optimization Strategy
6. Conclusions
- The given value and control way of excitation current, the control scheme of the governor, and the water head have great influence on the transient process of BTBS. The control scheme of excitation current and guide vane should be selected as the decision variables in the BTBS optimization; the worst BTBS condition can be identified by the lowest water head.
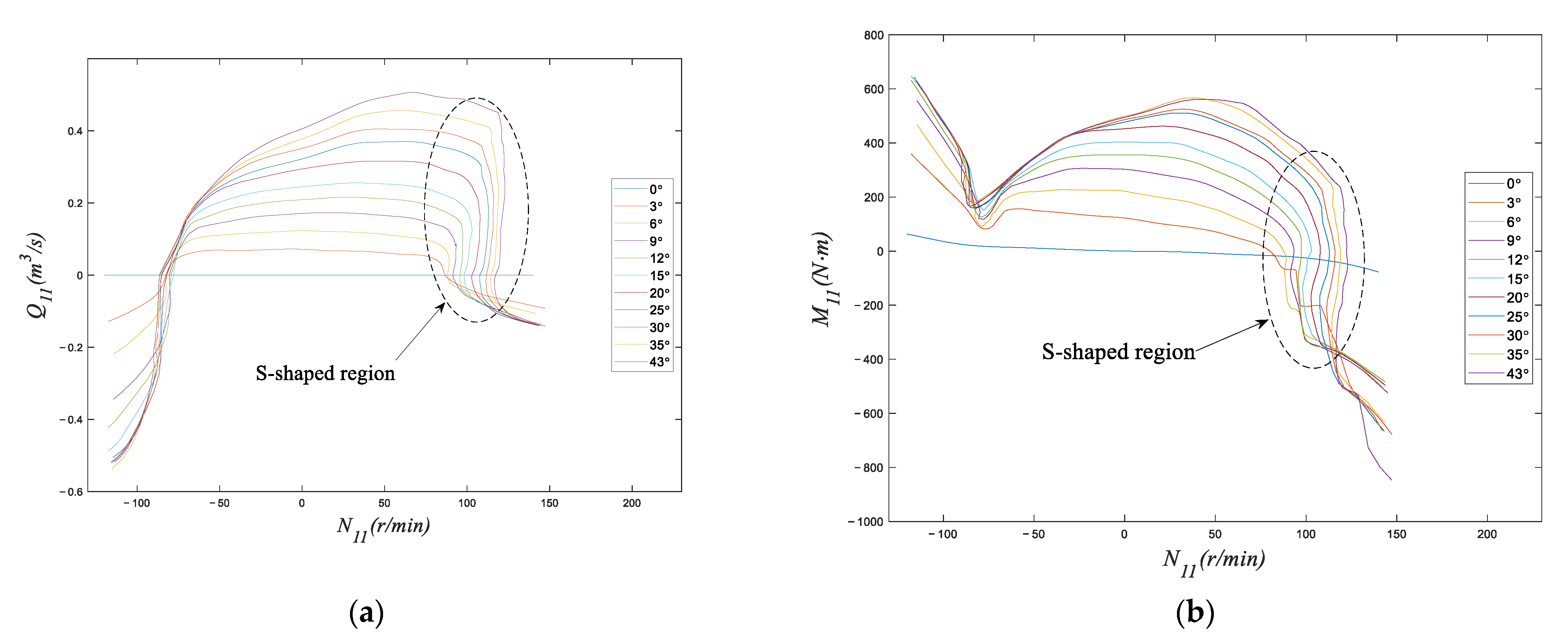
- The overshoot and stable time of the speed are contradictory. The traditional single-objective optimization scheme merely considers the single objective, which can very easily cause the unit to fall into the S-shaped area, resulting in severe fluctuations in speed and power.
- Compared with the single-objective, the optimization strategy proposed can considerably improve the speed overshoot and the speed stable time by at least 68.27% and by 3.22% under the worst working condition. The optimization results show that the multi-objective scheme is a better choice than the single-objective scheme.
- Compared with the MOCEC scheme, when the MOCEV scheme is adopted, the overshoot, rise time, and stable time are improved by 68.35%, 3.7%, and 3.2% in PSU-1, and 45.4%, 3.7%, and 3.2% in PSU-2. Thus, the MOCEV scheme is superior.
- The proposed MOCEV optimal control scheme can effectively keep away from the S-shaped area and is verified by a real PSU.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | |
| PSP | pumped storage plant |
| BTBS | back-to-back starting |
| PSU | pump storage unit |
| CEV | constant excitation voltage |
| CEC | constant excitation current |
| LCP | logarithmic curve projection |
| MOC | method of characteristics |
| GVO | gate valve opening |
| MOCEC | multi-objective CEC |
| MOCEV | multi-objective CEV |
| SOCEC | single-objective CEC |
| SOCEV | single-objective CEV |
| ITAE | integrated time and absolute error |
| pu | per-unit value |
| Symbols | |
| Parameters | |
| A | cross sectional area of pipeline (m2) |
| a | wave velocity (m/s) |
| bp | permanent difference coefficient (pu) |
| D | the diameter of the turbine runner (m) |
| d | pipeline diameter (m) |
| f | friction coefficient (pu) |
| g | acceleration of gravity (m/s2) |
| Kd | differential gain (pu) |
| Ke | self-excitation coefficient of exciter (pu) |
| Kf | damping coefficient (pu) |
| k0 | forward amplification factor (pu) |
| Ki | integral gain (pu) |
| Kp | proportional gain (pu) |
| Ra | resistance of stator winding (pu) |
| Se | exciter saturation factor (pu) |
| Ta | amplifier time constant (s) |
| Tb | lead lag time constant (s) |
| Tc | lead lag time constant (s) |
| x | distance calculated from upstream (m) |
| Td | differential time constant (s) |
| Te | exciter time constant (s) |
| Tf | damping time constant (s) |
| Tj | mechanical time constant (s) |
| Ty | main servomotor response time (s) |
| Ty1 | assistant servomotor response time (s) |
| transient and sub-transient time constants of open-circuit d-axis (s) | |
| transient and sub-transient time constants of open-circuit q-axis (s) | |
| synchronous, transient and sub-transient reactance of q-axis (pu) | |
| synchronous, transient and sub-transient reactance of q-axis (pu) | |
| Variables | |
| the transient and sub-transient internal EMF of d-axis (pu) | |
| Efd | excitation EMF (pu) |
| the transient and sub-transient internal EMF of q-axis (pu) | |
| H | piezometric head (m) |
| Ht | the working head of pump turbine (m) |
| the current of d- and q-axis (pu) | |
| ifd | excitation current (pu) |
| excitation current setting value of generator and motor (pu) | |
| Ka | amplifier coefficient (pu) |
| Me | electromagnetic torque (pu) |
| Mt | the moment of pump turbine (pu) |
| M11 | unit torque (N/m3) |
| N | the rotational speed of the turbine (r/min) |
| N11 | unit speed (m1/2/s) |
| N11r | rated unit speed (m1/2/s) |
| Q | the water flow rate (m3/s) |
| Qt | the flow of pump turbine (m3/s) |
| Q11 | unit flow (m1/2/s) |
| Q11r | rated unit flow (m1/2/s) |
| u | controller output signal (pu) |
| excitation voltage setting value of generator and motor (pu) | |
| d- and q-axis component of the voltage (pu) | |
| Y | guide vane opening (deg) |
| y | main servomotor output signal (pu) |
| ω, ω* | relative and given value angular shaft velocity (m) |
| the internal EMF of d- and q-axis (pu) | |
| rotor angle (rad) | |
Appendix A
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Rated speed (r/min) | 250 | Rated capacity (MVA) | 334 |
| Rated water-head (m) | 195 | Rated voltage (kV) | 15.75 |
| Rated water flow (m3/s) | 176.1 | Rated current (A) | 12,244 |
| Power rating (MW) | 306 | Rated frequency (Hz) | 50 |
| Turbine runner diameter (m) | 5.26 | Power factor | 0.90 |
| 100% guide-vane opening (°) | 43.01 | Moment of inertia (ton/m2) | 19,300 |
| Number | Length (m) | Diameter (m) | Wave Velocity (m/s) | Roughness |
|---|---|---|---|---|
| L1 | 1113.94 | 9.21 | 1100 | 0.014 |
| L2 | 206.71 | 8.97 | 1120 | 0.014 |
| L3 | 250.77 | 4.77 | 1204 | 0.011 |
| L4 | 173.52 | 6.90 | 1161 | 0.010 |
| L5 | 260.30 | 4.80 | 1204 | 0.011 |
| L6 | 173.52 | 6.89 | 1160 | 0.012 |
| L7 | 295.27 | 10.82 | 1050 | 0.014 |
| Sectional Area of the Impedance Hole (m2) | Inflow Loss Coefficient | Outflow Loss Coefficient | Sectional Area (m2) | Altitude (m) |
|---|---|---|---|---|
| 19.63 | 0.0009217 | 0.0006767 | 19.63 | 231.70~268.30 |
| 380.13 | 268.30~310.00 | |||
| 530.93 | 310.00~320.00 |
| Excitation System | Synchronous Machine | ||||
|---|---|---|---|---|---|
| Ta | 0.001 | Ra | 0.00125 | X’’d | 0.2 |
| Tb | 0 | Xd | 1.015 | X’’q | 0.195 |
| Tc | 0 | Xq | 0.627 | T’d0 | 12.6 |
| Te | 0 | X’d | 0.253 | T’’d0 | 0.189 |
| Tf | 0.1 | Tj | 10.8 | T’’q0 | 0.519 |
| Ka | 300 | Speed Regulation System | |||
| Ke | 1 | bp | 0.01 | k0 | 1 |
| Kf | 0.001 | Ty1 | 0.02 | Ty | 0.2 |
| Solutions | Kp | Ki | Kd | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000 | 61.1400 | 0.9805 | 0.6135 | 0.1923 | 3.4725 | 0.1000 | 5.1410 |
| 2 | 0.0000 | 60.9600 | 0.9881 | 0.6272 | 0.1924 | 3.5060 | 0.1000 | 4.9311 |
| 3 | 0.0001 | 60.8600 | 1.0098 | 0.6266 | 0.1932 | 3.4515 | 0.1000 | 5.0734 |
| 4 | 0.0002 | 60.3600 | 1.0188 | 0.5930 | 0.1938 | 3.6432 | 0.1000 | 5.2704 |
| 5 | 0.0003 | 60.2800 | 1.0329 | 0.6127 | 0.1942 | 3.5734 | 0.1000 | 5.1753 |
| 6 | 0.0003 | 60.2200 | 1.0125 | 0.6208 | 0.1945 | 3.5620 | 0.1000 | 5.3608 |
| 7 | 0.0003 | 60.0400 | 0.9989 | 0.6175 | 0.1944 | 3.5887 | 0.1000 | 5.1362 |
| 8 | 0.0004 | 59.8600 | 1.0071 | 0.5973 | 0.1949 | 3.5649 | 0.1000 | 5.1444 |
| 9 | 0.0005 | 59.7000 | 1.0080 | 0.6061 | 0.1954 | 3.3926 | 0.1000 | 4.9045 |
| 10 | 0.0006 | 59.3400 | 0.9943 | 0.6156 | 0.1964 | 3.5366 | 0.1000 | 5.3577 |
| 11 | 0.0007 | 59.2200 | 0.9977 | 0.6136 | 0.1962 | 3.4684 | 0.1000 | 4.9254 |
| 12 | 0.0007 | 59.1400 | 0.9970 | 0.6167 | 0.1970 | 3.4364 | 0.1000 | 5.1984 |
| 13 | 0.0008 | 59.0000 | 1.0160 | 0.6366 | 0.1971 | 3.5003 | 0.1000 | 5.0073 |
| 14 | 0.0009 | 58.8800 | 1.0035 | 0.6084 | 0.1968 | 3.3919 | 0.1000 | 4.6497 |
| 15 | 0.0010 | 58.6400 | 1.0143 | 0.6353 | 0.1984 | 3.3848 | 0.1000 | 5.1553 |
| 16 | 0.0010 | 58.5200 | 1.0118 | 0.6244 | 0.1980 | 3.3945 | 0.1000 | 4.7860 |
| 17 | 0.0011 | 58.4600 | 1.0115 | 0.6289 | 0.1988 | 3.3993 | 0.1000 | 5.1672 |
| 18 | 0.0012 | 58.1600 | 1.0112 | 0.6271 | 0.1997 | 3.3300 | 0.1000 | 5.1576 |
| 19 | 0.0012 | 57.8800 | 1.0027 | 0.6149 | 0.1999 | 3.4411 | 0.1000 | 5.2033 |
| 20 | 0.0015 | 57.7200 | 1.0255 | 0.6064 | 0.2001 | 3.2400 | 0.1000 | 4.5951 |
| 21 | 0.0016 | 57.2200 | 0.9945 | 0.6315 | 0.2014 | 3.3322 | 0.1000 | 4.9067 |
| 22 | 0.0018 | 57.0600 | 1.0057 | 0.6203 | 0.2022 | 3.2075 | 0.1000 | 4.8830 |
| 23 | 0.0018 | 56.8000 | 1.0073 | 0.6276 | 0.2028 | 3.3360 | 0.1000 | 5.0474 |
| 24 | 0.0020 | 56.7800 | 0.9945 | 0.6364 | 0.2038 | 3.3257 | 0.1000 | 5.1467 |
| 25 | 0.0020 | 56.7400 | 1.0045 | 0.6287 | 0.2029 | 3.1622 | 0.1000 | 4.6525 |
| Solutions | Kp | Ki | Kd | |||||
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0000 | 58.9400 | 0.6049 | 0.4437 | 0.1929 | 3.5941 | 0.1000 | 5.0779 |
| 2 | 0.0001 | 58.8800 | 0.5815 | 0.4172 | 0.1928 | 3.4206 | 0.1000 | 4.6254 |
| 3 | 0.0001 | 58.7200 | 0.5967 | 0.4302 | 0.1940 | 3.5515 | 0.1000 | 5.3448 |
| 4 | 0.0002 | 58.3600 | 0.6055 | 0.4150 | 0.1949 | 3.6035 | 0.1000 | 5.4766 |
| 5 | 0.0003 | 58.2200 | 0.5762 | 0.4380 | 0.1946 | 3.5755 | 0.1000 | 5.1809 |
| 6 | 0.0004 | 57.9400 | 0.5310 | 0.4862 | 0.1955 | 3.6367 | 0.1000 | 5.3869 |
| 7 | 0.0004 | 57.9200 | 0.5631 | 0.4490 | 0.1956 | 3.3992 | 0.1000 | 4.9775 |
| 8 | 0.0005 | 57.8800 | 0.5369 | 0.4775 | 0.1963 | 3.4578 | 0.1000 | 5.4568 |
| 9 | 0.0005 | 57.6000 | 0.5851 | 0.4409 | 0.1962 | 3.5772 | 0.1000 | 5.2510 |
| 10 | 0.0006 | 57.4600 | 0.5933 | 0.4596 | 0.1962 | 3.5212 | 0.1000 | 4.9430 |
| 11 | 0.0007 | 57.2600 | 0.6137 | 0.4421 | 0.1975 | 3.5201 | 0.1000 | 5.4057 |
| 12 | 0.0007 | 57.1400 | 0.5369 | 0.4708 | 0.1974 | 3.4673 | 0.1000 | 5.1295 |
| 13 | 0.0008 | 57.0000 | 0.5759 | 0.4408 | 0.1976 | 3.4549 | 0.1000 | 5.0178 |
| 14 | 0.0008 | 56.9400 | 0.5776 | 0.4511 | 0.1979 | 3.4562 | 0.1000 | 5.1085 |
| 15 | 0.0009 | 56.8600 | 0.5853 | 0.4415 | 0.1986 | 3.3694 | 0.1000 | 5.2359 |
| 16 | 0.0010 | 56.6200 | 0.5782 | 0.5092 | 0.1990 | 3.5058 | 0.1000 | 5.3278 |
| 17 | 0.0010 | 56.5000 | 0.5681 | 0.4310 | 0.1991 | 3.4715 | 0.1000 | 5.2946 |
| 18 | 0.0010 | 56.4200 | 0.5768 | 0.4593 | 0.1992 | 3.5151 | 0.1000 | 5.2587 |
| 19 | 0.0012 | 56.0000 | 0.5805 | 0.4346 | 0.2003 | 3.4980 | 0.1000 | 5.2770 |
| 20 | 0.0014 | 55.7800 | 0.5440 | 0.4646 | 0.2010 | 3.3650 | 0.1000 | 5.1138 |
| 21 | 0.0015 | 55.5800 | 0.5772 | 0.4403 | 0.2013 | 3.3715 | 0.1000 | 5.0147 |
| 22 | 0.0016 | 55.3200 | 0.5720 | 0.4422 | 0.2023 | 3.3496 | 0.1000 | 5.1389 |
| 23 | 0.0016 | 55.2200 | 0.5543 | 0.4567 | 0.2024 | 3.3941 | 0.1000 | 5.1392 |
| 24 | 0.0018 | 55.0600 | 0.5587 | 0.4434 | 0.2027 | 3.2578 | 0.1000 | 4.8341 |
| 25 | 0.0020 | 54.8600 | 0.5710 | 0.4508 | 0.2037 | 3.1818 | 0.1000 | 4.8972 |
References
- Zhang, Y.; Zang, W.; Zheng, J.; Cappietti, L.; Zhang, J.; Zheng, Y.; Fernandez-Rodriguez, E. The influence of waves propagating with the current on the wake of a tidal stream turbine. Appl. Energy 2021, 290, 116729. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Zheng, J.; Zhang, J.; Zheng, Y.; Zang, W.; Lin, X.; Fernandez-Rodriguez, E. Experimental investigation into effects of boundary proximity and blockage on horizontal-axis tidal turbine wake. Ocean Eng. 2021, 225, 108829. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Lin, X.; Wang, R.; Zhang, C.; Zhao, J. Experimental investigation into downstream field of a horizontal axis tidal stream turbine supported by a mono pile. Appl. Ocean Res. 2020, 101, 102257. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, Q.; Yan, D.; Liu, W. A two-stage numerical simulation framework for pumped-storage energy system. Energy Convers Manag. 2020, 210, 112676. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, Q.; Yan, D.; Zhang, H. Equivalent circuit modelling of large hydropower plants with complex tailrace system for ultra-low frequency oscillation analysis. Appl. Math. Model. 2021, 103, 176–194. [Google Scholar] [CrossRef]
- Feng, C.; Li, C.; Chang, L.; Ding, T.; Mai, Z. Advantage analysis of variable-speed pumped storage units in renewable energy power grid: Mechanism of avoiding S-shaped region. Int. J. Electr. Power Energy Syst. 2020, 120, 105976. [Google Scholar] [CrossRef]
- Zeng, W.; Yang, J.; Hu, J. Pumped storage system model and experimental investigations on S-induced issues during transients. Mech. Syst. Signal Process. 2017, 90, 350–364. [Google Scholar] [CrossRef]
- Wang, X.; Na, R. Simulation of asynchronous starting process of synchronous motors based on Matlab/Simulink. In Proceedings of the Sixth International Conference on Electrical Machines and Systems, ICEMS 2003 IEEE, Beijing, China, 9–11 November 2003; Volume 2, pp. 684–687. [Google Scholar]
- Wang, F.; Jiang, J. A novel static frequency converter based on multilevel cascaded H-bridge used for the startup of synchronous motor in pumped-storage power station. Energy Convers Manag. 2011, 52, 2085–2091. [Google Scholar] [CrossRef]
- Magsaysay, G.; Schuette, T.; Fostiak, R.J. Use of a static frequency converter for rapid load response in pumped-storage plants. IEEE Trans. Energy Convers. 1995, 10, 694–699. [Google Scholar] [CrossRef]
- Li, B.; Duan, Z.; Wu, J. Short-circuit analysis of pumped storage unit during back-to-back starting. IET Renew. Power Gener. 2015, 9, 99–108. [Google Scholar] [CrossRef]
- Konidaris, D.N. Investigation of back-to-back starting of pumped storage hydraulic generating units. IEEE Trans. Energy Convers. 2002, 17, 273–278. [Google Scholar] [CrossRef]
- Xu, Y.; Zhou, J.; Xue, X.; Fu, W.; Zhu, W.; Li, C. An adaptively fast fuzzy fractional order PID control for pumped storage hydro unit using improved gravitational search algorithm. Energy Convers. Manag. 2016, 111, 67–78. [Google Scholar] [CrossRef]
- Chaudhry, H. Applied Hydraulic Transients, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Osburn, G.D.; Atwater, P.L. Design and testing of a back-to-back starting system for pumped storage hydrogenerators at Mt. Elbert Powerplant. IEEE Trans. Energy Convers. 1992, 7, 280–288. [Google Scholar] [CrossRef]
- Rajamani, K.; Hariharan, M.V. Synchronous starting of synchronous machine. Electr. Mach. Power Syst. 1993, 21, 647–661. [Google Scholar] [CrossRef]
- Karmaker, H.; Mi, C. Improving the starting performance of large salient-pole synchronous machines. IEEE Trans. Magn. 2004, 40, 1920–1928. [Google Scholar] [CrossRef]
- Xiao, S.; Liu, J.; Kang, X. The coordination of Back-to-back starting and protections for pumped storage units. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4. [Google Scholar]
- Ghazvini, M.; Pourkiaei, S.M.; Pourfayaz, F. Thermo-economic assessment and optimization of actual heat engine performance by implemention of NSGA II. Renew. Energy Res. Appl. 2020, 1, 235–245. [Google Scholar]
- Beiranvand, A.; Ehyaei, M.A.; Ahmadi, A.; Silvaria, J.L. Energy, exergy, and economic analyses and optimization of solar organic Rankine cycle with multi-objective particle swarm algorithm. Renew. Energy Res. Appl. 2021, 2, 9–23. [Google Scholar]
- Sabbagh, O.; Fanaei, M.A.; Arjomand, A.; Ahmadi, M.H. Multi-objective optimization assessment of a new integrated scheme for co-production of natural gas liquids and liquefied natural gas. Sustain. Energy Technol. Assess. 2021, 47, 101493. [Google Scholar] [CrossRef]
- Pourkiaei, S.M.; Pourfayaz, F.; Mehrpooya, M.; Ahmadi, M.H. Multi-objective optimization of tubular solid oxide fuel cells fed by natural gas: An energetic and exergetic simultaneous optimization. J. Therm. Anal. Calorim. 2021, 145, 1575–1583. [Google Scholar] [CrossRef]
- Xu, Y.; Zheng, Y.; Du, Y.; Yang, W.; Peng, X.; Li, C. Adaptive condition predictive-fuzzy PID optimal control of start-up process for pumped storage unit at low head area. Energy Convers. Manag. 2018, 177, 592–604. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L.; Suo, L. Fluid transients in systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Chaudhry, M.H. Characteristics and Finite-Difference Methods. In Applied Hydraulic Transients; Springer: New York, NY, USA, 2014; pp. 65–113. [Google Scholar]
- Lai, X.; Li, C.; Zhou, J.; Zhang, N. Multi-objective optimization of the closure law of guide vanes for pumped storage units. Renew. Energy 2019, 139, 302–312. [Google Scholar] [CrossRef]
- Machowski, J.; Lubosny, Z.; Bialek, J.W. Power System Dynamics: Stability and Control; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Grigsby, L.L. Power System Stability and Control; CRC press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Yang, W.; Norrlund, P.; Bladh, J.; Yang, J.; Lundin, U. Hydraulic damping mechanism of low frequency oscillations in power systems: Quantitative analysis using a nonlinear model of hydropower plants. Appl. Energy. 2018, 212, 1138–1152. [Google Scholar] [CrossRef]
- Zhao, L.; Gong, Z.S. Application of ABB F series excitation regulator in synchronous motor. Electr. World 2006, 47, 1–5. (In Chinese) [Google Scholar]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1051–1056. [Google Scholar]
- Sheikholeslami, F.; Navimipour, N.J. Service allocation in the cloud environments using multi-objective particle swarm optimization algorithm based on crowding distance. Swarm Evol. Comput. 2017, 35, 53–64. [Google Scholar] [CrossRef]
- Hou, J.; Li, C.; Guo, W.; Fu, W. Optimal successive start-up strategy of two hydraulic coupling pumped storage units based on multi-objective control. Int. J. Electr. Power Energy Syst. 2019, 111, 398–410. [Google Scholar] [CrossRef]
- Qu, B.Y.; Suganthan, P.N. Constrained multi-objective optimization algorithm with an ensemble of constraint handling methods. Eng. Optim. 2011, 43, 403–416. [Google Scholar] [CrossRef]
- Song, H.Z. A method based on objective adjacent scale for multi-objective decision-making and its application. Math. Pract. Theory 2004, 5, 30–36. [Google Scholar]




| Unit Number | Category | Maximum Pressure at Measuring Point of Volute Inlet | Minimum Water Pressure at MEASURING Point of Draft Tube | Maximum Speed |
|---|---|---|---|---|
| 1# | Measurement | 299.32 m | 26.6 m | 140% |
| Refined model | 297.05 m | 27.9 m | 136% | |
| Absolute error | −2.27 m | 1.3 m | −4% | |
| Relative error | −0.75% | 4.88% | 2.85% |
| Initial Rotor Angel Difference (°) | Start Time of Speed Rise (s) | Rotor Angle Difference at Steady State (°) | Description of BTBS |
|---|---|---|---|
| 0 | 3 | 17.66 | Successful start; Slight oscillation |
| −90 | 8 | 19.24 | Successful start; Slight oscillation |
| −180 | 10 | 20.89 | Successful start; Moderate oscillation |
| −270 | 10 | 21.19 | Successful start; Moderate oscillation |
| Decision Variables | Boundaries | Values | |||||
|---|---|---|---|---|---|---|---|
| X1 | L1 | 0.1 | 0.1 | 0.1 | 1 | 0.1 | 0 |
| U1 | 2.0 | 2.0 | 0.4 | 6 | 1 | 6 | |
| X2 | L2 | 0.1 | 0.1 | 0.1 | 1 | 0.1 | 0 |
| U2 | 2.0 | 2.0 | 0.4 | 6 | 1 | 6 |
| Schemes | |||
|---|---|---|---|
| MOCEC | (0.90, 0.10) | (0.53, 0.47) | (0.91, 0.09) |
| MOCEV | (0.90, 0.10) | (0.63, 0.36) | (0.94, 0.06) |
| Schemes | SOCEC | SOCEV | MOCEC | MOCEV | |
|---|---|---|---|---|---|
| Variables | |||||
| 1.2331 | 0.6599 | 0.9881 | 0.6049 | ||
| 0.7422 | 0.5413 | 0.6272 | 0.4437 | ||
| yc | 0.3985 | 0.3976 | 0.1924 | 0.1929 | |
| Kp | 3.9083 | 4.6298 | 3.5060 | 3.5941 | |
| Ki | 0.3630 | 0.3900 | 0.1000 | 0.1000 | |
| Kd | 0.3190 | 0.7031 | 4.9311 | 5.0779 | |
| Schemes | SOCEC | SOCEV | MOCEC | MOCEV | |||||
|---|---|---|---|---|---|---|---|---|---|
| Indexes | PSU-1 | PSU-2 | PSU-1 | PSU-2 | PSU-1 | PSU-2 | PSU-1 | PSU-2 | |
| 0.0515 | 0.0518 | 0.0468 | 0.0472 | 2.7796 × 10−5 | 4.1466 × 10−5 | 8.7973 × 10−6 | 2.2633 × 10−5 | ||
| tr (s) | 28.20 | 28.18 | 26.84 | 26.82 | 50.74 | 50.74 | 48.86 | 48.84 | |
| ts (s) | 90.68 | 90.68 | 99.30 | 99.30 | 60.98 | 60.94 | 59.00 | 58.98 | |
| Working Conditions | Water Level | Water Head (m) | |
|---|---|---|---|
| Upstream (m) | Downstream (m) | ||
| N0 | 291 | 106 | 185 |
| N1 | 295 | 105 | 190 |
| N2 | 298 | 103 | 195 |
| N3 | 303 | 103 | 200 |
| N4 | 303 | 98 | 205 |
| N5 | 308 | 98 | 210 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, C.; Li, G.; Zheng, Y.; Zhou, D.; Mai, Z. Multi-Objective Optimization of Back-to-Back Starting for Pumped Storage Plants under Low Water Head Conditions Based on the Refined Model. Sustainability 2022, 14, 10289. https://doi.org/10.3390/su141610289
Feng C, Li G, Zheng Y, Zhou D, Mai Z. Multi-Objective Optimization of Back-to-Back Starting for Pumped Storage Plants under Low Water Head Conditions Based on the Refined Model. Sustainability. 2022; 14(16):10289. https://doi.org/10.3390/su141610289
Chicago/Turabian StyleFeng, Chen, Guilin Li, Yuan Zheng, Daqing Zhou, and Zijun Mai. 2022. "Multi-Objective Optimization of Back-to-Back Starting for Pumped Storage Plants under Low Water Head Conditions Based on the Refined Model" Sustainability 14, no. 16: 10289. https://doi.org/10.3390/su141610289
APA StyleFeng, C., Li, G., Zheng, Y., Zhou, D., & Mai, Z. (2022). Multi-Objective Optimization of Back-to-Back Starting for Pumped Storage Plants under Low Water Head Conditions Based on the Refined Model. Sustainability, 14(16), 10289. https://doi.org/10.3390/su141610289