1. Introduction
The transportation industry is the basic industry of the national economy. Sound construction and development of the transportation industry will help realize economic connectivity and sustainable economic growth [
1,
2]. After China’s reform and opening up, the transportation industry has been developing rapidly with the support of policies and funds, and a well-developed transportation system can help improve regional economic development [
3]. In recent years, road transportation and railway transportation have occupied an increasingly important position in the current transportation system of their own advantages. In terms of infrastructure, by the end of 2021, the total operating mileage of the National Railways exceeded 150,000 km, including 40,000 km of high-speed railways. The rate of railroad duplication was 59.5%, and the electrification rate was 73.3%. The density of the national railroad road network was 156.7 kilometers per 10,000 square kilometers. The total mileage of highways reached 5,280,700 kilometers, an increase of 82,600 kilometers over the end of the previous year. The road density was 55.01 km/100 km², an increase of 0.86 km/100 km². The road maintenance mileage was 5.2516 million kilometers, accounting for 99.4% of the total road mileage. In terms of passenger and cargo volume, railway transportation completed 2.612 billion passengers throughout the year, an increase of 18.5% over the previous year, and completed 956.781 billion passenger kilometers, an increase of 15.7%. The annual total cargo delivery volume was 4.774 billion tons, an increase of 4.9% over the previous year, and the total cargo turnover was 3323.8 million ton-kilometers, an increase of 8.9%. Road transportation completed 5.087 billion business passenger transportation in the whole year, a decrease of 26.2% over the previous year, and completed 362.754 billion person-kilometers, a decrease of 21.8%. The annual business freight was 39.139 billion tons, an increase of 14.2% over the previous year, to complete the cargo turnover of 690,865 million ton-kilometers, an increase of 14.8%. The annual average transportation volume of motor vehicles for the year was 14,993 vehicles per day, an increase of 4.9% over the previous year, and the annual average travel volume was 348,692,000 vehicle kilometers per day, an increase of 3.6% [
4].
According to the above data, inter-regional passenger transportation has increased, and the transportation demand has been growing [
5]. The demand for transportation promotes economic development, but the rapid expansion of market capacity also intensifies market competition. This has led to excessive differences in transport volumes undertaken by various modes of transportation, resulting in an imbalanced transportation structure. The unreasonable transportation structure indirectly increases additional economic expenditure. Some urban transportation is not combined with local resources, and the output value contribution is not high, which may be the reason for the wide gap in economic development between regions. China’s Fifth Plenary Session of the 19th Central Committee proposed accelerating the construction of a strong transportation country to promote the optimization and upgrading of the economic system. At the same time, it is also proposed to accelerate coordinated regional development, encourage the eastern region to speed up modernization, promote the rise of the central region and accelerate the development of the western region. Therefore, under the background of the rapid development of the national economy and transportation industry, how to effectively measure the transportation efficiency of the eastern, central and western regions and analyze the impact of transportation-related factors on regional economic development and economy has become an urgent problem to be discussed at this stage [
6].
The issue of transportation efficiency has attracted the attention of researchers with the rapid development of the transportation industry [
7,
8]. The efficiency of transportation is one of the important symbols to measure the regional transportation structure and the level of regional economic development [
9]. Through the study of transportation efficiency, we can analyze the investment and development direction of the transportation industry, which is of high guiding significance to improving the efficiency of transportation resource utilization [
9,
10]. The traditional data envelopment analysis (DEA) is widely used by scholars at home and abroad as a tool to evaluate the efficiency of transportation, which is essentially an evaluation of the relative effectiveness among decision-making units (DMUs) with multiple inputs and outputs. The main feature is that there is no need to assign relative weights to input and output indicators, which is free from the constraints of subjectivity in evaluation, so the DEA method can reflect the actual objective state in which the decision units are located. Due to the statistical errors and environmental factors in the traditional DEA method, Fried et al. [
11] developed a three-stage data envelopment analysis method. The three-stage data envelopment analysis (DEA) method can effectively remove environmental effects and statistical noise and has been widely used for efficiency analysis in various industries, such as hotel management [
12], the banking industry [
13], manufacturing industry [
14], education industry [
15], sports industry [
16], urban construction industry [
17] and transportation industry [
18,
19].
The transportation industry has experienced a variety of development modes in different stages of economic development, and the comprehensive transportation system structure also presents different characteristics. There are also differences in the allocation efficiency of transportation resources and the comprehensive transportation service level in each stage [
20]. The development of the comprehensive transportation system in developed countries has a distinct trend of gradual increment, and the main problem to be solved is how to allocate it. In contrast, China’s transportation industry is in a stage of rapid development, and all modes of transportation have greater room for development, so how to reasonably allocate the existing resources and how to coordinate the development of each mode of transportation is the most important problem to be solved in the development of China’s transportation industry at present. Promoting the reasonable division of labor and collaboration of various modes of transportation and improving the efficiency of the comprehensive transportation system are urgently needed to realize the optimal allocation of transportation resources, improve the structural system of the transportation industry and enhance the level of comprehensive transportation services. This requires us to conduct a comprehensive and systematic analysis of the evolution characteristics of the structure of China’s comprehensive transportation system and make an accurate assessment of the current stage of China’s comprehensive transportation structure. The result of transportation activities is the spatial displacement of people or goods, while the transportation volume is the measurement of the final product and the final embodiment of the interaction results of transportation resources. Due to the different industrial characteristics of passenger and freight transportation, the combined volume of passenger and freight transportation is chosen to measure the structure of the comprehensive transportation system in this paper.
The regional economy refers to the total value of the national economy distributed in each administrative region and is the general term for the interconnectedness of social production sectors, distribution sectors and other economic sectors constituted in the administrative region [
21,
22]. The development of the regional economy is inseparable from the support of the transportation industry, and the development of the regional economy will also promote the development of the transportation industry. As China’s economy shifts from high growth to high-quality development, the objective requirement is for each industry’s development direction and industrial structure to be more reasonable and balanced. The panel vector autoregressive model is widely used to study the correlation and influence degree between multiple variables. Based on the random coefficients panel vector autoregressive model, Mou and Wang [
23] conducted an empirical study on the impact of fiscal and monetary policies on employment and economic growth in 24 developed countries. Chen et al. [
24] conducted an empirical study on the relationship between technology selection, industrial structure upgrading, and economic growth based on the semi-parametric spatial panel vector autoregressive model. At present, there are many types of research on the relationship between multiple variables by using the panel vector autoregressive model, but there is little research on the relationship between the regional economy and other variables, especially the relationship between the transportation industry and regional economic development.
In summary, this paper uses the three-stage data envelopment analysis method to assess the efficiency of the transportation industry [
25,
26,
27]. With the help of information entropy theory, the equilibrium degree of the existing transportation structure is analyzed. Finally, from the point of view of coordinated development, the PVAR model is used to comprehensively analyze the relationship and influence of the degree of transportation efficiency, transportation structure, and regional economic development to promote the realization of high-quality, sustainable development of the transportation system and economy.
The contents of this study are as follows: firstly, we briefly introduce the advanced research and theoretical knowledge related to transportation efficiency, transportation structure, and regional economic development. Then, we introduce the corresponding measurement and evaluation methods and indicators for each variable in this paper, as well as present the data sources and data descriptions after analyzing the corresponding data and empirical studies. Finally, we put forward the conclusion, including research contributions, policy recommendations, research limitations, and future research directions.
The research objectives of this paper are as follows: (1) to analyze the current situation and trends of the development of the transportation industry in 28 provinces and cities in China, as well as the reasons for this current situation, using a combination of qualitative and quantitative analysis methods; (2) to introduce the concepts of structure information entropy and structural equilibrium of a comprehensive transportation system with the help of information entropy theory and to realize the most reasonable development direction of the transportation industry by studying the evolution characteristics and trends of structural equilibrium of comprehensive transportation; (3) to analyze the relationship between transportation efficiency, transportation structure and regional economic development through the panel vector autoregressive model, analyze the interrelationship and degree of influence and propose suggestions and directions for improvement.
The innovation of this paper is mainly reflected in the following aspects.
- (1)
There are few studies on the transportation industry, especially on transportation efficiency and transportation structure in China. Based on previous studies in the transportation industry, this study selects more appropriate input, output, and environmental variables from the real environment. Since the DEA model cannot directly eliminate random errors and external factors, an SFA regression analysis is needed to strip the external factors and noise from the solution results. The improved three-stage DEA model is used to better remove the external environmental factors and make the analysis results more accurate.
- (2)
The existing studies on the comprehensive transportation system are only qualitative studies on the scale quantity and proportional relationship. This paper introduces the concepts of information entropy and the equilibrium degree of the structure of a comprehensive transportation system with the help of information entropy theory. By studying the randomness and disorder degree of the comprehensive transportation system structure and the conversion efficiency between various transportation modes, we analyze the evolution characteristics and trends of the structure of China’s comprehensive transportation system and evaluate and analyze the structure of the comprehensive transportation system from both qualitative and quantitative aspects.
- (3)
The existing domestic and foreign scholars’ studies on the relationship between the transportation industry and economic development have only focused on the exploration of the relationship between infrastructure or a single mode of transportation and economic development and have not considered the internal factors of the transportation system. Therefore, this paper is an innovative approach to analyzing the interrelationship between transportation efficiency, transportation structural equilibrium, and regional economic development from the perspective of coordination by using a panel vector autoregressive model (PVAR).
3. Research Methods
3.1. Data Collection
The data source used in this study is the National Bureau of Statistics of China and the
National Statistical Yearbook [
43], as well as the
Provincial and Municipal Statistical Yearbook revised by the provincial statistical bureaus. The timespan of sample selection is 2011–2020. Due to the lack of original data in some provinces, only 11 provinces and cities in eastern China (Beijing, Tianjin, Hebei, Shandong, Liaoning, Jiangsu, Shanghai, Zhejiang, Fujian, Guangdong, and Hainan), 8 provinces in Central China (Shanxi, Jilin, Henan, Anhui, Heilongjiang, Hubei, Hunan, and Jiangxi), and 9 provinces and regions in Western China (Neimenggu, Guangxi, Chongqing, Sichuan, Guizhou, Yunnan, Shaanxi, Gansu, and Qinghai) are selected. The data from the National Bureau of Statistics and the
National Statistical Yearbook are more complete, and the official statistics are highly accurate and authoritative, which can guarantee the accuracy of the analysis results. The specific analysis process is as follows in
Figure 1.
3.2. Evaluation of Transportation Efficiency
In the empirical analysis, a modified three-stage DEA-CCR model was used. The DEA-CCR model was proposed by Charnes and Cooper in 1978 [
44]. The model method projects the decision-making unit (DMU) onto the frontier through linear programming and judges its relative effectiveness according to the distance between the DMU and the frontier [
24,
37]. Compared with the traditional DEA model, the three-stage DEA model considers the influence of external environmental factors and random errors and can evaluate transportation efficiency more accurately [
45]. The specific process is as follows:
In the first stage, the DEA-CCR model is used to evaluate the initial efficiency. Let be the input vector of a DMU, be the multiple output vectors corresponding to that DMU, and use , to represent the whole economic activity of all DMUs.
Assuming that there are
n DMUs and m input indicators, the model can be built as follows:
are the actual observations of input and output indicators, either cross-sectional, time-series, or panel data.
θ is the optimal value of the objective function;
λj is the optimal solution. To further analyze input redundancy and output deficiency, slack variables
s+ for inputs and
s− for outputs are introduced.
Based on the model, the output deficiency rate and input redundancy rate of ineffective DMUs can be further analyzed to find the direction of production adjustment and provide theoretical support to further improve industrial efficiency. The efficiency of each DMU can be evaluated using the results calculated by the CCR model. The evaluation rules are as follows:
If is DEA efficiency. The input redundancy rate and output deficiency rate are both equal to 0, i.e., there is no input redundancy and output deficiency.
If is a weak DEA efficiency, which is the presence of input redundancy or output deficiency.
If is DEA inefficiency; there are input redundancies and output shortfalls at this point.
When
is a DEA inefficiency, its input redundancy rate and output deficiency rate can be calculated. Let this input redundancy be
and the output deficiency be
is the solution of the linear programming model, and
is the objective value of the DEA effective for evaluated DMUs. At this point, the input redundancy
and the output deficiency
can be expressed, respectively, as:
Thus, the input redundancy rate and output deficiency rate can be calculated as follows:
In the second stage, the SFA model is used to regress first-stage performance measures against a set of environmental variables. The second stage of the SFA model allows the slack variables to be obtained from the first stage DEA [
11,
46]. The slack variable is used as the explanatory variable to separate the effects of environment and random error factors on the efficiency value, and the SFA regression model is constructed:
where
is the input slack variable;
is the external environmental variable;
is the parameter to be estimated for the external environmental variable, and
denotes the stochastic frontier function of the effect of environmental variables on input slack; and
and
denote the random error term and management inefficiency, respectively, both of which are mixed error terms. The purpose of a regression analysis is to remove the effects of environmental variables and random errors, adjust all decision units to the equivalent external environmental situation, and obtain the adjusted inputs after separating the environmental factors and random factors obtained. The adjustment formula is as follows:
where
is the adjusted input variable;
is the input variable before the adjustment;
and
respectively, represent the adjustment of external environment variables and random error terms, and all units are adjusted to the same environment.
In the third stage, the DEA-CCR model is used again to evaluate the transportation efficiency of the adjusted input indicators. As the input and output indicators are under the same external environment, the efficiency value calculated will be more accurate than the efficiency value obtained using the DEA model alone.
3.3. Evaluation of Transportation Structure
The structure of the transportation system can be described and measured mainly by the structure of technology, personnel, investment, transportation capacity, and transportation volume. The result of transportation activities is the spatial displacement of passengers or cargoes, while the transportation volume is the measurement of the final product and the final embodiment of the interaction results of transportation resources, so this paper mainly selects transportation volume to measure the structure of a comprehensive transportation system.
Transportation volume is measured by two indicators: volume and turnover. However, since the average distance of various modes of transportation varies, the size of the volume does not truly reflect the capacity of various modes of transportation, so it is difficult to accurately reflect the structure of a comprehensive transportation system through the transportation volume index. Turnover is the product of the number of passengers or tons of cargo carried and the distance traveled in a certain period [
43,
47,
48]. Turnover reflects not only the transportation volume but also the transportation distance. It is an important indicator to reflect the quantity of transportation products. Therefore, this paper selects turnover as the measurement indicator of transportation volume [
49].
Due to the different industrial characteristics of passenger and freight transportation, this paper converts passenger kilometer (
PK) and freight turnover (
FT) in the ratio of 10:1 and 1:1, respectively. The sum of the two is combined turnover (
CT). The unit is 100 million-tons kilometers. The formula is:
Based on the above discussion, assuming that the total conversion turnover is a conversion turnover of various transportation modes
A1,
A2, …,
An, and there are
, the proportions of various transportation modes are
P1,
P2, …,
Pn, where
Pi =
Ai/
A, and
. Thus, it can be concluded that the information entropy of the comprehensive transportation system structure is:
The level of information entropy can reflect the degree of stability of the comprehensive transportation system structure. When
P1 = 1, the value of information entropy is the smallest,
Hmin = 0. When
A1 =
A2 = … =
An,
P1 =
P2 = … =
Pn = 1/
n, the value of information entropy is the largest,
Hmax = lgn. Additionally, information entropy will generally be between the two; a good dissipative system state should be in order and chaos [
50,
51].
According to the definition of equilibrium degree in the information entropy theory, combined with the above discussion of the information entropy of the comprehensive transportation structure, the structural equilibrium degree of the transportation system can be expressed as:
B represents the transportation structure equilibrium degree, which is the ratio between the information entropy of the comprehensive transportation structure and the maximum information entropy, and B ∈ [0, 1]. The greater the combined equilibrium of the transportation system, the better the equilibrium of structure, the smaller the relative gap between various modes of transportation and the more reasonable the development of each mode of transportation.
3.4. Panel Vector Autoregressive Model
The panel vector autoregressive model (PVAR) was first proposed by Douglas Holtz Eakin [
52]. This model follows the strengths of the vector autoregression (VAR) model proposed by Sims [
53]. It does not require a causal relationship between variables in advance but rather treats each variable as an endogenous variable and analyzes the effect of each variable and its lag on the other variables in the model. The PVAR model could not only reduce the required length of time series but also capture the impact of individual heterogeneity on model parameters. The PVAR model analyzes the current and future effects of an endogenous variable on itself and other endogenous variables, thus reflecting the dynamic relationship between the variables comprehensively [
54]. Love, Inessa, and Lea [
55,
56] and Lian and Su [
57] improved the panel vector autoregressive model. In this paper, the PVAR model proposed by Love and Lian Yujun is used to select the three variables of China’s transportation efficiency, transportation structure equilibrium degree, and regional economic development, which correspond to the panel data from 2011 to 2020. According to the principle of the VAR model, the PVAR model can be established:
where
is the explained variable and
is the regression coefficient;
is the difference between the
th individual and other individuals;
is the time point effect of individual
;
is the residual term that obeys the normal distribution.
5. Conclusions
5.1. Research Summary
Based on the previous research, this paper takes the panel data of 28 provinces in China from 2011 to 2020 as a sample to evaluate and analyze the correlation and impact of transportation efficiency, transportation structure, and regional economic development in these regions.
First, the results of the three-stage DEA model are as follows. (1) In the first stage, the overall trend of the average comprehensive transportation efficiency of 28 provinces in China from 2011 to 2020 was to increase first and then decrease. The fluctuation range of the national comprehensive transportation efficiency is small, indicating that there is a big gap in the development level of the transportation industry in various regions of China. (2) In the third stage, 20 provinces have an increasing trend in the value of comprehensive transportation efficiency. This shows that after excluding the influence of factors such as the external environment and random disturbances, the resource allocation of the transportation industry in all regions is gradually rationalized, and all inputs play a better role. (3) From the perspective of the three economic regions, transportation efficiency is highest in the eastern region, followed by the central region, and it is lowest in the western region. In the third stage, the efficiency values of the central and western regions increase significantly, which indicates that environmental variables have a great influence on the development of the transportation industry in the central and western regions.
Second, the average value of the equilibrium degree of China’s comprehensive transportation structure from 2011 to 2020 is very stable, at around 0.75. This indicates that from a national perspective, the national transportation structure has not changed much from 2011 to 2020, the share of major transportation modes in each province is almost unchanged, and each region develops its regional transportation industry reasonably according to the resources and advantages of their respective regions.
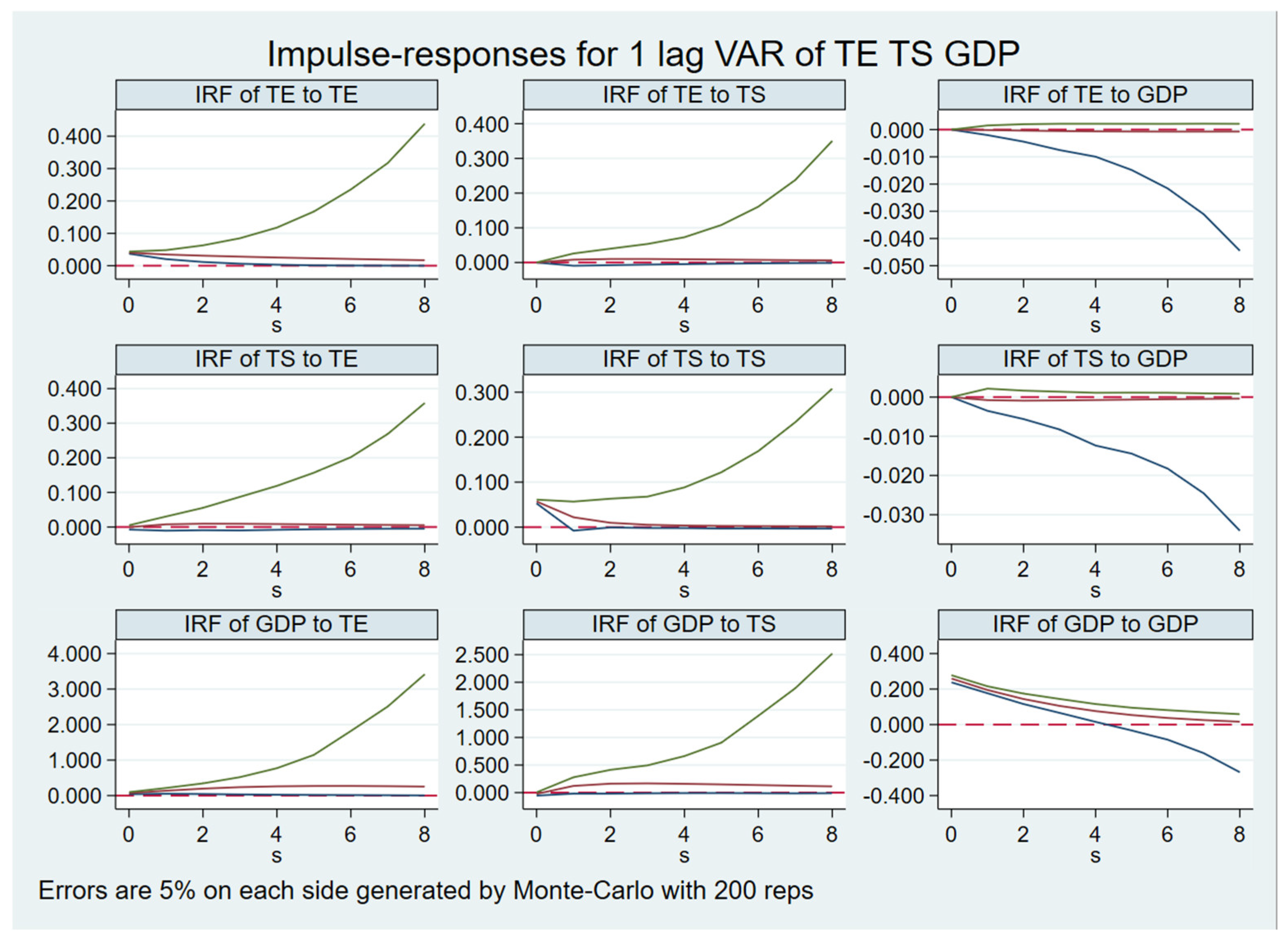
Third, the results of the relationship between transportation efficiency, transportation structure, and regional economic development are as follows: (1) transportation efficiency and transportation structure have a mutual promotion effect in the short term, but both are most influenced by themselves; (2) regional economic development has a long-term role in promoting transportation efficiency and structure improvement; (3) there is a two-way promotion effect between transportation efficiency, transportation structure and regional economic development. Among them, the level of transportation efficiency plays a leading role in regional economic development.
5.2. Discussion
In previous studies on the transportation industry, transportation efficiency has been used as a separate dimension to construct studies [
3,
8,
9,
29]. In our study, we found that transportation efficiency does not fully show the development of the transportation industry. Therefore, we introduced the concept of transport structural equilibrium to compensate for the deficiency of transport efficiency in measuring the development of the industry [
34,
35]. The results show that the combination of transport efficiency and transport structural balance can more fully reflect the development of the transportation industry [
20,
33,
49]. In the validation of the relationship between transport efficiency, transport structural equilibrium and regional economic development, the results indicate that transport efficiency is positively related to transport structural equilibrium, and regional economic development is positively related to the transport sector. These results support the previous study [
6,
62,
63,
64]. The results also provide new findings that transport efficiency plays a dominant role in regional economic development. This is supported by the empirical evidence that the efficiency level of the transportation industry is crucial to regional economic development.
5.3. Policy Recommendations
According to the current situation of each region, plans suitable for each region should be formulated to promote the coordinated development of the transportation system. From the perspective of transportation and economic development in all provinces, the overall development of the western region started late, so it is necessary to make up for its shortcomings according to its situation. The central region, as the core area connecting the east, west, north and south regions, needs to improve the channel capacity connecting the north and the south and connecting the east and the west. This should include accelerating the construction of key transportation projects in the central region and promoting the development of transportation. The eastern region needs to further optimize its transportation structure, create a synergistic transportation system, and strengthen cooperation with the central and western regions to strengthen inter-regional transportation and economic ties, enhance overall development, and enable coordinated development in all regions.
In terms of transportation efficiency, regions with unformed transportation systems need to improve their transportation development and increase investment in transportation infrastructure. Regions with more mature transportation systems should strengthen their hub functions, promote more efficient development of the transportation industry, and strengthen inter-regional cooperation to drive the reform and development of the transportation system in regions with less developed transportation systems.
In terms of transportation structure, the transportation configuration should be adjusted to reduce energy consumption and increase transportation supply. In the case of the surplus capacity of various modes of transportation, wasting resources should be avoided due to the excessive load of a single mode of transportation. In order to meet the increasing demand for transportation, it is also necessary to strengthen the reform of the transportation industry, improve the quality of all types of transportation services and optimize their organizational structure, improve the construction of comprehensive transportation hub infrastructure, and promote the reasonable and balanced development of all modes of transportation.
In terms of policy, we should avoid negative effects according to market demand. In some areas, the development of the transportation industry is too radical or seriously insufficient in the process of urbanization. In the process of policy formulation, it is necessary to fully consider the characteristics of its region and formulate its development direction. The development of transportation needs to be adjusted at any time according to social and economic development. It is not ideal to blindly pursue the equilibrium of transportation structure, which will lead to its advantages not being realized and affect economic development.
5.4. Limitations and Future Research
This paper mainly measures the transportation efficiency of 28 regions in China, analyzes the overall efficiency of the transportation industry in 28 provinces in China, and further analyzes the correlation and degree of influence between transportation efficiency, transportation structure, and regional economic development in 28 provinces in China. This paper adopts the method of empirical analysis, and the limitations mainly come from the collection and acquisition of data, the choice of research method, and the academic ability of the authors. The development of the transportation industry has promoted the development of society, but it has also created some environmental problems. Because of the limitation of data, transportation efficiency does not consider undesirable output variables. Therefore, there are some shortcomings in this paper, and we hope to further explore the following aspects in the future.
In the selection of the transportation efficiency evaluation model, the subsequent analysis can be tried by choosing the super-efficient SBM model, which considers the non-desired output. In addition to the DEA model, there are gray evaluation methods, fuzzy integrated evaluation methods, indicator evaluation methods, stochastic frontier methods, etc. There is no comparative study on these evaluation methods, so it is necessary to further analyze the advantages and disadvantages of these methods and select the most suitable evaluation method.
In the selection of efficiency evaluation indicators, only three input indicators and three output indicators were selected for the evaluation indicators of transportation efficiency. In the second stage, only three environmental variables were selected. Due to the differences in transportation environment and economy in each region, the results differed using the same residual coefficients to calculate the variables. Therefore, in future research, more reasonable evaluation indicators can be constructed in conjunction with the actual situation.
For some of the evaluation indicators selected for transportation efficiency, the data after 2020 have not yet been published and cannot completely reflect the current situation. This leads to a lack of continuity and validity of the data used in this paper, which can further deepen the study in the future.
For the indicators to measure the equilibrium of transportation structure, passenger turnover and cargo turnover are selected, and the evaluation indicators should be selected more comprehensively in future research.
In the panel vector autoregressive model, the selected variables are transportation efficiency, transportation structure equilibrium, and regional economic development. The relationship and influence of these variables have certain limitations. In future research, we can combine the previous research with the actual situation to build a more reasonable evaluation index and add some more representative variables.