Integration of Supercritical CO2 Recompression Brayton Cycle with Organic Rankine/Flash and Kalina Cycles: Thermoeconomic Comparison
Abstract
:1. Introduction
2. System Description and Assumptions
- Use of a dry working fluid is suggested for preventing turbine blade erosion [29]. This characteristic suggests having a superheated outflow from the turbine.
- A working fluid with high critical temperature and low critical pressure is recommended. A low critical pressure provides the opportunity for a superheated outflow from the turbine with low heat input.
- (1)
- The systems operate under steady state conditions.
- (2)
- Pressure drops in all heat exchangers and pipelines are negligible.
- (3)
- Turbines, pumps and compressors have constant isentropic efficiencies.
- (4)
- Changes in kinetic and potential energies are negligible.
- (5)
- The cooling water enters the pre-cooler and condenser at ambient temperature and pressure.
- (6)
- At the heater and condenser outlets, the working fluid is in a saturated liquid state [33].
- (7)
- The HTR and LTR have constant effectiveness values.
- (8)
- At the outlets of the separator and condenser, the ammonia-water mixture is in a saturated liquid state.
3. Modeling and Analysis
3.1. Thermodynamic Analysis
3.2. Thermoeconomic Analysis
3.3. Sustainability Analysis
4. Results and Discussion
4.1. Validation
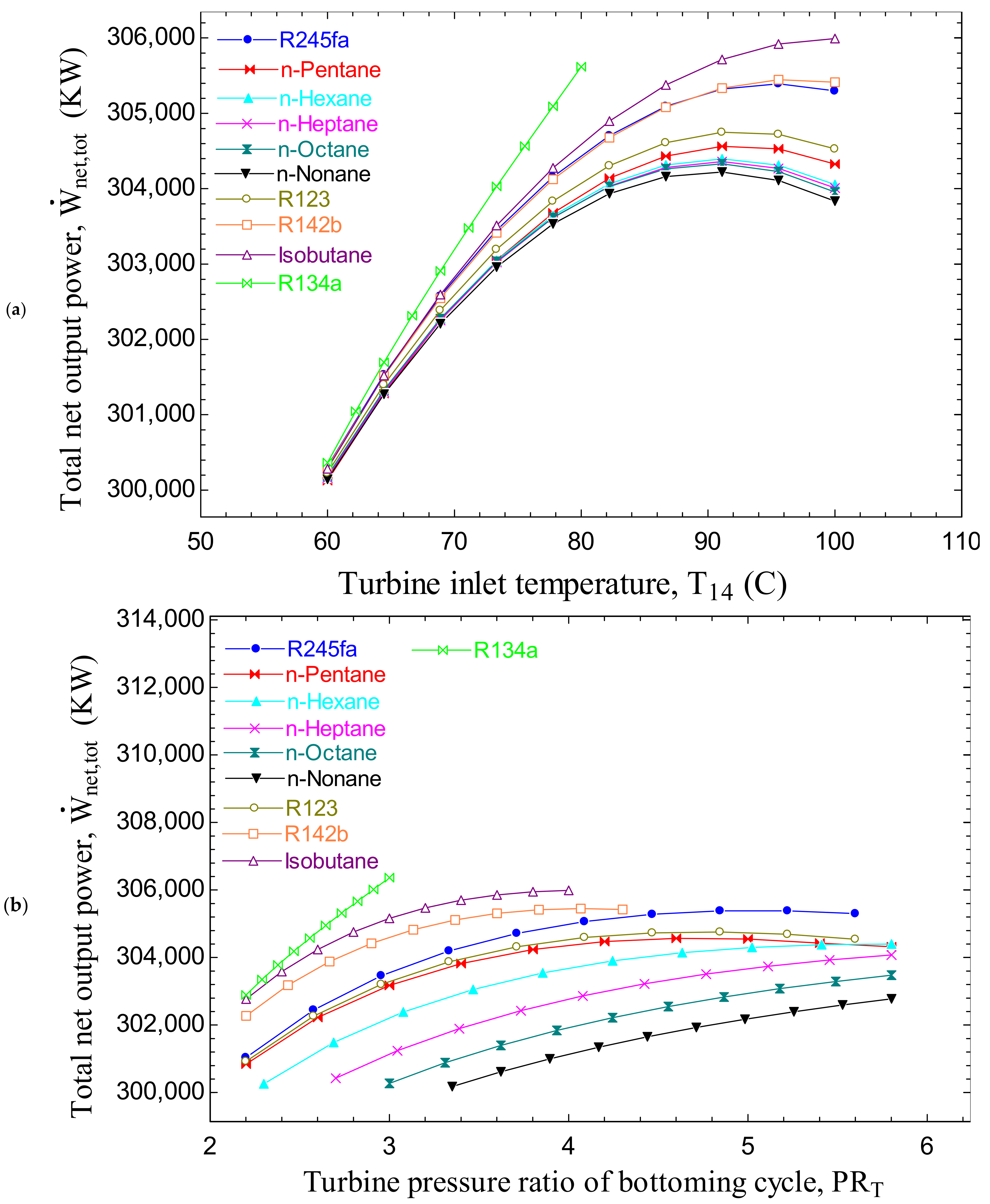
4.2. Working Fluid Selection
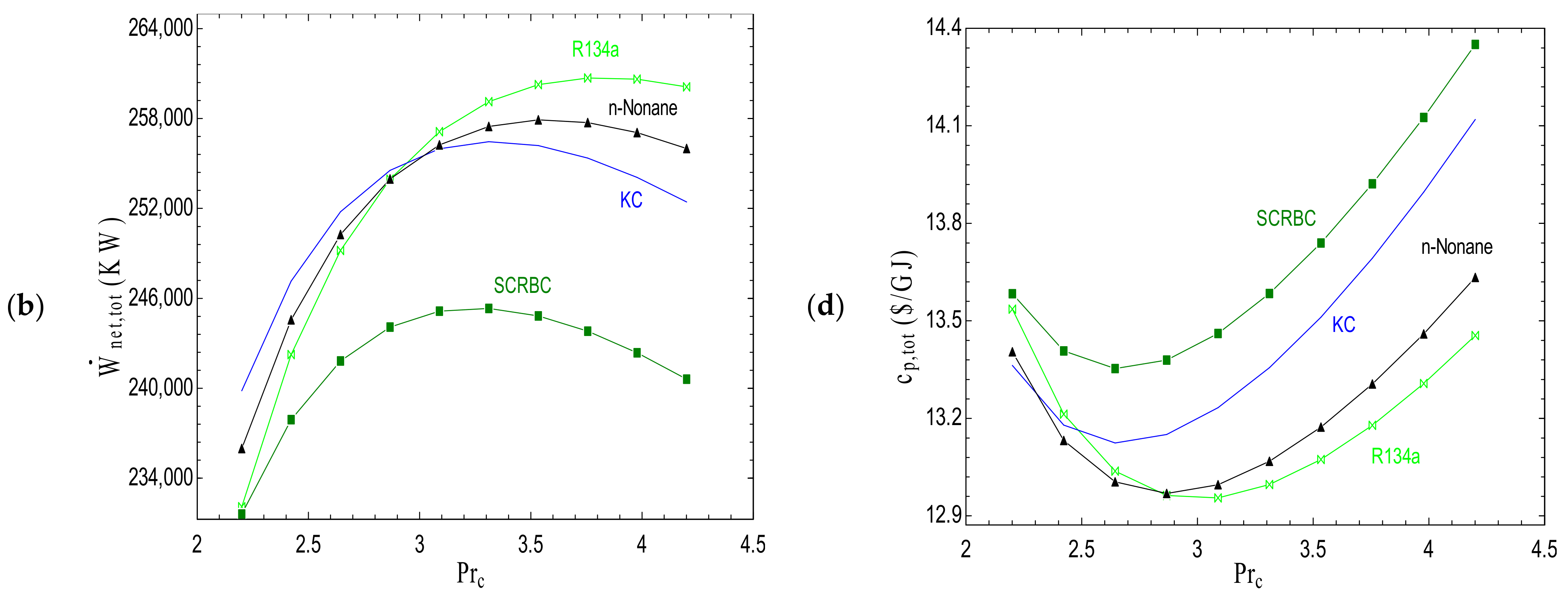
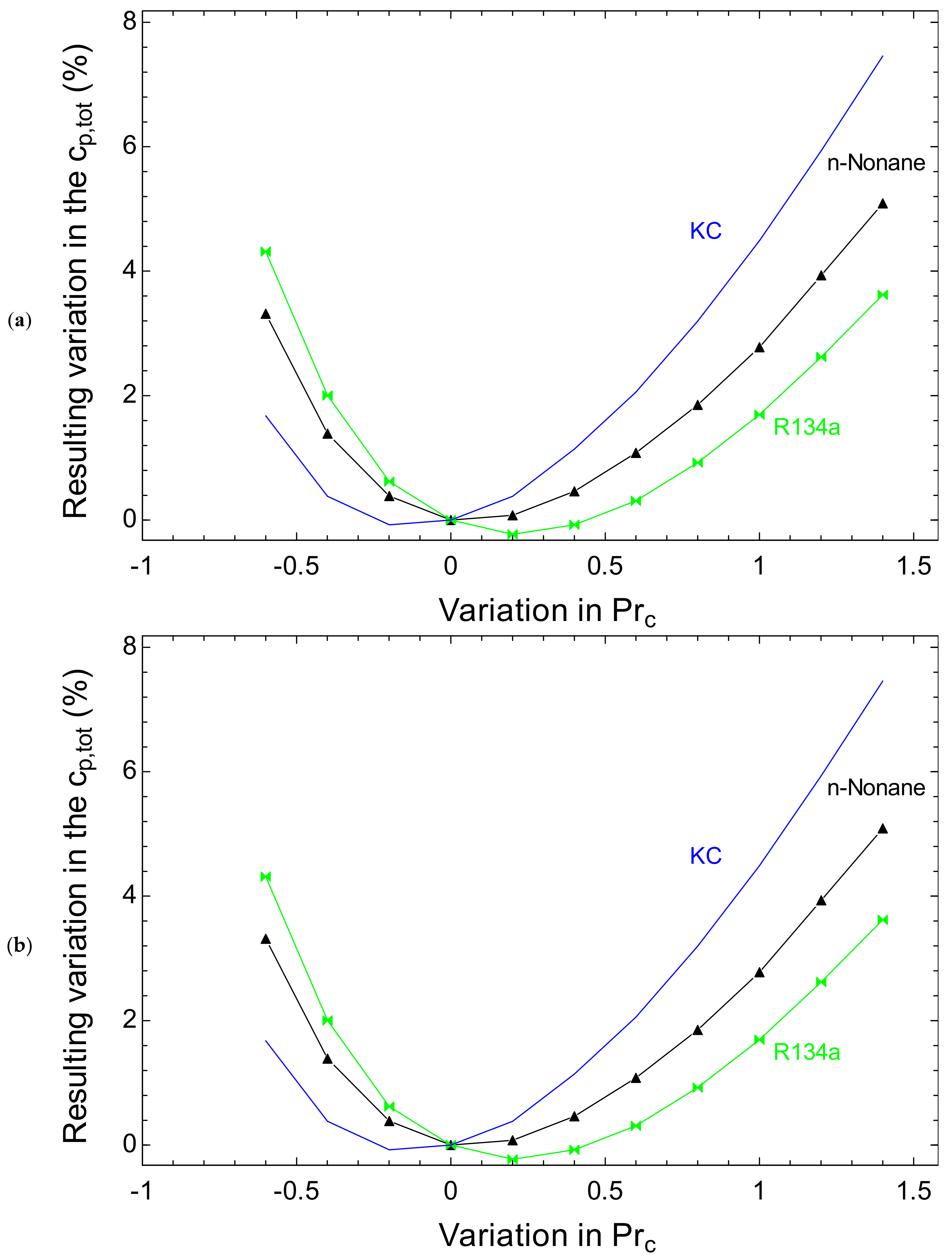
4.3. Parametric Study
4.4. Optimization
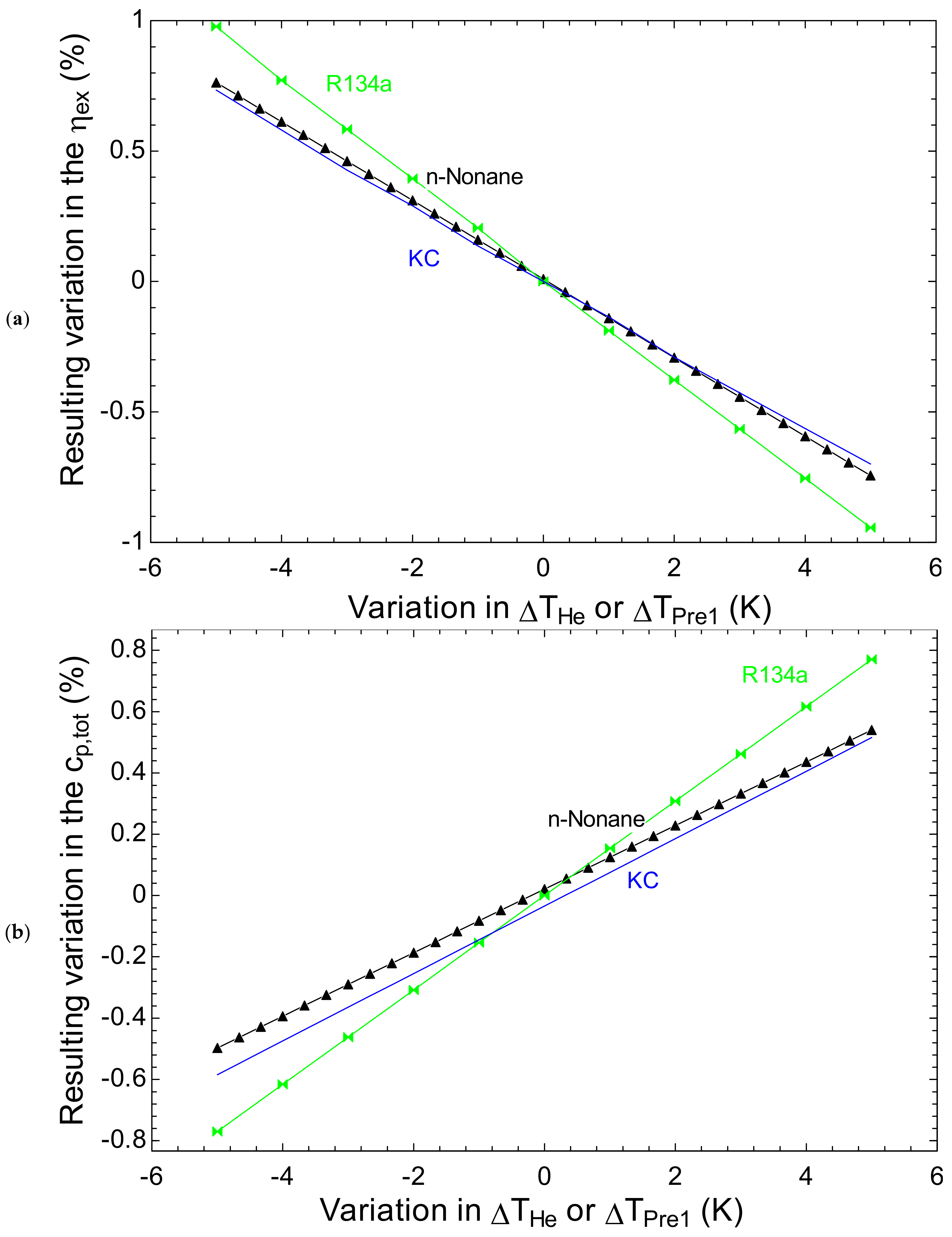
4.5. Sensitivity Analysis
5. Conclusions
- (1)
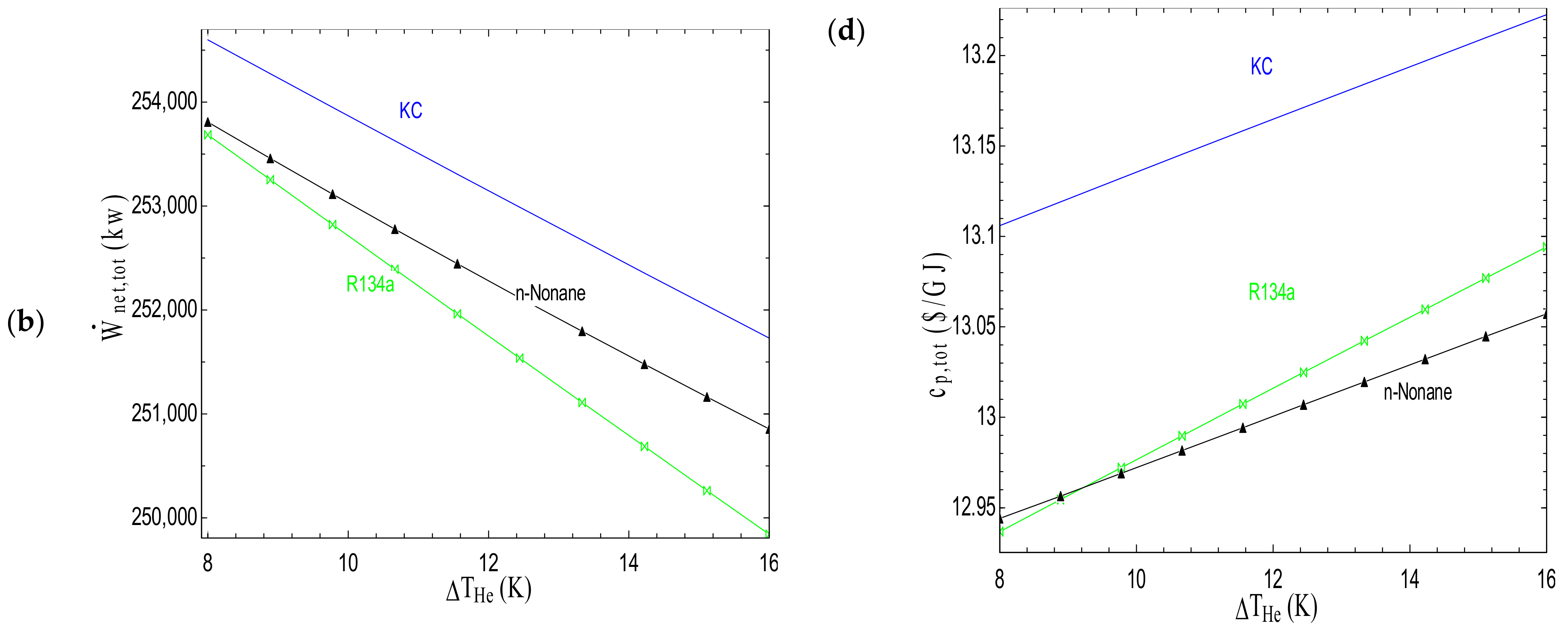
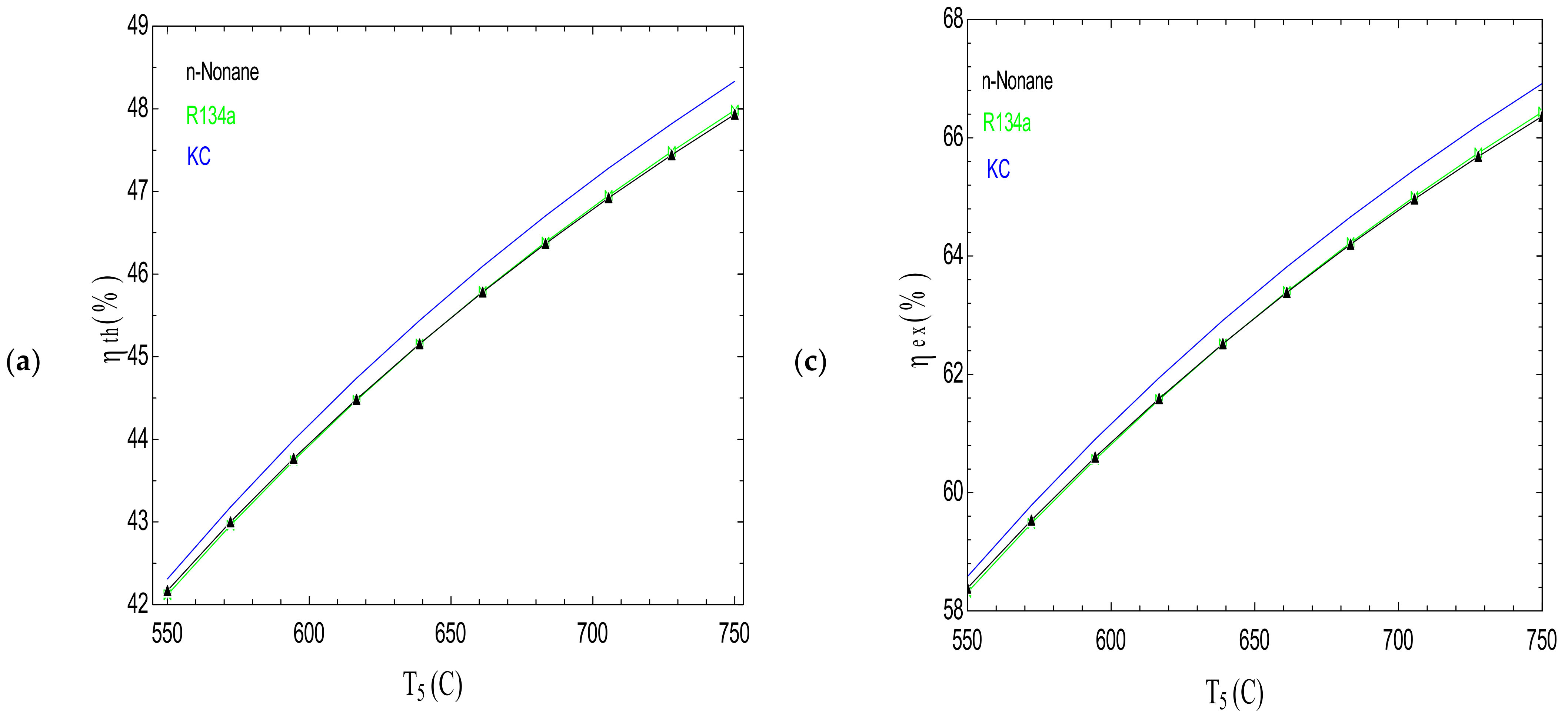
- The parametric studies show that the SCRB/OFC, SCRB/ORC and SCRB/KC systems perform thermodynamically and economically better when the pinch point temperature difference is at its own lowest value, which is 8 °C for this work. For achieving more desirable performances for the systems from the viewpoints of thermodynamics and economics, the turbine inlet temperature should be 750 °C, noting that this value is limited by material technology.
- (2)
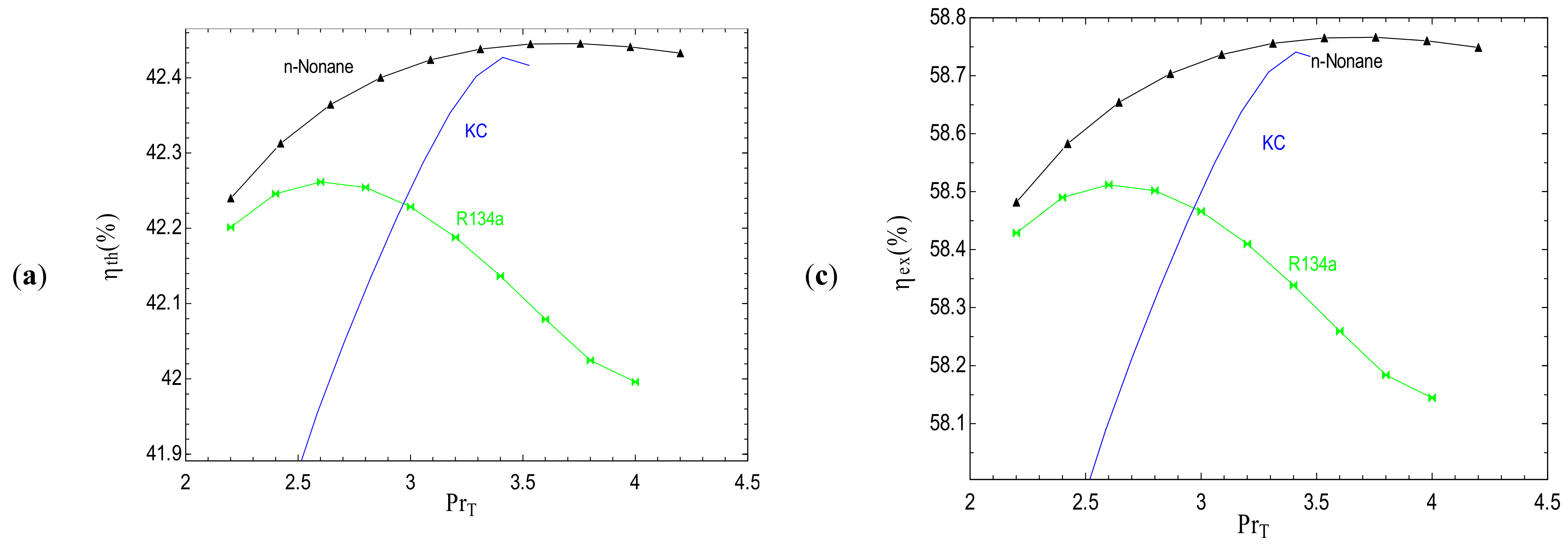
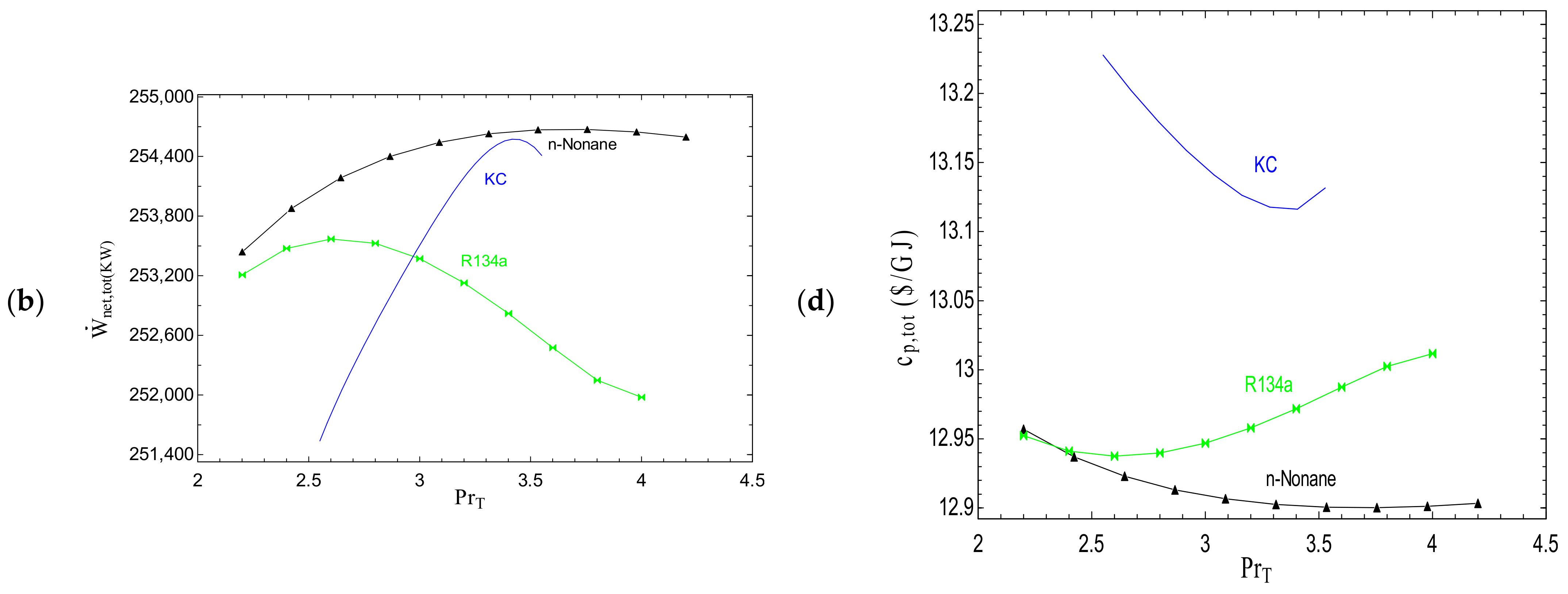
- Under the thermodynamic condition of T5 = 550 °C and or = 8K, there is an optimum value for the compressor pressure ratio at which the exergy efficiency is maximized and Cp, total is minimized.
- (3)
- Based on the working fluid selection strategy, the SCRB/OFC and SCRB/ORC cycles achieve their best performances from the viewpoints of exergy and economics, when n-nonane and R134a are used as the working fluid, respectively.
- (4)
- For operation at low pressure ratios, the SCRB/KC cycle exhibits better performance from the viewpoints of thermodynamic and exergoeconomic analyses; however, at high pressure ratios, the SCRB/ORC is the best system.
- (5)
- The optimization results show that the exergy efficiency of the SCRB/ORC cycle is higher than that of the SCRB/OFC and SCRB/KC cycles, by up to 1.3%. In addition, the unit cost of power production of the SCRB/ORC cycle is lower than those of the SCRB/KC and SCRB/OFC systems by up to 1.9% and 0.75%, respectively.
- (6)
- The optimization results indicate that the sustainability index for the SCRB/ORC system is 2.48% and 4.62% higher than those for the SCRB/OFC and SCRBB/KC systems, respectively.
- (7)
- From thermodynamic, exergoeconomic and sustainability perspectives, the SCRB/ORC system is the best option while the SCRB/OFC system can be a promising integrated cycle.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Area (m2) |
| Cost rate () | |
| Average cost per unit exergy () | |
| Total product unit cost ($/GJ) | |
| CRF | Capital recovery factor |
| Exergy rate (kW) | |
| Rate of exergy destruction (kW) | |
| f | Exergoeconomic factor (%) |
| h | Specific enthalpy (kJ/kg) |
| Interest rate (%) | |
| Logarithmic mean temperature difference (K) | |
| Mass flow rate (kg/s) | |
| n | Number of operating years |
| P | Pressure (bar) |
| Compressor pressure ratio | |
| Pump pressure ratio | |
| Turbine pressure ratio of bottoming cycle | |
| Heat transfer rate (kW) | |
| s | Specific entropy (kJ/kg·K) |
| SI | Sustainability index |
| T | Temperature (K) |
| U | Overall heat transfer coefficient (kW/m2K) |
| Work rate (kW) | |
| x | Mass flow ratio of CO2 |
| Z | Capital investment cost ($) |
| Capital investment cost rate ($/h) | |
| Subscripts | |
| 0 | Ambient state |
| 1,2, … | State points |
| Bot | Bottoming cycle |
| ch | Chemical exergy |
| CI | Capital investment |
| Cond | Condenser |
| D | Destruction |
| EOD | Economic optimal design |
| ex | Exergy |
| Fs | Flash separator |
| He | Heater |
| HTR | High temperature recuperator |
| L | Loss |
| LTR | Low temperature recuperator |
| MC | Main compressor |
| OM | Operation and maintenance |
| P | Product |
| Pre | Pre-cooler |
| ph | Physical exergy |
| pp | Pinch point |
| R | Reactor |
| RC | Recompression compressor |
| ST | S-CO2 turbine |
| sup | Superheat/Superheater |
| T | Turbine |
| th | Thermal |
| TOD | Thermodynamic optimal design |
| tot | Total |
| V | Valve |
| Greek symbols | |
| Efficiency (%) | |
| Effectiveness (%) | |
| Maintenance factor | |
| Annual plant operation hours | |
| Temperature difference (K) | |
Appendix A
| Component | Cost Function | Reference Year | CEPCI0 | Reference |
|---|---|---|---|---|
| Reactor | 2003 | 402.3 | [38] | |
| S-CO2 turbine | 1994 | 368.1 | [39] | |
| Compressors | 1994 | 368.1 | [39] | |
| HTR, LTR, Pre-cooler 1, Heater and Superheater | 1986 | 318.4 | [50] | |
| KCLTR, KCHTR, Condenser, Pre-cooler, Pre-cooler 2 | 1986 | 318.4 | [50] | |
| Turbine | 2005 | 468.2 | [51] | |
| Pump | 2005 | 468.2 | [51] |
References
- Sarkar, J. Second law analysis of supercritical CO2 recompression Brayton cycle. Energy 2009, 34, 1172–1178. [Google Scholar] [CrossRef]
- Zhang, X.R.; Yamaguchi, H.; Uneno, D. Thermodynamic analysis of the CO2-based Rankine cycle powered by solar energy. Int. J. Energy Res. 2007, 31, 1414–1424. [Google Scholar] [CrossRef]
- Ahn, Y.; Bae, S.J.; Kim, M.; Cho, S.K.; Baik, S.; Lee, J.I.; Cha, J.E. Review of supercritical CO2 power cycle technology and current status of research and development. Nucl. Eng. Technol. 2015, 47, 647–661. [Google Scholar] [CrossRef] [Green Version]
- Angelino, G. Carbon Dioxide Condensation Cycles For Power Production. J. Eng. Power 1968, 90, 287–295. [Google Scholar] [CrossRef]
- Dostal, V.; Driscoll, M.J.; Hejzlar, P. A Supercritical Carbon Dioxide Cycle for Next Generation Nuclear Reactors. Master’s Thesis, Massachusetts Institute of Technology, Department of Nuclear Engineering, Cambridge, MA, USA, 2004. [Google Scholar]
- Dostal, V.; Hejzlar, P.; Driscoll, M.J. The Supercritical Carbon Dioxide Power Cycle: Comparison to Other Advanced Power Cycles. Nucl. Technol. 2006, 154, 283–301. [Google Scholar] [CrossRef]
- Yari, M.; Mahmoudi, S.M.S. A thermodynamic study of waste heat recovery from GT-MHR using organic Rankine cycles. Heat Mass Transf. 2010, 47, 181–196. [Google Scholar] [CrossRef]
- Bao, J.; Zhao, L. A review of working fluid and expander selections for organic Rankine cycle. Renew. Sustain. Energy Rev. 2013, 24, 325–342. [Google Scholar] [CrossRef]
- Besarati, S.M.; Goswami, D.Y. Analysis of Advanced Supercritical Carbon Dioxide Power Cycles with a Bottoming Cycle for Concentrating Solar Power Applications. J. Sol. Energy Eng. 2013, 136, 10904. [Google Scholar] [CrossRef]
- Akbari, A.D.; Mahmoudi, S.M. Thermoeconomic analysis & optimization of the combined supercritical CO2 (carbon dioxide) recompression Brayton/organic Rankine cycle. Energy 2014, 78, 501–512. [Google Scholar] [CrossRef]
- Wang, X.; Dai, Y. Exergoeconomic analysis of utilizing the transcritical CO2 cycle and the ORC for a recompression supercritical CO2 cycle waste heat recovery: A comparative study. Appl. Energy 2016, 170, 193–207. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Wang, K.; Wang, J.; Markides, C.N. Combined supercritical CO2 (SCO2) cycle and organic Rankine cycle (ORC) system for hybrid solar and geothermal power generation: Thermoeconomic assessment of various configurations. Renew. Energy 2021, 174, 1020–1035. [Google Scholar] [CrossRef]
- Song, J.; Li, X.; Wang, K.; Markides, C.N. Parametric optimisation of a combined supercritical CO2 (S-CO2) cycle and organic Rankine cycle (ORC) system for internal combustion engine (ICE) waste-heat recovery. Energy Convers. Manag. 2020, 218, 112999. [Google Scholar] [CrossRef]
- Gutierrez, J.C.; Ochoa, G.V.; Duarte-Forero, J. A comparative study of the energy, exergetic and thermo-economic performance of a novelty combined Brayton S-CO2-ORC configurations as bottoming cycles. Heliyon 2020, 6, e04459. [Google Scholar] [CrossRef]
- Habibi, H.; Zoghi, M.; Chitsaz, A.; Javaherdeh, K.; Ayazpour, M.; Bellos, E. Working fluid selection for regenerative supercritical Brayton cycle combined with bottoming ORC driven by molten salt solar power tower using energy–exergy analysis. Sustain. Energy Technol. Assess. 2020, 39, 100699. [Google Scholar] [CrossRef]
- Wang, X.; Levy, E.K.; Pan, C.; Romero, C.E.; Banerjee, A.; Rubio-Maya, C.; Pan, L. Working fluid selection for organic Rankine cycle power generation using hot produced supercritical CO2 from a geothermal reservoir. Appl. Therm. Eng. 2018, 149, 1287–1304. [Google Scholar] [CrossRef]
- Liang, Y.; Bian, X.; Qian, W.; Pan, M.; Ban, Z.; Yu, Z. Theoretical analysis of a regenerative supercritical carbon dioxide Brayton cycle/organic Rankine cycle dual loop for waste heat recovery of a diesel/natural gas dual-fuel engine. Energy Convers. Manag. 2019, 197, 111845. [Google Scholar] [CrossRef]
- Chen, X.; Pan, M.; Li, X. Novel supercritical CO2/organic Rankine cycle systems for solid-waste incineration energy harvesting: Thermo-environmental analysis. Int. J. Green Energy 2021, 19, 786–807. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, C.; Luo, R.; Li, D.; Macián-Juan, R. Thermodynamic analysis and optimization of the combined supercritical carbon dioxide Brayton cycle and organic Rankine cycle-based nuclear hydrogen production system. Int. J. Energy Res. 2021, 46, 832–859. [Google Scholar] [CrossRef]
- Ma, H.; Liu, Z. An Engine Exhaust Utilization System by Combining CO2 Brayton Cycle and Transcritical Organic Rankine Cycle. Sustainability 2022, 14, 1276. [Google Scholar] [CrossRef]
- Javanshir, A.; Sarunac, N.; Razzaghpanah, Z. Thermodynamic Analysis of ORC and Its Application for Waste Heat Recovery. Sustainability 2017, 9, 1974. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Wang, S.-S.; Li, J. Exergoeconomic analysis and optimization of a combined supercritical carbon dioxide recompression Brayton/organic flash cycle for nuclear power plants. Energy Convers. Manag. 2018, 171, 936–952. [Google Scholar] [CrossRef]
- Ganesh, N.S.; Srinivas, T. Thermodynamic Assessment of Heat Source Arrangements in Kalina Power Station. J. Energy Eng. 2013, 139, 99–108. [Google Scholar] [CrossRef]
- Mahmoudi, S.M.S.; Akbari, A.D.; Rosen, M.A. Thermoeconomic Analysis and Optimization of a New Combined Supercritical Carbon Dioxide Recompression Brayton/Kalina Cycle. Sustainability 2016, 8, 1079. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wang, M.; Wang, J.; Dai, Y. Exergoeconomic Analysis and Optimization of a Supercritical CO2 Cycle Coupled with a Kalina Cycle. J. Energy Eng. 2017, 143, 4016055. [Google Scholar] [CrossRef]
- Feng, Y.; Du, Z.; Shreka, M.; Zhu, Y.; Zhou, S.; Zhang, W. Thermodynamic analysis and performance optimization of the supercritical carbon dioxide Brayton cycle combined with the Kalina cycle for waste heat recovery from a marine low-speed diesel engine. Energy Convers. Manag. 2020, 206, 112483. [Google Scholar] [CrossRef]
- Sadeghi, M.; Nemati, A.; Ghavimi, A.; Yari, M. Thermodynamic analysis and multi-objective optimization of various ORC (organic Rankine cycle) configurations using zeotropic mixtures. Energy 2016, 109, 791–802. [Google Scholar] [CrossRef]
- Roy, J.; Mishra, M.; Misra, A. Parametric optimization and performance analysis of a waste heat recovery system using Organic Rankine Cycle. Energy 2010, 35, 5049–5062. [Google Scholar] [CrossRef]
- Sadeghi, M.; Chitsaz, A.; Marivani, P.; Yari, M.; Mahmoudi, S. Effects of thermophysical and thermochemical recuperation on the performance of combined gas turbine and organic rankine cycle power generation system: Thermoeconomic comparison and multi-objective optimization. Energy 2020, 210, 118551. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. REFPROP Version 8.0: Reference Fluid Thermodynamic and Transport Properties; NIST Standard Reference Database 23; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007. [Google Scholar]
- Aljundi, I.H. Effect of dry hydrocarbons and critical point temperature on the efficiencies of organic Rankine cycle. Renew. Energy 2011, 36, 1196–1202. [Google Scholar] [CrossRef]
- Malafeev, I.I.; Il’In, G.A.; Sapozhnikov, V.B. Mathematical-Experimental Assessment of Energy Efficiency of High-Temperature Heat Pump Distiller. Chem. Pet. Eng. 2019, 55, 556–561. [Google Scholar] [CrossRef]
- Nemati, A.; Nami, H.; Yari, M. Assessment of different configurations of solar energy driven organic flash cycles (OFCs) via exergy and exergoeconomic methodologies. Renew. Energy 2018, 115, 1231–1248. [Google Scholar] [CrossRef]
- Wu, C.; Wang, S.-S.; Feng, X.-J.; Li, J. Energy, exergy and exergoeconomic analyses of a combined supercritical CO 2 recompression Brayton/absorption refrigeration cycle. Energy Convers. Manag. 2017, 148, 360–377. [Google Scholar] [CrossRef]
- Sarkar, J.; Bhattacharyya, S. Optimization of recompression S-CO2 power cycle with reheating. Energy Convers. Manag. 2009, 50, 1939–1945. [Google Scholar] [CrossRef]
- Lee, H.Y.; Park, S.H.; Kim, K.H. Comparative analysis of thermodynamic performance and optimization of organic flash cycle (OFC) and organic Rankine cycle (ORC). Appl. Therm. Eng. 2016, 100, 680–690. [Google Scholar] [CrossRef]
- Dincer, I.; Rosen, M.A. Exergy: Energy, Environment and Sustainable Development, 3rd ed.; Elsevier: Oxford, UK, 2021. [Google Scholar]
- Schultz, K.; Brown, L.; Besenbruch, G.; Hamilton, C. Large-Scale Production of Hydrogen by Nuclear Energy for the Hydrogen Economy; General Atomics: San Diego, CA, USA, 2003. [Google Scholar] [CrossRef] [Green Version]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design and Optimization; John Wiley & Sons: New York, NY, USA, 1995. [Google Scholar]
- Lazzaretto, A.; Tsatsaronis, G. SPECO: A systematic and general methodology for calculating efficiencies and costs in thermal systems. Energy 2006, 31, 1257–1289. [Google Scholar] [CrossRef]
- Sarabchi, N.; Yari, M.; Mahmoudi, S.S. Exergy and exergoeconomic analyses of novel high-temperature proton exchange membrane fuel cell based combined cogeneration cycles, including methanol steam reformer integrated with catalytic combustor or parabolic trough solar collector. J. Power Source 2020, 485, 229277. [Google Scholar] [CrossRef]
- Byun, M.; Kim, H.; Choe, C.; Lim, H. Conceptual feasibility studies for cost-efficient and bi-functional methylcyclohexane dehydrogenation in a membrane reactor for H2 storage and production. Energy Convers. Manag. 2020, 227, 113576. [Google Scholar] [CrossRef]
- Dincer, I.; Joshi, A.S. Solar Based Hydrogen Production Systems; Springer: Cham, Switzerland, 2013. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Exergo-environmental analysis of an integrated organic Rankine cycle for trigeneration. Energy Convers. Manag. 2012, 64, 447–453. [Google Scholar] [CrossRef]
- Nami, H.; Ranjbar, F.; Yari, M. Thermodynamic assessment of zero-emission power, hydrogen and methanol production using captured CO2 from S-Graz oxy-fuel cycle and renewable hydrogen. Energy Convers. Manag. 2018, 161, 53–65. [Google Scholar] [CrossRef]
- LaBar, M.P. The gas turbine–modular helium reactor: A promising option for near term deployment. In Proceedings of the International Congress on Advances in Nuclear Power Plants, Hollywood, FL, USA, 9–13 June 2002. [Google Scholar]
- Zare, V.; Mahmoudi, S.; Yari, M. On the exergoeconomic assessment of employing Kalina cycle for GT-MHR waste heat utilization. Energy Convers. Manag. 2015, 90, 364–374. [Google Scholar] [CrossRef]
- Mosaffa, A.; Zareei, A. Proposal and thermoeconomic analysis of geothermal flash binary power plants utilizing different types of organic flash cycle. Geothermics 2018, 72, 47–63. [Google Scholar] [CrossRef]
- Vieira, L.S.; Donatelli, J.L.; Cruz, M.E. Exergoeconomic improvement of a complex cogeneration system integrated with a professional process simulator. Energy Convers. Manag. 2009, 50, 1955–1967. [Google Scholar] [CrossRef]
- Guo-Yan, Z.; En, W.; Shan-Tung, T. Techno-economic study on compact heat exchangers. Int. J. Energy Res. 2008, 32, 1119–1127. [Google Scholar] [CrossRef]
- Dorj, P. Thermoeconomic Analysis of a New Geothermal Utilization CHP Plant in Tsetserleg, Mongolia. Master’s Thesis, University of Iceland, Departement of Mechanical and Industrial Engineering, Reykjavík, Iceland, 2005. [Google Scholar]
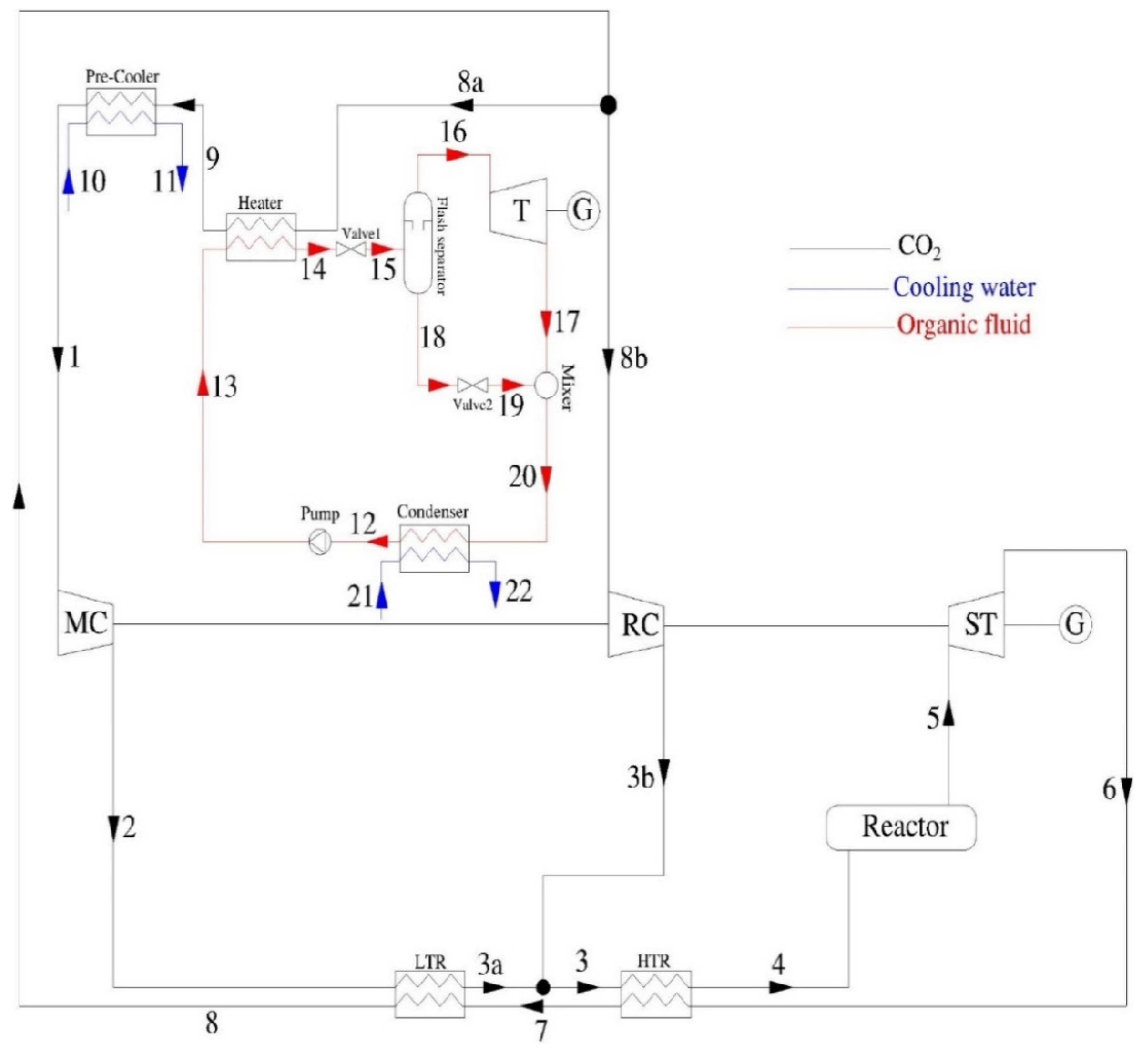
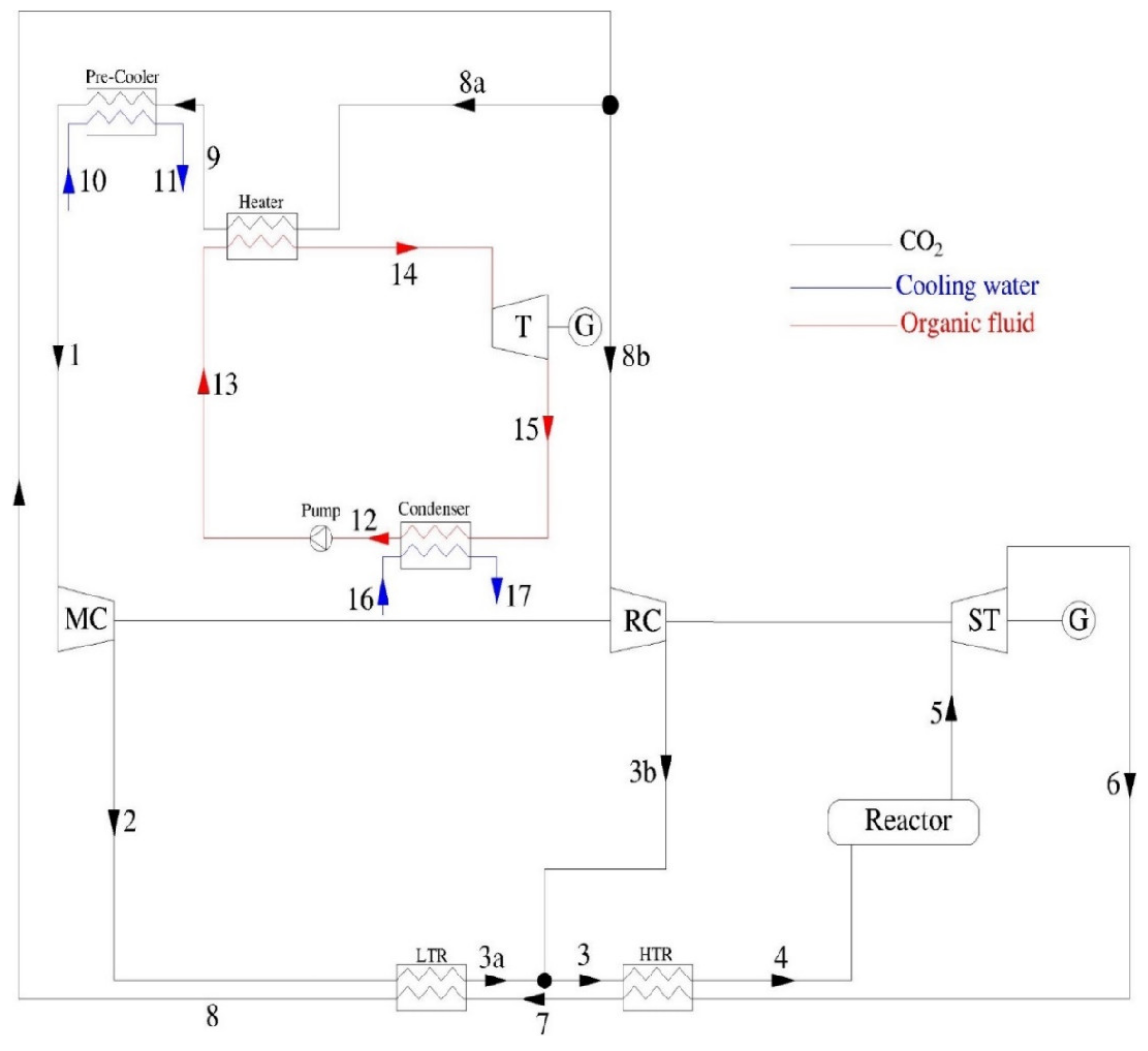





| Working Fluid | Thermophysical Properties | Environmental Properties | ||
|---|---|---|---|---|
| Critical Temperature (K) | Critical Pressure (kPa) | ODP | GWP (100 Year) (Relative to CO2) | |
| R245fa | 427.2 [30] | 3640 [30] | 0 [29] | 950 [29] |
| n-Pentane | 469.7 [30] | 3370 [30] | 0 [31] | 0 [31] |
| n-Hexane | 507.82 [30] | 3034 [30] | 0 [31] | 0 [31] |
| n-Heptane | 540.13 [30] | 2736 [30] | 0 [32] | 3 [32] |
| n-Octane | 569.32 [30] | 2497 [30] | ||
| n-Nonane | 594.55 [30] | 2281 [30] | ||
| R123 | 456.83 [29] | 3662 [29] | 0.012 [29] | 120 [29] |
| R142b | 479.96 [29] | 4460 [29] | 0.086 [29] | 700 [29] |
| R134a | 374.21 [29] | 4056 [29] | 0 [29] | 1300 [29] |
| Isobutane | 425.12 [29] | 3796 [29] | 0.12 [29] | 725 [29] |
| System | Parameter | Value Reference |
|---|---|---|
| S-CO2 Brayton cycle | Cycle minimum temperature (°C) | 32 [11,34] |
| Cycle maximum temperature (°C) | 550 [11,34] | |
| Main compressor inlet pressure (bar) | 74 [11,34] | |
| Compressor pressure ratio, Prc | 2.2–4.2 [11,34] | |
| LTR and HTR effectiveness, and (%) | 86 [1,5,35] | |
| S-CO2 turbine isentropic efficiency, (%) | 90 [1,5,35] | |
| Main compressor isentropic efficiency, (%) | 85 [1,5,35] | |
| Recompression compressor isentropic efficiency, (%) | 85 [1,5,35] | |
| Pinch point temperature difference in Heater, (K) | 8–16 [22] | |
| Pinch point temperature difference in Pre-cooler 1, (K) | 8–16 [22] | |
| Heat provided by Reactor, (MW) | 600 [1,5,35] | |
| Bottoming cycle Organic flash cycle | Reactor core temperature, (°C) Turbine isentropic efficiency, (%) Pump isentropic efficiency, (%) Flash separator inlet temperature, (°C) Pinch point temperature difference in Condenser, (K) | 800 [1,5,35] 80 [36] 80 [36] 80 [36] 10 [22] |
| Organic Rankine cycle | Turbine inlet temperature, (°C) Pinch point temperature difference in Condenser, (K) Degree of superheat, (K) | 90 [11] 10 [22] 0 [11] |
| Kalina cycle | Separator inlet temperature,
(°C) Ammonia concentration in ammonia-water mixture leaving the condenser, X20 (%) Pump pressure ratio, Prpump Minimum temperature difference in superheater, (K) Standard chemical exergy of ammonia, Standard chemical exergy of water, | 79.85 [24] 95 [24] 2.55–3.65 [24] 1 [11] 337,900 [37] 900 [37] |
| Economic data | Interest rate, Number of operation year, n Annual plant operation hours, Maintenance factor, Fuel cost, ($/MWh) | 0.12 [10] 20 [10] 8000 [10] 0.06 [10] 7.4 [38] |
| Ambient condition | Ambient temperature, T0 (k) | 298.15 |
| Ambient pressure, P0 (bar) | 1 |
| Component | Energy Balance | Exergy Balance | Cost Rate Balance and Ancillary Equation |
|---|---|---|---|
| Main compressor | |||
| Recompression compressor | |||
| S-CO2 turbine | |||
| Reactor | |||
| HTR | |||
| LTR | |||
| Pre-cooler | |||
| Heater | |||
| Valve 1 | |||
| Valve 2 | |||
| Flash separator | |||
| Mixer | |||
| Pump | |||
| Turbine | |||
| Condenser |
| Component | Energy Balance | Exergy Balance | Cost Rate Balance and Ancillary Equation |
|---|---|---|---|
| Main compressor | |||
| Recompression compressor | |||
| S-CO2 turbine | |||
| Reactor | |||
| HTR | |||
| LTR | |||
| Pre-cooler | |||
| Heater | |||
| Pump | |||
| Turbine | |||
| Condenser |
| Component | Energy Balance | Exergy Balance | Cost Rate Balance and Ancillary Equation |
|---|---|---|---|
| Main compressor | |||
| Recompression compressor | |||
| S-CO2 turbine | |||
| Reactor | |||
| HTR | |||
| LTR | |||
| Superheater | |||
| Pre-cooler 1 | |||
| Pre-cooler 2 | |||
| Separator | |||
| KCHTR | |||
| KCLTR | |||
| Mixer and Valve | |||
| Pump | |||
| Turbine | |||
| Condenser |
| State | T (K) | P (bar) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Present Work Ref. [22] Error (%) | Present Work Ref. [22] Error (%) | Present Work Ref. [22] Error (%) | |||||||
| 1 | 305.2 | 305.2 | 0 | 74 | 74 | 0 | 2098 | 2096 | 0.095 |
| 2 | 370.2 | 370.0 | 0.054 | 207.2 | 207.2 | 0 | 2098 | 2096 | 0.095 |
| 3 | 503.1 | 502.9 | 0.039 | 207.2 | 207.2 | 0 | 2939 | 2938 | 0.034 |
| 4 | 657.6 | 657.5 | 0.015 | 207.2 | 207.2 | 0 | 2939 | 2938 | 0.034 |
| 5 | 823.2 | 823.2 | 0 | 207.2 | 207.2 | 0 | 2939 | 2938 | 0.034 |
| 6 | 701.2 | 701.2 | 0 | 74 | 74 | 0 | 2939 | 2938 | 0.034 |
| 7 | 530.8 | 530.6 | 0.037 | 74 | 74 | 0 | 2939 | 2938 | 0.034 |
| 8 | 392.7 | 392.5 | 0.050 | 74 | 74 | 0 | 2939 | 2938 | 0.034 |
| 9 | 323.8 | 323.8 | 0 | 74 | 74 | 0 | 2098 | 2096 | 0.095 |
| 12 | 313.2 | 313.2 | 0 | 2.496 | 2.5 | 0.160 | 2072 | 2071 | 0.048 |
| 13 | 313.9 | 313.9 | 0 | 15.58 | 15.49 | 0.581 | 2072 | 2071 | 0.048 |
| 14 | 382.7 | 382.5 | 0.052 | 15.58 | 15.49 | 0.581 | 2072 | 2071 | 0.048 |
| 15 | 353.2 | 353.2 | 0 | 7.908 | 7.89 | 0.228 | 2072 | 2071 | 0.048 |
| 16 | 353.2 | 353.2 | 0 | 7.908 | 7.89 | 0.228 | 622.4 | 618.8 | 0.581 |
| 17 | 324.2 | 324.3 | 0.031 | 2.496 | 2.5 | 0.160 | 622.4 | 618.8 | 0.581 |
| 18 | 353.2 | 353.2 | 0 | 7.908 | 7.89 | 0.228 | 1449 | 1452 | 0.207 |
| 19 | 313.2 | 313.2 | 0 | 2.496 | 2.5 | 0.160 | 1449 | 1452 | 0.207 |
| 20 | 313.2 | 313.2 | 0 | 2.496 | 2.5 | 0.160 | 2072 | 2071 | 0.048 |
| State | T (K) | P (bar) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Present Work Ref. [22] Error (%) | Present Work Ref. [22] Error (%) | Present Work Ref. [22] Error (%) | |||||||
| 1 | 305.2 | 305.2 | 0 | 74 | 74 | 0 | 2084 | 2082 | 0.096 |
| 2 | 369.5 | 369.3 | 0.054 | 207.2 | 207.2 | 0 | 2084 | 2082 | 0.096 |
| 3 | 498.8 | 498.6 | 0.040 | 207.2 | 207.2 | 0 | 2917 | 2916 | 0.034 |
| 4 | 656.3 | 656.3 | 0 | 207.2 | 207.2 | 0 | 2917 | 2916 | 0.034 |
| 5 | 823.2 | 823.2 | 0 | 207.2 | 207.2 | 0 | 2917 | 2916 | 0.034 |
| 6 | 701.2 | 701.2 | 0 | 74 | 74 | 0 | 2917 | 2916 | 0.034 |
| 7 | 527.2 | 527.0 | 0.038 | 74 | 74 | 0 | 2917 | 2916 | 0.034 |
| 8 | 391.6 | 391.4 | 0.051 | 74 | 74 | 0 | 2917 | 2916 | 0.034 |
| 9 | 357.9 | 358.2 | 0.083 | 74 | 74 | 0 | 2084 | 2082 | 0.096 |
| 12 | 303.2 | 303.2 | 0 | 1.097 | 1.10 | 0.273 | 440 | 436.6 | 0.778 |
| 13 | 303.4 | 303.4 | 0 | 6.252 | 6.24 | 0.192 | 440 | 436.6 | 0.778 |
| 14 | 363.2 | 363.2 | 0 | 6.252 | 6.24 | 0.192 | 440 | 436.6 | 0.778 |
| 15 | 318.2 | 317.5 | 0.220 | 1.097 | 1.10 | 0.273 | 440 | 436.6 | 0.778 |
| State | T (K) | P (bar) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Present Work Ref. [22] Error (%) | Present Work Ref. [22] Error (%) | Present Work Ref. [22] Error (%) | |||||||
| 1 | 308.2 | 308.2 | 0 | 74 | 74 | 0 | 2187 | 2187 | 0 |
| 2 | 385.9 | 385.9 | 0 | 214.6 | 214.6 | 0 | 2187 | 2187 | 0 |
| 3 | 526.5 | 526.5 | 0 | 214.6 | 214.6 | 0 | 2980 | 2980 | 0 |
| 4 | 660.2 | 660.2 | 0 | 214.6 | 214.6 | 0 | 2980 | 2980 | 0 |
| 5 | 823.2 | 823.2 | 0 | 214.6 | 214.6 | 0 | 2980 | 2980 | 0 |
| 6 | 697.2 | 697.2 | 0 | 74 | 74 | 0 | 2980 | 2980 | 0 |
| 7 | 550.4 | 550.4 | 0 | 74 | 74 | 0 | 2980 | 2980 | 0 |
| 8 | 409 | 408.9 | 0.024 | 74 | 74 | 0 | 2980 | 2980 | 0 |
| 9 | 398.3 | 398.3 | 0 | 74 | 74 | 0 | 2187 | 2187 | 0 |
| 12 | 338.9 | 338.9 | 0 | 74 | 74 | 0 | 2187 | 2187 | 0 |
| 13 | 353 | 353 | 0 | 32.47 | 32.47 | 0 | 191.4 | 191.4 | 0 |
| 14 | 353 | 353 | 0 | 32.47 | 32.47 | 0 | 146.3 | 146.3 | 0 |
| 15 | 353 | 353 | 0 | 32.47 | 32.47 | 0 | 45.13 | 45.13 | 0 |
| 16 | 407.9 | 407.9 | 0 | 32.47 | 32.47 | 0 | 146.3 | 146.3 | 0 |
| 17 | 323.8 | 323.8 | 0 | 10.47 | 10.47 | 0 | 146.3 | 146.3 | 0 |
| 18 | 309 | 309.1 | 0.032 | 32.47 | 32.47 | 0 | 45.13 | 45.13 | 0 |
| 19 | 307.1 | 307.2 | 0.032 | 10.47 | 10.47 | 0 | 45.13 | 45.13 | 0 |
| 20 | 309 | 309.1 | 0.032 | 10.47 | 10.47 | 0 | 191.4 | 191.4 | 0 |
| 21 | 308.5 | 308.6 | 0.032 | 10.47 | 10.47 | 0 | 191.4 | 191.4 | 0 |
| 22 | 301.2 | 301.2 | 0 | 10.47 | 10.47 | 0 | 191.4 | 191.4 | 0 |
| 23 | 301.8 | 301.8 | 0 | 32.47 | 32.47 | 0 | 191.4 | 191.4 | 0 |
| 24 | 304 | 304.1 | 0.033 | 32.47 | 32.47 | 0 | 191.4 | 191.4 | 0 |
| 25 | 314.5 | 314.6 | 0.031 | 32.47 | 32.47 | 0 | 191.4 | 191.4 | 0 |
| Cycle | Working Fluid | Sustainability Index (SI) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Present work | Ref. | Error (%) | Present work | Ref. | Error (%) | Present work | Ref. | Error (%) | ||
| SCRB/OFC | R245fa | 58.02 | 58.02 [22] | 0 | 13.08 | 12.64 [22] | 3.48 | 2.439 | -- | -- |
| SCRB/ORC | R123 | 59.90 | 59.92 [11] | 0.03 | 13.04 | 9.7 [11] | 34.43 | 2.514 | 1.57 [18] | 60.12 |
| SCRB/KC | Ammonia-water | 59.83 | 59.83 [24] | 0 | 12.97 | 12.02 [24] | 7.9 | 2.5 - | -- | -- |
| Parameter | SCRB/OFC | SCRB/ORC | SCRB/KC | |||
|---|---|---|---|---|---|---|
| TOD | EOD | TOD | EOD | TOD | EOD | |
| Prc | 4.2 | 3.582 | 4.2 | 3.722 | 4.2 | 3.345 |
| T5 (°C) | 750 | 750 | 750 | 750 | 750 | 750 |
| (K) | 8 | 8 | 8 | 8 | 8 | 8 |
| (%) | 70.38 | 69.52 | 71.31 | 70.49 | 70.36 | 69.22 |
| ($/GJ) | 10.76 | 10.70 | 10.65 | 10.62 | 10.96 | 10.83 |
| (MW) | 305.0 | 301.3 | 309.0 | 305.5 | 304.9 | 300.0 |
| (MW) | 290.7 | 288.4 | 290.7 | 289.2 | 283.2 | 280.9 |
| (MW) | 14.28 | 12.82 | 18.30 | 16.25 | 21.68 | 19.06 |
| (kg/s) | 1944 | 2046 | 1944 | 2020 | 1987 | 2141 |
| (kg/s) | 801.9 | 898.2 | 1241 | 1102 | 187.7 | 177.5 |
| ($/h) | 8612 | 8399 | 8643 | 8469 | 8821 | 8488 |
| (MW) | 125.0 | 128.7 | 122.0 | 125.2 | 127.8 | 132.7 |
| (MW) | 3.348 | 3.444 | 2.349 | 2.697 | 0.640 | 0.651 |
| x | 0.255 | 0.232 | 0.255 | 0.238 | 0.240 | 0.197 |
| SI | 3.467 | 3.367 | 3.553 | 3.464 | 3.396 | 3.292 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seyed Mahmoudi, S.M.; Ghiami Sardroud, R.; Sadeghi, M.; Rosen, M.A. Integration of Supercritical CO2 Recompression Brayton Cycle with Organic Rankine/Flash and Kalina Cycles: Thermoeconomic Comparison. Sustainability 2022, 14, 8769. https://doi.org/10.3390/su14148769
Seyed Mahmoudi SM, Ghiami Sardroud R, Sadeghi M, Rosen MA. Integration of Supercritical CO2 Recompression Brayton Cycle with Organic Rankine/Flash and Kalina Cycles: Thermoeconomic Comparison. Sustainability. 2022; 14(14):8769. https://doi.org/10.3390/su14148769
Chicago/Turabian StyleSeyed Mahmoudi, Seyed Mohammad, Ramin Ghiami Sardroud, Mohsen Sadeghi, and Marc A. Rosen. 2022. "Integration of Supercritical CO2 Recompression Brayton Cycle with Organic Rankine/Flash and Kalina Cycles: Thermoeconomic Comparison" Sustainability 14, no. 14: 8769. https://doi.org/10.3390/su14148769
APA StyleSeyed Mahmoudi, S. M., Ghiami Sardroud, R., Sadeghi, M., & Rosen, M. A. (2022). Integration of Supercritical CO2 Recompression Brayton Cycle with Organic Rankine/Flash and Kalina Cycles: Thermoeconomic Comparison. Sustainability, 14(14), 8769. https://doi.org/10.3390/su14148769







