Predicting Pavement Structural Condition Using Machine Learning Methods
Abstract
:1. Introduction
2. Literature Review
3. Data Description
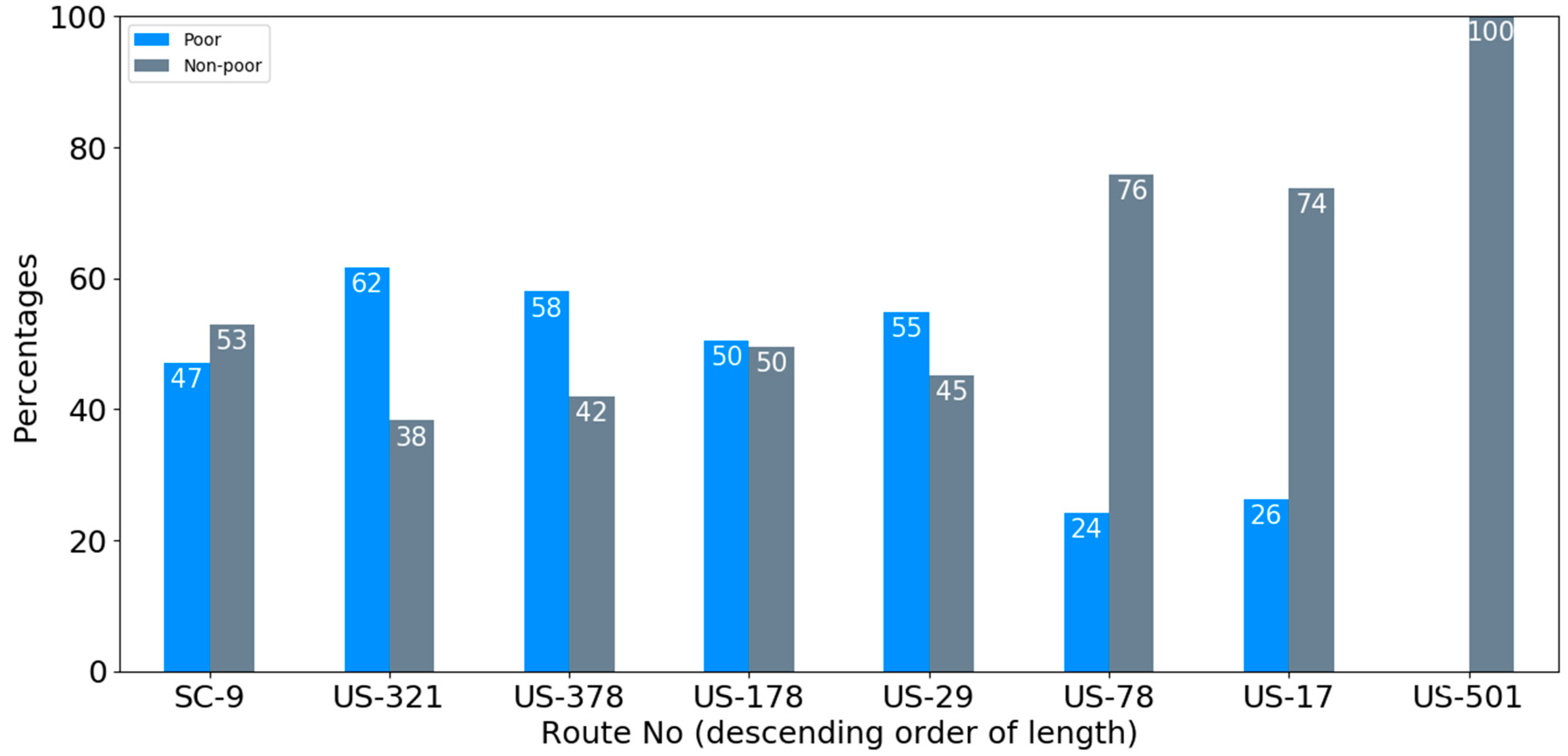
3.1. Source of TSD Data
- SC-9: 231 miles
- US-321: 216 miles
- US-378: 201 miles
- US-178: 181 miles
- US-29: 37 miles
- US-78: 36 miles
- US-17: 19 miles
- US-501: 12 miles
3.2. Data Preparation
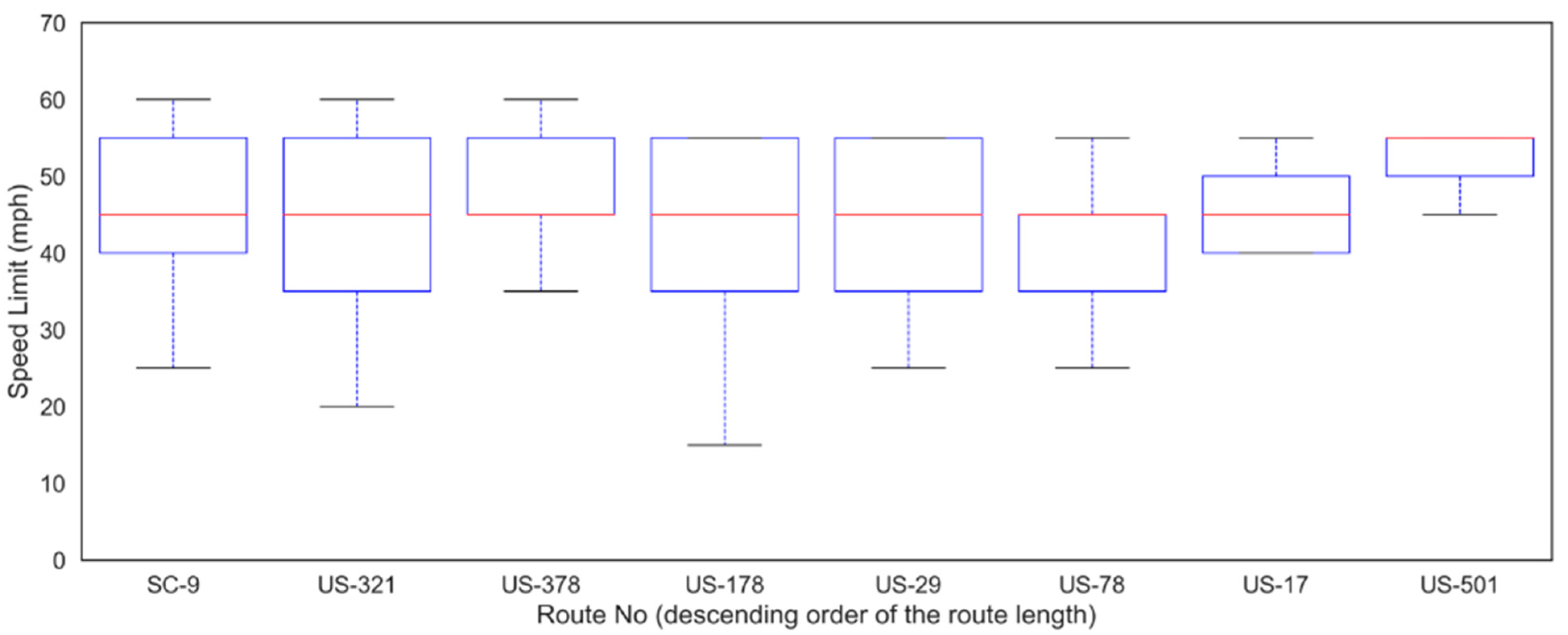
3.3. Descriptive Statistics
4. Methods
4.1. Random Forest
4.2. eXtreme Gradient Boosting (XGBoost)
4.3. Logistic Regression
4.4. Machine Learning Models’ Hyperparameters Tuning
4.5. Evaluation Metrics
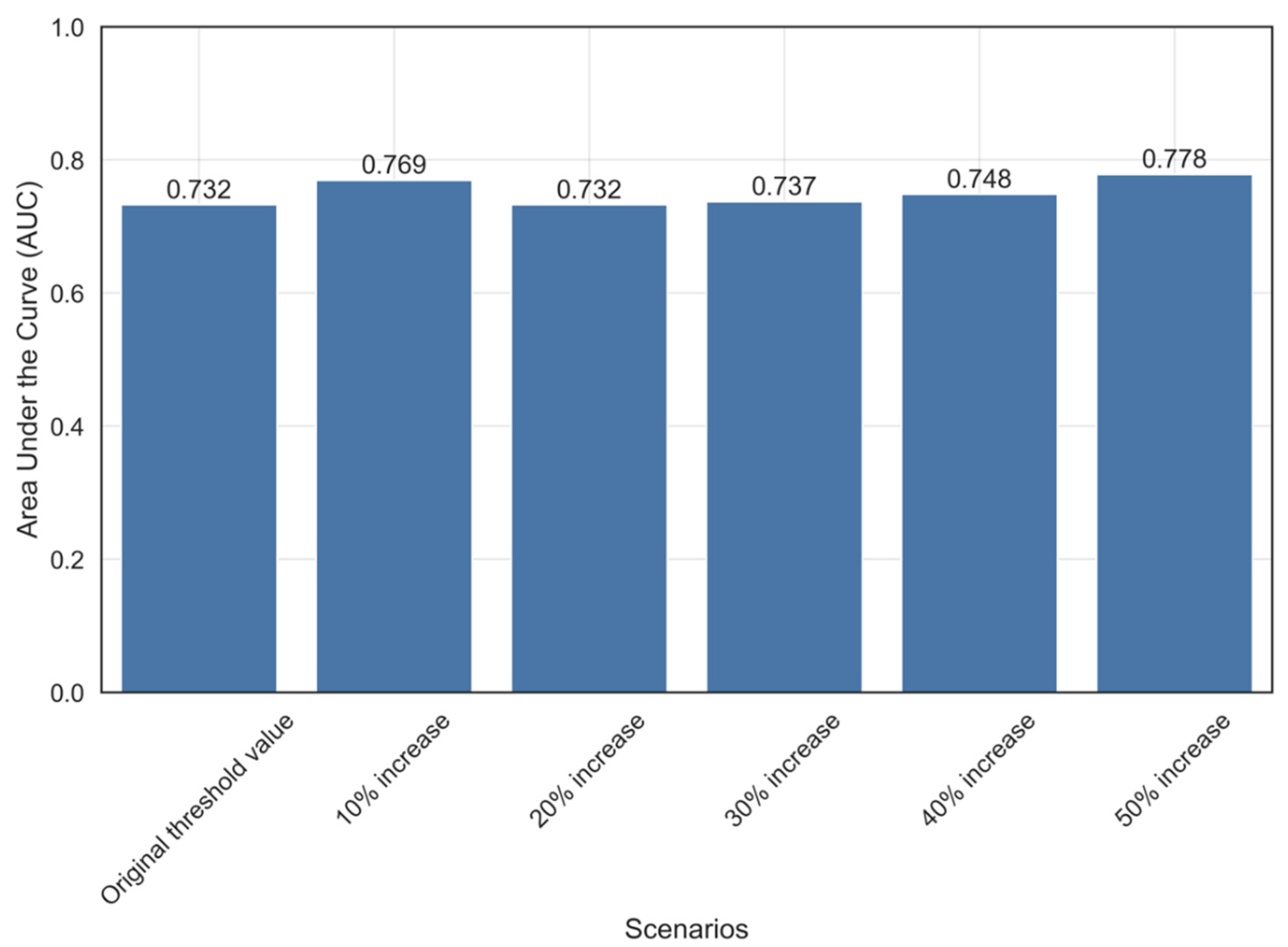
5. Results and Discussion
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shrestha, S.; Katicha, S.W.; Flintsch, G.W. Application of Traffic Speed Deflectometer for Network-Level Pavement Management. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 348–359. [Google Scholar] [CrossRef]
- Flora, W.F. Development of a Structural Index for Pavement Management: An Exploratory Analysis. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 2009. [Google Scholar]
- Bryce, J.; Flintsch, G.; Katicha, S.; Diefenderfer, B. Developing A Network-Level Structural Capacity Index for Asphalt Pavements. J. Transp. Eng. 2013, 139, 123–129. [Google Scholar] [CrossRef]
- Zaghloul, S.; He, Z.; Vitillo, N.; Kerr, J. Project Scoping Using Falling Weight Deflectometer Testing: New Jersey Experience. Transp. Res. Rec. J. Transp. Res. Board 1998, 1643, 34–43. [Google Scholar] [CrossRef]
- Ferne, B.; Langdale, P.; Wright, M.; Fairclough, R.; Sinhal, R. Developing and Implementing Traffic-Speed Network Level Structural Condition Pavement Surveys. In Proceedings of the 9th International Conference on the Bearing Capacity of Roads, Railways and Airfields, Trondheim, Norway, 25–27 June 2013. [Google Scholar]
- Steele, A.D.; Beckemeyer, C.A.; Van, T.P. Optimizing Highway Funds by Integrating RWD Data into Pavement Management Decision Making. In Proceedings of the 9th International Conference on Managing Pavement Assets, Washington, DC, USA, 18–21 May 2015. [Google Scholar]
- Katicha, W.S.; Ercisli, S.; Flintsch, G.W.; Bryce, J.M.; Diefenderfer, B.K. Development of Enhanced Pavement Deterioration Curves; VTRC 17-R7; Virginia Transportation Research Council: Charlottesville, VA, USA, 2016. [Google Scholar]
- Nasimifar, M.; Thyagarajan, S.; Chaudhari, S.; Sivaneswaran, N. Pavement Structural Capacity from Traffic Speed Deflectometer for Network Level Pavement Management System Application. Transp. Res. Rec. J. Transp. Res. Board 2019, 2673, 456–465. [Google Scholar] [CrossRef]
- Manoharan, S.; Chai, G.; Chowdhury, S. A Study of The Structural Performance of Flexible Pavements Using Traffic Speed Deflectometer. J. Test. Eval. 2018, 46, 1280–1289. [Google Scholar] [CrossRef] [Green Version]
- Chai, G.; Manoharan, S.; Golding, A.; Kelly, G.; Chowdhury, S. Evaluation of the Traffic Speed Deflectometer Data using Simplified Deflection Model. Transp. Res. Procedia 2016, 14, 3031–3039. [Google Scholar] [CrossRef] [Green Version]
- Shrestha, S.; Katicha, S.W.; Flintsch, G.W. Development of Traffic Speed Deflectometer Structural Condition Thresholds Based on Pavement Management Condition Data. In Proceedings of the 98th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 12–16 January 2018. [Google Scholar]
- Manoharan, S.; Chai, G.; Chowdhury, S. Structural Capacity Assessment of Queensland Roads Using Traffic Speed Deflectometer Data. Aust. J. Civ. Eng. 2020, 18, 219–230. [Google Scholar] [CrossRef]
- Zihan, A.U.; Elseifi, M.A.; Gaspard, K.; Zhang, Z. Development of Structural Capacity Prediction Model Based on Traffic Speed Deflectometer Measurements. Transp. Res. Rec. J. Transp. Res. Board 2018, 2672, 315–325. [Google Scholar] [CrossRef]
- Zhang, Y.; Haghani, A. A Gradient Boosting Method to Improve Travel Time Prediction. Transp. Res. Part C Emerg. Technol. 2015, 58, 308–324. [Google Scholar] [CrossRef]
- Kim, J.E.; Park, H.C.; Ham, S.W.; Kho, S.Y.; Kim, D.K. Extracting Vehicle Trajectories Using Unmanned Aerial Vehicles in Congested Traffic Conditions. J. Adv. Transp. 2019, 2019, 9060797. [Google Scholar] [CrossRef]
- Luo, X.; Li, D.; Yang, Y.; Zhang, S. Spatiotemporal Traffic Flow Prediction with KNN and LSTM. J. Adv. Transp. 2019, 2019, 4145353. [Google Scholar] [CrossRef] [Green Version]
- Eraqi, M.H.; Abouelnaga, Y.; Saad, M.H.; Moustafa, M.N. Driver Distraction Identification with an Ensemble Of Convolution Neural Networks. J. Adv. Transp. 2019, 2019, 4125865. [Google Scholar] [CrossRef]
- Xue, Q.; Wang, K.; Lu, J.J.; Liu, Y. Rapid Driving Style Recognition in Car-Following Using Machine Learning and Vehicle Trajectory Data. J. Adv. Transp. 2019, 2019, 9085238. [Google Scholar] [CrossRef] [Green Version]
- Shang, Q.; Tan, D.; Gao, S.; Feng, L. A Hybrid Method for Traffic Incident Duration Prediction Using Boa-Optimized Random Forest Combined With Neighborhood Components Analysis. J. Adv. Transp. 2019, 2019, 4202735. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Zhang, J.; Bi, J.; Wang, Y. A Machine Learning Method for Driving Range of Battery Electric Vehicles. J. Adv. Transp. 2019, 2019, 4109148. [Google Scholar] [CrossRef]
- Cheng, Y.; Chen, X.; Ding, X.; Zeng, L. Optimizing Location of Car-Sharing Stations Based On Potential Travel Demand And Present Operation Characteristic: The Case of Chengdu. J. Adv. Transp. 2019, 2019, 7546303. [Google Scholar] [CrossRef] [Green Version]
- Abdelaziz, N.; El-Hakim, R.T.A.; El-Badawy, S.M.; Afify, H.A. International Roughness Index prediction model for flexible pavements. Int. J. Pavement Eng. 2020, 21, 88–99. [Google Scholar] [CrossRef]
- Kaloop, R.M.; El-Badawy, S.M.; Ahn, J.; Sim, H.-B.; Hu, J.W.; El-Hakim, R.T.A. A Hybrid Wavelet-Optimally-Pruned Extreme Learning Machine Model for the Estimation of International Roughness Index Of Rigid Pavements. Int. J. Pavement Eng. 2022, 23, 862–876. [Google Scholar] [CrossRef]
- Guo, R.; Fu, D.; Sollazzo, G. An Ensemble Learning Model for Asphalt Pavement Performance Prediction Based on Gradient Boosting Decision Tree. Int. J. Pavement Eng. 2021; ahead-of-print. [Google Scholar] [CrossRef]
- Karballaeezadeh, N.; Tehrani, H.G.; Shadmehri, D.M.; Shamshirband, S. Estimation Of Flexible Pavement Structural Capacity Using Machine Learning Techniques. Front. Struct. Civ. Eng. 2020, 14, 1083–1096. [Google Scholar] [CrossRef]
- Justo-Silva, R.; Ferreira, A.; Flintsch, G. Review on Machine Learning Techniques for Developing Pavement Performance Prediction Models. Sustainability 2021, 13, 5248. [Google Scholar] [CrossRef]
- Rahman, M.M.; Uddin, M.M.; Gassman, S.L. Pavement Performance Evaluation Model for South Carolina. KSCE J. Civ. Eng. 2017, 21, 2695–2706. [Google Scholar] [CrossRef]
- Kim, S.; Kim, N. Development of Performance Prediction Models in Flexible Pavement Using Regression Analysis Method. KSCE J. Civ. Eng. 2017, 10, 91–96. [Google Scholar] [CrossRef]
- Qu, L.; Zhang, Y.; Harvey, J.T. Estimation of Truck Traffic Inputs for Mechanistic -Empirical Pavement Design in California. Transp. Res. Rec. J. Transp. Res. Board 2009, 2095, 62–72. [Google Scholar]
- Chou, C.P.J. Effect of Overloaded Heavy Vehicles On Pavement and Bridge Design. Transp. Res. Rec. J. Transp. Res. Board 1996, 1539, 58–65. [Google Scholar] [CrossRef]
- Salama, K.H.; Chatti, K.; Lyles, R.W. Effect of Heavy Multiple Axle Trucks on Flexible Pavement Damage Using In-Service Pavement Performance Data. J. Transp. Eng. 2006, 132, 763–770. [Google Scholar] [CrossRef] [Green Version]
- Mshali, R.M.; Steyn, W.J. Effect of Truck Speed on The Response of Flexible Pavement Systems to Traffic Loading. Int. J. Pavement Eng. 2020, 23, 1213–1225. [Google Scholar] [CrossRef]
- Jiang, X.; Abdel-Aty, M.; Hu, J.; Lee, J. Investigation Macro-Level Hotzone Identification and Variable Importance Using Big Data. Neurocomputing 2016, 181, 53–63. [Google Scholar] [CrossRef]
- Gong, H.; Sun, Y.; Huang, B. Gradient Boosted Models for Enhancing Fatigue Cracking Prediction In Mechanistic-Empirical Pavement Design Guide. J. Transp. Eng. Part B Pavements 2019, 145, 04019014. [Google Scholar] [CrossRef]
- Rezapour, M.; Molan, A.M.; Ksaibati, K. Analyzing Injury Severity of Motorcycle At-Fault Crashes Using Machine Learning Techniques, Decision Tree And Logistic Regression Models. Int. J. Transp. Sci. Technol. 2020, 9, 89–99. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A Random Forest Guided Tour. TEST 2016, 25, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Li, J.; An, X.; Li, Q.; Wang, C.; Yu, H.; Zhou, X.; Geng, Y. Application of XGBoost Algorithm in the Optimization of Pollutant concentration. Atmos. Res. 2022, 276, 106238. [Google Scholar] [CrossRef]
- McDowell, I. Measuring Health: A Guide to Rating Scales and Questionnaires; Oxford University Press: Oxford, UK, 2006. [Google Scholar]







| Pavement Condition | Percentage | SCI12 Thresholds |
|---|---|---|
| Good | 28% | <1.6 |
| Fair | 27% | 1.6–3.3 |
| Poor | 45% | >3.3 |
| Model | Parameters | Optimal Values |
|---|---|---|
| RF | Randomly Selected Predictors | 2 |
| XGBoost | Boosting Iterations | 250 |
| Maximum Tree Depth | 3 | |
| Shrinkage | 0.1 | |
| Minimum Loss Reduction | 0 | |
| Subsample Ratio of Columns | 1 | |
| Minimum Sum of Instance Weight | 0.8 | |
| Subsample Percentage | 1 |
| Predicted Class | True Class | Accuracy | Sensitivity/ Recall | Precision | F1-Score | ||
| Poor Structural Condition | Non-Poor Structural Condition | ||||||
| Poor Structural Condition | 82 | 47 | 0.65 | 0.68 | 0.64 | 0.66 | |
| Non-poor Structural Condition | 39 | 77 | |||||
| Predicted Class | True Class | Accuracy | Sensitivity/ Recall | Precision | F1-Score | ||
| Poor Structural Condition | Non-Poor Structural Condition | ||||||
| Poor Structural Condition | 91 | 45 | 0.69 | 0.75 | 0.67 | 0.71 | |
| Non-poor Structural Condition | 30 | 79 | |||||
| Predicted Class | True Class | Accuracy | Sensitivity/ Recall | Precision | F1-Score | ||
| Poor Structural Condition | Non-Poor Structural Condition | ||||||
| Poor Structural Condition | 90 | 74 | 0.57 | 0.74 | 0.55 | 0.63 | |
| Non-poor Structural Condition | 31 | 50 | |||||
| Model | Variable | Importance Value |
|---|---|---|
| RF | AADT | 100 |
| Truck Percentage | 77.7 | |
| Speed limit | 0 | |
| XGBoost | AADT | 100 |
| Truck Percentage | 58.94 | |
| Speed limit | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, N.S.; Huynh, N.; Gassman, S.; Mullen, R.; Pierce, C.; Chen, Y. Predicting Pavement Structural Condition Using Machine Learning Methods. Sustainability 2022, 14, 8627. https://doi.org/10.3390/su14148627
Ahmed NS, Huynh N, Gassman S, Mullen R, Pierce C, Chen Y. Predicting Pavement Structural Condition Using Machine Learning Methods. Sustainability. 2022; 14(14):8627. https://doi.org/10.3390/su14148627
Chicago/Turabian StyleAhmed, Nazmus Sakib, Nathan Huynh, Sarah Gassman, Robert Mullen, Charles Pierce, and Yuche Chen. 2022. "Predicting Pavement Structural Condition Using Machine Learning Methods" Sustainability 14, no. 14: 8627. https://doi.org/10.3390/su14148627
APA StyleAhmed, N. S., Huynh, N., Gassman, S., Mullen, R., Pierce, C., & Chen, Y. (2022). Predicting Pavement Structural Condition Using Machine Learning Methods. Sustainability, 14(14), 8627. https://doi.org/10.3390/su14148627







