Optimization of a Water-Saving and Fertilizer-Saving Model for Enhancing Xinjiang Korla Fragrant Pear Yield, Quality, and Net Profits under Water and Fertilizer Coupling
Abstract
:1. Introduction
2. Materials and Methods
2.1. Overview of the Study Area
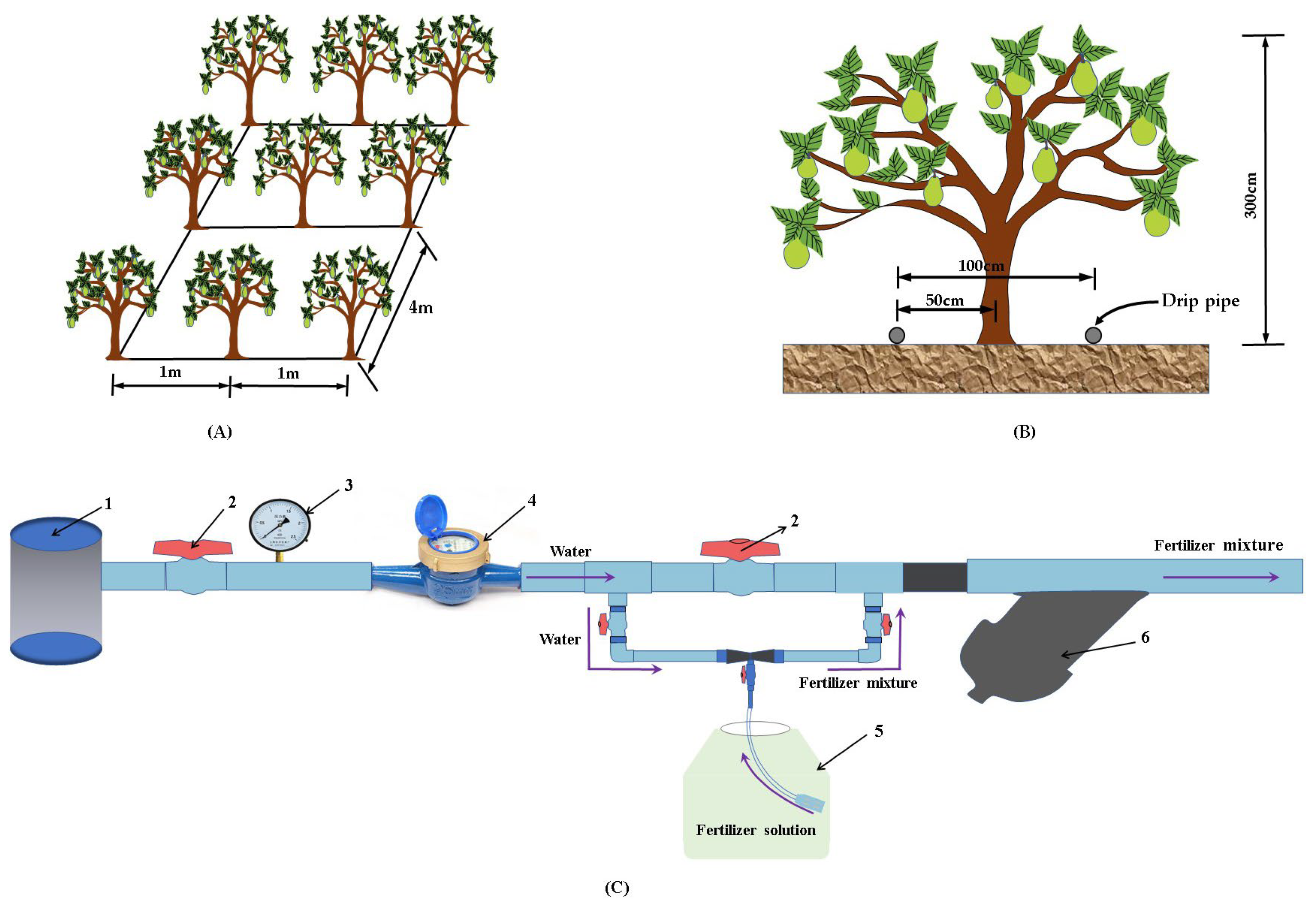
2.2. Experimental Design
2.3. Testing Indices and Methods
2.3.1. Single Fruit Weight and Yield
2.3.2. Fragrant Pear Quality
2.3.3. IWUE
2.3.4. PFP
2.3.5. Net Profits
2.3.6. Principal Component Analysis
2.4. Data Processing
3. Results
3.1. The Effect of Water and Fertilizer Coupling on the Comprehensive Quality of Fragrant Pear
3.2. A Comprehensive Evaluation Model of Fragrant Pear Quality
3.3. Effect of Water and Fertilizer Coupling on Fragrant Pear Yield
3.4. Effect of Water–Fertilizer Coupling on IWUE, PFP, and Net Profits of Fragrant Pear Irrigation
3.5. Multi-Objective Solution for Optimal Water and Fertilizer Amount
4. Discussion
4.1. Effect of Water–Fertilizer Coupling on the Comprehensive Quality of Fragrant Pear
4.2. Effect of Water–Fertilizer Coupling on the Comprehensive Quality of Fragrant Pear
4.3. Optimal Water and Fertilizer Solution
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, J.; Lu, J.; He, Z.; Zhang, F.; Zhang, S.; Zhang, H. Investigations into the production of volatile compounds in Korla fragrant pears (Pyrus sinkiangensis Yu). Food Chem. 2020, 302, 125337. [Google Scholar] [CrossRef] [PubMed]
- Niu, Y.; Chen, X.; Zhou, W.; Li, W.; Zhao, S.; Nasir, M.; Dong, S.; Zhan, S.; Liao, K. Genetic relationship between the ‘Korla fragrant pear’ and local pear varieties in xinjiang based on floral organ characteristics. Sci. Hortic. 2019, 257, 108621. [Google Scholar] [CrossRef]
- Feng, Z.; Zhiqin, J.; Xiaoguang, C.; Shiqiang, L.; Tianming, H. The Development Factors of Pyrus sinkiangensis ‘Korla Xiangli’lndustry. Chin. Agric. Sci. Bull. 2021, 37, 159–164, (In Chinese with English Abstract). [Google Scholar]
- Dou, M.; Wang, Y. The construction of a water rights system in China that is suited to the strictest water resources management system. Water Sci. Technol.-Water Supply 2017, 17, 238–245. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, E.; Miao, C. Fertilizer Use in China: The Role of Agricultural Support Policies. Sustainability 2019, 11, 4391. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.; Li, R.; Song, W.; Wu, T.; Sun, S.; Hu, S.; Han, T.; Wu, C. Responses of Branch Number and Yield Component of Soybean Cultivars Tested in Different Planting Densities. Agriculture 2021, 11, 69. [Google Scholar] [CrossRef]
- Jia, H.; Wang, Z.; Zhang, J.; Li, W.; Ren, Z.; Jia, Z.; Wang, Q. Effects of biodegradable mulch on soil water and heat conditions, yield and quality of processing tomatoes by drip irrigation. J. Arid. Land 2020, 12, 819–836. [Google Scholar] [CrossRef]
- Wezel, A.; Casagrande, M.; Celette, F.; Vian, J.-F.; Ferrer, A.; Peigne, J. Agroecological practices for sustainable agriculture. A review. Agron. Sustain. Dev. 2014, 34, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Hongbo, L.; Yungang, B.; Jianghui, Z.; Ping, D. Effect of water fertilizer coupling on yield of fragrant pear. J. Irrig. Drain. 2015, 34, 15–17, (In Chinese with English Abstract). [Google Scholar]
- Qing, Z.; Fangliang, L.; Qingbo, K.; Mulai, Z. Effect of different reduced fertigation modes on the yield, quality and economic benefits of honey pomelo. J. Fruit Sci. 2021, 38, 361–371. [Google Scholar] [CrossRef]
- Li, B.; Shukla, M.K.; Du, T. Combined environmental stresses induced by drip irrigation positively affect most solar greenhouse grown tomato fruit quality. Sci. Hortic. 2021, 288, 110334. [Google Scholar] [CrossRef]
- Yanan, L.; Meijian, B.; Baozhong, Z.; Xianbing, W.; Yuan, S. Responses of Pear Tree Growth and Fruit Quality Indexes to Water and Nitrogen Coupling and Correlation Degree Analysis. Water Sav. Irrig. 2020, 4, 52–56, (In Chinese with English Abstract). [Google Scholar]
- Liu, K.; Wang, X.; Young, M. Effect of bentonite/potassium sorbate coatings on the quality of mangos in storage at ambient temperature. J. Food Eng. 2014, 137, 16–22. [Google Scholar] [CrossRef]
- Chen, X.; Feng, S.; Qi, Z.; Sima, M.W.; Zeng, F.; Li, L.; Cheng, H.; Wu, H. Optimizing Irrigation Strategies to Improve Water Use Efficiency of Cotton in Northwest China Using RZWQM2. Agriculture 2022, 12, 383. [Google Scholar] [CrossRef]
- Zou, Y.; Saddique, Q.; Ali, A.; Xu, J.; Khan, M.I.; Qing, M.; Azmat, M.; Cai, H.; Siddique, K.H.M. Deficit irrigation improves maize yield and water use efficiency in a semi-arid environment. Agric. Water Manag. 2021, 243, 106483. [Google Scholar] [CrossRef]
- Sun, G.; Hu, T.; Liu, X.; Peng, Y.; Leng, X.; Li, Y.; Yang, Q. Optimizing irrigation and fertilization at various growth stages to improve mango yield, fruit quality and water-fertilizer use efficiency in xerothermic regions. Agric. Water Manag. 2022, 260, 107296. [Google Scholar] [CrossRef]
- Li, W.; Yang, M.; Wang, J.; Wang, Z.; Fan, Z.; Kang, F.; Wang, Y.; Luo, Y.; Kuang, D.; Chen, Z.; et al. Agronomic Responses of Major Fruit Crops to Fertilization in China: A Meta-Analysis. Agronomy 2020, 10, 15. [Google Scholar] [CrossRef] [Green Version]
- Xia, C.; Liu, Z.; Suo, X.; Cao, S. Quantifying the net benefit of land use of fruit trees in China. Land Use Policy 2020, 90, 104276. [Google Scholar] [CrossRef]
- Xiubing, C.; Lin, P.; Qingli, W.; Xinxin, X. Water-fertilizer coupling effects and its optimization in greenhouse tomato production. J. Nanjing Agric. Univ. 2006, 29, 138–141, (In Chinese with English Abstract). [Google Scholar]
- Pengbo, W.; Jianming, L.; Juanjuan, D.; Guoying, L.; Tonghua, P.; Qingjie, D.; Yibo, C. Effect of Water and Fertilizer Coupling on Quality, Yield and Water Use Efficiency of Tomato Cultivated by Organic Substrate in Bag. Sci. Agric. Sin. 2015, 48, 314–323, (In Chinese with English Abstract). [Google Scholar]
- Yi, C.; Yonghong, Z.; Geng, Z.; Zhonglili, Z.; Feifei, S.; Xin, Z. Effects of Water and Fertilizer Coupling on Yield, Quality and Utilization of Protected Grape. J. Agric. Mech. Res. 2021, 43, 186–193. [Google Scholar] [CrossRef]
- Yingying, X.; Fucang, Z.; Lifeng, W. Determination of optimal amount of irrigation and fertilizer under drip fertigated system based on tomato yield, quality, water and fertilizer use efficiency. Trans. Chin. Soc. Agric. Eng. 2015, 31, 110–121, (In Chinese with English Abstract). [Google Scholar]
- Thompson, T.L.; Doerge, T.A.; Godin, R.E. Nitrogen and water interactions in subsurface drip-irrigated cauliflower: II. Agronomic, economic, and environmental outcomes. Soil Sci. Soc. Am. J. 2000, 64, 412–418. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; Zeng, H.; Zhu, W.; Yan, N.; Ma, Z. Enhancing China’s Three Red Lines strategy with water consumption limitations Comment. Sci. Bull. 2021, 66, 2057–2060. [Google Scholar] [CrossRef]
- Bessho, H.; Kudo, K.; Omori, J.; Inomata, Y.; Wada, M.; Masuda, T.; Nakamoto, Y.; Fujisawa, H.; Suzuki, Y. A portable non-destructive quality meter for understanding fruit soluble solids in apple canopies. In Proceedings of the 8th International Symposium on Canopy, Rootstocks and Environmental Physiology in Orchard Systems, Budapest, Hungary, 13–18 June 2007; pp. 593–597. [Google Scholar]
- Lan, H.; Wang, Z.; Niu, H.; Zhang, H.; Zhang, Y.; Tang, Y.; Liu, Y. A nondestructive testing method for soluble solid content in Korla fragrant pears based on electrical properties and artificial neural network. Food Sci. Nutr. 2020, 8, 5172–5181. [Google Scholar] [CrossRef]
- Zhang, H.; Chi, D.; Wang, Q.; Fang, J.; Fang, X. Yield and Quality Response of Cucumber to Irrigation and Nitrogen Fertilization Under Subsurface Drip Irrigation in Solar Greenhouse. Agric. Sci. China 2011, 10, 921–930. [Google Scholar] [CrossRef]
- Jukneviciene, E.; Cerniauskiene, J.; Kulaitiene, J.; Jukneviciene, Z. Oil pumpkins—Important source of antioxidants. J. Food Agric. Environ. 2013, 11, 156–158, (In Chinese with English Abstract). [Google Scholar]
- De Oliveira, L.M.A.; Dos Santos, V.B.; Da Silva, E.K.N.; Lopes, A.S.; Dantas-Filho, H.A. An environment-friendly spot test method with digital imaging for the micro-titration of citric fruits. Talanta 2020, 206, 120219. [Google Scholar] [CrossRef]
- Sunderwirth, S.G.; Olson, G.G.; Johnson, G. Paper Chromatography-Anthrone Determination of Sugars. J. Chromatogr. 1964, 16, 176–180. [Google Scholar] [CrossRef]
- Inoue, H.; Tateishi, A. The application of non-destructive handy hardness meter for assessment of avocado fruit firmness. In Proceedings of the XXVth International Horticultural Congress, Brussels, Belgium, 2–7 August 1998. [Google Scholar]
- Xue, Y.; Xu, S.; Xue, C.; Wang, R.; Zhang, M.; Li, J.; Zhang, S.; Wu, J. Pearprocess: A new phenotypic tool for stone cell trait evaluation in pear fruit. J. Integr. Agric. 2020, 19, 1625–1634. [Google Scholar] [CrossRef]
- National Public Service Platform for Standards Information. Available online: http://std.samr.gov.cn/gb/search/gbDetailed?id=71F772D767C7D3A7E05397BE0A0AB82A (accessed on 1 January 2006).
- National Public Service Platform for Standards Information. Available online: http://std.samr.gov.cn/hb/search/stdHBDetailed?id=8B1827F18E5CBB19E05397BE0A0AB44A (accessed on 20 December 2002).
- Jia, H.; Zheng, L. Irrigation Water Use Efficiency Based on the Deficit Irrigation Theories. In Proceedings of the 3rd International Conference on Energy, Environment and Sustainable Development (EESD 2013), Shanghai, China, 12–13 November 2014. [Google Scholar]
- Omezzine, A.; Zaibet, L. Management of modern irrigation systems in oman: Allocative vs. irrigation efficiency. Agric. Water Manag. 1998, 37, 99–107. [Google Scholar] [CrossRef]
- Garavito, J.; Herrera, A.O.; Castellanos, D.A. A combined mathematical model to represent transpiration, respiration, and water activity changes in fresh cape gooseberry (Physalis peruviana) fruits. Biosyst. Eng. 2021, 208, 152–163. [Google Scholar] [CrossRef]
- Andreu, L.; Hopmans, J.W.; Schwankl, L.J. Spatial and temporal distribution of soil water balance for a drip-irrigated almond tree. Agric. Water Manag. 1997, 35, 123–146. [Google Scholar] [CrossRef]
- Ierna, A.; Pandino, G.; Lombardo, S.; Mauromicale, G. Tuber yield, water and fertilizer productivity in early potato as affected by a combination of irrigation and fertilization. Agric. Water Manag. 2011, 101, 35–41. [Google Scholar] [CrossRef]
- Zou, H.; Fan, J.; Zhang, F.; Xiang, Y.; Wu, L.; Yan, S. Optimization of drip irrigation and fertilization regimes for high grain yield, crop water productivity and economic benefits of spring maize in Northwest China. Agric. Water Manag. 2020, 230, 105986. [Google Scholar] [CrossRef]
- Subasi, I. Agro-Morphological Characterization and Some Seed Characteristics of Wild Crambe (Brassicaceae) Species in Turkey. Sustainability 2022, 14, 287. [Google Scholar] [CrossRef]
- Rajametov, S.N.; Lee, K.; Jeong, H.-B.; Cho, M.-C.; Nam, C.-W.; Yang, E.-Y. Physiological Traits of Thirty-Five Tomato Accessions in Response to Low Temperature. Agriculture 2021, 11, 792. [Google Scholar] [CrossRef]
- Li, X.; Liu, H.; Li, J.; He, X.; Gong, P.; Lin, E.; Li, K.; Li, L.; Binley, A. Experimental study and multi-objective optimization for drip irrigation of grapes in arid areas of northwest China. Agric. Water Manag. 2020, 232, 106039. [Google Scholar] [CrossRef]
- Hou, Y.; Wang, Z.; Ding, H.; Li, W.; Wen, Y.; Zhang, J.; Dou, Y. Evaluation of Suitable Amount of Water and Fertilizer for Mature Grapes in Drip Irrigation in Extreme Arid Regions. Sustainability 2019, 11, 2063. [Google Scholar] [CrossRef] [Green Version]
- Zhenhua, W.; Qingyong, B.; Wenhao, L.; Chaoyang, L. Suitable water and fertilizer amount for mature jujube with drip-irrigation under fertigation in southern Xinjiang sandy area. Trans. Chin. Soc. Agric. Eng. 2018, 34, 96–104, (In Chinese with English Abstract). [Google Scholar]
- Liu, X.; Li, S.; Feng, X.; Li, L. Study on Cell Wall Composition, Fruit Quality and Tissue Structure of Hardened ‘Suli’ Pears (Pyrus bretschneideri Rehd). J. Plant Growth Regul. 2021, 40, 2007–2016. [Google Scholar] [CrossRef]
- Zheng, P.; Zhang, M.; Wang, Z.; Wang, T.; Tang, L.; Ma, E.; Liu, J.; Shi, F. Comprehensive evaluation of the Fruit Quality of the Main Cultivars of Pear (Pyrus spp.) in North China. Erwerbs-Obstbau 2021, 64, 219–227. [Google Scholar] [CrossRef]
- Song, X.H.; Xie, K.; Zhao, H.B.; Li, Y.L.; Dong, C.X.; Xu, Y.C.; Shen, Q.R. Effects of Different Organic Fertilizers on Tree Growth, Yield, Fruit Quality, and Soil Microorganisms in a Pear Orchard. Eur. J. Hortic. Sci. 2012, 77, 204–210, (In Chinese with English Abstract). [Google Scholar]
- Melissa, V.; Luigi, M.; Demetrio, P.G.; Alexandra, B.; Kushtrim, B.; Luca, C.G.; Brunella, M. Deficit Irrigation as a Tool to Optimize Fruit Quality in Abbé Fetél Pear. Agronomy 2021, 11, 1141. [Google Scholar]
- Mattar, M.A.; Soliman, S.S.; Al-Obeed, R.S. Effects of Various Quantities of Three Irrigation Water Types on Yield and Fruit Quality of ‘Succary’ Date Palm. Agronomy 2021, 11, 796. [Google Scholar] [CrossRef]
- Sihua, Y.; Yanming, G.; Minjiao, T.; Yongqiang, T.; Jianshe, L. Comprehensive evaluation of effects of various carbon-rich amendments on tomato production under continuous saline water irrigation: Overall soil quality, plant nutrient uptake, crop yields and fruit quality. Agric. Water Manag. 2021, 255, 106995. [Google Scholar]
- Lu, J.; Shao, G.; Gao, Y.; Zhang, K.; Wei, Q.; Cheng, J. Effects of water deficit combined with soil texture, soil bulk density and tomato variety on tomato fruit quality: A meta-analysis. Agric. Water Manag. 2021, 243, 106427. [Google Scholar] [CrossRef]
- Babak, M.; Qifu, M.; Reza, T.A.; Reza, F.; Farzaneh, B. Nutritional, Yield, and Quality Responses of Apple, Pear, and Cherry to Calcium Nitrate Application. Commun. Soil Sci. Plant Anal. 2021, 52, 1132–1148. [Google Scholar]
- Jiankai, Z.; Hongxia, C.; Xiaoyan, P.; Xueping, N. Optimization of drip irrigation and topdressing nitrogen based on apple yield and quality in Northern Shaanxi. Agric. Res. Arid. Areas 2020, 38, 143–152, (In Chinese with English Abstract). [Google Scholar]
- Zhou, H.; Zhang, F.; Kjelgren, R.; Wu, L.; Gong, D.; Zhao, N.; Yin, D.; Xiang, Y.; Li, Z. Effects of Water and Fertilizer Coupling on Yield, Fruit Quality and Water and Fertilizer Use Efficiency of Young Apple Tree. J. Integr. Agric. 2017, 16, 1173–1183. [Google Scholar] [CrossRef]
- Shen, R.; Wang, K.; Zhang, Y.; Yang, L.; Mu, J.; Zhao, L. Experimental study on crop yield, water use and root nitrogen uptake under water fertilizer coupling. Trans. Chin. Soc. Agric. Eng. 2001, 5, 35–38, (In Chinese with English Abstract). [Google Scholar]
- Faloye, O.T.; Alatise, M.O.; Ajayi, A.E.; Ewulo, B.S. Effects of biochar and inorganic fertiliser applications on growth, yield and water use efficiency of maize under deficit irrigation. Agric. Water Manag. 2019, 217, 165–178. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, F.; Wang, G.; Chen, J.; Huang, G.; Liang, Y. Causes of low yield and measures for increasing yield of Korla Fragrant Pear. Deciduous Fruits 2021, 53, 77–78, (In Chinese with English Abstract). [Google Scholar]
- Feng, Y.; Wang, Y.; Wang, Y. Geng, W.; Fan, G.; Zhang, S. Effects of Different Fertilizer Treatments on Planting Benefit of Korla Fragrant Pear. Tianjin Agric. Sci. 2021, 27, 25–29, (In Chinese with English Abstract). [Google Scholar]
- Xiao, Z.; Jiang, W.; Yu, H. Research Progress on coupling effect of crop water and fertilizer. Crops 2007, 53, 18–22, (In Chinese with English Abstract). [Google Scholar]
- Wang, Q.D.; Chen, B.L.; Yusufujiang, Y.; Wang, C.; Chai, Z.P. Characteristics of absorption, utilization, and distribution of 15N-urea for Korla fragrant pear in spring. Ying Yong Sheng Tai Xue Bao J. Appl. Ecol. 2018, 29, 1443–1449. [Google Scholar] [CrossRef]
- He, C.; Ali, K.; Zare, M. Effects of Different Fertilizer Amount on Chloroplast Ultra-structure and Photosynthesis of Korla Fragrant Pear. In Proceedings of the 3rd Conference on Horticulture Science and Technology (CHST 2012), Beijing, China, 22–23 December 2012; pp. 6–14. [Google Scholar]






| Soil Depth (cm) | Soil Texture | Particle Mass Fraction (%) | Soil Salt Content (g kg−1) | Bulk Density (g cm−1) | Saturated Water Content (%) | Field Water Holding Capacity (%) | Wilting Point (%) | ||
|---|---|---|---|---|---|---|---|---|---|
| Sand | Silt | Clay | |||||||
| 0–20 | Sandy clay | 55.48 | 36.34 | 8.18 | 8.16 | 1.38 | 34.49 | 22.31 | 6.95 |
| 20–40 | Sandy clay | 57.72 | 35.18 | 7.1 | 10.77 | 1.43 | 34.36 | 19.14 | 7.31 |
| 40–60 | Sandy clay | 53.82 | 37.7 | 8.48 | 10.38 | 1.50 | 36.32 | 20.04 | 7.41 |
| 60–80 | Sandy clay | 45.94 | 47.07 | 6.99 | 9.01 | 1.50 | 34.47 | 19.54 | 7.55 |
| 80–100 | Sandy clay | 49.15 | 40.17 | 10.68 | 7.62 | 1.39 | 33.14 | 18.28 | 7.85 |
| Organic Matter (g kg−1) | Total Nitrogen (g kg−1) | Total Phosphorus (%) | Alkaline Hydrolyzed Nitrogen (mg kg−1) | Available Phosphorus (mg kg−1) | Available Potassium (mg kg−1) |
|---|---|---|---|---|---|
| 15.0 | 0.6 | 0.139 | 181.6 | 22.2 | 200.9 |
| Growth Period | Irrigation Date | Fertilization Date | Irrigation Amount (m3 ha−1) | Fertilization Amount (kg ha−1) | |||||
|---|---|---|---|---|---|---|---|---|---|
| W1 | W2 | W3 | F1 | F2 | F3 | F4 | |||
| Budding period (26 March 2021–8 April 2021) | 7 April 2021 | / | 477 | 614 | 750 | / | / | / | / |
| Florescence (9 April 2021–21 April 2021) | 21 April 2021 | / | 477 | 614 | 750 | / | / | / | / |
| Twig growth stage (22 April 2021–14 May 2021) | 10 May 2021 | / | 477 | 614 | 750 | / | / | / | / |
| Fruit setting period (15 May 2021–8 July 2021) | 26 May 2021 | 477 | 614 | 750 | / | / | / | / | |
| 14 June 2021 | 14 June 2021 | 477 | 614 | 750 | 112.5 | 125 | 137.5 | 150 | |
| 30 June 2021 | 30 June 2021 | 477 | 614 | 750 | 112.5 | 125 | 137.5 | 150 | |
| Fruit swelling period (9 July 2021–28 August 2021) | 16 July 2021 | 16 July 2021 | 477 | 614 | 750 | 112.5 | 125 | 137.5 | 150 |
| 28 July 2021 | 28 July 2021 | 477 | 614 | 750 | 112.5 | 125 | 137.5 | 150 | |
| 9 August 2021 | 9 August 2021 | 477 | 614 | 750 | 112.5 | 125 | 137.5 | 150 | |
| 21 August 2021 | 21 August 2021 | 477 | 614 | 750 | 112.5 | 125 | 137.5 | 150 | |
| Mature period (29 August 2021–14 September 2021) | 29 August 2021 | / | 477 | 614 | 750 | / | / | / | / |
| Total | / | / | 5250 | 6750 | 8250 | 675 | 750 | 825 | 900 |
| Quality Factors | Indicators | ||
|---|---|---|---|
| Grade A | Grade A | Grade A | |
| Soluble sugar | ≥12.5 | ≥12.0 | ≥11.0 |
| Fruit shape index | 1.0–1.1 | 1.1–1.2 | >1.2, <1.0 |
| Single fruit weigh | 120–160 | 100–120 | 80–100 |
| Pulp hardness | 4.9–6.8 | 6.8–7.8 | >7.8, <4.9 |
| Stone cell | ≤0.5 | ≤0.6 | ≤1.0 |
| Treatment | Soluble Solids (%) | Vitamin C (mg 100 g−1) | Titratable Acid (%) | Total Sugar (%) | Ratio of Sugar to Acid | Ratio of Soluble Sugar to Acid | Fruit Shape Index | Single Fruit Weight (g) | Peel Hardness (kg cm−2) | Pulp Hardness (kg cm−2) | Transverse Diameter of Kernel (mm) | Stone Cell (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| W1F1 | 11.86 ± 0.26 g | 3.67 ± 0.43 c | 0.24 ± 0.06 e | 7.08 ± 0.04 e | 30.76 ± 7.29 ab | 51.51 ± 12.33 ab | 1.14 ± 0.07 abc | 98.52 ± 19.45 c | 9.98 ± 0.12 f | 5.98 ± 0.06 e | 27.36 ± 3.21 ab | 0.21 ± 0.03 bcd |
| W1F2 | 12.90 ± 0.18 cde | 4.15 ± 1.30c | 0.47 ± 0.05 a | 7.22 ± 0.06 de | 15.49 ± 1.7 e | 27.64 ± 2.59 e | 1.18 ± 0.08 ab | 109.07 ± 21.89 abc | 10.68 ± 0.61 cdef | 6.50 ± 0.25 cde | 25.73 ± 1.97 b | 0.28 ± 0.03 a |
| W1F3 | 12.67 ± 0.37 de | 9.61 ± 1.22b | 0.33 ± 0.06 cd | 8.05 ± 0.41 ab | 24.99 ± 5.3 abc | 39.23 ± 7.51 cd | 1.20 ± 0.11 a | 106.35 ± 23.13 abc | 10.35 ± 0.1 def | 7.02 ± 0.21 bcd | 27.22 ± 2.25 ab | 0.11 ± 0.01 ef |
| W1F4 | 12.02 ± 0.13 fg | 12.29 ± 2.30ab | 0.44 ± 0.07 ab | 7.62 ± 0.71 abcde | 17.66 ± 3.71 de | 27.66 ± 3.69 e | 1.13 ± 0.07 abc | 101.25 ± 29.06 bc | 10.01 ± 0.32 f | 6.15 ± 0.55 cde | 29.39 ± 2.72 a | 0.10 ± 0.03 f |
| W2F1 | 12.01 ± 0.14 fg | 11.90 ± 1.75 ab | 0.37 ± 0.03 bc | 7.34 ± 0.19 cde | 19.97 ± 2.2 cde | 32.62 ± 2.6 de | 1.17 ± 0.07 ab | 112.62 ± 21.43 abc | 10.25 ± 0.3 ef | 7.12 ± 0.52 abc | 25.32 ± 7.51 b | 0.22 ± 0.02 bc |
| W2F2 | 13.65 ± 0.20 a | 11.63 ± 0.63 ab | 0.42 ± 0.04 ab | 7.44 ± 0.17 bcde | 17.84 ± 1.87 de | 32.69 ± 2.78 de | 1.18 ± 0.08 ab | 123.59 ± 24.39 a | 11.52 ± 0.21 ab | 8.00 ± 0.83 a | 24.35 ± 3.16 b | 0.18 ± 0.02 cde |
| W2F3 | 13.47 ± 0.44 ab | 11.68 ± 0.34 ab | 0.37 ± 0.02 bc | 8.26 ± 0.33 a | 22.35 ± 1.29 cde | 36.44 ± 1.51 cde | 1.13 ± 0.06 bc | 118.93 ± 24.32 ab | 11.00 ± 0.24 abcd | 7.01 ± 0.62 bcd | 27.53 ± 4.48 ab | 0.14 ± 0.01 efg |
| W2F4 | 12.66 ± 0.10 de | 11.39 ± 1.88 ab | 0.27 ± 0.02 de | 8.05 ± 0.38 ab | 29.90 ± 2.43 ab | 47.02 ± 2.96 abc | 1.16 ± 0.09 c | 106.96 ± 19.18 abc | 10.89 ± 0.37 bcde | 6.52 ± 0.33 cde | 26.22 ± 2.5 ab | 0.16 ± 0.02 def |
| W3F1 | 13.02 ± 0.10 bcd | 14.16 ± 1.03 a | 0.31 ± 0.02 cde | 7.86 ± 0.07 abcd | 25.43 ± 1.51 abc | 42.12 ± 2.57 bcd | 1.13 ± 0.08 bc | 107.36 ± 13.39 abc | 10.45 ± 0.24 cdef | 7.00 ± 0.02 bcd | 25.68 ± 4.52 b | 0.19 ± 0.03 bcd |
| W3F2 | 13.27 ± 0.26 abc | 11.95 ± 2.38ab | 0.25 ± 0.02 de | 7.91 ± 0.19 abc | 31.77 ± 2.83 a | 53.25 ± 3.77 a | 1.17 ± 0.06 ab | 121.00 ± 24.62 a | 11.67 ± 0.74 a | 7.80 ± 0.39 ab | 25.47 ± 5.01 b | 0.21 ± 0.02 bc |
| W3F3 | 13.01 ± 0.18 bcd | 10.36 ± 0.64 b | 0.32 ± 0.05 cde | 8.01 ± 0.35 ab | 25.53 ± 4.58 abc | 41.35 ± 6.3 bcd | 1.13 ± 0.07 bc | 113.31 ± 31.69 abc | 11.12 ± 0.22 abc | 6.98 ± 0.82 bcd | 27.52 ± 4.47 ab | 0.24 ± 0.02 ab |
| W3F4 | 12.48 ± 0.35 ef | 9.98 ± 1.80 b | 0.33 ± 0.03 cd | 8.01 ± 0.34 ab | 24.44 ± 2.39 bcd | 38.15 ± 4.59 cde | 1.09 ± 0.06 c | 105.6 ± 14.99 abc | 11.00 ± 0.18 abcd | 6.12 ± 0.31 de | 31.14 ± 3.31 a | 0.21 ± 0.02 bcd |
| Double factor variance analysis | ||||||||||||
| W | 21.900 ** | 32.422 ** | 8.557 ** | 5.927 ** | 6.228 ** | 6.785 ** | 5.639 ** | 2.495 * | 17.561 ** | 7.864 ** | 4.077 ** | 9.155 ** |
| F | 33.806 ** | 2.968 * | 4.752 * | 8.603 ** | 1.721 | 1.357 | 2.665 | 5.897 ** | 13.933 ** | 9.426 ** | 1.698 | 15.254 ** |
| W × F | 5.695 ** | 13.260 ** | 11.698 ** | 1.376 | 9.631 ** | 11.071 ** | 2.357 | 1.156 | 0.556 | 2.135 | 1.349 | 11.938 ** |
| Indicator Variables | Factor Loading | |||
|---|---|---|---|---|
| Principal Components | ||||
| 1 | 2 | 3 | 4 | |
| Soluble sugar (X1) | 0.885 | 0.003 | 0.143 | 0.219 |
| Vitamin C (X2) | 0.458 | 0.159 | 0.657 | −0.288 |
| Soluble solids (X3) | 0.058 | −0.950 | 0.269 | 0.090 |
| Total sugar (X4) | 0.311 | 0.510 | 0.695 | 0.009 |
| Fruit shape index (X5) | 0.396 | −0.355 | −0.471 | −0.579 |
| Peel hardness (X6) | 0.830 | 0.216 | 0.058 | 0.412 |
| Pulp hardness (X7) | 0.945 | −0.047 | −0.079 | −0.193 |
| Ratio of sugar to acid (X8) | −0.020 | 0.966 | −0.230 | −0.103 |
| Ratio of soluble sugar to acid (X9) | 0.074 | 0.923 | −0.357 | −0.071 |
| Fruit weight (X10) | 0.951 | −0.093 | 0.033 | 0.134 |
| Transverse diameter of kernel (X11) | −0.644 | 0.189 | 0.575 | 0.328 |
| Stone cell (X12) | 0.132 | −0.092 | −0.641 | 0.665 |
| Characteristic value | 4.171 | 3.199 | 2.161 | 1.266 |
| Variance contribution rates/% | 34.760 | 26.656 | 18.010 | 10.551 |
| Contribution rates/% | 34.760 | 61.416 | 79.426 | 89.977 |
| Treatment | Principal Component | Overall Score | Overall Ranking | |||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| W1F1 | 0.005 | 0.394 | −0.385 | 0.225 | 0.238 | 12 |
| W1F2 | 0.736 | −0.069 | −0.242 | 0.662 | 1.087 | 10 |
| W1F3 | 0.963 | 0.368 | 0.465 | −0.368 | 1.427 | 8 |
| W1F4 | 0.381 | 0.156 | 0.578 | −0.298 | 0.817 | 11 |
| W2F1 | 0.764 | 0.038 | 0.252 | 0.113 | 1.167 | 9 |
| W2F2 | 1.832 | 0.173 | 0.489 | 0.409 | 2.902 | 3 |
| W2F3 | 1.510 | 0.518 | 0.840 | 0.292 | 3.160 | 2 |
| W2F4 | 0.942 | 0.681 | 0.546 | 0.118 | 2.287 | 6 |
| W3F1 | 0.999 | 0.520 | 0.688 | 0.239 | 2.446 | 5 |
| W3F2 | 1.835 | 0.783 | 0.374 | 0.427 | 3.420 | 1 |
| W3F3 | 1.295 | 0.530 | 0.387 | 0.597 | 2.809 | 4 |
| W3F4 | 0.879 | 0.489 | 0.360 | 0.496 | 2.224 | 7 |
| Treatment | IWUE (kg m−3) | PFP (kg kg−1) | G(CNY ha−1) | WC(CNY ha−1) | FC(CNY ha−1) | L(CNY ha−1) | N(CNY ha−1) |
|---|---|---|---|---|---|---|---|
| W1F1 | 1.94 ± 0.04 f | 15.11 ± 0.3e | 77,907 ± 1528 i | 1117 | 3375 | 1050 | 72,365 ± 1528 g |
| W1F2 | 2.29 ± 0.19 bcd | 16.00 ± 1.33e | 105,600 ± 8800 efg | 1117 | 3750 | 1167 | 99,567 ± 8800 ef |
| W1F3 | 2.00 ± 0.10 ef | 12.73 ± 0.61f | 94,006 ± 4476 gi | 1117 | 4125 | 1283 | 87,481 ± 4476 fg |
| W1F4 | 2.23 ± 0.10 cd | 13.00 ± 0.56f | 90,894 ± 3884 efg | 1117 | 4500 | 1400 | 83,878 ± 3884 fg |
| W2F1 | 2.11 ± 0.05 bc | 21.11 ± 0.52c | 104,378 ± 6610 abc | 1438 | 3375 | 1350 | 95,856 ± 3211 ef |
| W2F2 | 2.56 ± 0.01 a | 23.00 ± 0.07b | 143,365 ± 416 abc | 1438 | 3750 | 1500 | 136,677 ± 416 bc |
| W2F3 | 2.33 ± 0.11 def | 19.09 ± 0.91d | 125,857 ± 9455 cde | 1438 | 4125 | 1650 | 121,396 ± 6632 cd |
| W2F4 | 2.00 ± 0.07 ef | 15.00 ± 0.56e | 115,133 ± 12,617 def | 1438 | 4500 | 1800 | 110,448 ± 10,162 de |
| W3F1 | 2.18 ± 0.10 abc | 26.67 ± 1.19a | 139,740 ± 29,157 bc | 1763 | 3375 | 1650 | 126,414 ± 24,365 bcd |
| W3F2 | 2.45 ± 0.09 ab | 27.00 ± 1.00 a | 151,441 ± 5609 ab | 1763 | 3750 | 1833 | 144,095 ± 5609 ab |
| W3F3 | 2.36 ± 0.18 cde | 23.64 ± 1.82 b | 163,281 ± 14,885 a | 1763 | 4125 | 2017 | 158,241 ± 13,127a |
| W3F4 | 2.00 ± 0.07 ef | 18.33 ± 0.67 d | 131,993 ± 4800 bcd | 1763 | 4500 | 2200 | 123,530 ± 4800 cd |
| W1F1 | 1.94 ± 0.04 f | 15.11 ± 0.3e | 77,907 ± 1528 i | 1117 | 3375 | 1050 | 72,365 ± 1528 g |
| Double factor variance analysis | |||||||
| W | 336,322 ** | 6674 ** | 10,669 ** | 17,970 ** | |||
| F | 91,067 ** | 21,657 ** | 70,008 ** | 90,656 ** | |||
| W × F | 8650 ** | 6787 ** | 1629 ** | 2323 | |||
| Output Variables Y | Regression Equation | R2 | p |
|---|---|---|---|
| Comprehensive fruit quality/Y1 | Y1= −3.24 × 10−7 W2 − 1.95 × 10−6 WF − 8.82 × 10−5 F2 + 6.53 × 10−3 W + 0.155 F − 83.1111 | 0.965 | <0.01 |
| Yield/Y2 | Y2= −2.11 × 10−4 W2 − 5.82 × 10−3 WF − 0.079 F2 + 10.003 W + 150.297 F – 80,397 | 0.986 | <0.01 |
| IWUE/Y3 | Y3= −5.64 × 10−8 W2 − 2.98 × 10−7 WF − 2.44 × 10 – 5 F2 + 1.06 × 10−3 W + 0.040 F − 83.111 | 0.875 | <0.01 |
| PFP/Y4 | Y4= −4.00 × 10−7 W2 − 7.01 × 10−6 WF − 1.94 × 10−4 F2 + 0.01438 W + 0.321 F − 83.111 | 0.988 | <0.01 |
| Net profits/Y5 | Y5= −2.49 × 10−3 W2 − 1.33 × 10−2 WF − 2.044 F2 + 41.569 W + 3138.541 F – 1,311,072 | 0.986 | <0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; He, X.; Gong, P.; Zhao, D.; Zhang, Y.; Wang, Z.; Zhang, J. Optimization of a Water-Saving and Fertilizer-Saving Model for Enhancing Xinjiang Korla Fragrant Pear Yield, Quality, and Net Profits under Water and Fertilizer Coupling. Sustainability 2022, 14, 8495. https://doi.org/10.3390/su14148495
Wang J, He X, Gong P, Zhao D, Zhang Y, Wang Z, Zhang J. Optimization of a Water-Saving and Fertilizer-Saving Model for Enhancing Xinjiang Korla Fragrant Pear Yield, Quality, and Net Profits under Water and Fertilizer Coupling. Sustainability. 2022; 14(14):8495. https://doi.org/10.3390/su14148495
Chicago/Turabian StyleWang, Jiaxin, Xinlin He, Ping Gong, Danqi Zhao, Yao Zhang, Zonglan Wang, and Jingrui Zhang. 2022. "Optimization of a Water-Saving and Fertilizer-Saving Model for Enhancing Xinjiang Korla Fragrant Pear Yield, Quality, and Net Profits under Water and Fertilizer Coupling" Sustainability 14, no. 14: 8495. https://doi.org/10.3390/su14148495
APA StyleWang, J., He, X., Gong, P., Zhao, D., Zhang, Y., Wang, Z., & Zhang, J. (2022). Optimization of a Water-Saving and Fertilizer-Saving Model for Enhancing Xinjiang Korla Fragrant Pear Yield, Quality, and Net Profits under Water and Fertilizer Coupling. Sustainability, 14(14), 8495. https://doi.org/10.3390/su14148495







