1. Introduction
In the past few decades, environmental pollution and its countermeasures have attracted high attention around the world. Environmental sustainability has become an important indicator to measure the success of supply chain management, and sustainable development has gradually become the common consensus of the whole society to deal with global climate change. The coordinated development of the economy and environment has gradually become a hot topic. While pursuing rapid economic growth, people also hope that the environment can be effectively protected and the economy can develop rapidly while protecting the environment [
1]. Since 2015, the Chinese government has provided consumers with 55,000 CNY electric vehicles (with a range greater than 250 km) to promote the development of new energy vehicles [
2].
Pressure from governments and consumers is forcing companies to take the environmental characteristics of their products seriously. In recent years, due to drastic changes in nature, 80% of consumers considered green characteristics before buying products, and one-third of them were more inclined to pay more for green products [
3,
4]. Therefore, in order to achieve comprehensive sustainable development and win competitive advantages, enterprises need to carry out a green transformation of traditional supply chains and establish the concept of green environmental protection. Through the study of real cases, we found that the state or government uses certain policy tools in a planned way to adjust and control the operation of the macro economy, which has reached certain policy goals. In the study of this paper, the government considers the impact of economic, environmental and social aspects, that is, stimulating manufacturers to invest in green technology innovation while ensuring social welfare stability under the premise of pursuing a maximum profit for the supply chain [
5].
Carbon emissions are one of the most important drivers of increasing global warming and an important issue that needs to be addressed seriously. Cap-and-trade regulation is widely used as one of the most effective market legislations to control the carbon emissions that manufacturers produce. Under a cap-and-trade scheme, companies receive a set number of free carbon credits, which manufacturers can sell in the carbon market. If insufficient free emission credits are received, the company has two options to maintain its production. One is to introduce green technologies to reduce carbon emissions, and the other is to purchase credits from the carbon trading market [
6]. The implementation of cap-and-trade affects the investment of manufacturers to produce green products, thus affecting the coordination of the whole supply chain. Thus, the decisions of the players in the game are also affected by cap-and-trade.
In addition, channel power structures that rely on members’ ability to control the channel decision-making process will have a substantial impact on channel performance [
7]. Traditionally, manufacturers have enjoyed enough power to be the first to make decisions, but the increasing power of some retailers, such as Carrefour and Amazon, has led to balanced power structures and even retailer-dominated supply chains. Therefore, it is necessary and useful to study the influence of different power structures on supply chain operation decisions.
How to design effective government intervention policies, which maximize social welfare and encourage stakeholders in the supply chain to improve their product green level, is an urgent problem that needs to be solved. By considering operational performance, resource efficiency and environmental impact, this paper discusses the balance and coordination of a green supply chain based on cap-and-trade and government interventions for optimal supply chain decisions and social welfare maximization. The main research issues of this paper are as follows:
- (1)
How do the profits of stakeholders, the price of green products and social welfare in the supply chain behave in different power structures?
- (2)
What is the impact of government intervention on green investment, profit and social welfare of supply chain enterprises?
- (3)
What are the effects of carbon prices and green investment cost coefficients on green investment levels, profits and social welfare in the context of cap-and-trade policies?
We constructed a consideration of the two-stage supply chain game model of government intervention to answer those questions, as well as: how the government will seek to maximize social welfare and determine the carbon cap limits and product greenness threshold; how manufacturers consider green investments to produce a green product; how retailers consider the green degree to promote sales; how manufacturers and retailers will seek profit maximization. The product sales price and level of green investment are the decision-making variables of the green products in the supply chain. In this study, four supply chain models with different power structures are established. Based on backward induction, the optimal solution is obtained, and the impacts of the optimal operating decisions, profits and carbon emissions on the environment and social welfare are compared and analyzed.
The innovation and contribution of this paper mainly include two aspects as follows:
- (1)
From the perspective of the government, this paper studies how to set the greenness threshold to reward or punish and if it can promote enterprises to actively invest in green technology innovation. On this basis, a cap-and-trade policy is considered: How will the level of green investment, profits and social welfare of enterprises change when they face the interaction of the investment cost and carbon price?
- (2)
Previous studies mostly consider whether government intervention has a positive or negative impact on enterprises. On this basis, this paper considers the index of social welfare, and the government sets the threshold value of the product’s greenness from three aspects of economy, environment and society to encourage enterprises to invest in green technology innovation. This paper also considers the power structure that has a significant influence on the supply chain. The purpose is to explore the effect of government intervention in different situations.
Through a comparative analysis, this paper can better explain the impact of cap-and-trade policy and government intervention on a product’s greenness and social welfare and draw relevant conclusions.
The rest of this article is arranged as follows.
Section 2 reviews the relevant literature.
Section 3 builds the model framework. In
Section 4, four supply chain models and corresponding equilibrium solutions are given. The model comparison and analysis are presented in
Section 5. A numerical analysis is carried out in
Section 6.
Section 7 discusses and compares the conclusions of this study with those of the existing literature.
Section 8 provides the conclusion and some directions for future research. To make the paper more readable, all proofs are provided in
Appendix A.
2. Literature Review
The theory of sustainable development originates from the triple bottom line (TBL) concept, which mainly includes three dimensions: environment, economy and society. There is no doubt that TBL is the cornerstone of the sustainable supply chain studied in this paper. However, with the change in the environment, the perspective of sustainable supply chain research is also changing. In the operation process of the supply chain, manufacturers’ investment in green technology innovation will undoubtedly have a positive impact on the environment, but the relationship between costs and profits also generates economic problems. In addition, the influence of the power of each decision-making unit in the supply chain on profit is also a part of our concern. Social welfare represents an important indicator of the social dimension in the sustainable supply chain. This paper discusses these concerns from three perspectives: green supply chain (environment), different power structures (economy) and social welfare (society).
2.1. Green Supply Chain Management
Green supply chain management considers the environmental problems in all links of the supply chain, pays attention to environmental protection and promotes the coordinated development of the economy and environment. In practice, it mainly includes green design, green procurement, green manufacturing, green packaging, green materials and green recycling [
8,
9,
10]. In previous works of literature, research on green supply chain management mainly focuses on the pricing decisions, system coordination and operation decisions of green supply chain management [
11,
12,
13]. With the further deterioration of the environment and the further increase in green investment, in order to stimulate enterprises to increase investment and promote the sustainable development of the supply chain, the study of green supply chain management has been extended to government intervention and low-carbon operations.
Government intervention in green supply chain management is mainly through setting green thresholds to reward and punish so as to promote enterprises to actively invest in green technology innovation. The greenness of a product is used to measure the degree of environmental friendliness of the product. The greater the negative impact, the smaller the greenness, and vice versa. For example, ref. [
14] studied and analyzed the problem of green coordination in a two-level supply chain, in which demand is a function of the selling price and green product quality. Retailers determine the selling price, while manufacturers control the green quality of their products. The aim is to provide an analytical approach to address the channel coordination and pricing issues in a green supply chain with consumer environmental awareness, while manufacturers have the ability to invest in improving the green quality of their products. Ref. [
15] introduced product greenness and established a game model for a green supply chain consisting of a manufacturer and a retailer to discuss the influence of a channel’s structure on product greenness, price and profit. Ref. [
16] investigated a supply chain that sold non-green products and intended to sell a new green product. In the supply chain, the retailer’s decision variable is the sales price and effort level of selling green products, while the manufacturer’s decision variable is the quality of the green products. Their study uses game theory to model and solve this problem. Ref. [
17] analyzed the pricing and coordination of green products and non-green products to a certain extent in two different scenarios (centralized and decentralized), and the conclusion showed that the centralized scenarios obtained a higher greenness than the decentralized scenarios.
In terms of low-carbon operations, there are currently three effective carbon policies: carbon emission tax, carbon cap-and-trade policy or subsidies provided by the government [
18]. Compared with other mechanisms, the cap-and-trade system has many advantages by introducing a market mechanism, which can be implemented more effectively and significantly to save public resources. Many scholars have studied the impact of the caps on supply chain coordination and profit. For example, ref. [
19] found that although emission cap policies reduce profitability, the cap-and-trade system not only reduces carbon emissions but also improves profitability. Ref. [
20] studied the influence of a carbon footprint and low-carbon preference for market supply and demand under the cap-and-trade mechanism, established a production optimization model and made optimization decisions. After the cap-and-trade policy became an emission reduction policy, many scholars studied the influence of the cap-and-trade system on supply chain operation. Ref. [
21] studied the relationship between manufacturers’ carbon emission levels and carbon trading prices. Their results show that the level of carbon reduction increases with the price of carbon trading. Ref. [
22] studied the channel selection and emission reduction decisions of manufacturers when considering carbon emission constraints. The results show that channel conflicts under the cap-and-trade system are alleviated, and retailers can accommodate more online channels under certain conditions. Ref. [
23] showed that carbon emission caps, carbon trading prices and consumers’ preferences for low-carbon products are key factors that influence retailers’ and manufacturers’ behaviors.
On the basis of green supply chain management, this paper considers government intervention and low-carbon operations at the same time, aiming to consider the impact of multiple factors and promote sustainable development of the supply chain.
2.2. Different Power Structures
Many scholars have studied and discussed different power structures among supply chain members, and they show that power structures influence decision-making and profits [
24,
25,
26]. Ref. [
27] considered the setup of one manufacturer and multiple retailers and compared the supply chain efficiency between the manufacturer-led and retailer-led cases. Numerical analysis shows that retailer dominance usually leads to higher supply chain efficiency. Ref. [
28] provides a comparison between the manufacturer-led, retailer-led and collector-led closed-loop supply chain models. Ref. [
29] determines the best effort level decision and corresponding profit under different supply chain power structures, given the demand on which quality and marketing efforts depend. Their research shows that under RS, an investment in marketing efforts is most profitable for retailers, while an investment in quality is most profitable for manufacturers under MS. Ref. [
30] developed a game model to explore the decision-making of the offer delivery lead time, price and channel structure of the customized duopoly system under three game scenarios, and found that decentralization can increase the offer lead time, and two manufacturers can choose different channel structure duopolies under symmetric conditions. Ref. [
31] studied centralized and different Stackelberg games and Nash games, while the researchers did not consider the validity of demand expansion, the collection effort and sales effort, and did not investigate the coordination of the closed-loop supply chain with a price and effort dependent demand. Ref. [
7] established a game theory model of the centralized and decentralized closed-loop supply chain of manufacturer and retailer and studied the optimal decision of collection effort, sales effort and pricing under different channel power structures, namely, the manufacturer Stackelberg, vertical Nash and retailer Stackelberg. The aim is to identify the most profitable channel power structures and propose coordination strategies. Ref. [
32] developed four different scenarios: one centralized model and three decentralized models based on the Stackelberg game. Stackelberg, a manufacturer, Stackelberg, a retailer and Stackelberg, a third-party collector, compared and analyzed optimal decisions in different scenarios. Ref. [
33] studied the green product supply chain composed of one manufacturer and two retailers and constructed Stackelberg game models that compared centralized decision-making and decentralized decision-making to study the changing internal performance rules of greenness and profit levels. The results show that the profit level of the whole supply chain in the centralized scenario is higher than that in the decentralized scenario.
Unlike the above literature, our study introduces the government as a participant in the supply chain. This paper aims to fill in the literature gaps and guide business decisions in practice.
2.3. Social Welfare
In the game analysis of the supply chain, social welfare maximization has been widely used to solve management problems. Many scholars have conducted modeling and calculations to study optimal social welfare in the context of the supply chain. For example, ref. [
34] used the three-stage game model to analyze the impact of government intervention on the competition. The results show that the government should adopt green tax and subsidy measures to ensure that the green profit generated by the production of green products is not negative. Compared with the situation without intervention, the social welfare and chain profit are increased by 27.8% and 306.6%, respectively. Ref. [
35] studied the use of environmental taxes to stimulate innovation and “green” choices, and analyzed the optimal policies of enterprises and the policies of regulators to maximize social welfare. The results show that if the regulator is limited to tax policy, then the tax level that maximizes social welfare will simultaneously encourage the choice of clean technology when the regulator pays moderate attention to the environmental impact. Ref. [
36] solved the optimal social welfare problem based on a mathematical modeling framework. Ref. [
37] discussed the interaction among multiple stakeholders of the green supply chain of trans-basin water diversion through game theory and the coordination of research methods, and considered the government’s subsidy for improving the green level of water resources to maximize social welfare. The results of analytical modeling with and without social welfare maximization were compared. Ref. [
38] analyzed and derived the social welfare function, proving that in a decentralized supply chain setting, a lower level of data quality would lead to a decline in social welfare and supply chain profits. From the perspective of social welfare maximization, ref. [
39] developed, analyzed and compared equilibrium and coordination-decision models for the inter-basin water transfer supply chain, considering equity concerns in the absence or presence of social welfare objectives.
Unlike the above literature, this paper studies the maximization of social welfare based on the profit and consumer surplus of all parties in the game under the environmental green and sustainable development considerations.
Table 1 shows the differences between our paper and the existing literature. The literature review and
Table 1 show that most studies are limited to the impact of a carbon quota policy or government intervention on a product’s greenness in the supply chain, and few pieces of literature consider both. On the other hand, there are few works of literature that consider the maximization of social welfare. In this study, four supply chain models with different power structures are established, in which the government seeks to maximize social welfare, and the limits of carbon credit and product greenness thresholds are determined, respectively. The manufacturers consider producing green products, and retailers consider greenness to promote sales. The manufacturers and retailers seeking profit maximization, product sales price and green degree are the decision-making variables of the green products in the supply chain. The impacts of optimal business decisions, profits and carbon emissions on the environment and social welfare are compared and analyzed.
3. Model Framework
In the context of cap-and-trade regulation and government intervention, the interaction mechanism among government, manufacturers and retailers under different power structures is studied considering the two-level green supply chain composed of manufacturers and retailers. The government sets the thresholds for enterprises’ carbon emissions and the greenness of products. The manufacturer invests in green technology to produce green products. The retailer wholesales green products from the manufacturer and sells green products to consumers. The structure of the model is shown in
Figure 1. We summarize the notations in
Table 2. To facilitate the calculation, the following assumptions were given.
Assumption 1. Market demand is deterministic and linearly dependent on the selling prices and the level of green investment. The demand function for green products is assumed to be .
Assumption 2. We consider that in order to promote enterprises to invest in green production, the government sets the threshold of product greenness θ0 and the subsidy per unit product . If , the government subsidizes the manufacturer , otherwise the government penalizes the manufacturer . The manufacturer’s cost of green investment is assumed to be λθ2 [2,15]. Assumption 3. The carbon emission per unit of product produced is related to the green investment, and the carbon emission function is considered as , that is, the level of green investment is negatively correlated with the carbon emission per unit of product. Thus, the total carbon footprint of the manufacturer is . If , the manufacturer needs to spend to purchase carbon emission permits in the carbon trading market; otherwise, the manufacturer can obtain profits of by selling excess carbon emission permits in the carbon trading market [40,41]. Assumption 4. We set the consumer surplus as . We consider that the environmental impact of the total carbon emissions of manufacturers producing green products is . The social welfare function is assumed to be [35].
4. Model Analysis
This paper will discuss supply chain operation decisions and social welfare with different power structures under cap-and-trade regulations and government intervention: supply chain centralized decision (C), manufacturer-led Stackelberg game (DM), retailer-led Stackelberg game (DR) and Cournot game (DN). The optimal operating decision, profit and impact of carbon emissions on each model’s environment and social welfare are further compared.
4.1. Supply Chain Centralized Decision (C)
In scenario (
C), the manufacturer and retailer are considered as one decision unit. Thus, the wholesale price does not exist in scenario (
C). ∏
C and
SWC are the total profit and social welfare of the green supply chain, respectively. We developed the model as follows:
Proposition 1. If , the supply chain optimal decisions, profit and social welfare in scenario C are given by:where , , , . 4.2. Manufacturer-Led Stackelberg Game (DM)
In the scenario (
DM), the manufacturer plays the leader of the green supply chain and the retailer is the follower.
,
and
are the manufacturer’s profit, retailer’s profit and social welfare of the green supply chain, respectively. We developed the model as follows:
Proposition 2. If , the supply chain optimal decisions, profit and social welfare in scenario DM are given by:where , , , . 4.3. Retailer-Led Stackelberg Game (DR)
In the scenario (
DR), the retailer plays the leader of the green supply chain, and the manufacturer is the follower.
,
and
are the manufacturer’s profit, retailer’s profit and social welfare of the green supply chain, respectively. We developed the model as follows:
Proposition 3. If , the supply chain optimal decisions, profit and social welfare in scenario DR are given by:where , , , . 4.4. Cournot Game (DN)
In the scenario (
DN), the manufacturer and the retailer have equal power in the green supply chain.
,
and
are the manufacturer’s profit, retailer’s profit and social welfare of the green supply chain, respectively. We developed the model as follows:
Proposition 4. If , the supply chain optimal decisions, profit and social welfare in scenario DR are given by:where , , , . 5. Model Comparison
In this section, we compare the optimal results in centralized and decentralized scenarios, especially the differences between the three different power structures.
Proposition 5. When the green supply chain is under the cap-and-trade policy of government intervention, the green investment level of manufacturers is as follows: .
Proposition 5 indicates that the level of green investment when the manufacturer produces green products depends on the competitive strategy and power of the manufacturer and the retailer in the green supply chain. Consistent with the research results of most articles, the green investment level of the manufacturer is higher under the centralized decision scenario. Under three decentralized decision scenarios of manufacturer and retailer, the Nash scenario can help manufacturers produce higher green level products, while the manufacturer leadership scenario can make manufacturers produce lower green level products. The reasons are as follows: In the manufacturer-led Stackelberg game, the manufacturer, in a dominant position in the supply chain, can steadily obtain high profits, so there is no need to actively increase the level of green investment to increase demand. When the manufacturer and the retailer have the same power, the manufacturer will increase the level of green investment in order to gain more profits and subsidies without knowing the other side’s decision. Similar to the Nash scenario, in the retailer-led Stackelberg game, the manufacturer would increase the level of green investment to obtain more profits and subsidies in order to reduce revenue losses.
Proposition 6. When the green supply chain is under the cap-and-trade policy of government intervention, the selling price and wholesale price are: , .
Proposition 6 shows that different power structures in the green supply chain will affect the wholesale price and selling price of green products, and the wholesale price set by the manufacturer is positively correlated with the manufacturer’s power in the green supply chain. The wholesale price is highest in the manufacturer-led Stackelberg game, and lowest in the retailer-led Stackelberg game.
Selling prices generally follow a similar trend to manufacturers’ wholesale prices. The reason behind this is that the higher the wholesale price set by the manufacturer, the higher the selling price will be set by the retailer in order to achieve a stable unit profit. In the retailer-led supply chain, because the retailer first sets the price of the product based on the profit of the unit product, the selling price of the product is higher than that of the product under the condition that both parties have equal power. In essence, the retailer gains a higher profit from the unit product. In the centralized decision-making scenario, both sides aim to obtain higher supply chain profits without a double marginalization effect. Therefore, lower selling prices are set to increase market demand and gain more profits from the market.
Proposition 7. When the green supply chain is under the cap-and-trade policy of government intervention, the manufacturer’s profit is as follows: .
Proposition 7 shows that green supply chains with different power structures have an impact on manufacturers’ profits. In the Stackelberg game scenario led by the manufacturer, the manufacturer will get higher profits, while in the Stackelberg game scenario led by the retailer, the manufacturer’s profits are the lowest. We find that, similar to wholesale prices, manufacturers’ profits positively correlate with manufacturers’ power in the green supply chain. The reason behind this is that when manufacturers have more power, they raise the wholesale price of their products. In order to maintain their own interests, retailers will maintain a stable market demand environment, and manufacturers’ profit per unit product will increase accordingly. Eventually, manufacturers’ profits will increase.
Proposition 8. When the green supply chain is under the cap-and-trade policy of government intervention, the retailer’s profit is as follows: .
Proposition 8 shows that a green supply chain with different power structures has an impact on retailers’ profits. In the retailer-led Stackelberg game, the retailer obtains higher profits, while in the manufacturer-led Stackelberg game, the retailer obtains the lowest profits. Similar to Propositions 6 and 7, the retailer’s profit is also positively correlated with the retailer’s power in the green supply chain. The reason behind this is that the retailer makes decisions based on the profit per unit of product. When the manufacturer leads the supply chain, the manufacturer sets a higher wholesale price, and the retailer also sets a higher selling price to ensure the profit per unit of product, thus reducing the market demand. As a result, retailers’ profits will decline as demand drops.
Due to the complexity of the optimal analytic solution for social welfare, we will analyze it in
Section 6 through numerical study.
6. Numerical Study
In this section, a numerical analysis will be applied to four models. We discuss the sensitivity of some key parameters in order to explore the influence of these parameters on the optimal solution. Due to the difficulty of data collection, we referred to [
2,
41] and made some adjustments. The parameters are as follows:
,
,
,
,
,
,
,
,
,
,
. Next, we analyzed the level of green investment, corporate profits and social welfare.
6.1. The Impact of Government Intervention
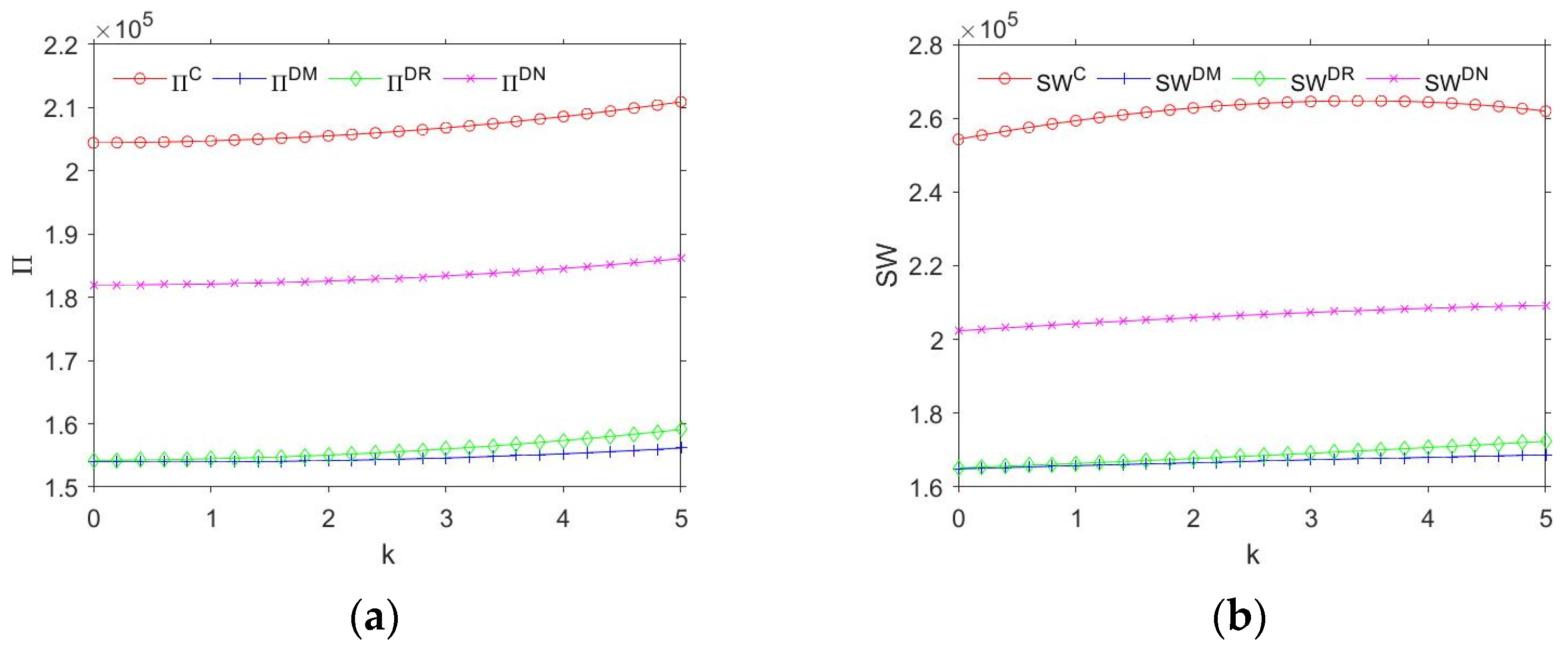
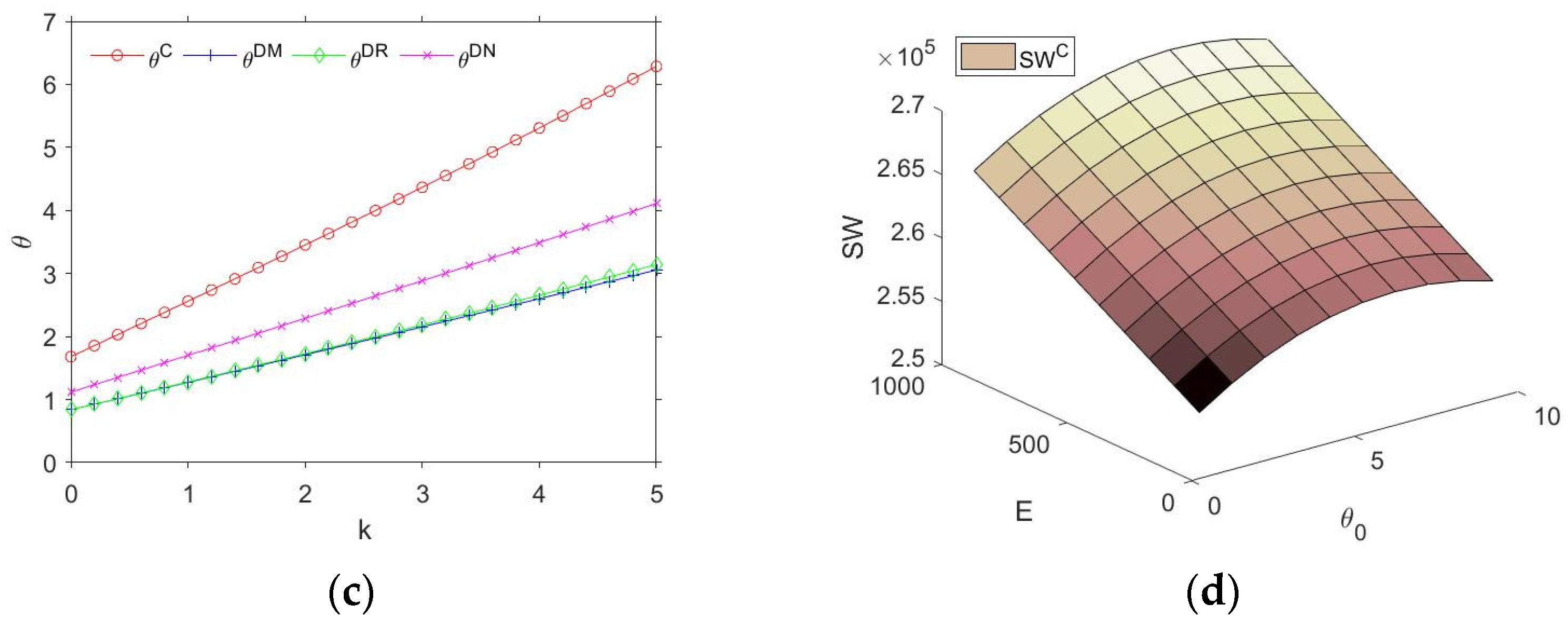
Figure 2 shows the impact of the various parameters of government intervention on the profits and social welfare of the supply chain system. Where
Figure 2a represents the influence of government intervention adjustment factor
k on supply chain profit;
Figure 2b represents the influence of government intervention adjustment factor
k on supply chain social welfare;
Figure 2c represents the influence of government intervention adjustment factor
k on the level of green investment;
Figure 2d represents the influence of product green threshold
θ0 preset by the government and enterprise carbon emission
E on social welfare in model C. The main results are shown below.
It is obvious from
Figure 2a, b that the supply chain profit and social welfare are at the highest level when a centralized decision is made. In the decentralized scenario with three different power structures, the scenario with equal power (
DN) is more conducive to the supply chain to obtain more profits and social welfare. At the same time, we observe that the supply chain profit is positively correlated with the government intervention adjustment factor
k; social welfare increases first and then decreases with the increase in
k. The reason behind this is that when government intervention becomes more and more intense, members of the supply chain system can increase the level of green investment, on the one hand, to increase the market demand, and on the other hand, they can obtain additional income, namely government subsidies. At the same time, social welfare will be reduced because the marginal expenditure of government subsidies is greater than the marginal income of the supply chain system.
Figure 2c shows that the level of green investment is positively correlated with the government intervention adjustment factor
k, and the level of green investment in the supply chain is at the highest level in the centralized scenario. Similar to the trend in
Figure 2a, the power parity scenario (
DN) can promote the manufacturer to improve the level of green investment, followed by the retailer-led scenario (
DR), and the manufacturer-led scenario (
DM) has the lowest level of green investment. This also verifies the result of proposition 5.
In addition, we are concerned that the threshold
θ0 of product greenness and
E of the corporate carbon quota set by the government may have an impact on social welfare. Since the social welfare values of different models differ greatly, we especially studied social welfare in concentrated scenarios. As can be seen from
Figure 1d, social welfare
SWC is positively correlated with
E, while social welfare increases first and then decreases with the increase in
θ0. The reason behind this is that when the carbon limit
E becomes larger and larger, enterprises are allowed to emit more carbon. At this time, increasing the level of green investment is conducive to obtaining additional income from the carbon trading market. At the same time, when the threshold
θ0 of product greenness becomes higher and higher, the manufacturer will increase the level of green investment in order to obtain excess income. When the marginal benefit is less than the marginal cost, the manufacturer will stop promoting the green investment level; thus, the green investment level will increase first and then decrease.
6.2. The Impact of Carbon Trading Markets
We mainly studied the impact of the carbon trading markets on supply chain profits, green investment levels and social welfare.
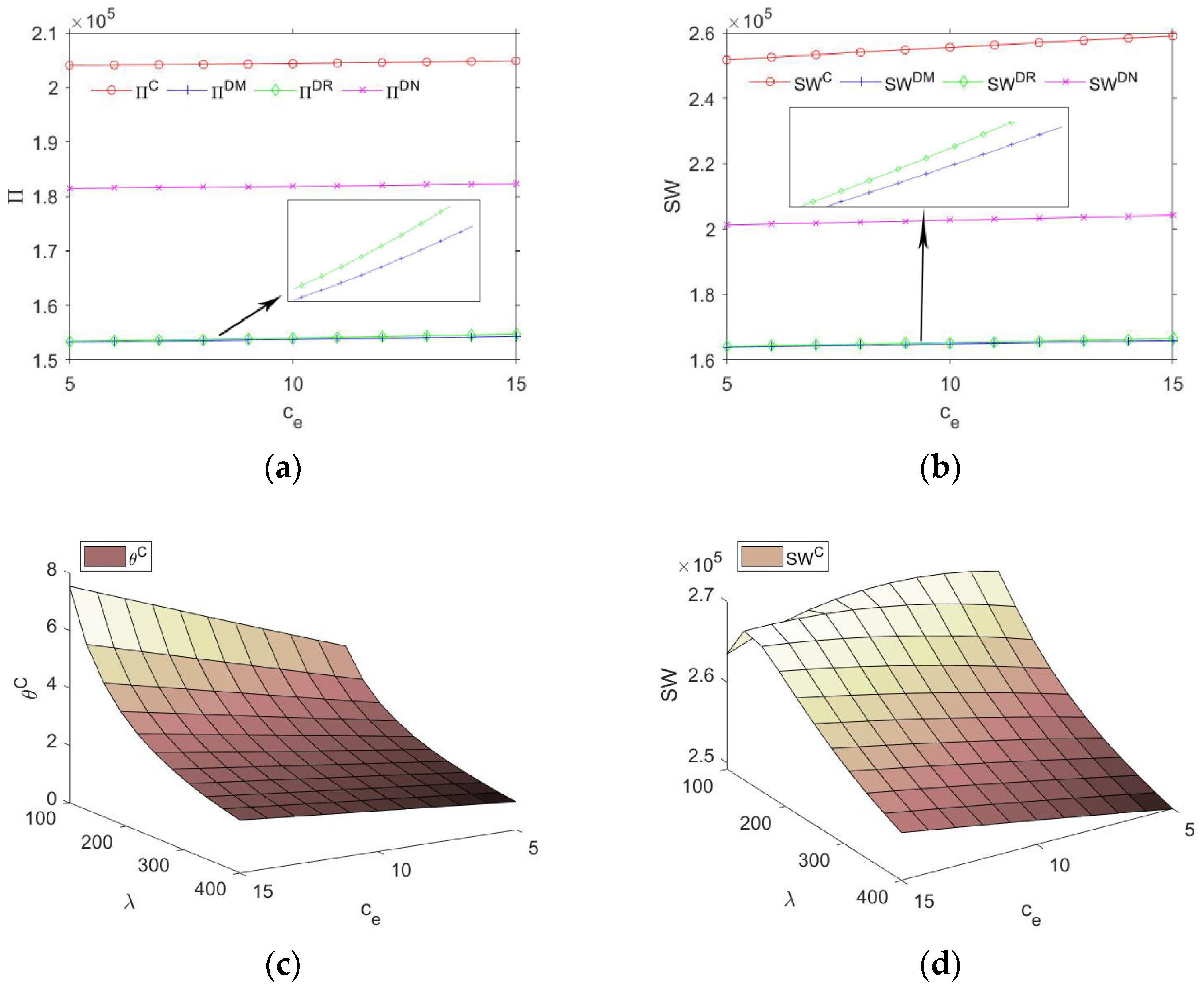
Figure 3a,b show the changes in profit ∏ and social welfare
SW of the four models with carbon trading prices
ce. On this basis, we consider the impact of the green investment cost coefficient
λ. Therefore, we specifically studied the changes in the green investment level
θC and social welfare
SWC with the carbon trading price
ce and green investment cost coefficient
λ under the centralized scenario.
Similar to
Figure 2a,b, the profit and social welfare of the supply chain in the centralized scenario are at the highest levels. In the decentralized scenario, profit and social welfare are the highest when the manufacturer and retailer have equal power (DN), followed by retailer leadership (DR), and the profit and social welfare are the lowest with the manufacturer leadership (DM). The reason behind this is that when carbon trading prices become higher and higher, the manufacturer will increase the level of green investment in order to increase market demand and reduce carbon emissions. As a result, excess carbon permits and increased market demand boost supply chain profits.
Furthermore, we considered the impact of the carbon trading price and green investment cost coefficient on the social welfare and green investment level of the supply chain.
Figure 3c shows that under the centralized scenario, the level of green investment of the manufacturer is negatively correlated with the cost coefficient of green investment. The reason behind this is that when the carbon trading price rises and the cost coefficient of green investment decreases, the manufacturer only needs to pay a small part of the cost to improve the level of green investment so that they can obtain additional profits from the carbon trading market.
As can be seen from
Figure 3d, when the carbon trading price is high, and the cost coefficient of green investment is low, social welfare will be reduced. This is an interesting result. In this scenario, the manufacturer continues to increase the level of green investment, which obviously adds to the profits of the supply chain system. However, from the perspective of the government, the expenditure of government subsidies is far greater than the additional benefits of the supply chain system, and therefore, social welfare will be reduced.
7. Discussion
In this section, we further summarize the results of the numerical analysis and compare them with those of previous literature. Next, we will discuss the content of this paper from three perspectives: the level of green investment of the manufacturer, corporate profits and social welfare.
First of all, we can find that the level of green investment in the centralized scenario is much higher than that in the decentralized scenario. Power parity in decentralized scenarios can promote manufacturers to invest in green technology innovation. Through
Figure 2c and
Figure 3c, we found that the intensity of government intervention and carbon trading price was positively correlated with the level of green investment, while the investment cost coefficient was negatively correlated with the level of green investment [
40].
Secondly, in
Section 5 and
Section 6, we compared the manufacturer and retailer in the supply chain profit under different power structure states in size and found that the corporate profits in the supply chain with power levels were positively correlated, and the whole supply chain profit was similar to the trend of green investment levels, and when both sides powered fairly, the highest overall supply chain profit was seen. In
Figure 2a and
Figure 3a, we found that government intervention and carbon trading prices did not significantly affect supply chain profits.
Finally, we found that for the three different kinds of power in decentralized situations, the level of government intervention positively correlated with social welfare, while in centralized situations, social welfare will increase first and then decrease with the increase in the government intervention level. We further studied the product greenness threshold and the carbon cap, the carbon trading price, and the green investment cost coefficient on the interaction of social welfare, as shown in
Figure 2d and
Figure 3d, and found that relative to the carbon cap, the product greenness threshold has more influence on social welfare, and when the carbon trading price is high, there is a low level of green investment in social benefits.
The above discussion shows that government intervention and cap-and-trade policy have positive effects on the green supply chain to improve profits, green investment levels and social welfare.
8. Conclusions
In the face of increasingly serious environmental problems, the government and stakeholders in the green supply chain are committed to coordinating progress in economic, social and environmental aspects. The popularity of cap-and-trade policies and government interventions have been used to encourage companies to reduce carbon emissions and improve product quality. At the same time, the negotiating position and pricing position of stakeholders in the supply chain (called ‘power level’ in this paper) makes the green supply chain business environment extremely complicated. In this case, this paper compares the impact of government intervention and cap-and-trade policies on corporate investment behavior, market demand, product price, corporate profits and social welfare by establishing mathematical models under four scenarios.
The main research results of this paper are summarized as follows. (1) Both government intervention and cap-and-trade policy encourage manufacturers to invest in green technology innovation, but excessive control and high carbon trading price will lead to a decline in social welfare. (2) In the decentralized scenario, the overall profit, social welfare and green investment levels of the green supply chain are at the highest level when the power of the manufacturer and retailer are equal (DN), and are at the lowest level when the power of the manufacturer is dominant (DM). (3) The low-cost coefficient of green investment will cause enterprises to give up carbon trading, and enterprises are more willing to bear the lower cost of green investment for carbon emission reduction.
This paper studies the impacts of government intervention and cap-and-trade policy on green innovation investment, corporate profits and social welfare under the framework of a green supply chain with different power structures. The results of this study stimulate some content worthy of further research. Firstly, this paper studies the optimal decision of a green supply chain from the perspective of maximizing government social welfare. Further research may look at green supply chains from the perspective of carbon trading markets. Secondly, this paper only considers the duopoly secondary supply chain. Extending the study to multiple manufacturers and retailers will increase its applicability. Thirdly, this paper finds that the results in the centralized state are far better than those in the three dispersed states. Therefore, it will be very valuable for research content in the future to develop a reasonable mechanism to bring the decentralized green supply chain closer to a centralized state.