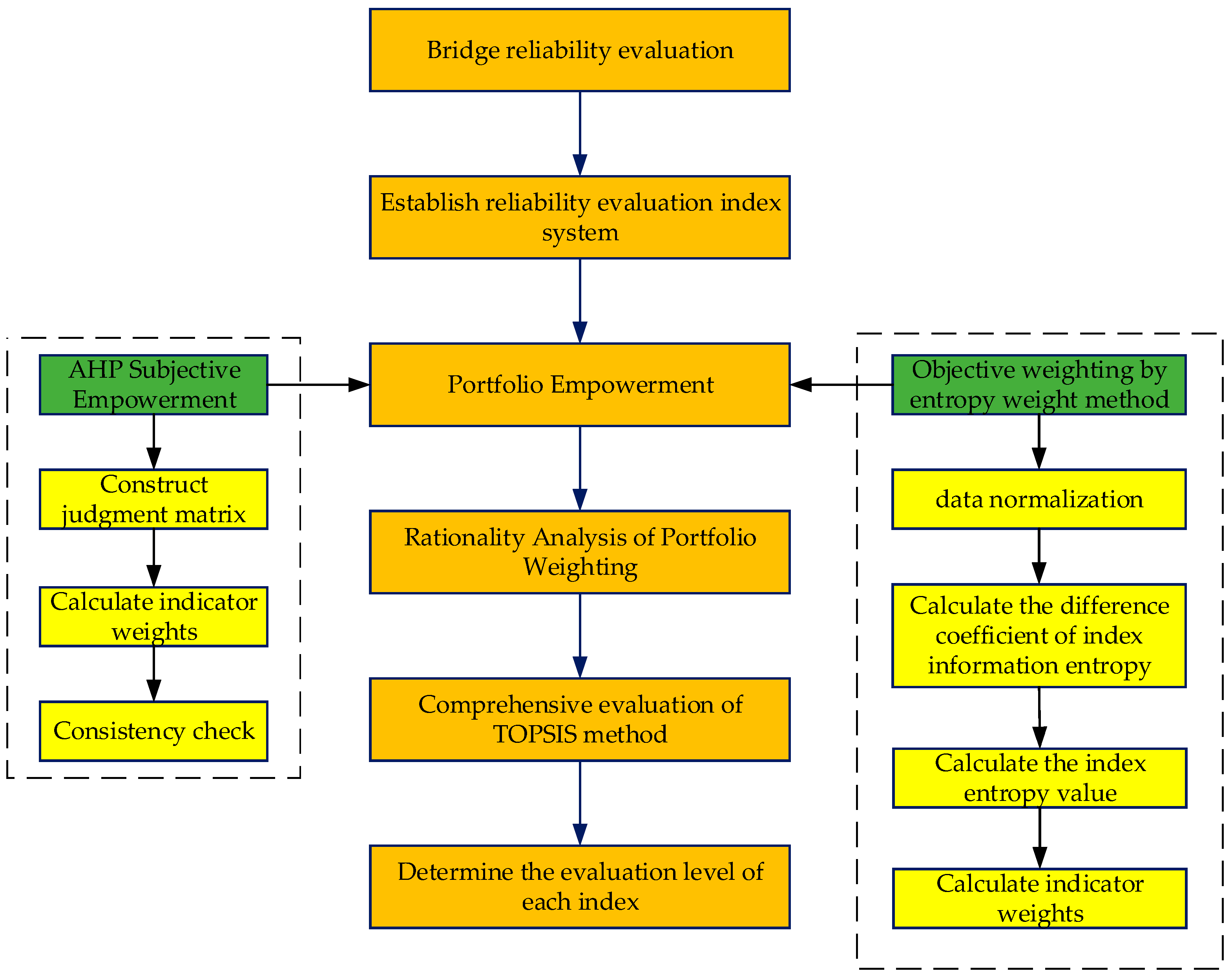
4.3. Bridge Superstructure Reliability Evaluation
- (1)
Calculation of subjective weights based on hierarchical analysis
According to the reliability evaluation indexes in
Table 6, expert scoring is used to analyze the 10 evaluation indexes in a two-by-two comparison based on a 1-9 scale, and the relative importance of the two indexes is quantified to obtain judgment matrix
of the evaluation indexes. The values in judgment matrix
A are obtained after the comprehensive balance based on the data, expert opinions and decision makers’ understanding as follows:
The subjective weight vector
= (0.071, 0.138, 0.120, 0.139, 0.085, 0.101, 0.087, 0.104, 0.079, 0.076) of each evaluation index can be calculated according to Equations (3)–(5). From Equations (6) and (7), we get
. Checking
Table 2, we know that when judgment matrix
A is of order
, the average random consistency index is
; using Equation (8),
—the consistency test meets the requirements, so subjective weight vector
is acceptable.
- (2)
Calculation of objective weights based on entropy weight
The measured data of the reliability indexes in
Table 6 are dimensionlessized using Equations (9) and (10), and the dimensionlessization matrix is obtained as
For dimensionless matrix B, the entropy = (0.624, 0.365, 0.410, 0.318, 0.526, 0.455, 0.602, 0.512, 0.545, 0.562) of each evaluation index can be calculated according to Equations (11)–(13), and then the difference coefficient = (0.376, 0.635,0.590, 0.682, 0.474, 0.545, 0.398, 0.488, 0.455, 0.438) of the information entropy of each index is derived according to Equation (14). Finally, the objective weight vector of each evaluation index based on the entropy weight is derived from Equation (15).
- (3)
Portfolio empowerment and rationalization analysis
Based on the index weights calculated by the above hierarchical analysis and entropy weighting, the weight values are ranked as shown in
Table 8.
The consistency coefficient can be obtained from Equation (18) and shows consistency between the weights calculated by hierarchical analysis and the entropy weighting; thus weights can be combined. Based on the weights and calculated by the above hierarchical analysis and entropy weighting, the combined weight vector can be obtained using Equation (17).
- (4)
Combination of weighting and TOPSIS
First, the initial decision matrix
E0 is established with the bridge reliability index rating criteria, and the initial decision matrix is obtained according to
Table 5 and Equation (19).
From Equations (20) and (21), the normalized decision matrix is
Then, based on Equation (22) and combined weights
= (0.086, 0.115, 0.109, 0.118, 0.095, 0.103, 0.091, 0.101, 0.092, 0.091), the weighted decisionalization matrix is obtained:
The positive ideal solution
= (0.086, 0.116, 0.110, 0.118, 0.095, 0.097, 0.093, 0.101, 0.093, 0.090) and negative ideal solution
of weighted decision matrix
A are obtained according to Equations (23) and (24). Then, the distance between each evaluation grade and the positive and negative ideal solutions is calculated according to Equations (25) and (26) as
and
, respectively. Finally, the relative closeness
of each evaluation grade to the positive ideal solution is calculated by Equation (27) as listed in
Table 8, and the bridge reliability classification criteria can be obtained from
Table 9 as listed in
Table 10.
The measured data of the reliability evaluation indexes in
Table 6 are dimensionlessized using Equations (20) and (21) to obtain the standard decision matrix as
Then, Equation (22) is used to multiply the data in the standardized decision matrix by the weight
of each corresponding indicator to obtain the weighted decisionalization matrix as
Then, the positive ideal solution
= (0.086, 0.115, 0.109, 0.118, 0.095, 0.103, 0.091, 0.101, 0.092, 0.091) and negative ideal solution
of the weighted decision matrix can be obtained using Equations (23) and (24). Then, the distance
and
between each object to be evaluated and the positive and negative ideal solutions plus the relative closeness
between each object and the positive ideal solution can be calculated by Equations (25)–(27). Finally, the results of the evaluation of the reliability grade of the three-span upper structure are listed in
Table 11.
- (5)
Analysis of evaluation results
From the evaluation results in
Table 10, it can be seen that the reliability grade of the bridge for the three spans is evaluated as Grade 2, Grade 2 and Grade 2, indicating that the bridge has slight deficiencies, which is consistent with the reliability grade evaluation results in the literature [
36]. Based on TOPSIS, the closer the relative closeness
of each evaluation object to the positive ideal solution is to 1, the closer the solution is to the optimal level, so the superiority ranking of the reliability of the superstructure of the three spans of this bridge is:
. When maintenance resources are limited, span 1 and span 2 can be given priority.
In summary, the combined assignment–TOPSIS method is well-tested in the reliability assessment of actual bridge projects and reflects the accuracy and applicability of the method, which provides a new method for the reliability assessment of highway bridges.
4.4. Comparative Study
In order to illustrate the rationality and scientificity of the method, this paper does a comparative study using the AHP–Extenics method. AHP calculates subjective weights, as was explained in detail in the previous section; thus we focus on Extenics here.
Extenics was first founded as a new discipline by scholars such as Wen Cai from Guangdong University of Technology and adopts a formal model to study the possibility of expansion of things and the laws and methods of pioneering innovation. It is widely used in multi-objective comprehensive determination problems, and is mainly divided into the objects, extensible sets and extensible logic, among which objects have a greater advantage in solving uncertainty and fuzziness of things [
37]. Objects mainly include the following three parts: determination of classical domain and nodal domain, determination of objects to be evaluated, and calculation of the correlation degree of the evaluation index [
38].
Let the highway bridge reliability assessment study be the object element
R with
m evaluation indicators under it, and also divide
n evaluation grades for each evaluation indicator
, the evaluation indicator set
and the evaluation grade set
[
39].
- (1)
The object element classical domain is denoted as:
where
—the
jth
grade of the evaluation object;
—the ith evaluation indicator of the evaluation object;
—the value of the corresponding indicator when the evaluation object belongs to the jth grade;
—the range of values when evaluation object
i belongs to the
jth evaluation grade
, i.e., the classical domain;
is the lower limit of the value of the quantity of the
ith indicator
; and
is the upper limit of the value of the quantity of the
ith indicator
[
40].
The nodal domain of the object element is expressed as:
where
—the whole of the evaluation grade;
—the range of all values of evaluation index , i.e., the section field; is the minimum value of the lower limit of the ith evaluation index in all evaluation grades; and is the maximum value of the upper limit of the ith index in all evaluation grades.
- (2)
Determination of the elements to be evaluated
where
W—an object to be evaluated;
— on the evaluation of the value range of indicator is the specific indicator data of the object to be evaluated.
- (3)
Calculation of the correlation of evaluation indicators
Correlation of reliability grade
j of the road bridge to be evaluated is as follows:
where
—the correlation degree of the object to be evaluated when for evaluation grade
j.
- (4)
Determine the reliability evaluation grade of highway bridges
Combining of the weight coefficients of each index with the calculated correlation function value synthesized to get the evaluation object’s grade correlation is shown in Equation (34). If
, then the evaluation object belongs to grade
j.
where
is the weight value of evaluation index
; the larger
is, the greater the degree of influence of the evaluation index on the evaluation object.
The classical domain and section domain in this bridge reliability evaluation index are in
Table 12, and the measured values of each evaluation index are shown in
Table 13.
From Equations (31)–(33), we can obtain the correlation degree of highway bridge reliability evaluation indexes to be evaluated, and the calculation results are as follows:
Note: The correlation degree represents the distance between the point and the interval and can have a positive or negative value. Positive values indicate that the degree of conformity of the point with the interval is large. correlation degree reflects the degree of connection between each evaluation index and each evaluation grade—the greater the correlation degree, the better the conformity between the evaluation index and the evaluation level.
The values of subjective weights calculated by hierarchical analysis are
= (0.071, 0.138, 0.120, 0.139, 0.085, 0.101, 0.087, 0.104, 0.079, 0.076). According to Equation (34), the comprehensive correlation of the reliability of this highway bridge regarding evaluation grade
j can be calculated as:
Based on maximum affiliation, the reliability level of this highway bridge is span (Grade 2), span (Grade 2), span (Grade 2), which indicates that all three spans of the bridge are in a slightly deficient condition.
Throughout the text, the comparison reveals that the reliability evaluation of the bridge using two different methods is consistent, and the evaluation grade is two, which is also consistent with the actual working condition of the bridge. In the control study, the traditional AHP method was used to calculate the weights, and it was difficult to ensure scientific and accurate weights due to the uneven level of experts. In contrast, this paper uses AHP and entropy to assign subjective and objective weights to each evaluation index separately, avoiding the one-sidedness of a single assignment method and taking into account the subjective intention of decision makers and the objective properties of the data itself. Further, this paper uses TOPSIS to calculate the relative closeness of each span and then determine its reliability level. The obtained evaluation results are consistent with those determined by AHP–Extenics. The comparative study highlights the rationality of the proposed method.