Abstract
This paper involves an analysis to determine appropriate cassava harvest practices and choose a pricing scheme between farmers and factories, cassava yards, and collectors in Thailand. Harvest practices represent all activities from land preparation to harvest. A key decision that governs the amount of resources required during cassava life cycle is the cassava’s harvesting age. The harvesting age can be from eight to 18 months in two patterns: fixed age, e.g., harvest every 12 months, and variable age, e.g., harvest at an age between 10 and 14 months. After harvesting, there are two common pricing schemes to consider, which are weight-based and starch-content-based. Factors that affect the two decisions made by Thai farmers at a given time are the market price, which highly varies within a season and between seasons, and yields in terms of weight and starch content, both of which change with cassava’s age and/or harvest month. Economic sustainability measure for Thai farmers is the average monthly profit that the farmers gain over cassava harvest cycle under uncertain market price. To handle uncertainties, a simulation model is constructed to imitate cassava planting activities from cultivation to harvest. The purpose is to evaluate various harvesting ages and two pricing schemes under uncertain cassava market prices. Market prices in 15 seasons (2006–2021) are grouped using the k-mean clustering into four price scenarios. As cassava grows in the simulation, the required resources are consumed until the decisions on harvesting time and pricing scheme are made with estimated selling probability under different price scenarios and uncertainty in cassava yield. Through simulation, harvesting age and pricing scheme that are most profitable and robust-to-system-variation are determined. Finally, a guideline for Thai farmers to choose a pricing scheme is developed based on the sensitivity analysis of the simulation model.
1. Introduction
Cassava is an important economic crop of Thailand. In 2020, Thailand’s cassava production amount (29 million tons) was at the third rank in the world [1]. Thailand cassava export, in the forms of cassava dried (chips and pellets) and cassava starches, was ranked first with approximately 57% of global market share due to relatively much lower domestic consumption [2]. The total export volumes had ever been around 11 million tons from 2014 to 2017 but have been decreasing since 2018 and were at 7.14 million tons in 2020 [3]. However, unlike most developed countries, where agricultural products are produced in large farms under contract farming with the buyers, there are a large number of small-sized cassava farms in Thailand, mostly without contract farming. In 2020, there were 587,754 cassava farming households with an average farm size of 2.57 hectares [4].
In general, fresh cassava root production (Figure 1) consists of the following activities: land preparation and cultivation, fertilizing, weed control, harvesting, and transportation. First, the land is ploughed at least once prior to ridging. Then, organic fertilizers, e.g., compost and chicken manure, are added, and stems are planted. After two months, fertilizer, usually a chemical type, is applied to enhance nutrients in the soil. Then, weed control is performed every three months, either by using herbicide or manual removal by human workers in order to protect the cassava stems from weeds. Finally, the cassava is harvested and transported to a cassava yard or starch factory.
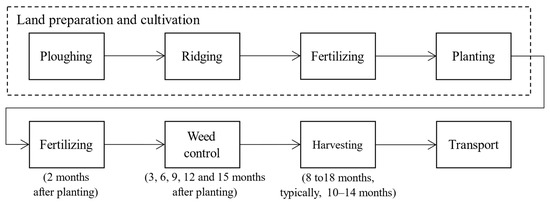
Figure 1.
Typical cassava production process in Thailand.
Factors that directly affect farmers’ profit from selling their harvests include the cost of cultivation activities that is directly driven by the harvesting age, yield (amount and starch content, expressed as a percentage), market price, and the pricing basis in which to sell the products to local buyers, defined as “pricing scheme” in this paper. Among these factors, market price and yield, to a lesser degree, are not under the farmers’ control. Although cultivation activities can affect yield, there are other uncontrollable external factors related to climate change, such as amounts of rainfall, drought, flood, pest and disease breakouts. Cassava yield also changes with harvesting age. Naturally, cassava root’s weight increases, while starch content tends to decrease, as cassava grows older. In addition, there is a relationship between the decrease in starch content and high rainfall during the harvesting period, as the cassava plant reinitiates its growth and creates new sprouts, and translocate the nutrients from the root to the top of the plant [5,6,7].
Since most Thai farmers perform common cultivation activities, the two important factors under farmers’ control that affect cost, revenue, and thus, profitability are the length of harvesting practices and pricing scheme. The amount of resources required for cassava’s harvesting practices is driven primarily by its harvesting age. The harvesting age can range from eight months (the earliest age that cassava is harvested) to 18 months (the oldest age of cassava sold in the market). Moreover, there is some variation in the length of harvesting practices that farmers prefer. Harvesting practices length may be fixed or varying within an interval. The most common practice among Thai farmers is to harvest once a year, i.e., a fixed harvest cycle of 12 months. However, some farmers consider market price when making their harvest timing decision. In other words, the market price trend directly affects the likelihood of harvesting, as farmers prefer to harvest when the market price is high, or they may postpone harvesting when the market price is low. This leads to harvesting practices with some variations in its length. For example, a 10-month to 14-month varying length implies that most farmers may harvest their cassavas as early as 10 months, or as late as 14 months after planting.
After harvesting, farmers have to choose where to sell their produce, based on factory-gate buying prices and pricing schemes. In Thailand, there are two pricing schemes: weight-based and starch-content-based. Weight-based pricing is widely used by collectors, cassava chip manufacturers, and some starch manufacturers, while the starch-content-based pricing is mainly used at starch manufacturers. With weight-based pricing, the harvest is sold according to the weight (in tons) only; whereas with starch-content-based pricing, the quality of the harvest is evaluated at the factory gate to determine the percentage of starch content and the per-kilogram buying price. The market price is quoted at a level of starch content, either at 30%, or 25%. When the cassava has lower starch content, the buyer decreases the buying price, depending on the measured starch content of the harvest. Usually, in a particular area, the quoted market price at 30% starch content is higher than the market price of the weight-based pricing.
As a commodity product, changes in cassava supply and market demand lead to price fluctuation. In the past decade, the market trend is somewhat positive due to increasing demand from emerging market (China) that uses cassava as raw material for producing alternative energy, i.e., biodiesel. In recent years, some influential events and factors, e.g., an outbreak of diseases, climate change, world economy, technological change, government policies, contribute to higher uncertainty in the demand and supply of cassava, which highly affects cassava market prices. Figure 2 illustrates the market price of cassava over the past decade. It can be seen that the price fluctuates in an unpredictable manner, i.e., the price pattern does not necessarily repeat itself from season to season. Making decisions under such volatile market situations to achieve economic sustainability is clearly a challenge for farmers.
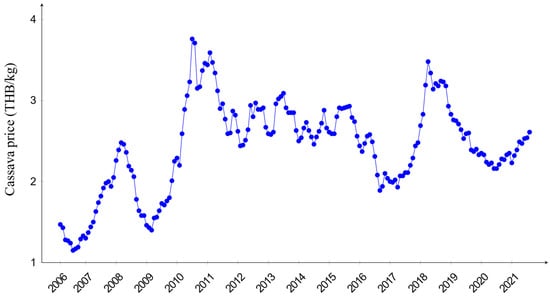
Figure 2.
Cassava price in the past decade. Source: Thai Tapioca Starch Association (TTSA) [8].
Thai cassava farmers usually choose the time to harvest and pricing scheme based on their experiences, financial needs, and market price, without proper guidelines on choosing the harvesting age and pricing scheme. This may not lead to optimal and/or robust decisions. Thus, the objective of this paper is to provide a guideline for choosing harvesting age and pricing scheme, while considering uncertainties regarding other factors including market price, amount of resources required, its cost, yield amount and percent starch that change with age, through the use of a computer simulation model.
Simulation modelling is a methodology that can be used to analyze such an agricultural system that contains various sources of uncertainty. A simulation model imitates the real system with a logical/mathematical, computerized model. The major benefit of using simulation is that the system behavior can be studied through computational experiment in advance without disrupting the real system. In this paper, a simulation model is developed to imitate cassava production processes under uncertainties. Using the model, farmers’ decision makings regarding the harvesting age and pricing scheme are analyzed under volatile market scenarios so as to maximize the economic benefit, i.e., profit, for the farmers. It is important to emphasize that the harvesting age governs the farming activities and resources required until harvest. Therefore, from this perspective, the harvesting age essentially represents the harvesting practices. Input data of the model are from an extensive survey study using face-to-face interviews with the farmers. After constructing the model, model verification and validation are properly performed to ensure that the model is a good representative of the real system. In addition, clustering analysis on market price is performed to identify common price scenarios that farmers may face. Different harvesting age and pricing scheme decisions are then tested under these market price scenarios in order to determine not only the optimal decisions that maximize profit, but also to obtain robust decisions. Analysis of the computational experiment results lead to the guideline for farmers to choose a harvesting age and a pricing scheme that maximize their average monthly profit. The guideline is based on a comparison between the market price posted at factory gate and the actual purchase price the farmer will receive based on the estimated starch content of their cassava roots.
Our contributions are two-fold. First, through simulation analysis, we develop a guideline to help Thai farmers choose an appropriate harvesting age and pricing scheme to achieve economic sustainability in terms of long-term profit under various market price scenarios. Second, we demonstrate the use of computer simulation, in a computational experiment environment, as a decision support tool to capture the simulated uncertainties in the external factors affecting cassava marketing and farmers’ financial benefits.
2. Literature Review
A number of research studies have been conducted in applying simulation modelling to various industries such as manufacturing, logistics, and agriculture. In the manufacturing industry, simulation is widely used as a decision support tool for productivity improvements such as reducing production lead-time and work-in-process inventory [9,10,11,12,13]. In the logistics industry, simulation played a role in transportation analysis for both domestic and export systems. For example, Mobini et al. [14] used simulation to investigate the logistics of supplying forest biomass to a potential power plant. Turner et al. [15] applied the simulation to assess the performance of a domestic grain transportation system in various scenarios while varying resources, which are truck and driver capacity, and considering uncertain parameters related to the transportation process.
Simulation was implemented to achieve productivity improvement and assist decision-making in agricultural production systems in the following studies. Stehfest et al. [16] adapted the agro-ecosystem model for the simulation of major crops at a global scale. The objective is to address the issue of the earth system as it changes global biogeochemical and water cycles, while global environmental change affects land productivity and future land-use decisions. Martin-Clouaire and Rellier [17] studied a computer simulation framework for production activities, flexible plans, and material resources in agricultural production systems. Van der Vorst et al. [18] proposed a new integrated approach towards logistics, sustainability, and food quality analysis, and implement the approach by introducing a new simulation environment. Martin et al. [19] presented a simulation framework to construct simulation models of grassland-based beef-cattle farms for evaluation and empirical design purposes.
Furthermore, in the past decade, Hameed et al. [20] developed and applied an object-oriented simulation model which simulates in detail in-field machine activities during the execution phase in order to deal with complex operations involving capacity constraints and cooperating units. Ooster et al. [21] presented a simulation of labor processes in a greenhouse with a rose cultivation system. The objective is to quantify the effects of production system changes by means of a flexible and generic model approach. Bergez et al. [22] built a specific modelling platform to help model, simulate and evaluate cropping systems to find new solutions to produce goods due to significant changes in agro-ecological contexts. Linker et al. [23] improved efficiency of water consumption in cultivating cotton, potato, and tomato by using simulation analysis results to perform irrigation scheduling. She et al. [24] presented an application of simulation in modelling a ground-based timber harvesting system to estimate machine performances including cycle times, productivities, and utilization. Gittins et al. [25] developed an approach that combines simulation result and interviews with farmers. The objective is to evaluate the impact of changing in socio-political circumstances and to find strategies for livestock management. The simulation was also applied to support seeding and harvesting decisions in two recent studies. Kadigi et al. [26] performed simulation experiments to evaluate alternative rice farming systems, specifically, traditional rice farming practices and the proposed rice intensification (SRI) practices, to improve farmers’ income. Deepradit et al. [27] presented a simulation model for aromatic coconut manufacturing to determine an appropriate harvest amount and harvesting age that maximize annual profit under uncertainty.
For cassava-based products, simulation-related studies and the study objective are as follows. Amamullah et al. [28] developed a simulation model to estimate cassava growth in order to identify the treatment combinations (forage intercropping and organic manures) that maximize cassava growth rate. Yu and Tao [29] implemented a Monte Carlo simulation to assess the energy efficiency of cassava-based ethanol fuel on the vehicle energy consumption. In another study by the same authors, Yu and Tao [30] constructed a Monte Carlo simulation of the life cycle emission models to assess and compare environmental emissions of three biomass-based fuel ethanol (BFE), including wheat-based, corn-based, and cassava-based, from different feedstock planting areas in China.
Da et al. [31] studied recycling process in cassava starch production process using continuous simulation model. Specifically, the reduction of effluents volume, measured in terms of water consumption, through a recycling process in the cassava extraction operation is modelled using MATLAB Simulink. Different strategies of recycling are tested and the most water-volume saving strategy is identified. Mithra et al. [32] proposed a process model for simulating the growth of cassavas. The objective is to predict the final yield under different field conditions, crop phenology, solar radiation and photosynthesis, levels of stress due to shortage of water, nitrogen and potassium. Zhang et al. [33] analyzed the cost of using cellulase enzyme and stream energy in cassava-based ethanol product. A flowsheet simulation model of the system is constructed using Aspen Plus.
Recently, Le et al. [34] proposed an environmental policy integrated climate (EPIC) model to assess the impact of conservation agriculture (CA) and conservation tillage (CT) on the yields of important crops, which also included cassava, in Cambodia. The model inputs include crop parameters, management practices, soil properties, plot topographic conditions, and daily weather. In particular, the simulations of cassava yield and cassava biomass show satisfactory results that the model can capture the behavior of the actual crop system. Jiao et al. [35] implemented a Monte Carlo simulation to analyze uncertainty in the development of cassava-based fuel ethanol in China. The objective is to identify the stages and factors that mostly affect the life cycle performance of cassava ethanol.
Based on the literature review, there is no past research study, to the best of our knowledge, that uses simulation to model the behavior of farmers regarding their selling practice and harvesting age with respect to fluctuation in market prices, cassava yield in terms of starch content and yield amounts. Currently, farmers’ decision making rely mainly on their experiences without a proper tool to consider such uncertainties. Therefore, this paper aims to fill this research gap and to demonstrate the practical use of simulation modelling to support the decision-making that impacts the economic aspect of an important group of stakeholders, cassava farmers, in this supply chain. Filling this research gap provides a framework for other agricultural products’ stakeholders to consider the simulation modeling approach as a decision support tool.
3. Methodology
Decision makings on the harvesting age and pricing scheme need to consider uncertainties in the market price, cassava yield in terms of amount and starch content, and the chance that farmers will sell their harvests. These factors interact with one another, e.g., the chance of selling depends on changes in the market price. A decision in one harvest cycle may affect the timing of another decision in the next harvest cycle. For example, consider a farmer who chooses the harvesting age between 12 and 18 months. Suppose at month 12, the farmer decides to keep the harvest, then the farmer has to make the selling decision again in the next months. However, if the farmer decides to harvest and sell at month 12, then cultivation of the new crop will start next month. In a span of 36 months, a farmer can have three 12-month harvest cycles (with a lower yield amount in each cycle), or two 18-month harvest cycles (with a higher yield amount in each cycle). In other words, this example represents a decision between harvesting every 12 months, i.e., selling to a starch manufacturer using starch-content based pricing scheme, and keeping the cassava longer to sell to a chips producer using weight-based pricing scheme. Considering the interaction of these factors under uncertainties can lead to more profitability for the farmers.
3.1. Data Collection Using Interview
Input data of this study are from face-to-face interviews with several groups of farmers in seven major provinces that grow cassava in Thailand. Specifically, these provinces, which produce more than one million metric tons of cassava per year, are selected from over 54 cassava-growing provinces. They also adequately represent all geographic regions that grow cassava. The sampling scheme is based on stratified random sampling with proportional allocation that uses expected yield amount of each province as stratifying variable.
The collected data from interviews include many pieces of information. Some of the collected data that directly affect harvesting practices and selling decision are used in this study, including buyer information and pricing scheme, cultivation and harvesting practices, harvesting ages and total yield (weight amount and starch content), related cost components from land preparation to harvesting.
3.2. Patterns of Harvesting Age and Pricing Scheme
To capture variation in harvesting practices (HP), this article considers nine different harvesting age patterns based on the practices of over 800 cassava farmers participating in our survey study as in Table 1.

Table 1.
Harvesting practices of cassava farmers.
For the varying harvesting age, it is assumed that a farmer may make decisions every two months in order to reduce the number of decision points. For example, a 10–14 month interval would have three decision points at 10, 12, and 14 months of cassava age. Each decision point consists of up to two decisions for a farmer to make: (1) keep or sell their harvest, and (2) if sell, a subsequent decision is to choose a pricing scheme between weight-based and starch-content-based. Together with the nine different harvesting age, there are a total of 18 combinations of practice alternatives.
3.3. Simulation Model
A simulation model was constructed in ARENA 16.0, a specialized software tool for discrete-event simulation modelling and analysis. The logic diagram of the simulation model is shown in Figure 3.
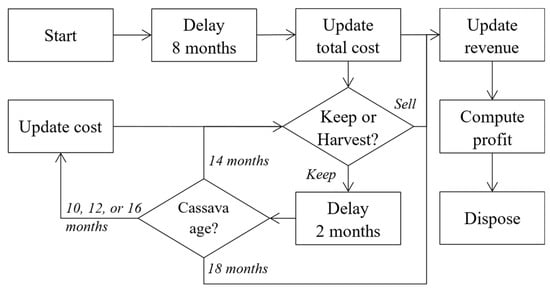
Figure 3.
Logic diagram of simulation model.
In the model, nine entities representing independent decision makers (farmers), one for each harvesting practice are created at the beginning. The entities go through initialization process, where the cultivations begin, and the costs associated with all cultivation activities in the first eight months are recorded. Then, the entities enter a keep-or-harvest decision point. While the three fixed harvesting age entities always harvest their produce at their specified times, the six varying harvesting age entities make a keep-or-harvest decision at their respective decision points. At a decision point, the decision to harvest is subject to two conditions: (1) the entity must be eligible in terms of timing, and (2) if eligible, then harvesting decision follows a probability distribution as shown in Table 2. These harvesting probabilities are a non-decreasing function of cassava age and market price, i.e., the better the price and/or the older the age, the higher the probability of harvesting. The probability values are estimated from data collected from face-to-face interviews with many farmers during a field survey.

Table 2.
Probability of harvesting.
For example, at the first time all entities reach the decision point (with a cassava age of 8 months), only the entities representing HP7 and HP9 are eligible to harvest, while all other seven entities must keep their produces. The two entities then check the price scenario. Suppose the cassava market price increases by 2% from the previous month, then the probability of harvesting is 60%.
For an entity that decides to harvest and sell its produce, the cost, revenue, and monthly profit are updated, and the entity is disposed. For entities that keep the produce, they go through a delay of two months. After a delay, if the cassava age is 10, 12, or 16 months, then the cost (incurred from weed control activity at cassava age of 9, 12, and 15 months) is updated and the entity is redirected to the keep-or-harvest decision point again. If the cassava age is 14 months, then it is routed back to the keep-or-harvest decision point without updating the cost. Otherwise, the cassava is 18 months old at which time the cassava must be harvested and sold, and the simulation run is terminated at 18 months.
3.4. Cost Parameters
In each harvest cycle, there are several cost components: land preparation cost incurred at cultivation time, land rental cost, stem and stem preparation cost, fertilizer cost (at cultivation and two months after cultivation), weed control cost (every three months), harvesting and transportation cost, as shown in Table 3. The last three cost components are incurred at harvesting time. These cost components are estimated from over 800 farmer interviews in 20 provinces in Thailand. These cost parameters are used to update the total cost in the simulation model at cultivation time (month 0), at cassava ages of 8, 10, 12, and 16 months, and at harvest time, as entities go through their harvest cycles.

Table 3.
Relevant costs of cultivation and harvesting.
3.5. Market Prices
Market prices of cassava are highly volatile, both within a season and from season to season. This is due to two components of cassava demand in Thailand. The first component is the normal demand for cassava roots as raw materials of cassava products and by-products. This component together with the harvesting practices mainly drive the within-season variation of the market price. The other component, which is associated with the season-to-season variation, is cassava demand as a substitute product for other agricultural products. For example, cassava roots and cassava chips are alternative raw materials of other raw materials such as maize, molasses from sugarcane for producing ethanol. In a season when market prices of these raw materials are relatively high, or when their harvests are low, there would be a higher demand for cassava, which in turn affects cassava market price.
Because the market price is one of the major sources of variation in the cassava agricultural system, investigating the harvesting practices and pricing scheme decisions under various price scenarios is important. Cassava market prices used in our study are from 2006 to 2018, i.e., 13 seasons. In a season, each harvest cycle may begin as early as March and end as late as August next year, or 18 months later for the oldest harvesting age. That is, market prices of the first harvest cycle of our data are prices in March 2006 to prices in August 2007, market prices of the second harvest cycle are prices in March 2007 to prices in August 2008, and so on. To add market price variability, the quoted market prices in the simulation model are randomly generated using a triangular distribution with three parameters: minimum, average, and maximum market prices within a month. The Source of market price data is the Thai Tapioca Starch Association (TTSA) [8].
Due to season-to-season and within-season price variability, it is difficult to accurately forecast the future market price as it is influenced by several uncertain factors such as production yield, weather, government policy, and other commodity prices. Market prices in 13 seasons are classified using k-means clustering algorithm [36] into common patterns of prices. The purpose of market price clustering is that it helps to refine our research question to determine the most robust and profitable harvesting age and pricing scheme for every price scenario (or market price cluster). The steps of the algorithm are shown in Figure 4. The algorithm starts with selecting the number of clusters (k). The centroid of each cluster is then randomly initialized. Each sample containing a market price data set (18 observations of monthly market prices in a harvest cycle) is assigned to one of the clusters according to the nearest distance to the cluster’s centroid. The algorithm searches for the centroid of each cluster so as to minimize the total distance of all samples to their assigned centroid. The search stops when the new centroids are not different from the current centroids. Otherwise, the new centroids will replace the current centroids, and the samples will be repeatedly assigned to their nearest centroid.
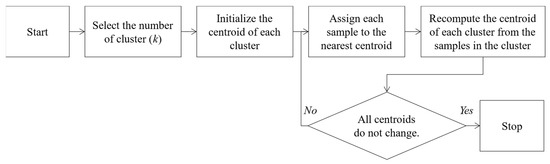
Figure 4.
k-mean procedure.
The k-mean algorithm is run from k = 2 to 10 clusters. The suitable number of clusters is four because it gives the highest average value of Silhouette [37], as in Figure 5. Note that the silhouette value is the measure that reflects the minimal total distance between samples and their cluster centroids, and the maximum distance between different centroids.
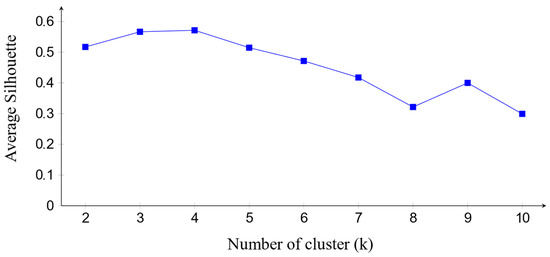
Figure 5.
Average Silhouette and number of clusters.
The resulting four clusters of market price data are illustrated in Figure 6. The high price cluster contains seven samples (2010/11–2015/16, and 2018/19). These are the seasons when in-season market prices were relatively stable with some fluctuations around 2.50–3.50 THB/kg. Moderate price cluster contains market prices of four harvest seasons, 2007/08, 2016/17, 2019/20, and 2020/21. These are the seasons when market prices, although started differently, became very similar after month 6 in their respective seasons. The lowprice cluster is when market prices were relatively low in 2006/07 and 2008/09, approximately 1.50–2.00 THB/kg, compared to other seasons. Finally, the increasing price cluster contains seasons when market prices surged, from 2.00 to 3.20 THB/kg in 2017/18, and from 1.40 to 3.50 THB/kg in 2009/10 (due to government intervention policy.
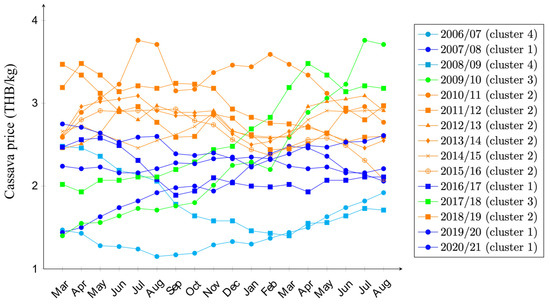
Figure 6.
Classification of cassava market prices of 13 harvest seasons into four clusters.
3.6. Cassava Yields
The cassava yields in terms of amount (weight) and starch content are other sources of system variation. Usually, cassava yield amount increases with cassava age. Figure 7 shows estimates of yield amount at various cassava ages from our survey data. Cassava starch content is mostly related to the harvesting month, rainfall and weather condition in a season, and geographical factors (see Figure 8). In the simulation model, the starch content is randomly generated from a triangular distribution, whose parameters (minimum, average, and maximum values) change with cassava age according to the estimated data in Figure 8.
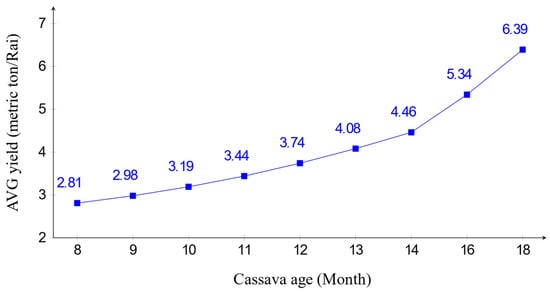
Figure 7.
Cassava yield vs. age.
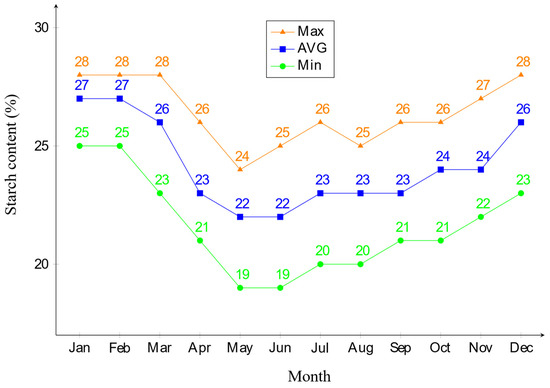
Figure 8.
Cassava starch content vs. harvest month.
3.7. Revenue Functions
When a farmer decides to harvest and sell their cassava, the revenue for both weighted-based and starch content-based pricing schemes are updated using Equations (1) and (2), respectively.
where
- denotes revenue from weight-based pricing, (THB),
- denotes quoted market price of cassava roots, (THB/kg),
- denotes percent price reduction from the quoted market price for weight-based pricing, (%),
- y denotes yield, (mt/Rai),
- denotes revenue from starch content-based pricing, (THB),
- s denotes starch content of cassava, (%),
- denotes percent price reduction from the quoted market price for every percent starch content below 30%, (%),
- a denotes age of cassava, (month), and
- denotes percent price reduction from the quoted market price if the cassava age is 14 months or older for starch content-based pricing, (%); this parameter follows a triangular distribution, .
The weight-based revenue is simply computed from the market price, the percent reduction from quoted market price when there are too many soils or foreign materials mixed with the roots, and the yield amount. On the other hand, the starch content-based revenue relies on the market price at 30% starch content, yield amount, and two other price reduction percentages. The first one is the percent reduction, , from the quoted market price at 30% starch content. For example, = 2% means that there is a 2% price reduction for every 1% starch content below 30%. The other percent reduction is , which is applied when the cassava age is 14 months or older.
3.8. Verification and Validation of the Simulation Model
Logics of the simulation model are verified by setting the market price scenarios that affect the harvesting and selling of cassava to two extreme cases: when price constantly increases by 4% each month and when price constantly decreases by 4% each month. These cases are chosen so that the measures of system performance can be calculated manually such that a comparison of results can be made. Then, two key measures of performance, including the length of HPs and monthly profit, from the simulation model and from the manual calculation are compared to see whether the results match. These cases have no effects on the performance measures of three fixed harvesting age (10, 12, and 18 months). However, for six varying harvesting age, 4% increase in market price would always result in selling as early as possible (i.e., the youngest harvesting age), whereas 4% decrease leads to selling as late as possible. The simulation results of both performance measures match exactly with manual calculation results, which verifies the simulation model logic.
Simulation model validation was performed by comparing the collected data of monthly profit from a survey study and the monthly profit from the simulation model. First, the cost and revenue data were obtained from questionnaires, which can be used to calculate the monthly profit. These questionnaires were filled by farmers at Nakhon Ratchasima, the province with the largest cassava production in Thailand. The same cost data from each questionnaire is put into the simulation model and the monthly profits are generated from the simulation runs. Finally, a 95% prediction interval of the monthly profit from the simulation model is constructed. After comparison, all the average monthly profit data were within the prediction interval from the simulation model, which indicates that the simulation model is valid and can be used for the analysis.
3.9. Computational Experimentation with Simulation
To evaluate the harvesting practices and pricing schemes, the simulation model was set to run for 18 months. In each simulation run, all nine harvesting practices are set to start the cassava cultivation in the same month (March). The harvesting age may vary from eight months up to 18 months. Therefore, a simulation run ends at 18 months (the oldest harvesting age). Key system measure of performance is the average monthly profit, which is computed from the total revenue, the total cost, and the harvesting age. The number of replications is 30 runs. This is determined by specifying that a difference of 10% in the average monthly profits between any two HPs can be detected as being statistically different with a probability of 95% (i.e., a type II error of 5%), at the level of confidence of 95% (i.e., a type I error of 5%).
In addition, the market prices from 13 harvest seasons (2006–2018) are arranged into 13 datasets. Each dataset represents a market price scenario. The simulation model is run for 30 replications for each of the 13 market price scenarios, or 390 simulation runs. In each run, 18 monthly profits (from 18 combinations of nine harvesting ages and two pricing schemes) are recorded, which results in a total of 7020 monthly profit data to analyze.
4. Results and Discussion
4.1. Statistical Data Analysis of the Results
Statistical analysis of average monthly profits is performed using analysis of variance (ANOVA). The factor effects of interest are the nine harvesting practices and two pricing schemes. Note that different replications are treated as blocks in this analysis because all treatment combinations of harvesting practices and pricing schemes face the same set of randomly generated data and are evaluated at the same time in each replication. The ANOVA is shown in Table 4.

Table 4.
AVONA for average monthly profit.
From the ANOVA, since the interaction between harvesting practices and pricing scheme is significant (p-value < 0.001), further analysis must be performed at the interaction level. Multiple comparisons on the average monthly profit are conducted by using Tukey’s method. The average monthly profits for the 18 combinations of harvesting practices and pricing schemes are shown in Figure 9.
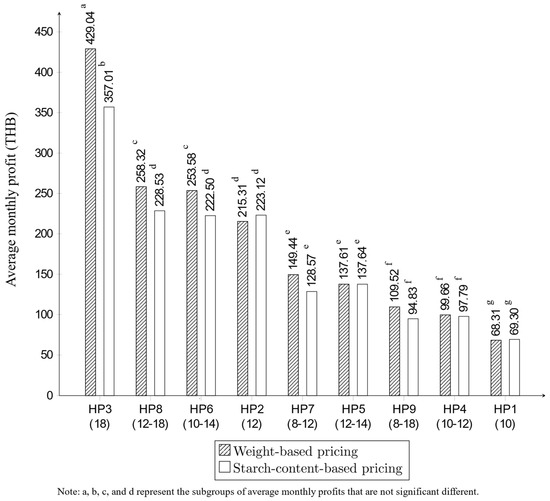
Figure 9.
Average monthly profit of nine HPs and two pricing schemes. Note: Average monthly profits that share the same letter are not statistically different.
From Figure 9, the average monthly profits that share the same letter are not statistically different based on Tukey’s multiple comparisons. For the pricing scheme, due to the significance of interaction between harvesting practices and pricing schemes, the average monthly profits of weight-based pricing are statistically higher than those of starch content-based pricing in three harvesting practices. Differences are found in the fixed 18-month harvesting age (HP3), varying 12–18 months harvesting age (HP8), and varying 10–14 months harvesting age (HP6), while the two pricing schemes perform statistically the same for the other harvesting practices.
For fixed age-at harvest, when cassava root is relatively young (i.e., 10 months), both pricing schemes give relatively the same monthly profit. At a common harvesting age of 12 months, the profit becomes significantly higher than those of 10 months harvesting age, with starch content-based pricing giving a slightly higher monthly profit than weight-based pricing. This implies that at the age of 12 months, it is more profitable to sell the cassava at a factory gate, rather than at a cassava yard. As cassava age reaches its maximum harvest age (18 months), the profit is maximized due to a significantly larger harvest yield amount. However, at such old age, the cassava roots contain lower percent starch that starch content-based pricing gives a much lower average monthly profit than the weight-based pricing. The cassava roots at such old age are only appropriate to be processed into cassava chips or pellets, but not into tapioca starch. A similar trend can be seen for the varying harvesting age. That is, monthly profit seems to be higher as cassava age is older, and between the two pricing schemes, weight-based pricing generally gives no lower profit than starch content-based pricing.
Effects of the harvesting practices are also interpreted in terms of the interaction between the harvesting practices and the clusters of price scenarios. Tukey’s multiple comparisons of the average monthly profits from different harvesting practices are performed for each price scenario. The results are displayed in Figure 10a–d. In seasons when the cassava market prices are low and moderate, i.e., Figure 10a,b, there are differences in the statistical grouping of the average monthly profits with respect to the nine harvesting practices. In the figure, harvesting practices in the different statistical groups are separated by different letters. The fixed 18-month harvesting age significantly gives a higher average monthly profit. This follows by three harvesting practices with varying harvesting age of 12–18 months and 10–14 months, relatively old-aged cassava, and a fixed, most common harvesting age of 12 months. For the 8–12 months, 12–14 months, 10–12 months, and 8–18 months varying harvesting age, as well as the fixed 10-month harvesting age, which are the harvesting practices that may begin harvesting at a relatively young age that gives lower average profit. Another noticeable finding is that only the fixed 18-month harvesting age can generate a profit in low-price seasons, while varying harvesting age of 12–18 months, 10–14 months, and a 12-month fixed harvesting age perform mostly around break-even, and all other harvesting practices result in economic losses.
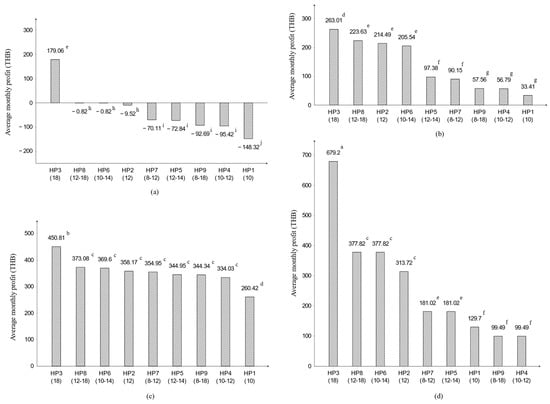
Figure 10.
Average monthly profit of nine harvesting practices for each price scenario: (a) Average monthly profit of low price scenario, (b) Average monthly profit of moderate price scenario, (c) Average monthly profit of high price scenario, and (d) Average monthly profit of increasing price scenario.
From Figure 10c, in the seasons when cassava market prices are high, all harvesting practices result in a profit for farmers. The fixed 18-month harvesting age generates the highest average monthly profit, whereas the fixed 10-month harvesting age generates the lowest average monthly profit. All other harvesting practices perform statistically in the same group.
Finally, when the market price seems to be increasing during the season, Figure 10d, the trend in the average monthly profit remains the same as those of the other price scenarios, but with a much larger difference between the most profitable harvesting practice (fixed 18-month harvesting age) and the worst one (fixed 10-month harvesting age). This is because the later the farmers harvest their cassava, the higher the price becomes.
4.2. Guideline for Pricing Scheme Decision
A further analysis is conducted to develop a guideline for choosing between the two pricing schemes for the farmers. Recall that is the percentage of a price reduction from the quoted market price for every percent reduction in the starch content and is the percentage of a price reduction from the quoted market price that is applied to the weight-based pricing. The analysis is performed by varying from 0.5% to 5% (the current value is approximately 2%) in the simulation model. Then, the values of that lead to break-even points between the average monthly profits of the two pricing schemes are determined. Analysis results are shown in Table 5. Each entry in the table represents that can help farmers decide whether to sell their cassava based on starch content-based or weight-based pricing. The guideline for using Table 5 is presented in Figure 11.

Table 5.
Break-even values of at increasing values of .
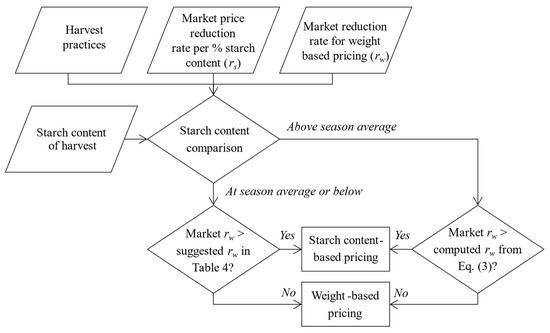
Figure 11.
Flow chart of using the break-even of average monthly profit table.
Initially, based on one’s harvesting practices, a farmer must know the current market value of and current market value of . Then, the farmer decides whether the starch content of their harvest is close to the season average value (e.g., the % starch is around 27% in January in Figure 7). If so, the farmer may use the value of from Table 4. If the market value of is higher than the break-even value in the table (i.e., the market weight-based price has too much price reduction), then the farmer should sell their harvest based on starch content-based pricing. Otherwise, the weight-based pricing is suggested. However, if the farmer estimates that their harvests have higher starch content than the season average, then the calculation according to the Equation (3) would be performed.
where is the calculated break-even . Similar to using the value in Table 4, if the market is higher than the calculated from Equation (3), then starch content-based pricing should be chosen; otherwise, the farmer should sell by weight. Note that Equation (3) is derived from equating Equations (1) and (2).
For example, suppose a farmer, who uses a fixed 12-month harvesting age, assesses that his harvest’s percent starch is close to the season average, and decides to use Table 4. Also, suppose that the market value of is 2% reduction in price per each percent starch below 30%, and the market value of is 5%. The farmer would find the break-even value of from Table 4 at 8.8% (row 2, column 5). In this case, the farmer would choose weight-based pricing, because the market is better than the break-even value. However, if the farmer estimates that their harvests have starch content higher than the season average, say s = 29%, then = 2% which leads to starch content-based pricing. Note that is assumed at its mode value of 2.5%.
5. Conclusions
This paper presents the use of a simulation model to support Thai farmers’ decision makings regarding the harvesting practices and pricing scheme for selling cassava roots. Usually, Thai cassava farmers consider their financial needs, the current market price, and rely on their experience, which may not provide optimal and/or robust decisions. The simulation model is developed to imitate the cassava planting process from cultivation to harvesting. The model can effectively capture inherited uncertainties of the real system that affect the profitability of producing, harvesting, and selling cassava. These include market price fluctuation within and between seasons, probability of harvesting under different price scenarios, and harvest yield in terms of weight and starch content. The simulation model is verified under extreme price scenarios. In addition, market prices in 15 different seasons are grouped into four price scenarios with the k-mean clustering methods. The four price scenarios cover the market characteristics over the past decade, including high price, moderate price, low price, and increasing price.
Using the constructed simulation model, different harvesting ages and pricing schemes are evaluated under various market price scenarios to enhance economic sustainability for farmers. The results lead to a guideline that can help Thai farmers to choose a pricing scheme so as to maximize the average monthly profit by comparing the market price posted at factory gate and the actual price the farmer will receive based on the estimated starch content of their cassava roots. Our findings can be transferred to representative of farmers through training activities that are often organized by key stakeholders, such as starch factories, agricultural co-operatives, and related government agencies. We demonstrate that the approach can be used to support the decisions for cassava farmers. The approach should also be applicable to other agricultural products. Our findings could be significant to other developing countries whose cassava farmers have similar characteristics as those in Thailand, where cassava farms are relatively small in size, but many in terms of the number of farms. Finally, two future research directions for further study are (1) to study the impact of chemical and organic fertilisers and pesticides on the economic viability of cassava production, and (2) to integrate prediction models that can accurately predict or estimate key input parameters of our simulation model, specifically, starch content, and cassava price, rather than relying on the triangular distributions. Two previous studies that are related to the extension of this work include starch content prediction models [38] and cassava export forecasting models using machine learning algorithms [39].
Author Contributions
Conceptualization, P.P. and J.B.; Data curation, P.P.; Formal analysis, W.P. and J.B.; Funding acquisition, J.B.; Investigation, W.P., P.P. and J.B.; Methodology, W.P., P.P. and J.B.; Project administration, P.P.; Resources, P.P. and J.B.; Software, J.B.; Supervision, P.P. and J.B.; Validation, W.P., P.P. and J.B.; Visualization, W.P.; Writing—original draft, W.P. and J.B.; Writing—review & editing, W.P., P.P. and J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Bangchak Public Company Limited and the Center of Excellence in Logistics and Supply Chain System Engineering and Technology (COE LogEn), Sirindhorn International Institute of Technology (SIIT), Thammasat University.
Institutional Review Board Statement
Not applicable. The authors declare that this study did not report on or involve the use of any animal or human data or tissue. All data were from computer simulation, expert consultation, and overview statistics which were not sensitive personal data from individuals.
Informed Consent Statement
Not applicable.
Acknowledgments
We would like to express our gratitude to the supports provided by Bangchak Public Company Limited and the Center of Excellence in Logistics and Supply Chain System Engineering and Technology (COE LogEn), Sirindhorn International Institute of Technology (SIIT), Thammasat University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Office of Agricultural Economics (OAE). Agricultural Statistics of Thailand 2020; Ministry of Agriculture and Cooperatives: Bangkok, Thailand, 2012.
- Office of Agricultural Economics (OAE). Situation of Important Agricultural Products and Trends in 2021; Ministry of Agriculture and Cooperatives: Bangkok, Thailand, 2012. (In Thai)
- Information Technology and Communication Center, Ministry of Commerce of Thailand. Exports Structure. 2021. Available online: https://tradereport.moc.go.th/Report/ReportEng.aspx?Report=MenucomRecode&Option=5&Lang=Eng (accessed on 13 September 2021).
- Office of Agricultural Economics (OAE). Cassava: Planted Area, Number of Households, and Average Planted Area per Planted Area by Province in 2020; Ministry of Agriculture and Cooperatives: Bangkok, Thailand, 2012. Available online: https://www.oae.go.th/assets/portals/1/fileups/prcaidata/files/Casava Holdland 63.pdf (accessed on 13 September 2021). (In Thai)
- Rojanaridpiched, C.; Pulsanguan, P.; Phuddachareon, S.; Jeamjamnanja, J.; Saengkaewsook, W. Study on planting season of cassava. Agric. Nat. Resour. 1987, 21, 119–125. (In Thai) [Google Scholar]
- Ceballos, H.; Perez, J.C.; Calle, F.; Jaramillo, G.; Lenis, J.I.; Morante, N.; López, J. A new evaluation scheme for cassava breeding at CIAT. In Cassava Research and Development in Asia: Exploring New Opportunities for an Ancient Crop. Proceedings of the Seventh Regional Workshop, Bangkok, Thailand, 28 October—1 November 2002; Howeler, R.H., Ed.; The Centro Internacional de Agricultura Tropical (CIAT) and the Department of Agriculture (DOA): Bangkok, Thailand, 2007; pp. 125–135. [Google Scholar]
- Moreno, L.P.; Gourdji, S.M. Cassava Starch Content and Its Relationship with Rainfall; CCAFS Info Brief; CGIAR Research Program on Climate Change, Agriculture and Food Security (CCAFS): Copenhagen, Denmark, 2015. [Google Scholar]
- Thai Tapioca Starch Association. Weekly Tapioca Starch Price. 2019. Available online: http://www.thaitapiocastarch.org/en/information/statistics/weekly_tapioca_starch_market (accessed on 3 October 2019).
- Abdulmalek, F.A.; Rajgopal, J. Analyzing the benefits of lean manufacturing and value stream mapping via simulation: A process sector case study. Int. J. Prod. Econ. 2007, 107, 223–236. [Google Scholar] [CrossRef]
- Parthanadee, P.; Buddhakulsomsiri, J. Simulation modeling and analysis for production scheduling using real-time dispatching rules: A case study in canned fruit industry. Comput. Electron. Agric. 2010, 70, 245–255. [Google Scholar] [CrossRef]
- Kampa, A.; Gołda, G.; Paprocka, I. Discrete event simulation method as a tool for improvement of manufacturing systems. Computers 2017, 6, 10. [Google Scholar] [CrossRef]
- Lidberg, S.; Aslam, T.; Pehrsson, L.; Ng, A.H. Optimizing real-world factory flows using aggregated discrete event simulation modelling. Flex. Serv. Manuf. J. 2020, 32, 888–912. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.L.; Xu, Z.G.; Li, G.Z.; Wang, J.Y. Assembly transport optimization for a reconfigurable flow shop based on a discrete event simulation. Adv. Prod. Eng. Manag. 2020, 15, 69–80. [Google Scholar] [CrossRef]
- Mobini, M.; Sowlati, T.; Sokhansanj, S. Forest biomass supply logistics for a power plant using the discrete-event simulation approach. Appl. Energ. 2011, 88, 1241–1250. [Google Scholar] [CrossRef]
- Turner, A.P.; Sama, M.P.; McNeill, L.S.G.; Dvorak, J.S.; Mark, T.; Montross, M.D. A discrete event simulation model for analysis of farm scale grain transportation systems. Comput. Electron. Agric. 2019, 167, 105040. [Google Scholar] [CrossRef]
- Stehfest, E.; Heistermann, M.; Priess, J.A.; Ojima, D.S.; Alcamo, J. Simulation of global crop production with the ecosystem model DayCent. Ecol. Modell. 2007, 209, 203–219. [Google Scholar] [CrossRef]
- Martin-Clouaire, R.; Rellier, J.P. Modelling and simulating work practices in agriculture. Int. J. Metadata Semant. Ontol. 2009, 4, 42–53. [Google Scholar] [CrossRef] [Green Version]
- van der Vorst, J.G.; Tromp, S.O.; Zee, D.J.V.D. Simulation modelling for food supply chain redesign; integrated decision making on product quality, sustainability and logistics. Int. J. Prod. Res. 2009, 47, 6611–6631. [Google Scholar] [CrossRef]
- Martin, G.; Martin-Clouaire, R.; Rellier, J.P.; Duru, M. A simulation framework for the design of grassland-based beef-cattle farms. Environ. Model. Softw. 2011, 26, 371–385. [Google Scholar] [CrossRef]
- Hameed, I.A.; Bochtis, D.D.; Sørensen, C.G.; Vougioukas, S. An object-oriented model for simulating agricultural in-field machinery activities. Comput. Electron. Agric. 2012, 81, 24–32. [Google Scholar] [CrossRef]
- Ooster, A.; van’t Bontsema, J.; van Henten, E.J.; Hemming, S. GWorkS–A discrete event simulation model on crop handling processes in a mobile rose cultivation system. Biosyst. Eng. 2012, 112, 108–120. [Google Scholar] [CrossRef]
- Bergez, J.E.; Chabrier, P.; Gary, C.; Jeuffroy, M.H.; Makowski, D.; Quesnel, G.; Ramat, E.; Raynal, H.; Rousse, N.; Wallach, D.; et al. An open platform to build, evaluate and simulate integrated models of farming and agro-ecosystems. Environ. Modell. Softw. 2013, 39, 39–49. [Google Scholar] [CrossRef]
- Linker, R.; Ioslovich, I.; Sylaios, G.; Plauborg, F.; Battilani, A. Optimal model-based deficit irrigation scheduling using AquaCrop: A simulation study with cotton, potato and tomato. Agric. Water Manag. 2016, 163, 236–243. [Google Scholar] [CrossRef]
- She, J.; Chung, W.; Kim, D. Discrete-event simulation of ground-based timber harvesting operations. Forests 2018, 9, 683. [Google Scholar] [CrossRef] [Green Version]
- Gittins, P.; McElwee, G.; Tipi, N. Discrete event simulation in livestock management. J. Rural Stud. 2020, 78, 387–398. [Google Scholar] [CrossRef]
- Kadigi, I.L.; Mutabazi, K.D.; Philip, D.; Richardson, J.W.; Bizimana, J.-C.; Mbungu, W.; Mahoo, H.F.; Sieber, S. An Economic Comparison between Alternative Rice Farming Systems in Tanzania Using a Monte Carlo Simulation Approach. Sustainability 2020, 12, 6528. [Google Scholar] [CrossRef]
- Deepradit, S.; Ongkunaruk, P.; Pisuchpen, R. Tactical Procurement Planning under Uncertainty in Aromatic Coconut Manufacturing. Int. J. Technol. 2020, 11, 698–709. [Google Scholar] [CrossRef]
- Amanullah, M.; Kailasam, C.; Safiullah, A.M.; Selvam, S.; Sivakumar, K. Crop simulation growth model in cassava. Res. J. Agric. Biol. Sci. 2007, 3, 255–259. [Google Scholar]
- Yu, S.; Tao, J. Energy efficiency assessment by life cycle simulation of cassava-based fuel ethanol for automotive use in Chinese Guangxi context. Energy 2009, 34, 22–31. [Google Scholar] [CrossRef]
- Yu, S.; Tao, J. Simulation based life cycle assessment of airborne emissions of biomass-based ethanol products from different feedstock planting areas in China. J. Clean. Prod. 2009, 17, 501–506. [Google Scholar] [CrossRef]
- Da, G.; Ferret, E.; Marechal, P.A.; Le Thanh, M.; Marouze, C.; Dufour, D. Modeling small-scale cassava starch extraction. Simulation of the reduction of water consumption through a recycling process. Process Biochem. 2010, 45, 1837–1842. [Google Scholar] [CrossRef]
- Mithra, V.S.; Sreekumar, J.; Ravindran, C.S. Computer simulation of cassava growth: A tool for realizing the potential yield. Arch. Agron. Soil Sci. 2013, 59, 603–623. [Google Scholar] [CrossRef]
- Zhang, J.; Fang, Z.; Deng, H.; Zhang, X.; Bao, J. Cost analysis of cassava cellulose utilization scenarios for ethanol production on flowsheet simulation platform. Bioresource Technol. 2013, 134, 298–306. [Google Scholar] [CrossRef] [PubMed]
- Le, K.N.; Jeong, J.; Reyes, M.R.; Jha, M.K.; Gassman, P.W.; Doro, L.; Hok, L.; Boulakia, S. Evaluation of the performance of the EPIC model for yield and biomass simulation under conservation systems in Cambodia. Agric. Syst. 2018, 166, 90–100. [Google Scholar] [CrossRef]
- Jiao, J.; Li, J.; Bai, Y. Uncertainty analysis in the life cycle assessment of cassava ethanol in China. J. Clean. Prod. 2019, 206, 438–451. [Google Scholar] [CrossRef]
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Berkeley Symposium on Mathematical Statistics and Probability; Le Cam, L.M., Neyman, J., Eds.; University of California Press: Berkeley, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Buddhakulsomsiri, J.; Parthanadee, P.; Pannakkong, W. Prediction models of starch content in fresh cassava roots for a tapioca starch manufacturer in Thailand. Comput. Electron. Agric. 2018, 154, 296–303. [Google Scholar] [CrossRef]
- Pannakkong, W.; Huynh, V.N.; Sriboonchitta, S. A novel hybrid autoregressive integrated moving average and artificial neural network model for cassava export forecasting. Int. J. Comput. Intell. Syst. 2019, 12, 1047–1061. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).