Abstract
This study discusses how to create strategic value through energy big data and how to promote stakeholder interaction mechanisms in the evolution of the energy big data ecosystem. We use differential game methods to study the interaction between one power grid enterprise (PG) and one technology supplier (TS) under three different cost-sharing contracts: without cost-sharing contract, cost-sharing contract, and two-way subsidy contract. The effectiveness of the dynamic equilibrium strategies under different contracts is verified via numerical simulations. The results show that under the centralized decision scenario, the technological innovation investment, the degree of technological advancement of PG and TS, and the total profit of the supply chain system are superior to the decentralized decision scenario. The extent of TS technology innovation investment depends on the share rate of PG. Technology innovation investment and the profits of energy big data service supply chain stakeholders will increase with the sensitivity coefficient of technological advancement. Compared with contracts without cost-sharing and with cost-sharing, the two-way subsidy contract can provide the Pareto optimal solution for the investment trajectory of technological innovation and long-term profits. Theoretically, this study reveals a new perspective in the research on the relationship between power grid enterprises and technology suppliers under dynamic technology innovation. In practice, this study facilitates power grid enterprises and technology suppliers to form a closer cooperative relationship in the energy big data ecosystem. More importantly, it is helpful for power grid enterprises to make optimal transaction decisions at different stages of energy big data ecosystem evolution.
1. Introduction
Faced with the rapid development of the Internet of Things, edge computing, and artificial intelligence, enterprises are interested in exploring the value of big data for competitive advantage [1]. The COVID-19 pandemic and the pressure of carbon neutrality have further accelerated the digitalization of various industries [2,3]. In the energy sector, information and communication technology (ICT) has penetrated the whole process, from energy production to consumption [4]. During the process, a large amount of energy data is generated. For example, in the Smart Grid, the advanced metering infrastructure has stimulated the large utility enterprise to accelerate the number of readings from 24 million per year to 220 million per day [5]. In this context, it is urgent for energy enterprises to build new energy data businesses and form new economic growth points [6].
New economic opportunities are making possible the creation of an energy big data ecosystem where the advanced information and communication technology in the energy sector will improve the reliability of energy systems [7,8], and reduce the cost [9,10] and environmental impact [11,12]. Energy big data is an important strategic resource for energy enterprises and information technology leaders because it is disruptive and transformative in the entire value chain of information (data, information, services, decisions, and action) [13]. It is under the dual drive of technological innovation and profit that closer cooperation of energy big data supply chain enterprises should be developed [14]. Channel coordination is an effective way to improve the profit of the supply chain [15]. For example, Jocevski et al. [16] deeply analyzed the relationship between omni-channel strategy and digital transformation of the retail industry from the perspective of the business model. Kim et al. [17] investigated the internet retailing competition effects on the business model of omni-channel strategies. Meanwhile, understanding how strategic value creation from big data services is the premise of supply chain cooperation. However, the strategic value created from energy big data services is still unclear [18].
The business model is the key issue for energy big data supply chain management because it determines the logic of value created by energy big data and it mediates the link between technology innovation and enterprise performance. For example, some business models have been designed in the literature [19,20,21,22] for value delivery through different incentive contracts. Qian et al. [20] developed four contracts to investigate the channel coordination of sustainable supply chains, including wholesale price, two-part tariff, Nash bargaining, and Rubinstein bargaining. Jabarzare et al. [21] investigated the coordination of dual-channel supply chains under three scenarios, such as a non-cooperative game, cooperative games through revenue-sharing contracts, and cooperative games through profit-sharing contracts. To identify the business value of big data, many scholars dedicate themselves to the related study of big data. Most of them focus on the static and general framework of big data strategic business value [23,24] but have ignored the dynamic impact of technology evolution on big data business value in specific industries. To the best of the authors’ knowledge, studies on considering the dynamic impact of technological innovation on the business strategic value of big data remain sparse, especially in the energy sector. Furthermore, the technology innovation of energy big data is a dynamic process, and the effects of technological innovation can be inter-temporal. Hence, the dynamics of technological innovation with time should be taken into account. To extend the study on energy big data, we connect the evolution of the energy big data ecosystem and supply chain coordination, and we consider the dynamics of technological innovation by using differential game theory and optimal control theory. We studied the following key questions:
- What are the respective impacts of technological advancement degrees on the decisions of supply chain players?
- How can a power grid enterprise incent a technology supplier to improve the investment of energy big data services from overall supply chain aspects? What kind of contract should be used for this purpose?
- What are the equilibrium technology innovation investment, sales price, and cost subsidy when supply chain stakeholders take into account the effects of their decisions in the dynamics of technological advancement degree in different scenarios?
To address the above questions, this study analyzes the energy big data service supply chain, composed of a power grid enterprise that provides energy big data services and a technology supplier that provides technological development. Compared with the static game that takes into account current interests, this study discusses the optimal operation strategy of energy big data service enterprises utilizing differential game and optimal control theory. This method aims at maximizing the long-term profits of energy big data service enterprises and considers the comprehensive impact of current decisions on current and future benefits, which is more conducive to the sustainable development of the supply chain system. In addition, this study extends the differential game model to three stages (without cost-sharing contract, cost-sharing contract, and two-way subsidy contract) by describing the impact of technological innovation on the development of energy big data (technological development drives the evolution of the enterprise development stage). This change contributes to energy companies developing appropriate strategies when they envision the occurrence of technological innovation. Finally, this study explores the impact of technological innovation on the effectiveness of cooperation strategy and Pareto improvement effects on the energy big data service supply chain.
The rest of this study is structured as follows. In Section 2, the related literature is reviewed. Section 3 presents the definition and evolution framework of the energy big data ecosystem. Three contracts are designed according to the evolving framework of the energy big data ecosystem, i.e., without cost-sharing contract, cost-sharing contract, and two-way subsidy contract in Section 4. Simulation and sensitivity analysis are conducted in Section 5, and the conclusion and discussion are presented in Section 6.
2. Literature Review
This study is closely related to four main streams of literature: (1) big data ecosystem, (2) the strategic value of big data services, (3) coordination supply chain, and (4) differential game model. These related studies are reviewed as follows.
Big data is becoming a vital resource to address unique customer requirements and gain competitive advantages. The development of big data is still in the initial stage, and relevant studies focused on the definition and particular technology or solution of big data [25,26,27,28,29,30,31,32,33]. Laney [25] proposed a well-known definition of 3Vs based on the attributes of big data, including volume, velocity, and variety. Later studies [26,27], except 3Vs, veracity, and value, were added to explain the definition of big data. To deal with the above attributes of big data, many relevant algorithms, analytics technologies, and solutions have emerged [29,30,31,32,33]. With the sharpness of big data definition and the development of big data technology, the “value” of big data is becoming the dominant attribute. Bao et al. [34] studied the supply chain coordination of energy big data services based on the value attribute of energy big data. Therefore, the key challenge of big data for enterprises and researchers is “how to translate big data into equivalent valuable information and business insights via technology innovation to support the investment decisions? [35]”.
It is vital for enterprises to investigate the strategic value of big data services before investment programs. Kitchens et al. [36] developed the framework of big data for designing advanced customer analytics solutions based on relationship marketing theory. Mamonov et al. [37] proposed the value strategy of big data resources in emergent industries combined with the resource-based view and the relational view theories. Kathuria et al. [38] proposed a big data service value appropriation framework drawn on the resource-based view and dynamic capability hierarchy concepts. Grover et al. [39] investigated the strategic business value framework of big data analytics from five different theoretical logics, including resources, alignment, real options, dynamics, and absorptive capacity. They also proposed that technological innovation plays a fundamental role to mine the business value of products, especially for big data services or products. Therefore, it is feasible to construct a strategic value framework of big data based on resources, relational, and dynamics.
The research on the strategic value of big data services will inevitably lead to coordination problems among supply chain stakeholders [40]. Effective contracts can improve the performance of supply chain members and strengthen the cooperative relationships among them. For example, Dai et al. [41] analyzed and compared cartelization and cost-sharing contracts in the green supply chain with the method of game theory. Tao Li et al. [42] found that revenue-sharing and cost-sharing contracts can achieve the coordination of the supply chain, but the proportion of sharing is affected by the bargaining power of supply chain members and the environmental awareness of consumers. The choice of contracts is determined by the competition and cooperation relationships between stakeholders under evolution of the supply chain system [43]. However, due to the pricing of big data services and the data sharing barriers of the energy sector [44], there are few studies on supply chain collaboration with energy big data services as the transaction object [45].
Game theory is a common theory to solve the relationship strategy between stakeholders. Wu et al. [46] considered the trade-off between privacy and utility in the big data supply chain and formulated a Nash game model of multiple players. Liu et al. [47] applied a three-party evolutionary game theory to put forward a governance mechanism among big data service platforms, governments, and consumers. However, relative game analyses of big data services in the energy sector are deficient. Considering the bounded rationality of members of the energy big data ecosystem, Xiang and Xu [48] designed a differential game model of closed-loop supply chains involving internet recycling platforms to better introduce the dynamic processes of recycling manufacturing.
The difference between the present study and related literature is as follows: (1) Few studies introduce the problems of the microscopic operation level into the macroscopic evolutionary framework. This study analyzes the coordination strategy between power grid enterprises and technology suppliers under the framework of energy big data ecosystem evolution. Moreover, to eliminate double marginalization, a two-way subsidy contract between the participants in the energy big data supply chain at the microscopic operation level is taken into account. (2) Technological innovation is constantly iterated over time, which is considered dynamically. In this study, both the power grid enterprise and technology supplier are assumed to be far-sighted because they focus on technology investment and profit maximization in the evolution of the energy big data ecosystem. Therefore, a differential game model considering technology innovation is proposed, which is capable of reflecting the dynamic of technology innovation in the supply chain. (3) To the best of our knowledge, studies on the framework of the energy big data ecosystem based on relational view and dynamic view are sparse [49,50].
3. Model Assumptions and Notations
With the development of big data, the operation of the energy sector is increasingly driven by data, which gives birth to the energy big data ecosystem. Energy enterprises have shown keen attention to monetizing the data assets efficiently, especially for the power grid enterprises and technology suppliers. However, few studies have addressed the value chain of energy big data dynamically by considering big data monetization with technology innovation. This section aims to provide a framework which is intended to manage data from capture to decision-making and support a variety of supply chain members and their technologies, and the model assumptions are proposed based on the evolution framework.
3.1. Evolution Framework of Energy Big Data Ecosystem
According to the definition of the energy big data ecosystem [34], which not only focuses on data flow, but also includes value flow between the ecosystem members. Technological innovation is the link between data flow and value flow [51] because it can realize the transformation from raw data flow (generation, acquisition, storing, processing, querying, analytics) to business flow (software as a service, platform as a service, infrastructure as a service) [52]. However, the previous studies mainly focused on the implementation and development of technology (Cloud technology, 5G, Flume, MapReduce, HIVE, etc.) [53,54], with less information on how new business models are emerging through the integration of those technological innovations and how to impact the operational strategies of the ecosystem members.
In the context of the energy big data ecosystem, there will be multiple emerging participants (power grid enterprises, technology suppliers, government, etc.) in the energy big data service supply chain. Power grid enterprises and technology suppliers are important players in the energy big data ecosystem. Power grid enterprises occupy a dominant position, because of their strong investment capacity and abundant energy data volume. Technology suppliers play an important role in the game because their technical development capability has a significant influence on the quality of the energy big data service. There is no doubt that complex competition and competitive relationships between multiple participants will emerge under the evolution framework of the energy big data ecosystem.
Based on the relational view theories [55] and the business model innovation theory proposed by Osterwalder et al. [56], the evolution of the energy big data ecosystem has been proven in three successive stages in this study:
- Initial stage: this stage represents an incremental innovation that optimizes the original business without big changes, namely the new technologies (cloud computing, telecommunication technology, etc.) being introduced to realize the digitization of the internal business of the enterprise. The power grid enterprise and technology suppliers will independently decide their technology innovation investment to optimize the value creation architecture (key resources and activities) with the aim of maximizing profits. It is suitable for the non-cooperative Nash equilibrium game model.
- Growing stage: the business model has achieved a radical innovation at this stage, which is focused on several core value-added big data services and shared data resources and uncertainty with a cooperator. Specifically, energy consumers have a higher demand for data services (such as energy-saving services, energy management, consulting services, power equipment charging, etc.). It is extremely urgent to explore the added value of energy big data and develop new technologies. However, more technological innovation investment should be required. It is necessary to promote open sharing of energy data and cooperative innovation between power grid enterprises and technology suppliers. Thus, to further increase the technological innovation enthusiasm of technology suppliers, power grid enterprises must share the cost of technological investment with technology suppliers. This scenario is suitable for the Stackelberg game model.
- Mature stage: this stage represents a disruptive innovation that provides supply chain enterprises with the opportunity to differentiate or expand the market. The platform for energy big data services is constructed, and both the buyer and the seller can freely trade energy big data services on the platform. To maximize profits, power grid enterprises and technology suppliers form a supply chain alliance. This scenario belongs to the centralized decision-making model.
The mechanism of energy big data service coordination under the energy big data ecosystem can be described in Figure 1 as follows.
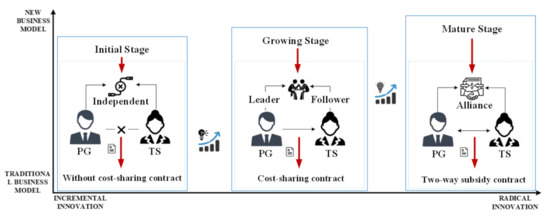
Figure 1.
The evolutionary framework of the energy big data ecosystem.
3.2. Model Assumptions and Notations
This study assumes that the energy big data ecosystem is composed of a technology supplier (TS) and a power grid enterprise (PG), in which the PG occupies a dominant position. TS plays an important role in the game because its technology level is advanced in the supply chain system. In the context of energy digital transformation and the pushing power of competitiveness, the PG tends to increase investment in energy big data services. This does not only require the PG to invest in big data technology but also to purchase energy big data services from the TS. Thus, the power grid enterprise registers the energy big data services on the data platform and sells the energy big data services to the customers based on their service requests. To motivate the TS to develop energy big data services, the power grid enterprise considers sharing the cost or giving subsidies to the TS. This study concentrates on the problem of channel coordination in the energy big data service supply chain considering technology innovation. Table 1 presents the notation and definitions used in this study.

Table 1.
Notation and definitions.
Assumption 1.
Technology innovation is a time-varied dynamic process [57]. The technology investment level of PG and the TS are both conducive to the improvement of technology innovation of energy big data services. The degree of technological advancement evolves according to the Nerlove and Arrow model [58]. When there is no effort toward technology innovation, which is decay, the related infrastructure will depreciate with time [59]. Therefore, the differential equation of the degree of technological advancement can be formulated as:
where I(t) represent the technological advancement degree of energy big data service at time t; iTS(t) and iPG(t) refer to the technology innovation levels of TS and PG, respectively. β1 and β2 represent the impact factors of the technology innovation levels of TS and PG on technological advancement degree, respectively; δ (δ > 0) denotes the decay rate of the technological advancement degree; parameter I (0) = I0 denotes the initial degree of technological advancement.
Assumption 2.
The quadratic cost function of the technology investment means that to achieve a higher level of technology innovation, the cost will increasingly accelerate [60]. The technology investment costs have diminishing returns with C′ (i) > 0, C″ (i) > 0. Hence, the cost of investment toward technology innovation by the PG and TS at time t can be equation as:
where CTS (iTS), CPG (iPG) denote the unit technology investment cost of TS and PG. f1 (f1 > 0), f2 (f2 > 0) represent the cost coefficient of technology innovation levels of the TS and the PG, respectively.
Assumption 3.
With the development of ICT technology and electrification of energy end-users, the demand for energy big data services is increasingly digitized. Based on the models of [61], this study assumes that there is a linear relationship between market demand and the technological advancement degree of energy big data services. To be consistent with the previous study, we assume that demand will decrease with the market price. Therefore, the demand for the energy big data service can be written as:
where D (t) represents the market demand for energy big data service; ε(ε > 0) represents the basic market capacity of energy big data service; θ(θ > 0) denotes the negative impact of service price on market demand; p (t) represents the unit market price of energy big data service, which is determined by PG; μ (μ > 0) refers to the market demand coefficient of the technological advancement degree.
Assumption 4.
In the energy big data service supply chain, PG takes a dominant position in the process of cooperation with TS depending on their own strong strengths. To encourage the TS to increase the technology development efforts, PG is willing to share part or all of the technology investment costs for the TS, the sharing proportion is φ (t) (0 ≤ φ (t) ≤ 1). In addition, PG bears fixed costs (EPG) including the maintenance of hardware infrastructure and data platform.
Assumption 5.
Without losing generality, the inventory cost and shortage cost of supply chain members are assumed to be 0, and the marginal profits of PG and TS are assumed to be πPG and πTS (πPG > 0; πTS > 0), respectively; In the infinite time, PG and TS have the same discount rate at any time
ρ (ρ > 0).
Based on the above assumption, the objective functions of the PG and TS are:
By Assumptions 1–5, this study proposed a PGTS infinite-horizon differential game with a state variable of the technological advancement degree of energy big data service and two control variables of energy big data service supply chain members’ the cost of technology innovation investment. The objectives of the power grid enterprise and the technology supplier ΠTS, ΠPG are to achieve their optimal technology innovation investment by maximizing their profits.
With the high integration of information technology and energy, maximizing profit through cooperation has become the consensus of the energy big data service supply chain members. The PG mainly has three types of contracts: without cost-sharing contracts; cost-sharing contracts; and two-way subsidy contracts in the three evolution stages of the energy big data ecosystem. Because different contracts have a great influence on the equilibrium strategy, the following discusses the coordination strategies of the ecosystem members under the three contracts. Table 1 presents the notation and definitions used in this study.
4. Differential Game Equilibrium Analysis
Technology innovation in the energy big data service supply chain is a long-term dynamic process, and the effect of the degree of technological advancement can be inter-temporal. Both the PG and the TS are far-sighted: they seek technology investment effectiveness and profit maximization in the long revolution energy big data ecosystem by considering the effects of technological innovation. It is urgent to introduce the evolution framework into the study on energy big data service management in the supply chain. Therefore, the differential game is used to analyze the problem in this section. To better compare the members’ decisions in different evolution stages of the energy big data ecosystem, this section classified the energy big data ecosystem into three models: the without cost-sharing contract (non-cooperative game), cost-sharing contract (cooperative game), two-way subsidy contract (cooperative game). The participants’ and systems’ profits throughout the evolution stage are analyzed. Furthermore, the key parameters under the different decision-making models are compared and statistically analyzed to give different decision management insights of the models in order to provide a basis for decision-making for the relevant participants in the energy big data supply chain.
4.1. Decentralized Decision Scenario
4.1.1. Without Cost-Sharing Contracts
In the without cost-sharing contract, both the TS and the PG will independently decide their own technology investment costs and technology innovation levels to maximize profits. This scenario belongs to the Nash non-cooperative game, which is denoted by superscript N. The objective functions (profit function) of TS and PG are expressed as:
In the non-cooperative game equilibrium, the optimal profit functions of TS and PG are valued functions VTSN and VPGN. According to Equation (5), the Hamilton Jacobi Bellman (HJB) equation of TS and PG can be given as:
Proposition 1.
Under the without cost-sharing model, the optimal technology innovation levels of TS and PG are:
The optimal profits function of TS, PG, and supply chains are, respectively:
The optimal trajectory of degree of technological advancement as follows:
Proof see the Appendix A.
Proposition 1 shows that under the without cost-sharing contract, the optimal technology innovation levels of TS and PG are only related to their marginal profit, which means that supply chain members will not change their technological innovation investment according to the change in each other’s or the overall profit of the supply chain. Secondly, the value functions of TS and PG are convex functions of the degree of technological advancement, indicating that with the increase of technology advancement, the profits of TS and PG increase, that is, they can benefit from technology innovation.
4.1.2. Cost-Sharing Contracts
In the cost-sharing contracts, PG will share a certain proportion of technological innovation costs considering the incentive for technology innovation level of TS and the demand for technological innovation to seize the market in the early stage of the formation of the energy big data market. In this scenario (superscript S), the differential game problem considering the infinite time interval and the evolution of energy big data technology is given as follows:
The above differential game problem includes two control variables i(t), p(t), and one state variable I(t). Assuming that VTSS and VPGS respectively represent the value function of the TS and the PG, according to Formula (3)–(18), the HJB equation of the TS and the PG can be given as:
Through the above HJB equation and decision order, the equilibrium strategy between TS and PG in the cost-sharing model in Proposition 2 can be obtained.
Proposition 2.
The optimal technology investment level and share ratio of TS and PG under the cost-sharing model are:
The optimal profits of TS, PG, and supply chains are:
Under the cost-sharing contract, the optimal trajectory of the degree of technological advancement with respect to time is:
Proof similar to the proof of Proposition 1, thus it will not repeated here.
Proposition 2 shows the PG’s optimal technology investment level is only related to its own marginal profit, and the optimal sharing proportion is related to the marginal profits of both stakeholders. At the same time, the optimal technology investment level of TS is also related to the marginal profit of both stakeholders. It shows that in this game scenario, because the marginal profits of both stakeholders will affect the sharing proportion of PGs to TSs, TSs should consider their own technology investment costs from the overall perspective of the supply chain.
Corollaries 1–3 follow from Proposition 2.
Corollary 1.
Under the cost-sharing model, only when the marginal profit of the PG and the TS meets 2 πPG − πTS > 0, the PG will consider taking part in the technology innovation cost to encourage the TS to improve the technology innovation level, and the share ratio φ is positively correlated with the marginal profit of the PG, and negatively correlated with the marginal profit of the TS. Therefore, PG tends to cooperate with TS, and this will result in a higher marginal profit, or lower unit cost and a mastery of cutting-edge core technologies to obtain higher profits.
Corollary 2.
Under the cost-sharing model, the optimal technology innovation investment of TS and PG are positively affected by their marginal profit πPG, πTS, and their respective technological advancement coefficients β1, β2, and demand influence coefficient μ. The discount factor ρ, technology decline rate δ, and its innovation cost coefficients f1, f2 are negatively affected. The difference is that the optimal technological innovation level of the TS is not only related to its marginal profit but also depends on the marginal profit of the PG. The reason is that the PG, as the leader of supply chain decision-making, can adjust the proportion of cost according to the marginal profit of the TS to maximize its own profit.
4.2. Centralized Decision Scenario
With the development of the energy big data ecosystem, the main stakeholders in the supply chain need to adopt a collaborative cooperation mechanism. Compared with the above two scenarios, the cooperative games (denoted by superscript C) can be used as a benchmark for the non-cooperative games. Both stakeholders consider the overall profit of the supply chain, so it can be seen that there is only one decision-maker. To sum up, the objective function of the energy big data ecosystem can be:
Its optimal profit function must satisfy the HJB equation:
Proposition 3.
Under the centralized decision scenario, the optimal technological innovation investment levels of TS and PG are as follows:
The optimal profit of energy big data supply chain system is:
Under centralized decision scenario, the optimal trajectory of the degree of technological advancement with respect to time is:
Proposition 3 shows that in the centralized decision scenario, the optimal technology innovation level of TS and PG are positively correlated with the marginal profit of both stakeholders, and both of them will adjust their technological investment from the perspective of maximizing the overall profit of the supply chain. Under this scenario, TS and PG need to rationally allocate resources, promote better data service products, form sales characteristics, and tap more potential consumers. However, this model has the problem of benefit distribution among supply chain members, and it is difficult to form a complete unified decision in the actual supply chain.
Proof see the Appendix B.
4.3. A Two-Way Subsidy Contract
To tackle the problem of benefit distribution under the centralized decision scenario and to avoid the existence of the double marginal effect, a new contract, called a two-way subsidy contract, is proposed. Under a two-way subsidy contract, PG and TS share the cost of technology investment for each other. Meanwhile, compared with the profits of cost-sharing contracts, the one with more profits needs to provide transfer payment as a subsidy to the other with fewer profits, to achieve a win-win situation for both stakeholders and the overall supply chain.
We assume that the parameter φ1 (0 < φ1 < 1) represents the proportion that the TS gets of the cost generated from the PG, and the parameter φ2 (0 < φ2 < 1) represents the proportion that the PG gets from the cost generated from the TS, and R is the profit subsidy between them, in which φ1, φ2, and R are exogenous variables. Therefore, the profit functions of PG and TS under the two-way subsidy contract (superscript M) are as follows:
Assuming that VTSM and VPGM represent the value function of the TS and the PG, respectively, according to Equation (28), the HJB equation of the TS and the PG can be given as:
Proposition 4.
The optimal technical investment level and share ratio of TS and PG under the centralized decision scenario are:
Under the hybrid contract model, the evolution trajectory of the level of technical investment with respect to time is:
Proof see the Appendix C.
Proposition 5 is obtained from Propositions 3 and 4.
Proposition 5.
When φ1 and φ2 satisfy iTSC** = iTSM**, iPGS** = iPGM**, that is, the sharing ratios of TS and PG are respectively φ1 = πPG/(πTS + πPG), φ2 = πTS/(πTS + πPG), the supply chain system coordination can be realized. Proposition 5 shows that the greater the proportion of marginal profits of supply chain members in the overall supply chain benefits, the higher the proportion of costs they are willing to bear for each other, and vice versa. Compared with the cost-sharing model, it can be further concluded that in the hybrid contract model, PG needs to increase cost-sharing efforts to fully encourage TS to improve the level of technological innovation and achieve maximum profit.
The long-term optimal profits of TS, PG, and supply chains are:
The profits of supply chain members and the whole supply chain system under the two models of hybrid contract and cost-sharing contract are compared as follows:
Proposition 6.
The optimal cost-sharing ratio can only ensure the increase of the profit of the supply chain system, but not the increase of the profit of the supply chain members. Therefore, only when the profit of the coordinated supply chain members is higher than the profit under the cost-sharing model, namely ΔVTS ≥ 0, ΔVPG ≥ 0, both stakeholders of the supply chain be willing to reach the mixed contract. According to the above formula, when R is greater than or equal to , ; when R is less than or equal to , Proposition 7 can be obtained from the above comparative analysis.
Proposition 7.
When , , and, When, the two-way sharing-sharing contract can be reached so that the overall profit of TS, PG and the supply chain will be Pareto improved.
4.4. Comparative Analysis
According to Equations (7), (8), (16), (16), (24) and (25), it can be concluded that under the three contract models, the comparison of the balanced technological innovation investment level of TS is: iTSN < iTSS < iTSC; the balance of technological innovation investment of PG is as follows: iPGN = iPGS < iPGC. Combining Equations (12), (21) and (27), it is easy to get IN*(t) ≤ IS*(t) ≤ IC*(t). Therefore, Corollary 3 can be drawn.
Corollary 3.
Compared with the without cost-sharing model and the cost-sharing model, the technological innovation investment level, technological advancement at the same time, and its stable value in the centralized decision-making model are improved.
According to Equation (33), it can be concluded that ΔVTP ≥ 0, while ΔVTS ≥ 0 and ΔVPG ≥ 0 need to meet certain conditions, that is, R ∈ [Rmin, Rmax]. Therefore, Corollary 4 can be drawn.
Corollary 4.
Under centralized decision-making, the overall long-term profit of the energy big data service supply chain has improved, which is only a necessary condition for realizing supply chain coordination. Only when
ΔVTS and
ΔVPG are greater than or equal to 0, that is, the long-term overall profit of the TS and the PG is higher than that under the cost-sharing model, can the two stakeholders be willing to enter into a two-way subsidy contract.
5. Simulations and Sensitivity Analysis
To verify the rationality of the propositions obtained, a comparative analysis will be conducted through data simulation examples. The relevant parameters are as follows, among which demand parameters: ε = 18, θ = 1, μ = 0.5, p = 6; cost parameters: f1 = 0.5, f2 = 0.3; technical advanced parameters: δ = 0.2, I(0) = I0 = 1.8, β1 = 0.4, β2 = 0.3, discount rate: ρ = 0.23; the fixed costs EPG = 1; the marginal profit under the without cost-sharing contract is set to πTS = 0.6, πPG = 0.8. The above parameters were selected based on references [62,63,64].
5.1. Integrity Analysis
By substituting the above parameters into Propositions 1–6, the optimal profit level and the supply chain profit of the supply chain system of the TS and the PG under the without cost-sharing model, cost-sharing model, and centralized decision-making scenario of the two-way subsidy model can be obtained (the result is shown in Figure 2):
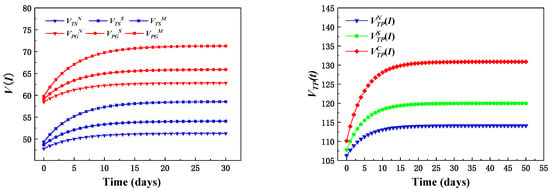
Figure 2.
Supply chain members and system equilibrium profit changes with t under different contracts.
VTSN(I) = −3.48e − 0.2t + 51.29; VPGN(I) =−4.35e − 0.2t + 62.83; VTPN(I) = −7.83 e − 0.2t + 114.12
VTSS(I) = −5.43e − 0.2t + 54.0813; VPGS(I) = −6.78e − 0.2t + 65.8964; VTPS(I) = −12.21e − 0.2t + 119.98
VTSM(I) = −9.221e − 0.2t + 58.56; VPGM(I) = −11.53e − 0.2t + 71.32; VTPM(I) = −20.75e − 0.2t + 129.88
As can be seen from Figure 2, under the three contracts, the overall profits of TS, PG, and supply chains increase over time and gradually tend to be stable. Regardless of the equilibrium profit of supply chain members or the long-term profit of the supply chain system, under a without cost-sharing contract is always lower than the cost-sharing contract, and the cost-sharing model is far lower than the profit in the centralized decision-making scenario, which is consistent with the above Corollary 3. The results show that in the dynamic development process of the energy big data ecosystem, supply chain members should adopt long-term and stable cooperative relationships to continuously improve their profits, which is conducive to the stability of the supply chain system.
5.2. Sensitivity Analysis
According to the above system parameters, the optimal trajectory of technological advancement degree with time under different contracts is obtained, as shown in Figure 3. As can be seen from Figure 3, the technological advancement degree of the three contracts keeps increasing over time and tends to be stable. Among them, the increase rate of technological advancement degree under a without cost-sharing contract is the slowest, and the increase rate under the two-way subsidy contract is the fastest. At the same time, the technological advancement degree of the three contracts is always IN*(t) ≤ IS*(t) ≤ IC*(t). The results show that the two-way subsidy contract can motivate supply chain members to jointly improve the investment level of technology innovation to maximize the profits of the whole supply chain.
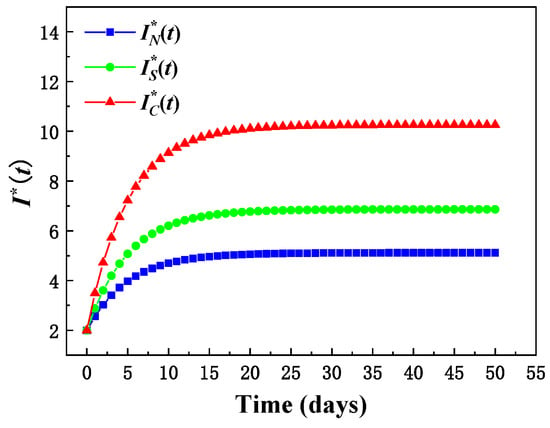
Figure 3.
The optimal trajectory of the degree of technological advancement changes with t under different contracts.
Further analysis of the sensitivity of the technological advancement parameter η to the level of innovation investment and the profit of supply chain members under the three contracts, as shown in Figure 4. It can be seen from Figure 4 that the increase in the sensitivity coefficient of technological advancement will prompt TS and PG to increase the level of investment in technological innovation, and with the continuous increase of μ, the faster the level of technological innovation investment will increase. This is due to the increasing demand for energy big data services in the current market, and the existing data service products cannot meet the diversified needs of energy users. Therefore, the more sensitive the market is to energy big data technology innovation, the more data service supply chain members pay attention to technological innovation, which in turn will increase investment in technological innovation. Supply chain members also use this as a core resource to seize opportunities in the fierce market competition.
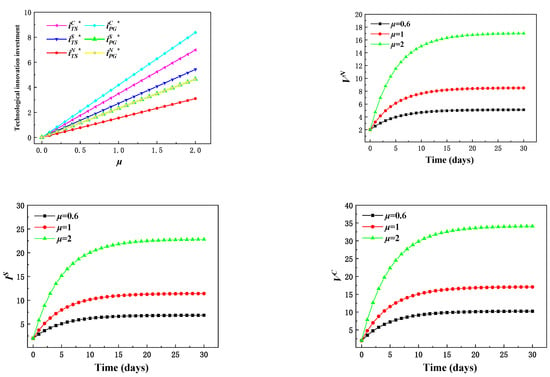
Figure 4.
Influence of technological advance coefficient μ on innovation investment level and profits of supply chain members.
It can be seen in Figure 4 that with the increase of the sensitivity coefficient of technological advance, the profits of TS and PG under the three contract models all increase, and the larger the sensitivity coefficient μ is, the higher the long-term equilibrium profits of supply chain members will be. Due to the without cost-sharing model, supply chain members do not consider the strategies of other members and make decisions alone. The cost of technological innovation is too high, resulting in lower profits. Under the cost-sharing model, PG has gradually adopted part of the cost of technological innovation to incentivize TS to invest in innovation, which in turn reduces the cost of technological innovation for members of the supply chain and increases profits. However, with the increasing income of PG, only taking part of the income as compensation can promote TS to continuously improve the level of technological innovation. This means that, regardless of the sensitivity coefficient of technological advances, supply chain members should choose the strategy of cooperation and coordination to obtain higher profits and achieve a win-win scenario in the supply chain system.
5.3. Coordination Effect of Two-Way Subsidy Contract
Substituting the parameters into Proposition 6 can obtain the relationship between the long-term equilibrium profits of supply chain members and the subsidy fund R after the coordination of the two-way subsidy contract, as shown in Figure 5. As can be seen from Figure 5, when the transfer payment R is in the range [−0.08,0.38], the profit growth of TS and PG is greater than or equal to 0, that is, compared with the cost-sharing model, the profit of both TS and PG will increase after the coordination of the two-way subsidy contract. When R is equal to −0.08, the coordinated profit increment is obtained by the TS; when R is equal to 0.38, both are obtained by the PG; when R is equal to 0.09, the profit increment of the supply chain member is the largest, and the supply chain system is balanced and coordinated.
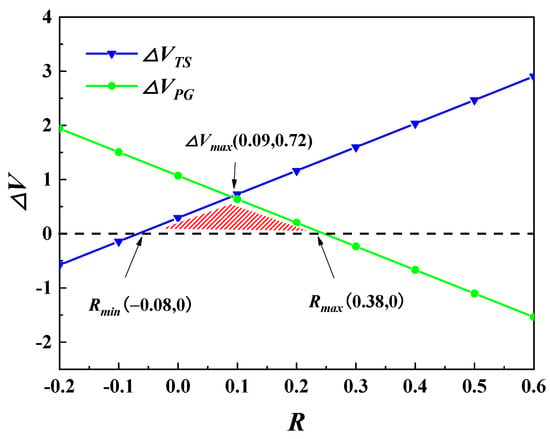
Figure 5.
The relationship between increased long-term equilibrium profit and transfer payment R under the two-way subsidy contract.
6. Discussion and Conclusions
With the rapid penetration of ICT technology in the energy sector and under the pressure of carbon neutrality, the digitalization of the energy sector is an inevitable trend. To tap new economic growth points, it is urgent to explore the energy big data business for energy enterprises. However, under the dual drive of technological innovation and profit, the interaction mechanism between energy big data supply chain enterprises has been highlighted. This study finds that technological innovation will be constantly updated and iterated. Energy enterprises should adjust their technology innovation investment decisions according to the evolutionary stage of the energy big data ecosystem. Meanwhile, with the development of the energy big data ecosystem, supply chain enterprises are more inclined to adopt cooperative and collaborative strategies to maximize profits.
This study considers the impact of technological innovation on the development of the energy big data ecosystem. Previous related studies focused on the technical aspects of implementing big data services [30,31,32] or exploring the static strategic value framework of big data [36,37,38,39]. Based on the relational view theories and the business model innovation theory, this study proposes three evolutionary stages (initial stage, growth stage, and mature stage) of the energy big data ecosystem and explores the interrelationship between technology innovation and the strategic value of energy big data services. We find that the dynamic relationship between supply chain enterprises is influenced by the evolutionary relationship between technological innovation and business models.
This study adopts differential game theory to analyze the dynamic relationship between PG and TS under the evolution framework of the energy big data ecosystem, which is different from the previous studies on the static and short-term relationships between supply chain enterprises [40,41,42]. Considering the three evolutionary stages of the ecosystem, this study adopts three contracts (without cost-sharing, cost-sharing, and two-way subsidy) to establish three differential models for investigating the interaction mechanism between the PG and the TS. Our results indicate that the positive interaction between supply chain enterprises can effectively promote the maximization of each enterprise as well as overall supply chain profits.
In the context of the digital revolution in the energy sector, this study investigates the two-stage supply chain, including one PG and one TS, under the evolution framework of the energy big data ecosystem. The primary conclusions are as follows: (1) The sensitivity coefficient of technological innovation has a positive linear relationship with the level of technological innovation investment and the profit of supply chain members. This finding implies that members of the energy big data services supply chain benefit from technology innovation in the face of energy customers who increasingly emphasize technological advanced quality. (2) The two-way subsidy contracts can promote the optimal trajectory and stable value of the technological advancement of TS and PG and the overall long-term profit of the supply chain. This suggests that to avoid the existence of the double marginal effect, the decision-making behavior of supply chain members needs to be coordinated to guarantee the overall coordination of the supply chain.
Compared with the existing studies, the contribution of this study lies in two aspects. (1) The evolution framework of the energy big data ecosystem is proposed for the first time. The research related to the strategic value framework of big data in previous studies mainly focused on manufacturing, retail, health care, and the public sector. In addition, they ignored the impact of dynamic changes in technological innovation on the evolution framework of the system. (2) The differential game theory is adopted to investigate the dynamic relationship between energy big data service supply chain enterprises. Rarely do studies apply the differential game method in the energy big data topic. (3) The interaction mechanism of PG and TS is proposed in this paper under three contracts: without cost-sharing contract, cost-sharing contract, and two-way subsidy contract. Previously, scholars mainly carried out research on the static strategic value framework and technology development of big data services.
Although this study has contributed to the energy big data service supply chain management, several directions remain for future investigation. This paper considers the impact of technological innovation on the market demand for energy big data services but does not consider the dynamic pricing of energy big data services. Pricing decisions can be introduced into the energy big data ecosystem evolution framework in future studies. In addition, this study only considers the two-stage supply chain, including one technology supplier and one power grid enterprise. However, the energy big data ecosystem is a complex system, including multiple stakeholders such as power grid enterprises, technology suppliers, governments, energy suppliers, and energy consumers, and there are data sharing barriers among stakeholders [65]. Therefore, in future research, the game strategy of a multi-level supply chain considering data openness can be further explored.
Author Contributions
J.D., methodology and writing of the original draft; A.-R.-H.B., visualization, supervision review, and editing; Y.L., X.-H.D., D.-R.L. and G.-Y.X., preliminary investigations. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Project of State Grid Corporation of China “Construction of Provincial Energy Big Data Ecosystem and Application practice of Data Value-added Service Oriented to Park” (Program NO. 5400-202018223A-0-0-00).
Data Availability Statement
Not applicable.
Acknowledgments
The authors gratefully acknowledge support from the Science and Technology Foundation of State Grid Corporation of China “Construction of Provincial Energy Big Data Ecosystem and Application practice of Data Value-added Service Oriented to Park” (Program NO. 5400-202018223A-0-0-00).
Conflicts of Interest
The authors declare that there is no conflict of interest.
Appendix A
Proof of Proposition 1.
Using the inverse induction method, this study obtained optimal technology innovation levels, optimal profits, and the time trajectory of the accumulated degree of technological advancement under without cost-sharing contracts. Thus, the optimal strategies of the ecosystem members under the initial stage of energy big data ecosystem are decided.
The Nash game model for maximizing the profit of the TS and PG in the initial evolution stage of energy big data ecosystem can be expressed as:
Denote the optimal net profit of TS and PG after time t in the Hamilton–Jacobi–Bellman Equation as VTS and VPG, the optimal value function of the TS’s and PG’s long-term profit are:
According to the optimal control theory, for all I(t) ≥ 0, VTS and VPG should satisfy the equations as follows:
It can be seen from the Equation (A4), considering the maximization of their own interests, PG do not provide any subsidies to TS (φ = 0). Equations (A4) and (A5) are the concave functions of the optimal technology innovation level of VTS and VPG, respectively. In addition, the optimal technology innovation level of TS and PG can be obtained from the first-order partial derivatives, respectively.
Substituting Equation (A6) into (A4) and (A5) to obtain the Hamilton–Jacobi–Bellman Equation as VT and VPG as follows:
According to the structures of Equations (A7) and (A8), it can be assumed that the linear analytical expressions of the optimal value functions VNTS (I) and VNPG (I) with respect to I are respectively as follows:
where a1, a2, b1, b2 are the constant coefficients of the value function.
The first-order deriving for IN:
The Equations (A9)–(A12) substituted into the Equations (A7) and (A8), we obtain the formulas by the undermined coefficient method as follows:
By substituting Equations (A11)–(A14) into Equation (A6), the technology innovation investment equilibrium strategy of TS and PG in the situation of Nash non-cooperative game are obtained as Equations (7) and (8).
Substituting equilibrium strategies (7) and (8) into (1), we can get
Solving the differential Equation (A15), the optimal trajectory of the technological advancement degree of energy big data service in the Nash non-cooperative game situation as follows:
where .
By substituting Equations (A13), (A14) into Equations (A9), (A10), the optimal profit functions of TS, PG, and supply chain system in the situation of Nash non-cooperative as Equations (9)–(11). □
Appendix B
Proof of Proposition 3.
In the centralized decision situation, the goal of TS and PG is to maximize the overall profit of the supply chain system. Therefore, they need to jointly determine the optimal value of iTS and iPG. The objective functions (profit function) of the overall supply chain can be expressed as:
The optimal value function of the overall supply chain is:
The optimal profit function VC should satisfy the HJB equation as follow:
And the optimal technology innovation level of TS and PG can be obtained from the first-order partial derivatives, respectively.
And substituting Equation (A20) into (A19) to obtain the Hamilton–Jacobi–Bellman Equation VC as follows:
According to Equation (A21), the solution of the HJB equation is the optimal net profit function of IC:
where a1, a2 are the constant coefficients of the value function.
The first-order deriving for IC:
The Equations (A22) and (A23) substituted into the Equation (A21), we obtain the formulas by the undermined coefficient method as follows:
By substituting Equations (A22) and (A23) into Equation (A20), the technology innovation investment equilibrium strategy of the overall supply chain in the centralized decision scenario is obtained as Equations (23) and (24).
Substituting equilibrium strategies (23) and (24) into (1), we can get:
Solving the differential Equation (A25), the optimal trajectory of the technological advancement degree of energy big data service in the centralized decision scenario, as follows:
where .
By substituting Equation (A24) into Equation (A22), the optimal profit functions of overall supply chain system in the centralized decision scenario as Equation (26). □
Appendix C
Proof of Proposition 4.
The profit functions of PG and TS under the two-way subsidy contract (superscript M) are as follows:
Assuming that VTSM and VPGM represent the value function of the TS and the PG, respectively, the HJB equation of the TS and the PG can be given as:
And the optimal technology innovation level of TS and PG can be obtained from the first-order partial derivatives, respectively
And substituting Equation (A29) into (A28) to obtain the Hamilton–Jacobi–Bellman Equation as VTS and VPG as follows:
According to Equations (A28) and (A29), the solution of the HJB equation is the optimal net profit function of I:
where a1, a2, b1, b2 are the constant coefficients of the value function. The value function and its first-order derivative substituted into the Equations (A28) and (A29), respectively.
By substituting Equations (A33) and (A34) into Equation (A32), the optimal profit function of TS and PG are obtained. Add the two formulas to obtain Equation (32) for the optimal profits function of supply chains. Then the two formulas are substituted into Formula (A29) to obtain Formulas (30) and (31) for the optimal technological innovation level of TS and PG. □
References
- Labrinidis, A.; Jagadish, H.V. Challenges and opportunities with big data. Proc. Vldb Endow. 2012, 5, 2032–2033. [Google Scholar] [CrossRef]
- Mak, H.W.L. From COVID-19 Pandemic of Five Selected East Asian Cities to Assessment of Data Openness and Integration for Future City Development. 2021. Available online: https://www.researchgate.net/publication/354293725_From_COVID-19_Pandemic_of_Five_Selected_East_Asian_Cities_to_Assessment_of_Data_Openness_and_Integration_for_Future_City_Development (accessed on 1 April 2022).
- De La Peña, L.; Guo, R.; Cao, X.; Ni, X.; Zhang, W. Accelerating the energy transition to achieve carbon neutrality. Resour. Conserv. Recy. 2022, 177, 105957. [Google Scholar] [CrossRef]
- Zhou, K.; Fu, C.; Yang, S. Big data driven smart energy management: From big data to big insights. Renew. Sustain. Energy Rev. 2016, 56, 215–225. [Google Scholar] [CrossRef]
- Ponce-Jara, M.A.; Ruiz, E.; Gil, R.; Sancristóbal, E.; Pérez-Molina, C.; Castro, M. Smart Grid: Assessment of the past and present in developed and developing countries. Energy Strateg. Rev. 2017, 18, 38–52. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, K.; Wang, Y.; Gao, M.; Zhang, Y. Energy big data: A survey. IEEE Access 2016, 4, 3844–3861. [Google Scholar] [CrossRef]
- Shoreh, M.H.; Siano, P.; Shafie-khah, M.; Loia, V.; Catalão, J.P. A survey of industrial applications of Demand Response. Electr. Power Syst. Res. 2016, 141, 31–49. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Fuerst, F.; Warren-Myers, G. Does voluntary disclosure create a green lemon problem? Energy-efficiency ratings and house prices. Energy Econ. 2018, 74, 1–12. [Google Scholar] [CrossRef]
- Gebrehiwot, K.; Mondal, M.A.H.; Ringler, C.; Gebremeskel, A.G. Optimization and cost-benefit assessment of hybrid power systems for off-grid rural electrification in Ethiopia. Energy 2019, 177, 234–246. [Google Scholar] [CrossRef]
- Jiang, A.; Yuan, H.; Li, D.; Tian, J. Key technologies of ubiquitous power Internet of Things-aided smart grid. J. Renew. Sustain. Energy 2019, 11, 062702. [Google Scholar] [CrossRef]
- Fan, S.; Liu, J.; Wu, Q.; Cui, M.; Zhou, H.; He, G. Optimal coordination of virtual power plant with photovoltaics and electric vehicles: A temporally coupled distributed online algorithm. Appl. Energy 2020, 277, 115583. [Google Scholar] [CrossRef]
- Hu, J.; Vasilakos, A.V. Energy big data analytics and security: Challenges and opportunities. IEEE Trans. Smart Grid 2016, 7, 2423–2436. [Google Scholar] [CrossRef]
- Krykavskyy, Y.; Pokhylchenko, O.; Hayvanovych, N. Supply chain development drivers in industry 4.0 in Ukrainian enterprises. Oecon. Copernic. 2019, 10, 273–290. [Google Scholar] [CrossRef]
- Xu, L.; Wang, C.; Zhao, J. Decision and coordination in the dual-channel supply chain considering cap-and-trade regulation. J. Clean. Prod. 2018, 197, 551–561. [Google Scholar] [CrossRef]
- Jocevski, M.; Arvidsson, N.; Miragliotta, G.; Ghezzi, A.; Mangiaracina, R. Transitions towards omni-channel retailing strategies: A business model perspective. Int. J. Retail. Distrib. 2019, 47, 78–93. [Google Scholar] [CrossRef]
- Kim, J.C.; Chun, S.H. Cannibalization and competition effects on a manufacturer’s retail channel strategies: Implications on an omni-channel business model. Decis. Support Syst. 2018, 109, 5–14. [Google Scholar] [CrossRef]
- Grover, V.; Chiang, R.H.; Liang, T.P.; Zhang, D. Creating strategic business value from big data analytics: A research framework. J. Manag. Inf. Syst. 2018, 35, 388–423. [Google Scholar] [CrossRef]
- Alamdar, S.F.; Rabbani, M.; Heydari, J. Pricing, collection, and effort decisions with coordination contracts in a fuzzy, three-level closed-loop supply chain. Expert Syst. Appl. 2018, 104, 261–276. [Google Scholar] [CrossRef]
- Qian, X.; Chan, F.T.; Zhang, J.; Yin, M.; Zhang, Q. Channel coordination of a two-echelon sustainable supply chain with a fair-minded retailer under cap-and-trade regulation. J. Clean. Prod. 2020, 244, 118715. [Google Scholar] [CrossRef]
- Jabarzare, N.; Rasti-Barzoki, M. A game theoretic approach for pricing and determining quality level through coordination contracts in a dual-channel supply chain including manufacturer and packaging company. Int. J. Prod. Econ. 2020, 221, 107480. [Google Scholar] [CrossRef]
- Nolden, C.; Barnes, J.; Nicholls, J. Community energy business model evolution: A review of solar photovoltaic developments in England. Renew. Sust. Energy Rev. 2020, 122, 109722. [Google Scholar] [CrossRef]
- Wamba, S.F.; Akter, S.; Edwards, A.; Chopin, G.; Gnanzou, D. How ‘big data’can make big impact: Findings from a systematic review and a longitudinal case study. Int. J. Prod. Econ. 2015, 165, 234–246. [Google Scholar] [CrossRef]
- Chiang, R.H.; Grover, V.; Liang, T.P.; Zhang, D. Strategic value of big data and business analytics. J. Manag. Inf. Syst. 2018, 35, 383–387. [Google Scholar] [CrossRef]
- McCord, S.E.; Webb, N.P.; Van Zee, J.W.; Burnett, S.H.; Christensen, E.M.; Courtright, E.M.; Tweedie, C. Provoking a cultural shift in data quality. Bioscience 2021, 71, 647–657. [Google Scholar] [CrossRef]
- Hu, H.; Wen, Y.; Chua, T.S.; Li, X. Toward scalable systems for big data analytics: A technology tutorial. IEEE Access 2014, 2, 652–687. [Google Scholar] [CrossRef]
- Johnson, J.S.; Friend, S.B.; Lee, H.S. Big data facilitation, utilization, and monetization: Exploring the 3Vs in a new product development process. J. Prod. Innovat. Manag. 2017, 34, 640–658. [Google Scholar] [CrossRef]
- Rialti, R.; Zollo, L.; Ferraris, A.; Alon, I. Big data analytics capabilities and performance: Evidence from a modelrated multi-mediation model. Technol. Forecast. Soc. 2019, 149, 119781. [Google Scholar] [CrossRef]
- Santana, E.F.Z.; Chaves, A.P.; Gerosa, M.A.; Kon, F.; Milojicic, D.S. Software platforms for smart cities: Concepts, requirements, challenges, and a unified reference architecture. Acm. Comput. Surv. 2017, 50, 1–37. [Google Scholar] [CrossRef]
- Liu, Z.H.; Zhang, Q.L. Research overview of big data technology. J. Zhejiang Univ. 2014, 48. [Google Scholar] [CrossRef]
- Oussous, A.; Benjelloun, F.Z.; Lahcen, A.A.; Belfkih, S. Big Data technologies: A survey. J King Saud Univ-Com. 2018, 30, 431–448. [Google Scholar] [CrossRef]
- Ogbuke, N.J.; Yusuf, Y.Y.; Dharma, K.; Mercangoz, B.A. Big data supply chain analytics: Ethical, privacy and security challenges posed to business, industries and society. Prod. Plan. Control 2022, 33, 123–137. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. A survey towards an integration of big data analytics to big insights for value-creation. Inf. Process. Manag. 2018, 54, 758–790. [Google Scholar] [CrossRef]
- Bao, A.-R.-H.; Liu, Y.; Dong, J.; Chen, Z.-P.; Chen, Z.-J.; Wu, C. Evolutionary Game Analysis of Co-Opetition Strategy in Energy Big Data Ecosystem under Government Intervention. Energies 2022, 15, 2066. [Google Scholar] [CrossRef]
- Raghupathi, W.; Raghupathi, V. Big data analytics in healthcare: Promise and potential. Health Inf. SCI Syst. 2014, 2, 1–10. [Google Scholar] [CrossRef]
- Kitchens, B.; Dobolyi, D.; Li, J.; Abbasi, A. Advanced customer analytics: Strategic value through integration of relationship-oriented big data. J. Manag. Inf. Syst. 2018, 35, 540–574. [Google Scholar] [CrossRef]
- Mamonov, S.; Triantoro, T.M. The strategic value of data resources in emergent industries. Int. J. Inf. Manag. 2018, 39, 146–155. [Google Scholar] [CrossRef]
- Kathuria, A.; Mann, A.; Khuntia, J.; Saldanha, T.J.; Kauffman, R.J. A strategic value appropriation path for cloud computing. J. Manag. Inf. Syst. 2018, 35, 740–775. [Google Scholar] [CrossRef]
- Büchi, G.; Cugno, M.; Castagnoli, R. Smart factory performance and Industry 4.0. Technol Forecast Soc. 2020, 150, 119790. [Google Scholar] [CrossRef]
- Tallman, S.; Luo, Y.; Buckley, P.J. Business models in global competition. Glob. Strateg. J. 2018, 8, 517–535. [Google Scholar] [CrossRef]
- Dai, R.; Zhang, J.; Tang, W. Cartelization or Cost-sharing? Comparison of cooperation models in a green supply chain. J. Clean. Prod. 2017, 156, 159–173. [Google Scholar] [CrossRef]
- Li, T.; Zhang, R.; Zhao, S.; Liu, B. Low carbon strategy analysis under revenue-sharing and cost-sharing contracts. J. Clean. Prod. 2019, 212, 1462–1477. [Google Scholar] [CrossRef]
- Salunke, S.; Weerawardena, J.; McColl-Kennedy, J.R. The central role of knowledge integration capability in service innovation-based competitive strategy. Ind. Market. Manag. 2019, 76, 144–156. [Google Scholar] [CrossRef]
- Mak, H.W.L.; Lam, Y.F. Comparative assessments and insights of data openness of 50 smart cities in air quality aspects. Sustain. Cities Soc. 2021, 69, 102868. [Google Scholar] [CrossRef]
- Ruan, J.; Yan, Z.; Dong, B.; Zheng, Q.; Qian, B. Identifying suspicious groups of affiliated-transaction-based tax evasion in big data. Inf. Sci. 2019, 477, 508–532. [Google Scholar] [CrossRef]
- Wu, X.; Wu, T.; Khan, M.; Ni, Q.; Dou, W. Game theory based correlated privacy preserving analysis in big data. IEEE Trans. Big Data 2017, 7, 643–656. [Google Scholar] [CrossRef]
- Liu, W.; Long, S.; Xie, D.; Liang, Y.; Wang, J. How to govern the big data discriminatory pricing behavior in the platform service supply chain? An examination with a three-party evolutionary game model. Int. J. Prod. Econ. 2021, 231, 107910. [Google Scholar] [CrossRef]
- Xiang, Z.; Xu, M. Dynamic game strategies of a two-stage remanufacturing closed-loop supply chain considering Big Data marketing, technological innovation and overconfidence. Comput. Ind. Eng. 2020, 145, 106538. [Google Scholar] [CrossRef]
- Busca, L.; Bertrandias, L. A framework for digital marketing research: Investigating the four cultural eras of digital marketing. J. Interact. Mark. 2020, 49, 1–19. [Google Scholar] [CrossRef]
- Cloarec, J. The personalization–privacy paradox in the attention economy. Technol. Forecast. Soc. 2020, 161, 120299. [Google Scholar] [CrossRef]
- Bai, C.; Dallasega, P.; Orzes, G.; Sarkis, J. Industry 4.0 technologies assessment: A sustainability perspective. Int. J. Prod. Econ. 2020, 229, 107776. [Google Scholar] [CrossRef]
- Martín-Hernández, P.; Gil-Lacruz, M.; Gil-Lacruz, A.I.; Azkue-Beteta, J.L.; Lira, E.M.; Cantarero, L. Fostering University Students’ Engagement in Teamwork and Innovation Behaviors through Game-Based Learning (GBL). Sustainability 2021, 13, 13573. [Google Scholar] [CrossRef]
- Miller, H.G.; Mork, P. From data to decisions: A value chain for big data. It Prof. 2013, 15, 57–59. [Google Scholar] [CrossRef]
- Munshi, A.A.; Yasser, A.R.M. Big data framework for analytics in smart grids. Electr. Pow. Syst. Res. 2017, 151, 369–380. [Google Scholar] [CrossRef]
- Kabalci, Y.; Kabalci, E.; Padmanaban, S.; Holm-Nielsen, J.B.; Blaabjerg, F. Internet of things applications as energy internet in smart grids and smart environments. Electronics 2019, 8, 972. [Google Scholar] [CrossRef]
- Min, Q.; Lu, Y.; Liu, Z.; Su, C.; Wang, B. Machine learning based digital twin framework for production optimization in petrochemical industry. Int. J. Inf. Manag. 2019, 49, 502–519. [Google Scholar] [CrossRef]
- Osterwalder, A.; Pigneur, Y.; Oliveira, M.A.Y.; Ferreira, J.J.P. Business Model Generation: A handbook for visionaries, game changers and challengers. Afr. J. Bus. Manag. 2011, 5, 22–30. [Google Scholar]
- El Ouardighi, F. Supply quality management with optimal wholesale price and revenue sharing contracts: A two-stage game approach. Int. J. Prod. Econ. 2014, 156, 260–268. [Google Scholar] [CrossRef]
- Dierickx, I.; Cool, K. Asset stock accumulation and sustainability of competitive advantage. Manag. Sci. 1989, 35, 1504–1511. [Google Scholar] [CrossRef]
- Li, Y. Research on supply chain CSR management based on differential game. J. Clean. Prod. 2020, 268, 122171. [Google Scholar] [CrossRef]
- De Giovanni, P. Digital supply chain through dynamic inventory and smart contracts. Mathematics 2019, 7, 1235. [Google Scholar] [CrossRef]
- Wang, Y.; Su, M.; Shen, L.; Tang, R. Decision-making of closed-loop supply chain under Corporate Social Responsibility and fairness concerns. J. Clean. Prod. 2021, 284, 125373. [Google Scholar] [CrossRef]
- Xia, L.; Bai, Y.; Ghose, S.; Qin, J. Differential game analysis of carbon emissions reduction and promotion in a sustainable supply chain considering social preferences. Ann. Oper. Res. 2020, 6, 1–36. [Google Scholar] [CrossRef]
- Zu, Y.; Chen, L.; Fan, Y. Research on low-carbon strategies in supply chain with environmental regulations based on differential game. J. Clean. Prod. 2018, 177, 527–546. [Google Scholar] [CrossRef]
- Mak, H.W.L.; Ng, D.C.Y. Spatial and Socio-Classification of Traffic Pollutant Emissions and Associated Mortality Rates in High-Density Hong Kong via Improved Data Analytic Approaches. Int. J. Environ. Res. Public Health 2021, 18, 6532. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).