Incentive Compensation Mechanism for the Infrastructure Construction of Electric Vehicle Battery Swapping Station under Asymmetric Information

Abstract

Driven by the application and promotion of the electric vehicle battery swapping station (BSS), this paper addresses a key challenge in the BSS’s infrastructure construction, which is information asymmetry between the government and BSS. First, inspired by the insights of financial contracting, this study constructs the government’s capital allocation and compensation models for the BSS via the principal–agent approach. This paper is the first developing an incentive-compatible (IC) compensation mechanism for improving the operation of BSS in the presence of two kinds of asymmetric information (operation level and effort level). Next, this paper derives the government and BSS’s equilibrium strategies under two scenarios of symmetry and asymmetry information, respectively. Finally, this paper compares the equilibrium solutions obtained in the above two scenarios to verify the effectiveness of the allocation scheme and compensation mechanism. This paper finds that the capital allocation scheme and compensation mechanism proposed in this paper can incentivize the BSS to report its actual operation level and take the corresponding effort level. Moreover, the government and BSS’s underinvestment problems become smaller when the BSS’s operation level is relatively high. Several important managerial insights are derived based on our analytical and numerical results.

1. Introduction

The effects of global warming on humans are no longer just a theory. Recently, many countries and regions worldwide have suffered huge losses due to extreme climates mainly caused by global warming. For example, in July 2021, devastating floods in Germany, Austria, and Belgium killed approximately 200 people [1]. Meanwhile, a rare flood caused by heavy rainfall in China’s Henan Province displaced nearly 1.5 million people [2]. Similar natural disasters occur frequently, and these natural disasters are gradually increasing the awareness of reducing greenhouse gas emissions. Governments and international organizations have taken some actions to reduce the harm of greenhouse gas emissions to the circular economy and sustainability [3,4,5,6,7]. For example, the Paris Climate Agreement has set a target of zero-carbon solutions being competitive in sectors representing over 70% of global emissions by 2030 [5]. The European Union is committed to achieving carbon neutrality by 2050 and has announced an ambitious plan to reduce its carbon emissions by 60% by 2030 compared to 1990 levels [6]. In particular, the world’s leading carbon emitter, China, has pledged to reach its peak carbon dioxide emissions by 2030. Moreover, the country is striving to achieve carbon neutrality by 2060 [7]. Therefore, reducing carbon emissions has become the unanimous direction of global efforts, and many countries are undertaking industrial restructuring and energy transformation to reduce carbon emissions as much as possible [8,9,10].

The transportation sector is a substantial contributor to carbon dioxide emissions, accounting for approximately 20% of all carbon emissions globally [11]. Hence, it is urgent to reduce carbon emissions in transportation. Due to the clean energy transition, especially the improvement of vehicle battery technology, electric vehicles (EVs) are widely favored by many countries/regions, creating optimistic prospects for low-carbon transportation. For example, Japanese carmaker Nissan expects four of 10 vehicles it sells in China to be electrified by 2026, and the figure would be 75% in Europe and 55% in Japan by the same year [12]. Biden is aiming for 50% EVs by 2030 with industry support [13]. Regarding the image of EVs, Tesla and NiO have a high market share and development prospects, which is inspiring many manufacturers (such as Volkswagen and Toyota) to produce EVs [14]. Although EVs can address carbon emissions from transportation, they still present disadvantages such as high costs, slow charging capacities, and a lack of corresponding public service facilities. Hence, the automotive industry is still dominated by fuel vehicles (FVs) [15]. Especially, some manufacturers have introduced EV battery swapping models to eliminate long wait times for EV battery charging, boosting EV prospects.

Battery Swapping Stations (BSSs) propose an alternative method of refueling electric vehicles (EVs) that can lead to a sustainable transportation ecosystem. However, the construction and operation of an electric vehicle battery swapping station (BSS) require a lot of capital, which is usually unaffordable for electric vehicle operators, who need to seek government investment and compensation. As Xu et al. [16] said, the government’s investment and compensation for the BSS need to be based on the BSS’s operation level, which is unknown and unverifiable to the government. In such a case, the BSS has an incentive to overstate the operation level so as to enhance the government’s valuation. The matter is further complicated by the fact that the BSS’s actual effort level is also unknown and unverifiable to the government. Hence, a major problem faced by the government is how to design a capital allocation scheme and an incentive compensation mechanism to induce a true operation level and effort level from the BSS.

To date, there have been a number of studies on BSSs. However, most of them focus on swapping techniques [17,18], optimal locations for BSSs [19,20], and optimal charging-discharging scheduling [21,22], and little attention has been given to the investment and construction of BSSs. At present, Revankar and Kalkhambkar [23] divided the research of BSSs into: charging strategy for BSS batteries, BSS and battery life, battery swapping techniques, BSS and EV scheduling, energy management in BSSs, optimization strategies of BSSs, and so on. Moreover, although many scholars have demonstrated that the performance of agents is improved through incentive compensation mechanisms [24], the principal–agent approach in public transport management has received little attention. Recently, Sun et al. [25] proposed an incentive-compatible mechanism to regulate monopoly public transport operators with asymmetric cost information. Unfortunately, this direct disclosure mechanism cannot be applied to this paper, because the BSS has two kinds of private information (i.e., operation level and effort level).

To fill the gap, this paper proposes an optimal capital allocation scheme and incentive compensation mechanism for the BSS with asymmetric information. In this paper, the government is the principal and the BSS is the agent. Both participants are risk-neutral and aim to maximize their utility. In the government’s valuation function, operation level and capital allocation are complementary. For the government, capital allocation and the BSS’s effort level are also complementary. As in the literature of mechanism design [25], the hazard rate is assumed to be increasing in gross margin. In addition, this paper supposes the government commits to the compensation scheme at the beginning of the game.

In particular, the paper addresses the following questions. (1) Under symmetric information, what are the government’s capital allocation scheme and compensation mechanism (first-best solution)? (2) Under asymmetric information, what are the government’s capital allocation scheme and compensation mechanism (optimal solution)? (3) What is the impact of asymmetric information on the government and BSS?

This study summarizes our contributions as follows:

First, this paper derives the government’s capital allocation scheme and compensation mechanism for the BSS, which has two kinds of private information of operation level and effort level, in two scenarios of information symmetry and asymmetry.

Second, through a comparison of the equilibrium results and numerical experiments, this paper finds that asymmetric information will cause a loss of government profits and hinder the sustainable development of the BSS.

Finally, this paper provides the following insights. For the government, it should seek to cooperate with the BSS with a higher operation level. For the BSS, under the capital allocation scheme and compensation mechanism provided by the government, it is more beneficial to report truthfully.

The paper is organized as follows. Section 2 reviews the relevant literature. Section 3 presents this paper’s model. Section 4 presents the analysis results in symmetric and asymmetric information scenarios. Section 5 carries out a numerical experiment to verify the propositions obtained in this study. Section 6 presents conclusions and potential directions for future work.

2. Literature Review

Two streams of research in the literature are closely related to our paper, namely, the electric vehicle battery swapping station and the application of principal–agent theory in optimal compensation mechanisms.

2.1. Electric Vehicle Battery Swapping Station

Electric vehicles (EVs), which are powered by batteries instead of traditional fuels, are considered to have the capability to reduce the transportation sector’s carbon emissions, improve consumer comfort, and protect the ecological environment [26]. Given these advantages above, the EVs’ development has attracted extensive attention from governments, manufactures, consumers, environmentalists, academics, etc., [27]. However, the long battery charging time has seriously hindered the development of the EV industry. Thus, some manufacturers have introduced EV battery swapping models to eliminate long wait times for EV battery charging, boosting EV prospects.

There have been a number of studies on EV battery swapping stations (BSSs), and they focus on swapping techniques [17,18], optimal locations for BSSs [19,20], and optimal charging–discharging scheduling [21,22]. Sarker et al. [28] proposed an optimization framework for the BSS’s operating model, considering the day-ahead scheduling process and battery demand uncertainty. Yang et al. [29] proposed a dynamic operation model of BSSs in the electricity market. Wu et al. [30] studied a new model of a viable battery swapping station and proposed an integrated algorithm to determine an optimal charging schedule. Mahoor et al. [31] developed a mathematical model for the uncertainty-constrained BSS optimal operation and proposed mixed-integer linear programming for solving this model. Asadi et al. [32] studied the problem of optimal power scheduling in charging and swapping stations and proposed an optimal power scheduling and inventory allocation mechanism for charging and swapping stations. Esmaeili et al. [33] took microgrid and battery swapping stations, two stakeholders with inherent conflicting goals, and proposed a two-layer scheduling framework for optimal decision-making between the microgrid and battery swapping station. Raeesi and Zografos [34] studied the EV routing problem with time windows and synchronized mobile battery swapping, and developed a method of in-route charging for freight electric commercial vehicles. Verma [35] found that under the constraints of a short delivery time window in the last kilometer of logistics delivery, battery swapping in a swapping station can better optimize the transportation route and reduce the total transportation cost than charging in a traditional charging station. Zhang et al. [36] proposed a hybrid charging management framework combining plug-in charging and battery swapping to optimize the electric taxis’ charging and swapping path, thus reducing the trip delay of electric taxis. For an excellent review of BSSs, readers can refer to [23].

As mentioned above, although there is a lot of research literature on BSSs, little attention has been given to the investment and construction of BSSs. Mak et al. [37] and Xu et al. [16] studied the infrastructure planning for BSSs. In [37], Mak et al. considered the scenario of EV manufacturers’ participation in the construction of BSSs. In [16], although Xu et al. comprehensively considered the scenario of government investment in the construction of BSSs, they ignored the influence of the BSS’s private information (operation level and effort level). Therefore, given these shortcomings of the above literature, this paper studies the government’s investment and construction of BSSs under asymmetry information.

2.2. The Application of Principal–Agent Theory in Optimal Compensation Mechanisms

The principal–agent theory is based on asymmetric information game theory, aiming to eliminate (or reduce) the loss caused by asymmetric information through a reasonable incentive and constraint mechanism to achieve a “win–win” between principal and agent. In recent years, many scholars have conducted rich and in-depth research on principal–agent theory. Holmstrom [38] proposed a performance evaluation method based on the principal–agent theory to measure agents’ genuine efforts accurately. Baron and Myerson [39] proposed a direct revelation mechanism to regulate a monopolistic firm with unknown costs. Aghion and Bolton [40] studied the incomplete social contract based on the design idea of contract theory and obtained the optimal voting strategy. Demarzo and Sannikov [41] studied the capital structure and securities pricing according to principal–agent theory. Biais et al. [42] studied the dynamic principal–agent model with high risk and limited debt characteristics. He [43] adopted the principal–agent theory to study the relationship between the principal–agent relationship and the optimal capital structure of enterprises. Gryglewicz and Hartman [44] studied the investment problem of enterprises with asymmetric information to explore the impact of incentive costs on investment timing. Sun et al. [25] addressed the monopolistic public transit regulation problem with asymmetric cost information.

In addition to the above studies, principal–agent models are also widely used in financial regulation [45], public–private partnerships [46], ecological environment development and protection [47], marketing with the sales staff incentive mechanism [48], and repurchase contracts [49]. For an excellent review of general principal–agent models, readers can refer to [50].

To sum up, there are many studies on principal–agent theory, which has been widely applied in many fields. Therefore, sufficient empirical evidence shows that agent performance can be improved through incentive compensation mechanisms [24]. However, in the existing literature, few scholars pay attention to the principal–agent method of public transport management. Recently, Sun et al. [25] proposed an incentive compatibility mechanism to regulate monopolistic bus operators under asymmetric cost information. In their study, the only asymmetrical information examined was cost. However, in real life, much asymmetric information (e.g., operation level, transportation cost, effort level) widely exists in the public transportation system. Unlike Sun et al. [25], this paper assumes that both the operation level and effort level of the BSS are unknown and unverifiable to the government.

3. The Model

Consider a simple model in which an EV battery swapping station (BSS) provides battery replacement services for EV owners. Due to the current constraints of capital and market, the BSS needs to seek government investment for infrastructure construction, which will promote its sustainable development [16]. The quantity of capital invested by the government in the BSS depends on the BSS’s operation level, which is private information of the BSS and is unknown and unverifiable to the government. However, the BSS has an incentive to defraud the government for more capital by overstating its operation level. Therefore, the government’s problem will be to design an optimal capital allocation scheme and compensation mechanism to induce the BSS to report its true operation level.

Specifically, this paper assumes that the government’s valuation for the BSS V depends on the BSS’s operation level, denoted s; the BSS’s effort level, denoted e; and the quantity of capital allocated to the BSS by the government, denoted k.

Therefore, the government’s valuation V is given by

$$V=nk+\sigma sk+\alpha ek-\lambda k^2$$

(1)

where $n$ is a positive constant, $\sigma >0$ represents the importance of the BSS’s operation level $s$ to the government’s valuation $V$, $\alpha >0$ represents the importance of the BSS’s effort level $e$ to the government’s valuation $V$, and $\lambda >0$ represents the cost coefficient of government investment capital.

It is worth mentioning that the BSS’s operation level ($s$) and the government’s investment capital ($k$) are complementary [47,51]. Intuitively, the government is more willing to invest more capital in the BSS with a high operation level. Similarly, the BSS’s effort level ($e$) and the government’s investment capital are also complementary, implying that the marginal product of $e$ increases in $k$, and vice versa. This is simply because the government prefers the BSS with a higher effort level [47,51].

The government does not know the BSS’s true operation level ($s$) but only knows that $s$ follows a cumulative distribution $F\left(s\right)$ within an interval $\left[0,s^{+}\right]$, where $F^{\prime }\left(s\right)=f\left(s\right)>0$ for $\forall s>0$. Without loss of generality, this paper assumes that the hazard rate of $F\left(·\right)$, denoted by $\mu \left(s\right)=f\left(s\right)/\left(1-F\left(s\right)\right)$, increases in $s$. This is a standard assumption in the literature of mechanism design [25,47,50]. It is well known that many common distributions (e.g., uniform, exponential, normal, Poisson, gamma) have increasing hazard rates.

The BSS can enhance the government’s valuation by improving its effort level $e$. For tractability, this paper assumes that the BSS’s cost associated with $e$ is given by $0.5\gamma e^2$, where $\gamma >0$ represents the BSS’s effort-aversion parameter, which is a common operation in the model solution of operations management-related research [47,51]. Specifically, the BSS’s expected utility $U_S$ is given by

$$U_S=w+sk-0.5\gamma e^2$$

(2)

where $w$ is the government’s compensation and $sk$ is the BSS’s operating profit.

The purpose of the government is to design an incentive mechanism to induce the BSS to truthfully report its operation level and provide a corresponding effort level. Specifically, the incentive mechanism consists of a capital allocation policy $k\left(\widehat{s}\right)$ depending on the BSS’s report about operation level, $\widehat{s}$, and a compensation mechanism $w\left(\widehat{s},V\right)$ depending on both the BSS’s report and the government’s valuation.

Therefore, the problem faced by the government turns to maximizing its expected utility $U_G$, which is given by

$$U_G=V-w$$

(3)

The sequence of events for our research question is as follows:

Time 0: The government provides a compensation mechanism $\left\{w\left(\widehat{s},V\right),k\left(\widehat{s}\right)\right\}$ to the BSS, and gives a recommendation of effort level $e\left(\widehat{s}\right)$.

Time 1: The BSS reports its operation level $\widehat{s}$.

Time 2: The government allocates the capital $k\left(\widehat{s}\right)$.

Time 3: The BSS chooses effort level $e$.

Time 4: The government’s valuation $V$ is realized, and pays compensation $w\left(\widehat{s},V\right)$ to the BSS.

Moreover, this paper needs to assume that the government commits to the compensation mechanism $\left\{w\left(\widehat{s},V\right),k\left(\widehat{s}\right)\right\}$ at Time 0 [47,51]. Without such an assumption, in Time 2, the government would allocate a quantity of capital different to the quantity specified in Time 0, resulting in the BSS not telling the truth.

4. Equilibrium Solutions

In this section, we first study the interaction between the government and the BSS under two scenarios of symmetry and asymmetry information, respectively, then compare these equilibrium results.

4.1. First-Best Solution: Symmetric Information

We first consider the benchmark case, in which the BSS’s operation level $\left(s\right)$ and effort level $\left(s\right)$ are common knowledge. Therefore, we can obtain the first-best solution by maximizing the total utility of the government and BSS $\left(U\right)$:

$$\underset{k\left(s\right),e\left(s\right)}{\max }U=U_S+U_G=nk-0.5\gamma e^2-\lambda k^2+\alpha ek+sk+\sigma sk$$

(4)

Proposition 1.

The first-best capital allocation and effort level are given as follows:

$$k^{*}\left(s\right)=\frac{\gamma \left(n+s+\sigma s\right)}{2\gamma \lambda -{\alpha }^2}$$

(5)

$$e^{*}\left(s\right)=\frac{\alpha \left(n+s+\sigma s\right)}{2\gamma \lambda -{\alpha }^2}$$

(6)

Proof. 

For readability, all the proofs are included in Appendix A. □

Notice that this study requires $2\gamma \lambda -{\alpha }^2$ to satisfy the second-order conditions for Equation (4). This inequality is thus assumed throughout this paper. Substituting Equations (5) and (6) into (4), this paper obtains the total utility of the government and BSS $U$ in the first-best solution:

$$U=\frac{\gamma {\left(n+s+\sigma s\right)}^2}{2\left(2\gamma \lambda -{\alpha }^2\right)}$$

(7)

According to Equations (5)–(7), this study can find that $U=0.5k^{*}\left(s\right)\left(n+s+\sigma s\right)=0.5\gamma e^{*}\left(s\right)$. Therefore, the total utility $U$ is increasing in $k^{*}\left(s\right)$ and $e^{*}\left(s\right)$. Moreover, from Equations (5) and (6), it is seen that both $k^{*}\left(s\right)$ and $e^{*}\left(s\right)$ increase with the BSS’s operation level $\left(s\right)$. This result is consistent with the realistic observation that the more efficiently the BSS operates, the higher the capital allocation and effort level will be [16].

To sum up, this paper can conclude that if the government could observe both the BSS’s operation level $s$ and effort level $e$, a complete contract with the first-best solution specified by Equations (5) and (6) can be easily reached. Ideally, once the first-best solution is achieved, the government’s monetary compensation ($w$) should be set to levels satisfying the BSS’s participation constraint.

The management implication of proposition 1: As the government’s capital allocation and the BSS’s effort level are complementary, the total utility increases with the government’s capital allocation and the BSS’s effort level. Therefore, for the government, it can allocate more capital to the BSS to incentivize it to provide higher-level effort, and for the BSS, it can attract more government capital allocation by increasing its effort level. A virtuous cycle between the government’s allocation capital and the BSS’s effort level would maximize their total utility.

4.2. Optimal Mechanism: Asymmetric Information

This study next considers the scenario in which the government does not know the BSS’s operation level $\left(s\right)$ or effort level $\left(e\right)$. To induce truthful report from the BSS, this paper designs an incentive compensation mechanism for the government, which is formulated as a linear function of the government’s valuation $\left(V\right)$.

This paper constructs the compensation mechanism as follows:

$$w\left(\widehat{r},V\right)=a\left(\widehat{r}\right)+b\left(\widehat{r}\right)V$$

(8)

where $a\left(·\right)$ represents a fixed compensation and $b\left(·\right)$ represents the valuation sharing ratio. This study has no restriction on the sign of $a\left(·\right)$, but $b\left(·\right)$ is restricted to be nonnegative. Note that although the compensation mechanism is a linear function of $V$, $a\left(·\right)$ and $b\left(·\right)$ can be nonlinear functions of the reported operation level $\left(\widehat{s}\right)$.

According to the compensation mechanism specified by Equation (8), the BSS’s expected utility can be rewritten as follows:

$$U_S\left(s,\widehat{s},e\right)=a\left(\widehat{s}\right)+b\left(\widehat{s}\right)V\left(s,k\left(\widehat{s}\right)\right)+sk-0.5\gamma e^2$$

(9)

Recall that in the sequence of movements in our problem, the BSS puts effort level $e$ after knowing the capital allocation $k\left(\widehat{s}\right)$ and reporting $\widehat{s}$. Therefore, the optimal effort level can be derived by maximizing $U_S\left(s,\widehat{s},e\right)$. As $U_S\left(s,\widehat{s},e\right)$ is a concave function in $e$, and the first-order condition is $bak=\gamma e$, this study can obtain the BSS’s optimal effort level $e$, which is given by

$$e=\frac{bak}{\gamma }$$

(10)

Substituting Equation (10) into Equation (9), this paper obtains the BSS’s expected utility when its operation level is $s$ but reports $\widehat{s}$:

$$U_S\left(s,\widehat{s}\right)=a+\left(s+bn+bs\sigma \right)k-b\lambda k^2+\frac{{\alpha }^2{b}^2{k}^2}{2\gamma }$$

(11)

where $\widehat{s}$ is omitted in $a\left(·\right)$, $b\left(·\right)$, and $k\left(·\right)$.

Next, this paper turns to the government’s mechanism design problem. If the BSS reports the operation level truthfully, then its expected utility is exactly $U_S\left(s\right)=U_S\left(s,s\right)$. Referring to the revelation principle [50], true reporting is the optimal strategy of the BSS. Therefore, the government’s mechanism design problem can be stated as follows:

$$\underset{a\left(\widehat{s}\right),b\left(\widehat{s}\right),k\left(\widehat{s}\right)}{\max }{U}_G={{\displaystyle \int }}_0^{s^{+}}\left[V-a\left(s\right)-b\left(s\right)V\right]\mathrm{d}F\left(s\right)$$

(12)

subject to

(i)

$s\in \arg \max U_S\left(s,\widehat{s}\right)$ (IC),

(ii)

$\forall s, U_S\left(s,s\right) \ge U_S\left(0\right)$ (IR),

(iii)

$\forall s, b\left(s\right) \ge 0, k\left(s\right) \ge 0$.

The government designs the fixed compensation $a\left(\widehat{s}\right)$, the valuation sharing ratio $b\left(\widehat{s}\right)$, and the capital allocation $k\left(\widehat{s}\right)$ to maximize its expected utility $U_G$. The constraint (i) guarantees that the BSS can obtain the maximum utility when it reports the operation level truthfully. The constraint (ii) guarantees that the BSS should achieve at least their reservation utility $U_S\left(0\right)$ for all possible values of $s$, where $U_S\ge 0$. The constraint (iii) guarantees that the capital allocation and valuation sharing ratio must be nonnegative. It should be noted again that this paper does not impose a nonnegative restriction on $a\left(\widehat{s}\right)$, allowing us to design a more flexible compensation mechanism.

Next, to conduct a more accurate analysis of the government’s incentive mechanism, this paper calculates two special values of $s$, $s_1$, and $s_2$, which represent the boundaries of the BSS’s operation level. Specifically, $s_1$ represents the value of $s$ when the capital allocation $k\left(s\right)=0$, and $s_2$ represents the value of $s$ when the valuation sharing ratio $b\left(s\right)=0$. According to $s_1$ and $s_2$, the whole interval $\left[0,s^{+}\right]$ is divided into three sub-intervals, where $s\in \left[0,s_1\right)$ represents the BSS with low operation level, $s\in \left[s_1,s_2\right)$ represents the BSS with medium operation level, and $s\in \left[s_2,s^{+}\right]$ represents the BSS with high operation level. The detailed calculation process of $s_1$ and $s_2$ is shown in Definition 1.

Definition 1.

Let $s_1$be the solution to $\left[n\mu \left(s\right)+\left(s\mu (s\right)-1)\left(1+\sigma \right)\right]=-\sigma$and $s_2$be the solution to $\left[n\mu \left(s\right)+\left(s\mu (s\right)-1)\left(1+\sigma \right)\right]=\sigma \left[2\gamma \lambda -{\alpha }^2\right]/{\alpha }^2$.

As the hazard rate function $\mu \left(s\right)$ is increasing in $s$, the left-hand sides of both equations in definition 1 increase with $s$. Therefore, there exists a unique solution in either of the two equations. In addition, by $2\gamma \lambda >{\alpha }^2$, we can derive that $s_1\le s_2$. For simplicity, this study assumes $s_2\le s^{+}$ for the rest of this paper. Then, this paper concludes that for $0\le s<s_1$, $\left[n\mu \left(s\right)+\left(s\mu (s\right)-1)\left(1+\sigma \right)\right]<-\sigma$; for $s_1\le s<s_2$, $-\sigma \le \left[n\mu \left(s\right)+\left(s\mu (s\right)-1)\left(1+\sigma \right)\right]<\sigma \left[2\gamma \lambda -{\alpha }^2\right]]/{\alpha }^2$; and for $s_2\le s$, $\left[n\mu \left(s\right)+\left(s\mu (s\right)-1)\left(1+\sigma \right)\right]\ge \sigma \left[2\gamma \lambda -{\alpha }^2\right]/{\alpha }^2$.

Proposition 2 presents the government’s optimal mechanism with a linear compensation mechanism.

Proposition 2.

The government’s optimal mechanism with a linear compensation and its outcome can be described as follows.

Region 1: Low operation level. When $s\in \left[0,s_1\right)$, the government allocates no capital, and pays the BSS a fixed compensation that is equal to its reservation utility $U_S\left(0\right)$. For the BSS, as there is no capital, the effort level is zero. That is,

$$a\left(s\right)=U_S\left(0\right), b\left(s\right)=0, k\left(s\right)=0, e\left(s\right)=0.$$

Region 2: Medium operation level. When $s\in \left[s_1,s_2\right)$, the government allocates some capital but only pays the BSS a fixed compensation. For the BSS, as $b\left(s\right)=0$, the effort level is also zero. That is,

$$\begin{array}{c}a\left(s\right)=U_S\left(0\right)+{{\displaystyle \int }}_{s_1}^{s}k\left(t\right)\mathrm{d}t-sk\left(s\right)\hfill \\ b\left(s\right)=0\hfill \\ k\left(s\right)=\frac{n\mu \left(s\right)+s\mu \left(s\right)+s\mu \left(s\right)\sigma -1}{2\mu \left(s\right)\lambda }\hfill \\ e\left(s\right)=0\hfill \end{array}$$

Region 3: High operation level. When $s\in \left[s_2, s^{+}\right]$, the government allocates more capital, and pays the BSS with a fixed compensation and valuation sharing incentives. For the BSS, as $0\le b\left(s\right)<1$ and there are more capitals, it will take a corresponding effort level. That is,

$$\begin{array}{l}a\left(s\right)=U_S\left(0\right)+{{\displaystyle \int }}_{s_1}^s\left[\left(\sigma b\left(t\right)+1\right)k\left(t\right)\right]\mathrm{d}t-\left(s+b\left(s\right)n+b\left(s\right)\sigma s\right)k\left(s\right)-\left(\frac{2\lambda \gamma b\left(s\right)-{\alpha }^{2}b{\left(s\right)}^2}{2\gamma }\right)k{\left(s\right)}^2\\ b\left(s\right)=1-\frac{\sigma \left[2\gamma \lambda -{\alpha }^2\right]]}{{\alpha }^2\left[n\mu \left(s\right)+\left(s\mu (s\right)-1)\left(1+\sigma \right)\right]}\\ k\left(s\right)=\frac{\gamma \left[n\mu \left(s\right)+\left(s\mu (s\right)-1)\left(1+\sigma \right)\right]}{\mu \left(s\right)\left[2\gamma \lambda -{\alpha }^2\right]}\\ e\left(s\right)=\frac{\alpha b\left(s\right)k\left(s\right)}{\gamma }\end{array}$$

Proposition 2 shows that the optimal incentive mechanism consists of three parts. When the BSS’s operation level is low, i.e., $s\in \left[0,s_1\right)$, the government does not allocate capital but provides a fixed compensation such as $U_S\left(0\right)$ to the BSS, although the BSS makes no effort. This is because, although some BSSs are poorly run, they are an essential service to society, so the government must subsidize them. When the BSS’s operation level is medium, i.e., $s\in \left[s_1,s_2\right)$, the government would like to allocate a number of capitals and provides corresponding compensations. Especially, when the BSS’s operation level is high, i.e., $s\in \left[s_2,s^{+}\right]$, the government will not only offer a fixed compensation but also share a certain ratio of its valuation. In such a case, the BSS makes a positive response to the government’s compensation via high effort levels.

The above results are consistent with Proposition 1 that the virtuous circle between the government allocation of capital and BSS effort level is beneficial to both parties. Furthermore, some important properties of the optimal mechanism are presented in the following proposition.

Proposition 3.

Over the whole interval $\left[0, s^{+}\right]$, the derived capital allocation $k\left(s\right)$, effort level $e\left(s\right)$, and valuation sharing ratio $b\left(s\right)$ are continuous and nondecreasing, while the fixed compensation $a\left(s\right)$ is continuous and nonincreasing.

Proposition 3 shows that the government will allocate more capital quantity and a higher ratio of the valuation to the BSS with a higher operation level, but will provide a lower fixed compensation. Interestingly, the BSS will also provide a higher effort level, generating a positive response to the greater (true) operation level and monetary compensation. That is, the optimal mechanism realizes a win–win solution for both parties and increases the possibility of practical implementation to a large extent.

The above results are also intuitive. In real life, the BSS with a poor operation level needs significant support from the government. In contrast, the BSS with a better operation level can achieve a win–win situation for itself and the government [16].

4.3. Comparison between the Optimal Mechanism and the First-Best Solution

In this subsection, this paper compares the optimal mechanism (asymmetric information) with the first-best solution (symmetric information). Specifically, this study concentrates on the capital allocation, effort level, and total utility in the two scenarios.

Let $\Delta k\left(s\right)=k^{*}\left(s\right)-k\left(s\right)$, where $k^{*}\left(s\right)$ is the first-best capital allocation, and $k\left(s\right)$ is the optimal capital allocation under asymmetric information. According to Propositions 1 and 2, we have

$$\Delta k\left(s\right)=\left\{\begin{array}{cc}\frac{\gamma \left(n+s+\sigma s\right)}{2\gamma \lambda -{\alpha }^2},\hfill & 0\le s<s_1;\hfill \\ \frac{2\gamma \lambda +{\alpha }^2\left(n\mu \left(s\right)+s\mu \left(s\right)\left(1+\sigma \right)-1\right)}{2\mu \left(s\right)\lambda \left(2\gamma \lambda -{\alpha }^2\right)},\hfill & s_1\le s<s_2;\hfill \\ \frac{\gamma \left(1+\sigma \right)}{\mu \left(s\right)\left(2\gamma \lambda -{\alpha }^2\right)},\hfill & s\ge s_2.\hfill \end{array}\right.$$

As $2\gamma \lambda >{\alpha }^2$, we can easily find that for any $s$,

$$\Delta k\left(s\right)\ge 0$$

(13)

Similarly, next, let $\Delta e\left(s\right)=e^{*}\left(s\right)-e\left(s\right)$, where $e^{*}\left(s\right)$ is the first-best effort level, and $e\left(s\right)$ is the optimal effort level under asymmetric information. According to Propositions 1 and 2, we have

$$\Delta e\left(s\right)=\left\{\begin{array}{cc}\frac{\alpha \left(n+s+\sigma s\right)}{2\gamma \lambda -{\alpha }^2},\hfill & \hfill 0\le s<s_2;\\ \frac{{\alpha }^2+2\gamma \lambda \sigma }{\alpha \mu \left(s\right)\left(2\gamma \lambda -{\alpha }^2\right)},& \hfill s\ge s_2.\end{array}\right.$$

We can also easily find that for any $s$,

$$\Delta e\left(s\right)\ge 0$$

(14)

Finally, let $\Delta U\left(s\right)=U^{*}\left(s\right)-U\left(s\right)$, and we have

$$\Delta U\left(s\right)=\left\{\begin{array}{cc}\frac{\gamma \left(n+s+\sigma s\right)}{2\gamma \lambda -{\alpha }^2},\hfill & \hfill 0\le s<s_1;\\ \frac{2\gamma \lambda +{\alpha }^2\left(n^2\mu {\left(s\right)}^2+2ns\left(1+\sigma \right)\mu {\left(s\right)}^2+s^2\mu {\left(s\right)}^2{\left(1+\sigma \right)}^2-1\right)}{4\mu {\left(s\right)}^2\lambda \left(2\gamma \lambda -{\alpha }^2\right)},\hfill & \hfill s_1\le s<s_2;\\ \frac{\gamma \left(2\gamma \lambda {\sigma }^2+{\alpha }^2\left(1+2\sigma \right)\right)}{2\mu {\left(s\right)}^2{\alpha }^2\left(2\gamma \lambda -{\alpha }^2\right)},\hfill & \hfill s\ge s_2\end{array}\right.$$

Likewise, we can find that for any $s$,

$$\Delta U\left(s\right)\ge 0$$

(15)

As in Equations (13)–(15), the government underinvests the capital quantity and the BSS underinvests the effort level in the optimal mechanism relative to the first-best solution. Clearly, such underinvestment problems are caused by asymmetric information, which further leads to the loss of total utility. Fortunately, our following proposition demonstrates that the impact of asymmetric information stated above will be smaller in some realistic conditions.

Proposition 4.

Over the whole interval $\left[0, s^{+}\right]$, $\Delta q\left(s\right)$, $\Delta e\left(s\right)$, and $\Delta U\left(s\right)$ are nonincreasing in $s$.

Proposition 4 implies that the government and BSS’s underinvestment problems will become smaller as the BSS’s operation level increases. Moreover, when the precondition is satisfied, the total utility loss $\Delta U\left(s\right)$ decreases with the operation level. Surprisingly, as in the proof of Proposition 4, if $s$ approaches $s^{+}$, the impact of asymmetric information will implicitly disappear; that is, $\Delta k\left(s\right)=0$, $\Delta e\left(s\right)=0$, and $\Delta U\left(s\right)=0$ when $s\to s^{+}$. These results highlight the advantages of high operation level in terms of mitigating the government and BSS’s underinvestment problems, as well as reducing the loss of total utility.

The management implication of proposition 4: For the government, it can reduce the loss caused by information asymmetry by seeking the BSS with a high operation level. For the BSS, it should enhance its operation level with might and main to sharpen its competitive edge. In addition, from a comprehensive perspective, achieving a high operation level is suitable for individuals and society.

5. Numerical Results

To further study the government’s optimal mechanism and test the correctness of the previous propositions, this paper adopts a numerical simulation in this section. Referring to [16,37], the specific values of the parameters used are shown in Table 1.

Table 1. Parameter setting.

Parameters	$\mathit{n}$	$\mathit{\gamma }$	$\mathit{a}$	$\mathit{\lambda }$	$\mathit{\sigma }$	${\mathit{U}}_{\mathit{s}}\left(0\right)$
Value	0.1	0.3	0.1	0.1	0.4	300,000

Furthermore, this paper assumes that the operation level $s$ follows a uniform distribution within the interval $\left[0,100\right]$, and we can obtain $f\left(s\right)=1/100$, $F\left(s\right)=s/100$, and $\mu \left(s\right)=1/\left(100-s\right)$. According to Definition 1, we can derive that $s_1=41.63$ and $s_2=70.81$. The impact of operation level on valuation sharing ratio $b\left(s\right)$, fixed compensation $a\left(s\right)$, capital allocation $k\left(s\right)$, effort level $e\left(s\right)$, and total utility $U$ are illustrated in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5, respectively.

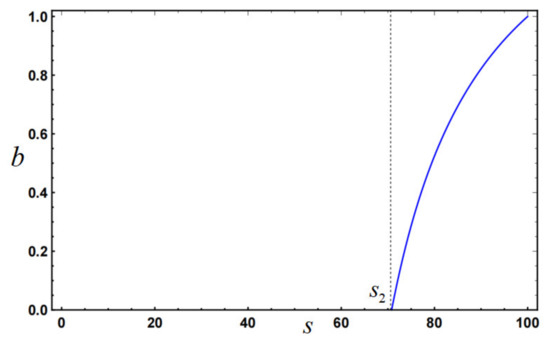
Figure 1. The impact of operation level on valuation sharing ratio $b\left(r\right)$.

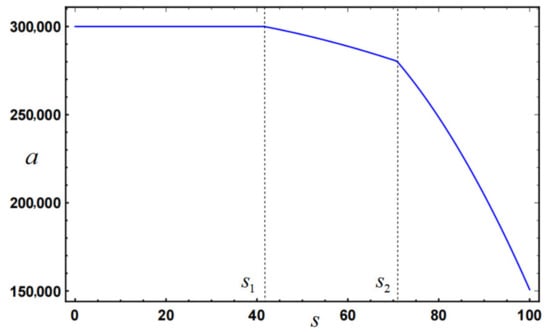
Figure 2. The impact of operation level on fixed compensation $a\left(r\right)$.

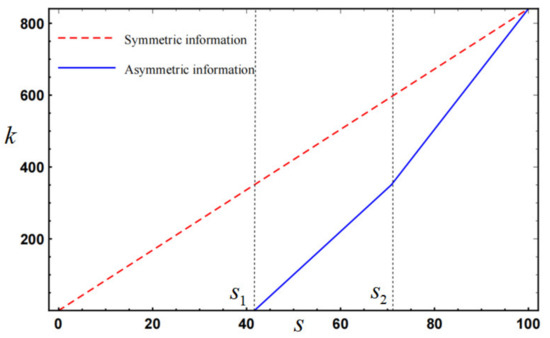
Figure 3. The impact of operation level on optimal capital allocation.

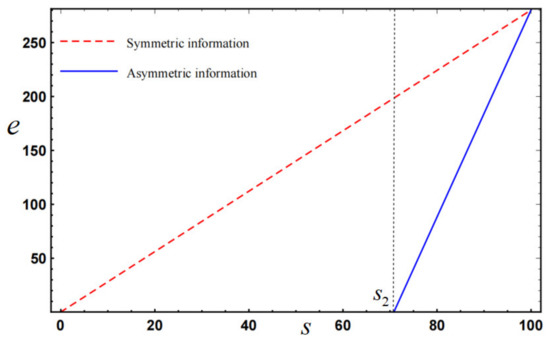
Figure 4. The impact of operation level on optimal effort level.

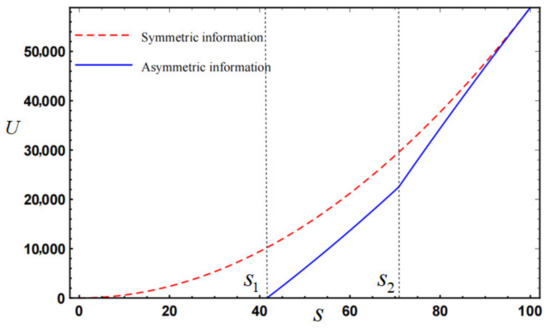
Figure 5. The impact of operation level on total utility.

From Figure 1, we can see that only when the BSS’s operation level $s<s_2$ (Region 3), the government will provide the valuation sharing ratio to the BSS. Moreover, as the BSS’s operation level increases, the valuation sharing ratio will also increase. These observations validate the conclusions about $b\left(s\right)$ in Propositions 2 and 3.

Similarly, from Figure 2, we can see that if the BSS’s operation level $s\ge s_1$ (Region 1), the government will provide a fixed compensation ($U_S\left(0\right)$) to the BSS, and if $s\ge s_1$ (Region 2, 3), the government will provide a fixed compensation $a\left(s\right)$ less than $U_S\left(0\right)$. Moreover, as the BSS’s operation level increases, the fixed compensation will decrease. These observations validate the conclusions about $a\left(s\right)$ in Propositions 2 and 3.

From Figure 3, Figure 4 and Figure 5, we can see that: (1) the government will allocate capital to the BSS with better operating level (Regions 2 and 3), but the BSS will only pay the effort level at the higher operation level (Region 3); (2) asymmetric information will cause the government and BSS underinvestment problems ($\Delta k\left(s\right)>0$, $\Delta e\left(s\right)>0$), which will further lead to the loss of total utility ($\Delta U\left(s\right)>0$); (3) as the BSS’s operation level increases, the underestimation problems will become smaller and smaller, and the total utility will gradually increase. These observations validate the conclusions about $k\left(s\right)$, $e\left(s\right)$, $U\left(s\right)$, $\Delta k\left(s\right)$, $\Delta e\left(s\right)$, and $\Delta U\left(s\right)$ in Propositions 2, 3, and 4.

6. Conclusions

This paper is motivated by the application and promotion of the electric vehicle battery changing station (BSS). In a principal–agent framework, this study designs the government’s optimal capital allocation scheme and compensation mechanism to induce the BSS to report its true operation level and take the corresponding effort level.

To our best knowledge, this paper is the first developing optimal compensation mechanisms for improving the operation of BSS in the presence of two kinds of asymmetric information. In other words, this study derives the government’s capital allocation scheme and compensation mechanism for the BSS, which has two kinds of private information of operation level and effort level, in two scenarios of information symmetry and asymmetry. This paper finds that the capital allocation scheme and compensation mechanism proposed in this paper can incentivize the BSS to report its actual operation level and take the corresponding effort level. Moreover, the government and BSS’s underinvestment problems become smaller when the BSS’s operation level is relatively high. Then, through a comparison of the equilibrium results and numerical experiments, this paper finds that asymmetric information will cause a loss of government profits and hinder the sustainable development of the BSS. Specifically, in the optimal (asymmetric information) capital allocation scheme and compensation mechanism, the government is underinvesting in capital allocation and the BSS’s effort level relative to the first-best solution (symmetric information). This result is consistent with the information rents that an agent with private information receives from the principal. On the other side of the coin, this result is also important to support the win–win cooperation in some conditions where the information rents are too high to be feasible. In addition, our results highlight the advantages of a high operation level in terms of mitigating the government’s underinvestment problems, as well as reducing the loss of total utility.

Some important managerial insights are summarized as follows: First, from a system perspective, the government should adopt the linear compensation mechanisms due to the simplicity for practical implementation. However, if the information rents caused by hidden information are too high to be feasible, it is urgent for both parties to think over the win–win cooperation with complete information. Second, our results highlight the advantages of the BSS’s operation level in terms of mitigating the government and BSS’s underinvestment problems, as well as reducing the loss of total utility. Hence, achieving a high operation level is beneficial for individuals and the whole of society.

This paper highlights a few potential directions for future work. First, this paper only considers BBS’s two kinds of asymmetric information: operation level and effort level, so one can extend our model to other asymmetric information scenarios (e.g., uncertain market demand, investment risk information.) [20,44,45]. Secondly, this paper only studies the case of government investment and subsidy for one BSS, and it is more practical and worthy of study to consider multiple competing BSSs [15,17,19]. Finally, the competition and subsidy strategies between the electric vehicle charging mode and battery swapping mode are also worth studying [16,30].