Prediction of Future Lake Water Availability Using SWAT and Support Vector Regression (SVR)
Abstract
:1. Introduction
2. Materials and Methods
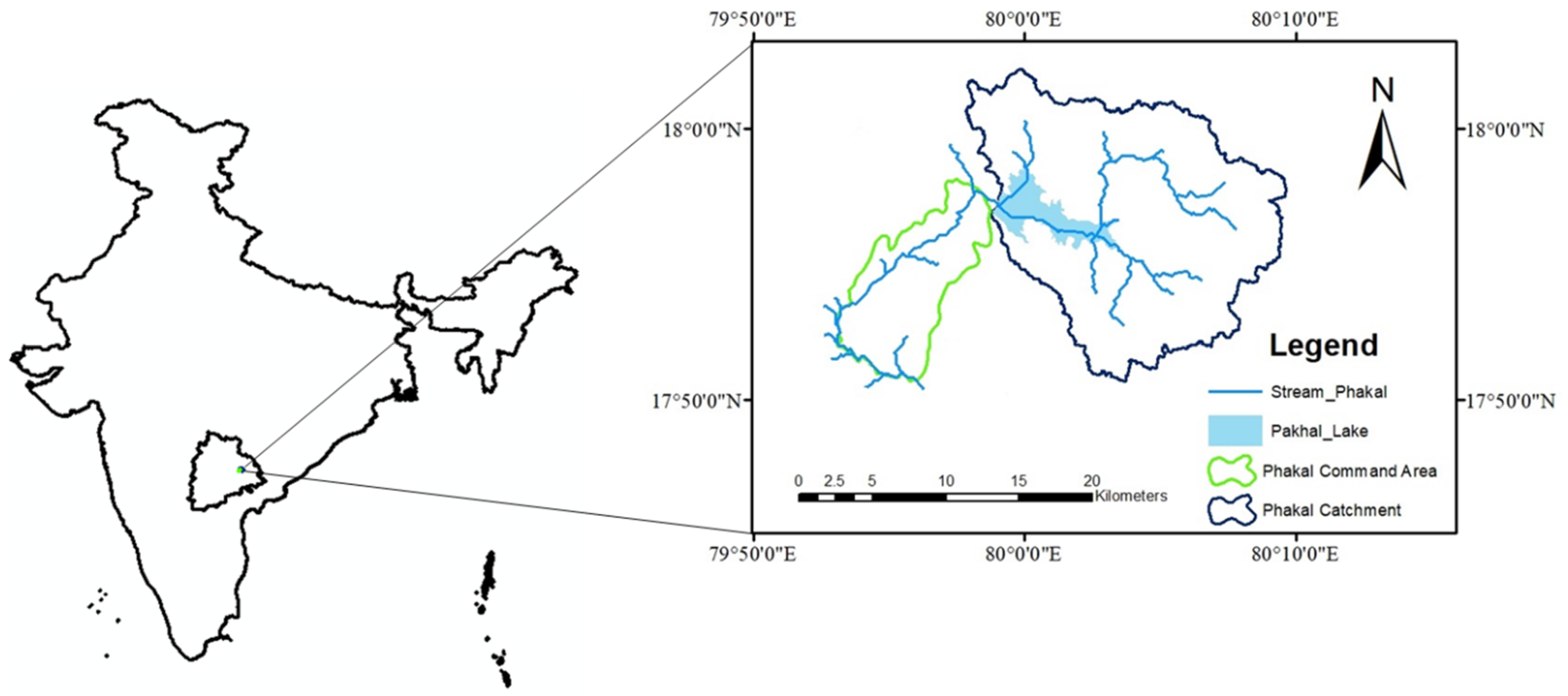
2.1. Study Area Description
2.2. Methodology
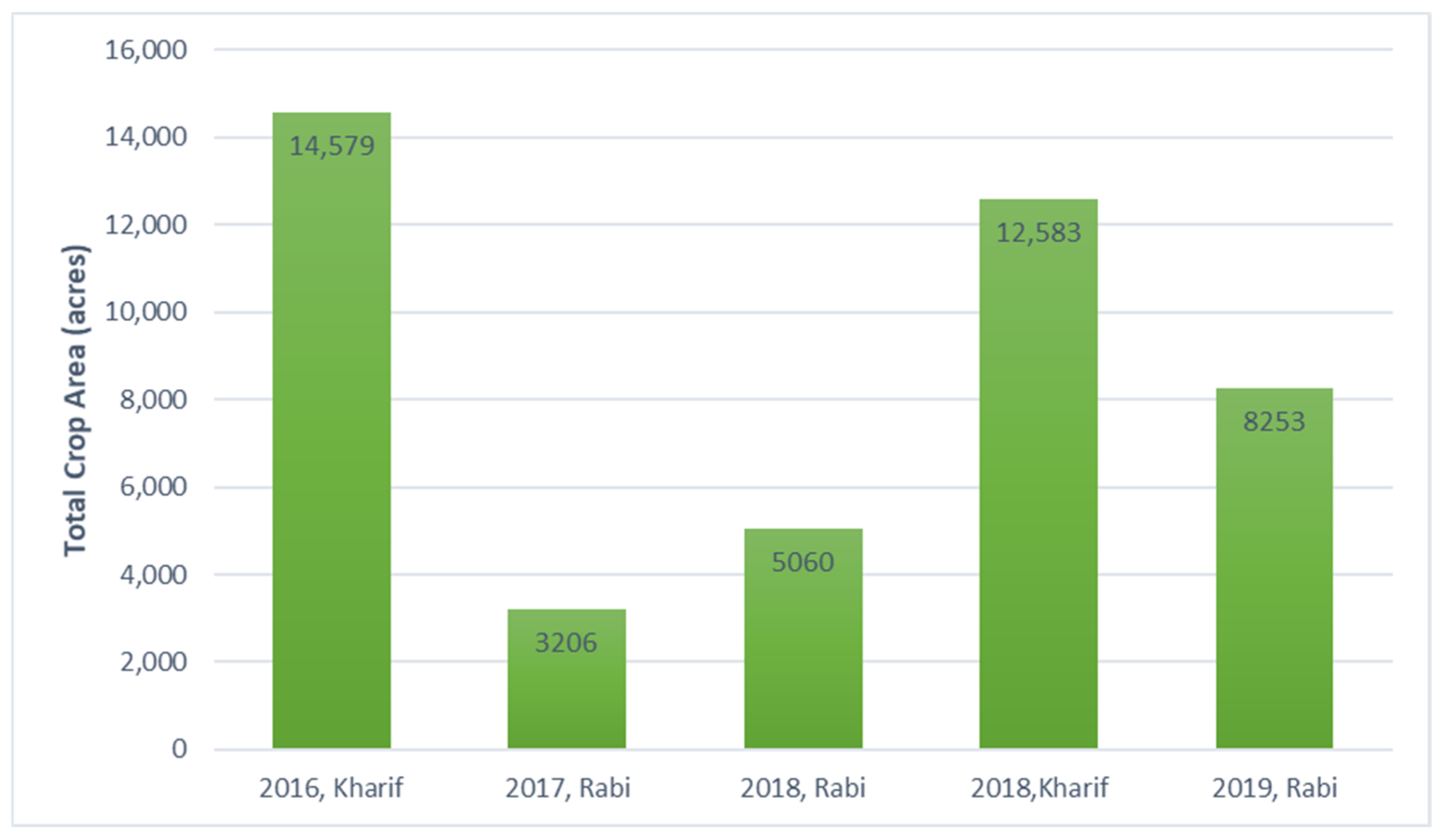
2.3. Data Used
2.4. REA_QM Method
2.5. Support Vector Regression (ν-SVR)
2.6. Linking SWAT with ν-SVR
3. Results
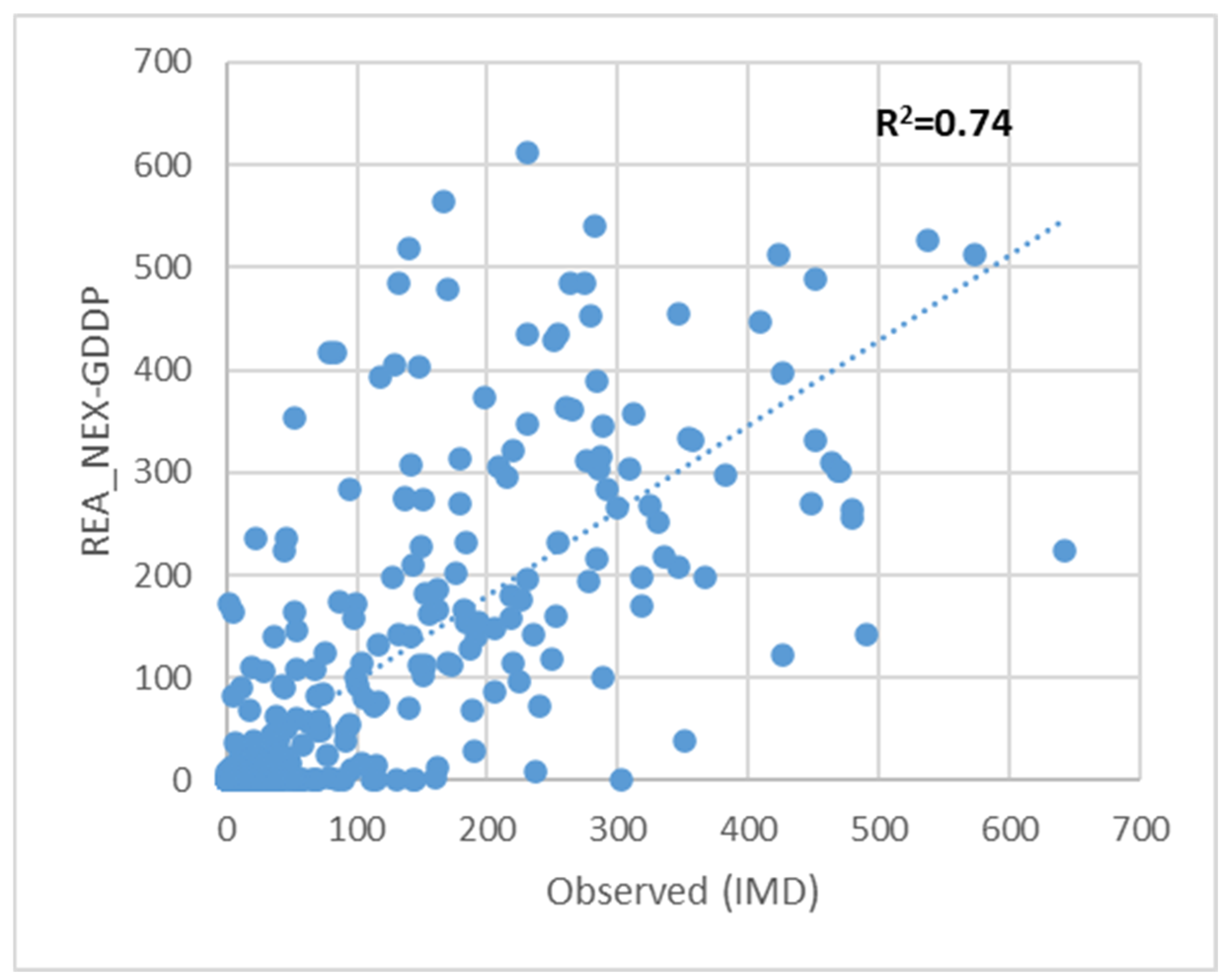
3.1. Climate Variables from REA_QM
3.2. Historic and Future NEX-GDDP Climate Data Analysis
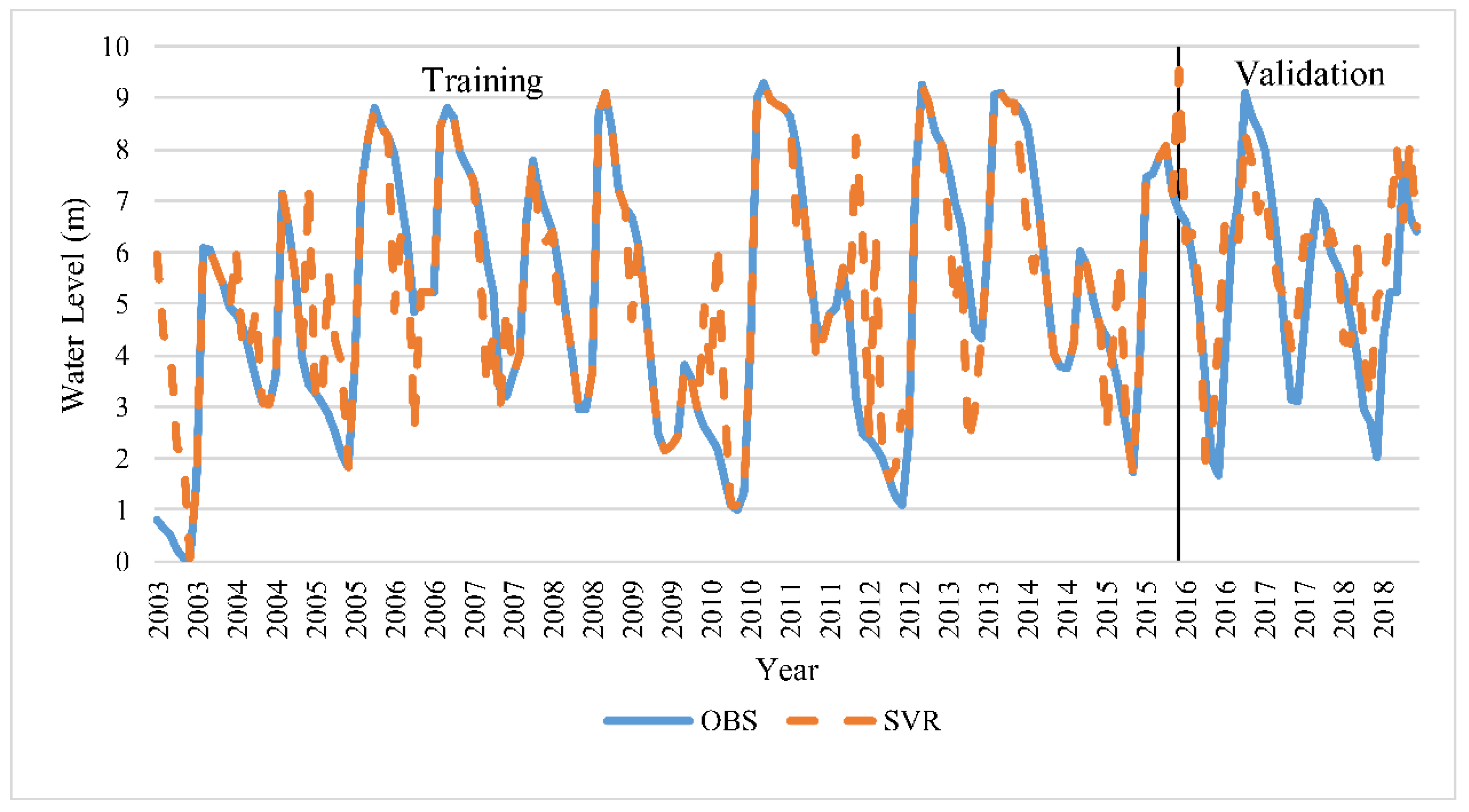
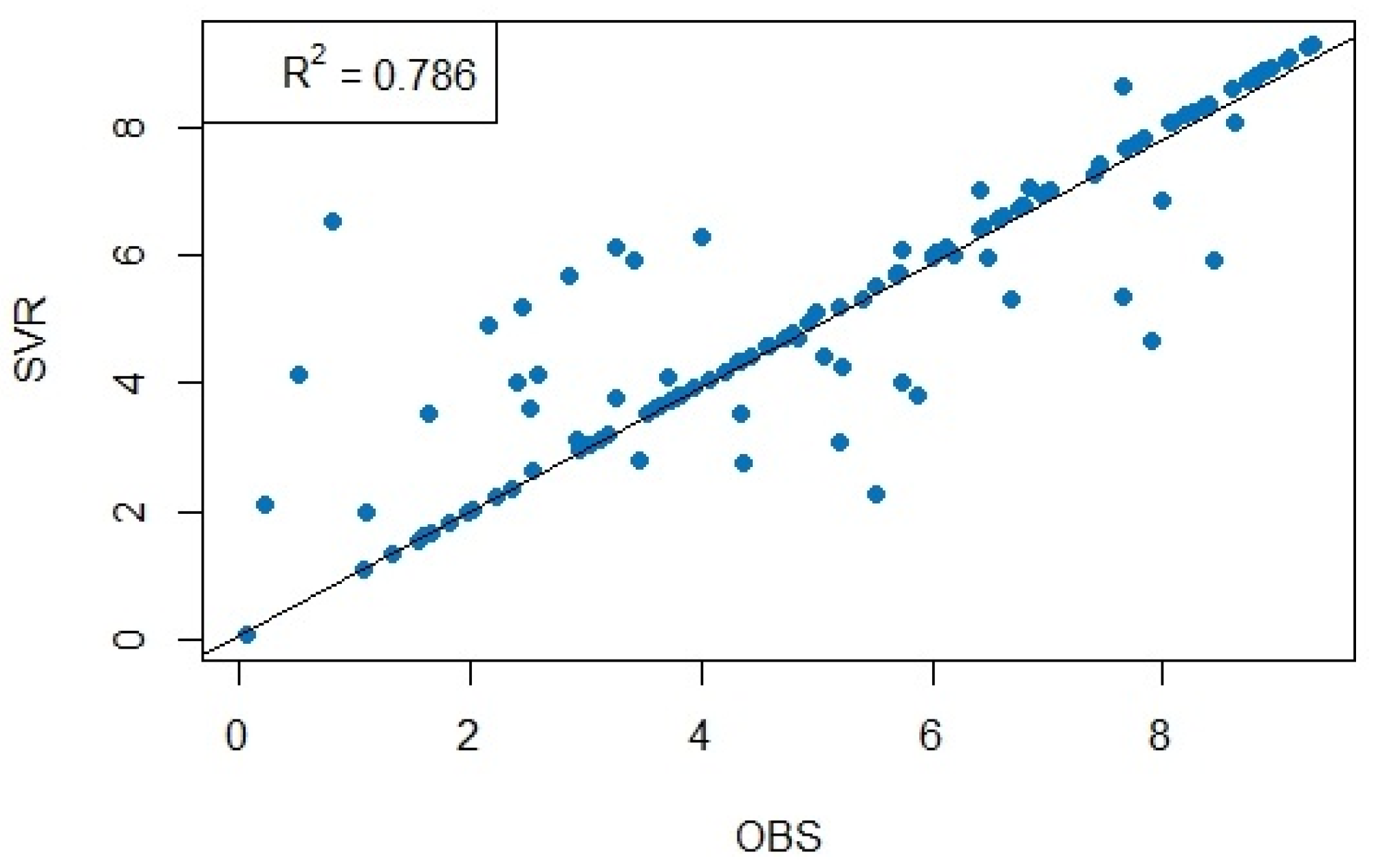
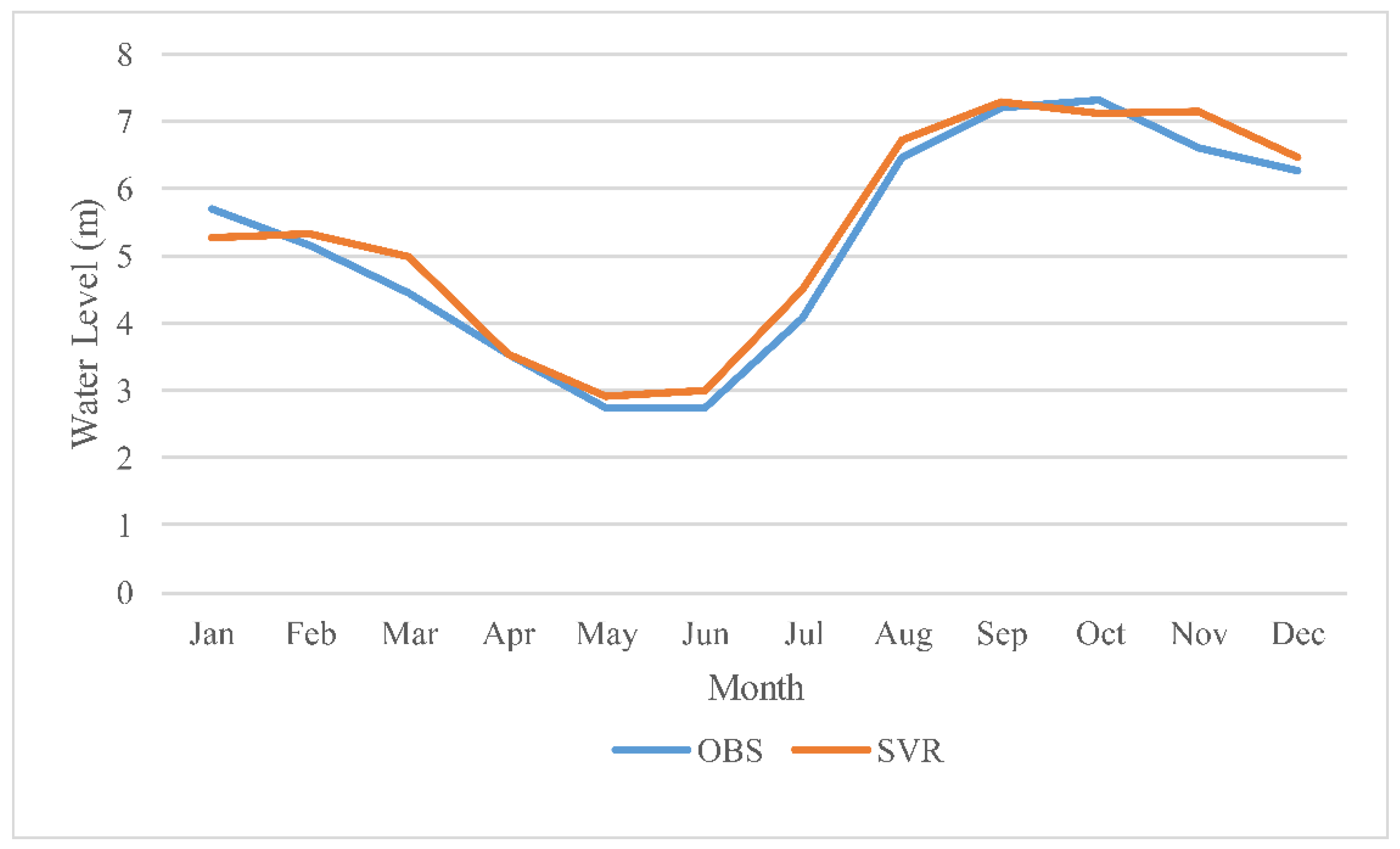
3.3. Performance of the ν-SVR Model
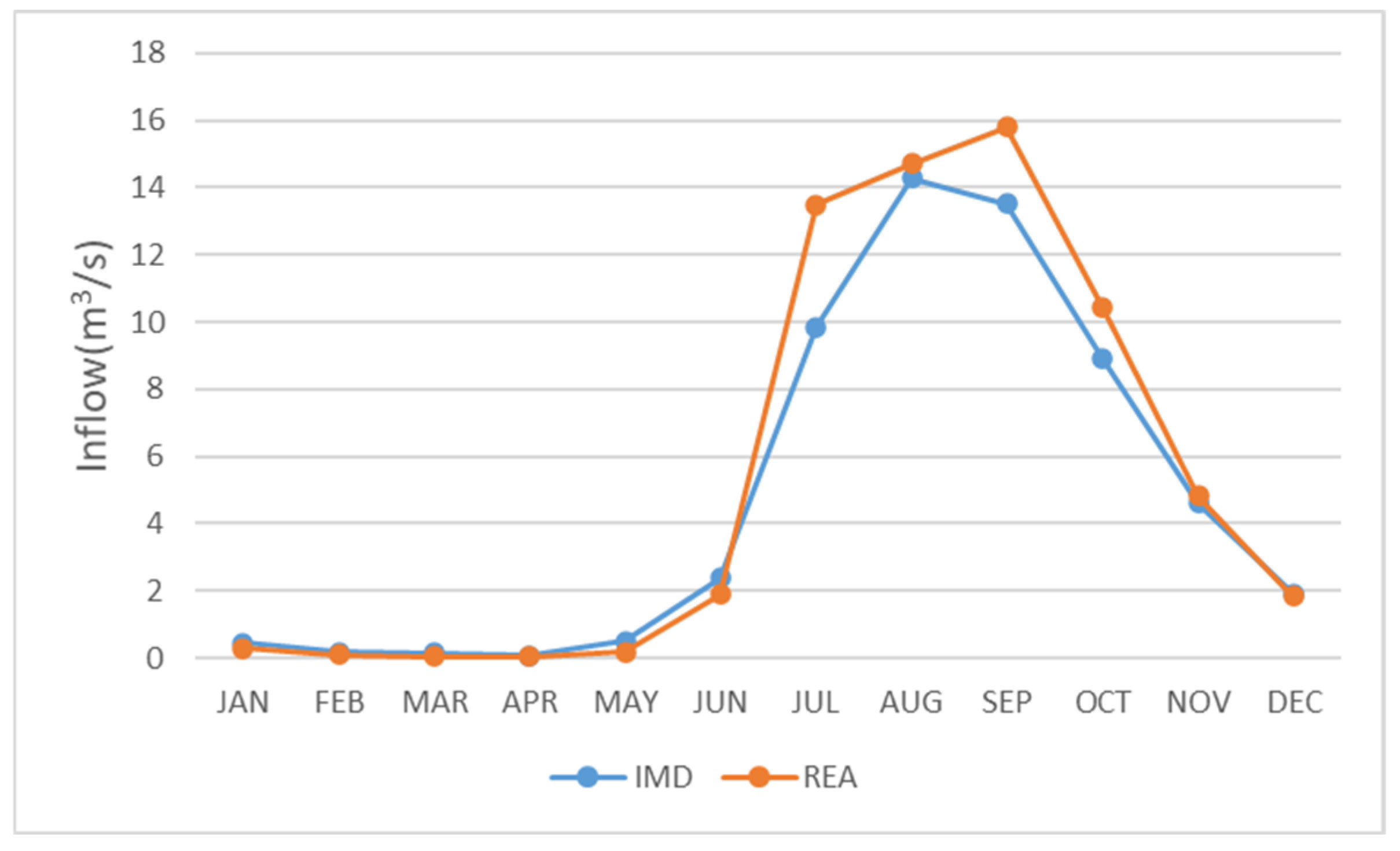
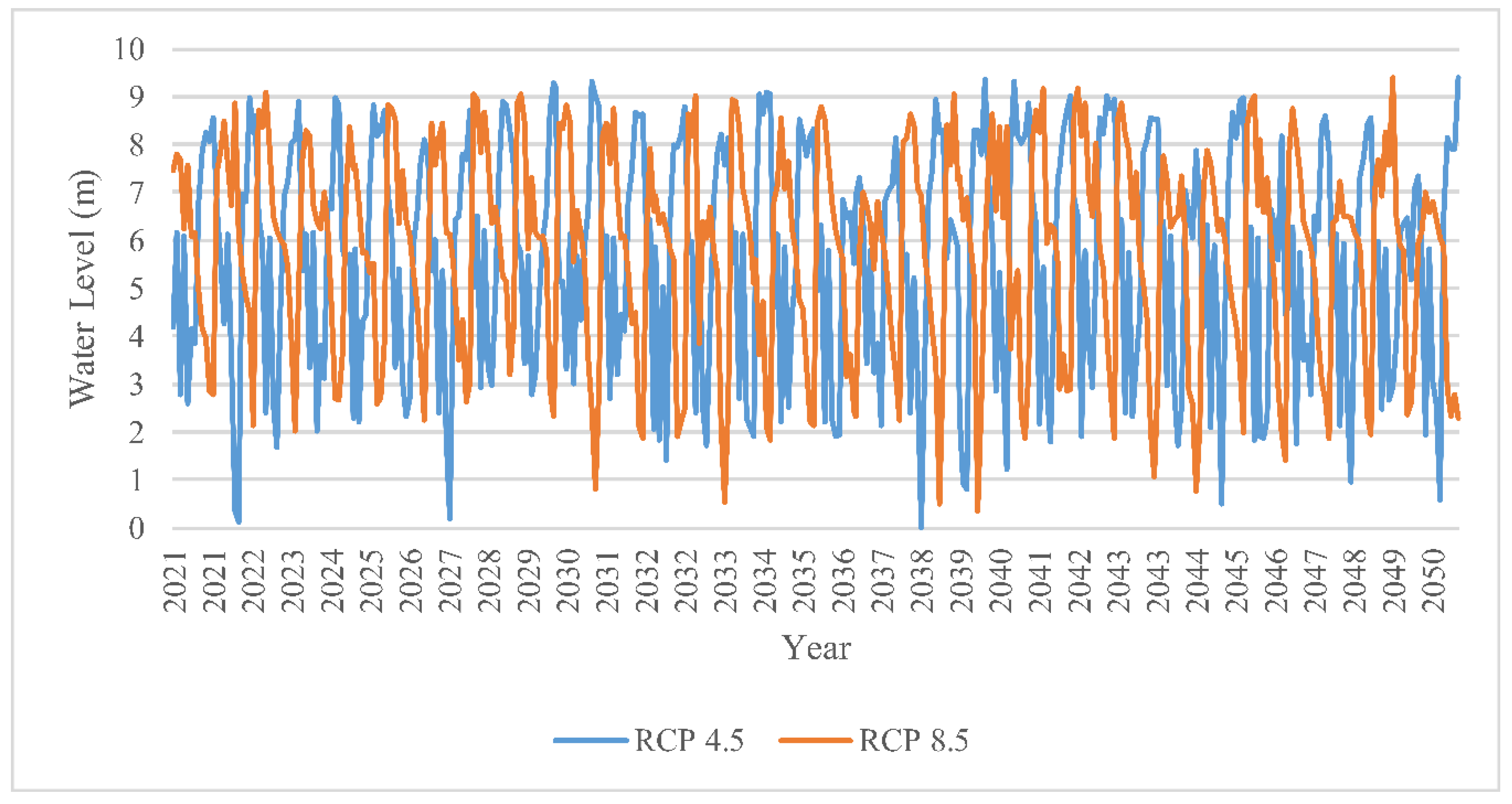
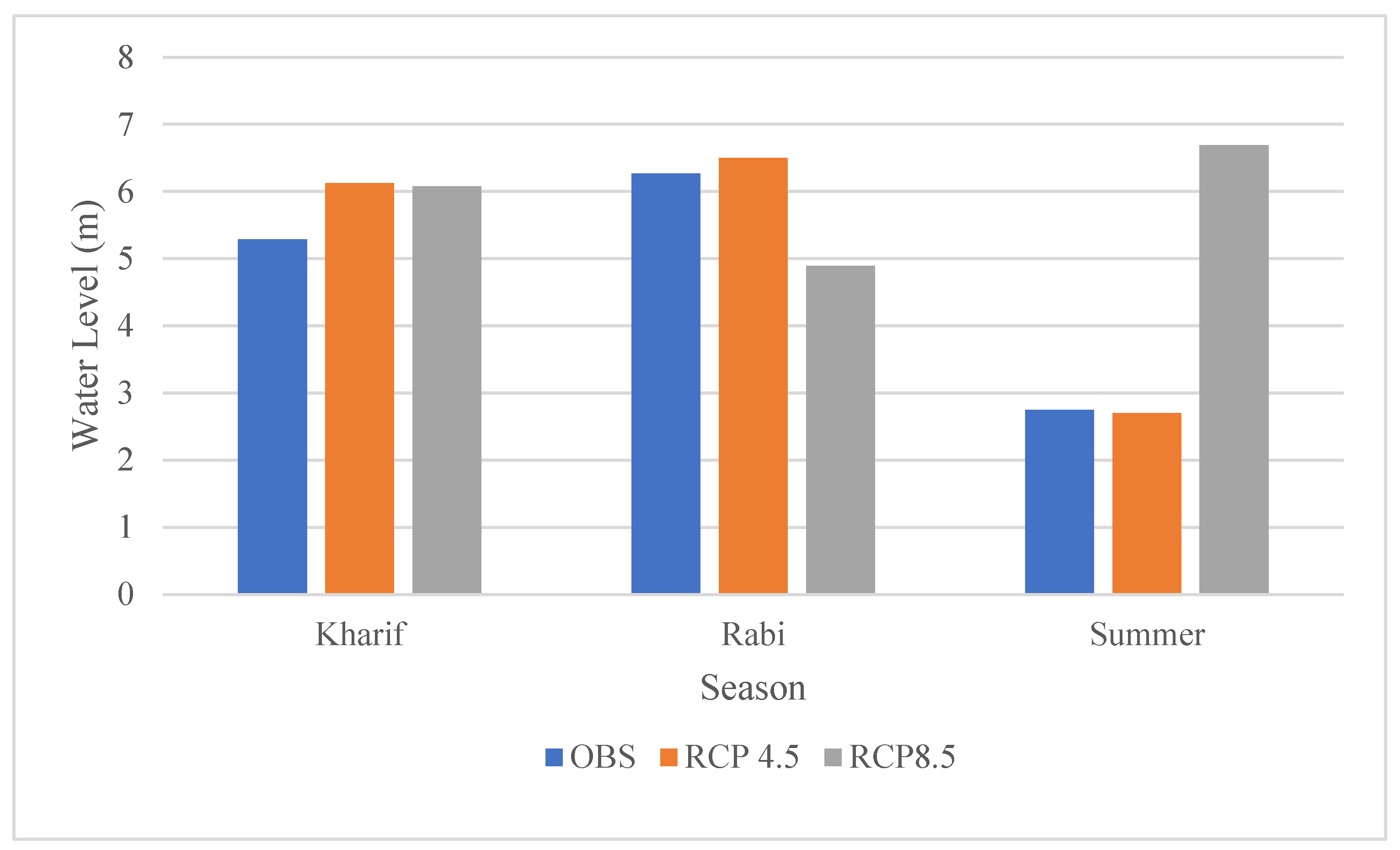
3.4. Effect of Climate Change on Water Availability
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kwarteng, E.A.; Gyamfi, C.; Anyemedu, F.O.K.; Adjei, K.A.; Anornu, G.K. Coupling SWAT and Bathymetric Data in Modelling Reservoir Catchment Hydrology. Spat. Inf. Res. 2021, 29, 55–69. [Google Scholar] [CrossRef]
- Chen, Y.D.; Chen, X.; Xu, C.-Y.; Shao, Q. Downscaling of Daily Precipitation with a Stochastic Weather Generator for the Subtropical Region in South China. Hydrol. Earth Syst. Sci. Discuss. 2006, 3, 1145–1183. [Google Scholar] [CrossRef]
- Qin, X.S.; Huang, G.H.; Chakma, A.; Nie, X.H.; Lin, Q.G. A MCDM-Based Expert System for Climate-Change Impact Assessment and Adaptation Planning—A Case Study for the Georgia Basin, Canada. Expert Syst. Appl. 2008, 34, 2164–2179. [Google Scholar] [CrossRef]
- Das, J.; Umamahesh, N.V. Assessment of Uncertainty in Estimating Future Flood Return Levels under Climate Change. Nat. Hazards 2018, 93, 109–124. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; Van Deursen, W. Estimates of Future Discharges of the River Rhine Using Two Scenario Methodologies: Direct versus Delta Approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Mohammed, R.; Scholz, M. Adaptation Strategy to Mitigate the Impact of Climate Change on Water Resources in Arid and Semi-Arid Regions: A Case Study. Water Resour. Manag. 2017, 31, 3557–3573. [Google Scholar] [CrossRef] [Green Version]
- Sowjanya, P.N.; Reddy, V.K.; Shashi, M. Intra- and Interannual Streamflow Variations of Wardha Watershed under Changing Climate. ISH J. Hydraul. Eng. 2018, 26, 197–208. [Google Scholar] [CrossRef]
- Ramabrahmam, K.; Keesara, V.R.; Srinivasan, R.; Pratap, D.; Sridhar, V. Flow Simulation and Storage Assessment in an Ungauged Irrigation Tank Cascade System Using the SWAT Model. Sustainability 2021, 13, 13158. [Google Scholar] [CrossRef]
- Buri, E.S.; Keesara, V.R.; Loukika, K.N. Spatio-Temporal Analysis of Climatic Variables in the Munneru River Basin, India, Using NEX-GDDP Data and the REA Approach. Sustainability 2022, 14, 1715. [Google Scholar] [CrossRef]
- Güntner, A.; Krol, M.S.; De Araújo, J.C.; Bronstert, A. Simple Water Balance Modelling of Surface Reservoir Systems in a Large Data-Scarce Semiarid Region/Modélisation Simple Du Bilan Hydrologique de Systèmes de Réservoirs de Surface Dans Une Grande Région Semi-Aride Pauvre En Données. Hydrol. Sci. J. 2004, 49, 37–41. [Google Scholar] [CrossRef]
- Huang, J.; Ji, M.; Xie, Y.; Wang, S.; He, Y.; Ran, J. Global Semi-Arid Climate Change over Last 60 Years. Clim. Dyn. 2016, 46, 1131–1150. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Li, X.; Huang, C.; Nan, Z. A Decision Support System for Irrigation Water Allocation along the Middle Reaches of the Heihe River Basin, Northwest China. Environ. Model. Softw. 2013, 47, 182–192. [Google Scholar] [CrossRef]
- Jayanthi, S.L.S.V.; Keesara, V.R. Climate Change Impact on Water Resources of Medium Irrigation Tank. ISH J. Hydraul. Eng. 2019, 27, 322–333. [Google Scholar] [CrossRef]
- Dong, H.; Song, Y.; Zhang, M. Hydrological Trend of Qinghai Lake over the Last 60 Years: Driven by Climate Variations or Human Activities? J. Water Clim. Chang. 2018, 10, 524–534. [Google Scholar] [CrossRef]
- Wang, Z.; Ficklin, D.L.; Zhang, Y.; Zhang, M. Impact of Climate Change on Streamflow in the Arid Shiyang River Basin of Northwest China. Hydrol. Processes 2012, 26, 2733–2744. [Google Scholar] [CrossRef]
- Palanisami, K.; Meinzen-Dick, R.; Giordano, M. Climate Change and Water Supplies: Options for Sustaining Tank Irrigation Potential in India. Econ. Political Wkly. 2010, 45, 183–190. [Google Scholar]
- Sanchez-Cohen, I.; Díaz-Padilla, G.; Velasquez-Valle, M.; Slack, D.C.; Heilman, P.; Pedroza-Sandoval, A. A Decision Support System for Rainfed Agricultural Areas of Mexico. Comput. Electron. Agric. 2015, 114, 178–188. [Google Scholar] [CrossRef]
- Lin, P.; Yang, Z.L.; Cai, X.; David, C.H. Development and Evaluation of a Physically-Based Lake Level Model for Water Resource Management: A Case Study for Lake Buchanan, Texas. J. Hydrol. Reg. Stud. 2015, 4, 661–674. [Google Scholar] [CrossRef] [Green Version]
- Davraz, A.; Sener, E.; Sener, S. Evaluation of Climate and Human Effects on the Hydrology and Water Quality of Burdur Lake, Turkey. J. Afr. Earth Sci. 2019, 158, 103569. [Google Scholar] [CrossRef]
- Rani, S.; Sreekesh, S. Evaluating the Responses of Streamflow under Future Climate Change Scenarios in a Western Indian Himalaya Watershed. Environ. Processes 2019, 6, 155–174. [Google Scholar] [CrossRef]
- Chien, H.; Yeh, P.J.F.; Knouft, J.H. Modeling the Potential Impacts of Climate Change on Streamflow in Agricultural Watersheds of the Midwestern United States. J. Hydrol. 2013, 491, 73–88. [Google Scholar] [CrossRef]
- Rocha, J.; Carvalho-Santos, C.; Diogo, P.; Beça, P.; Keizer, J.J.; Nunes, J.P. Impacts of Climate Change on Reservoir Water Availability, Quality and Irrigation Needs in a Water Scarce Mediterranean Region (Southern Portugal). Sci. Total Environ. 2020, 736, 139477. [Google Scholar] [CrossRef]
- Gosain, A.K.; Rao, S.; Arora, A. Climate Change Impact Assessment of Water Resources of India. Curr. Sci. 2011, 101, 356–371. [Google Scholar]
- Musie, M.; Sen, S.; Srivastava, P. Application of CORDEX-AFRICA and NEX-GDDP Datasets for Hydrologic Projections under Climate Change in Lake Ziway Sub-Basin, Ethiopia. J. Hydrol. Reg. Stud. 2020, 31, 100721. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Faramarzi, M.; Ghasemi, S.S.; Yang, H. Assessing the Impact of Climate Change on Water Resources in Iran. Water Resour. Res. 2009, 45, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Pandey, B.K.; Gosain, A.K.; Paul, G.; Khare, D. Climate Change Impact Assessment on Hydrology of a Small Watershed Using Semi-Distributed Model. Appl. Water Sci. 2017, 7, 2029–2041. [Google Scholar] [CrossRef] [Green Version]
- Narsimlu, B.; Gosain, A.K.; Chahar, B.R. Assessment of Future Climate Change Impacts on Water Resources of Upper Sind River Basin, India Using SWAT Model. Water Resour. Manag. 2013, 27, 3647–3662. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef] [Green Version]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R. Soil and Water Assessment Tool User’s Manual; TWRI Report TR-192; Texas Water Resources Institute, USDA Agricultural Research Service: College Station, TX, USA, 2002; Volume 202, p. 412. [Google Scholar]
- Gosain, A.K.; Rao, S.; Basuray, D. Special section: Climate change and india climate change impact assessment on hydrology of indian river basins. Curr. Sci. 2006, 90, 346–353. [Google Scholar]
- Yin, Z.; Feng, Q.; Zou, S.; Yang, L. Assessing Variation in Water Balance Components in Mountainous Inland River Basin Experiencing Climate Change. Water 2016, 8, 472. [Google Scholar] [CrossRef] [Green Version]
- Uniyal, B.; Jha, M.K.; Verma, A.K. Assessing Climate Change Impact on Water Balance Components of a River Basin Using SWAT Model. Water Resour. Manag. 2015, 29, 4767–4785. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Luo, Y.; Luedeling, E.; Zhang, M. Climate Change Sensitivity Assessment of a Highly Agricultural Watershed Using SWAT. J. Hydrol. 2009, 374, 16–29. [Google Scholar] [CrossRef]
- Khalilian, S.; Shahvari, N. A SWAT Evaluation of the Effects of Climate Change on Renewable Water Resources in Salt Lake Sub-Basin, Iran. AgriEngineering 2018, 1, 44–57. [Google Scholar] [CrossRef]
- Devia, G.K.; Ganasri, B.P.; Dwarakish, G.S. A Review on Hydrological Models. Aquat. Procedia 2015, 4, 1001–1007. [Google Scholar] [CrossRef]
- Mehan, S.; Neupane, R.P.; Kumar, S. Coupling of SUFI 2 and SWAT for Improving the Simulation of Streamflow in an Agricultural Watershed of South Dakota. Hydrol. Curr. Res. 2017, 8, 1–11. [Google Scholar] [CrossRef]
- Saade, J.; Atieh, M.; Ghanimeh, S.; Golmohammadi, G. Modeling Impact of Climate Change on Surface Water Availability Using Swat Model in a Semi-Arid Basin: Case of El Kalb River, Lebanon. Hydrology 2021, 8, 134. [Google Scholar] [CrossRef]
- Bucak, T.; Trolle, D.; Andersen, H.E.; Thodsen, H.; Erdoğan, Ş.; Levi, E.E.; Filiz, N.; Jeppesen, E.; Beklioğlu, M.; Bucak, T. Future Water Availability in the Largest Freshwater Mediterranean Lake Is at Great Risk as Evidenced from Simulations with the SWAT Model. Sci. Total Environ. 2017, 581–582, 413–425. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J.; Karimi, S.; Shamshirband, S.; Motamedi, S.; Petković, D.; Hashim, R. A Survey of Water Level Fluctuation Predicting in Urmia Lake Using Support Vector Machine with Firefly Algorithm. Appl. Math. Comput. 2015, 270, 731–743. [Google Scholar] [CrossRef]
- Buyukyildiz, M.; Tezel, G.; Yilmaz, V. Estimation of the Change in Lake Water Level by Artificial Intelligence Methods. Water Resour. Manag. 2014, 28, 4747–4763. [Google Scholar] [CrossRef]
- Mohammadi, B.; Guan, Y.; Aghelpour, P.; Emamgholizadeh, S.; Zolá, R.P.; Zhang, D. Simulation of Titicaca Lake Water Level Fluctuations Using Hybrid Machine Learning Technique Integrated with Grey Wolf Optimizer Algorithm. Water 2020, 12, 3015. [Google Scholar] [CrossRef]
- Khan, M.S.; Coulibaly, P. Application of Support Vector Machine in Lake Water Level Prediction. J. Hydrol. Eng. 2006, 11, 199–205. [Google Scholar] [CrossRef]
- Çimen, M.; Kisi, O. Comparison of Two Different Data-Driven Techniques in Modeling Lake Level Fluctuations in Turkey. J. Hydrol. 2009, 378, 253–262. [Google Scholar] [CrossRef]
- Hipni, A.; El-shafie, A.; Najah, A.; Karim, O.A.; Hussain, A.; Mukhlisin, M. Daily Forecasting of Dam Water Levels: Comparing a Support Vector Machine (SVM) Model With Adaptive Neuro Fuzzy Inference System (ANFIS). Water Resour. Manag. 2013, 27, 3803–3823. [Google Scholar] [CrossRef]
- TWRIS Dashboard. Available online: https://bhuvan-app1.nrsc.gov.in/twris/geoportal/twris.php?type=Medium&status=Completed&project=Pakhal%20Lake# (accessed on 21 April 2022).
- Gitau, M.W.; Chaubey, I. Regionalization of SWAT Model Parameters for Use in Ungauged Watersheds. Water 2010, 6, 849–871. [Google Scholar] [CrossRef]
- Yang, X.; Magnusson, J.; Rizzi, J.; Xu, C.Y. Runoff Prediction in Ungauged Catchments in Norway: Comparison of Regionalization Approaches. Hydrol. Res. 2018, 49, 487–505. [Google Scholar] [CrossRef]
- Emam, A.R.; Kappas, M.; Hoang, L.; Nguyen, K.; Renchin, T. Hydrological Modeling in an Ungauged Basin of Central Vietnam Using SWAT Model. Hydrol. Earth Syst. Sci. 2016, 44. [Google Scholar] [CrossRef] [Green Version]
- Thrasher, B.; Maurer, E.P.; McKellar, C.; Duffy, P.B. Technical Note: Bias Correcting Climate Model Simulated Daily Temperature Extremes with Quantile Mapping. Hydrol. Earth Syst. Sci. 2012, 16, 3309–3314. [Google Scholar] [CrossRef] [Green Version]
- Sajjad, H.; Ghaffar, A. Observed, Simulated and Projected Extreme Climate Indices over Pakistan in Changing Climate. Theor. Appl. Climatol. 2019, 137, 255–281. [Google Scholar] [CrossRef]
- Nauman, S.; Zulkafli, Z.; Bin Ghazali, A.H.; Yusuf, B. Impact Assessment of Future Climate Change on Streamflows Upstream of Khanpur Dam, Pakistan Using Soil and Water Assessment Tool. Water 2019, 11, 1090. [Google Scholar] [CrossRef] [Green Version]
- Raghavan, S.V.; Hur, J.; Liong, S.Y. Evaluations of NASA NEX-GDDP Data over Southeast Asia: Present and Future Climates. Clim. Chang. 2018, 148, 503–518. [Google Scholar] [CrossRef]
- Bao, Y.; Wen, X. Projection of China’s near- and Long-Term Climate in a New High-Resolution Daily Downscaled Dataset NEX-GDDP. J. Meteorol. Res. 2017, 31, 236–249. [Google Scholar] [CrossRef]
- Pai, D.S.; Sridhar, L.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadhyay, B. Development of a New High Spatial Resolution (0.25° × 0.25°) Long Period (1901–2010) Daily Gridded Rainfall Data Set over India and Its Comparison with Existing Data Sets over the Region. Mausam 2014, 65, 1–18. [Google Scholar] [CrossRef]
- Srivastava, A.K.; Rajeevan, M.; Kshirsagar, S.R. Development of a High Resolution Daily Gridded Temperature Data Set (1969–2005) for the Indian Region. Atmos. Sci. Lett. 2009, 10, 249–254. [Google Scholar] [CrossRef]
- Chen, H.P.; Sun, J.Q.; Li, H.X. Future Changes in Precipitation Extremes over China Using the NEX-GDDP High-Resolution Daily Downscaled Data-Set. Atmos. Ocean. Sci. Lett. 2017, 10, 403–410. [Google Scholar] [CrossRef] [Green Version]
- Xu, R.; Chen, Y.; Chen, Z. Future Changes of Precipitation over the Han River Basin Using NEX-GDDP Dataset and the SVR_QM Method. Atmosphere 2019, 10, 688. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Mearns, L.O. Calculation of Average, Uncertainty Range, and Reliability of Regional Climate Changes from AOGCM Simulations via the “Reliability Ensemble Averaging” (REA) Method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Mujumdar, P.P.; Ghosh, S. Modeling GCM and Scenario Uncertainty Using a Possibilistic Approach: Application to the Mahanadi River, India. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Xu, Y.; Gao, X.; Giorgi, F. Upgrades to the Reliability Ensemble Averaging Method for Producing Probabilistic Climate-Change Projections. Clim. Res. 2010, 41, 61–81. [Google Scholar] [CrossRef] [Green Version]
- Chandra, R.; Saha, U.; Mujumdar, P.P. Model and Parameter Uncertainty in IDF Relationships under Climate Change. Adv. Water Resour. 2015, 79, 127–139. [Google Scholar] [CrossRef]
- Das, J.; Treesa, A.; Umamahesh, N.V. Modelling Impacts of Climate Change on a River Basin: Analysis of Uncertainty Using REA & Possibilistic Approach. Water Resour. Manag. 2018, 32, 4833–4852. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias Correction of Regional Climate Model Simulations for Hydrological Climate-Change Impact Studies: Review and Evaluation of Different Methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Fang, G.H.; Yang, J.; Chen, Y.N.; Zammit, C. Comparing Bias Correction Methods in Downscaling Meteorological Variables for a Hydrologic Impact Study in an Arid Area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef] [Green Version]
- Ringard, J.; Seyler, F.; Linguet, L. A Quantile Mapping Bias Correction Method Based on Hydroclimatic Classification of the Guiana Shield. Sensors 2017, 17, 1413. [Google Scholar] [CrossRef] [Green Version]
- Bong, T.; Son, Y.-H.; Yoo, S.-H.; Hwang, S.-W. Nonparametric Quantile Mapping Using the Response Surface Method–Bias Correction of Daily Precipitation. J. Water Clim. Chang. 2017, 9, 525–539. [Google Scholar] [CrossRef]
- Yang, T.; Asanjan, A.A.; Welles, E.; Gao, X.; Sorooshian, S.; Liu, X. Developing Reservoir Monthly Inflow Forecasts Using Artificial Intelligence and Climate Phenomenon Information. Water Resour. Res. 2017, 53, 2786–2812. [Google Scholar] [CrossRef]


| Model | Country and Institution |
|---|---|
| ACCESS | Commonwealth Scientific and Industrial Research Organization and Bureau of Meteorology, Australia |
| BCC-CSM1 | Beijing Climate Center, China Institute of global change and Earth System Sciences, Beijing Normal University, China |
| BNU-ESM | Institute of global change and Earth System Sciences, Beijing Normal University, China |
| CCSM4 | National Center for Atmospheric Research, America |
| MIROC5 | Atmosphere and Ocean Research Institute, Japan Atmosphere |
| MIROCESM | Atmosphere and Ocean Research Institute, Japan Atmosphere |
| MIROCHEM | Atmosphere and Ocean Research Institute, Japan Atmosphere |
| CanEsm | Canadian Centre for Climate Modelling and Analysis, Canada |
| CESM1-BGC | National Center for Atmospheric Research, America Centre National de Recherches Meteorologiques, Centre. |
| CNRM-CM5 | Centre Europeen de Recherche et Formation Avancees en Calcul Scientifique, France Commonwealth Scientific and Industrial Research |
| CSIRO-MK3 | Organization/Queensland Climate Change Centre of Excellence, Australia |
| GFDL-CM3 | Geophysical Fluid Dynamics Laboratory, America |
| GFDL-ESM2G | Geophysical Fluid Dynamics Laboratory, America |
| GFDL-ESM2M | Geophysical Fluid Dynamics Laboratory, America |
| INMCM4 | Institute of Numerical Calculation, Russia |
| IPSL-CM5A-LR | Institut Pierre-Simon Laplace, France |
| IPSL-CM5A-MR | Institut Pierre-Simon Laplace, France |
| MPI-ESM-LR | Max Planck Institute for Meteorology, Germany |
| MPI-ESM-MR | Max Planck Institute for Meteorology, Germany |
| MPRI-CGCM3 | Max Planck Institute for Meteorology, Germany |
| NORESM1-M | Norway Consumer Council, Norway |
| Precipitation | Maximum Temperature | Minimum Temperature | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | Historic | RCP 4.5 | RCP 8.5 | Historic | RCP 4.5 | RCP 8.5 | Historic | RCP 4.5 | RCP 8.5 |
| ACCESS1-0 | 0.0848 | 0.0379 | 0.0091 | 0.0531 | 0.0470 | 0.0454 | 0.0356 | 0.0480 | 0.0480 |
| BCC-CSM1-1 | 0.0229 | 0.0527 | 0.0575 | 0.0437 | 0.0482 | 0.0475 | 0.0438 | 0.0469 | 0.0469 |
| BNU-ESM | 0.0272 | 0.0560 | 0.0612 | 0.0492 | 0.0481 | 0.0483 | 0.0398 | 0.0484 | 0.0484 |
| CanESM2 | 0.0166 | 0.0640 | 0.0424 | 0.0392 | 0.0479 | 0.0472 | 0.0332 | 0.0472 | 0.0472 |
| CCSM4 | 0.0309 | 0.0355 | 0.0480 | 0.0542 | 0.0472 | 0.0475 | 0.0576 | 0.0483 | 0.0483 |
| CESM1-BGC | 0.1612 | 0.0543 | 0.0255 | 0.0409 | 0.0466 | 0.0454 | 0.0427 | 0.0449 | 0.0449 |
| CNRM-CM5 | 0.0403 | 0.0390 | 0.0427 | 0.0508 | 0.0480 | 0.0486 | 0.0439 | 0.0483 | 0.0482 |
| CSIRO-Mk3-6-0 | 0.0322 | 0.0360 | 0.0353 | 0.0541 | 0.0484 | 0.0487 | 0.0799 | 0.0486 | 0.0485 |
| GFDL-CM3 | 0.0311 | 0.0424 | 0.0420 | 0.0445 | 0.0473 | 0.0483 | 0.0592 | 0.0468 | 0.0468 |
| GFDL-ESM2G | 0.0362 | 0.0439 | 0.0555 | 0.0525 | 0.0494 | 0.0486 | 0.0420 | 0.0498 | 0.0498 |
| GFDL-ESM2M | 0.1678 | 0.0361 | 0.0450 | 0.0413 | 0.0477 | 0.0483 | 0.0408 | 0.0479 | 0.0479 |
| INMCM4 | 0.0613 | 0.0467 | 0.0330 | 0.0518 | 0.0485 | 0.0479 | 0.0703 | 0.0490 | 0.0491 |
| IPSL-CM5A-LR | 0.0281 | 0.0535 | 0.0613 | 0.0426 | 0.0478 | 0.0476 | 0.0498 | 0.0493 | 0.0493 |
| IPSL-CM5A-MR | 0.0400 | 0.0392 | 0.0493 | 0.0462 | 0.0474 | 0.0484 | 0.0365 | 0.0482 | 0.0481 |
| MIROC5 | 0.0285 | 0.0441 | 0.0657 | 0.0473 | 0.0478 | 0.0485 | 0.0719 | 0.0475 | 0.0475 |
| MIROCESM | 0.0222 | 0.0740 | 0.0786 | 0.0452 | 0.0473 | 0.0474 | 0.0363 | 0.0470 | 0.0471 |
| MIROCHEM | 0.0285 | 0.0572 | 0.0720 | 0.0459 | 0.0473 | 0.0473 | 0.0297 | 0.0467 | 0.0467 |
| MPI-ESM-LR | 0.0328 | 0.0454 | 0.0312 | 0.0502 | 0.0469 | 0.0473 | 0.0415 | 0.0464 | 0.0464 |
| MPI-ESM-MR | 0.0220 | 0.0499 | 0.0412 | 0.0535 | 0.0472 | 0.0464 | 0.0348 | 0.0462 | 0.0462 |
| MRI-CGCM3 | 0.0637 | 0.0411 | 0.0456 | 0.0478 | 0.0471 | 0.0477 | 0.0612 | 0.0469 | 0.0469 |
| NorESM1-M | 0.0219 | 0.0511 | 0.0578 | 0.0460 | 0.0468 | 0.0477 | 0.0497 | 0.0478 | 0.0478 |
| Period | P (mm) | ΔP (%) | SF | ΔSF (%) | Tmax (°C) | ΔTmax | Tmin (°C) | ΔTmin | ET (mm) | ΔET (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| IMD | 1143.04 | 56.76 | 33.42 | 22.07 | 595.66 | |||||
| 1988–2018 | ||||||||||
| Historic | 1120.81 | −1.95 | 63.63 | 12.10 | 33.35 | −0.07 | 22.10 | 0.03 | 510.55 | −14.29 |
| 1988–2018 | ||||||||||
| Future RCP4.5 | 1020.25 | −10.74 | 54.99 | −3.12 | 34.63 | 1.21 | 23.29 | 1.22 | 511.62 | −14.11 |
| 2021–2050 | ||||||||||
| Future RCP8.5 | 1178.94 | 3.14 | 68.53 | 20.73 | 34.84 | 1.42 | 23.55 | 1.48 | 517.63 | −13.10 |
| 2021–2051 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jayanthi, S.L.S.V.; Keesara, V.R.; Sridhar, V. Prediction of Future Lake Water Availability Using SWAT and Support Vector Regression (SVR). Sustainability 2022, 14, 6974. https://doi.org/10.3390/su14126974
Jayanthi SLSV, Keesara VR, Sridhar V. Prediction of Future Lake Water Availability Using SWAT and Support Vector Regression (SVR). Sustainability. 2022; 14(12):6974. https://doi.org/10.3390/su14126974
Chicago/Turabian StyleJayanthi, Sri Lakshmi Sesha Vani, Venkata Reddy Keesara, and Venkataramana Sridhar. 2022. "Prediction of Future Lake Water Availability Using SWAT and Support Vector Regression (SVR)" Sustainability 14, no. 12: 6974. https://doi.org/10.3390/su14126974
APA StyleJayanthi, S. L. S. V., Keesara, V. R., & Sridhar, V. (2022). Prediction of Future Lake Water Availability Using SWAT and Support Vector Regression (SVR). Sustainability, 14(12), 6974. https://doi.org/10.3390/su14126974







