A Group Contribution Method for Predicting the Alkyl Ester and Biodiesel Densities at Various Temperatures
Abstract
:1. Introduction
2. Methods
2.1. Experimental Database
2.2. Predictive Model for the Alkyl Ester Density
2.3. Predictive Model for the Biodiesel Density
2.4. Statistical Analysis
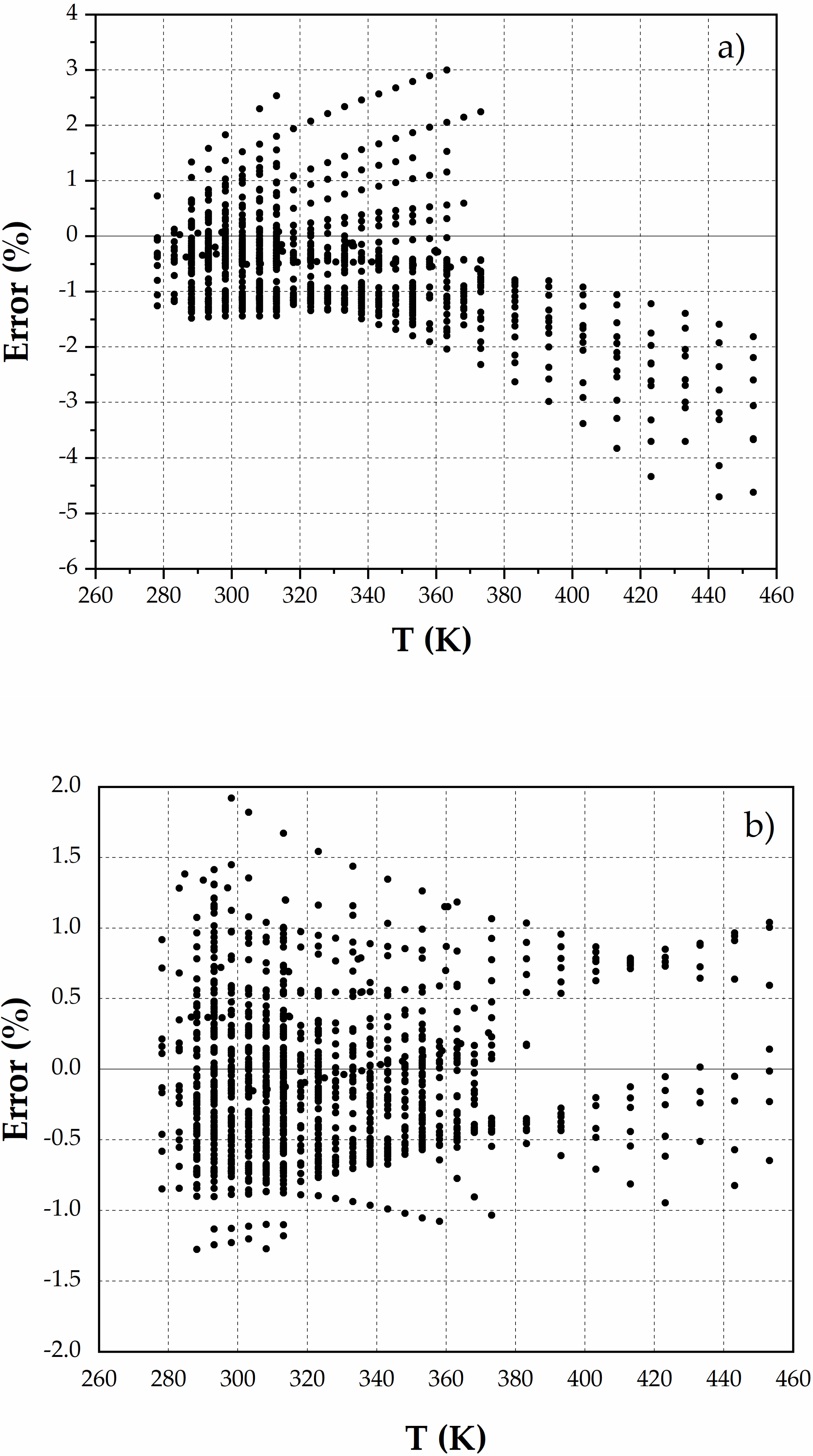
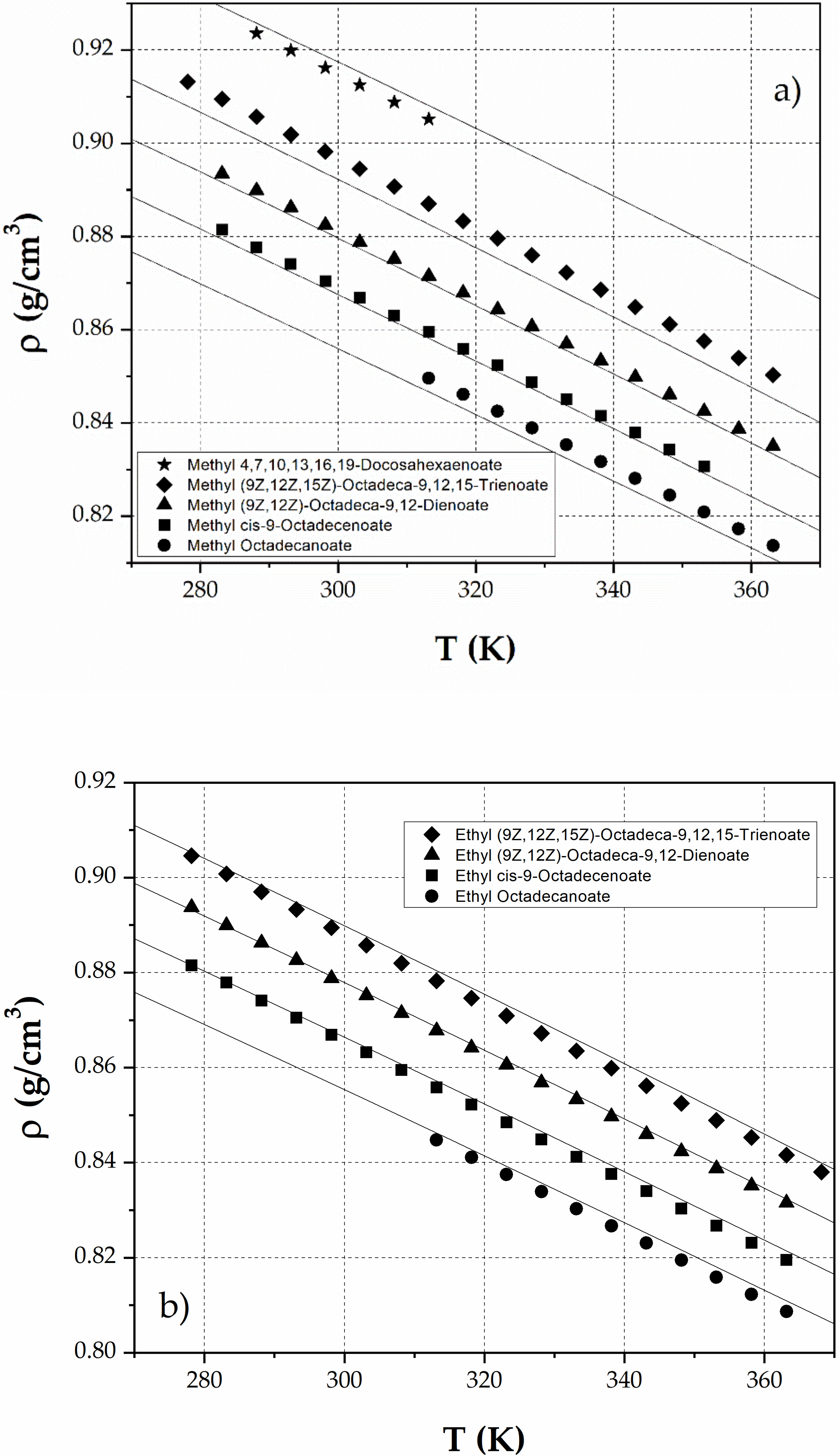
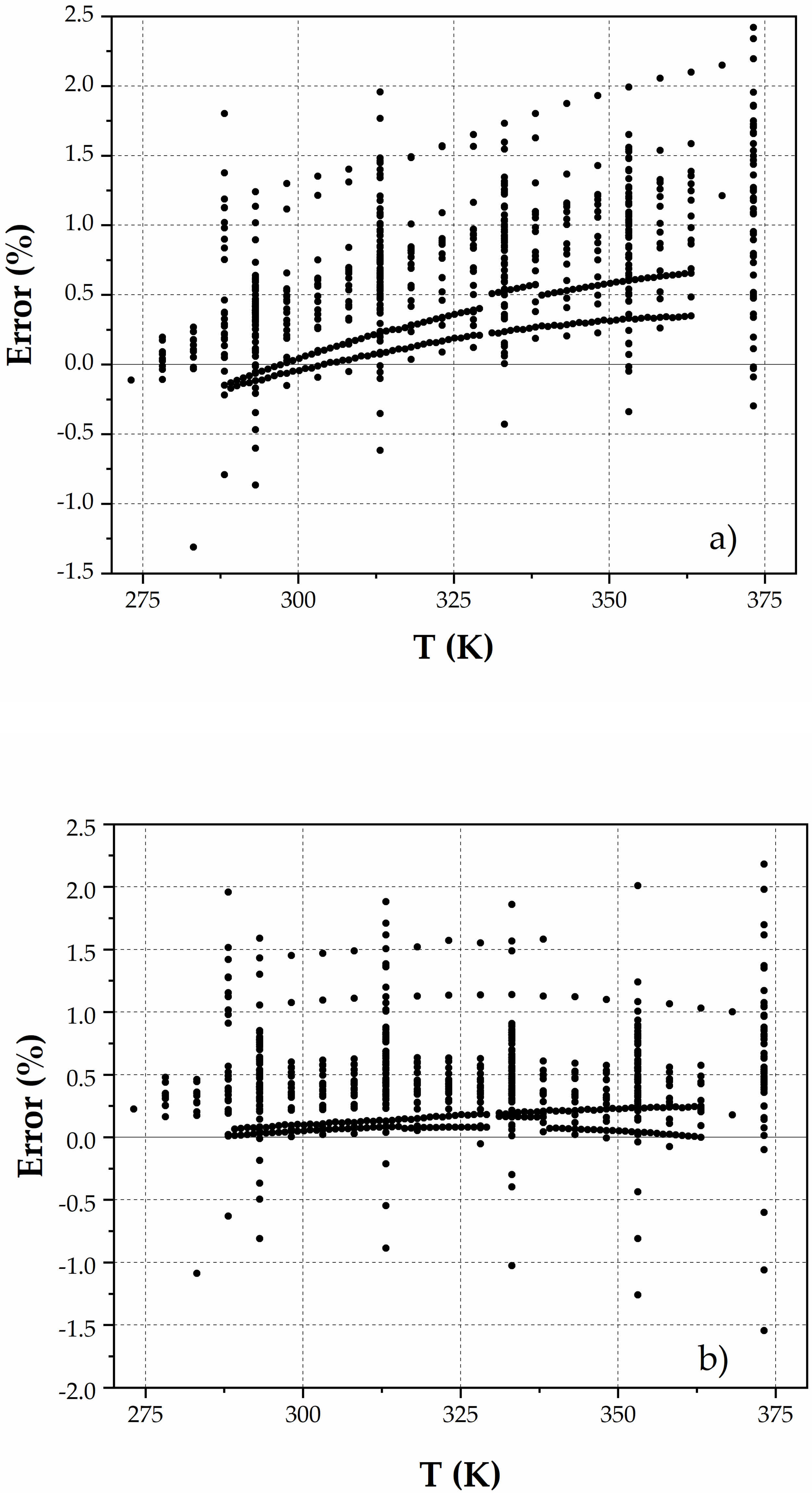
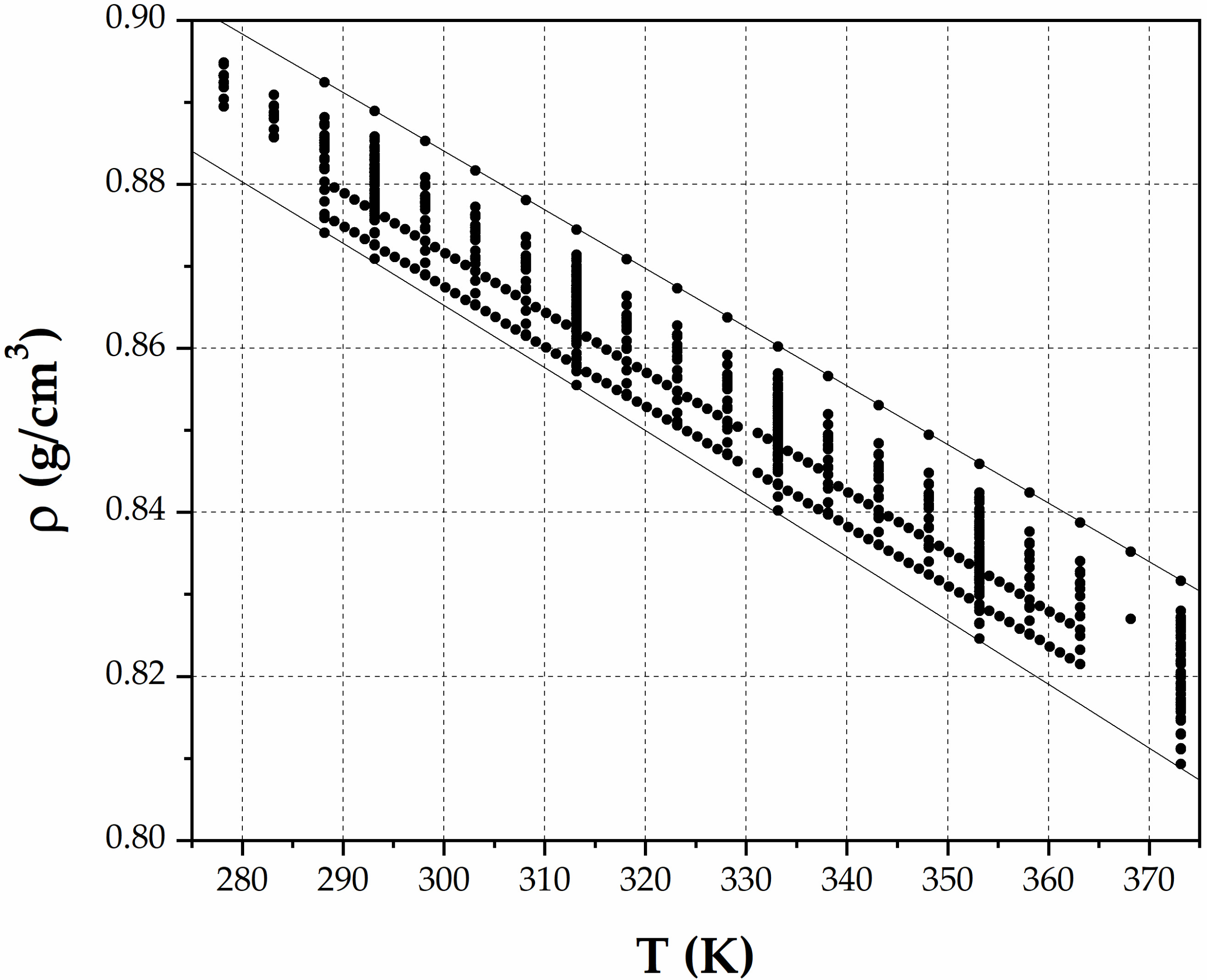
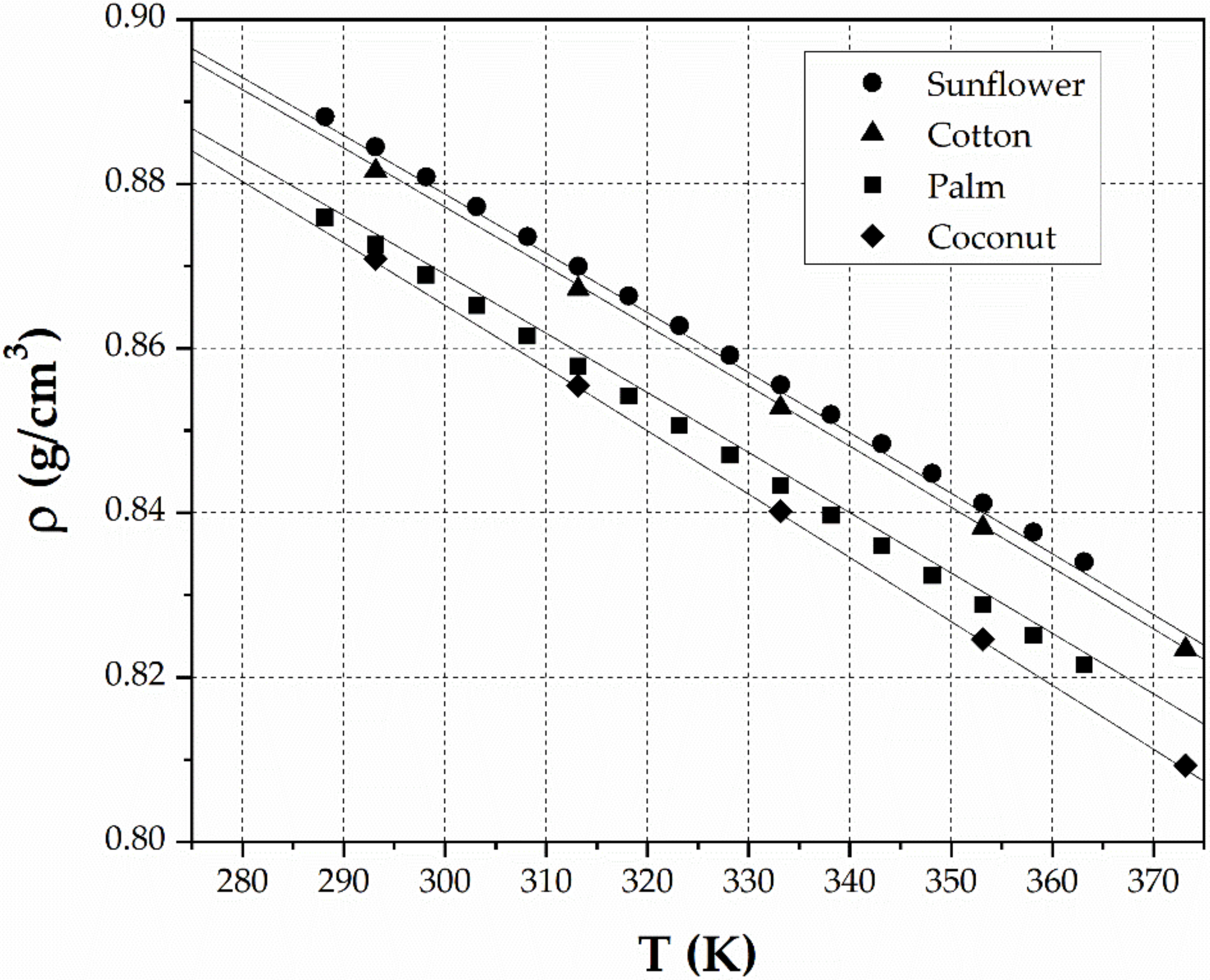
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Compound | Chemical Structure | -CH3 | -CH2 | =CH- | -COO- |
|---|---|---|---|---|---|
| Methyl octadecanoate |  | 2 | 16 | 0 | 1 |
| Methyl cis-9-octadecanoate |  | 2 | 14 | 2 | 1 |
| Methyl (9Z,12Z)-octadeca-9,12-dienoate |  | 2 | 12 | 4 | 1 |
| Methyl (9Z,12Z,15Z)-octadeca-9,12,15-trienoate |  | 2 | 10 | 6 | 1 |
Appendix B
- (a)
- MWmethyl hexadecanoate = [17(12.0107) + 34(1.00794) + 2(15.9994)] g/mol = 270.4507 g/mol.
- (b)
- MWmethyl octadecanoate = [19(12.0107) + 38(1.00794) + 2(15.9994)] g/mol = 298.5038 g/mol.
- (c)
- MWmethyl cis-9-octadecenoate = [19(12.0107) + 36(1.00794) + 2(15.9994)] g/mol = 296.4879 g/mol.
- (d)
- MWmethyl (9Z,12Z)-octadeca-9,12-dienoate = [19(12.0107) + 34(1.00794) + 2(15.9994)] g/mol = 294.4721 g/mol.
- (a)
- n-CH3 = 2, n-CH2 = 14, n=CH- = 0, n-COO- = 1 (methyl hexadecanoate).
- (b)
- n-CH3 = 2, n-CH2 = 16, n=CH- = 0, n-COO- = 1 (methyl octadecanoate).
- (c)
- nCH3 = 2, n-CH2 = 14, n=CH- = 2, n-COO- = 1 (methyl cis-9-octadecenoate).
- (d)
- nCH3 = 2, n-CH2 = 12, n=CH- = 4, n-COO- = 1 (methyl (9Z,12Z)-octadeca-9,12-dienoate).
- (a)
- Vmethyl hexadecanoate = {2[15.74 + 1.62 × 10−3(303.15) + 10.01 × 10−5(303.15)2] + 14[14.42 + 5.1 × 10−3(303.15) + 0.76 × 10−5(303.15)2] + 0[11.98 + 1.19 × 10−3(303.15) + 0.89 × 10−5(303.15)2] + 1[30.77 + 1.31 × 10−3(303.15) + 1.08 × 10−5(303.15)2]} cm3/mol = 316.3233 cm3/mol.
- (b)
- Vmethyl octadecenoate = {2[15.74 + 1.62 × 10−3(303.15) + 10.01 × 10−5(303.15)2] + 16[14.42 + 5.1 × 10−3(303.15) + 0.76 × 10−5(303.15)2] + 0[11.98 + 1.19 × 10−3(303.15) + 0.89 × 10−5(303.15)2] + 1[30.77 + 1.31 × 10−3(303.15) + 1.08 × 10−5(303.15)2]} cm3/mol = 349.6523 cm3/mol.
- (c)
- Vmethyl cis-9-octadecenoate = {2[15.74 + 1.62 × 10−3(303.15) + 10.01 × 10−5(303.15)2] + 14[14.42 + 5.1 × 10−3(303.15) + 0.76 × 10−5(303.15)2] + 2[11.98 + 1.19 × 10−3(303.15) + 0.89 × 10−5(303.15)2] + 1[30.77 + 1.31 × 10−3(303.15) + 1.08 × 10−5(303.15)2]} cm3/mol = 342.6406 cm3/mol.
- (d)
- Vmethyl (9Z,12Z)-octadeca-9,12-dienoate = {2[15.74 + 1.62 × 10−3(303.15) + 10.01 × 10−5(303.15)2] + 12[14.42 + 5.1 × 10−3(303.15) + 0.76 × 10−5(303.15)2] + 4[11.98 + 1.19 × 10−3(303.15) + 0.89 × 10−5(303.15)2] + 1[30.77 + 1.31 × 10−3(303.15) + 1.08 × 10−5(303.15)2]} cm3/mol = 335.6289 cm3/mol.
- (a)
- ρmethyl hexadecanoate = [270.4507 ÷ 316.3233] g/cm3 = 0.85498 g/cm3.
- (b)
- ρmethyl octadecenoate = [298.5038 ÷ 349.6523] g/cm3 = 0.85372 g/cm3.
- (c)
- ρ methyl cis-9-octadecenoate = [296.4879 ÷ 342.6406] g/cm3 = 0.8653 g/cm3.
- (d)
- ρmethyl (9Z,12Z)-octadeca-9,12-dienoate = [294.4721 ÷ 335.6289] g/cm3 = 0.87737 g/cm3.
References
- Demirbas, A. Importance of biodiesel as transportation fuel. Energy Policy 2007, 35, 4661–4670. [Google Scholar] [CrossRef]
- Issariyakul, T.; Dalai, A.K. Biodiesel from vegetable oils. Renew. Sustain. Energy Rev. 2014, 31, 446–471. [Google Scholar] [CrossRef]
- Meher, L.C.; Vidya Sagar, D.; Naik, S.N. Technical aspects of biodiesel production by transesterification—A review. Renew. Sustain. Energy Rev. 2006, 10, 248–268. [Google Scholar] [CrossRef]
- Sayin, C.; Gumus, M.; Canakci, M. Influence of injector hole number on the performance and emissions of a DI diesel engine fueled with biodiesel–diesel fuel blends. Appl. Therm. Eng. 2013, 61, 121–128. [Google Scholar] [CrossRef]
- Yusuf, N.N.A.N.; Kamarudin, S.K.; Yaakub, Z. Overview on the current trends in biodiesel production. Energy Convers. Manag. 2011, 52, 2741–2751. [Google Scholar] [CrossRef]
- Atabani, A.E.; Silitonga, A.S.; Badruddin, I.A.; Mahlia, T.M.; Masjuki, H.H.; Mekhilef, S. A comprehensive review on biodiesel as an alternative energy resource and its characteristics. Renew. Sustain. Energy Rev. 2012, 16, 2070–2093. [Google Scholar] [CrossRef]
- Knothe, G. Analyzing biodiesel: Standards and other methods. J. Am. Oil Chem. Soc. 2006, 83, 823–833. [Google Scholar] [CrossRef]
- Pratas, M.J.; Freitas, A.V.D.; Oliveira, M.B.; Monteiro, S.C.; Lima, A.S.; Coutinho, J.A.P. Biodiesel Density: Experimental Measurements and Prediction Models. Energy Fuels 2011, 25, 2333–2340. [Google Scholar] [CrossRef]
- Phankosol, S.; Sudaprasert, K.; Lilitchan, S.; Aryusuk, K.; Krisnangkura, K. Estimation of Density of Biodiesel. Energy Fuels 2014, 28, 4633–4641. [Google Scholar] [CrossRef]
- Wang, X.; Kang, K.; Zhu, S.; Gao, B. High-pressure liquid densities of fatty acid methyl esters: Measurement and prediction with PC-SAFT equation of state. Fluid Phase Equilib. 2018, 471, 8–16. [Google Scholar] [CrossRef]
- Pratas, M.J.; Freitas, S.; Oliveira, M.B.; Monteiro, S.C.; Lima, A.S.; Coutinho, J.A.P. Densities and Viscosities of Minority Fatty Acid Methyl and Ethyl Esters Present in Biodiesel. J. Chem. Eng. Data 2011, 56, 2175–2180. [Google Scholar] [CrossRef]
- Pratas, M.J.; Freitas, S.; Oliveira, M.B.; Monteiro, S.C.; Lima, A.S.; Coutinho, J.A.P. Densities and Viscosities of Fatty Acid Methyl and Ethyl Esters. J. Chem. Eng. Data 2010, 55, 3983–3990. [Google Scholar] [CrossRef]
- Prieto, N.M.C.T.; Ferreira, A.G.M.; Portugal, A.T.G.; Moreira, R.J.; Santos, J.B. Correlation and prediction of biodiesel density for extended ranges of temperature and pressure. Fuel 2015, 141, 23–38. [Google Scholar] [CrossRef] [Green Version]
- Tesfa, B.; Mishra, R.; Gu, F.; Powles, N. Prediction models for density and viscosity of biodiesel and their effects on fuel supply system in CI engines. Renew. Energy 2010, 35, 2752–2760. [Google Scholar] [CrossRef] [Green Version]
- Evangelista, N.S.; do Carmo, F.R.; de Sant’Ana, H.B. Estimation of Vapor Pressures and Enthalpies of Vaporization of Biodiesel-Related Fatty Acid Alkyl Esters. Part 1. Evaluation of Group Contribution and Corresponding States Methods. Ind. Eng. Chem. Res. 2017, 56, 2298–2309. [Google Scholar] [CrossRef]
- García, M.; Alba, J.-J.; Gonzalo, A.; Sánchez, J.L.; Arauzo, J. Comparison of Methods for Estimating Critical Properties of Alkyl Esters and Its Mixtures. J. Chem. Eng. Data 2012, 57, 208–218. [Google Scholar] [CrossRef]
- Pankow, J.F.; Asher, W.E. SIMPOL.1: A simple group contribution method for predicting vapor pressures and enthalpies of vaporization of multifunctional organic compounds. Atmos. Chem. Phys. 2008, 8, 2773–2796. [Google Scholar] [CrossRef] [Green Version]
- Nguyen Thi, T.X.; Tamouza, S.; Tobaly, P.; Passarello, J.-P.; de Hemptinne, J.-C. Application of group contribution SAFT equation of state (GC-SAFT) to model phase behaviour of light and heavy esters. Fluid Phase Equilib. 2005, 238, 254–261. [Google Scholar] [CrossRef]
- Evangelista, N.S.; do Carmo, F.R.; de Sant’Ana, H.B. Estimation of Physical Constants of Biodiesel-Related Fatty Acid Alkyl Esters: Normal Boiling Point, Critical Temperature, Critical Pressure, and Acentric Factor. Ind. Eng. Chem. Res. 2018, 57, 8552–8565. [Google Scholar] [CrossRef]
- Espinosa, S.; Diaz, S.; Brignole, E.A. Thermodynamic Modeling and Process Optimization of Supercritical Fluid Fractionation of Fish Oil Fatty Acid Ethyl Esters. Ind. Eng. Chem. Res. 2002, 41, 1516–1527. [Google Scholar] [CrossRef]
- Del Pozo, I.; Cartes, M.; Llovell, F.; Mejía, A. Densities and interfacial tensions for fatty acid methyl esters (from methyl formate to methyl heptanoate) + water demixed mixtures at atmospheric pressure conditions. J. Chem. Thermodyn. 2018, 121, 121–128. [Google Scholar] [CrossRef]
- Zhao, G.; Yuan, Z.; Yin, J.; Ma, S. Thermophysical properties of fatty acid methyl and ethyl esters. J. Chem. Thermodyn. 2019, 134, 195–212. [Google Scholar] [CrossRef]
- Knothe, G.; Steidley, K.R. A Comprehensive Evaluation of the Density of Neat Fatty Acids and Esters. J. Am. Oil Chem. Soc. 2014, 91, 1711–1722. [Google Scholar] [CrossRef]
- Lapuerta, M.; Rodríguez-Fernández, J.; Armas, O. Correlation for the estimation of the density of fatty acid esters fuels and its implications. A proposed Biodiesel Cetane Index. Chem. Phys. Lipids 2010, 163, 720–727. [Google Scholar] [CrossRef] [PubMed]
- Gouw, T.H.; Vlugter, J.C. Physical properties of fatty acid methyl esters. I. density and molar volume. J. Am. Oil Chem. Soc. 1964, 41, 142–145. [Google Scholar] [CrossRef]
- Vogel, A.I. 130. Physical properties and chemical constitution. Part XIII. Aliphatic carboxylic esters. J. Chem. Soc. 1948, 2, 624–644. [Google Scholar] [CrossRef]
- Li, D.; Guo, M.; Wang, X.; Lin, S.; Jia, W.; Wang, G. Measurement and correlation of density and viscosity of binary mixtures of fatty acid (methyl esters + methylcyclohexane). J. Chem. Thermodyn. 2019, 137, 86–93. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Chen, J. Experimental investigations of density and dynamic viscosity of n-hexadecane with three fatty acid methyl esters. Fuel 2016, 166, 553–559. [Google Scholar] [CrossRef]
- Aissa, M.A.; Ivaniš, G.R.; Radović, I.R.; Kijevčanin, M.L. Experimental Investigation and Modeling of Thermophysical Properties of Pure Methyl and Ethyl Esters at High Pressures. Energy Fuels 2017, 31, 7110–7122. [Google Scholar] [CrossRef]
- Liew, K.Y.; Seng, C.E. Molal volumes of somen-Fatty acids and their methyl and ethyl esters. J. Am. Oil Chem. Soc. 1992, 69, 734–740. [Google Scholar] [CrossRef]
- Ndiaye, E.H.I.; Habrioux, M.; Coutinho, J.A.P.; Paredes, M.L.L.; Daridon, J.L. Speed of Sound, Density, and Derivative Properties of Ethyl Myristate, Methyl Myristate, and Methyl Palmitate under High Pressure. J. Chem. Eng. Data 2013, 58, 1371–1377. [Google Scholar] [CrossRef]
- Rasulov, S.M.; Isaev, I.A.; Orakova, S.M. Viscosity and Density of Methyl Palmitate. High Temp. 2019, 57, 269–271. [Google Scholar] [CrossRef]
- Sheu, Y.-W.; Tu, C.-H. Densities, Viscosities, Refractive Indices, and Surface Tensions for 12 Flavor Esters from T = 288.15 K to T = 358.15 K. J. Chem. Eng. Data 2005, 50, 1706–1710. [Google Scholar] [CrossRef]
- Shigley, J.W.; Bonhorst, C.W.; Liang, P.M.; Althouse, P.M.; Triebold, H.O. Physical characterization of (a) a series of ethyl esters and (b) a series of ethanoate esters. J. Am. Oil Chem. Soc. 1955, 32, 213–215. [Google Scholar] [CrossRef]
- Ivaniš, G.R.; Radović, I.R.; Veljković, V.B.; Kijevčanin, M.L. Biodiesel density and derived thermodynamic properties at high pressures and moderate temperatures. Fuel 2016, 165, 244–251. [Google Scholar] [CrossRef]
- Parente, R.C.; Nogueira, C.A.; Carmo, F.R.; Lima, L.P.; Fernandes, F.A.N.; Santiago-Aguiar, R.S.; de Sant’Ana, H.B. Excess Volumes and Deviations of Viscosities of Binary Blends of Sunflower Biodiesel + Diesel and Fish Oil Biodiesel + Diesel at Various Temperatures. J. Chem. Eng. Data 2011, 56, 3061–3067. [Google Scholar] [CrossRef]
- Baroutian, S.; Shahbaz, K.; Mjalli, F.S.; Hashim, M.A.; AlNashef, I.M. Densities and Viscosities of Binary Blends of Methyl Esters + Ethyl Esters and Ternary Blends of Methyl Esters + Ethyl Esters + Diesel Fuel from T = (293.15 to 358.15) K. J. Chem. Eng. Data 2012, 57, 1387–1395. [Google Scholar] [CrossRef]
- Baroutian, S.; Aroua, M.K.; Raman, A.A.A.; Sulaiman, N.M.N. Density of Palm Oil-Based Methyl Ester. J. Chem. Eng. Data 2008, 53, 877–880. [Google Scholar] [CrossRef]
- Latinwo, G.K.; Aribike, D.S.; Kareem, S.A. Comparative Study of Biodiesels Produced from Unrefined Vegetable Oils. Nat. Sci. 2010, 8, 102–106. [Google Scholar]
- Veny, H.; Baroutian, S.; Aroua, M.K.; Hasan, M.; Raman, A.A.; Sulaiman, N.M.N. Density of Jatropha curcas seed oil and its methyl esters: Measurement and estimations. Int. J. Thermophys. 2009, 30, 529–541. [Google Scholar] [CrossRef]
- Nogueira, C.A.; Feitosa, F.X.; Fernandes, F.A.N.; Santiago, R.S.; de Sant’Ana, H.B. Densities and Viscosities of Binary Mixtures of Babassu Biodiesel + Cotton Seed or Soybean Biodiesel at Different Temperatures. J. Chem. Eng. Data 2010, 55, 5305–5310. [Google Scholar] [CrossRef]
- Feitosa, F.X.; Rodrigues, M.L.; Veloso, C.B.; Cavalcante, C.L.; Albuquerque, M.C.G.; de Sant’Ana, H.B. Viscosities and Densities of Binary Mixtures of Coconut + Colza and Coconut + Soybean Biodiesel at Various Temperatures. J. Chem. Eng. Data 2010, 55, 3909–3914. [Google Scholar] [CrossRef]
- Huber, M.L.; Lemmon, E.W.; Kazakov, A.; Ott, L.S.; Bruno, T.J. Model for the Thermodynamic Properties of a Biodiesel Fuel. Energy Fuels 2009, 23, 3790–3797. [Google Scholar] [CrossRef]
- Mesquita, F.M.R.; Feitosa, F.X.; Santiago, R.S.; de Sant’Ana, H.B. Density, Excess Volumes, and Partial Volumes of Binary Mixtures of Soybean Biodiesel + Diesel and Soybean Biodiesel + n-Hexadecane at Different Temperatures and Atmospheric Pressure. J. Chem. Eng. Data 2011, 56, 153–157. [Google Scholar] [CrossRef]
- Barabás, I. Predicting the temperature dependent density of biodiesel–diesel–bioethanol blends. Fuel 2013, 109, 563–574. [Google Scholar] [CrossRef]
- Cano-Gómez, J.J.; Iglesias-Silva, G.A.; Rivas, P.; Díaz-Ovalle, C.O.; de Jesús Cerino-Córdova, F. Densities and Viscosities for Binary Liquid Mixtures of Biodiesel + 1-Butanol, + Isobutyl Alcohol, or + 2-Butanol from 293.15 to 333.15 K at 0.1 MPa. J. Chem. Eng. Data 2017, 62, 3391–3400. [Google Scholar] [CrossRef]
- Gülüm, M.; Bilgin, A. Measurements and empirical correlations in predicting biodiesel-diesel blends’ viscosity and density. Fuel 2017, 199, 567–577. [Google Scholar] [CrossRef]
- Vargas-Ibáñez, L.T.; Iglesias-Silva, G.A.; Cano-Gómez, J.J.; Escamilla-Alvarado, C.; Berrones-Eguiluz, M.A. Densities and Viscosities for Binary Liquid Mixtures of Biodiesel + 1-Pentanol, 2-Pentanol, or 2-Methyl-1-Butanol from (288.15 to 338.15) K at 0.1 MPa. J. Chem. Eng. Data 2018, 63, 2438–2450. [Google Scholar] [CrossRef]
- Davis, J.P.; Geller, D.; Faircloth, W.H.; Sanders, T.H. Comparisons of Biodiesel Produced from Unrefined Oils of Different Peanut Cultivars. J. Am. Oil Chem. Soc. 2009, 86, 353–361. [Google Scholar] [CrossRef]
- Nogueira, C.A.; Nogueira, V.M.; Santiago, D.F.; Machado, F.A.; Fernandes, F.A.N.; Santiago-Aguilar, R.S.; de Sant’Ana, H.B. Density and Viscosity of Binary Systems Containing (Linseed or Corn) Oil, (Linseed or Corn) Biodiesel and Diesel. J. Chem. Eng. Data 2015, 60, 3120–3131. [Google Scholar] [CrossRef]
- Elbro, H.S.; Fredenslund, A.; Rasmussen, P. Group contribution method for the prediction of liquid densities as a function of temperature for solvents, oligomers, and polymers. Ind. Eng. Chem. Res. 1991, 30, 2576–2582. [Google Scholar] [CrossRef]
- Ihmels, E.C.; Gmehling, J. Extension and Revision of the Group Contribution Method GCVOL for the Prediction of Pure Compound Liquid Densities. Ind. Eng. Chem. Res. 2003, 42, 408–412. [Google Scholar] [CrossRef]
- Kehiaian, H.V. Group contribution methods for liquid mixtures: A critical review. Fluid Phase Equilib. 1983, 13, 243–252. [Google Scholar] [CrossRef]
- Biegler, L.T. Solution of dynamic optimization problems by succesive quadratic programming and orthogonal collocation. Comput. Chem. Eng. 1984, 8, 243–247. [Google Scholar] [CrossRef]
- Kay, W. Gases and vapors at high temperature and pressure-density of hydrocarbon. Ind. Eng. Chem. 1936, 28, 1014–1019. [Google Scholar] [CrossRef]
- Ramírez-Verduzco, L.F. Density and viscosity of biodiesel as a function of temperature: Empirical models. Renew. Sustain. Energy Rev. 2013, 19, 652–665. [Google Scholar] [CrossRef]
- Poling, B.E.; Prausnitz, J.M.; O’Connell, J.P. The Properties of Gases and Liquids, 5th ed.; McGraw Hill: New York, NY, USA, 2001. [Google Scholar]


| Group | Group Contribution Parameters | Statistical Parameters | ||||
|---|---|---|---|---|---|---|
| A (cm3/mol) | 103·B (cm3/mol·K) | 105·C (cm3/mol·K2) | R | AAD (%) | σ (g/cm3) | |
| This work | 0.9941 | 0.36 | 0.00339 | |||
| -CH3 | 15.74 | 1.62 | 10.01 | |||
| -CH2 | 14.42 | 5.1 | 0.76 | |||
| =CH- | 11.98 | 1.19 | 0.89 | |||
| -COO- | 30.77 | 1.31 | 1.08 | |||
| Elbro et al. [51] | 0.9788 | 0.83 | 0.00866 | |||
| -CH3 | 18.96 | 45.58 | - | |||
| -CH2 | 12.52 | 12.94 | - | |||
| =CH- | 6.761 | 23.97 | - | |||
| -COO- | 14.23 | 11.93 | - | |||
| Ihmels and Gmehling [52] | 0.9894 | 0.44 | 0.00457 | |||
| -CH3 | 16.43 | 55.62 | - | |||
| -CH2 | 12.04 | 14.1 | - | |||
| =CH- | −1.651 | 93.42 | −14.39 | |||
| -COO- | 61.15 | −248.2 | 36.81 | |||
| Pratas et al. [8] | 0.9911 | 0.81 | 0.00827 | |||
| -CH3 | 18.96 | 45.58 | - | |||
| -CH2 | 12.52 | 12.94 | - | |||
| =CH- | 11.43 | 6.756 | - | |||
| -COO- | 14.23 | 11.93 | - | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Verduzco, L.F. A Group Contribution Method for Predicting the Alkyl Ester and Biodiesel Densities at Various Temperatures. Sustainability 2022, 14, 6804. https://doi.org/10.3390/su14116804
Ramírez-Verduzco LF. A Group Contribution Method for Predicting the Alkyl Ester and Biodiesel Densities at Various Temperatures. Sustainability. 2022; 14(11):6804. https://doi.org/10.3390/su14116804
Chicago/Turabian StyleRamírez-Verduzco, Luis Felipe. 2022. "A Group Contribution Method for Predicting the Alkyl Ester and Biodiesel Densities at Various Temperatures" Sustainability 14, no. 11: 6804. https://doi.org/10.3390/su14116804
APA StyleRamírez-Verduzco, L. F. (2022). A Group Contribution Method for Predicting the Alkyl Ester and Biodiesel Densities at Various Temperatures. Sustainability, 14(11), 6804. https://doi.org/10.3390/su14116804






