Prediction of WEEE Recycling in China Based on an Improved Grey Prediction Model

Abstract

Accurate waste electrical and electronic equipment (WEEE) recycling forecast is an essential reference for optimizing e-waste industry layout and division of labor policies, conducive to better guiding enterprises’ recycling activities and improving the efficiency of WEEE recycling in China. The nonlinear grey Bernoulli model (NGBM (1,1)) was constructed by analyzing the recycling data characteristics of WEEE from 2012 to 2020, and a particle swarm optimization (PSO) algorithm was introduced to solve the model parameters and optimize the background value coefficients. The prediction results were compared with other grey prediction models to verify the effectiveness of the improved NGBM (1,1) model for WEEE recycling prediction in China and the applicability of the PSO algorithm for improving the prediction accuracy of each grey model. Statistical data were used to forecast the WEEE recycling volume in China from 2021 to 2023, and the results show that the value of WEEE recycling will continue to grow at 9%. The value of recycling will reach 16 billion yuan by 2023, while the quantity of WEEE recycling will see a slight decline. Based on the calculation results, the WEEE recycling industry development trend is predicted to guide the promotion of the WEEE industry recycling program and the national circular economy program.

1. Introduction

Urbanization, advances in science and technology, and diversification of consumer demand have led to exponential growth in electrical and electronic equipment. The annual growth rate of global e-waste volume has exceeded the population growth rate. However, only 17.4% of the e-waste is appropriately disposed of globally, and China is the most significant contributor to global e-waste production [1]. In May 2020, the National Development and Reform Commission and seven departments issued the “Implementation Plan on Improving the Recycling and Processing System of Waste Home Appliances and Promoting the Renewal and Consumption of Household Appliances,” proposing requirements for localities and relevant departments to improve the recycling and processing system of waste household appliances. Therefore, the reasonable scientific layout of the waste electrical and electronic equipment (WEEE) recycling network and construction of the WEEE treatment system is of great significance for implementing the “Plan” [2].

The recycling of WEEE is beneficial for reducing resource waste, environmental pollution, and human health risks [3,4]. In China, about 63% of WEEE enters the informal recycling sector that has not obtained official certification [5]. These sectors use pickling, firing, and other treatment methods to save recycling costs, resulting in waste of resources and secondary pollution. Officially authorized companies can manage e-waste to protect the environment and conserve resources and are responsible to the public, but authorized companies recycle less than 40% of the total WEEE. With the continuous improvement of pilot projects and China’s domestic e-waste legislation, China’s legal e-waste recycling industry has made excellent processing capacity and quality [6,7]. As of 2020, China has established 109 authorized WEEE recycling and processing enterprises, which recycle about 3.9 million tons and 170 million units of waste electrical and electronic products annually [8]. The complexity and unpredictability of WEEE recycling and disposal have always been the reason that it is difficult for the industry to develop on a large scale. Efficiently predicting the WEEE recycling volume of authorized enterprises is significant for guiding corporations to formulate scientific recycling plans, inventory plans, and developing remanufacturing plans [9], and it can also help government decision-making departments develop and improve e-waste recycling plans and promote China’s circular economy plan [10,11].

Numerous studies have provided methods for WEEE recycling forecasting, mainly input-output models, time series models, econometric models, and direct waste analysis models [12], which rely on quantifying the flows and stocks and their life cycle assessment. These methods require extensive data to provide highly accurate predictions [13]. China’s WEEE recycling market is not developing well. The lack of data, the coexistence of formal and informal recycling channels, and other reasons make the available data limited and unreliable. Therefore, this study chooses the grey prediction model suitable for “small sample” and “poor information” to predict the recycling amount of WEEE in China’s formal channels.

The contributions of this paper are as follows:

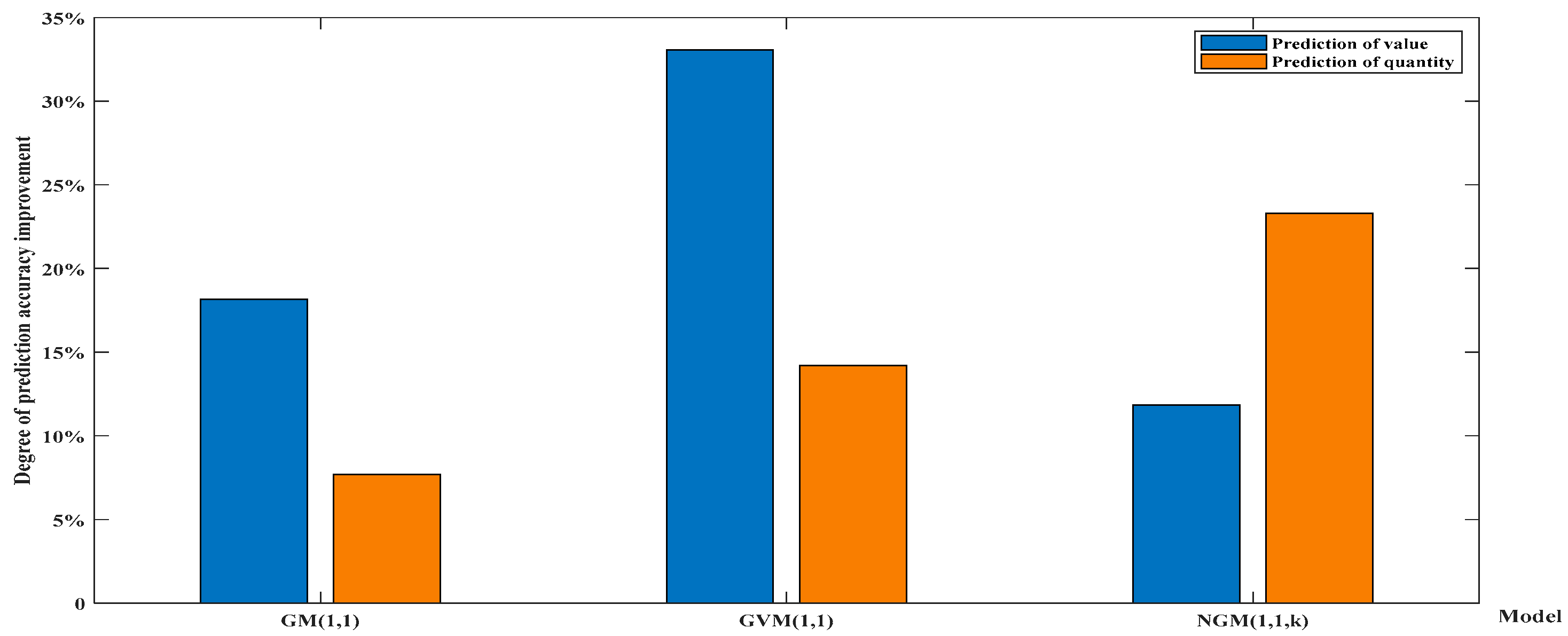
• According to the characteristics of the sample data, a non-linear grey Bernoulli model (NGBM (1,1)) is constructed, particle swarm optimization (PSO) is applied to optimize parameters, and the PSO-NGBM (1,1) model has higher prediction accuracy compared with the traditional grey prediction model (GM (1,1)), grey Verhulst model (GVM (1,1)), discrete grey prediction model (DGM (1,1)) and non-homogeneous grey prediction model (NGM (1,1,k));
• Using particle swarm optimization (PSO) to optimize the background value coefficient, it is verified that the PSO optimization algorithm is applicable for improving the prediction accuracy of various grey prediction models;
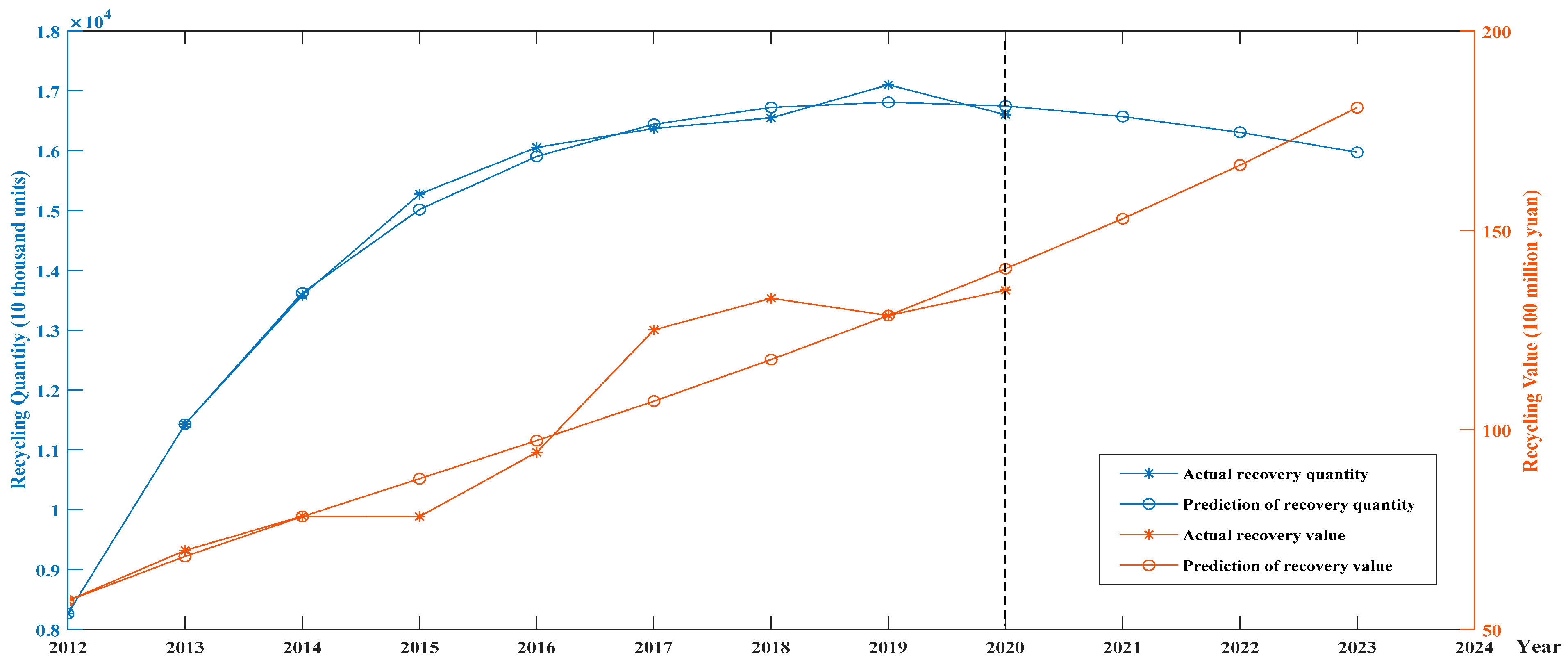
• The PSO-NGBM (1,1) model was used to forecast the WEEE recycling quantity and recycling value from 2021 to 2023, unlike previous studies, which showed an upward trend. The WEEE recycling quantity will show a slight decrease in the short term, and the recycling value will show a steady increase. This finding has implications for government policy formulation and enterprise optimization of development strategies in the context of COVID-19.

The rest of this paper is organized as follows: Section 2 reviews the research progress of WEEE recycling prediction studies, the grey prediction model, and its improved models; Section 3 introduces relevant models and algorithms, including the NGBM (1,1) model, PSO algorithm, and NGBM (1,1) model improved by PSO; Section 4 verifies through empirical analysis that the NGBM (1,1) model improved by the PSO algorithm is the best model for predicting WEEE recycling in China, and the PSO algorithm is effective for improving the prediction accuracy of all forms of grey models; Section 5 presents the results and discussion.

2. Literature Review

2.1. Related Research on WEEE Recycling Prediction

Scholars have constructed various models of WEEE generation and recycling prediction, such as input-output models, factor models, time series models, direct waste analysis models, econometric models, etc. [12]. Among them, the combination of input-output models and factor models is particularly widely used. Abbondanza [14] and Shoki et al. [10] estimated the potential amount of WEEE by incorporating electronic product lifetime factors into input-output analysis models. Lase et al. [15] used multivariate input-output analysis models to predict the amount of WEEE generated in Belgium and the Netherlands in 2030. Mairizal et al. [16] proposed a multivariate input-output analysis model (IOA) based on sales-inventory-life and a dynamic time-varying product life approach through the Weibull distribution function to estimate and predict the amount of e-waste generated in Indonesia. Material flow analysis (MFA) is an extension of the input-output model. It is also widely used for WEEE prediction. De Meester et al. [17] combined MFA and life cycle assessment (LCA) to predict the potential environmental benefits of e-waste material flow and its recycling chain to guide policymakers and enterprises in effective decision making. Econometric methods are also commonly used to predict the amount of electrical e-waste. Petridis et al. [18] applied a series of models such as Bass, Gompertz, and Logistic to predict and estimate the accumulation of waste computers in different regions of the world. Chen [19] and Liang et al. [20] used the pollution coefficient method, consumption and use method, retention coefficient method, and market value method to predict the generation of five types of household electronic waste (TV, refrigerator, air conditioner, washing machine, and computer) in Beijing-Tianjin-Hebei and Guangdong regions, respectively. Li et al. [2] used Stata multiple regression to analyze the influencing factors of WEEE end-of-life and then used the Holt model to predict the end-of-life of WEEE in the Yangtze River Delta region. The latest study incorporated spatial and temporal elements into the WEEE recycling prediction model, and Tong et al. [21] estimated the inter-regional flow pattern of WEEE within informal recycling channels in China using the Wilson spatial interaction model based on the actual amount of WEEE recycled by formal processing enterprises in China. Liu et al. [22] proposed a new model for estimating appliance usage and e-waste generation at the 1 km × 1 km grid-level by combining geographic information systems (GIS) and material flow analysis (MFA). Lv et al. [9] proposed a kriging-based spatial mathematical model for WEEE recycling based on the spatial structure of the recycling network. Wang et al. [23] proposed a multi-source data hybrid method based on quarterly sales data, survey data, and Internet data to estimate the amount of e-waste generated for domestic electrical storage water heaters (DESWH), namely the SMK-GDSGM (1,1)-MSA method, which can deal with seasonal trend features hidden in time series in e-waste forecast modeling.

The above studies on WEEE focus on predicting WEEE generation and overall recycling, lacking attention to WEEE recycling from different recycling channels. The prediction results are usually high relative to the actual values. In addition, Chinese WEEE recycling is characterized by uncertainty and small data samples. The above models usually require a large amount of data to ensure the accuracy of the model predictions. They do not apply to recycle prediction studies in China, so a grey prediction model that requires only a small amount of data is a more suitable choice. Few scholars have applied the grey prediction model to research WEEE recycling. Zhao et al. [24] developed a GM (1,1) model to predict WEEE in China based on home appliance ownership. Xu et al. [25] designed a prediction model combining the GM (1,1) model and FTS model to forecast electronics recycling. Wang et al. [11] proposed a decomposition-integrated hybrid forecasting method integrating the variable mode decomposition (VMD) and exponential smoothing model (ESM) in the grey model (GM) for WEEE quantity forecasting.

2.2. Grey Prediction Model and Its Optimization

Professor Deng proposed the grey system theory in the 1980s, and the grey prediction model is the core of it, which has the advantages of requiring less modeling data, simple calculation, and high simulation accuracy, so it is widely used in economic analysis, engineering construction, and other fields [26]. The traditional GM (1,1) model assumes that the original data series obeys homogeneous exponential growth, but different forms of improved grey prediction models have emerged for data series with other characteristics. Zhang et al. [27] proposed a GVM (1,1) model integrating the Verhulst method into the grey model when the data series grows in an “S” curve or a saturation stage. To solve the problem of “non-uniformity” between parameter estimation and model expressions in the traditional GM (1,1) model, Xie et al. [28] proposed the discrete grey model (DGM (1,1)). Cui et al. [29] constructed the NGM (1,1,k) model, which is suitable for approximating the characteristics of nonlinear exponential growth series, to compensate for the lack of accuracy of the GM (1,1) model for simulating nonlinear exponential series. Chen et al. [30] proposed the nonlinear grey Bernoulli model (NGBM (1,1)) for solving the small nonlinear sample forecasting problem.

Improving the accuracy of the grey prediction model is a fundamental task, and the main ways to improve the accuracy of the prediction include changing the initial conditions, background value selection, grey derivative improvement, and parameter solution [31,32]. Among them, scholars have conducted more studies on the optimization of background values. Based on the reconstruction of the background value formula, Jiang and Zhang [33] proposed the construction method of replacing the traditional trapezoidal area with an irregular trapezoidal area to optimize the background value based on the principle of Riemann integration. Xiao et al. [34] used the Lagrange interpolation function and variable step trapezoidal algorithm to optimize the background value. Song [35] and Zheng et al. [36] used the integral median theorem to fit the real background value, Liu et al. [37] applied the golden mean optimization method to optimize the background values, and Jiang [38] and Wei [39] et al. used the Newton–Cotes product formula to optimize the background values. Based on background value coefficient optimization, Li et al. [40] derived a solution method for the optimal sequence of background value coefficients and translations, and Zeng [41] and Huang [42] et al. optimized the background value coefficients using particle swarm optimization (PSO) algorithm. Zhang et al. [43] used a genetic algorithm to optimize the weight coefficients of the grey model. Intelligent algorithms are increasingly used in the optimization of background value coefficients.

Various intelligent optimization algorithms have been integrated into traditional or improved grey prediction models due to their simplicity and ease of implementation to improve model prediction accuracy. Zhao et al. [44] optimized the GM (1,1) model parameters using the ant-lion optimization algorithm. Zhao [45] used the moth flame optimization algorithm (MFO) to optimize parameters a and b of the GM (1,1) model. Xu et al. [46] used the particle swarm optimization (PSO) algorithm to optimize the traditional grey prediction model. Wang and Li [47] developed a new grey Verhulst model combined with the PSO algorithm to predict CO₂ emissions in China. Zhang et al. [48] proposed a fractional-order cumulative NGM (1,1,k) model based on optimal background values by optimizing the model parameters using the PSO algorithm. Hu [49] used a genetic algorithm to optimize the background value coefficients for a multivariate grey prediction model constructed for the bankruptcy prediction problem. Zhi et al. [50] proposed a method that combines a nonlinear grey Bernoulli model (NGBM (1,1)) with a genetic algorithm. Yuan et al. [51] combined an adaptive artificial fish swarm algorithm and metabolic method to select optimal parameters and established an optimized nonlinear grey Bernoulli model (AF-MNGBM (1,1)). Kong and Ma [52] simultaneously applied genetic algorithm (GA), particle swarm optimization algorithm (PSO), grey wolf optimization algorithm (GWO), and the novel ant-lion optimization algorithm (ALO) for a comparative study of the optimization effect of the parameters of the nonlinear grey Bernoulli model (NGBM (1,1)).

The NGBM (1,1) model is widely used in the energy field because of its applicability to data with nonlinear and non-stationary characteristics by varying the nonlinear parameters [53]. The NGBM (1,1) model is a reasonable choice for the lack of formal WEEE recycling data and nonlinear data series in China. The above optimization methods for grey prediction models are usually effective for specific data and models. The intelligent PSO algorithm can optimize the background values without restriction for the commonality in different structures of gray prediction models, which is applicable and significantly improves model accuracy. Therefore, in this paper, we will construct a PSO–NGBM (1,1) model to predict the recycling trend of WEEE in China’s official channels and verify that the PSO–NGBM (1,1) model has a better prediction effect compared with the traditional GM (1,1), GVM (1,1), DGM (1,1), and NGM (1,1,k) models. Second, the PSO algorithm is applied to the GM (1,1), GVM (1,1), and NGM (1,1,k) models to optimize the background values to verify the general effectiveness of the PSO algorithm for improving the prediction results of the grey prediction models.

3. Methodology

3.1. Nonlinear Grey Bernoulli Model (NGBM (1,1))

NGBM (1,1) is a power model of the traditional GM (1,1) model, with better prediction accuracy for data dealing with nonlinear characteristics. The modeling process is as follows:

Step 1. For the number of non-negative samples, the original time series $X^{\left(0\right)}$ is given as Equation (1):

$$X^{\left(0\right)}=\{x^{\left(0\right)}\left(1\right),x^{\left(0\right)}\left(2\right),\cdots x^{\left(0\right)}\left(n\right)\}$$

(1)

The once accumulated generating operation (1-AGO) transforms the original data into a monotonically increasing data sequence, reducing the disorder of the original data sequence to obtain the accumulation sequence $X^{\left(1\right)}$=$\{x^{\left(1\right)}\left(1\right),x^{\left(1\right)}\left(2\right),\cdots x^{\left(1\right)}\left(n\right)\}$, where $x^{\left(1\right)}\left(k\right)$ is expressed as Equation (2):

$$x^{\left(1\right)}\left(k\right)={\displaystyle \sum }_{i=1}^k{x}^{\left(0\right)}\left(i\right),k=1,2\cdots \mathrm{n}$$

(2)

The mean generating sequence of $Z^{\left(1\right)}=\left\{z^{\left(1\right)}\left(2\right),z^{\left(1\right)}\left(3\right),\cdots ,z^{\left(1\right)}\left(n\right)\right\}$, where $z^{\left(1\right)}\left(k\right)$ is expressed as Equation (3):

$$z^{\left(1\right)}\left(k\right)=0.5{\mathrm{x}}^{\left(1\right)}\left(k\right)+0.5{\mathrm{x}}^{\left(1\right)}\left(k-1\right), k=2,3,\cdots n$$

(3)

$z^{\left(1\right)}\left(k\right)$ is the background value, and $0.5$ is the background value generation coefficient.

Step 2. The model is built using a Bernoulli differential equation, as shown in Equation (4):

$$\frac{\mathrm{d}{x}^{\left(1\right)}\left(k\right)}{\mathrm{dk}}+a{x}^{\left(1\right)}\left(k\right)=b{\left(x^{\left(1\right)}\left(k\right)\right)}^r$$

(4)

$r$ is the exponential parameter.

The obtained whitening differential equation is expressed as Equation (5):

$$x^{\left(0\right)}\left(k\right)+a{z}^{\left(1\right)}\left(k\right)=b{\left(z^{\left(1\right)}\left(k\right)\right)}^r$$

(5)

$a$ is the development coefficient, $b$ is the amount of grey effect, and the parameters $a$ and $b$ can be estimated by the least-squares method to find the estimates $\widehat{a}$ and $\widehat{b}$, as in Equation (6):

$$\left[\begin{array}{c}a\\ b\end{array}\right]={\left[B^{T}B\right]}^{-1}{B}^{T}Y$$

(6)

where $B$ is denoted as Equation (7):

$$B=\left[\begin{array}{c}-{\mathrm{z}}^{\left(1\right)}\left(2\right) \\ -z^{\left(1\right)}\left(3\right) \\ ⋮\\ -z^{\left(1\right)}\left(\mathrm{n}\right) \end{array}\begin{array}{c}{z}^{\left(1\right)}{\left(2\right)}^r\\ z^{\left(1\right)}{\left(3\right)}^r\\ ⋮\\ z^{\left(1\right)}{\left(\mathrm{n}\right)}^r\end{array}\right],\mathrm{Y}=\left[\begin{array}{c}{x}^{\left(0\right)}\left(2\right)\\ x^{\left(0\right)}\left(3\right)\\ ⋮\\ x^{\left(0\right)}\left(n\right)\end{array}\right]$$

(7)

Step 3. The time response equation of the NGBM (1,1) model is Equation (8):

$${\widehat{x}}^{\left(1\right)}\left(k\right)={\left[\left(x^{\left(0\right)}{\left(1\right)}^{\left(1-r\right)}-\frac{\widehat{b}}{\widehat{a}}\right)e^{-a\left(1-r\right)\left(k-1\right)}+\frac{\widehat{b}}{\widehat{a}}\right]}^{\frac{1}{1-r}}$$

(8)

${\widehat{x}}^{\left(1\right)}\left(k\right)$ denotes the predicted value of $x^{\left(1\right)}\left(k\right)$ at time $k$ with the initial condition of $x^{\left(1\right)}\left(1\right)=x^{\left(0\right)}\left(1\right)$. When $r=0$, Equation (8) is the GM (1,1) model; when $r=1$, Equation (8) has no solution; when $r=2$, Equation (8) is the GVM (1,1) model.

The predicted value is obtained by $\mathrm{Equation} \left(8\right)-\mathrm{Equation} \left(2\right)$, as shown in Equation (9):

$${\widehat{x}}^{\left(0\right)}\left(k\right)={\widehat{x}}^{\left(1\right)}\left(k\right)-{\widehat{x}}^{\left(1\right)}\left(k-1\right), k=2,3,\dots ,n$$

(9)

Step 4. In this paper, the mean absolute error (MAE), mean absolute percentage error (MAPE), root mean square error (RMSE), and R-square ($R^2$) are used to measure the prediction error, as in Equations (10)–(13):

$$\mathrm{MAE}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n \left|x^{\left(0\right)}\left(k\right)-{\widehat{x}}^{\left(0\right)}\left(k\right)\right|$$

(10)

$$\mathrm{MAPE}=\left[\frac{1}{n}{\displaystyle \sum }_{i=1}^n\frac{\left|x^{\left(0\right)}\left(k\right)-{\widehat{x}}^{\left(0\right)}\left(k\right)\right|}{x^{\left(0\right)}\left(k\right)}\right]\times 100\%$$

(11)

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{(x^{\left(0\right)}\left(k\right)-{\widehat{x}}^{\left(0\right)}\left(k\right))}^2}$$

(12)

3.2. Particle Swarm Optimization Algorithm (PSO)

PSO is a global optimization algorithm proposed by Eberhart and Kennedy in 1995, which originated from the study of bird flock predation behavior [54]. PSO has the advantages of easy conceptual understanding, few adjustment parameters, and easy programming implementation and is widely used in fields such as neural network training and function optimization.

The PSO algorithm’s basic idea is to start as a set of random particles (random solutions) in the search space, and then iteration is used to find the best solution. In each iteration, all particles have fitness determined by the optimized function. Based on fitness, the optimal solution found by the particles themselves is called the extreme individual value ($P_{best}^k$), and the optimal solution currently found by the whole population is the extreme global value ($G_{best}^k$). Each particle updates its velocity and position based on the individual and global extremes to find these two optimal values. The velocity update of each particle is expressed as Equation (13):

$$V_{id}^{k+1}=w{V}_{id}^k+c_1{r}_1\left(P_{best}^k-X_{id}^k\right)+c_2{r}_2\left(G_{best}^k-X_{id}^k\right)$$

(13)

The position update of each particle is expressed as Equation (14):

$$X_{id}^{k+1}=X_{id}^k+V_{id}^{k+1}$$

(14)

The interpretation of each notation is described in

Table 1. Notation interpretation.

Notation	Interpretation
$i$	Particle number
$d$	Particle dimension number
$k$	Number of iterations
$w$	Inertia weight
$c_1$	Individual learning factor
$c_2$	Group learning factor
$r_1$,$r_2$	Random number in the interval [0,1] to increase the randomness of the search
$V_{id}^k$	Velocity vector of particle $i$ in the $d$th dimension in the $k$th iteration
$X_{id}^k$	Position vector of particle $i$ in the $d$th dimension in the $k$th iteration
$P_{best}^k$	The optimal solution obtained by the search of the $i$th particle (individual) after the $k$th iteration
$G_{best}^k$	The optimal solution in the whole particle population after the $k$th iteration

.

3.3. Improved Grey Prediction Model

The NGBM (1,1) model improves the whitening differential equation of the traditional GM (1,1) model into a nonlinear grey Bernoulli exponential differential equation. By adjusting the value of the exponential coefficient $r$ to make the solution of the equation better adapt to the trend and regularity of the original series after the cumulative operation, the flexibility of the model application and the prediction accuracy are improved. The value of $r$ was mainly determined empirically or through multiple experiments in previous studies, which lacked a theoretical basis [31]. The optimal parameters determined by the PSO algorithm with the minimization of the MAPE value as the objective function can avoid the subjective problem. The objective function is shown in Equation (15):

$$\min MAPE=\min f\left(r\right)=min\left[\frac{1}{n}{\displaystyle \sum }_{i=1}^n\frac{\left|x^{\left(0\right)}\left(k\right)-{\widehat{x}}^{\left(0\right)}\left(k\right)\right|}{x^{\left(0\right)}\left(k\right)}\right]\times 100\%$$

(15)

Scholars pay less attention to optimizing the background value $z^{\left(1\right)}\left(k\right)$ after determining the optimal NGBM (1,1) model index coefficient $r$. The background value coefficient is the key to optimizing the background value. The background value coefficients are the weights occupied by adjacent elements in constructing the mean series [55]. The classical grey prediction model artificially specifies that old information is equally as important as new information [56] and sets the background value coefficient in Equation (3) to 0.5, with no strict theoretical basis. When the trend of the once accumulated generating operation (1-AGO) series is relatively flat and the time interval is small, a background value coefficient of 0.5 is appropriate; however, when the 1-AGO series is highly volatile, a background value coefficient of 0.5 will cause large errors. In this study, the background value coefficient is set to the variable $p$, as shown in equation (16):

$$z^{\left(1\right)}\left(k\right)=p{\mathrm{x}}^{\left(1\right)}\left(k\right)+\left(1-p\right){\mathrm{x}}^{\left(1\right)}\left(k-1\right), k=2,3,\cdots n$$

(16)

$p$ is the background value generation coefficient, which takes the value range [0,1]. The PSO algorithm is again applied to optimize the background value coefficients with the objective function as in Equation (17):

$$\min MAPE=\min f\left(p\right)=min\left[\frac{1}{n}{\displaystyle \sum }_{i=1}^n\frac{\left|x^{\left(0\right)}\left(k\right)-{\widehat{x}}^{\left(0\right)}\left(k\right)\right|}{x^{\left(0\right)}\left(k\right)}\right]\times 100\%$$

(17)

Then, we can obtain the NGBM (1,1) model in which the background values and parameters are optimized. The relevant parameter settings of the PSO algorithm in this study are shown in

Table 2. PSO algorithm parameter setting.

Nomenclature	Parameter
Population size	100
Number of iterations	1000
$\mathrm{Inertia} \mathrm{weights} w$	1.0
$\mathrm{Random} \mathrm{number} r_1, r_2$	[0,1]
$\mathrm{Learning} \mathrm{factor} c_1$	1.5
$\mathrm{Learning} \mathrm{factor} c_2$	1.5
$\mathrm{Range} \mathrm{for} r$	(−1,1)
$\mathrm{Range} \mathrm{for} p$	(0,1)

.

4. Empirical Analysis

China is a major producer of WEEE. Given the environmental problems and recycling value of WEEE, a more regulated dismantling process is bound to become the mainstream trend. The construction of a recycling system for WEEE in China has gone through three phases. The first phase was a regional pilot phase. Before 2009, the WEEE recycling pilot enterprises were set up in Zhejiang Province, Qingdao City, and Guiyu Town, Guangdong, to achieve a circular economy. However, most WEEE flowed into informal recycling channels, so authorized enterprises faced the dilemma of not having WEEE to recycle. The second phase was the “trade-in” and WEEE recycling legal system standardization phase from 2009 to 2011. The promotion of the “trade-in” policy led to a significant increase in WEEE recycling in 2011. The expiration of the trade-in policy at the end of 2011 and the promulgation of the WEEE Recycling Regulations curbed informal enterprises’ crude and highly polluting dismantling and recycling activities, leading to a significant decrease in the total amount of WEEE recycling in 2012. The third stage is establishing a multi-level recycling system led by enterprises that have obtained WEEE processing qualifications after 2012, and the amount of WEEE recycled increases year by year. Figure 1 shows the recycling quantity of WEEE (TVs, microcomputers, washing machines, refrigerators, and air conditioners) in official channels from 2008 to 2020 and Figure 2 shows the value of WEEE recycled from 2012 to 2019. The data come from the official websites of the Ministry of Commerce of the People’s Republic of China, China Solid Waste Chemicals Management, and China Household Electric Appliance Research Institute, and precisely reflect the changing trend of WEEE recycling in China.

4.1. Data

The WEEE recycling system in China has gone through three stages. The government has introduced different WEEE recycling policies at different stages, significantly affecting the amount of WEEE recycled by authorized companies and the value of WEEE recycling. China is currently in the third phase of the WEEE recycling system and will remain in this phase for a long time. Using only the data from the third phase (2012–2020) for recycling forecasting will provide better forecasting results by excluding the “noise” data from the first and second phases. The experimental data are shown in

Table 3. Quantity and value of formal channel WEEE recycling in China, 2012–2020.

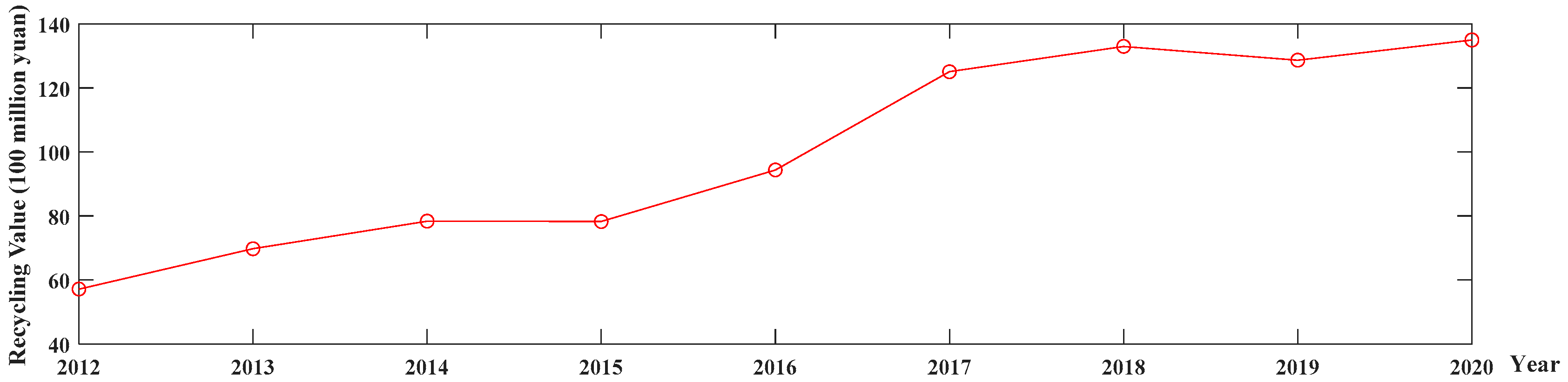
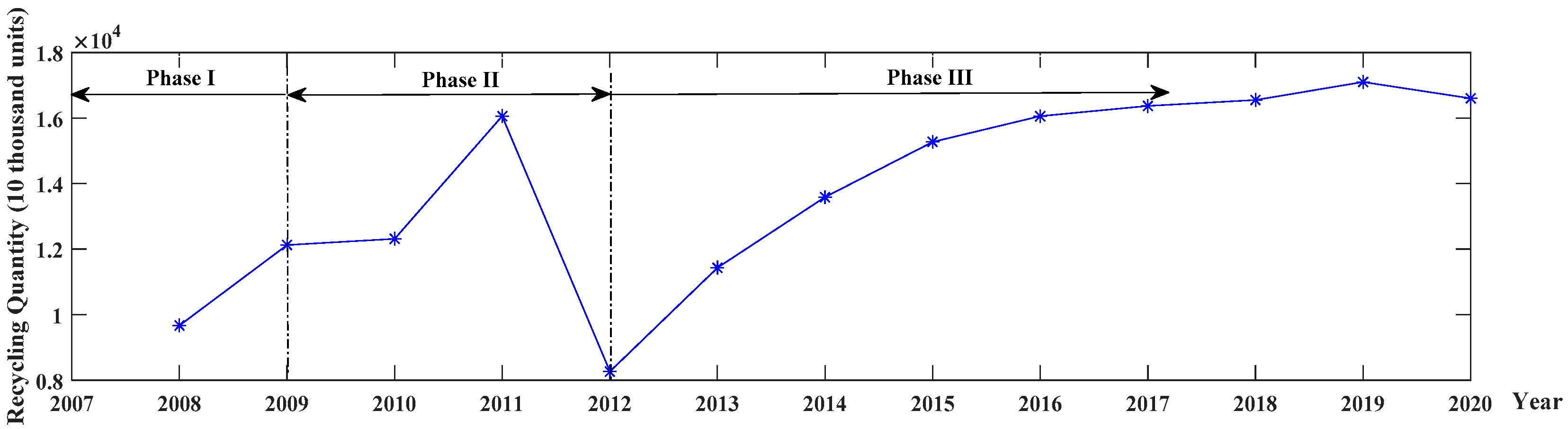
Year	2012	2013	2014	2015	2016	2017	2018	2019	2020
Recycling Quantity (10 thousand units)	8264	11,430	13,583	15,274	16,055	16,370	16,550	17,100	16,600
Recycling Value (100 million yuan)	57.2	69.8	78.4	78.3	94.4	125.1	133	128.7	135

.

4.2. Example Analysis

First, the data of recovery quantity from 2012 to 2018 were used to construct the NGBM (1,1) model. The model’s optimal exponential coefficient and background value coefficient were solved by applying the PSO algorithm with MAPE minimization as the objective function. Then, the determined optimal parameters were substituted into the NGBM (1,1) model for forecasting. Meanwhile, the predictive effects of the model were analyzed using data from 2019 and 2020. The prediction effects of the NGBM (1,1) model were compared with those of the GM (1,1), GVM (1,1), DGM (1,1), and NGM (1,1,k) models. All models were run on MATLAB 2018b, and the results of the operations are shown in

Table 4. Waste electrical and electronic equipment recovery quantity prediction for each model.

Year	Recovery Quantity (10 Thousand Units)	GM (1,1)	GVM (1,1)	DGM (1,1)	NGM (1,1,k)	NGBM(1,1)	PSO-NGBM (1,1)
2012	8264	8264	8264	8264	8264	8264	8264
2013	11,430	12,604	5791	12,625	7878	10,540	11,430
2014	13,583	13,437	9048	12,876	11,730	13,264	13,635
2015	15,274	14,326	12,982	13,721	13,951	15,084	15,022
2016	16,055	15,273	16,518	14,622	15,230	16,198	15,889
2017	16,370	16,283	18,083	15,582	15,968	16,767	16,394
2018	16,550	17,360	16,808	16,605	16,393	16,920	16,635
MAE		563.75	2182.5	818.69	1158.9	329.86	82.64
RMSE		714.43	2947.8	1001.1	1633	421.72	120.39
MAPE (%)		3.98%	16.09%	5.7%	8.85%	2.42%	0.53%
2019	17,100	18,507	13,408	17,695	16,638	16,757	16,677
2020	16,600	19,731	9451	18,857	16,779	16,363	16,568
MAE		2269	5420.5	1426	320.5	290	227.5
RMSE		2427.22	5689.42	1650.47	350.35	294.80	299.96
MAPE (%)		13.54%	32.33%	8.54%	1.89%	1.72%	1.33%

.

As shown in Table 4, the improved NGBM (1,1) model has the best prediction effect on the WEEE recycling of officially authorized enterprises as its MAPE is 0.53%. In contrast, the GM (1,1), GVM (1,1), DGM (1,1), and NGM (1,1,k) models have prediction errors of 3.98%, 16.09%, 5.7%, and 8.85%, respectively. The optimal index coefficients $r$ and background value $p$ of the PSO–NGBM (1,1) model for predicting WEEE recovery quantities are 0.3529 and 0.5036, and its relative error of out-of-sample forecasting result from 2019 to 2020 is 1.33%, which is much lower than that of other models.

Then, the PSO–NGBM (1,1) model will be constructed by applying the WEEE recycling value data for 2012–2020, as its superiority in WEEE recycling prediction has been verified above. It will also be compared with GM (1,1), GVM (1,1), DGM (1,1), and NGM (1,1,k) models simultaneously. The optimal index coefficients $r$ and background value $p$ of the PSO–NGBM (1,1) model for predicting WEEE recovery values are 0.1163 and 0.6512 and it has the lowest prediction error. The results of the operations are shown in

Table 5. Waste electrical and electronic equipment recovery value prediction for each model.

Year	Recovery Value (100 Million Yuan)	GM (1,1)	GVM (1,1)	DGM (1,1)	NGM (1,1,k)	NGBM (1,1)	PSO-NGBM (1,1)
2012	57.2	57.2	57.2	57.2	57.2	57.2	57.2
2013	69.8	72.89	28.67	73.23	55.89	58.43	68.29
2014	78.4	80.45	41.55	74.27	69.85	75.28	78.29
2015	78.3	88.78	58.54	81.91	82.81	89.97	87.77
2016	94.4	97.98	79.28	90.33	94.85	102.7	97.33
2017	125.1	108.13	101.8	99.62	106.03	113.68	107.23
2018	133	119.34	122.15	109.86	116.42	123.05	117.64
2019	128.7	131.7	135.19	121.16	126.07	130.98	128.67
2020	135	145.35	136.87	133.6181	135.03	137.59	140.41
MAE		7.02	17.26	8.09	7.3	6.75	5.85
RMSE		8.99	22.05	12.03	10.18	8.07	8.72
MAPE (%)		6.45%	20.04%	7.08%	7.43%	7.14%	5.26%

.

The above two sets of examples verify that the PSO–NGBM (1,1) model has the best results for predicting the quantity and value of WEEE recycling. Moreover, it is verified that the PSO–NGBM (1,1) model has significantly improved the prediction accuracy over the NGBM (1,1) model after using the PSO algorithm to optimize the parameters. The PSO algorithm is applied to optimize the background values of the GM (1,1), GVM (1,1), and NGM (1,1,k) models, and the DGM (1,1) model does not need to apply the PSO algorithm to optimize the background value coefficients because it does not contain the mean sequence as in Equation (3). After optimizing the background value coefficients by the PSO algorithm, the prediction accuracy of each model is improved to a certain extent, as shown in Figure 3. The prediction accuracy has mostly improved by more than 10%.

The NGBM (1,1) model with optimized exponential coefficients and background value coefficients by the PSO algorithm is used to forecast WEEE recycling in China from 2021 to 2023, and the forecast results are shown in Figure 4. Unlike the continued growth in WEEE recycling predicted in previous studies, this study shows a slight decline in the amount of WEEE recycled from 2021 to 2023, while the recycling value will maintain an average annual growth rate of 9%, which is a more realistic prediction.

The decrease in the number of authorized companies implementing WEEE recycling may seem unreasonable, but it is the most likely scenario over the next three years. From the perspective of recycling enterprises, China’s WEEE dismantling industry revenue mainly comes from the sales of dismantled goods and dismantling fund subsidies. The dismantling subsidy income is the most important source of income for enterprises. Due to the continued impact of COVID-19, the delay in the dismantling fund subsidy has brought a crisis to the enterprises. At present, about 90 out of 109 domestic dismantling companies are carrying out WEEE recycling and dismantling activities, and the decrease in the amount of WEEE recycling will continue for some time. From the consumer perspective, the aging population and the downgrading of consumption under the influence of the epidemic have led to a reduction in WEEE production from both source reduction of electrical and electronic product consumption and the extension of product life cycles. On the market side, the entry of electrical and electronic product manufacturing companies into the WEEE recycling industry has impacted professional WEEE recycling and dismantling companies.

While WEEE recycling volumes have declined, the value of product recycling will maintain an optimistic trend of continued growth. The predicted data show that the value of WEEE recycled by authorized enterprises from 2021 to 2023 will maintain an annual growth rate of about 9%. The value of product recovery is a more important indicator for the WEEE recycling industry, and growth in recovery value means attracting more investment, creating more jobs, and a more dynamic market outlook. The recycling value of WEEE will grow from 13.5 billion yuan in 2020 to 16 billion yuan by 2023. The decrease in the amount of WEEE recycled and the increase in recycling value are not contradictory. This phenomenon indicates that the Chinese WEEE recycling industry is transitioning from simple dismantling to refined, high-value automation [57] to maximize the value of WEEE resources, supported by WEEE recycling-related legislation and technological advances.

On the whole, China’s WEEE recycling industry has strong prospects for development, but the risk of a decrease in the amount of WEEE recycling cannot be ignored. A stable or growing amount of WEEE recycling can guarantee the continued healthy development of the industry. To avoid operational difficulties, government agencies should issue timely subsidy funds and take active incentives, such as adjusting the tax system and using it to help companies reduce energy, labor, and resource costs during economic downturns. WEEE recycling companies should continue innovating disassembly and processing technologies while integrating emerging technologies such as industrial internet, big data, cloud computing, and artificial intelligence into the recycling–disassembly–reuse process. The recycled WEEE products are reused with high value, supported by technological empowerment.

5. Result and Discussion

China is committed to developing a green and circular economy and improving the efficiency of resource utilization and the use of renewable resources. WEEE is the core of the “urban mine,” and its pollution control and recycling are receiving increasing attention. An accurate forecast of WEEE recycling in China will provide a scientific basis for government agencies to implement effective policies and qualified enterprises to carry out recycling activities. It is vital to promote the standardized recycling activities of qualified regions and enterprises and is essential for establishing a green, low-carbon, and circular economic system.

The NGBM (1,1) model constructed based on the characteristics of WEEE recycling data from official channels in China has better prediction results than GM (1,1), GVM (1,1), DGM (1,1), and NGM (1,1,k) models. The PSO–NGBM (1,1) model has the optimal prediction effect by optimizing the parameters of the NGBM (1,1) model using the PSO algorithm to forecast the WEEE recycling volume and recycling value in China from 2021 to 2023. The PSO algorithm can improve the model’s prediction accuracy by optimizing the background value coefficients of different forms of grey prediction models, and this intelligent algorithm is valuable and applicable in improving grey prediction. This intelligent algorithm has practicality and applicability in improving the performance of grey prediction models.

The PSO–NGBM (1,1) model was used to predict the amount and value of WEEE recycling in the formal channel in China. In the short term, there will be a downward trend in the amount of WEEE recycled, which the government should implement timely incentives to curb. The value of WEEE recycling is predicted to grow at 9%, thanks to technological advances empowering the value of WEEE products. It should be the focus of future development for WEEE recycling companies.

Regarding the limitations of this study, using a small amount of data for forecasting enhances the prediction effect, but the prediction results are good only in the short term; based on past statical data forecasting, the prediction results are valid only in the case of the stable external environment. Future research directions include how to construct dynamic models with minimal data samples and maintain high prediction accuracy and how to develop an intelligent algorithm that can be more generally applied to model optimization than the PSO algorithm, which cannot be used to optimize the DGM (1,1) model in this study.