Abstract
With the increasing complexity of application situations in multi-core processing systems, how to assure task execution reliability has become a focus of scheduling algorithm research in recent years. Most fault-tolerant algorithms achieve hard reliability requirements through task redundancy, which increases energy consumption and contradicts the concept of sustainable development. In this paper, we propose a new algorithm called HDFE (Heterogeneous-Dag-task-fault-tolerance-energy-efficiency algorithm) that combines DVFS technology and task replication technology to solve the scheduling problem of DAG applications concerning energy-saving and hard reliability requirements in heterogeneous multi-core processor systems. Our algorithm is divided into three phases: the priority calculation phase, the task replication phase, and the task assignment phase. The HDFE algorithm achieved energy savings while meeting hard reliability requirements for applications, which was based on the interrelationship between reliability and energy consumption in filtering task replicas. In the experimental part of this paper, we designed four comparison experiments between the EFSRG algorithm, the HRRM algorithm, and the HDFE algorithm. The experimental results showed that the energy consumption of task scheduling using the HDFE algorithm is lower than other algorithms under different scales, thus achieving energy savings and complying with the concept of sustainable development.
1. Introduction
1.1. Background
Since the late 1990s, with the development of semiconductor technology, the number of transistors on a single chip has greatly increased, while multi-core processors have also seen a lot of development [1]. Artificial intelligence applications have also gradually penetrated various industries such as intelligent medicine, autonomous driving, aerospace, and security surveillance, owing to the powerful computing power brought by multi-core processors. These industries have rigid requirements for the reliability of task execution. On the other hand, energy savings is also an eternal research topic with regard to embedded systems. In the field of task scheduling algorithms in multi-core processors, the discussion about the improvement of energy savings and reliability has never been interrupted.
1.2. Motivation
Task replication techniques are widely used in fault-tolerant scheduling algorithms for multi-core systems. However, redundant task replicas cause a surge in energy consumption while guaranteeing the reliability of task execution [2]. Therefore, how to save energy in scheduling algorithms based on task replication techniques has become a concern for scholars. Considering energy savings, the DVFS technique is undoubtedly the best choice. The DVFS technique achieves energy savings by reducing the processing frequency of processor cores. Existing studies [3,4] have shown that the failure rate increases when the processor cores are at a low frequency, which easily leads to task execution failure and thus reduces the system’s reliability. There are some algorithms that have been proposed, which combine task replication techniques with DVFS techniques to satisfy both application reliability requirements and energy efficiency. For example, the EFSRG algorithm, by filtering application replicas in an ascending order of energy consumption, allows the reliability of the application to be satisfied [5]. In the process of screening task replicas, such scheduling algorithms take the energy consumption of task replicas as the ranking basis and the reliability of task replicas as the condition constraint; this is accomplished without considering the comprehensive performance of task replicas in the screening process. Therefore, for this paper, we considered how to take into account the comprehensive performance of task replicas in the screening process of task replicas, as it is possible to find the task replica that meets the task reliability requirements and has lower energy consumption.
1.3. Contribution
In this paper, we focus on the problem of scheduling computational tasks with reliability and security requirements in heterogeneous multi-core processors for various domains, while considering energy savings. We consider task replication techniques, which guarantee the successful execution of a task by duplicating application replicas; we also ensure the continuation of an application as the execution of a task fails due to a transient failure of the processor. Each core in a multi-core processor system can be independently frequency-regulated by the DVFS technique, and we consider regulating the execution frequency of task replicas in order to achieve energy savings. The main contributions of this paper are the following:
- 1.
- In this paper, we propose a static heuristic scheduling algorithm, HDFE, for solving the scheduling problem of DAG applications with energy-saving requirements and hard reliability requirements in heterogeneous multi-core processor systems. The algorithm is divided into three phases: the priority calculation phase, the task replication phase, and the task assignment phase.
- 2.
- In the task priority calculation stage, this paper presents a new priority calculation method based on the execution time uncertainty of tasks.
- 3.
- This paper proposes a task replica screening method that combines the comprehensive performance of reliability and energy consumption in the task replication phase.
- 4.
- In the experimental part, the simulation experiments designed for this paper compare the differences in energy consumption between the EFSRG algorithm [5], the HRRM algorithm [6], and the HDFE algorithm proposed in this paper and are based on simulation scheduling experiments on an actual application and a random application.
2. Related Work
This section discusses the key research works related to energy-saving task scheduling and reliability task scheduling.
Energy consumption is an extremely important evaluation property of scheduling algorithms; the discussion on energy-saving scheduling algorithms has never stopped in various environments such as single-core processor systems, multi-core processor systems, real-time systems, or non-real-time systems. Most of the discussions on energy savings in heterogeneous processor systems rely on techniques such as VFI, DPM, DVS, and DVFS to dynamically regulate the voltage or frequency of processor cores in order to achieve energy savings [7]. The scheduling algorithm proposed in [8] aimed to achieve energy savings by dynamically adjusting processor voltage using the DVS technique. The DPM algorithm mainly achieves static energy consumption reduction by adjusting the processor state [9]. The VFI technique, on the other hand, discusses energy savings by regulating the voltage of processor cores in groups within processor systems that have a large number of cores [10,11,12]. The DVFS technique is most widely used in energy-efficient scheduling algorithms [13,14,15]. However, the DVFS technique also has a drawback in that the transient failure rate increases when the processor core is running at low frequencies, which leads to a higher probability of task execution failure. This drawback of the DVFS technique causes a conflict between its energy-saving capability and its reliability. How to explore a highly reliable and low energy consumption scheduling algorithm in the conflict between has thus become the focus of research.
Most of the research on fault-tolerant scheduling discusses how to ensure that the final execution results of tasks are not affected in case of transient or permanent processor failures. Many factors can cause processor failures, including high temperature, hardware failures, etc. [16,17]. The study of fault-tolerant scheduling mainly considers transient failures because the probability of permanent failures during task execution is much lower than that of transient failures [18]. Existing fault-tolerant scheduling algorithms generally quantify the probability of successful task execution by defining it as the reliability of the task. In this regard, many fault-tolerant techniques have been proposed in order to achieve the task reliability requirement; these include the task replication [19,20], primary-backup [21], and checkpoint [22] techniques.
Niraj Kumar et al. in [2] discussed the reliable energy-efficient scheduling of non-preemptive real-time tasks in heterogeneous multi-core processing systems, but the diverse ideas presented in their discussion about heterogeneous multi-core systems is reflected in the fact that each core can independently adjust its operating frequency without discussing the heterogeneity of the hardware parameters of the processor cores.
The HRRM algorithm proposed in [6] considers the hard reliability requirements of an application through task replication, but it does not consider energy savings while achieving the reliability requirement.
The EFSRG algorithm was proposed in [5] to satisfy the hard reliability requirements of tasks by task replication while achieving energy savings by regulating the execution frequency of task replicas. However, as stated in the previous section, the EFSRG algorithm does not consider the energy consumption and reliability of task replicas together when screening the task replicas, and it does not fully utilize the interrelationship between energy consumption and reliability.
In this paper, we will discuss the dynamic scheduling algorithm for DAG applications in heterogeneous multi-core systems based on the relationship between the energy consumption and the reliability of task execution, as well as the energy saved while satisfying hard reliability requirements.
3. System Model
3.1. Task Model
As shown in Figure 1, an application is represented by a DAG G. Let G = (V, E), where V is a set of v tasks, which is represented by V = , and E is a set of directed edges among tasks. Each edge represents task , dependency constraints between , i.e., task must finish its execution and transfer the resulting data to solve the data dependency before task starts. The weight of each edge represents the communication cost between task and and is denoted by .
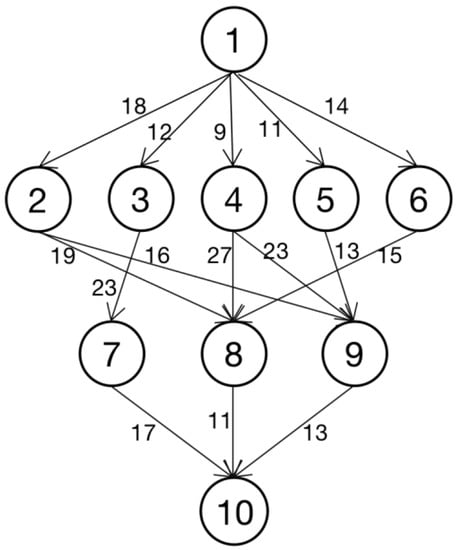
Figure 1.
DAG diagram shows the application.
As a supplement to DAG, W is a matrix of n * m, n is the number of tasks in the application, and m is the number of processors in this processor system. represents the estimated execution time of on processor .
3.2. Processor Model
This paper adopts a heterogeneous multi-core processor structure, and the cores in the processor are connected together by a bus, as shown in Figure 2. The processor is expressed as represents a core of a processor, where indicates the conversion capacitance of the processor, which is a hardware parameter. indicates the dynamic power index, while , indicates frequency-dependent dynamic power and frequency-independent static power. , indicates the maximum and minimum frequencies of processor core operation. According to DVFS technology, the processor core operating frequency can be adjusted between the minimum and maximum frequencies. indicates the processor core failure rate, is a static parameter related to the hardware. The above parameters will be used in the reliability model and the energy consumption model in the following sections. The related parameters of the processor structure in Figure 2 are shown in Table 1.
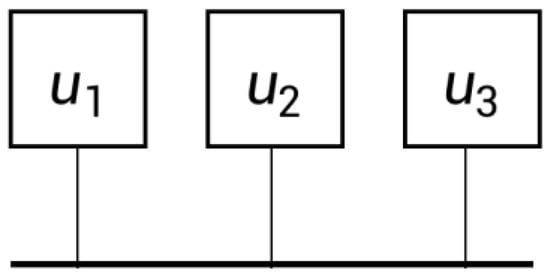
Figure 2.
Three-core processor architecture.

Table 1.
Hardware parameters.
3.3. Reliability Model
Due to hardware failure, high temperature, and other unknown reasons, the task may fail to complete. This paper proposes a reliability model based on transient failure probability, which is based on previous reliability scheduling research. The model uses the exponential function based on execution time and fault rate to express mission reliability.
When a task is executed, the fault rate can be expressed by , and fault rate is only related to the hardware parameter. When the processor is executed at the frequency f, the fault rate can be expressed as follows:
where is the fault rate executed at frequency of the processor ; is a static parameter related to the hardware, reflecting the sensitivity of the probability of failure to frequency changes; and is the minimum frequency of . Furthermore, the reliability of the task replica could be expressed by r, and the reliability of task executed at frequency on the processor is expressed as follows:
In particular, when = 0, it means that the task has no replica on this processor, =0. The reliability of task is calculated by the reliability of each replica of the task, which is expressed as:
Therefore, the reliability of the application could be represented as follows:
Our target is to let
Since the reliability given by the application represents the reliability of the entire application, and each task is dynamically allocated both processor and operating frequencies during the scheduling process, needs to be decomposed into task reliability requirements , expressed as:
where allocated represents the applications that have been allocated before task in the priority queue, and unallocated represents the applications that have not been allocated after task in the priority queue. Then, if each task in the application satisfies , then the inequality (5) can be satisfied, that is, the reliability requirement of the application can be satisfied.
3.4. Power Model
The power consumption of a processor is mainly composed of frequency-related dynamic consumption, frequency-independent dynamic consumption, and static consumption. Among these, the frequency-related dynamic power consumption is the main component, and the total power of the processor is represented by P; thus, the power model is expressed as follows:
means frequency-independent static power, means frequency-independent dynamic power, means frequency-dependent dynamic power, g means system state, g = 0 when the system is in sleep, g = 1 when the system is running, and means the switching capacitance of the processor, which is a hardware parameter, and represents the dynamic power exponent. Furthermore, the dynamic energy consumption of the replicated task executed on the processor at frequency can be expressed as follows:
The scheduling dynamic energy consumption of task is calculated by the dynamic energy consumption of each replica of the task.
The static energy consumption of application is related to the SL (schedule length) of the task.
The total energy consumption of the application is expressed as follows:
In particular, when = 0, it means that the task has no replica on this processor, .
4. Algorithm
Our algorithm consists of three parts: task priority calculation, task replication, and task scheduling. In the task priority calculation stage, the task priority sequence of the application is obtained, and in the task replication stage, the reliability requirements of the tasks are first calculated according to the task priority sequence. Then, the tasks are copied according to the determined reliability requirements. Finally, a group of task replicas that meet the requirements and save energy is screened out. In the task scheduling stage, the scheduling scheme of tasks in the application and in the task replica of the processor is obtained according to the previous two stages.
4.1. Calculation of Task Priority
Before replicating tasks in the application, its reliability requirements should be determined first. According to Formula (3), which was derived in the reliability model, we know that the reliability requirement of tasks is related to the processing order of tasks in the application, so we need to give the method of calculating tasks priority in the first step of the scheduling algorithm to determine the priority sequence of the tasks.
Because our scheduling algorithm will combine DVFS technology to scale the execution frequency of the tasks, the execution time of tasks on the processor cannot be determined in the priority calculation stage. Therefore, in the task priority calculation stage, we ignore the influence of task execution time and focus on the influence of communication cost between tasks.
We use the rank value to express the ranking weight of tasks, and the rank is calculated as shown in Formula (12). The priority sequence can be obtained by ranking tasks in descending order of rank value.
Taking the application in Figure 1 as an example, the task sequences calculated by Formula (12) are , , , , , , , , , and .
4.2. Task Replication
In the previous section, we obtained the priority sequence of tasks. In the task replication stage, we first need to decompose the reliability requirements of the application into the reliability requirements of the tasks, and then replicate the tasks according to their reliability requirements. The algorithm for the task replication phase is shown in Algorithm 1.
The first function of the task replication phase is to take out the first task from the priority sequence according to the reliability requirements in the reliability model, then perform Equation (3) to calculate the reliability requirements, as shown in line 3 of Algorithm 1.
Taking task as an example, the calculation of the reliability requirements is as follows:
After determining the reliability requirements of the tasks, how to use task replication to meet the reliability requirements has become a problem to be considered. According to the research in [2], given the task reliability requirements, the number of task replicas and the execution frequency of the task replicas are negatively correlated; that is, if the number of task replicas increases, the minimum execution frequency of each task replica will decrease. Therefore, the key to task replication is how to select the number of replicas and the frequency of the task replicas.
| Algorithm 1: Task replication phase. |
| Input:
Output: frequency
|
Because the hardware parameters of each core in the processor system being considered are different, it is impossible to calculate the execution frequency of each replica when determining the task reliability requirements and the number of replicas. We assume that the task has a task replica on each core, and that the initial execution frequency is 0. Search for the task execution frequency on each core until we find the replica combination that meets the requirements of task reliability. In the final result, if the execution frequency of a task replica is equal to 0, it means that there is no replica of the task on the processor .
If energy savings is not considered, we can always choose the most reliable replica for the next iteration when traversing the execution frequency of task replicas on each core. However, with regard to energy savings, we need to define a comprehensive index that includes reliability and energy consumption, and which is used to screen the task replicas that are able to enter the next iteration. For a group of task replicas that have finally been screened out, we hope it can achieve high reliability with low energy consumption. Hence, we take the energy consumption required to achieve the unit reliability goal as our comprehensive parameter, and the calculation method applied is as follows:
According to Formulas (2) and (8),
We assume that the task has a task replica on each core. In the process of task replica screening, our algorithm selects each task replica , a replica with the lowest value, so that its frequency is increased; the reliability of tasks is calculated according to Formula (3). If the reliability requirement is met, this group of task replicas will be output; otherwise, the screening process will continue. This is shown in lines 5–9 of Algorithm 1.
Figure 1 shows the tasks in the application . An example of the screening process for task replicas is shown in Table 2.

Table 2.
Tasks —task replica filtering process.
4.3. Task Scheduling Stage
In the task scheduling phase, we need to schedule the tasks based on the previously obtained task priority queue from task replication scheme. Tasks are scheduled according to the following rules.
- The task replica has the same priority as the primary task.
- When all replicas of the task have successfully been executed, its child nodes can start to receive the data of the task.
- The task cannot be preempted during execution.
Taking the application in Figure 1 as an example, the final scheduling result obtained by our scheduling algorithm is shown in Table 3. AST is the start execution time of the task replica on the corresponding core, and AFT is the end execution time.

Table 3.
Application task replication results.
5. Experiment
For this paper, we used MATLAB, a mighty data processing tool, to conduct simulation experiments in task scheduling. Since the EFSRG algorithm and HRRM algorithm are similar to the models in this paper, we will compare the performance of the EFSRG algorithm, HRRM algorithm, and HDFE algorithm in the experiments. The range of the relevant parameters of the processor in the simulation experiments is shown in Table 4.

Table 4.
Relevant parameter range of the processor in the simulation experiment.
5.1. FFT (Fast Fourier Transform) Application Scheduling Experiment
The Fourier transform is mainly used in signal processing to convert time domain signals to frequency domain signals. The Fast Fourier Transform is an efficient algorithm for computing the discrete Fourier transform in a computer. The use of the Fast Fourier Transform allows the number of multiplications required for the discrete Fourier transform to be greatly reduced. As shown in Figure 3, the dependencies between tasks when using the Fast Fourier Transform with four size of input vectors are plotted. The number of tasks n in the Fast Fourier Transform application is related to the number of size of input vectors N, as shown in Equation (15) [23], where N = 2.
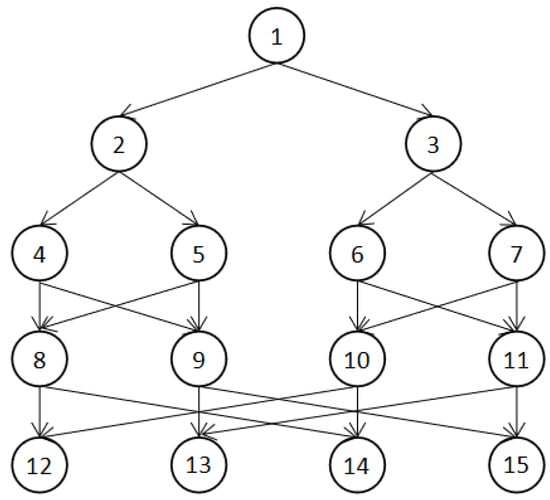
Figure 3.
Fast Fourier Transform application when the number of size of input vectors is four.
We randomly generated the FFT application when the number of size of input vectors N = 16, 32, 64, and 128 (that is, the number of tasks is 95, 223, 511, and 1151), and when the number of processor cores was set to eight. We increased the reliability requirement of the application from 0.90 to 0.99 in steps of 0.01, randomly generated 100 FFT applications, and compared the average energy consumption of various algorithms for scheduling applications with various reliability goals. Then, we scheduled the application by using the EFSRG algorithm, the HRRM algorithm, and our proposed HDFE algorithm and compared the scheduling results. The comparison index is the energy consumption required to meet the reliability requirements. The experimental data were subsequently drawn into a bar chart, as shown in Figure 4.
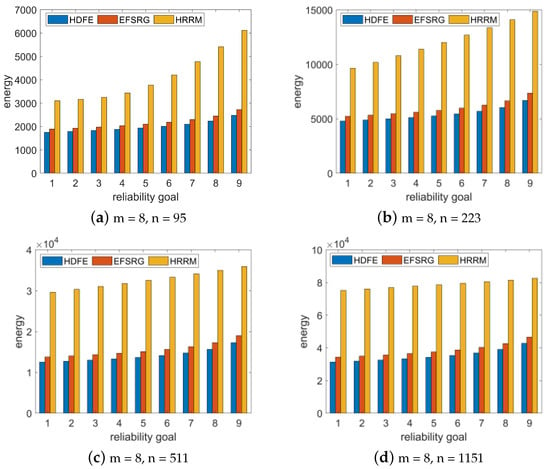
Figure 4.
Comparative experimental results of energy consumption required by different specifications of FFT application under different reliability requirements.
To study whether the number of processor cores has an impact on the experimental results, we randomly generated a Fast Fourier Transform application with size of input vectors n = 4 and N = 95 and compared the experimental results when the number of processors m was 4, 8, 16, and 20. The experimental results are shown in Figure 5.
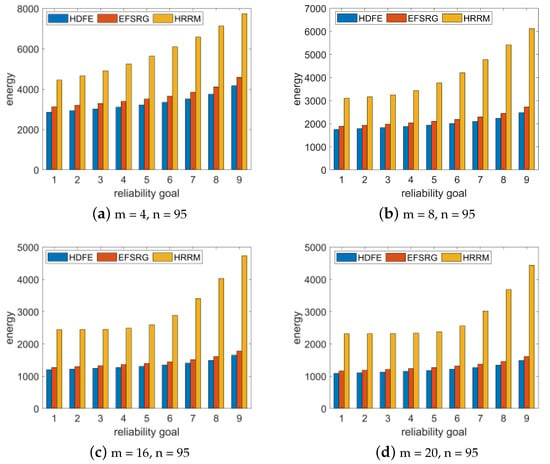
Figure 5.
Comparative experimental results of energy consumption required by the same FFT application specifications under different reliability requirements for different numbers of processor environments.
The analysis results show that in the same processor environment, the same Fast Fourier Transform application is scheduled. The HDFE algorithm proposed in this paper satisfies the required reliability requirements with a lower energy consumption than the other two algorithms, and this result is not affected by the number of task nodes and the number of processors.
5.2. Ge (Gaussian Elimination) Application Scheduling Experiment
The Gaussian elimination method, an algorithm in linear algebraic programming, can be used to solve linear equations, find out the rank of the matrix, and find out the inverse matrix of the reversible equation. Figure 6 is a 5 × 5 dependency diagram of Gaussian elimination calculation based on the matrix. The relationship between the number of tasks n of the Gaussian elimination application and the number of size of input vectors n is shown in Formula (16) [23].
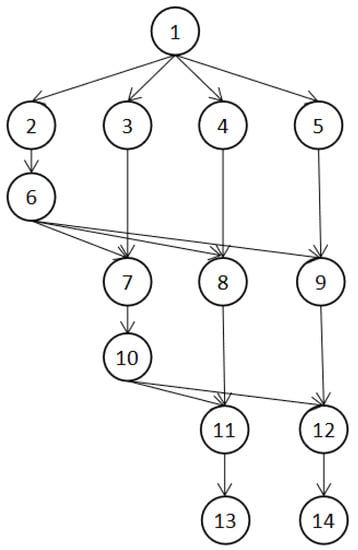
Figure 6.
Gaussian Elimination application when the number of size of input vectors is four.
We randomly generated the Gaussian elimination application when the number of size of input vectors n = 13, 21, 32, and 48 (i.e., the number of tasks is 90, 23, 05, 27, and 11, 75). We increased the reliability requirement of the application from 0.90 to 0.99 in steps of 0.01, randomly generated 100 GE applications, and compared the average energy consumption of various algorithms for scheduling applications with various reliability goals. Then, we scheduled the application by using the EFSRG algorithm, the HRRM algorithm, and our proposed HDFE algorithm and compared the scheduling results. The comparison index is the energy consumption required to meet reliability requirement. The experimental data were subsequently drawn into a bar chart, as shown in Figure 7.
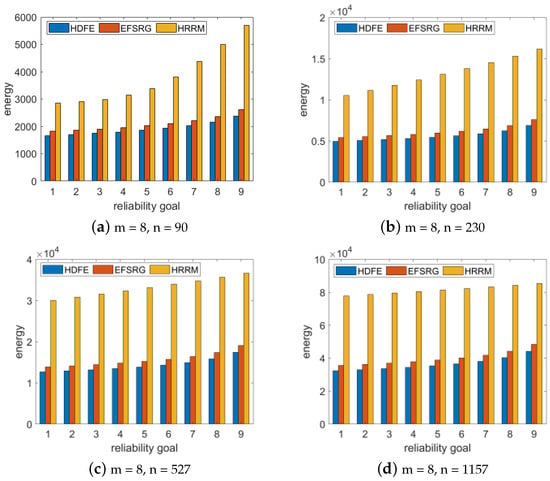
Figure 7.
Comparative experimental results of energy consumption required by the GE application with different specifications under different reliability requirements.
To study whether the number of processor cores affects the experimental results, we randomly generated the Gaussian elimination application with matrix dimensions of n = 13 and n = 90 and compared the experimental results when the number of processors m was 4, 8, 16, and 20. The experimental results are shown in Figure 8.
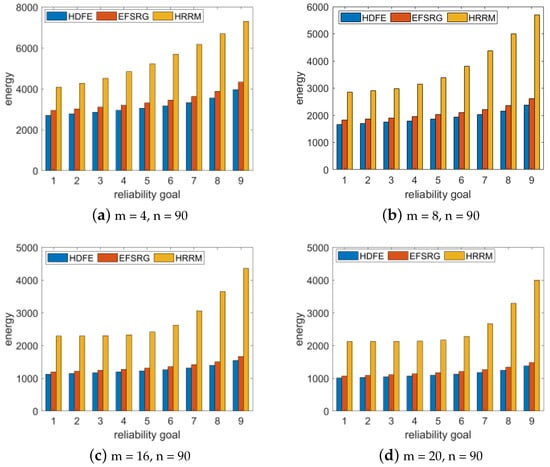
Figure 8.
Comparative experimental results of energy consumption required by the GE application with the same specifications under different reliability requirements for different numbers of processor environments.
The experimental results show that the same Gaussian cancellation application is scheduled in the same processor environment, and that the energy consumption of the HDFE algorithm proposed in this paper to meet the given reliability requirements is lower than that of the other two algorithms; this result is not affected by the number of task nodes and processors.
6. Conclusions
In this paper, we tried to solve the problem of scheduling DAG applications with hard reliability requirements in heterogeneous multiprocessor systems while keeping the energy consumption as low as possible. Algorithms that adopt task replication techniques to meet the reliability requirements performed well in terms of energy savings, but task replication techniques led to a surge in overall energy consumption. In this paper, we also proposed a static heuristic scheduling algorithm, HDFE, which can achieve energy savings while satisfying the hard reliability requirements of applications. The algorithm combines task replication technology with DVFS technology based on a thorough study of the correlation between task reliability and energy consumption, it performs task replica selection based on the combined parameters of task energy consumption and reliability, and finally, it selects application replicas that meet the reliability requirements and have low energy consumption. In the experimental part, we designed a comparison experiment based on the FFT and GE applications, and the comparison algorithm we used was the EFSRG algorithm and the HRRM algorithm. Upon analysis of the experimental results, it can be concluded that the scheduling which made use of the HDFE algorithm proposed in this paper requires less energy to achieve the hard reliability requirements of the application. In future research, we will consider complicating the task model with the processor model in order to explore the task scheduling problem in complex environments.
Our proposed algorithm is for embedded, heterogeneous multi-core systems with high, soft, real-time reliability requirements. In future work, we can put emphasis on combining real-time performance, energy savings, and reliability. For example, the task deadlines will be required in the model assumptions.
Author Contributions
Data curation, J.W.; Resources, J.W.; Software, Y.G.; Validation, Q.C. and Y.G.; Visualization, Y.H.; Writing—original draft, Q.C.; Writing—review & editing, Q.C. and Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Burger, D.; Goodman, J.R. Billion-transistor architectures: There and back again. Computer 2004, 37, 22–28. [Google Scholar] [CrossRef]
- Kumar, N.; Mayank, J.; Mondal, A. Reliability aware energy optimized scheduling of non-preemptive periodic real-time tasks on heterogeneous multiprocessor system. IEEE Trans. Parallel Distrib. Syst. 2019, 31, 871–885. [Google Scholar] [CrossRef]
- Zhu, D.; Melhem, R.; Mossé, D. The effects of energy management on reliability in real-time embedded systems. In Proceedings of the IEEE/ACM International Conference on Computer Aided Design, 2004. ICCAD-2004, San Jose, CA, USA, 7–11 November 2004; pp. 35–40. [Google Scholar]
- Ernst, D.; Das, S.; Lee, S.; Blaauw, D.; Austin, T.; Mudge, T.; Kim, N.S.; Flautner, K. Razor: Circuit-level correction of timing errors for low-power operation. IEEE Micro 2004, 24, 10–20. [Google Scholar] [CrossRef]
- Xie, G.; Chen, Y.; Xiao, X.; Xu, C.; Li, R.; Li, K. Energy-efficient fault-tolerant scheduling of reliable parallel applications on heterogeneous distributed embedded systems. IEEE Trans. Sustain. Comput. 2017, 3, 167–181. [Google Scholar] [CrossRef]
- Xie, G.; Zeng, G.; Chen, Y.; Bai, Y.; Zhou, Z.; Li, R.; Li, K. Minimizing redundancy to satisfy reliability requirement for a parallel application on heterogeneous service-oriented systems. IEEE Trans. Serv. Comput. 2017, 13, 871–886. [Google Scholar] [CrossRef] [Green Version]
- Sheikh, S.Z.; Pasha, M.A. Energy-Efficient Cache-Aware Scheduling on Heterogeneous Multicore Systems. IEEE Trans. Parallel Distrib. Syst. 2021, 33, 206–217. [Google Scholar] [CrossRef]
- Kang, J.; Ranka, S. DVS based energy minimization algorithm for parallel machines. In Proceedings of the 2008 IEEE International Symposium on Parallel and Distributed Processing, Miami, FL, USA, 14–18 April 2008; pp. 1–12. [Google Scholar]
- Devadas, V.; Aydin, H. On the interplay of voltage/frequency scaling and device power management for frame-based real-time embedded applications. IEEE Trans. Comput. 2010, 61, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Han, J.J.; Wu, X.; Zhu, D.; Jin, H.; Yang, L.T.; Gaudiot, J.L. Synchronization-aware energy management for VFI-based multicore real-time systems. IEEE Trans. Comput. 2012, 61, 1682–1696. [Google Scholar] [CrossRef] [Green Version]
- Kong, F.; Yi, W.; Deng, Q. Energy-efficient scheduling of real-time tasks on cluster-based multicores. In Proceedings of the 2011 Design, Automation & Test in Europe, Grenoble, France, 14–18 March 2011; pp. 1–6. [Google Scholar]
- Wu, X.; Lin, Y.; Han, J.J.; Gaudiot, J.L. Energy-efficient scheduling of real-time periodic tasks in multicore systems. In IFIP International Conference on Network and Parallel Computing; Springer: Berlin/Heidelberg, Germany, 2010; pp. 344–357. [Google Scholar]
- Zhang, Y.W. Energy-aware mixed-criticality sporadic task scheduling algorithm. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 40, 78–86. [Google Scholar] [CrossRef]
- Salami, B.; Noori, H.; Naghibzadeh, M. Fairness-aware energy efficient scheduling on heterogeneous multi-core processors. IEEE Trans. Comput. 2020, 70, 72–82. [Google Scholar] [CrossRef]
- Liu, Y.; Du, C.; Chen, J.; Du, X. Scheduling energy-conscious tasks in distributed heterogeneous computing systems. Concurr. Comput. Pract. Exp. 2022, 34, e6520. [Google Scholar] [CrossRef]
- Iyer, R.K.; Rossetti, D.J.; Hsueh, M.C. Measurement and modeling of computer reliability as affected by system activity. ACM Trans. Comput. Syst. (TOCS) 1986, 4, 214–237. [Google Scholar] [CrossRef]
- Castillo, X.; McConnel, S.R.; Siewiorek, D.P. Derivation and calibration of a transient error reliability model. IEEE Trans. Comput. 1982, 31, 658–671. [Google Scholar] [CrossRef]
- Shatz, S.M.; Wang, J.P. Models and algorithms for reliability-oriented task-allocation in redundant distributed-computer systems. IEEE Trans. Reliab. 1989, 38, 16–27. [Google Scholar] [CrossRef]
- Zhao, B.; Aydin, H.; Zhu, D. On maximizing reliability of real-time embedded applications under hard energy constraint. IEEE Trans. Ind. Inform. 2010, 6, 316–328. [Google Scholar] [CrossRef] [Green Version]
- Haque, M.A.; Aydin, H.; Zhu, D. On reliability management of energy-aware real-time systems through task replication. IEEE Trans. Parallel Distrib. Syst. 2016, 28, 813–825. [Google Scholar] [CrossRef]
- Roy, A.; Aydin, H.; Zhu, D. Energy-aware primary/backup scheduling of periodic real-time tasks on heterogeneous multicore systems. Sustain. Comput. Inform. Syst. 2021, 29, 100474. [Google Scholar] [CrossRef]
- Kada, B.; Kalla, H. A fault-tolerant scheduling algorithm based on checkpointing and redundancy for distributed real-time systems. In Research Anthology on Architectures, Frameworks, and Integration Strategies for Distributed and Cloud Computing; IGI Global: Hershey, PA, USA, 2021; pp. 770–788. [Google Scholar]
- Topcuoglu, H.; Hariri, S.; Wu, M.Y. Performance-effective and low-complexity task scheduling for heterogeneous computing. IEEE Trans. Parallel Distrib. Syst. 2002, 13, 260–274. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).