Prediction of Ozone Hourly Concentrations Based on Machine Learning Technology
Abstract
1. Introduction
- (1)
- We proposed a feature construction algorithm which can analyze the interaction strength between ozone and itself and other atmospheric pollutants from the perspectives of time and space, and built a feature set for ozone prediction based on this algorithm.
- (2)
- We proposed an ozone concentration prediction model, FC-LsOA-KELM, which comprehensively uses the feature construction algorithm, the kernel extreme learning machine and the lioness optimization algorithm.
- (3)
- We evaluated the prediction performance of FC-LsOA-KELM using 2015–2019 air pollution data from 11 cities on the Fenwei Plain in China. The results showed that the O3 prediction model proposed in this paper can obtain better prediction results and has a better performance compared with other prediction models.
2. Related Work
- (1)
- Prediction method based on linear regression. The linear regression prediction method is to study the linear causal relationship between the predictor (historical data of air pollutants) and the explanatory variable (future ozone concentration). The most commonly used linear regression methods in O3 prediction include ARIMA [8,9] and multiple linear regression (MLR) [10,11,12,13]. Although these statistical methods have been widely used for near-earth O3 concentration prediction, they also have many limitations. For example, when using MLR prediction, a large number of predictors need to be used, and these predictors often have multicollinearity problems [14]. In addition, the formation process of O3 is strongly nonlinear, and the concentration of ozone also depends on many other factors, such as meteorological factors (temperature, relative humidity, etc.), atmospheric transport process, and the concentration of ozone precursor compounds (VOC, NOx, etc.). These characteristics mean that the prediction accuracy of existing statistical models is often not ideal when predicting ozone concentration; especially when predicting some extreme values, the prediction error is large [15].
- (2)
- Prediction method based on artificial neural network (ANN). ANN is one of the most commonly used machine learning methods for ozone prediction. The ANN, derived with limited prior knowledge, is a nonlinear prediction model [15,16]. Therefore, it can find the nonlinear relationship between meteorological and photochemical processes and ozone concentration at a particular site, and then realize the prediction of ozone concentration. By comparing the prediction results of ANN with MLR and ARIMA, scholars found that ANN is more effective than statistical models such as ARIMA and MLR [17,18,19,20].
- (3)
- Prediction method based on support vector machine (SVM). SVM is a machine learning technique that has been widely applied to regression cases and classification problems [21]. Like ANN, SVM is a machine learning technique commonly used for ozone prediction [22,23,24]. Through studies, scholars have found that SVR has greater superiority and accuracy compared with statistical prediction methods such as ARIMA and MLR [25]. However, some researchers [26] have pointed out that ANN and SVM are not perfect, and they believed that these two methods still have certain limitations in ozone prediction. They proposed that ANN and SVM are easy to produce overfitting and local minimum problems, resulting in a poor prediction stability of the prediction model.
- (4)
- Prediction method based on fuzzy set theory. In 1993, Song and Chissom proposed a fuzzy time series (FTS) based on fuzzy set theory. Subsequently, scholars tried to apply this theory to O3 prediction. Domanska and Wojtylak [27] proposed a prediction method based on fuzzy set theory which uses a fuzzy time series model to predict O3, CO, NO and other pollutants. Although the prediction results were satisfactory, the lack of uncertainty and instability analysis in this paper led to doubts about the reliability of the prediction method [28].
- (5)
- Prediction method based on deterministic models. Deterministic models are based on mathematical equations describing chemical and physical processes in the atmosphere [29], and follow the principle of cause and effect [15]. When using a deterministic model for prediction, the O3 reaction equation must be established first, and then a large amount of ozone precursor and meteorological parameter data should be collected. In these two works, the design of the reaction equation is the key. If the equation design is not considered properly, or the parameters are not appropriate, the accuracy of the prediction model will be greatly reduced.
3. Method Design
3.1. Design of Feature Construction Algorithm
| Algorithm 1. Feature Construction algorithm | |
| 1 | Inputs: The Original multivariate time series V, Maximum time delay, |
| 2 | Correlation coefficient threshold , Feature set |
| 3 | Outputs: Feature set |
| 4 | Whilei <= do % i is the time series delay value |
| 5 | While j <= m % m is the number of variables in |
| 6 | Calculate the correlation coefficient between and |
| 7 | if >= |
| 8 | = , = = j, % C is used to record candidate feature information |
| 9 | end if |
| 10 | End while |
| 11 | End while |
| 12 | Sort C in descending order according to the first column value of C% Sort by correlation coefficient |
| 13 | While |
| 14 | Generate feature based on the values of and |
| 15 | F = |
| 16 | End while |
| 17 | ReturnF |
3.2. Kernel Extreme Learning Machine (KELM)
3.3. Lioness Optimization Algorithm (LsOA)
- (1)
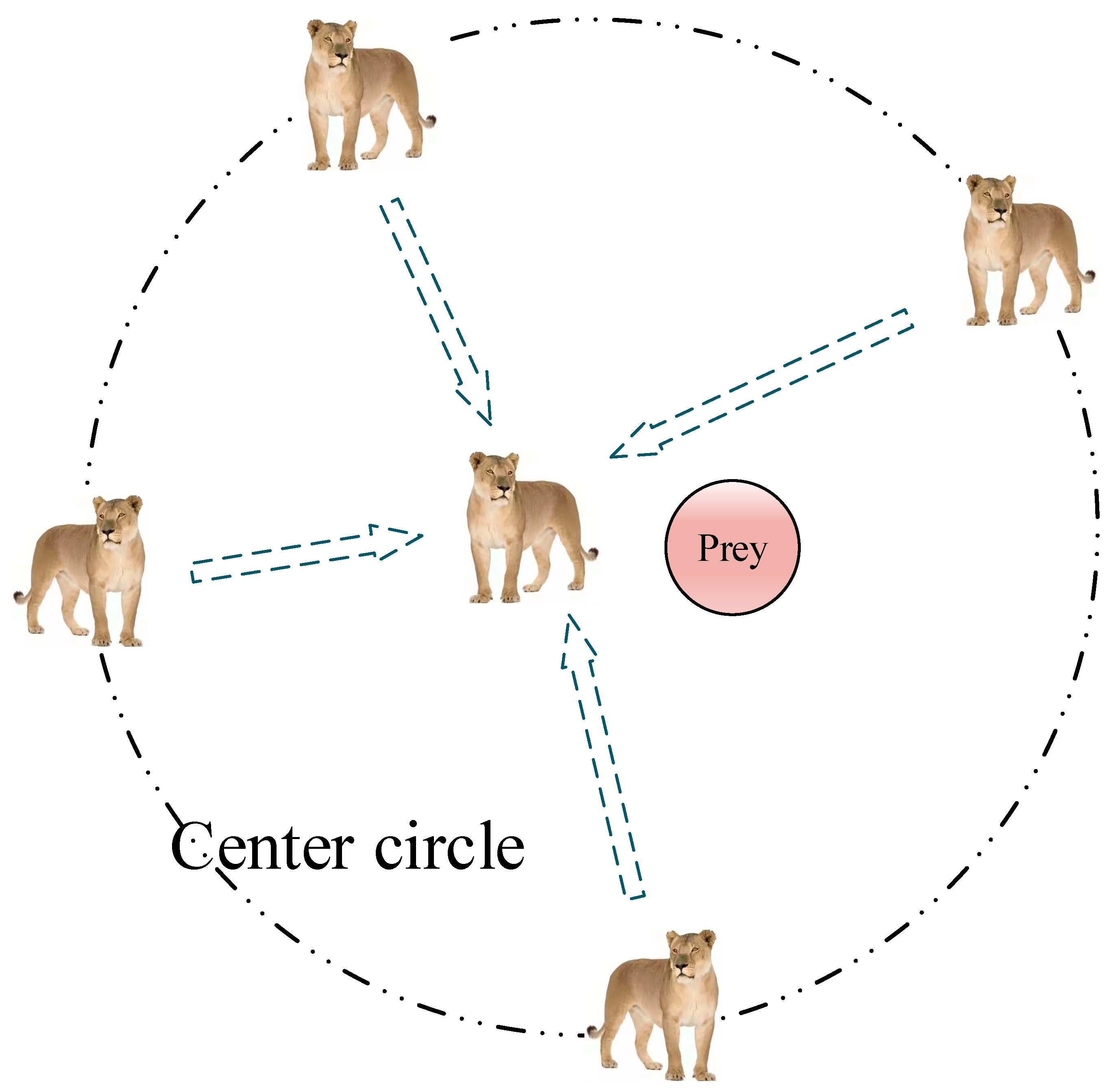
- Team hunting mechanism. This mechanism refers to the lionesses in the lion pride hunting in a cooperative way. When hunting in groups, lionesses often form a team for collective hunting. One part of the lioness (“wings”) surrounds the prey, and another part of the lioness (“center”) moves relative to the position of the other lioness (“wings”) and the prey. When a part of the lioness at the “wings” begins to charge towards the prey, the lioness in the “center” role will cautiously approach the target and use all the barriers that can be used as a cover to hide as much as possible. When the “central” lioness is close enough to its prey, it can suddenly pounce on the target and catch the prey. This mathematical model is as follows:where is the current iteration number, is the position vector of the lioness, is the distance between the current lioness and the prey, represents the dot product, and is the position vector of the prey. In these formulas, the calculation formulas of and are as follows:where , decreasing with the increase in iteration times. are both random vectors between [0, 1].
- (2)
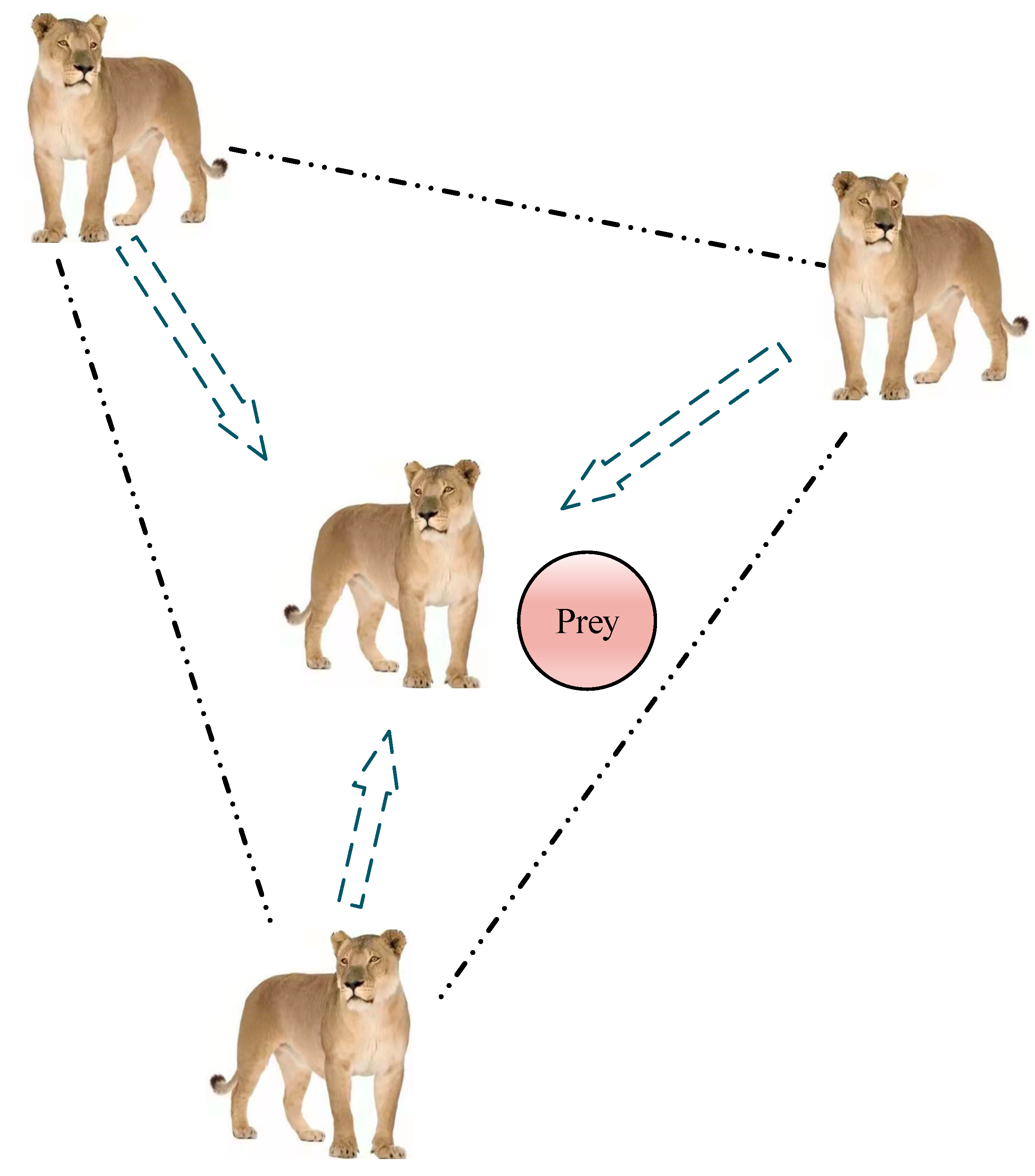
- Elite hunting mechanism. In addition to the team hunting, according to the theory of the survival of the fittest, the top lioness (the most physically strong lioness) sometimes hunts alone, that is, using the elite hunting mechanism. At this time, the population evolves into some agents of the elite through these agents to constantly test the direction and position of the elite and finally achieve the goal of capturing the prey. In order to avoid the risk of falling into a local optimum caused by relying only on a single elite position, here we draw on the principle of triangular stability, and replace the common method for determining the position of the elite from the common last-round best to a joint decision by the top three agent positions in the last-round fitness value. Figure 2 shows the construction process of the elite matrix.
- (3)
- The march strategy. With the increasing number of optimization iterations, the risk of the lions falling into local optimization increases. In order to enable the lions to quickly explore a new area, this paper designed the march strategy. The implication is that when , all dimensions of the predator are unified into a unique value. Otherwise, each dimension will randomly select a value in the to be updated with the following formula:where is used to generate pseudo-random integers and size() is used to return the size of the vector. M indicates the degree of influence of the march strategy on the process. The prey here is a matrix with the same dimension as the elite matrix.
- (4)
- Phase-focused strategy. The focus of the phase is to divide the lion hunting process into three phases, namely, the early iteration, the middle iteration and the late iteration [36]. Different search mechanisms were used for each stage. At the beginning of the iteration, the prey is energetic and moves fast. At this time, the lions disperse randomly in the search area and use Brownian motion to find the prey. This phase of the algorithm focuses on exploration. When the number of iterations reaches one-third, the lions begin to narrow the encircling circle to encircle the target prey. The prey being chased by the lions uses Levy flight to escape and flee, and individual elites of the lions also adopt Levy flight to chase the prey. At this phase, exploration is as important as exploitation. At the end of the iteration, as the physical strength of the target prey decreases and its speed slows down, it is no longer able to flee for a long distance. Meanwhile, the encircling circle of the lions becomes smaller and smaller, and the probability of capturing the prey increases greatly.
| Algorithm 2. Lioness Optimization Algorithm | |
| 1 | Initialize search agents(Prey) population = 1, …, n |
| 2 | Assign free parameters: = 0.2; = 0.5; = 0.5; = 0.9 |
| 3 | While Iter < Max_iter |
| 4 | Calculate the fitness of each search agent |
| 5 | = the best search agent |
| 6 | = the second best search agent |
| 7 | = the third best search agent |
| 8 | = the fourth best search agent |
| 9 | Update , , |
| 10 | If () % Team hunting |
| 11 | For each search agent |
| 12 | Update and by the Equations (12) and (13) |
| 13 | Use and to calculate |
| 14 | Calculate , , and by the Equation (15) |
| 15 | |
| 16 | Construct the “center circle”: |
| 17 | If () |
| 18 | Update the position of the current search agent by the Equation (19) |
| 19 | else if () |
| 20 | Update the position of the current search agent by the Equation (20) |
| 21 | end if |
| 22 | End for |
| 23 | Else if () % Elite hunting |
| 24 | Top_lioness_pos = |
| 25 | Construct the Elite matrix and accomplish memory saving |
| 26 | For each search agent |
| 27 | If Iter < Max_iter/3 |
| 28 | Update the position of the current search agent by the Equation (21) |
| 29 | else if Max_iter/3 < Iter < 2Max_iter/3 |
| 30 | For the first half of the populations (i = 1, …, n/2) |
| 31 | Update the position of the current search agent by the Equation (22) |
| 32 | End for |
| 33 | For the other half of the populations (i = n/2, …, n) |
| 34 | Update the position of the current search agent by the Equation (23) |
| 35 | End for |
| 36 | else if Iter > 2Max_iter/3 |
| 37 | Update the position of the current search agent by the Equation (24) |
| 38 | end if |
| 39 | End for |
| 40 | End if |
| 41 | Update Top_lioness_pos if there is a better solution |
| 42 | Applying FADs effect and update the position of the current search agent |
| 43 | Iter = Iter + 1 |
| 44 | End while |
| 45 | ReturnTop_lioness_pos |
3.4. Design of the Prediction Model
- (1)
- Randomly select 10% of the data from the training set excluding as the model validation set , which was used to test the performance of the KELM trained by the training set on the untrained data set. Its purpose is to test the generalization performance of the prediction model.
- (2)
- Instead of taking the training results of the model training set as the optimization object in common optimization algorithms, this paper redesigned the fitness function:where is the fitness function, is the position of the lioness, which is also the kernel parameter of KELM; as above, is the model training set and is the model validation set; means the absolute value. is the evaluation indicator of the fitting accuracy of KELM. In this paper, MAPE (mean absolute percentage error) was used, which is calculated as follows:
3.5. Comparison Methods
- (1)
- Multiple linear regression [37]. When performing regression analysis, we call regression with two or more independent variables under linear correlation conditions multiple linear regression (MLR). This method of predicting dependent variables using an optimal combination of several independent variables is usually more efficient than using only one independent variable for prediction or estimation. The mathematical equation of MLR is as follows:where is the observed value of the dependent variable, , is the value of the -th dimension of the input variable , is the regression coefficient of the input variable, , and its value is estimated using the ordinary least squares.
- (2)
- Gaussian process regression [38]. Gaussian process regression (GPR) is a nonparametric model that uses Gaussian process priors to perform a regression analysis on data, which provides flexibility for modeling stochastic processes. Compared with other models based on data parameters, GPR specifies a prior distribution over the function space, where the relationship between the data is encoded in the covariance function of the multivariate Gaussian distribution. The exponential square function, which is commonly used in many covariance functions, is shown in Equation (28).where is the variance and represents the noise degree of the data; is the characteristic length scale parameter (the larger the value, the smoother the function).
- (3)
- Back propagation neural network [39]. The back propagation neural network (BPNN) is a multi-layer feedforward network trained according to error back-propagation. The basic idea of BPNN is the gradient descent method, which uses gradient search technology to achieve the minimum mean square error between the real output value and the expected output value of the network. It is the most widely used neural network.
- (4)
- Support vector regression [40]. SVM is a class of generalized linear classifiers that perform binary classification of data in a supervised learning manner. Support vector regression (SVR) is an application model of support vector machine in regression problems. The core idea is to find a hyperplane (hypersurface) that minimizes the expected risk.
- (5)
- Kernel ridge regression [41]. Ridge regression [42] is a well-known technique from multiple linear regression that implements a regularized form of least-squares regression. Kernel ridge regression (KRR) introduces the kernel function on the basis of ridge regression, realizes the mapping of low-dimensional data in high-dimensional space, and further constructs a linear ridge regression model in high-dimensional feature space to realize nonlinear regression [41]. At present, KRR is widely used in pattern recognition, data mining and other fields.
- (6)
- Decision tree. Decision tree (DT) is a non-parametric supervised learning method used for classification and regression. The goal is to create a model that learns simple decision rules from data features to predict the value of a target variable.
- (7)
- Stochastic gradient descent regression [43]. Stochastic gradient descent (SGD) is a simple but highly efficient method which is mainly used for the discriminant learning of linear classifiers under convex loss functions, such as (linear) support vector machines and logistic regression. Stochastic gradient descent regression supports different loss functions and penalties to fit linear regression models.
- (8)
- GCN [44]. A graph convolutional network (GCN) is actually a feature extractor, which is the same as a convolutional neural network (CNN), but its object is graph data. It can be applied to richer topological structure data, such as social networks, recommendation systems, transportation networks, etc. These data are characterized by disorderly connections. GCN cleverly designs a method to extract features from graph data, so that we can use these features to perform node classification, graph classification and edge prediction, and also obtain embedded representation of the graph by the way, which is widely used.
- (9)
- GAT [45]. Graph attention network (GAT) aggregates neighbor nodes through the attention mechanism and realizes the adaptive allocation of different neighbor weights. This is different from GCN. The weights of different neighbors in GCN are fixed, and they all come from the normalized Laplacian matrix. GAT greatly improves the expressive ability of the graph neural network model.
- (10)
- LsOA-KELM. The LsOA-KELM model uses the LsOA for the parameter optimization of KELM. Compared with the model in this paper, the data processed by the LsOA-KELM model are all original data without feature construction. When using the LsOA-KELM model, the population size of LsOA was 30, and the number of iterations was set as 50. The kernel function of KELM was set to ‘RBF’, and the other parameters were the default values of the original algorithm.
- (11)
- FC-LsOA-KELM--. The FC-LsOA-KELM-- model adds a feature construction step on the basis of LsOA-KELM, and reconstructs the original data and hands it to LsOA-KELM for training and prediction. The main difference between this model and the FC-LsOA-KELM model is the lack of a correction step for the predicted values. The parameter setting of the FC-LsOA-KELM model was consistent with LsOA-KELM.
3.6. Evaluation Indicators
4. Research Results
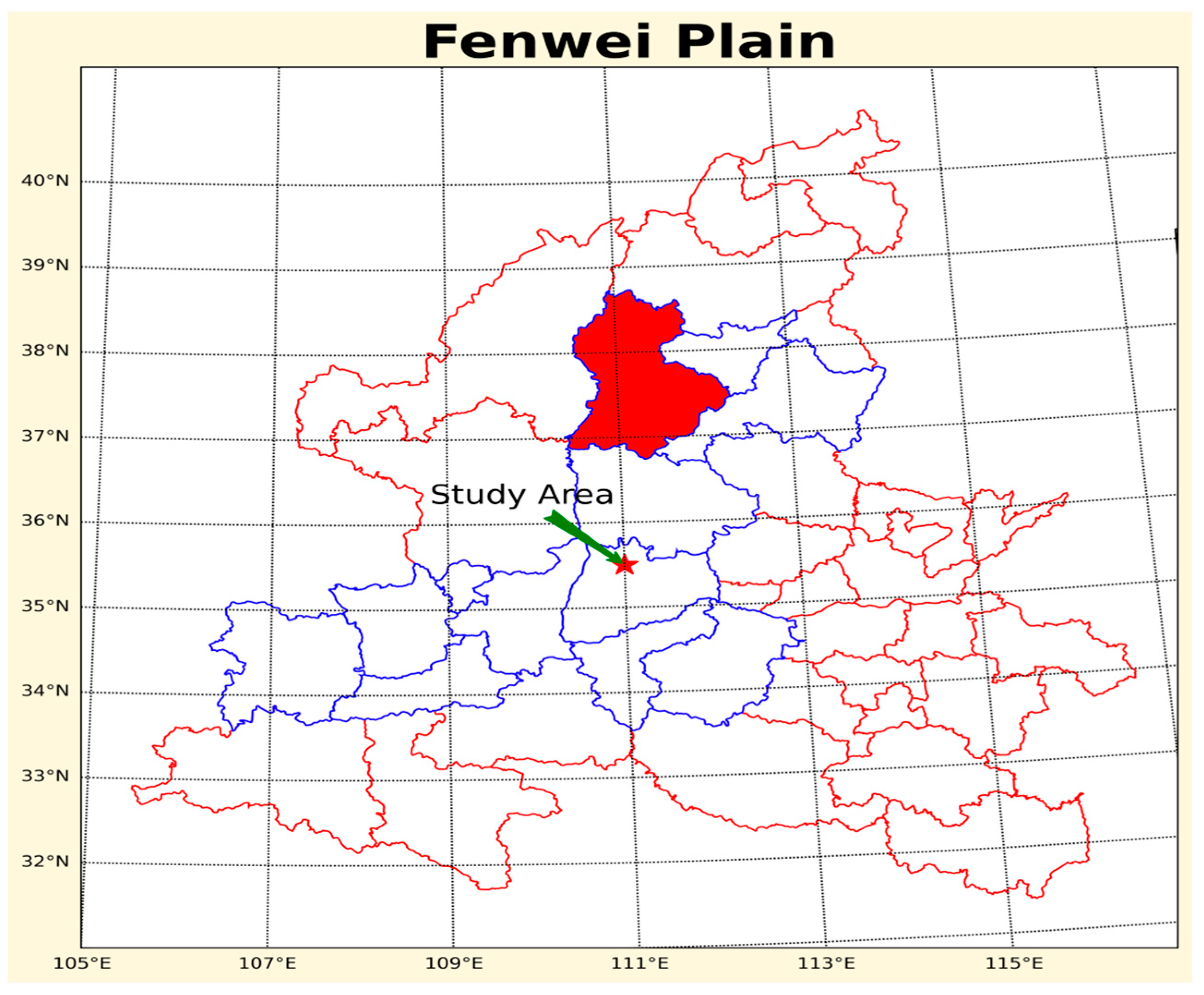
4.1. Research Area
4.2. Research Data
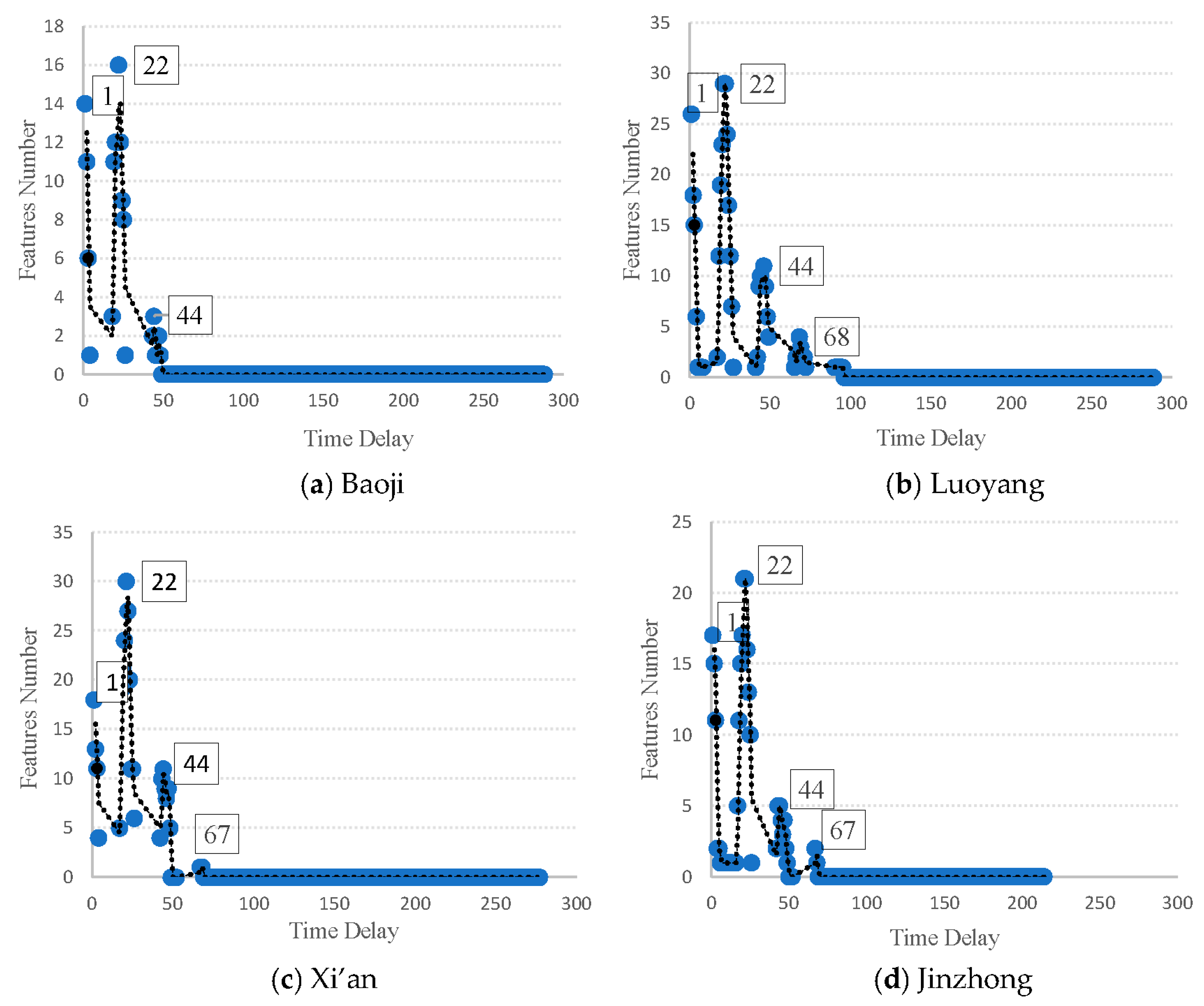
4.3. Feature Construction
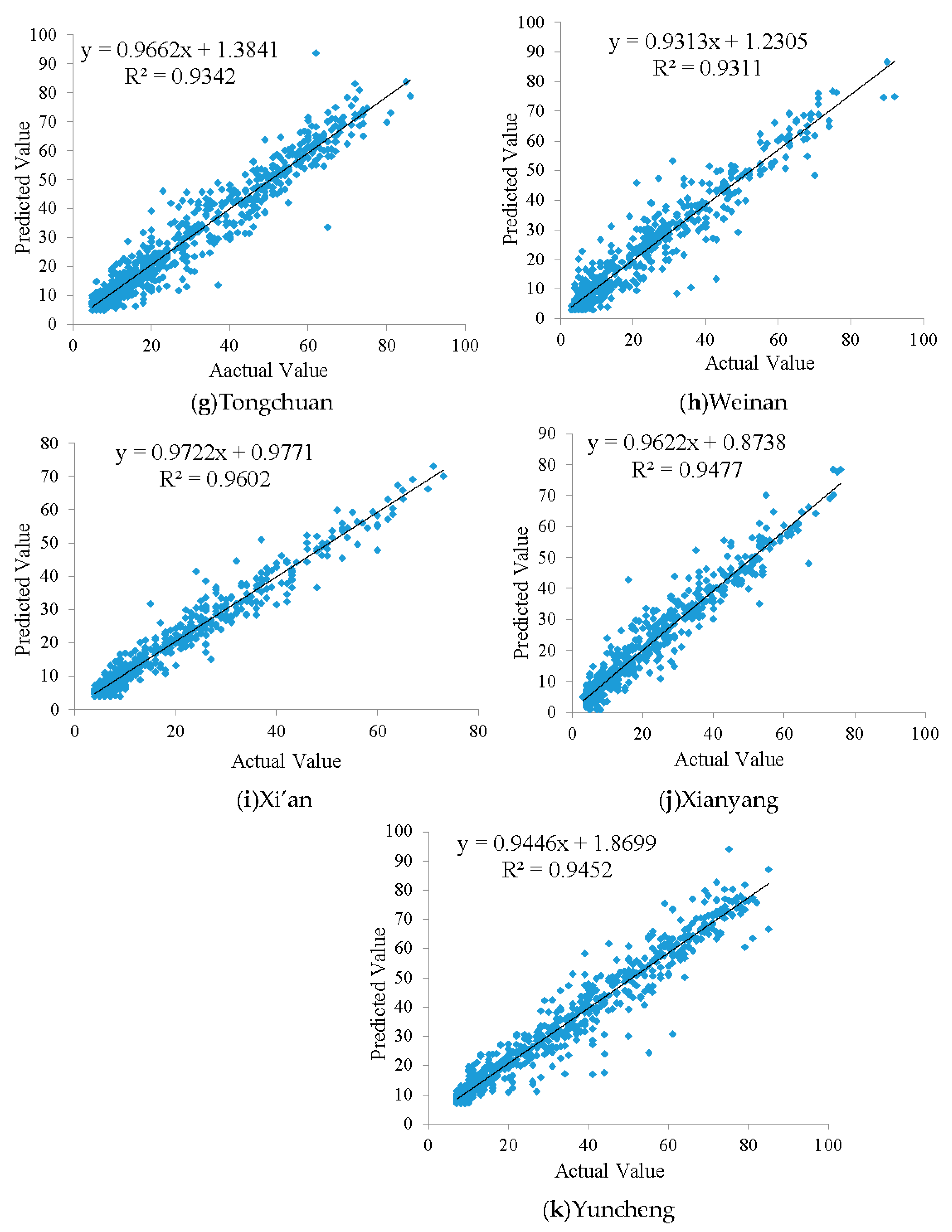
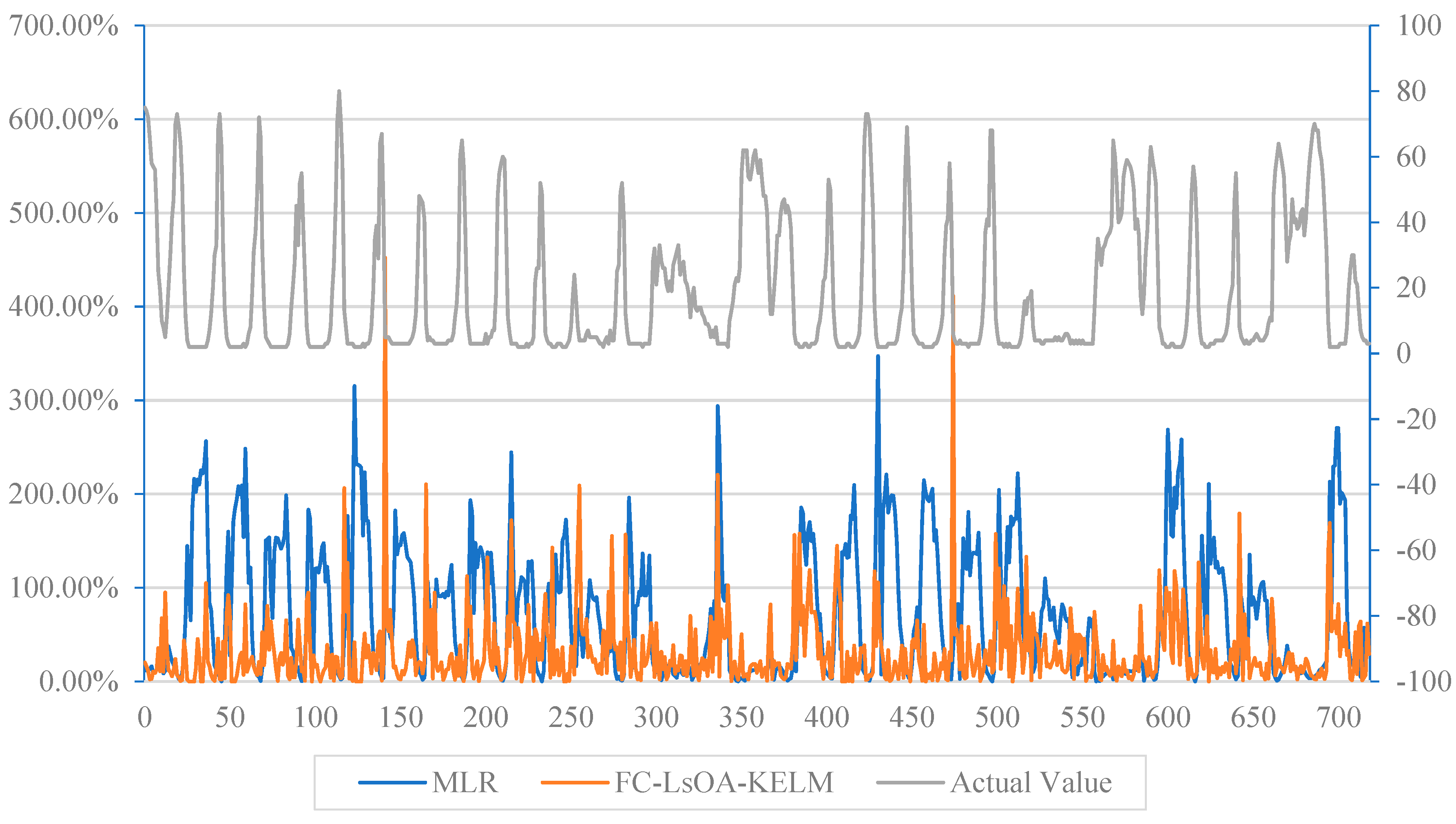
4.4. Result Analysis
4.5. Statistical Analysis
5. Conclusions
- (1)
- The selection and use of prediction features have a significant impact on the prediction performance of the prediction model. In this paper, when we used LsOA-KELM to train unselected and reconstructed air pollution data to build a predictive model to predict future values of O3 concentration, the prediction results were not ideal. In the evaluation of MAPE, RMSE and , LsOA-KELM was worse than BPNN, MLR and other methods. However, when LsOA-KELM was faced with the air pollution data reconstructed by the FC, its prediction performance was significantly improved.
- (2)
- The prediction feature set constructed by the feature construction method (FC) can not only mine the potential relationship between air pollutants, but also analyze the impact of historical pollutants on future pollutants, which is helpful for enriching the source of O3 prediction features, thereby helping the prediction model improve the accuracy of O3 predictions.
- (3)
- Using historical data to revise the prediction results can reduce the outliers in the model prediction caused by insufficient training of the prediction model, thereby helping the prediction model to improve the prediction accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| record candidate feature information | FC | coefficient vector | LsOA | ||
| coefficient vector | |||||
| threshold for correlation coefficient | coefficient vector | ||||
| correlation coefficient | adaptive parameter | ||||
| number of subsequences of the time series | distance between the lioness and the prey | ||||
| number of historical time points | hunting team’s “center circle” | ||||
| multivariate time series | elite matrix | ||||
| the th subsequence | current iteration number | ||||
| candidate features of the th subsequence | constant | ||||
| feature set | maximum iteration number | ||||
| a time delay | position vector of the prey | ||||
| maximum time delay | constant | ||||
| bias of the th hidden node | KELM | random vectors between [0, 1] | |||
| regularization coefficient | random number vector of Brownian motion | ||||
| activation function | uniform random vector in [0, 1] | ||||
| output matrix of the hidden layer | random number vector of Levy’s flight | ||||
| Moore-Penrose generalized inverse of matrix H | current iteration number | ||||
| identity matrix | position vector of the elite lioness | ||||
| kernel function | position vector of the lioness | ||||
| total number of samples | position vector of the lioness A with the best fitness | ||||
| input weight vector | position vector of the lioness B with the second highest fitness | ||||
| input vector | position vector of the lioness C with the third highest fitness | ||||
| expected output vector | position vector of the lioness D with the fourth highest fitness | ||||
| output matrix of the output layer | position vector adjusted by lioness A | ||||
| output weight matrix | position vector adjusted by lioness B | ||||
| output weight vector | position vector adjusted by lioness C | ||||
| inverse of the regularization coefficient | position vector adjusted by lioness D | ||||
| kernel matrix | the mean of |
Appendix A
| Methods | 2 | 3 | 4 | 5 | 6 | 7 |
| q0.05 | 1.960 | 2.241 | 2.394 | 2.498 | 2.576 | 2.638 |
| q0.10 | 1.645 | 1.960 | 2.128 | 2.241 | 2.326 | 2.394 |
| Methods | 8 | 9 | 10 | 11 | 12 | 13 |
| q0.05 | 2.690 | 2.724 | 2.774 | 3.219 | 3.268 | 3.313 |
| q0.10 | 2.450 | 2.498 | 2.539 | 2.978 | 3.030 | 3.077 |
References
- Hemming, B.L.; Harris, A.; Davidson, C.; U.S. EPA. Air Quality Criteria for Lead (2006) Final Report; U.S. Environmental Protection Agency: Washington, DC, USA, 2006; EPA/600/R-05/144aF-bF. [Google Scholar]
- Khatibi, R.; Naghipour, L.; Ghorbani, M.A.; Smith, M.S.; Karimi, V.; Farhoudi, R.; Delafrouz, H.; Arvanaghi, H. Developing a predictive tropospheric ozone model for Tabriz. Atmos. Environ. 2013, 68, 286–294. [Google Scholar] [CrossRef]
- Ordieres-Merè, J.; Ouarzazi, J.; Johra, B.E.; Gong, B. Predicting ground level ozone in Marrakesh by machine-learning techniques. J. Environ. Inform. 2020, 36, 93–106. [Google Scholar] [CrossRef]
- Yang, L.; Xie, D.; Yuan, Z.; Huang, Z.; Wu, H.; Han, J.; Liu, L. Quantification of regional ozone pollution characteristics and its temporal evolution: Insights from the identification of the impacts of meteorological conditions and emissions. Atmosphere 2021, 12, 279. [Google Scholar] [CrossRef]
- Bell, M.L.; Peng, R.D.; Dominici, F. The Exposure–Response Curve for Ozone and Risk of Mortality and the Adequacy of Current Ozone Regulations. Environ. Health Perspect. 2006, 114, 532–536. [Google Scholar] [CrossRef] [PubMed]
- Mills, G.; Buse, A.; Gimeno, B.; Bermejo, V.; Holland, M.; Emberson, L.; Pleijel, H. A synthesis of AOT40-based response functions and critical levels of ozone for agricultural and horticultural crops. Atmos. Environ. 2007, 41, 2630–2643. [Google Scholar] [CrossRef]
- Riga, M.; Stocker, M.; Ronkko, M.; Karatzas, K.; Kolehmainen, M. Atmospheric Environment and Quality of Life Information Extraction from Twitter with the Use of Self-Organizing Maps. J. Environ. Inform. 2015, 26, 27–40. [Google Scholar] [CrossRef]
- Duenas, C.; Fernandez, M.C.; Canete, S.; Carretero, J.; Liger, E. Stochastic model to forecast ground-level ozone concentration at urban and rural areas. Chemosphere 2005, 61, 1379–1389. [Google Scholar] [CrossRef]
- Kumar, K.; Yadav, A.K.; Singh, M.P.; Hassan, H.; Jain, V.K. Forecasting Daily Maximum Surface Ozone Concentrations in Brunei Darussalam—An ARIMA Modeling Approach. J. Air Waste Manag. Assoc. 2004, 54, 809–814. [Google Scholar] [CrossRef]
- Hubbard, M.C.; Cobourn, W.G. Development of a regression model to forecast ground-level ozone concentration in Louisville, KY. Atmos. Environ. 1998, 32, 2637–2647. [Google Scholar] [CrossRef]
- Kovač-Andrić, E.; Sheta, A.; Faris, H.; Gajdošik, M.Š. Forecasting ozone concentrations in the east of Croatia using nonparametric neural network models. J. Earth Syst. Sci. 2016, 125, 997–1006. [Google Scholar] [CrossRef][Green Version]
- Allu, S.K.; Srinivasan, S.; Maddala, R.K.; Reddy, A.; Anupoju, G.R. Seasonal ground level ozone prediction using multiple linear regression (MLR) model. Model. Earth Syst. Environ. 2020, 6, 1981–1989. [Google Scholar] [CrossRef]
- Iglesias-Gonzalez, S.; Huertas-Bolanos, M.E.; Hernandez-Paniagua, I.Y.; Mendoza, A. Explicit Modeling of Meteorological Explanatory Variables in Short-Term Forecasting of Maximum Ozone Concentrations via a Multiple Regression Time Series Framework. Atmosphere 2020, 11, 1304. [Google Scholar] [CrossRef]
- Oufdou, H.; Bellanger, L.; Bergam, A.; Khomsi, K. Forecasting daily of surface ozone concentration in the Grand Casablanca region using parametric and nonparametric statistical models. Atmosphere 2021, 12, 666. [Google Scholar] [CrossRef]
- Pawlak, I.; Jarosawski, J. Forecasting of Surface Ozone Concentration by Using Artificial Neural Networks in Rural and Urban Areas in Central Poland. Atmosphere 2019, 10, 52. [Google Scholar] [CrossRef]
- Kumar, P.; Lai, S.H.; Wong, J.K.; Mohd, N.S.; Kamal, M.R.; Afan, H.A.; Ahmed, A.N.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Review of Nitrogen Compounds Prediction in Water Bodies Using Artificial Neural Networks and Other Models. Sustainability 2020, 12, 4359. [Google Scholar] [CrossRef]
- Spellman, G. An application of artificial neural networks to the prediction of surface ozone concentrations in the United Kingdom. Appl. Geogr. 1999, 19, 123–136. [Google Scholar] [CrossRef]
- Chaloulakou, A.; Saisana, M.; Spyrellis, N. Comparative assessment of neural networks and regression models for forecasting summertime ozone in Athens. Sci. Total Environ. 2003, 313, 1–13. [Google Scholar] [CrossRef]
- Sousa, S.; Martins, F.G.; Alvim-Ferraz, M.; Pereira, M.C. Multiple linear regression and artificial neural networks based on principal components to predict ozone concentrations. Environ. Model. Softw. 2007, 22, 97–103. [Google Scholar] [CrossRef]
- AlOmar, M.K.; Hameed, M.M.; AlSaadi, M.A. Multi hours ahead prediction of surface ozone gas concentration: Robust artificial intelligence approach. Atmos. Pollut. Res. 2020, 11, 1572–1587. [Google Scholar] [CrossRef]
- Faris, S.; Alivernini, A.; Conte, A.; Maggi, F. Ozone and particle fluxes in a Mediterranean forest predicted by the AIRTREE model. Sci. Total Environ. 2019, 682, 494–504. [Google Scholar] [CrossRef]
- Luna, A.S.; Paredes, M.; Oliveira, G.; Corrêa, S.M. Prediction of ozone concentration in tropospheric levels using artificial neural networks and support vector machine at Rio de Janeiro, Brazil. Atmos. Environ. 2014, 98, 98–104. [Google Scholar] [CrossRef]
- Quej, V.H.; Almorox, J.; Arnaldo, J.A.; Saito, L. ANFIS, SVM and ANN soft-computing techniques to estimate daily global solar radiation in a warm sub-humid environment. J. Atmos. Sol.-Terr. Phys. 2017, 155, 62–70. [Google Scholar] [CrossRef]
- Faleh, R.; Bedoui, S.; Kachouri, A. Ozone monitoring using support vector machine and K-nearest neighbors methods. J. Electr. Electron. Eng. 2017, 10, 49–52. [Google Scholar]
- Su, X.; An, J.; Zhang, Y.; Zhu, P.; Zhu, B. Prediction of ozone hourly concentrations by support vector machine and kernel extreme learning machine using wavelet transformation and partial least squares methods. Atmos. Pollut. Res. 2020, 11, 51–60. [Google Scholar] [CrossRef]
- Lu, W.Z.; Wang, D. Learning machines: Rationale and application in ground-level ozone prediction. Appl. Soft Comput. J. 2014, 24, 135–141. [Google Scholar] [CrossRef]
- Domanska, D.; Wojtylak, M. Application of fuzzy time series models for forecasting pollution concentrations. Expert Syst. Appl. 2012, 39, 7673–7679. [Google Scholar] [CrossRef]
- Yafouz, A.; Najah, A.; Zaini, A.; El-Shafie, A. Ozone Concentration Forecasting Based on Artificial Intelligence Techniques: A Systematic Review. Water Air Soil Pollut. 2021, 232, 79. [Google Scholar] [CrossRef]
- Vautard, R.; Beekmann, M.; Roux, J.; Gombert, D. Validation of a hybrid forecasting system for the ozone concentrations over the Paris area. Atmos. Environ. 2001, 35, 2449–2461. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme Learning Machines: A Survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004. [Google Scholar]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme Learning Machine for Regression and Multiclass Classification. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2012, 42, 513–529. [Google Scholar] [CrossRef] [PubMed]
- Holland, J.H. Genetic algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, MHS’95, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A Nature-inspired Metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Yuchi, W.; Gombojav, E.; Boldbaatar, B.; Galsuren, J.; Enkhmaa, S.; Beejin, B.; Naidan, G.; Ochir, C.; Legtseg, B.; Byambaa, T.; et al. Evaluation of random forest regression and multiple linear regression for predicting indoor fine particulate matter concentrations in a highly polluted city. Environ. Pollut. 2019, 245, 746–753. [Google Scholar] [CrossRef]
- Cao, Q.D.; Miles, S.B.; Choe, Y. Infrastructure recovery curve estimation using Gaussian process regression on expert elicited data. Reliab. Eng. Syst. Saf. 2022, 217, 108054. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Chen, T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Support vector machines for classification and regression. Analyst 2010, 135, 230–267. [Google Scholar] [CrossRef]
- Cawley, G.C.; Talbot, N.; Foxall, R.J.; Dorling, S.R.; Mandic, D.P. Heteroscedastic kernel ridge regression. Neurocomputing 2004, 57, 105–124. [Google Scholar] [CrossRef]
- Banerjee, K.S.; Carr, R.N. Ridge regression-Biased estimation for non-orthogonal problems. Technometrics 1971, 12, 55–67. [Google Scholar] [CrossRef]
- Ighalo, J.O.; Adeniyi, A.G.; Marques, G. Application of linear regression algorithm and stochastic gradient descent in a machine-learning environment for predicting biomass higher heating value. Biofuels Bioprod. Biorefining 2020, 14, 1286–1295. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. arXiv 2017, arXiv:1710.10903. [Google Scholar]
- Zar, J.H. Biostatistical Analysis. Q. Rev. Biol. 2010, 18, 797–799. [Google Scholar] [CrossRef]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar] [CrossRef]




| Key Parameters | Parameter Introduction (Accessed on 1 May 2022) | Advantages and Disadvantages | |
|---|---|---|---|
| MLR | fit_intercept=True, normalize=‘False’ | https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression | advantages: simple modeling; easy explanation; fast running speed disadvantages: does not fit nonlinear data very well |
| SVR | kernel=‘poly’, C=1.1, gamma=‘auto’, degree=3, epsilon=0.1, coef0=1.0 | https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVR.html#sklearn.svm.SVR | advantages: robust to outliers; solve high-dimensional problems; excellent generalization ability disadvantages: not suitable for large-scale data; sensitive to missing data |
| BPNN | hidden layer nodes=30 | advantages: self-learning and adaptive ability; high-speed optimization; parallel processing capability disadvantages: a large number of parameters; difficult to explain; a risk of falling into local optimal | |
| GPR | kernel=DotProduct() + WhiteKernel(), random_state=0 | https://scikit-learn.org/stable/modules/generated/sklearn.gaussian_process.GaussianProcessRegressor.html#sklearn.gaussian_process.GaussianProcessRegressor | advantages: fits nonlinear data; predicted values are probabilistic; interpretability disadvantages: determination of covariance function; nonparametric model; high complexity when the amount of data is large |
| KRR | alpha=1, kernel=‘linear’, gamma=None, degree=3, coef0=1 | https://scikit-learn.org/stable/modules/generated/sklearn.kernel_ridge.KernelRidge.html | advantages: kernel function, which is more flexible; fits nonlinear relationships well; data can be mapped to high-dimensional space disadvantages: high computational cost and large amount of computation |
| DT | criterion=‘squared_error’ | https://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeRegressor.html#sklearn.tree.DecisionTreeRegressor | advantages: easy to understand and explain; easy to implement; insensitive to missing values; disadvantages: prone to overfitting |
| SGD | loss=‘squared_error’, penalty=‘l2’, alpha=0.0001, max_iter=1000, tol=0.001 | https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.SGDRegressor.html#sklearn.linear_model.SGDRegressor | advantages: fast running speed disadvantages: poor convergence performance; local minimum may be obtained, and the accuracy is not high |
| GCN | hidden layer nodes=6 | advantages: suitable for nodes and graphs of any topology; disadvantages: all neighbor nodes are assigned the same weight; completely dependent on the graph structure | |
| GAT | hidden layer nodes=6 | advantages: using the attention mechanism, different weights can be assigned to different neighbor nodes; not completely dependent on the graph structure disadvantages: when the neighborhoods are highly overlapping, a lot of redundant computations are involved |
| Region | Baoji | Jinzhong | Linfen | Luoyang | Lvliang | Sanmenxia | Tongchuan | Weinan | Xi’an | Xianyang | Yuncheng |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Number of Features | 126 | 215 | 195 | 328 | 79 | 232 | 111 | 218 | 278 | 202 | 309 |
| CITY | MLR | GPR | BPNN | SVR | KRR | DT | SGD | GCN | GAT | LsOA- KELM | FC- LsOA- KELM-- | FC- LsOA- KELM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baoji | 18.43% | 20.17% | 15.01% | 36.08% | 18.08% | 21.42% | 27.51% | 46.33% | 35.05% | 18.52% | 10.99% | 10.96% |
| Jinzhong | 29.28% | 46.11% | 23.71% | 36.53% | 36.53% | 30.27% | 34.71% | 50.20% | 48.77% | 29.78% | 20.48% | 20.09% |
| Linfen | 38.40% | 73.25% | 40.18% | 140.49% | 40.37% | 34.52% | 59.60% | 52.49% | 79.49% | 96.91% | 23.79% | 22.00% |
| Luoyang | 31.09% | 40.56% | 31.79% | 95.34% | 36.67% | 29.74% | 44.18% | 69.16% | 82.85% | 32.58% | 20.91% | 20.83% |
| Lvliang | 72.50% | 97.01% | 61.00% | 297.32% | 76.58% | 38.91% | 85.12% | 57.07% | 75.03% | 76.66% | 34.53% | 31.71% |
| Sanmenxia | 32.28% | 44.91% | 25.61% | 103.66% | 35.37% | 36.45% | 39.43% | 36.86% | 50.31% | 31.79% | 20.79% | 20.66% |
| Tongchuan | 24.97% | 28.82% | 19.37% | 42.41% | 27.23% | 29.80% | 30.19% | 46.30% | 38.13% | 24.93% | 17.12% | 16.77% |
| Weinan | 45.83% | 49.57% | 33.18% | 175.69% | 50.94% | 41.61% | 61.73% | 60.27% | 88.39% | 42.19% | 22.00% | 21.63% |
| Xi’an | 32.58% | 41.42% | 21.21% | 58.56% | 32.33% | 25.75% | 57.70% | 54.91% | 83.77% | 20.82% | 17.04% | 16.33% |
| Xianyang | 39.36% | 48.00% | 38.23% | 121.86% | 49.11% | 30.35% | 66.77% | 52.84% | 66.73% | 37.68% | 20.46% | 20.38% |
| Yuncheng | 21.75% | 31.47% | 19.27% | 55.65% | 25.23% | 21.25% | 27.95% | 36.46% | 33.42% | 23.09% | 14.69% | 14.56% |
| Average | 35.13% (5) | 47.39% (8) | 29.87% (3) | 105.78% (12) | 38.95% (6) | 30.92% (4) | 48.63% (9) | 51.17% (10) | 61.99% (11) | 39.54% (7) | 20.25% (2) | 19.63% (1) |
| CITY | MLR | GPR | BPNN | SVR | KRR | DT | SGD | GCN | GAT | LsOA- KELM | FC- LsOA- KELM-- | FC- LsOA- KELM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baoji | 6.0387 | 6.2340 | 4.9951 | 7.3118 | 5.9949 | 7.6410 | 7.1130 | 13.7306 | 11.0259 | 6.0634 | 3.8903 | 3.8899 |
| Jinzhong | 6.7307 | 7.9415 | 6.4126 | 7.1433 | 7.1433 | 9.5298 | 7.5211 | 11.4633 | 10.4303 | 6.6280 | 5.4699 | 5.4377 |
| Linfen | 7.6286 | 10.5295 | 7.4877 | 13.7167 | 7.9837 | 9.3066 | 8.8934 | 10.6429 | 12.3162 | 12.5136 | 5.8552 | 5.7987 |
| Luoyang | 5.7315 | 6.2975 | 5.2057 | 9.2403 | 5.8818 | 7.6821 | 6.7448 | 11.8725 | 13.6997 | 5.8018 | 4.0487 | 4.0454 |
| Lvliang | 4.3497 | 6.5708 | 5.8295 | 14.0666 | 5.6420 | 10.6836 | 4.6932 | 9.9392 | 8.6261 | 6.9900 | 6.3899 | 6.3164 |
| Sanmenxia | 6.5610 | 7.6068 | 6.3408 | 10.4989 | 6.8107 | 9.3511 | 7.3729 | 10.3181 | 9.3824 | 6.4893 | 5.2770 | 5.2595 |
| Tongchuan | 6.7897 | 7.1010 | 6.5860 | 8.2193 | 6.8189 | 9.8223 | 7.3982 | 14.8928 | 11.2797 | 6.7131 | 5.2050 | 5.1898 |
| Weinan | 6.8271 | 7.3700 | 6.0154 | 12.9803 | 7.1069 | 8.1725 | 7.6357 | 9.6211 | 11.6963 | 6.4087 | 4.8395 | 4.8250 |
| Xi’an | 5.0065 | 5.4275 | 4.1472 | 6.8488 | 4.9635 | 6.1154 | 6.6992 | 10.0322 | 11.8799 | 3.8726 | 2.9850 | 2.9415 |
| Xianyang | 5.8522 | 6.2894 | 5.6366 | 11.0173 | 6.1698 | 7.3127 | 7.8243 | 9.1366 | 8.9809 | 5.8797 | 3.9272 | 3.9186 |
| Yuncheng | 7.3365 | 8.4255 | 6.9595 | 10.1973 | 7.4415 | 8.4045 | 8.3762 | 14.1279 | 12.7037 | 7.3362 | 5.2392 | 5.2369 |
| Average | 6.2593 (4) | 7.2540 (7) | 5.9651 (3) | 10.1128 (10) | 6.5415 (5) | 8.5474 (9) | 7.2975 (8) | 11.4343 (12) | 11.0928 (11) | 6.7906 (6) | 4.8297 (2) | 4.8054 (1) |
| CITY | MLR | GPR | BPNN | SVR | KRR | DT | SGD | GCN | GAT | LsOA- KELM | FC- LsOA- KELM-- | FC- LsOA- KELM |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Baoji | 0.1191 | 0.1269 | 0.0815 | 0.1746 | 0.1174 | 0.1907 | 0.1653 | 0.6158 | 0.3971 | 0.1201 | 0.0494 | 0.0494 |
| Jinzhong | 0.1123 | 0.1563 | 0.1019 | 0.1265 | 0.1265 | 0.2251 | 0.1402 | 0.3258 | 0.2697 | 0.1089 | 0.0742 | 0.0733 |
| Linfen | 0.1332 | 0.2538 | 0.1284 | 0.4308 | 0.1459 | 0.1983 | 0.1811 | 0.2593 | 0.3473 | 0.3585 | 0.0785 | 0.0770 |
| Luoyang | 0.0814 | 0.0983 | 0.0672 | 0.2116 | 0.0857 | 0.1462 | 0.1127 | 0.3493 | 0.4651 | 0.0834 | 0.0406 | 0.0406 |
| Lvliang | 0.0434 | 0.0991 | 0.0780 | 0.4543 | 0.0731 | 0.2621 | 0.0506 | 0.2268 | 0.1708 | 0.1122 | 0.0937 | 0.0916 |
| Sanmenxia | 0.1292 | 0.1737 | 0.1207 | 0.3309 | 0.1392 | 0.2625 | 0.1632 | 0.3196 | 0.2642 | 0.1264 | 0.0836 | 0.0830 |
| Tongchuan | 0.1152 | 0.1260 | 0.1084 | 0.1688 | 0.1162 | 0.2410 | 0.1367 | 0.5541 | 0.3178 | 0.1126 | 0.0677 | 0.0673 |
| Weinan | 0.1380 | 0.1608 | 0.1071 | 0.4989 | 0.1496 | 0.1978 | 0.1726 | 0.2741 | 0.4051 | 0.1216 | 0.0693 | 0.0689 |
| Xi’an | 0.1197 | 0.1407 | 0.0821 | 0.2240 | 0.1177 | 0.1786 | 0.2143 | 0.4807 | 0.6740 | 0.0716 | 0.0426 | 0.0413 |
| Xianyang | 0.1173 | 0.1355 | 0.1089 | 0.4159 | 0.1304 | 0.1832 | 0.2098 | 0.2860 | 0.2764 | 0.1184 | 0.0528 | 0.0526 |
| Yuncheng | 0.1076 | 0.1419 | 0.0968 | 0.2079 | 0.1107 | 0.1412 | 0.1403 | 0.3991 | 0.3227 | 0.1076 | 0.0549 | 0.0548 |
| Average | 0.1106 (4) | 0.1467 (7) | 0.0983 (3) | 0.2949 (10) | 0.1193 (5) | 0.2024 (9) | 0.1533 (8) | 0.3719 (12) | 0.3555 (11) | 0.1310 (6) | 0.0643 (2) | 0.0636 (1) |
| CITY | Baoji | Jinzhong | Linfen | Luoyang | Lvliang | Sanmenxia | Tongchuan | Weinan | Xi’an | Xianyang | Yuncheng |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.5 | 617 | 2066 | 1553 | 3043 | 365 | 1354 | 589 | 972 | 1356 | 901 | 2737 |
| 0.6 | 126 | 215 | 195 | 328 | 79 | 232 | 111 | 218 | 278 | 202 | 309 |
| 0.7 | 18 | 23 | 29 | 38 | 6 | 27 | 18 | 31 | 57 | 28 | 34 |
| NO. | Friedman Mean Rank | MAPE | RMSE | |
|---|---|---|---|---|
| 1 | Multiple Linear Regression(MLR) | 5.18 | 4.45 | 4.45 |
| 2 | Gaussian Process Regression(GPR) | 8.45 | 7.55 | 7.55 |
| 3 | Back Propagation Neural Network(BPNN) | 3.82 | 3.18 | 3.18 |
| 4 | Support Vector Regression(SVR) | 11.41 | 10.41 | 10.41 |
| 5 | Kernel Ridge Regression(KRR) | 6.77 | 5.41 | 5.41 |
| 6 | Decision Tree(DT) | 4.91 | 9.00 | 9.00 |
| 7 | Stochastic Gradient Descent(SGD) | 9.09 | 7.27 | 7.27 |
| 8 | Graph Convolutional Network(GCN) | 9.36 | 11.00 | 11.00 |
| 9 | Graph Attention Network(GAT) | 10.27 | 10.73 | 10.73 |
| 10 | LsOA-KELM | 5.73 | 5.27 | 5.27 |
| 11 | FC-LsOA-KELM-- | 2.00 | 2.36 | 2.36 |
| 12 | FC-LsOA-KELM | 1.00 | 1.36 | 1.36 |
| FC-LsOA-KELM vs. | Rank | z-Value | p-Value | a/i(0.05) | a/i(0.1) |
|---|---|---|---|---|---|
| MLR | 5.18 | −2.934 | 0.00335 | 0.00455 | 0.00909 |
| GPR | 8.45 | −2.934 | 0.00335 | 0.005 | 0.01 |
| BPNN | 3.82 | −2.934 | 0.00335 | 0.00556 | 0.01111 |
| SVR | 11.41 | −2.934 | 0.00335 | 0.00625 | 0.0125 |
| KRR | 6.77 | −2.934 | 0.00335 | 0.00714 | 0.01429 |
| DT | 4.91 | −2.934 | 0.00335 | 0.00833 | 0.01667 |
| SGD | 9.09 | −2.934 | 0.00335 | 0.01 | 0.02 |
| GCN | 9.36 | −2.934 | 0.00335 | 0.0125 | 0.025 |
| GAT | 10.27 | −2.934 | 0.00335 | 0.01667 | 0.03333 |
| LsOA-KELM | 5.73 | −2.934 | 0.00335 | 0.025 | 0.05 |
| FC-LsOA-KELM-- | 2.00 | −2.934 | 0.00335 | 0.05 | 0.1 |
| FC-LsOA-KELM vs. | Rank | z-Value | p-Value | a/i(0.05) | a/i(0.1) |
|---|---|---|---|---|---|
| GPR | 7.55 | −2.934 | 0.00335 | 0.00455 | 0.00909 |
| SVR | 10.41 | −2.934 | 0.00335 | 0.005 | 0.01 |
| DT | 9.00 | −2.934 | 0.00335 | 0.00556 | 0.01111 |
| GCN | 11.00 | −2.934 | 0.00335 | 0.00625 | 0.0125 |
| GAT | 10.73 | −2.934 | 0.00335 | 0.00714 | 0.01429 |
| LsOA-KELM | 5.27 | −2.934 | 0.00335 | 0.00833 | 0.01667 |
| FC-LsOA-KELM-- | 2.36 | −2.934 | 0.00335 | 0.01 | 0.02 |
| BPNN | 3.18 | −2.845 | 0.00444 | 0.0125 | 0.025 |
| KRR | 5.41 | −2.845 | 0.00444 | 0.01667 | 0.03333 |
| SGD | 7.27 | −2.845 | 0.00444 | 0.025 | 0.05 |
| MLR | 4.45 | −2.934 | 0.02080 | 0.05 | 0.1 |
| FC-LsOA-KELM vs. | Rank | z-Value | p-Value | a/i(0.05) | a/i(0.1) |
|---|---|---|---|---|---|
| GPR | 7.55 | −2.934 | 0.00335 | 0.00455 | 0.00909 |
| SVR | 10.41 | −2.934 | 0.00335 | 0.005 | 0.01 |
| DT | 9.00 | −2.934 | 0.00335 | 0.00556 | 0.01111 |
| GCN | 11.00 | −2.934 | 0.00335 | 0.00625 | 0.0125 |
| GAT | 10.73 | −2.934 | 0.00335 | 0.00714 | 0.01429 |
| LsOA-KELM | 5.27 | −2.934 | 0.00335 | 0.00833 | 0.01667 |
| FC-LsOA-KELM-- | 2.36 | −2.934 | 0.00335 | 0.01 | 0.02 |
| BPNN | 3.18 | −2.845 | 0.00444 | 0.0125 | 0.025 |
| KRR | 5.41 | −2.845 | 0.00444 | 0.01667 | 0.03333 |
| SGD | 7.27 | −2.845 | 0.00444 | 0.025 | 0.05 |
| MLR | 4.45 | −2.490 | 0.01279 | 0.05 | 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Ren, X. Prediction of Ozone Hourly Concentrations Based on Machine Learning Technology. Sustainability 2022, 14, 5964. https://doi.org/10.3390/su14105964
Li D, Ren X. Prediction of Ozone Hourly Concentrations Based on Machine Learning Technology. Sustainability. 2022; 14(10):5964. https://doi.org/10.3390/su14105964
Chicago/Turabian StyleLi, Dong, and Xiaofei Ren. 2022. "Prediction of Ozone Hourly Concentrations Based on Machine Learning Technology" Sustainability 14, no. 10: 5964. https://doi.org/10.3390/su14105964
APA StyleLi, D., & Ren, X. (2022). Prediction of Ozone Hourly Concentrations Based on Machine Learning Technology. Sustainability, 14(10), 5964. https://doi.org/10.3390/su14105964






