Modeling HDV and CAV Mixed Traffic Flow on a Foggy Two-Lane Highway with Cellular Automata and Game Theory Model
Abstract
:1. Introduction
- To the best of our knowledge, this study is among the first to address a new problem of modeling mixed traffic flow in foggy weather. Foggy weather would affect the visibility and make the mixed traffic flow more complicated. Thus, we aim to model the mixed traffic flow and analyze its characteristics under different visibility levels.
- We propose four different car-following models within a two-lane highway scenario for mixed traffic flow by considering the limited visibility in foggy weather.
- We develop a game-theoretical approach to lane-changing policies for CAVs, considering the interaction between CAVs and surrounding vehicles (HDV/CAV). Compared with the traditional lane-changing rules, such as the lane-changing rule in STCA, the proposed lane-changing strategy could increase the speed of the mixed traffic flow.
2. Literature Review
2.1. Driving Behavior in Foggy Conditions
2.2. Mixed Traffic Flow Models in Highway
2.3. Cellular Automata Model in Traffic Simulation
3. Problem Formulation
3.1. The Car-Following Rules
3.1.1. HDV–HDV/CAV
- Acceleration.
- (1)
- When , and the preceding vehicle is in the scope of visibility, which means , if , then the HDV will accelerate with the probability according to the following acceleration rule:
- (2)
- When , and the preceding vehicle is not in the scope of visibility, which means , then the HDV will adjust its speed within the visible distance. The acceleration rule is as follows:
- Deceleration.
- (1)
- When , if , the HDV will decelerate to ensure safety:
- (2)
- When , if , the HDV cannot judge the distance to the preceding vehicle. In that case, the HDV can adjust its speed within its visible distance to ensure traffic safety; the speed of the vehicle at the next timestep is defined as
- Randomization.HDV slows down randomly according to Equation (5) with the probability .
- Update position.The state of the HDV in this situation from time to can be described as
3.1.2. CAV–CAV
3.1.3. CAV-HDV
- Acceleration.If
- Deceleration.If
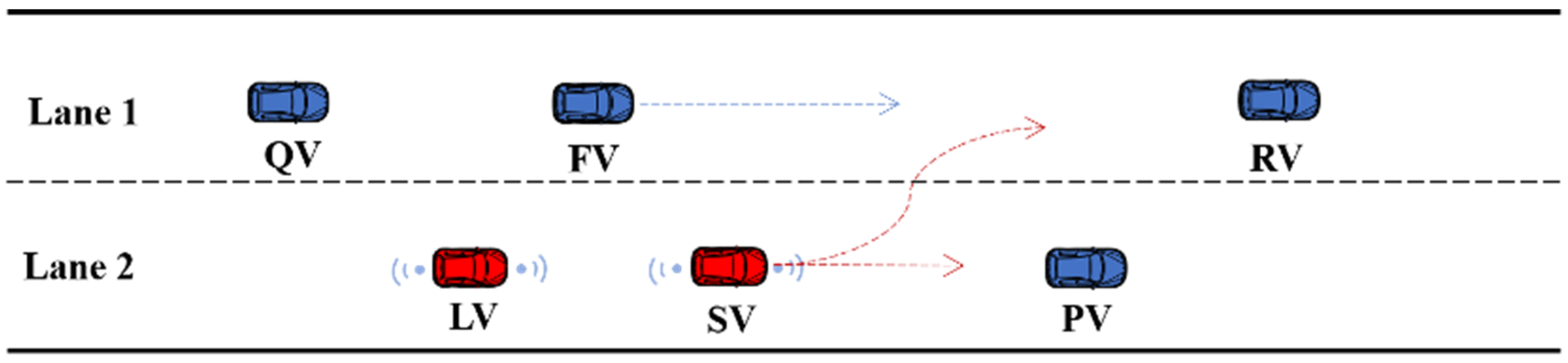
3.2. The Lane-Changing Rules
3.2.1. The Lane-Changing Rules for HDVs
3.2.2. The Lane-Changing Rules for CAVs
4. Numerical and Simulation Experiments
4.1. Scenarios and Setting
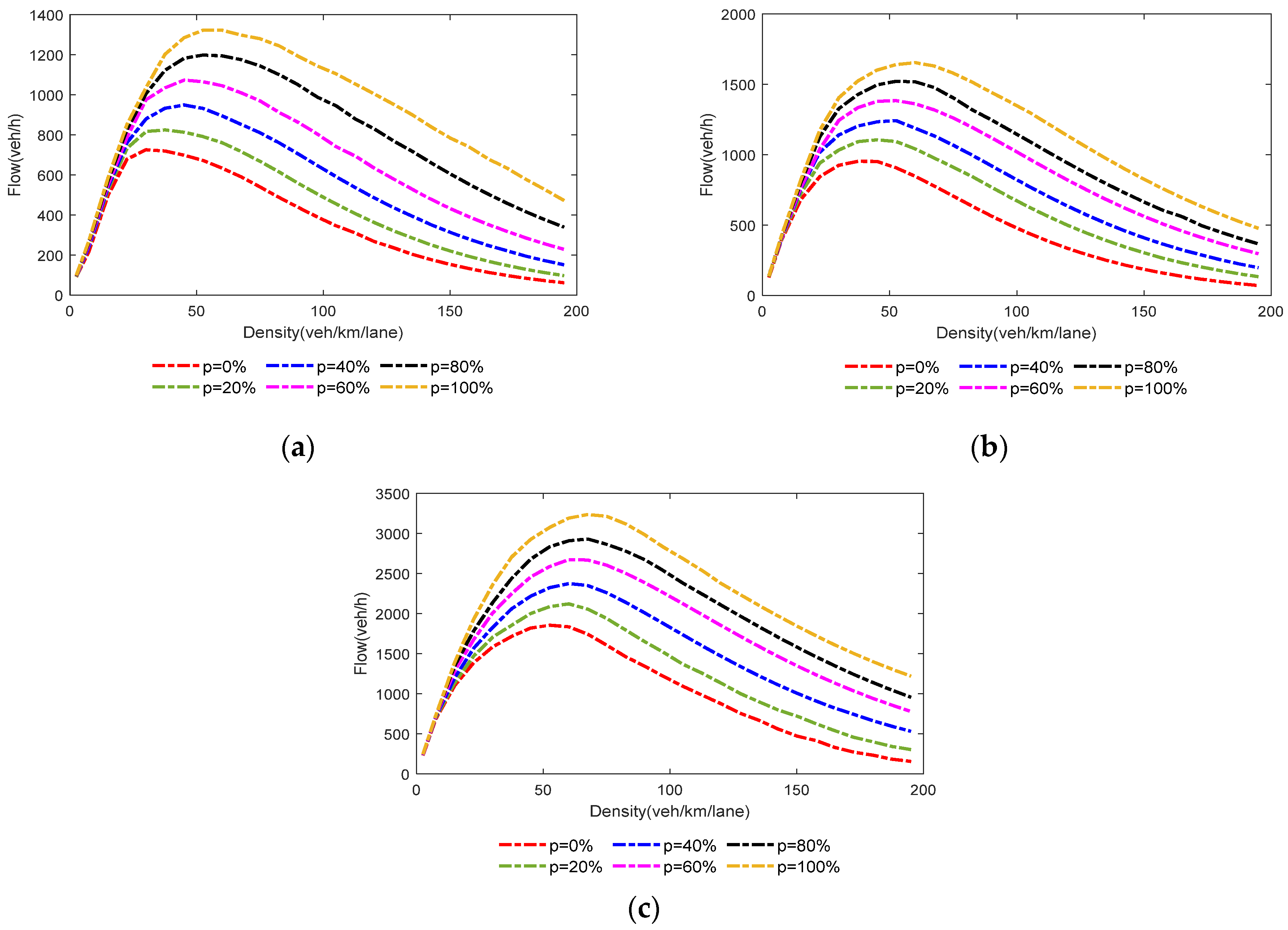
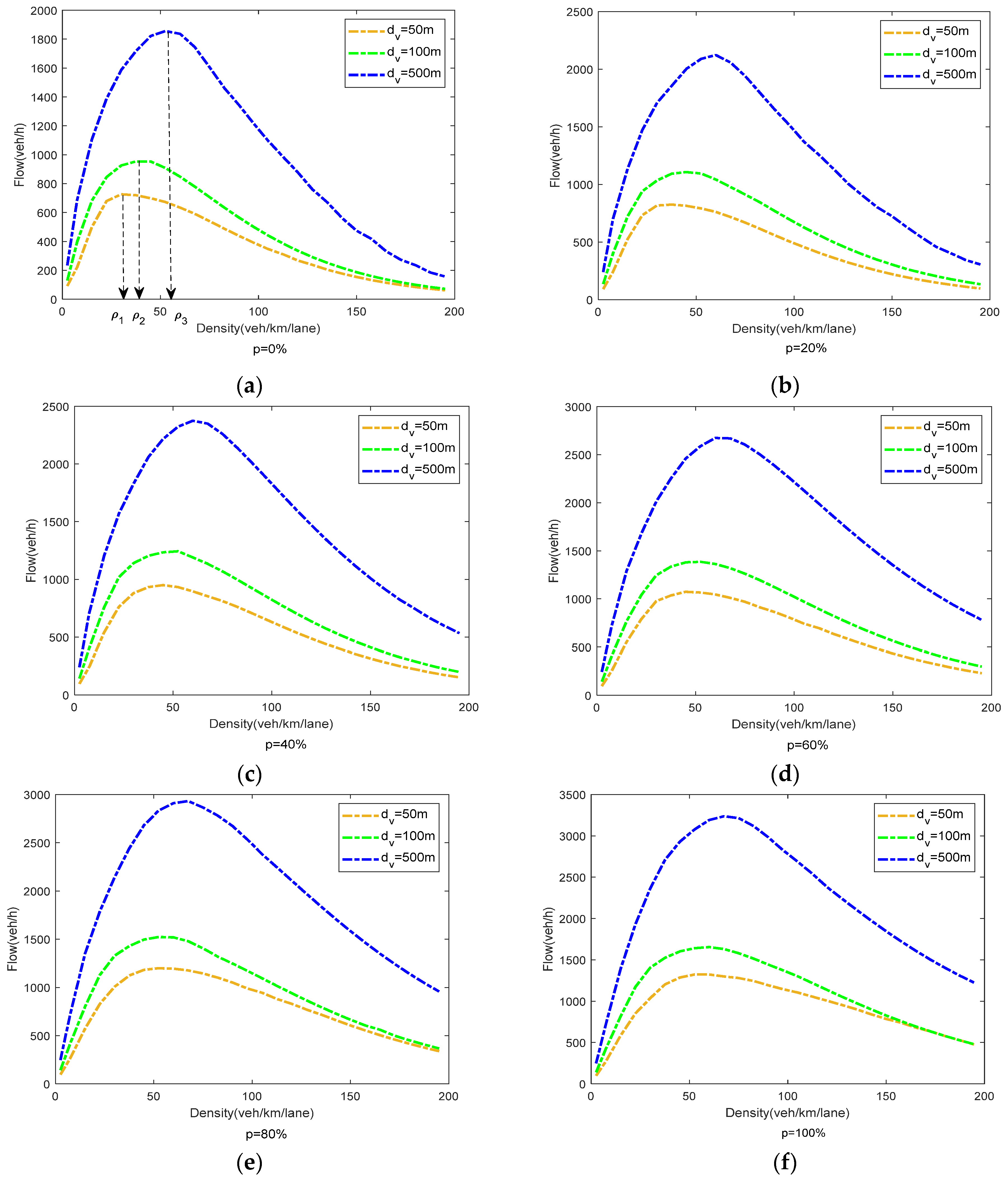
4.2. Simulation Results
4.3. Comparison with Other Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Talebpour, A.; Mahmassani, H. Influence of connected and autonomous vehicles on traffic flow stability and throughput. Transp. Res.-Emerg. Technol. 2016, 71, 143–163. [Google Scholar] [CrossRef]
- Chen, D.; Ahn, S.; Chitturi, M.; Noyce, D. Towards vehicle automation: Roadway capacity formulation for traffic mixed with regular and automated vehicles. Transp. Res.-Methodol. 2017, 100, 196–221. [Google Scholar] [CrossRef] [Green Version]
- Bahrami, S.; Roorda, M. Optimal traffic management policies for mixed human and automated traffic flows. Transp. Res.-Policy Pract. 2020, 135, 130–143. [Google Scholar] [CrossRef]
- Cao, Z.; Lu, L.; Chen, C.; Chen, X. Modeling and Simulating Urban Traffic Flow Mixed With Regular and Connected Vehicles. IEEE Access 2021, 9, 10392–10399. [Google Scholar] [CrossRef]
- Wang, Y.; Liang, L.; Evans, L. Fatal crashes involving large numbers of vehicles and weather. J. Saf. Res. 2017, 63, 1–7. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, J. Research on the fixation transition behavior of drivers on expressway in foggy environment. Saf. Sci. 2019, 119, 70–75. [Google Scholar]
- Zhao, C.; Jiang, S.; Lei, Y.; Wang, C. A Study on an Anthropomorphic Car-Following Strategy Framework of the Autonomous Coach in Mixed Traffic Flow. IEEE Access 2020, 8, 64653–64665. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Xu, Q.; Wang, J.; Li, K. Mixed platoon control of automated and human-driven vehicles at a signalized intersection: Dynamical analysis and optimal control. Transp. Res.-Emerg. Technol. 2021, 127, 103138. [Google Scholar] [CrossRef]
- Hidalgo, C.; Lattarulo, R.; Flores, C.; Perez Rastelli, J. Platoon Merging Approach Based on Hybrid Trajectory Planning and CACC Strategies. Sensors 2021, 21, 2626. [Google Scholar] [CrossRef]
- Liu, H.; Kan, X.; Shladover, S.; Lu, X.; Ferlis, R. Modeling impacts of Cooperative Adaptive Cruise Control on mixed traffic flow in multi-lane freeway facilities. Transp. Res.-Emerg. Technol. 2018, 95, 261–279. [Google Scholar] [CrossRef]
- Zheng, F.; Liu, C.; Liu, X.; Jabari, S.; Lu, L. Analyzing the impact of automated vehicles on uncertainty and stability of the mixed traffic flow. Transp. Res.-Emerg. Technol. 2020, 112, 203–219. [Google Scholar] [CrossRef]
- Li, C.; Feng, H.; Zhi, X.; Zhao, N. Intelligent guidance system for foggy area traffic safety operation. In Proceedings of the 2011 14th International IEEE Conference on Intelligent Transportation Systems (ITSC), Washington, DC, USA, 5–7 October 2011; pp. 428–432. [Google Scholar]
- Yan, X.; Li, X.; Liu, Y.; Zhao, J. Effects of foggy conditions on drivers’ speed control behaviors at different risk levels. Saf. Sci. 2014, 68, 275–287. [Google Scholar] [CrossRef]
- Saffarian, M.; Happee, R.; Winter, J. Why do drivers maintain short headways in fog? A driving-simulator study evaluating feeling of risk and lateral control during automated and manual car following. Ergonomics 2012, 55, 971–985. [Google Scholar] [CrossRef] [PubMed]
- Hoogendoorn, R.; Tamminga, G.; Hoogendoorn, S.; Daamen, W. Longitudinal driving behavior under adverse weather conditions: Adaptation effects, model performance and freeway capacity in case of fog. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, Funchal, Portugal, 19–22 September 2010; pp. 450–455. [Google Scholar]
- Broughton, K.; Switzer, F.; Scott, D. Car following decisions under three visibility conditions and two speeds tested with a driving simulator. Accid. Anal. Prev. 2007, 39, 106–116. [Google Scholar] [CrossRef]
- Peng, Y.; Abdel-Aty, M.; Shi, Q.; Yu, R. Assessing the impact of reduced visibility on traffic crash risk using microscopic data and surrogate safety measures. Transp. Res.-Emerg. Technol. 2017, 74, 295–305. [Google Scholar] [CrossRef] [Green Version]
- Deng, C.; Wu, C.; Cao, S.; Lyu, N. Modeling the effect of limited sight distance through fog on car-following performance using QN-ACTR cognitive architecture. Transp. Res.-Traffic Psychol. Behav. 2019, 65, 643–654. [Google Scholar] [CrossRef]
- Gao, K.; Tu, H.; Sun, L.; Sze, N.; Song, Z.; Shi, H. Impacts of reduced visibility under hazy weather condition on collision risk and car-following behavior: Implications for traffic control and management. Int. J. Sustain. Transp. 2019, 14, 635–642. [Google Scholar] [CrossRef]
- Gong, B.; Wei, R.; Wu, D.; Lin, C. Fleet Management for HDVs and CAVs on Highway in Dense Fog Environment. J. Adv. Transp. 2020, 2020, 8842730. [Google Scholar] [CrossRef]
- Ye, L.; Yamamoto, T. Modeling connected and autonomous vehicles in heterogeneous traffic flow. Phys. Stat. Mech. Appl. 2018, 490, 269–277. [Google Scholar] [CrossRef]
- Jafaripournimchahi, A.; Hu, W.; Sun, L. An Asymmetric-Anticipation Car-following Model in the Era of Autonomous-Connected and Human-Driving Vehicles. J. Adv. Transp. 2020, 2020, 8865814. [Google Scholar] [CrossRef]
- Wang, M.; Daamen, W.; Hoogendoorn, S.; van Arem, B. Rolling horizon control framework for driver assistance systems. Part II: Cooperative sensing and cooperative control. Transp. Res.-Emerg. Technol. 2014, 40, 290–311. [Google Scholar] [CrossRef]
- Milanes, V.; Shladover, S.; Spring, J.; Nowakowski, C.; Kawazoe, H.; Nakamura, M. Cooperative Adaptive Cruise Control in Real Traffic Situations. IEEE Trans. Intell. Transp. Syst. 2014, 15, 296–305. [Google Scholar] [CrossRef] [Green Version]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 62, 1805–1824. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shladover, S.; Su, D.; Lu, X. Impacts of Cooperative Adaptive Cruise Control on Freeway Traffic Flow. Transp. Res. Rec. 2012, 2324, 63–70. [Google Scholar] [CrossRef] [Green Version]
- Milanés, V.; Shladover, S. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data. Transp. Res. Emerg. Technol. 2014, 48, 285–300. [Google Scholar] [CrossRef] [Green Version]
- Chen, N.; Wang, M.; Alkim, T.; van Arem, B. A Robust Longitudinal Control Strategy of Platoons under Model Uncertainties and Time Delays. J. Adv. Transp. 2018, 2018, 9852721. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Wang, Y. Cooperative Adaptive Cruise Control for String Stable Mixed Traffic: Benchmark and Human-Centered Design. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3473–3485. [Google Scholar] [CrossRef]
- Gong, S.; Du, L. Cooperative platoon control for a mixed traffic flow including human drive vehicles and connected and autonomous vehicles. Transp. Res.-Methodol. 2018, 116, 25–61. [Google Scholar] [CrossRef]
- Karoui, O.; Khalgui, M.; Koubaa, A.; Guerfala, E.; Li, Z.; Tovar, E. Dual mode for vehicular platoon safety: Simulation and formal verification. Inf. Sci. 2017, 402, 216–232. [Google Scholar] [CrossRef]
- Nie, L.; Guan, J.; Lu, C.; Zheng, H.; Yin, Z. Longitudinal speed control of autonomous vehicle based on a self-adaptive PID of radial basis function neural network. IET Intell. Transp. Syst. 2018, 12, 485–494. [Google Scholar] [CrossRef]
- Gupta, A.; Anpalagan, A.; Guan, L.; Khwaja, A.S. Deep learning for object detection and scene perception in self-driving cars: Survey, challenges, and open issues. Array 2021, 10, 100057. [Google Scholar] [CrossRef]
- Olovsson, T.; Svensson, T.; Wu, J. Future connected vehicles: Communications demands, privacy and cyber-security. Commun. Transp. Res. 2022, 2, 100056. [Google Scholar] [CrossRef]
- Peng, B.; Keskin, M.F.; Kulcsár, B.; Wymeersch, H. Connected autonomous vehicles for improving mixed traffic efficiency in unsignalized intersections with deep reinforcement learning. Commun. Transp. Res. 2021, 1, 100017. [Google Scholar] [CrossRef]
- Wang, P.; Chan, C.Y.; Fortelle, A. A Reinforcement Learning Based Approach for Automated Lane Change Maneuvers. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium, Changshu, China, 26–30 June 2018. [Google Scholar]
- Kang, K.; Rakha, H. Game Theoretical Approach to Model Decision Making for Merging Maneuvers at Freeway On-Ramps. Transp. Res. Rec. 2017, 2623, 19–28. [Google Scholar] [CrossRef]
- Hang, P.; Lv, C.; Xing, Y.; Huang, C.; Hu, Z. Human-Like Decision Making for Autonomous Driving: A Noncooperative Game Theoretic Approach. IEEE Trans. Intell. Transp. Syst. 2021, 22, 2076–2087. [Google Scholar] [CrossRef]
- Wang, M.; Hoogendoorn, S.; Daamen, W.; van Arem, B.; Happee, R. Game theoretic approach for predictive lane-changing and car-following control. Transp. Res.-Emerg. Technol. 2015, 58, 73–92. [Google Scholar] [CrossRef]
- Yu, H.; Tseng, H.; Langari, R. A human-like game theory-based controller for automatic lane changing. Transp. Res.-Emerg. Technol. 2018, 88, 140–158. [Google Scholar] [CrossRef]
- Talebpour, A.; Mahmassani, H.; Hamdar, S. Modeling lane-changing behavior in a connected environment: A game theory approach. Transp. Res. Emerg. Technol. 2015, 59, 216–232. [Google Scholar] [CrossRef]
- Lin, D.; Li, L.; Jabari, S. Pay to change lanes: A cooperative lane-changing strategy for connected/automated driving. Transp. Res.-Emerg. Technol. 2019, 105, 550–564. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Zhu, C.; Jiang, R.; Treiber, M. Review of the cellular automata models for reproducing synchronized traffic flow. Transp. Transp. Sci. 2020, 17, 766–800. [Google Scholar] [CrossRef]
- Muhammad, T.; Kashmiri, F.; Naeem, H.; Qi, X.; Chia-Chun, H.; Lu, H. Simulation Study of Autonomous Vehicles’ Effect on Traffic Flow Characteristics including Autonomous Buses. J. Adv. Transp. 2020, 2020, 4318652. [Google Scholar] [CrossRef]
- Nagel, K.; Schreckenberg, M. A cellular automaton model for freeway traffic. J. Phys. 1992, 2, 2221–2229. [Google Scholar] [CrossRef]
- Takayasu, M.; Takayasu, H. 1/f noise in a traffic model. Fractals 1993, 1, 860–866. [Google Scholar] [CrossRef]
- Ning, W.U.; Brilon, W. Cellular Automata for Highway Traffic Flow Simulation. 1999. Available online: https://www.researchgate.net/publication/255571908_Cellular_Automata_for_Highway_Traffic_Flow_Simulation (accessed on 1 January 1999).
- Li, X.; Wu, Q.; Jiang, R. Cellular automaton model considering the velocity effect of a car on the successive car. Phys. Rev. 2001, 64, 066128. [Google Scholar] [CrossRef]
- Habel, L.; Schreckenberg, M. Asymmetric lane change rules for a microscopic highway traffic model. In Proceedings of the International Conference on Cellular Automata, Krakow, Poland, 22–25 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 620–629. [Google Scholar]
- Pottmeier, A.; Thiemann, C.; Schadschneider, A.; Schreckenberg, M. Mechanical restriction versus human overreaction: Accident avoidance and two-lane traffic simulations. In Traffic and Granular Flow’05; Springer: Berlin/Heidelberg, Germany, 2007; pp. 503–508. [Google Scholar]
- Chen, B.; Sun, D.; Zhou, J.; Wong, W.; Ding, Z. A future intelligent traffic system with mixed autonomous vehicles and human-driven vehicles. Inf. Sci. 2020, 529, 59–72. [Google Scholar] [CrossRef]
- Hu, X.; Huang, M.; Guo, J. Feature Analysis on Mixed Traffic Flow of Manually Driven and Autonomous Vehicles Based on Cellular Automata. Math. Probl. Eng. 2020, 2020, 7210547. [Google Scholar] [CrossRef]
- Vranken, T.; Sliwa, B.; Wietfeld, C.; Schreckenberg, M. Adapting a cellular automata model to describe heterogeneous traffic with human-driven, automated, and communicating automated vehicles. Phys.-Stat. Mech. Appl. 2021, 570, 125792. [Google Scholar] [CrossRef]
- Gipps, P. A behavioural car-following model for computer simulation. Transp. Res. Methodol. 1981, 15, 105–111. [Google Scholar] [CrossRef]
- Yang, D.; Qiu, X.; Ma, L.; Wu, D.; Zhu, L.; Liang, H. Cellular Automata-Based Modeling and Simulation of a Mixed Traffic Flow of Manual and Automated Vehicles. Transp. Res. Rec. 2017, 2622, 105–116. [Google Scholar] [CrossRef]
- Vranken, T.; Schreckenberg, M. Modelling multi-lane heterogeneous traffic flow with human-driven, automated, and communicating automated vehicles. Phys.-Stat. Mech. Appl. 2022, 589, 126629. [Google Scholar] [CrossRef]
- Das, A.; Ahmed, M.M. Exploring the effect of fog on lane-changing characteristics utilizing the SHRP2 naturalistic driving study data. J. Transp. Saf. Secur. 2021, 13, 477–502. [Google Scholar] [CrossRef]
- Levin, M.W.; Boyles, S.D. A multiclass cell transmission model for shared human and autonomous vehicle roads. Transp. Res. Emerg. Technol. 2016, 62, 103–116. [Google Scholar] [CrossRef] [Green Version]
- Tanveer, M.; Kashmiri, F.A.; Yan, H.; Wang, T.; Lu, H. A Cellular Automata Model for Heterogeneous Traffic Flow Incorporating Micro Autonomous Vehicles. J. Adv. Transp. 2022, 2022, 8815026. [Google Scholar] [CrossRef]
- Chowdhury, D.; Wolf, D.; Schreckenberg, M. Particle hopping models for two-lane traffic with two kinds of vehicles: Effects of lane-changing rules. Phys.-Stat. Mech. Appl. 1997, 235, 417–439. [Google Scholar] [CrossRef]
- Fei, L.; Zhu, H.; Han, X. Analysis of traffic congestion induced by the work zone. Phys.-Stat. Mech. Appl. 2016, 450, 497–505. [Google Scholar] [CrossRef]



| Notion | Explanation |
|---|---|
| the space of the gap between the subject vehicle and the preceding vehicle in the target lane | |
| the space of the gap between the subject vehicle and the succeeding vehicle in the target lane | |
| the space of the gap that needs to be satisfied to be safe | |
| the visible distance in foggy environment | |
| the length of the single lane | |
| the total number of vehicles | |
| the CAV proportion in traffic flow | |
| the lane-changing probability | |
| the acceleration probability | |
| the randomization deceleration probability | |
| the traffic flow | |
| the timestep in the simulation | |
| the simulation time horizon | |
| the maximum speed | |
| the minimum speed | |
| the average speed | |
| the space gap between the subject vehicle and the preceding vehicle in the current lane | |
| the vehicle density |
| Decision Making | FV. | ||
|---|---|---|---|
| Accelerate (n) | Decelerate (1 − n) | ||
| SV. | ) | ) | |
| ) | ) | ||
| Parameter | Scenario 1 | Scenario 2 | Scenario 3 |
|---|---|---|---|
| 50 | 100 | 500 | |
| 40 | 60 | 100 | |
| 0.2 | 0.3 | 0.4 | |
| 0.4 | 0.2 | 0.1 |
| in STCA- | in GT-Based | Increase | in STCA- | in GT-Based | Increase | ||
|---|---|---|---|---|---|---|---|
| (veh/km/h) | LC (km/h) | LC (km/h) | (%) | LC (km/h) | LC (km/h) | (%) | |
| 0% | 29.61 | 31.94 | 7.87 | 71.26 | 73.67 | 3.38 | |
| 20% | 30.97 | 33.49 | 8.13 | 72.09 | 75.85 | 5.22 | |
| 40% | 31.01 | 34.62 | 8.15 | 79.77 | 80.17 | 5.01 | |
| 60% | 32.49 | 35.44 | 8.4 | 81.89 | 85.91 | 4.91 | |
| 80% | 34.03 | 36.76 | 8.02 | 85.09 | 89.99 | 5.76 | |
| 100% | 35.18 | 37.77 | 7.36 | 87.66 | 92.91 | 5.99 | |
| 0% | 4.36 | 7.2 | 65.14 | 11.44 | 21.42 | 87.23 | |
| 20% | 5.29 | 8.91 | 68.43 | 13.39 | 25.86 | 93.13 | |
| 40% | 6.13 | 10.81 | 76.35 | 16.15 | 30.15 | 86.69 | |
| 60% | 7.28 | 12.93 | 77.61 | 17.74 | 34.73 | 95.77 | |
| 80% | 8.49 | 15.26 | 79.74 | 20.73 | 38.2 | 84.27 | |
| 100% | 9.36 | 17.07 | 82.37 | 24.53 | 42.86 | 74.72 | |
| 0% | 1.42 | 1.52 | 7.04 | 3.16 | 4.97 | 57.28 | |
| 20% | 1.85 | 2.12 | 14.59 | 4.47 | 6.68 | 49.44 | |
| 40% | 2.47 | 2.92 | 18.21 | 4.92 | 9.08 | 84.55 | |
| 60% | 3.35 | 3.92 | 17.01 | 6.29 | 11.79 | 87.44 | |
| 80% | 4.56 | 5.32 | 16.67 | 7.42 | 13.62 | 83.56 | |
| 100% | 5.49 | 6.57 | 19.67 | 8.03 | 15.59 | 94.15 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, B.; Wang, F.; Lin, C.; Wu, D. Modeling HDV and CAV Mixed Traffic Flow on a Foggy Two-Lane Highway with Cellular Automata and Game Theory Model. Sustainability 2022, 14, 5899. https://doi.org/10.3390/su14105899
Gong B, Wang F, Lin C, Wu D. Modeling HDV and CAV Mixed Traffic Flow on a Foggy Two-Lane Highway with Cellular Automata and Game Theory Model. Sustainability. 2022; 14(10):5899. https://doi.org/10.3390/su14105899
Chicago/Turabian StyleGong, Bowen, Fanting Wang, Ciyun Lin, and Dayong Wu. 2022. "Modeling HDV and CAV Mixed Traffic Flow on a Foggy Two-Lane Highway with Cellular Automata and Game Theory Model" Sustainability 14, no. 10: 5899. https://doi.org/10.3390/su14105899
APA StyleGong, B., Wang, F., Lin, C., & Wu, D. (2022). Modeling HDV and CAV Mixed Traffic Flow on a Foggy Two-Lane Highway with Cellular Automata and Game Theory Model. Sustainability, 14(10), 5899. https://doi.org/10.3390/su14105899









