Novel Recommendation-Based Approach for Multidisciplinary Development of Future Universities
Abstract
:1. Introduction
- Rather than directly wading through massive high-dimensional data, we judiciously formulate the cumbersome configurations of disciplines as a discipline recommendation problem.
- An efficient non-negative matrix factorization-based algorithm is developed to solve the resultant recommendation problem with a low (polynomial-time) complexity.
- A promising off-the-shelf subject list can be readily given by the proposed recommendation engine and used as a cost-effective, powerful and practical tool in the decision process of discipline configuration for a future university.
2. Problem Formulation
2.1. Problem Mapping
- In the classical recommendation-based problem of retail business, there are two types of roles: users and items. As shown in the left subfigure of Figure 1, the solid blue line refers to an actual purchase of an item by a user, and the green dashed line refers to a recommended item by the recommendation engine. In such a scenario, the users freely purchase the preferred ones from thousands of items. Typically, it can be inefficient for the user to fetch the mostly matched targets via brute-force search in many high-dimensional candidates. This induces the so-called information overload problem. To solve the problem, the recommendation engine is utilized to transform the cumbersome high-dimensional searching space into the low-dimensional space, and based on neighborhood or historical data similarities and correlations in the low-dimensional space, further recommend a Top-K (K is usually a small number) number of most needed items to users [29,30].As for the configuration of disciplines for universities, there are also two types of roles: universities and disciplines. As shown in the right sub-figure of Figure 1, the solid blue line refers to a preponderant discipline included in published data by a third party for a university, and the green dashed line refers to a recommended discipline by the recommendation engine to be the promising discipline for a university. In such a case, the objective of a university is to determine a series of disciplines as the focus of further developments. Correspondingly, we resort to the recommendation engine to transform the original high-dimensional features of both universities and disciplines into the low-dimensional ones. Based on neighborhood or historical data similarities and correlations in the low-dimensional space, we subsequently recommend an adequate configuration of disciplines to direct the decision process on the development of disciplines.
- In the recommendation case of retail business, the recommendation engine often relies on the explicit feedback of users, e.g., the rating for a specific item given by users. Based on a specific item’s neighborhood or historical usage rating data, the recommendation engine can readily provide the recommendation list of items with a neighborhood-based collaborative filtering approach or model-based approach [31]. As for the problem of discipline configuration for universities, the score on a specific discipline by a third party can be seen as a preferred configuration of the discipline for a university. Based on the scores on disciplines by the third party, the recommendation engine can be readily used to handle the recommendation task as in retail business scenarios and provide an appropriate list of disciplines for universities.
2.2. Discipline Recommendation Problem
| Algorithm 1 The proposed iterative-based algorithm to solve problem (3) |
| Initialize: Randomly initialize and with each entry in (0, 1), fill the unknown entries of as 0, an accuracy level , select a step size , a regularization parameter , and set . |
Repeat:
|
3. Numerical Results
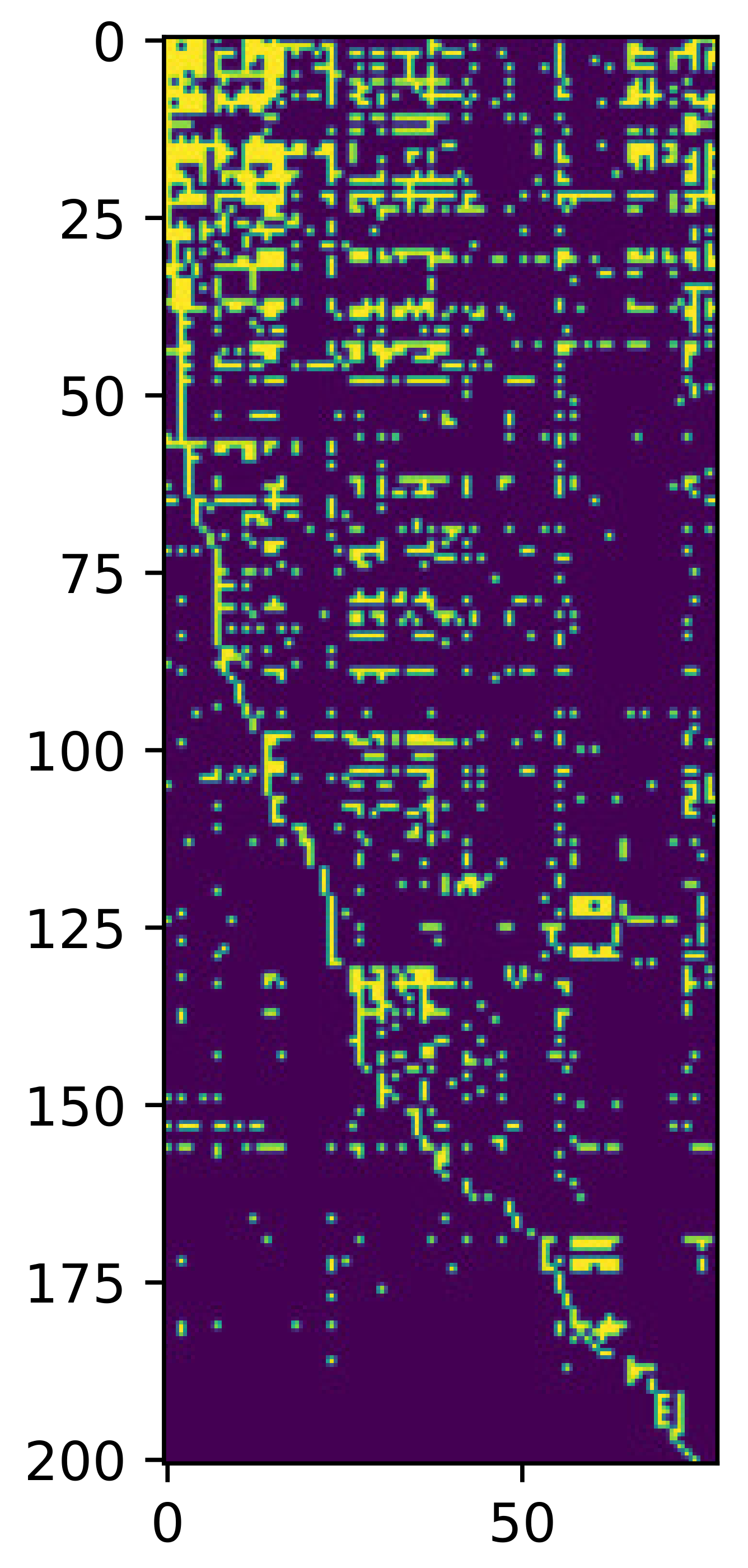
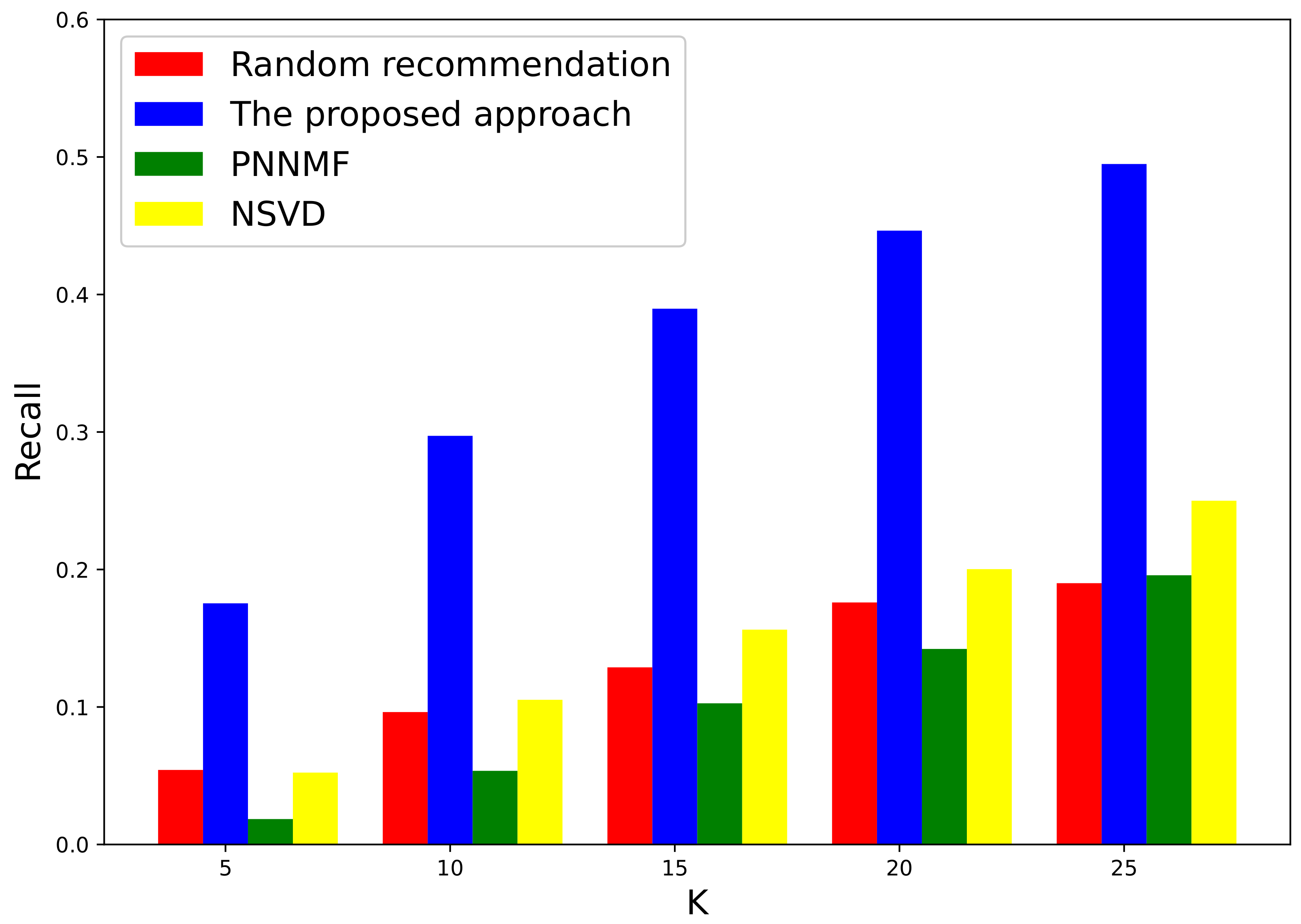
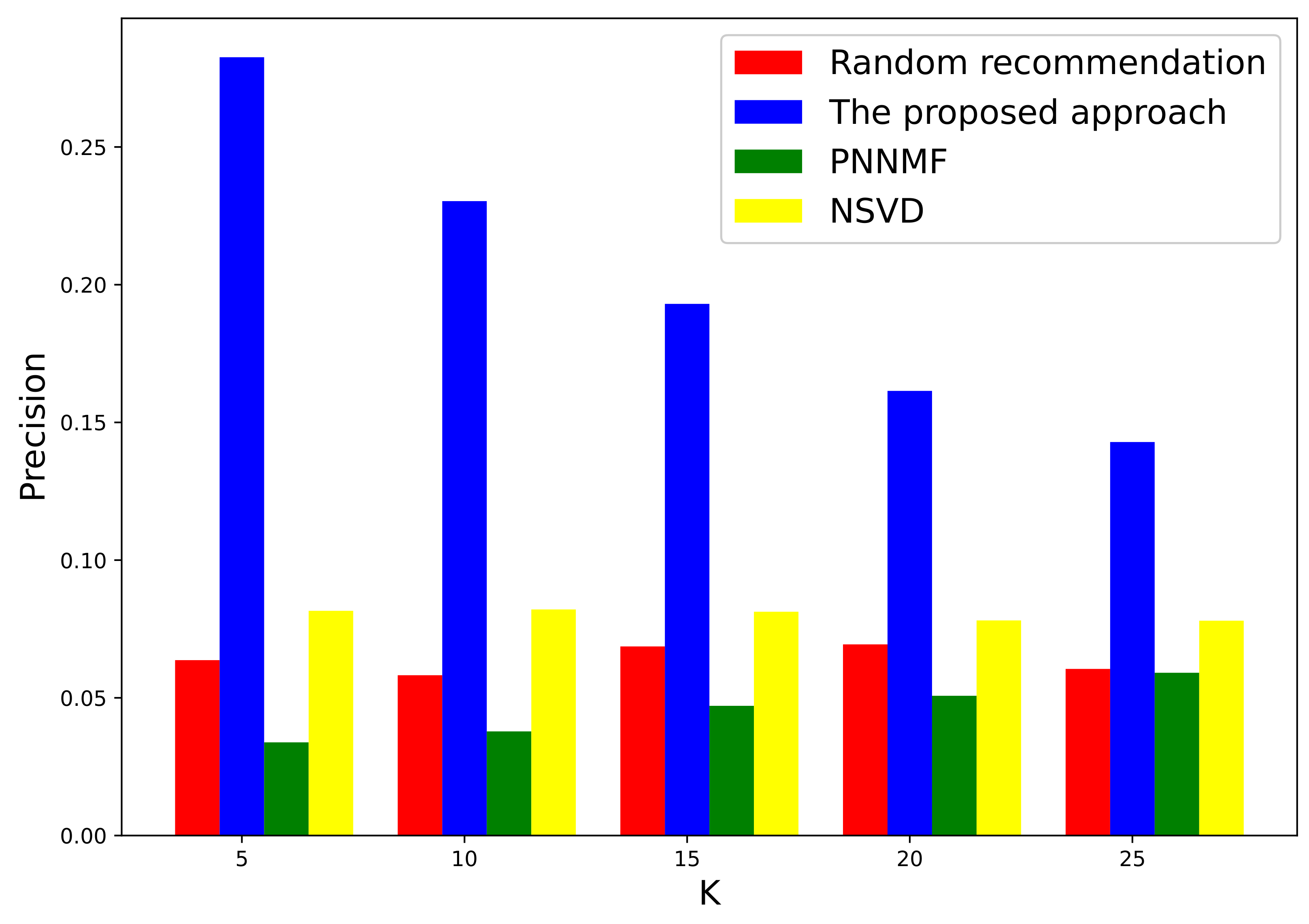
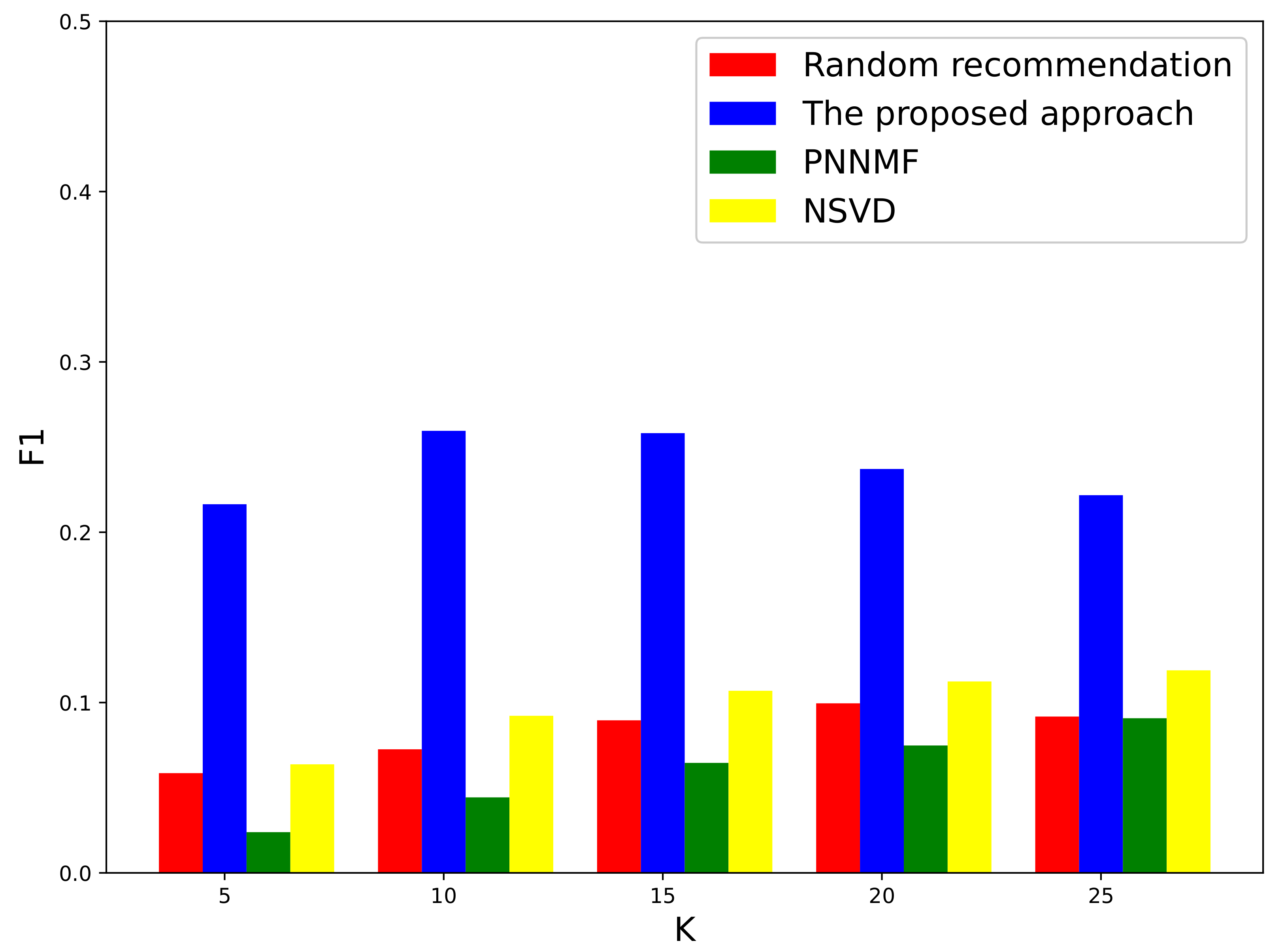
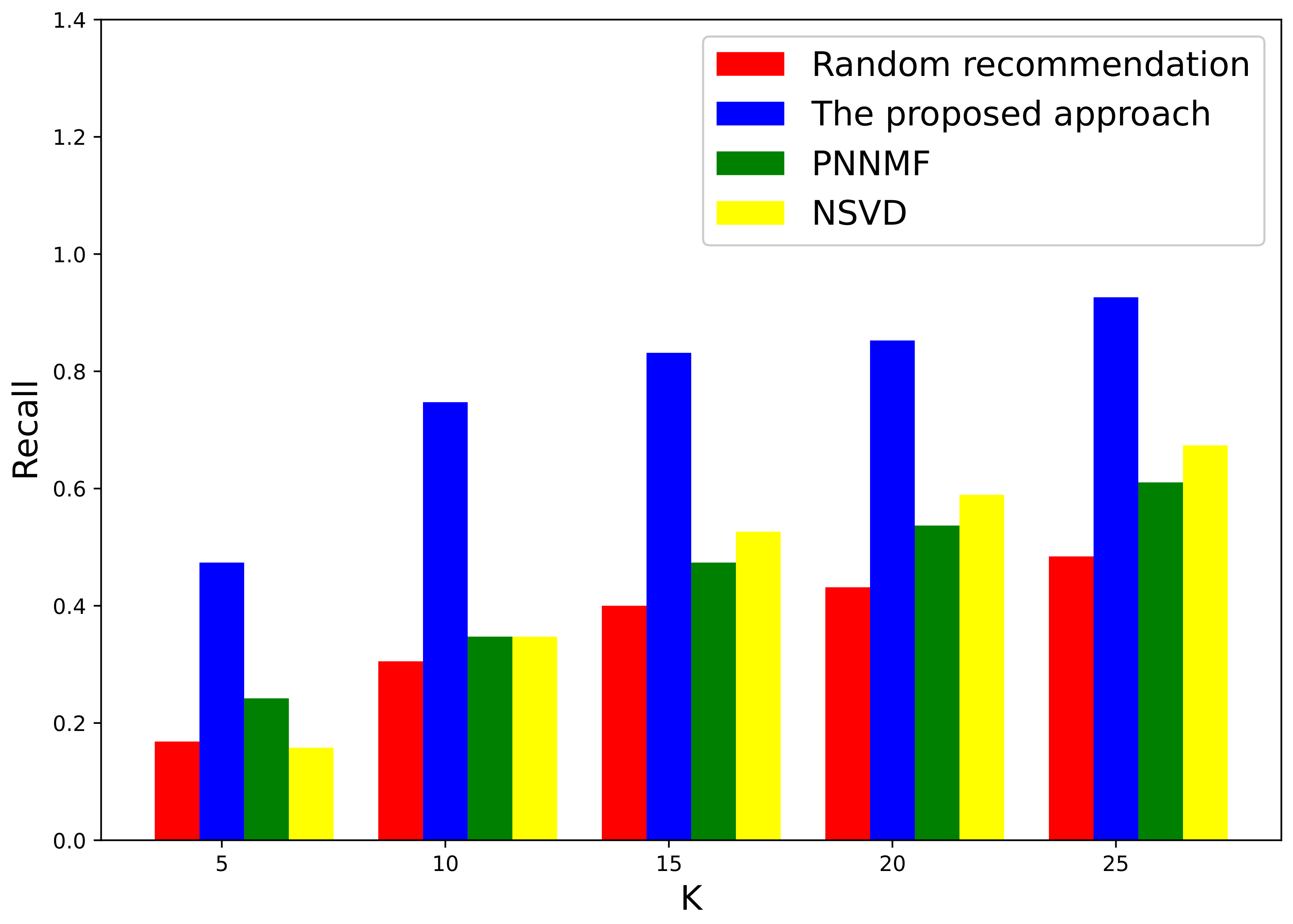
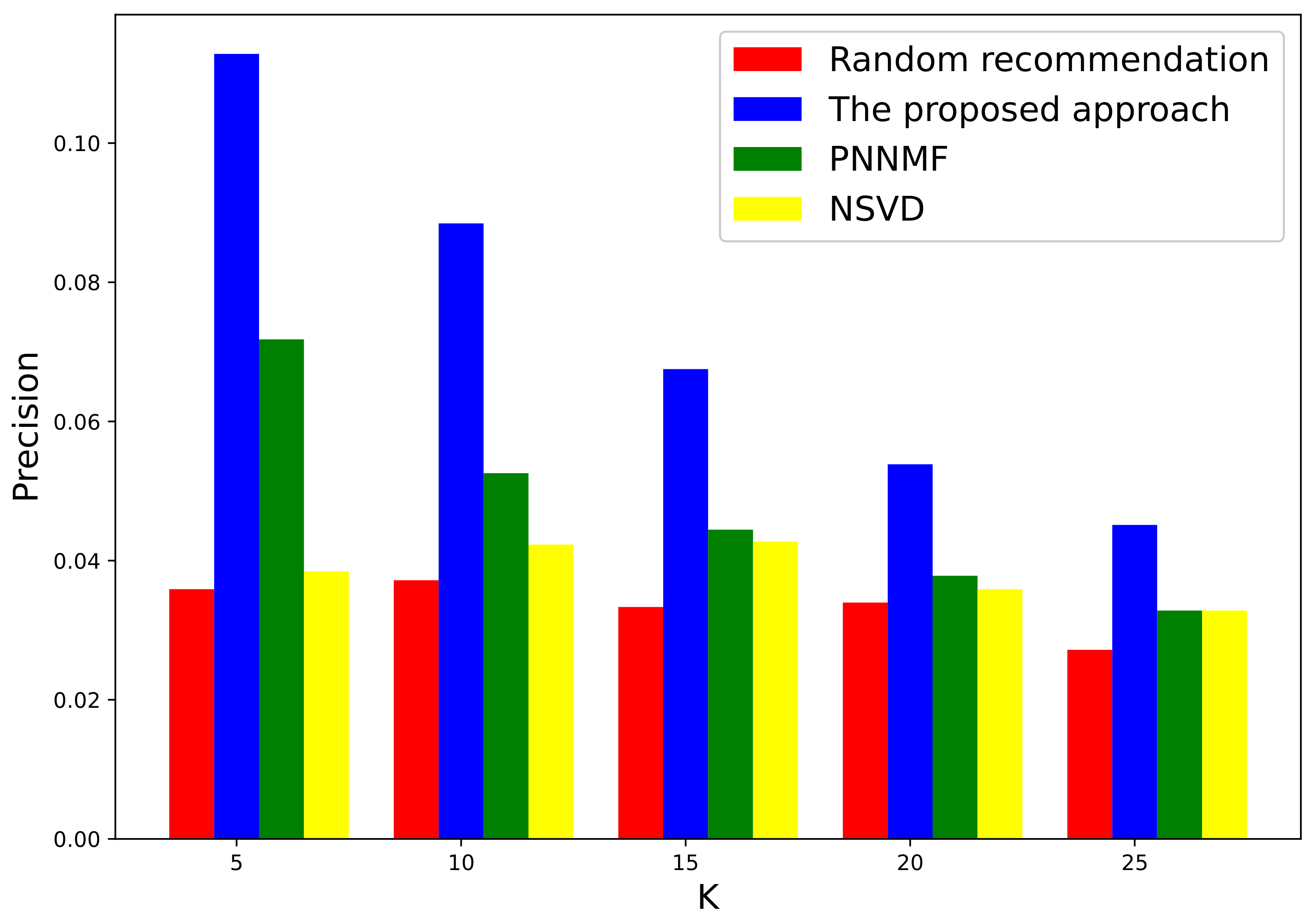
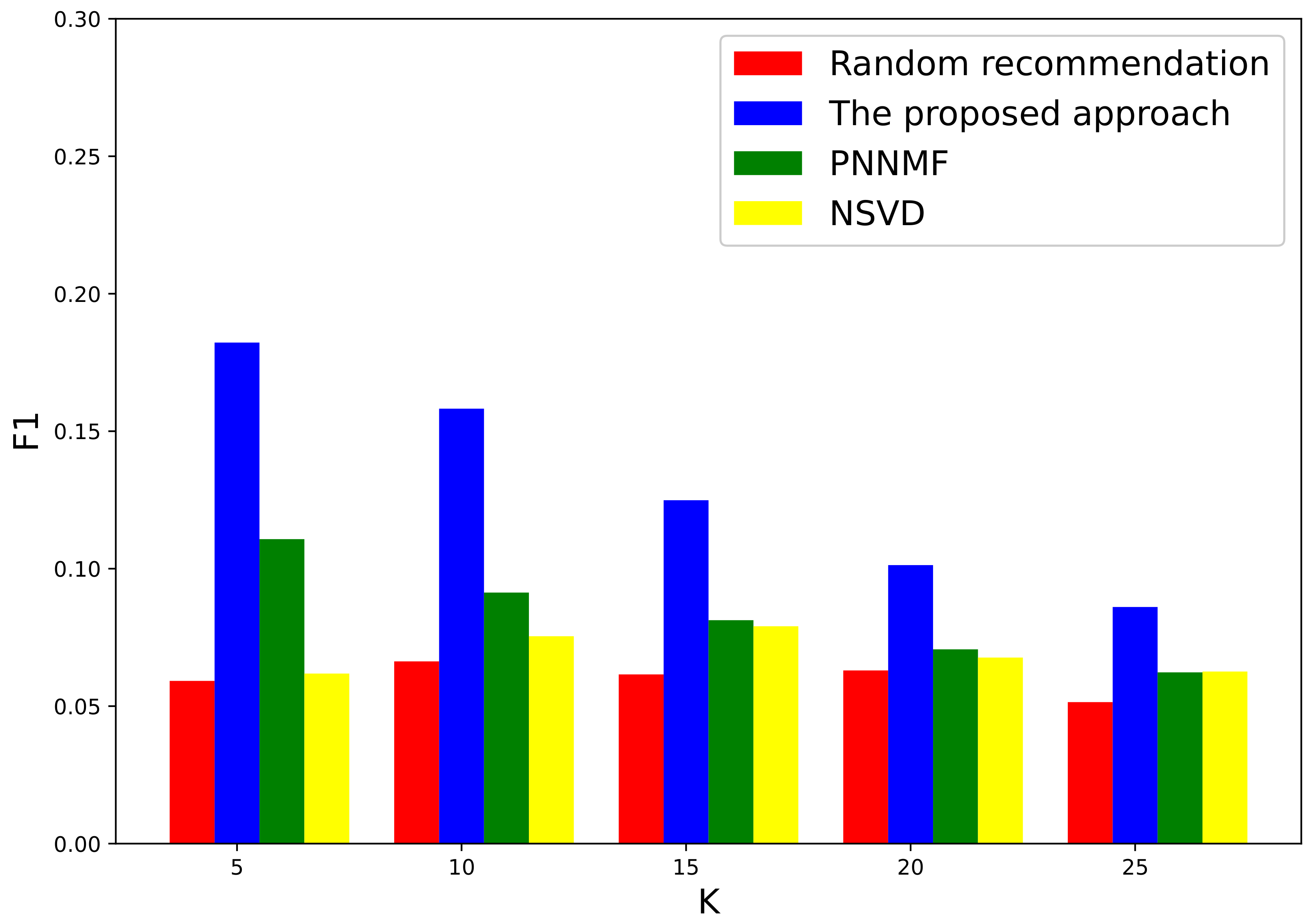
3.1. Evaluation on a Local Authoritative Data Set
3.2. Further Evaluation of Well-Known International Data Set
4. Discussions and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Monteiro, S.; Isusi-Fagoaga, R.; Almeida, L.; García-Aracil, A. Contribution of Higher Education Institutions to Social Innovation: Practices in Two Southern European Universities. Sustainability 2021, 13, 3594. [Google Scholar] [CrossRef]
- García-Aracil, A.; Monteiro, S.; Almeida, L.S. Students’ Perceptions of Their Preparedness for Transition to Work after Graduation. Act. Learn. High. Educ. 2021, 22, 49–62. [Google Scholar] [CrossRef]
- Puente, C.; Fabra, M.E.; Mason, C.; Puente-Rueda, C.; Sáenz-Nuño, M.A.; Viñuales, R. Role of the Universities as Drivers of Social Innovation. Sustainability 2021, 13, 13727. [Google Scholar] [CrossRef]
- Huang, Z.; Kougianos, E.; Ge, X.; Wang, S.; Chen, P.D.; Cai, L. A Systematic Interdisciplinary Engineering and Technology Model using Cutting-Edge Technologies for STEM Education. IEEE Trans. Educ. 2021, 64, 390–397. [Google Scholar] [CrossRef]
- Corazza, L.; Saluto, P. Universities and Multistakeholder Engagement for Sustainable Development: A Research and Technology Perspective. IEEE Trans. Eng. Manag. 2021, 68, 1173–1178. [Google Scholar] [CrossRef]
- García-Aracil, A. Understanding Productivity Changes in Public Universities: Evidence from Spain. Res. Eval. 2013, 22, 351–368. [Google Scholar] [CrossRef] [Green Version]
- Su, W.; Wang, D.; Xu, L.; Zeng, S.; Zhang, C. A Nonradial Super Efficiency DEA Framework using a MCDM to Measure the Research Efficiency of Disciplines at Chinese Universities. IEEE Access 2020, 8, 86388–86399. [Google Scholar] [CrossRef]
- Baturina, D. Pathways towards Enhancing HEI’s Role in the Local Social İnnovation Ecosystem. In Social Innovation in Higher Education: Landscape, Practices, and Opportunities; Springer: Cham, Switzerland, 2022; pp. 37–60. [Google Scholar]
- Dryjanska, L.; Kostalova, J.; Vidović, D. Higher Education Practices for Social Innovation and Sustainable Development. In Social Innovation in Higher Education: Landscape, Practices, and Opportunities; Springer: Cham, Switzerland, 2022; pp. 107–128. [Google Scholar]
- Piccardo, C.; Goto, Y.; Koca, D.; Aalto, P.; Hughes, M. Challenge-based, Interdisciplinary Learning for Sustainability in Doctoral Education. Int. J. Sustain. High. Educ. 2022, in press. [Google Scholar] [CrossRef]
- Xu, Z.; Xia, M.; Yang, Z. Interactive research of university discipline construction and development of science park. In Proceedings of the International Conference on Information Management, Innovation Management and Industrial Engineering, Shenzhen, China, 26–27 November 2011; pp. 499–502. [Google Scholar]
- Zong, F.; Hou, J.; Yang, Y. Evaluation of the first-class engineering discipline construction: A method based on d-number preference relation matrix. In Proceedings of the IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 914–923. [Google Scholar]
- QS World University Rankings by Subject. Available online: https://www.topuniversities.com/subject-rankings/2021 (accessed on 28 March 2022).
- THE World University Rankings by Subject. Available online: https://www.timeshighereducation.com/world-university-rankings/by-subject (accessed on 28 March 2022).
- Best-Global-Universities. Available online: https://www.usnews.com/education/best-global-universities (accessed on 28 March 2022).
- Project 985. Available online: http://www.moe.gov.cn/srcsite/A22/s7065/200612/t20061206_128833.html (accessed on 16 March 2022).
- Project 211. Available online: http://www.moe.gov.cn/srcsite/A22/s7065/200512/t20051223_82762.html (accessed on 16 March 2022).
- Double-First. Available online: http://www.moe.gov.cn/srcsite/A22/s7065/202202/t20220211_598710.html (accessed on 16 March 2022).
- MOE. Available online: http://www.moe.gov.cn/srcsite/A11/s7057/202102/t20210205_512709.html (accessed on 16 March 2022).
- World Bank. Available online: https://ieg.worldbankgroup.org/sites/default/files/Data/Evaluation/files/highereducation.pdf (accessed on 20 February 2022).
- Sun, F. Higher education quality evaluation: A game-theory approach. In Proceedings of the 7th International Conference on Information Technology in Medicine and Education (ITME), Huangshan, China, 13–15 November 2015; pp. 473–475. [Google Scholar]
- Deng, H.; Wang, J.; Liu, X.; Liu, B.; Lei, J. Evaluating the Outcomes of Medical Informatics Development as a Discipline in China: A Publication Perspective. Comput. Methods Programs Biomed. 2018, 164, 75–85. [Google Scholar] [CrossRef]
- Zhou, M.; Zhou, J. Discipline construction plan of undergraduate studies in applied universities for China’s guangdong baiyun university based on the McKinsey 7S model. In Proceedings of the 2020 International Conference on Modern Education and Information Management (ICMEIM), Dalian, China, 25–27 September 2020; pp. 68–71. [Google Scholar]
- Zhang, Y.; Cen, G.; Feng, T. University discipline construction progress monitoring system. In Proceedings of the 14th International Conference on Computer Science & Education (ICCSE), Toronto, ON, Canada, 19–21 August 2019; pp. 176–179. [Google Scholar]
- Uhoman, A. Level of Discipline among University Academic Staff as a Correlate of University Development in Nigeria. J. Educ. Pract. 2017, 8, 21–29. [Google Scholar]
- Tongji. Available online: https://en.tongji.edu.cn/Academic_Research/Discipline_Development.htm (accessed on 14 March 2022).
- Dadgar, M.; Hamzeh, A. How to Boost the Performance of Recommender Systems by Social Trust? Studying the Challenges and Proposing a Solution. IEEE Access 2022, 10, 13768–13779. [Google Scholar] [CrossRef]
- Coba, L.; Confalonieri, R.; Zanker, M. RecoXplainer: A Library for Development and Offline Evaluation of Explainable Recommender Rystems. IEEE Comput. Intell. Mag. 2022, 17, 46–58. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, L.; He, X.; Peng, J.; Zheng, Z.; Tang, J. Modelling High-Order Social Relations for Item Recommendation. IEEE Trans. Knowl. Data Eng. 2022, in press. [Google Scholar] [CrossRef]
- Chang, J.; Gao, C.; He, X.; Jin, D.; Li, Y. Bundle Recommendation and Generation with Graph Neural Networks. IEEE Trans. Knowl. Data Eng. 2022, in press. [Google Scholar] [CrossRef]
- Aggarwal, C. Recommender Systems; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Luo, X.; Zhou, M.; Xia, Y.; Zhu, Q. An Efficient Non-Negative Matrix-Factorization-Based Approach to Collaborative Filtering for Recommender Systems. IEEE Trans. Industr. Inform. 2014, 10, 1273–1284. [Google Scholar]
- Li, W.; He, Q.; Luo, X.; Wang, Z. Assimilating Second-Order Information for Building Non-Negative Latent Factor Analysis-based Recommenders. IEEE Trans. Syst. Man. Cybern. 2022, 52, 485–497. [Google Scholar] [CrossRef]
- Song, Y.; Li, M.; Zhu, Z.; Yang, G.; Luo, X. Non-Negative Latent Factor Analysis-Incorporated and Feature-Weighted Fuzzy Double C-Means Clustering for Incomplete Data. IEEE Trans. Fuzzy Syst. 2022, in press. [CrossRef]
- Selesnick, I. Sparse Regularization via Convex Analysis. IEEE Trans. Signal Process. 2017, 65, 4481–4494. [Google Scholar] [CrossRef]
- Second Round Discipline Assessment. Available online: http://www.chinadegrees.cn/xwyyjsjyxx/zlpj/xksppm/ (accessed on 12 January 2022).
- Third Round Discipline Assessment. Available online: http://www.chinadegrees.cn/xwyyjsjyxx/xxsbdxz/index.shtml (accessed on 12 January 2022).
- Gao, X.; Feng, F.; He, X.; Huang, H.; Guan, X.; Feng, C.; Ming, Z.; Chua, T. Hierarchical Attention Network for Visually-Aware Food Recommendation. IEEE Trans. Multimed. 2020, 22, 1647–1659. [Google Scholar] [CrossRef] [Green Version]
- Wu, B.; He, X.; Chen, Y.; Nie, L. Modeling Product’s Visual and Functional Characteristics for Recommender Systems. IEEE Trans. Knowl. Data Eng. 2022, 34, 1330–1343. [Google Scholar] [CrossRef]
- Yan, C.; Zhang, Y.; Zhong, W.; Zhang, C.; Xin, B. A Truncated SVD-based ARIMA Model for Multiple QoS Prediction in Mobile Edge Computing. Tsinghua Sci. Technol. 2022, 27, 315–324. [Google Scholar] [CrossRef]
- Wu, Y.; Tong, T. The First-Class Discipline Construction from the Perspective of Supply Side Reform. Univ. Educ. Sci. 2017, 4, 10–16. [Google Scholar]
- Chinadegrees. Available online: http://www.chinadegrees.cn/xwyyjsjyxx/cde/en/ (accessed on 5 May 2022).
- QS Methodology. Available online: https://www.topuniversities.com/qs-world-university-rankings/methodology (accessed on 5 May 2022).
- Liu, X.; Song, R.; Wang, Y.; Xu, H. A Multi-Granular Aggregation-Enhanced Knowledge Graph Representation for Recommendation. Information 2022, 13, 229. [Google Scholar] [CrossRef]
- Gao, M.; Lu, J.; Chen, F. Medical Knowledge Graph Completion Based on Word Embeddings. Information 2022, 13, 205. [Google Scholar] [CrossRef]
- Najafi, B.; Parsaeefard, S.; Leon-Garcia, A. Missing Data Estimation in Temporal Multilayer Position-Aware Graph Neural Network (TMP-GNN). Mach. Learn. Knowl. Extr. 2022, 4, 397–417. [Google Scholar] [CrossRef]

| University | Discipline | Scores |
|---|---|---|
| University 1 | mathematics | 89 |
| University 2 | mathematics | 82 |
| University 3 | physics | 85 |
| University 4 | physics | 75 |
| University 2 | chemistry | 82 |
| University 3 | chemistry | 81 |
| Discipline | Mathematics | Physics | Chemistry |
|---|---|---|---|
| University | |||
| University 1 | 89 | ? | ? |
| University 2 | 82 | ? | 82 |
| University 3 | ? | 85 | 81 |
| University 4 | ? | 75 | ? |
| Rank | University | Rating |
|---|---|---|
| 1 | Peking University | 90 |
| 2 | Renmin University of China | 89 |
| 3 | Sun Yat-sen University | 84 |
| 4 | Fudan University | 83 |
| 5 | Nanjing University | 81 |
| 6 | Wuhan University | 79 |
| 7 | Beijing Normal University | 77 |
| 8 | Nankai University | 76 |
| 9 | Jilin University | 75 |
| Zhejiang University | ||
| 10 | Tsinghua University | 74 |
| 11 | East China Normal University Xiamen University | 72 |
| Rank | University | Rating |
|---|---|---|
| 1 | Peking University | 95 |
| 2 | Renmin University of China | 92 |
| 3 | Fudan University Sun Yat-sen University | 87 |
| 4 | Nanjing University Wuhan University | 85 |
| 5 | Beijing Normal University | 83 |
| 6 | Nankai University Jilin University | 79 |
| 7 | Tsinghua University Heilongjiang University Zhejiang University | 78 |
| 8 | Shanxi University East China Normal University | 76 |
| The Scale of Universities | The Scale of Disciplines | Sparsity |
|---|---|---|
| 201 | 78 | 86.8% |
| University | Disciplines Hit in the Top-5 Recommendation |
|---|---|
| Northwestern Polytechnical University | business administration biomedical engineering electrical engineering public administration software engineering biology design |
| China University of Mining and Technology | mechanics material science and engineering information and communication engineering mechanical engineering physical education physics safety science and engineering Marxist theory |
| Dalian Jiaotong University | management science and engineering mechanics computer science and technology control science and engineering business administration mathematics software engineering transportation engineering environmental science and engineering Marxist theory |
| Shandong Agricultural University | agricultural engineering horticulture biology agricultural and forestry economic management ecology landscape architecture agricultural resources and environment foreign language and literature |
| The Scale of Universities | The Scale of Disciplines | Sparsity |
|---|---|---|
| 78 | 49 | 81.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bi, S.; Ni, W.; Jiang, Y.; Wang, X. Novel Recommendation-Based Approach for Multidisciplinary Development of Future Universities. Sustainability 2022, 14, 5881. https://doi.org/10.3390/su14105881
Bi S, Ni W, Jiang Y, Wang X. Novel Recommendation-Based Approach for Multidisciplinary Development of Future Universities. Sustainability. 2022; 14(10):5881. https://doi.org/10.3390/su14105881
Chicago/Turabian StyleBi, Siguo, Wei Ni, Yi Jiang, and Xin Wang. 2022. "Novel Recommendation-Based Approach for Multidisciplinary Development of Future Universities" Sustainability 14, no. 10: 5881. https://doi.org/10.3390/su14105881
APA StyleBi, S., Ni, W., Jiang, Y., & Wang, X. (2022). Novel Recommendation-Based Approach for Multidisciplinary Development of Future Universities. Sustainability, 14(10), 5881. https://doi.org/10.3390/su14105881






