An IndoorGeoBML Model Based IORP Algorithm for Indoor Operation
Abstract
:1. Introduction
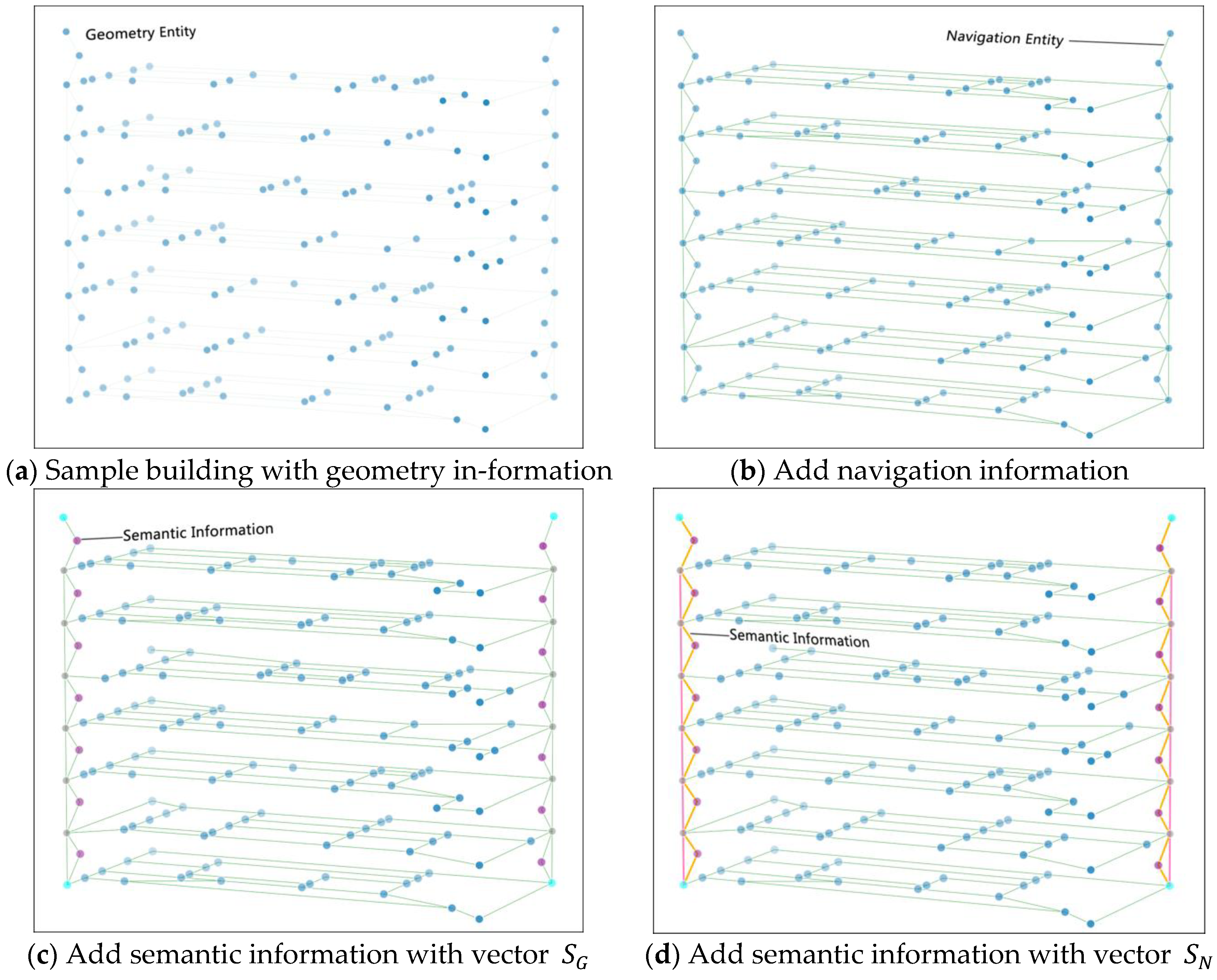
2. The Design of IndoorGeoBML Model
2.1. Geometry Information
2.2. Navigation Information
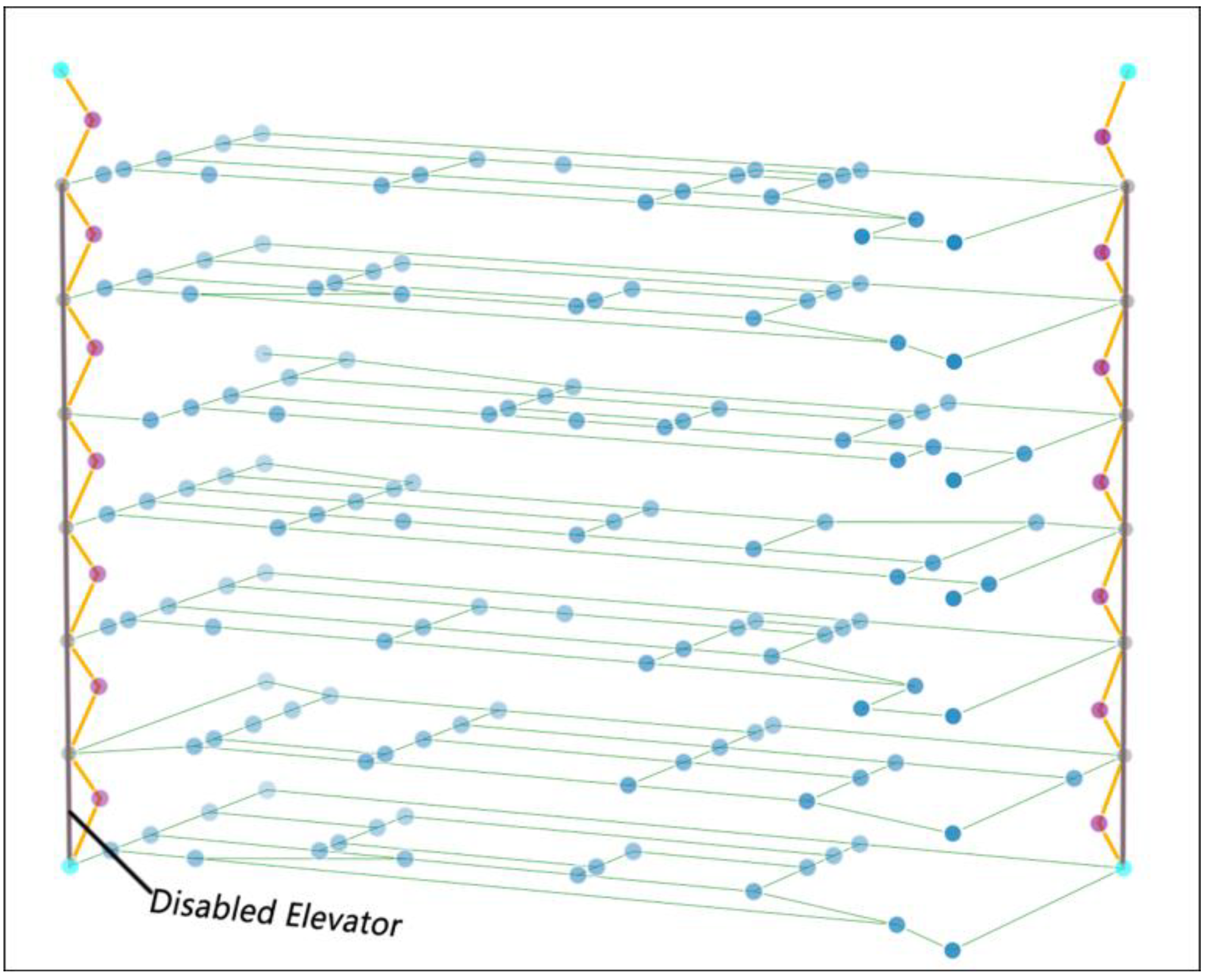
2.3. Semantic Information
- IGBMLSpace is the entity used to represent a space as the area or volume of a functional region. It is often associated with entities with empty space (e.g., hall, room, bathroom). The speed within those entities can be around 30 m per minute, and we can set the military difficulty factor of those entities as a standard unit 1.
- IGBMLElevator is a vertical entity, which merges or splits the space. Although the use of elevators is discouraged in operations with fire, some research still shows that they are a necessity and their usage is unavoidable, especially when we can monitor it with IoT technology. The speed within those entities can be at an average of 6 m per second, the military difficulty factor of those entities is higher, such as 15, in comparison with IGBMLSpace entities.
- IGBMLStair also represents a vertical passage allowing for movement from one floor to the other. It can contain an intermediate landing. The speed within those entities is considered at 15 m per minute, the military difficulty factor of those entities is a little bit higher, at 5, compared to IGBMLSpace entities.
2.4. Outdoor Information
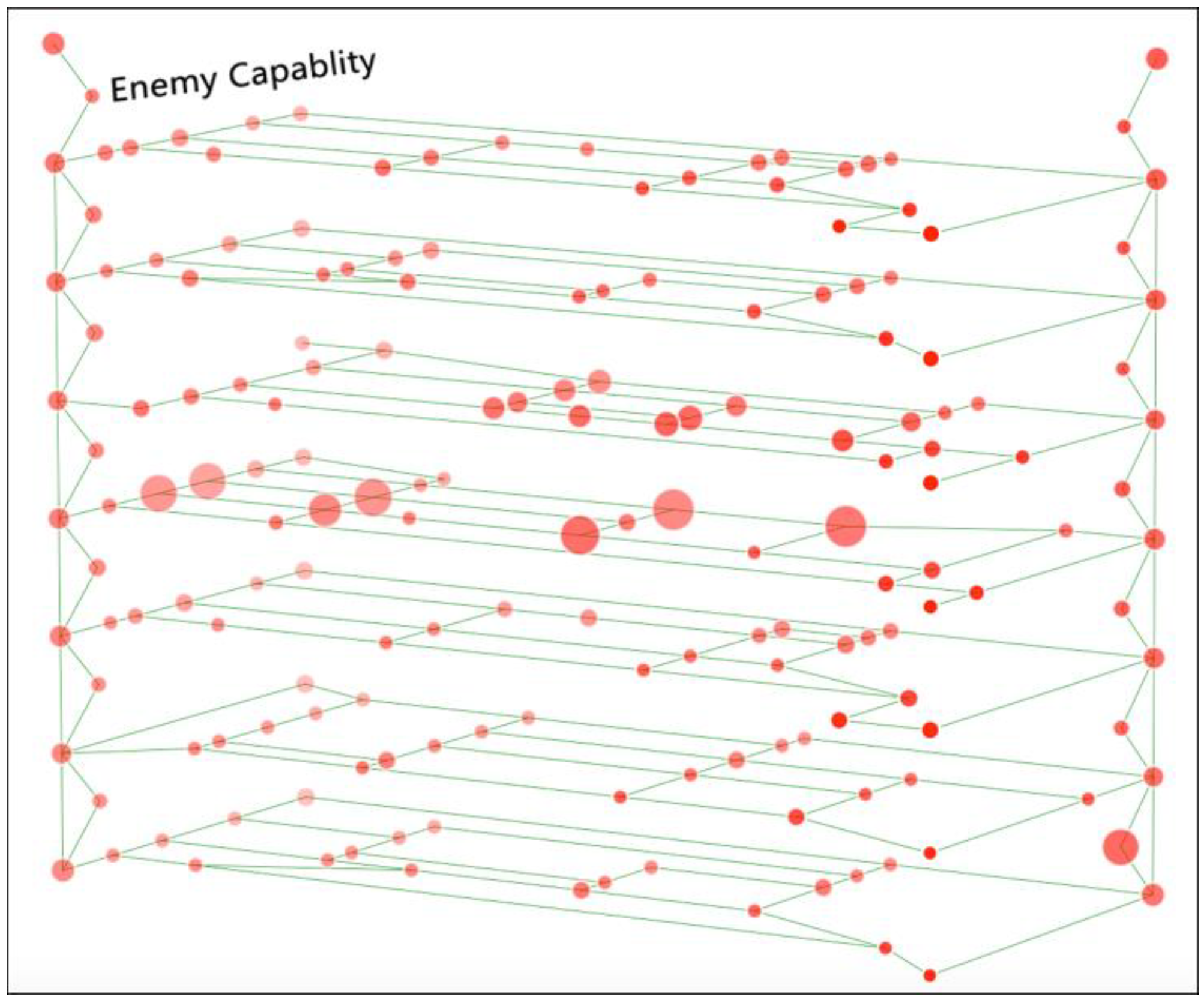
2.5. Intelligence Information
- IGBMLPeople is the detailed information about the enemy and victims (for some rescue operations). This includes the number of enemy and victims, the military ranks and positions of enemy, etc.
- IGBMLWeapon describes the number and categories of the enemy’s weapons.
- IGBMLLocation is the location of people and weapons.
2.6. Event Information
3. IORP Algorithm for Indoor Operation Route Planning
3.1. The Core Concept of IORP Algorithm
3.1.1. Route Selection
3.1.2. Parameters Setting
3.1.3. Pheromone Update
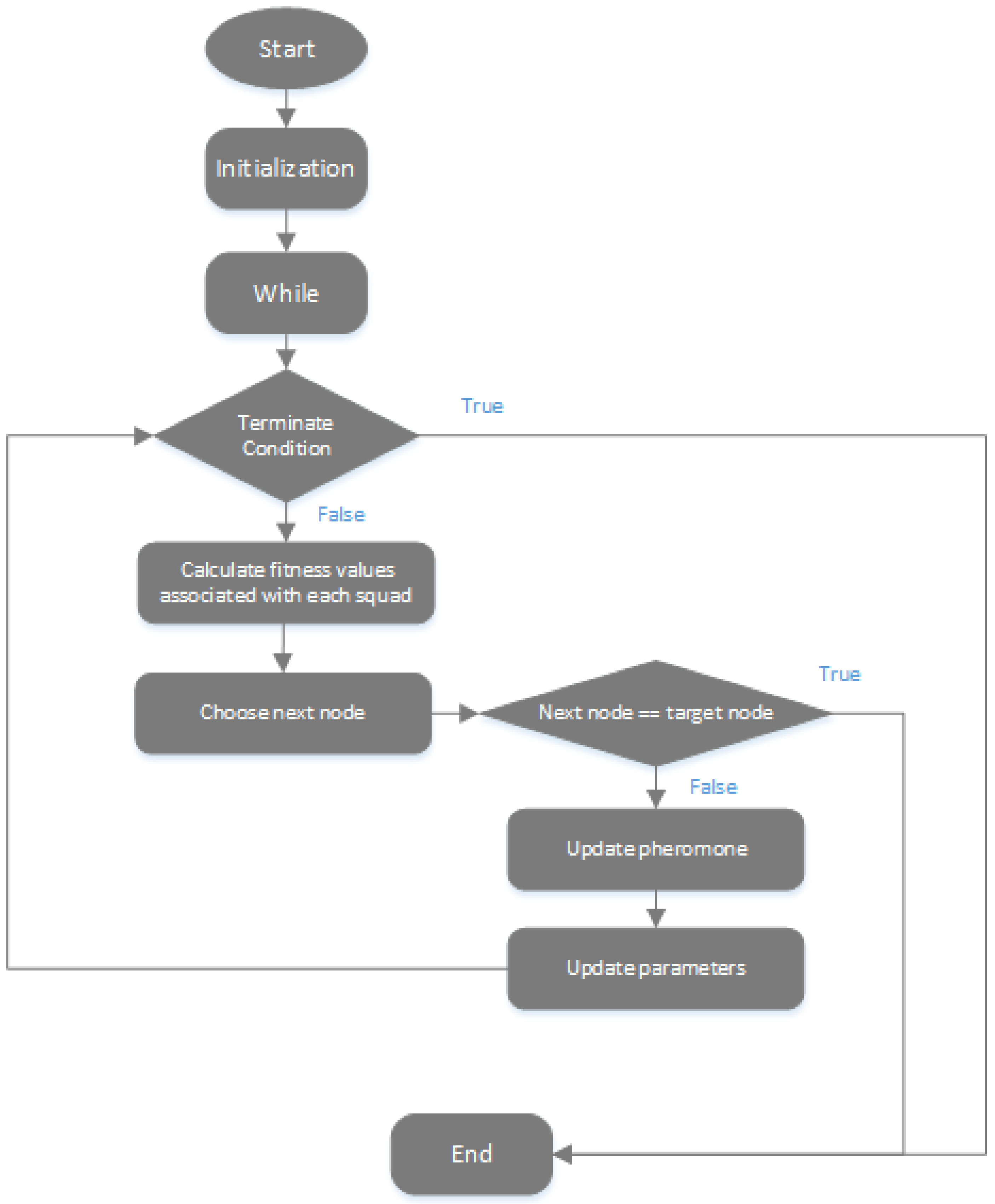
3.2. IORP Algorithm for Single Destination Short Route Planning
| Algorithm 1. Pseudo code of IORP algorithm for the single destination route planning | |
| 1. | initialization; |
| 2. | while not terminate condition do |
| 3. | calculate fitness values associated with each squad; |
| 4. | choose next node; |
| 5. | if next node != target node then |
| 6. | update pheromone; |
| 7. | update parameters; |
| 8. | end |
| 9. | end |
3.3. IORP Algorithm for Whole Searching Route Planning
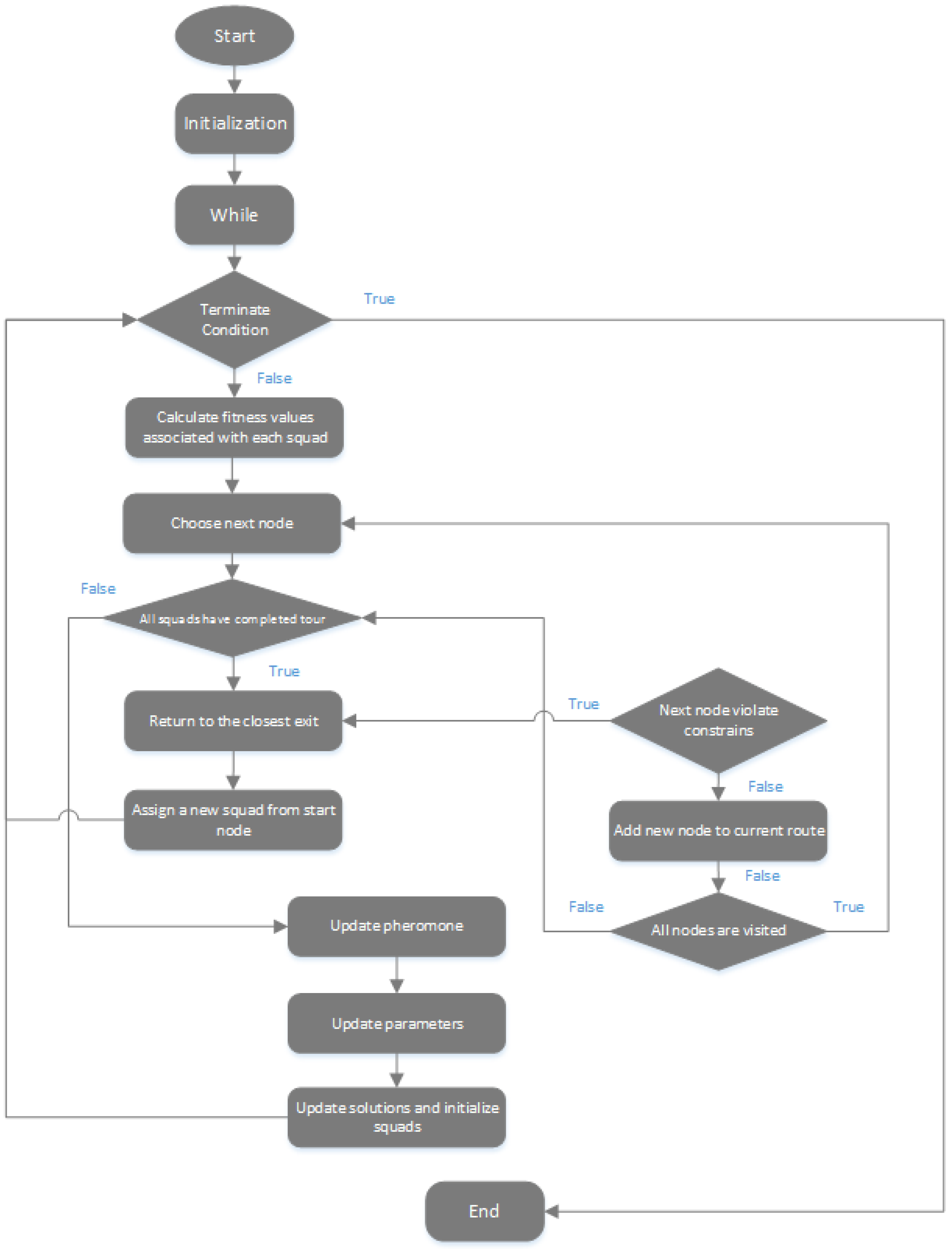
3.3.1. Implementation Steps of IORP Algorithm for Whole Searching Route Planning
3.3.2. Simplified Code of IORP Algorithm for Whole Searching Route Planning
| Algorithm 2. Pseudo code of IORP algorithm for whole searching route planning | |
| 1. | initialization; |
| 2. | while not terminate condition do |
| 3. | calculate fitness values associated with each squad; |
| 4. | if not all squads have completed tour then |
| 5. | choose next node; |
| 6. | if next node violates constrains then |
| 7. | return to closest exit; |
| 8. | assign a new squad from start node; |
| 9. | else |
| 10. | add a new node to current route; |
| 11. | if not all nodes are visited then |
| 12. | choose next node; |
| 13. | continue while loop; |
| 14. | else |
| 15. | update pheromone; |
| 16. | update parameters; |
| 17. | solution and initialize squads; |
| 18. | end |
| 19. | end |
3.3.3. Flow Chart of IORP Algorithm for Whole Searching Route Planning
4. Experiment and Result Analysis
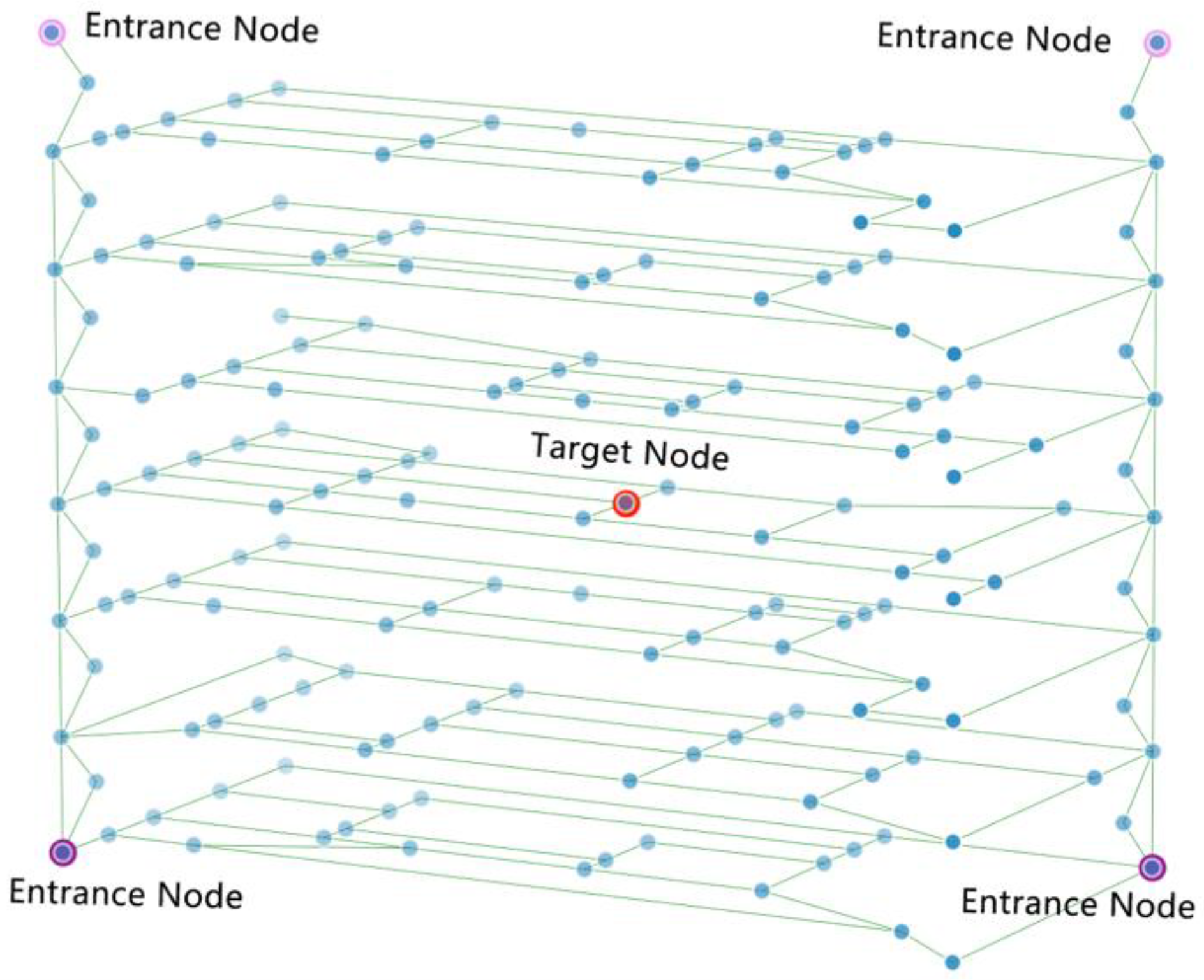
4.1. Experimental Design
4.2. The Single Destination Route Planning Result
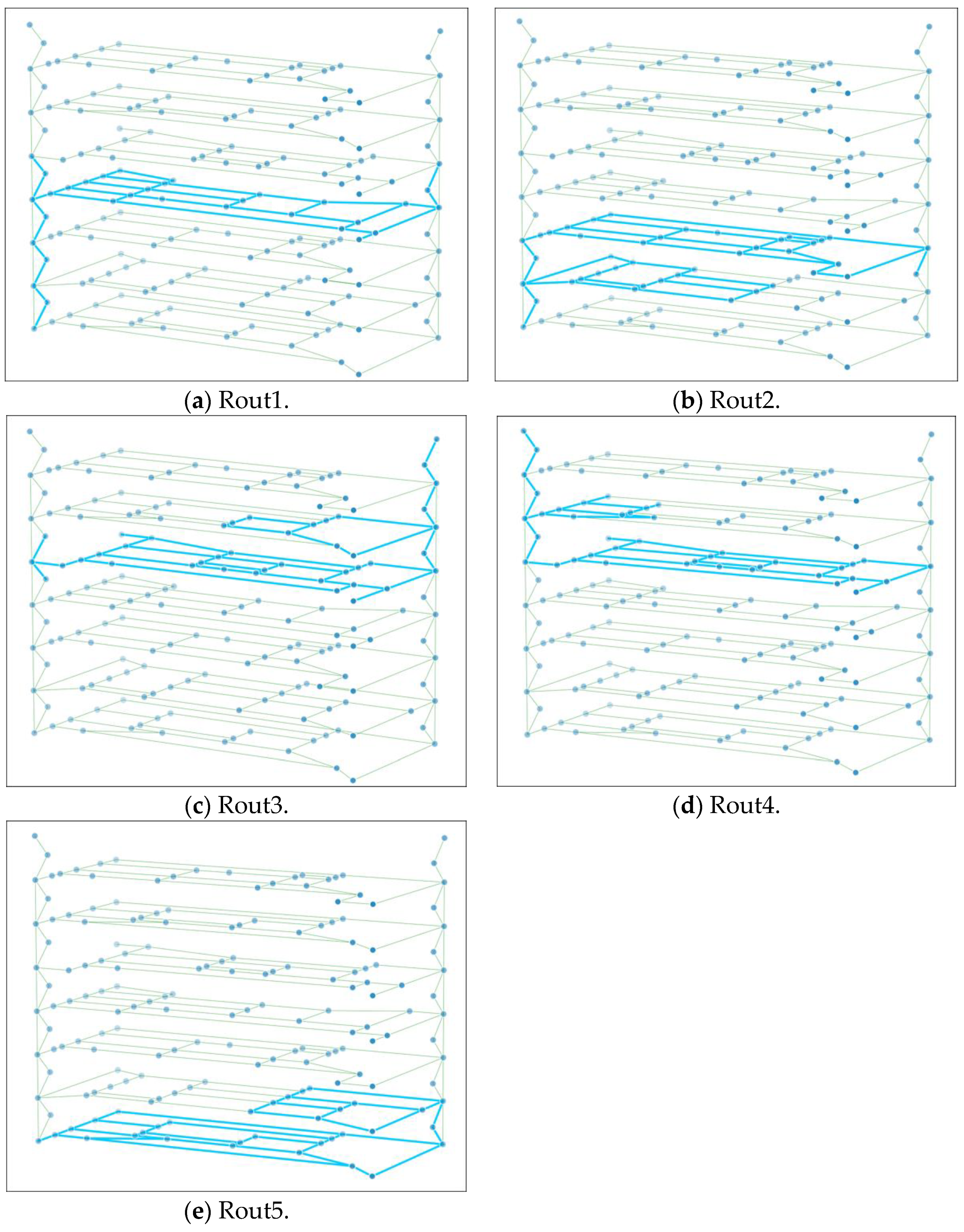
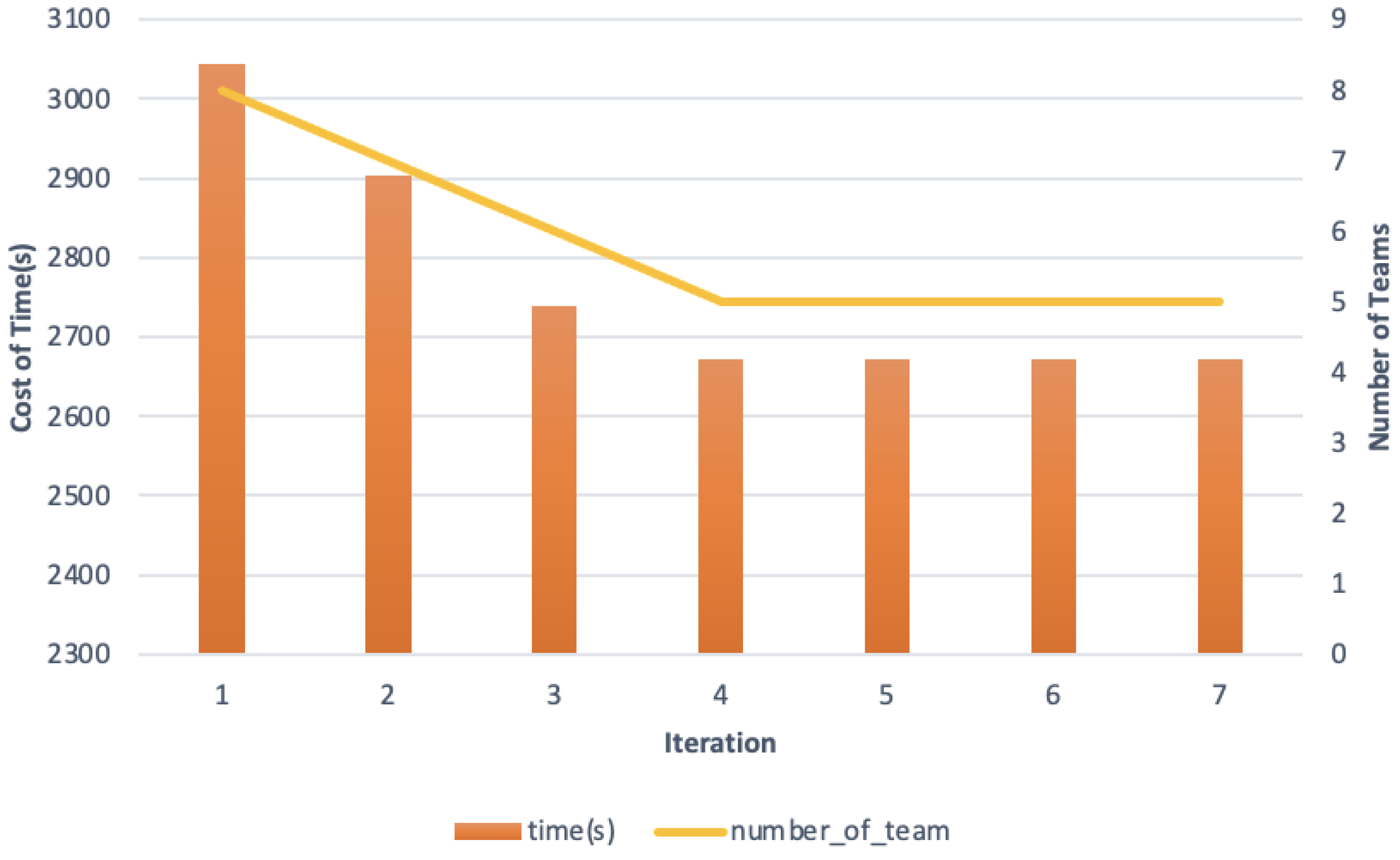
4.3. The Whole Searching Route Planning Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Meaning | Meaning of Subscript and Superscript | |
| V | Geometry entities vector | None |
| vi | Geometry entity coordinate | i: node number |
| AG | Geometry entity attribute vector | G: geometry entity |
| Geometry entity attribute node | i: node number G: geometry entity | |
| G(V,AG) | Geometry information vector | V: geometry entity coordinate AG: geometry entity attribute |
| gi | Geometry information node | i: node number |
| E | Navigation entities vector | None |
| ej | Navigation entity coordinate | j: node number |
| AN | Navigation entity attribute vector | N: navigation entity |
| Navigation entity attribute node | i: node number N: navigation entity | |
| N(E,AN) | Navigation information vector | E: navigation entity coordinate AN: navigation entity attribute |
| gj | Navigation information node | j: node number |
| U(G,N) | Matrix of relationship between geometry and navigation information | G: geometry information vector N: navigation information vector |
| SG | Semantic information of geometry entities | G: geometry information |
| SN | Semantic information of navigation entities | N: navigation information |
| sx | Speed of entity | x: type of entity, sp represents IGBMLSpace, el represents IGBMLElevator, st represents IGBMLStair, ro represents road |
| ψx | Military difficulty factor | x: type of entity, sp represents IGBMLSpace, el represents IGBMLElevator, st represents IGBMLStair, ro represents road |
| Judge if node in route | x: type of entity, sp represents IGBMLSpace, el represents IGBMLElevator, st represents IGBMLStair, ro represents road ij: node number | |
| B | Outdoor information vector | None |
| bp | Outdoor entity coordinate | p: node number |
| μy | Coefficient in intelligence information | y: type of coefficient, p represents IGBMLPeople, w represents IGBMLWeapon |
| Number of IGBMLPeople | p: represents IGBMLPeople i: node number | |
| Number of IGBMLWeapon | w: represents IGBMLWeapon i: node number | |
| Power of IGBMLWeapon | w: represents IGBMLWeapon i: node number | |
| Enemy capability | E: represents enemy xy: node number | |
| axy | Nodes can accessible or not | xy: node number |
| txy | Traversing time between nodes | xy: node number |
| dxy | Distance between nodes | xy: node number |
| θxy | Cost between nodes | xy: node number |
| D | Event information tuple | None |
| f | Function of event information | None |
| Own max casualty can bear | O: represents own s: represents casualty | |
| Probability to choose next node | k: squad number xy: node number | |
| Probability influence τ | α: parameter to control τ xy: node number | |
| Probability influence θ | β: parameter to control θ xy: node number | |
| Imax | Total number of iterations | max: total number |
| I | Current number of iterations | None |
| Coefficient with enemy’s capability and own side capability | None | |
| Coefficient with enemy’s capability and own side capability | None | |
| Coefficient with enemy’s capability and own side capability | None | |
| Coefficient with enemy’s capability and own side capability | None | |
| Initial pheromone value | 0: initial state : Probability to choose next node | |
| τ0 | Initial value | 0: initial state |
| dH,max | Maximum distance of horizontal | H,max: horizontal maximum |
| dV,max | Maximum distance of vertical | V,max: vertical maximum |
| Distance from the node to the straight line L | : Probability to choose next node L: straight line | |
| λ | Map scale factor | None |
| len(k) | Path length of the kth squad | k: the kth squad |
| rank(k) | The rank of ant k | k: the kth squad |
| ϑ · M | Number of squads to be updated | None |
| ρ | Pheromone volatility factor | None |
| Q | Pheromone constant | None |
| ρ(k) | The kth squad pheromone update | k: the kth squad |
| Preset value of pheromone volatilization rate | min: preset value | |
| Route vector | k: the kth squad xy: node number |
References
- Carey, S.; Kleiner, M.; Hieb, M.R.; Brown, R. Standardizing Battle Management Language–A Vital Move Towards the Army Transformation. In Proceedings of the IEEE Fall Simulation Interoperability Workshop, Orlando, FL, USA, 9–14 September 2001. [Google Scholar]
- Hieb, M.R.; Pullen, M.; Kleiner, M.; Powers, M. A geospatial battle management language (geoBML) for terrain reasoning. In Proceedings of the 11th International Command and Control Research and Technology Symposium, Cambridge, MA, USA, 20–22 June 2006. [Google Scholar]
- Hieb, M.R.; Mackay, S.; Powers, M.W.; Yu, H.; Kleiner, M.; Pullen, J.M. Geospatial challenges in a net centric environment: Actionable information technology, design, and implementation. In Proceedings of the Defense and Security Symposium, Orlando, FL, USA, 9 April 2007; Defense Transformation and Net-Centric Systems. International Society for Optics and Photonics: Bellingham, DC, USA, 2007; Volume 6578. [Google Scholar]
- Ulrich, S.; Hieb, M.R. Battle management language: A grammar for specifying reports. In Proceedings of the IEEE Spring Simulation Interoperability Workshop, San Diego, CA, USA, 25–29 March 2007. [Google Scholar]
- Ulrich, S.; Hieb, M.R. Formalizing battle management language: A grammar for specifying orders. In Proceedings of the 2006 Spring Simulation Interoperability Workshop, Arlington, VA, USA, 18–23 April 2006. [Google Scholar]
- Sudnikovich, W.P.; Pullen, J.M.; Kleiner, M.S.; Carey, S.A. Extensible battle management language as a transformation enabler. Simulation 2004, 80, 669–680. [Google Scholar] [CrossRef]
- Pullen, J.M.; Tolk, A.; Blais, C. Joint Battle Management Language (JBML)-US Contribution to the C-BML PDG and NATO MSG-048 TA. 2014. Available online: https://netlab.gmu.edu/pubs/07E-SIW-029.pdf (accessed on 27 March 2022).
- Martin, K.; Carey, S.; Roberts, J.; Altenau, M.; Yu, H.; Gates, B.Q.; Nielsen, E. Geospatial battle management language: Bridging GIS, C2 and simulations. In Proceedings of the ESRI Users Conference, San Diego, CA, USA, 18–22 June 2007. [Google Scholar]
- Zhou, J.; You, X.; Xia, Q. Object-oriented Battlefield Environment Simulation Process Object Model Based on Task-driven. J. Geod. Geoinf. Sci. 2020, 2, 31–43. [Google Scholar]
- Shiau, Y.-C.; Tsai, Y.Y.; Hsiao, J.-Y.; Chang, C.T. Development of building fire control and management system in BIM environment. Stud. Inform. Control 2013, 22, 15–24. [Google Scholar] [CrossRef]
- Wang, B.; Li, H.; Rezgui, Y.; Bradley, A.; Ong, H.N. BIM based virtual environment for fire emergency evacuation. Sci. World J. 2014, 2014, 589016. [Google Scholar] [CrossRef] [PubMed]
- Cheng, M.-Y.; Chiu, K.-C.; Hsieh, Y.-M.; Yang, I.-T.; Chou, J.-S.; Wu, Y.-W. BIM integrated smart monitoring technique for building fire prevention and disaster relief. Autom. Constr. 2017, 84, 14–30. [Google Scholar] [CrossRef]
- Fu, X.; Yao, H.; Yang, Y. Modeling and optimizing the cascading robustness of multisink wireless sensor networks. IEEE Trans. Reliab. 2020, 70, 121–133. [Google Scholar] [CrossRef]
- Yiquan, S.; Niu, L.; Li, Y. Combinatorial spatial data model for building fire simulation and analysis. ISPRS Int. J. Geo-Inf. 2019, 8, 408. [Google Scholar] [CrossRef] [Green Version]
- Fu, X.; Wang, Y.; Yang, Y.; Postolache, O. Analysis on cascading reliability of edge-assisted Internet of Things. Reliab. Eng. Syst. Saf. 2022, 108463. [Google Scholar] [CrossRef]
- Benton, J.R.; Iyengar, S.S.; Deng, W.; Brener, N.; Subrahmanian, V.S. Tactical route planning: New algorithms for decomposing the map. Int. J. Artif. Intell. Tools 1996, 5, 199–218. [Google Scholar] [CrossRef]
- Singhal, K.; Sahu, S. Fire evacuation using ant colony optimization algorithm. Int. J. Comput. Appl. 2016, 139, 0975–8887. [Google Scholar] [CrossRef]
- Wu, C.H.; Chen, L.C. 3D spatial information for fire-fighting search and rescue route analysis within buildings. Fire Saf. J. 2012, 48, 21–29. [Google Scholar] [CrossRef]
- Tashakkori, H.; Rajabifard, A.; Kalantari, M. Facilitating the 3d indoor search and rescue problem: An overview of the problem and an ant colony solution approach. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 4, 233. [Google Scholar] [CrossRef] [Green Version]
- Fu, X.; Pace, P.; Aloi, G.; Li, W.; Fortino, G. Cascade Failures Analysis of Internet of Things under Global/Local Routing Mode. IEEE Sens. J. 2021, 22, 1705–1719. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Liu, Y.-S.; Gao, G.; Han, X.-G.; Lai, C.-Y.; Gu, M. The IFC-based path planning for 3D indoor spaces. Adv. Eng. Inform. 2013, 27, 189–205. [Google Scholar] [CrossRef] [Green Version]
- Monmarché; Nicolas; Guinand, F.; Siarry, P. Artificial Ants; Wiley-ISTE: Hoboken, NJ, USA, 2010. [Google Scholar]
- Rachmawati, D.; Gustin, L. Analysis of Dijkstra’s Algorithm and A* Algorithm in Shortest Path Problem. J. Phys. Conf. Series. 2020, 1566, 012061. [Google Scholar] [CrossRef]
- Houssein, E.H.; Gad, A.G.; Hussain, K.; Suganthan, P.N. Major advances in particle swarm optimization: Theory, analysis, and application. Swarm Evol. Comput. 2021, 63, 100868. [Google Scholar] [CrossRef]
- Venkateswaran, C.; Ramachandran, M.; Chinnasamy, S.; Chinnasami, S. An Extensive Study on Gravitational Search Algorithm. In Materials and Its Characterization; REST Publisher: Krishnagiri, India, 2022. [Google Scholar]
- Nama, S.; Saha, A.K. A Bio-Inspired Multi-Population-Based Adaptive Backtracking Search Algorithm. Cogn. Comput. 2022, 14, 900–925. [Google Scholar] [CrossRef] [PubMed]
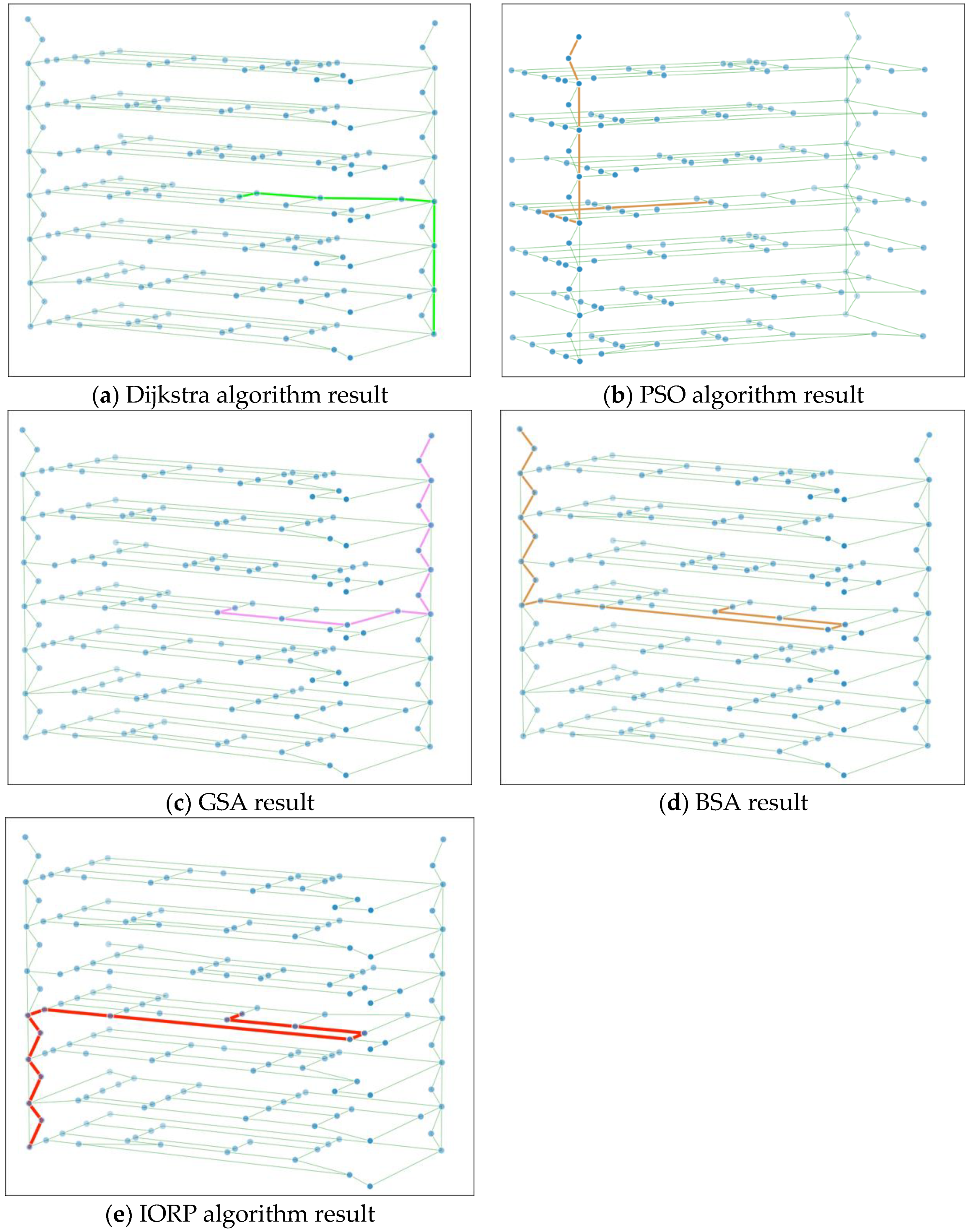
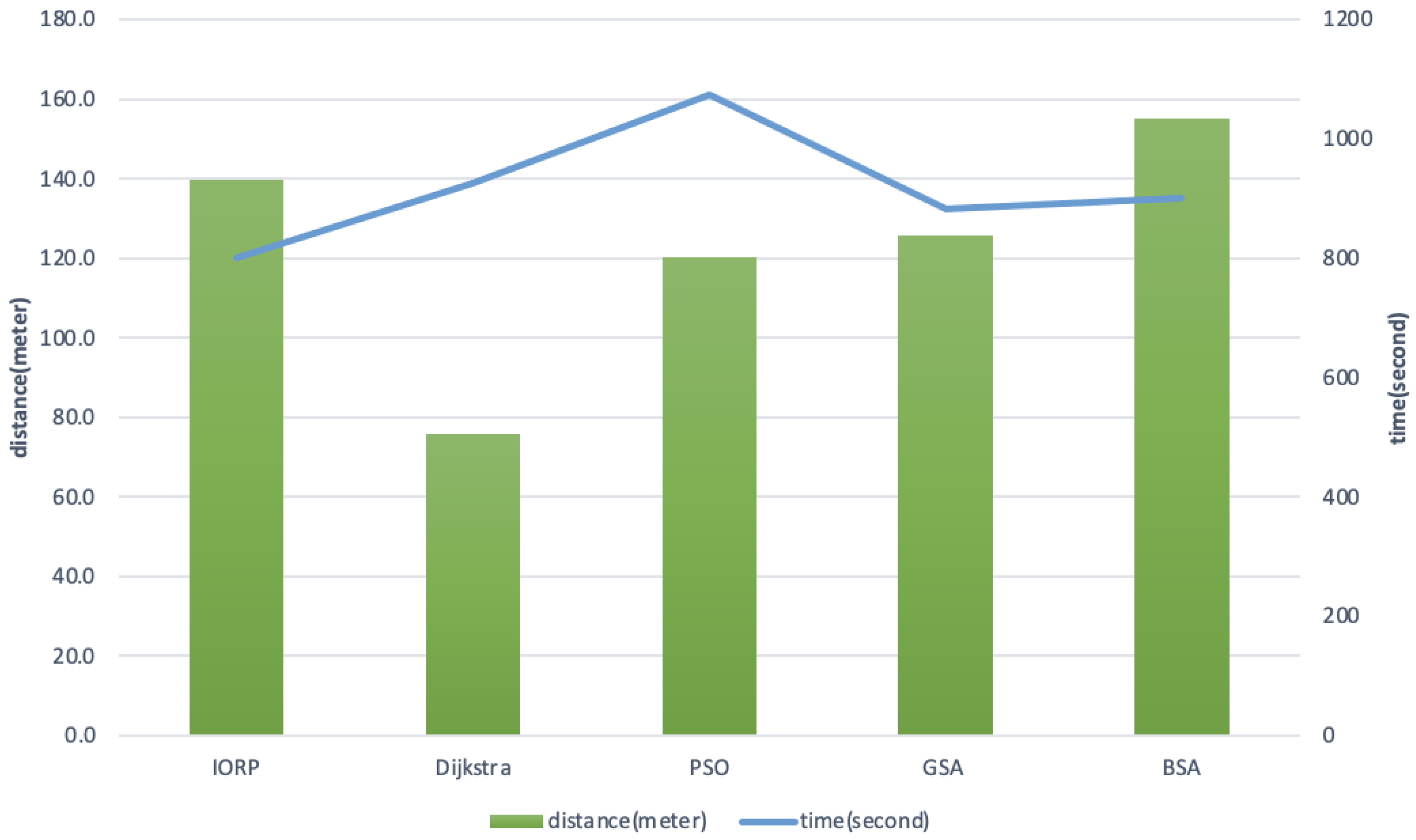
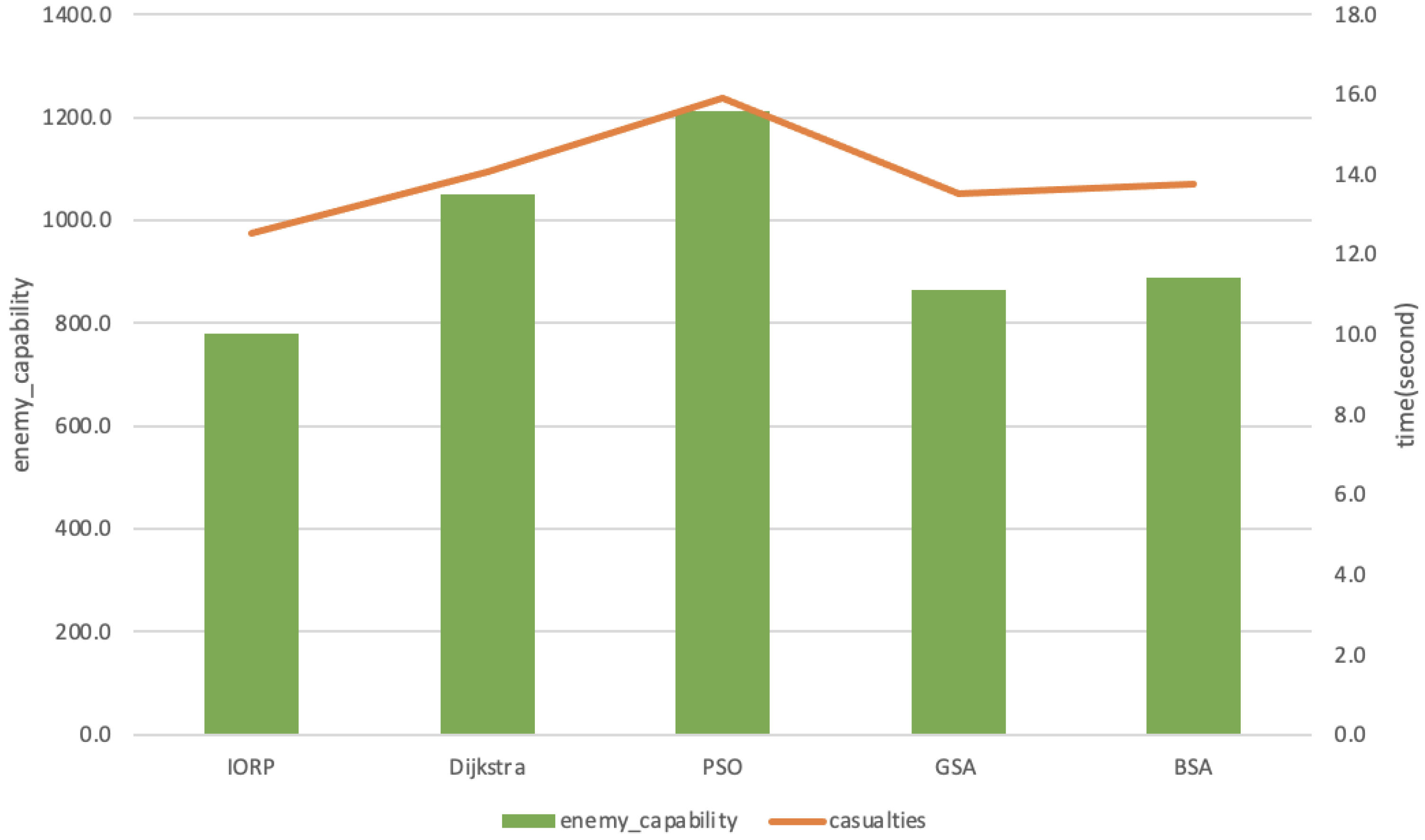
| Algorithm | Distance (m) | Enemy Capability | Time (s) | Casualties |
|---|---|---|---|---|
| Dijkstra | 75.8 | 1049.0 | 925 | 14.1 |
| PSO | 120.1 | 1211.1 | 1073 | 15.9 |
| GSA | 125.7 | 864.8 | 882 | 13.5 |
| BSA | 155.1 | 887.3 | 902 | 13.8 |
| IORP | 139.6 | 779.2 | 801 | 12.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, M.; Wang, G.; Chen, L.; Zhang, X. An IndoorGeoBML Model Based IORP Algorithm for Indoor Operation. Sustainability 2022, 14, 5760. https://doi.org/10.3390/su14105760
Su M, Wang G, Chen L, Zhang X. An IndoorGeoBML Model Based IORP Algorithm for Indoor Operation. Sustainability. 2022; 14(10):5760. https://doi.org/10.3390/su14105760
Chicago/Turabian StyleSu, Mingzhan, Guangxia Wang, Lingyu Chen, and Xin Zhang. 2022. "An IndoorGeoBML Model Based IORP Algorithm for Indoor Operation" Sustainability 14, no. 10: 5760. https://doi.org/10.3390/su14105760
APA StyleSu, M., Wang, G., Chen, L., & Zhang, X. (2022). An IndoorGeoBML Model Based IORP Algorithm for Indoor Operation. Sustainability, 14(10), 5760. https://doi.org/10.3390/su14105760






