Abstract
State of charge (SOC) of the lithium-ion battery is an important parameter of the battery management system (BMS), which plays an important role in the safe operation of electric vehicles. When existing unknown or inaccurate noise statistics of the system, the traditional unscented Kalman filter (UKF) may fail to estimate SOC due to the non-positive error covariance of the state vector, and the SOC estimation accuracy is not high. Therefore, an improved adaptive unscented Kalman filter (IAUKF) algorithm is proposed to solve this problem. The IAUKF is composed of the improved unscented Kalman filter (IUKF) that is able to suppress the non-positive definiteness of error covariance and Sage–Husa adaptive filter. The IAUKF can improve the SOC estimation stability and can improve the SOC estimation accuracy by estimating and correcting the system noise statistics adaptively. The IAUKF is verified under the federal urban driving schedule test, and the SOC estimation results are compared with IUKF and UKF. The experimental results show that the IAUKF has higher estimation accuracy and stability, which verifies the effectiveness of the proposed method.
1. Introduction
With the increasing global energy crisis and environmental pollution, pollution-free and zero-emission electric vehicles have been developing rapidly [1]. Lithium-ion batteries are extensively used in power systems of electric vehicles due to their high energy density, low self-discharge rate, and long cycle life. State of charge (SOC) of the lithium-ion battery is an indicator that describes the remaining power of the battery [2]. It can be used to prevent the battery from being overcharged or overdischarged, predict the driving range of electric vehicles, and reduce the inconsistency of different cells. It is one of the most important parameters of the electric vehicle battery management system (BMS) [3]. However, the SOC cannot be directly measured, and various factors such as ambient temperature, battery aging levels, and charging/discharging current rate will affect the accuracy of SOC estimation [4]. Therefore, estimating SOC precisely is a difficult subject that restricts the rapid development of electric vehicles.
Roughly, SOC estimation methods can be divided into three categories: experiment-based method, data-based method, and model-based method. The SOC estimation method based on experiments such as the discharge test method [5], open-circuit voltage method [6], and electrochemical impedance spectroscopy method [7] can obtain accurate SOC estimation. However, these kinds of methods are rarely used on large scale in BMS because of the long test time, high costs, etc. The data-based SOC estimation methods mainly include artificial neural network method [8], support vector machine method [9], Gaussian regression method [10], etc. Through a large amount of data training, these methods obtain the relationship between SOC and battery external measurement variables such as battery terminal voltage, working current, and ambient temperature and then realize the estimation of battery SOC. However, the SOC estimation accuracy of this kind of method is highly dependent on the training data. The model-based SOC estimation method has been tremendously studied because it can realize the closed-loop self-correction of the SOC estimation. The typical representatives of this method are Kalman filter (KF) and particle filter (PF). Compared with KF, PF [11] does not require the system noise statistics to satisfy Gaussian distribution, but the calculation of this method is complex, which affects its practicability. In order to solve the nonlinear of the battery model, an extended Kalman filter [12] (EKF) is used for SOC estimation. EKF realizes the linearization of the battery model through Taylor series expansion, which inevitably introduces the unnecessary linearization error. Through the unscented transformation, the unscented Kalman filter (UKF) [13] directly transmits the mean value and covariance of the state vector nonlinearly, thereby solving the problem of linearization error of the EKF. Moreover, the UKF does not need to calculate the Jacobian matrix, and the computational burden is much lower than EKF. However, when UKF is used to estimate the battery SOC, the filtering failure is often caused by the non-positive error covariance. Reference [14] uses the square root of the UKF to improve the stability of the SOC estimation. However, due to the roundoff error of the computer, it still cannot guarantee the positive definiteness of the error covariance.
At present, most of the battery SOC estimation methods based on UKF assume that the system process and measurement noise are known and fixed. However, the actual working environment of the battery is relatively complex, and the system noise statistical characteristics are usually difficult to accurately obtain. When existing unknown or inaccurate noise statistics of the system, the traditional unscented Kalman filter may fail to estimate SOC due to the non-positive error covariance of the state vector, and the SOC estimation accuracy is low. Therefore, a new SOC estimation algorithm for lithium-ion batteries based on an improved adaptive unscented Kalman filter is proposed in this paper. In order to realize the adaptive estimation of SOC by the improved adaptive unscented Kalman filter (IAUKF), firstly, the second-order resistor–capacitor (RC) equivalent circuit is selected to characterize the dynamic behaviors of the battery, and the model parameters are identified to obtain the state–space equation and output equation required by the IAUKF to estimate SOC. Secondly, singular value decomposition (SVD) is used to replace the Cholesky decomposition in the traditional UKF, and an improved unscented Kalman filter (IUKF) that can suppress the non-positive definiteness of the error covariance is proposed. Thirdly, IAUKF is proposed by combining IUKF with Sage–Husa adaptive filter. Finally, IAUKF is applied to SOC estimation based on the battery state–space equation and output equation. The IAUKF method is verified by experimental data under the federal urban driving schedule (FUDS) test [15]. The SOC estimation results are compared with IUKF and traditional UKF.
2. Battery State–Space Model
2.1. Second-Order Thevenin Equivalent Circuit Model
When using KF to estimate battery SOC, it is necessary to establish an accurate battery equivalent model. Usually, the selection of the battery equivalent model needs to meet the following requirements: firstly, the model can accurately simulate the dynamic and static characteristics of the battery in actual work conditions; secondly, the physical meaning of the model is clear, which is convenient for parameters identification and simple for calculation. The equivalent circuit model of the battery is widely used in battery SOC estimation for meeting the above two requirements. The commonly used battery equivalent circuit models include [16,17] Rint model, PNGV model, GNL model, and Thevenin model. According to the order of series-connected RC network that is composed of the resistors and capacitors parallel circuits, the Thevenin equivalent circuit model can be divided into the first-order Thevenin model and n-order Thevenin model [18]. The more RC networks are in series, the more accurate the model is, but the more complex the calculation is. Considering the accuracy and computational costs of the model, the second-order Thevenin model is used to characterize the battery in this paper. The second-order Thevenin equivalent circuit model is shown in Figure 1.
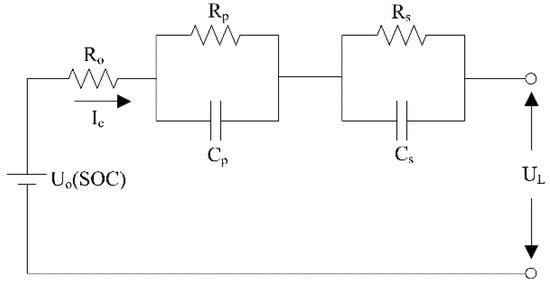
Figure 1.
Second-order Thevenin equivalent circuit model.
Here, Uo(SOC) denotes the open-circuit voltage (OCV) of the battery and its value changes with the SOC; UL denotes the terminal voltage; Ic denotes the charging/discharging current, and it is a positive number in the discharge process in this paper; Rp and Rs denote the polarization resistance; Cp and Cs denote the polarization capacitance; RpCp parallel network, and RsCs parallel network that simulates the concentration polarization and the electrochemical polarization of the battery. The polarization voltage across Cp and Cs are Up and Us, respectively.
According to the second-order Thevenin equivalent circuit model of the battery illustrated in Figure 1, the state–space equation and output equation of the battery can be obtained by using Kirchhoff’s law as follows:
Combined with the Ampere-hour (AH) counting method [19], SOC of the battery, the polarization voltage Up, and Us of the two RC networks are selected as system state variables. Equation (1) is discretized to obtain the discrete battery state–space equation and output equations as follows:
where, x = [SOC Up Us]T; k represents the time step; xk and Ic,k denote the state variable of the system and the charging/discharging current at time step k, respectively; τp and τs are time parameters, τp = RpCp, τs = RsCs; denotes the time interval of discretization; η denotes the Coulombic efficiency, which is assumed to be 1 for lithium-ion batteries; and CN denotes the nominal capacity of the battery. It should be noted that the analogous definition will apply throughout the paper if not otherwise stated.
Here, define
where yk denotes the measurement variable, and uk denotes the input variable.
Considering the system process noise and measurement noise, the state–space equation and output equation of the battery can be further written as
where, ωk denotes the process noise of the system, whose mean value is qk and covariance value is Qk, and vk denotes the measurement noise of the system, whose mean value is rk and covariance value is Rk.
2.2. Relationship between OCV and SOC
The OCV of the battery is a one-to-one correspondence with SOC, which plays an important role in SOC estimation [20]. Taking the Samsung 18,650 power lithium battery as the research object, the SOC–OCV relationship is obtained by OCV–SOC mapping tests [21]. In order to reduce the error of the battery model, the average value of OCV in charging and discharging direction under the same SOC is taken, and then the SOC–OCV relationship is fitted by the sixth-order polynomial. The fitted curve is shown in Figure 2.
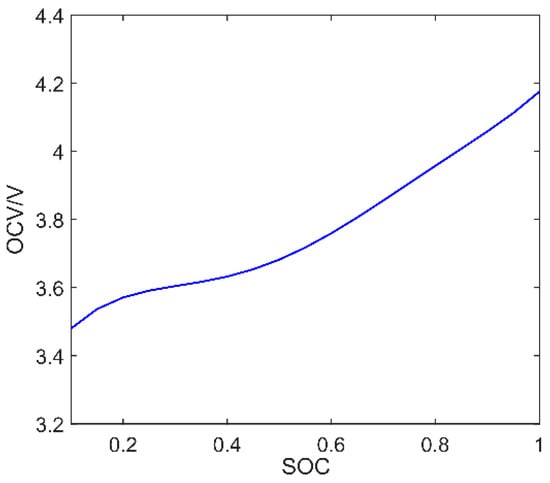
Figure 2.
Fitted SOC–OCV curve.
The OCV–SOC function relationship obtained by fitting is as follows:
2.3. Parameters Identification of Battery Model
When estimating the SOC, it is necessary to identify the relevant parameters including Ro, Rp, Rs, Cp, and Cs in the second-order RC equivalent circuit model of the battery. As one of the most commonly used methods in parameters identification, the least squares method has the characteristics of small computational effort and no requirement for prior statistical knowledge. In this paper, the offline recursive least squares method [22] is applied to identify the model parameters Ro, Rp, Rs, Cp, and Cs under dynamic stress test (DST) [23]. In order to reduce the error of model parameters identification, this paper takes the average values of multiple battery parameters obtained by the offline recursive least squares as the final identification results. The identification results are shown in Table 1.

Table 1.
Identified battery parameters.
The sixth-order SOC–OCV fitting polynomial obtained in Section 2.2 and second-order RC equivalent circuit model parameters Ro, Rp, Rs, Cp, and Cs identified in Section 2.3 are substituted into Equation (8) to obtain the state–space equation and output equation of 18,650 power lithium battery. Based on the state–space equation and output equation, the IAUKF can realize the real-time optimal estimation of the battery SOC.
3. State of Charge Estimation
When the UKF is used to estimate the SOC of the battery, the Cholesky decomposition is employed to factorize the error covariance of the state vector to obtain Sigma sampling points for nonlinear transmission. The Cholesky decomposition requires the error covariance matrix must be positive definite. However, the operating conditions of electric vehicles are complicated and the calculation rounding errors of the computer are unavoidable. As a matter of fact, the error covariance cannot always be guaranteed to be positive definite. If the error covariance is non-positive, the UKF will estimate SOC unsuccessfully. In addition, the process noise and measurement noise of the system should be set in advance when using UKF to estimate battery SOC. Usually, the system process noise and measurement noise are set to a constant value. If the system noise characteristics are known before the SOC estimation and the preset values of process noise and measurement noise are consistent with the actual noise statistical characteristics, UKF can estimate SOC accurately. However, in practical applications, the system noise statistics are usually unknown or inaccurate, sometimes even time varying. Additionally, if the operating mode and working environment of electric vehicles have changed, then the preset values of the system noise will no longer match the actual noise statistics. It will cause large SOC estimation errors and even lead to filtering failure. Therefore, for the sake of reducing the influence of system noise on SOC estimation accuracy, it is necessary to adaptively estimate system noise statistics in the process of SOC estimation. In order to address the two problems mentioned above when estimating SOC, the IAUKF is proposed in this paper. Additionally, based on the state–space equation and output equation of the lithium-ion battery obtained from Section 2.1, Section 2.2 and Section 2.3, the IAUKF is applied for battery SOC estimation.
3.1. Singular Value Decomposition
The singular value decomposition (SVD), proposed by Beltrami and Jordan, is a matrix orthogonalization decomposition method with good stability and accuracy used on a computer. Compared with Cholesky factorization, when the matrix to be factorized is positive definite, the two have the same decomposition results. When the matrix to be factorized is non-positive definite, the numerical stability of SVD is better than Cholesky factorization.
Providing P is an m × n matrix to be factorized over the real number field, where m ≥ n, then the SVD of P is
where U denotes a square matrix of degree m and its column vector is a left singular vector of matrix P; is an m × n semidefinite diagonal matrix; G is a square matrix of degree n, and its column vector is the right singular vector of matrix P; S = diag (s1, s2, … , sr) is a diagonal matrix, which is composed of singular values of matrix P; and r is the rank of matrix P, and s1 ≥ s2 ≥ … ≥ sr > 0.
3.2. Description of the IUKF
The numerical stability of SVD is much better than Cholesky factor decomposition. Therefore, in order to improve the stability of the UKF for SOC estimation, the Cholesky factor decomposition in traditional UKF is replaced by SVD in this paper, and then the IUKF is proposed.
For a discrete-time nonlinear system
where f and g are the nonlinear process and measurement models, respectively.
The detailed steps of IUKF can be summarized as follows:
- (1)
- Initialize the mean value of the system state variable x0, the error covariance P0, and the weighted coefficient.where E(·) denotes the expectation mean value.where and are mean weighted factor and covariance weighted factor, respectively; n is the dimension of the state vector; β is a non-negative weighted coefficient, which restrains the error caused by the higher-order term, and it is set to 2 for Gaussian random variables; α is a scaling parameter, which determines the distribution of Sigma sampling points around the state variable, its range is 1 × 10−4~1; λ is a composite coefficient, which can be expressed aswhere κ is another scaling parameter that is usually set to 3 − n.
- (2)
- Calculate Sigma sampling points of the state variable at time step k − 1 using SVD.where xi,k−1 denotes the Sigma sampling point; the symbol “^” denotes the estimated value and is the optimal estimate of the state variable at time step k − 1; is the error covariance at time step k − 1; and (·)i denotes the ith column of the matrix.
- (3)
- Time update for the mean and covariance of the state variable: use 2n + 1 Sigma sampling points obtained in step (2) to calculate the predicted mean and error covariance of the state variable in time step k.where k|k − 1 denotes the predicted value of the variable at time step k calculated based on the data at time step k − 1, and the intermediate variable is defined as follows:
- (4)
- Use SVD again to obtain new Sigma sampling points based on the predicted mean and error covariance of the state variable obtained in step (3).where denotes the regained Sigma sampling point, and the symbol “-” is used to distinguish the Sigma points obtained here from those obtained in step (2).
- (5)
- Time update for the mean of the measurement variable: calculate the predicted values of the measurement variable at time step k based on regained Sigma points in step (4).
- (6)
- Calculate the IUKF gain matrix Kk.wherewhere the intermediate variable is defined as follows:
- (7)
- Measurement correction of the state variable: calculate the corrected state variable estimated value and the optimal covariance matrix at time step k.
3.3. Description of Sage–Husa Adaptive Filter
The Sage–Husa adaptive filter is widely used in noise estimation due to the quality of simple principles and good practicability. Through the time-varying noise estimator, the Sage–Husa adaptive filter uses the measured data to realize the real-time estimation and correction of the system process and measurement noise statistics. Therefore, it can decrease the system model error, suppress the filter divergence and improve the filtering accuracy [24]. The estimation steps of the system process and measurement noise using a Sage–Husa adaptive filter can be summarized as follows [25,26]:
- (1)
- Calculate the estimated mean value of the system process noise.where dk can be expressed aswhere b is the forgetting factor, and its range is usually 0.95~1.
- (2)
- Calculate the estimated covariance value of the system process noise.where ek is a residual, which can be expressed as
- (3)
- Calculate the estimated mean value of the system measurement noise.
- (4)
- Calculate the estimated covariance value of the system measurement noise.
For a stable system, when using the Sage–Husa adaptive filter for noise estimation, the estimated state and measurement covariance will converge to a very small value or even zero when the filtering process begins to converge [27]. Therefore, we can attain
Then, the Sage–Husa adaptive filter can be further simplified as follows:
3.4. Estimate SOC Using IAUKF
As a matter of fact, the adaptive unscented Kalman filter (AUKF) can be formed by directly combining the traditional UKF with the Sage–Husa adaptive filter [28]. When the AUKF is applied to estimate SOC, the system noise statistics can be adaptively estimated through the Sage–Husa adaptive filter, thus reducing the influence of system noise on SOC estimation accuracy. However, due to the intrinsic characteristic of the traditional UKF, the error covariance is also required to be positive definite in the process of SOC estimation with AUKF. In addition, since the AUKF adaptively updates the system noise statistics while estimating SOC, the increase of computational complexity will further aggravate the uncertainty of error covariance in the calculation process, and it becomes more difficult to guarantee the error covariance to be positive definite. In order to overcome the shortcomings of AUKF, the IUKF is used to combine with the Sage–Husa adaptive filter, then the IAUKF is proposed in this paper. The only difference between IAUKF and AUKF is that the IAUKF replaces Cholesky factorization in AUKF with SVD. Depending on the outstanding numerical decomposition characteristic of SVD, the IAUKF can improve the stability of SOC estimation and the advantages of AUKF are retained as well. The main steps to estimate battery SOC using IAUKF are shown in Figure 3.
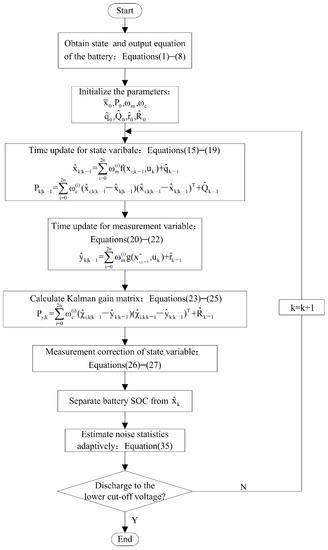
Figure 3.
SOC estimation flowchart using IAUKF.
Firstly, based on the second-order RC equivalent circuit model of the battery, the state–space equation and output equation required for IAUKF to estimate SOC are obtained. The fitted polynomial of the OCV–SOC relationship is obtained through OCV–SOC mapping tests. The parameters of the battery model are identified by the offline recursive least squares method. The state–space equation and output equation are transformed into the form of Equation (11). Secondly, some system parameters are initialized, including the initial value of the battery state variable, the initial value P0 of error covariance, the initial mean value and covariance value of process noise, the initial mean value , and covariance value of measurement noise. Additionally, the weighted coefficients and are also calculated. Thirdly, according to IAUKF calculation steps, the optimal estimated value of system state variable at time step k is obtained through Equations (15)–(27). The estimated SOC at time step k can be separated from the state variable optimal estimated value . It should be noted that when estimating the SOC of the battery at time step k, it is necessary to replace in Equation (17), in Equation (18), in Equation (22) and in Equation (24) with , , and , which are calculated based on the principle of Equation (35) using the relevant parameters at time step k − 1. Fourthly, based on the relevant parameters at the time step k, , , and are calculated through Equation (35) for the SOC estimation at time step k + 1; finally, determine whether the battery discharges to the lower cutoff voltage. If the battery has discharged to the lower cutoff voltage, then, end the SOC estimation. Otherwise, continue the SOC estimation.
4. Experimental Simulation and Verification
In practical applications, the operating conditions of electric vehicles are complex, and the working current of the lithium-ion battery changes dramatically. In order to verify the effectiveness of IAUKF, based on the state–space and output equations of Samsung 18,650 power lithium-ion battery obtained from Section 2.1, Section 2.2 and Section 2.3, the proposed estimation method is verified under sophisticated FUDS conditions. At the same time, the SOC estimated by IAUKF is compared with that estimated by IUKF and traditional UKF. The theoretical reference value of SOC is obtained by the AH counting method. The measured working current Ic and terminal voltage UL curves of the lithium-ion battery under the FUDS test are shown in Figure 4 and Figure 5. In Figure 4, the plus value represents the discharging current, and the minus value represents the charging current.
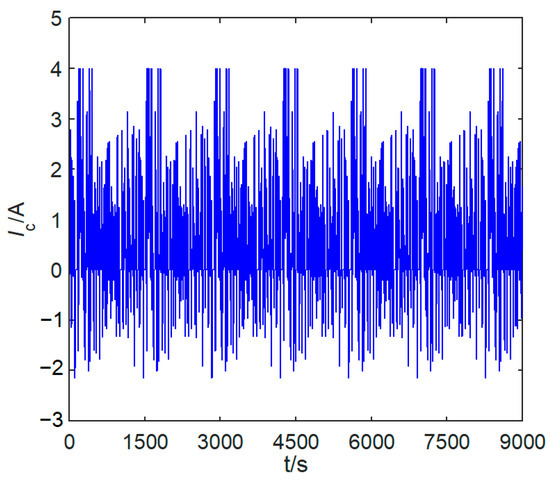
Figure 4.
Current curve of FUDS test.
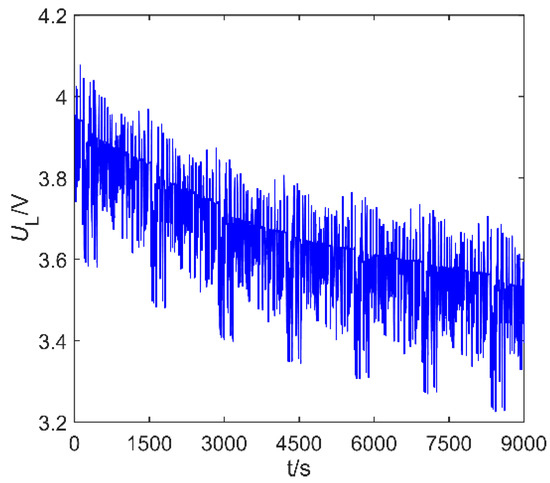
Figure 5.
Voltage curve of FUDS test.
When the traditional UKF, IUKF, and IAUKF are applied to estimate SOC, the selection of initial values of the three methods will pose a great impact on estimation results. Generally, the initial values of the UKF and its variants are tuned through a certain number of trial-and-error experiments based on experience because the noise characteristics of the system are difficult to accurately obtain. In order to compare the behaviors of different battery models effectively and avoid the interference of initial values on experimental results, particle swarm optimization is used creatively to calculate the initial values of EKF in the literature [29]. Since the main purpose of this paper is to study how to improve the stability of SOC estimation and reduce the influence of system noise on SOC estimation accuracy, very accurate initial values are not required. Furthermore, for reducing the influence of other factors on the experimental results and realizing the effective comparison of the three algorithms for SOC estimation, the initial values of the traditional UKF, IUKF and IAUKF are set the same in this paper. In other words, the stability and accuracy of SOC estimation among the three methods are analyzed and compared under the same initial conditions. Therefore, in this paper, the traditional UKF is taken as the test object and the initial values required by the three methods are obtained through an appropriate number of trial-and-error experiments. The preset values of the three methods are = [0.8 0 0]T, P0 = 10−1 × E3×3, , , , , where E3×3 denotes the unit matrix of degree 3.
The SOC estimation results of different methods and the SOC theoretical reference result are shown in Figure 6. As can be seen from Figure 6, IAUKF, IUKF, and UKF can estimate the SOC successfully, and the trend of SOC estimation curves are all consistent with the SOC theoretical reference curve. However, compared with the other two approaches, the SOC estimation result obtained by IAUKF is much closer to the theoretical reference curve.
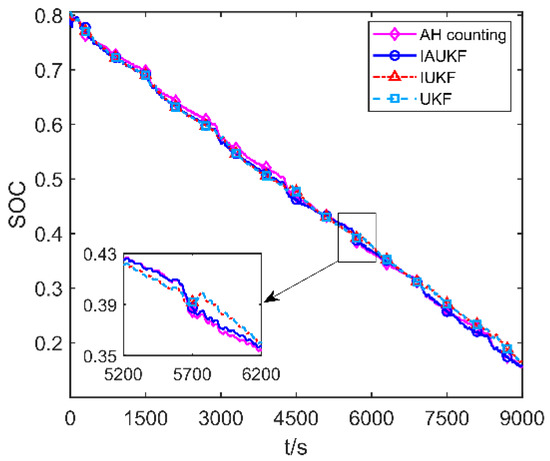
Figure 6.
SOC estimation comparative curves of FUDS test.
The error curves between the estimated SOC and reference SOC are shown in Figure 7. At the early state of SOC estimation, the estimation error of IAUKF for SOC is higher than IUKF and UKF. The reason is that during this period, the Sage–Husa adaptive filter is dynamically estimating the actual noise statistics of the system, and the estimated system noise statistics have not matched the actual noise statistics yet. As for the IUKF and UKF, the parameters of the noise statistics are preset, and the preset values are consistent with the actual noise statistical characteristics after the battery starts to work. Therefore, these two methods can obtain accurate SOC estimation, which is superior to IAUKF. About 300 s later, as the discharge progresses, the actual noise statistics changes, and the preset noise values cannot reflect the noise statistical characteristics any longer. As a result, the SOC estimation error curves of the IUKF and UKF fluctuate up and down dramatically. However, the IAUKF can estimate and correct the actual noise statistics of the system in real time through the Sage–Husa adaptive filter; thus, IAUKF can still obtain accurate SOC estimates, and the fluctuation of the SOC estimation error curve is significantly slighter than IUKF and UKF. Additionally, it is not difficult to find that the difference in SOC estimation accuracy between IUKF and traditional UKF is very small. This indicates that replacing the Cholesky factor decomposition in traditional UKF with SVD will not decrease the SOC estimation accuracy. Furthermore, as illustrated in Figure 7, we can also conclude that the estimation error of the three algorithms for SOC all exist with some certain offsets, namely, the estimation error curves of the three algorithms for SOC do not fluctuate around “SOC error = 0.” The reason for this phenomenon may be that when the offline least recursive squares method is used to identify the parameters of the battery model, the input noise of the system that can cause biased identification of the model parameters has not been taken into consideration. Consequently, there is a certain error between the identified battery model parameters and the real values [30]. The existence of this error reduces the accuracy of the battery model, which, in turn, leads to a certain deviation of the SOC estimation errors of the three methods.
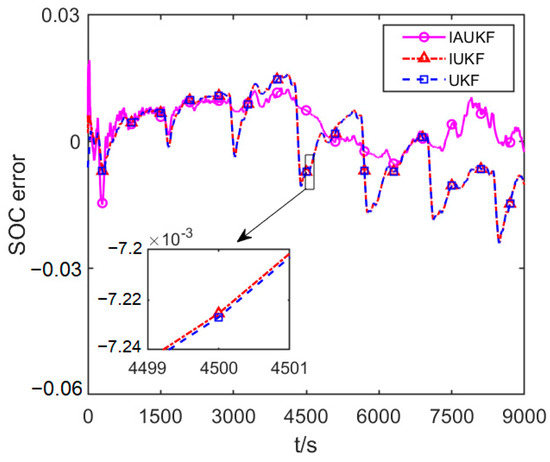
Figure 7.
SOC estimation error comparative curves of FUDS test.
In order to compare the accuracy of the three algorithms for SOC estimation quantitatively, the maximum absolute error (MAE) and root-mean-square error (RMSE) are employed in this paper to evaluate the three estimation methods. The smaller the MAE and RMSE are, the higher the SOC estimation accuracy is [31]. MAE and RMSE are calculated as follows:
where k is the step with a sample interval; Sk denotes the theoretical value of SOC; denotes the estimated value of SOC; L is the number of samples; |·| denotes the absolute value; and max (·) represents the maximum value of all samples.
The comparisons of MAE, RMSE of IAUKF, IUKF, and UKF under the FUDS test are shown in Table 2.

Table 2.
Comparisons of MAE and RMSE between IAUKF, IUKF, and UKF of FUDS test.
It can be inferred from Table 2 that the MAE and RMSE of the IAUKF are smaller than IUKF and UKF, indicating that the accuracy of IAUKF for SOC estimation is better than the other two estimation methods. Considering the character length limits of the computer, the MAE and RMSE of the IUKF and traditional UKF are the same, which also suggests that the IUKF and UKF can achieve almost the same SOC estimation accuracy.
To verify the suppression ability of IAUKF on the non-positive definiteness of error covariance further, the initial value of error covariance of the IAUKF, IUKF, and UKF are set as negative definite in this paper, namely, P0 = −10−1 × E3×3, and the other initial parameters are unchanged. In this case, the UKF cannot carry out the Cholesky factor decomposition due to the non-positive error covariance, which leads to the failure of SOC estimation. However, the IUKF and IAUKF can still complete the SOC estimation. When the error covariance is negative definite and positive definite, the SOC estimation error comparative curves of the IUKF are shown in Figure 8, and the SOC estimation error comparative curves of the IAUKF are shown in Figure 9.
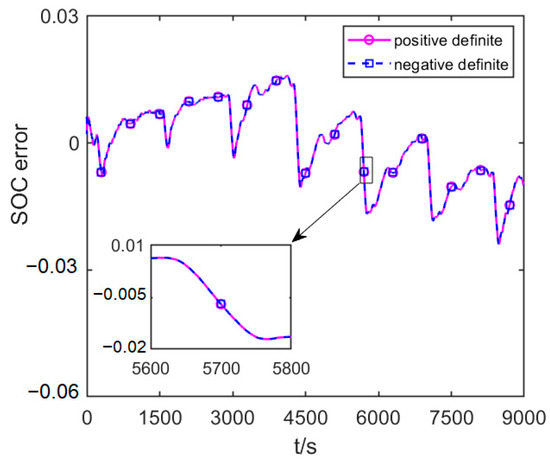
Figure 8.
SOC estimation error comparative curves of FUDS test when the initial error covariance matrix is positive and negative definite of the IUKF.
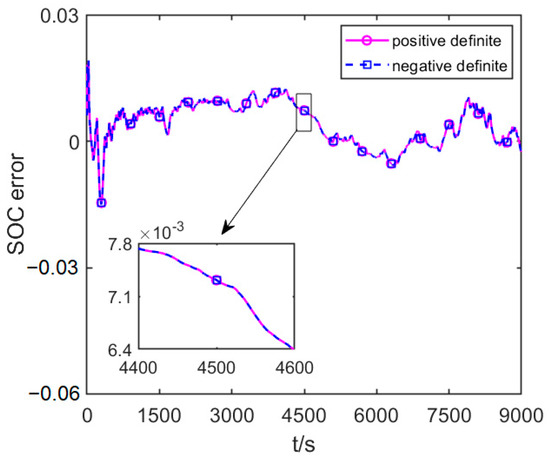
Figure 9.
SOC estimation error comparative curves of FUDS test when the initial error covariance matrix is positive and negative definite of the IAUKF.
As can be observed from Figure 8 and Figure 9, although the initial error covariance is negative definite, the IUKF can still achieve the same accurate SOC estimation since its initial error covariance is positive definite, and so does the IAUKF. It can be concluded that compared with UKF, because of the excellent numerical stability of SVD, the IUKF can suppress the non-positive definiteness of the error covariance and improve the stability of SOC estimation. Additionally, this characteristic has been effectively extended in IAUKF.
5. Conclusions
The SOC of the lithium-ion battery is the core parameter of BMS. Accurate SOC estimation is the premise to realize the functions of BMS and ensure the safe operation of electric vehicles. However, the traditional UKF fails to estimate SOC due to the non-positive error covariance of the state variable and the SOC estimation accuracy is not high because of the unknown or inaccurate system noise statistics. In this paper, a lithium-ion battery SOC estimation method based on an improved adaptive unscented Kalman filter is proposed to solve this problem. Experiments have been carried out to verify the effectiveness of the IAUKF by comparing it with traditional UKF and IUKF in terms of SOC estimation stability and accuracy. Based on the experimental results, the main concluding remarks can be made below:
- (1)
- Replacing the Cholesky decomposition in traditional UKF with SVD will not decrease the SOC estimation accuracy, and the IUKF and UKF can achieve almost the same SOC estimation results. The MAE of the traditional UKF and IUKF both are 2.4%, and the RMSE of the two methods both are 0.0094 when the character length limits of the computer are taken into consideration.
- (2)
- With the fantastic numerical stability of SVD, the IUKF can suppress the non-positive definiteness of the error covariance, so as to improve the stability of SOC estimation, and this characteristic can also be found in IAUKF, namely, whether the initial error covariance is positive definite or negative definite, both the IUKF and IAUKF can still complete the SOC estimation of the battery. However, when the initial error covariance is negative definite, the traditional UKF fails to estimate the SOC because the Cholesky decomposition cannot be carried out any longer.
- (3)
- The IAUKF is formed by combining IUKF with the Sage–Husa adaptive filter. With the help of the Sage–Husa adaptive filter, the IAUKF can realize the adaptive estimation of the system process and measurement noise during the process of SOC estimation.
- (4)
- The influence of the unknown or inaccurate system noise statistics on SOC estimation precision can be reduced by the IAUKF; thereby the SOC estimation accuracy can be improved. The MAE of the IAUKF is 1.92%, and the RMSE is 0.005; the two values are all smaller than those of IUKF and traditional UKF.
Although the IAUKF proposed in this paper improves the stability and accuracy of SOC estimation, the IAUKF still has the following limitations when applied in practical applications: firstly, in the actual operation of electric vehicles, the battery model parameters are not fixed, and complex operating conditions may lead to the changes in battery model parameters. Secondly, when the offline recursive least squares method is used to identify the battery model parameters, the identified parameters will deviate from the true values if the input noise is not compensated. Additionally, inaccurate parameters will reduce the accuracy of the battery model, which leads to an increase in SOC estimation error. Therefore, more attention will be focused on the method that can accurately identify the battery model parameters in real time by the authors, then combine the method with the IAUKF proposed in this paper to improve the estimation accuracy of SOC further.
Author Contributions
Conceptualization, J.X. and P.W.; methodology, J.X. and P.W.; software, P.W.; validation, J.X. and P.W.; formal analysis, J.X. and P.W.; investigation, J.X. and P.W.; resources, P.W.; data curation, P.W.; writing—original draft preparation, J.X.; writing—review and editing, P.W.; visualization, J.X.; supervision, P.W.; project administration, P.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, Y.; Tan, Z.; Ren, Y. Research on Factors That Influence the Fast Charging Behavior of Private Battery Electric Vehicles. Sustainability 2020, 12, 3439. [Google Scholar] [CrossRef]
- Wang, S.; Lu, C.; Liu, C.; Zhou, Y.; Bi, J.; Zhao, X. Understanding the Energy Consumption of Battery Electric Buses in Urban Public Transport Systems. Sustainability 2020, 12, 10007. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, C.; Chen, Z.J.A.E. On-line battery state-of-charge estimation based on an integrated estimator. Appl. Energy 2017, 185, 2026–2032. [Google Scholar] [CrossRef]
- Gantenbein, S.; Schönleber, M.; Weiss, M.; Ivers-Tiffée, E. Capacity Fade in Lithium-Ion Batteries and Cyclic Aging over Various State-of-Charge Ranges. Sustainability 2019, 11, 6697. [Google Scholar] [CrossRef]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Source 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Piller, S.; Perrin, M.; Jossen, A. Methods for state-of-charge determination and their applications. J. Power Source 2001, 96, 113–120. [Google Scholar] [CrossRef]
- Yang, F.; Li, W.; Li, C.; Miao, Q. State-of-charge estimation of lithium-ion batteries based on gated recurrent neural network. Energy 2019, 175, 66–75. [Google Scholar] [CrossRef]
- Sheng, H.; Xiao, J. Electric vehicle state of charge estimation: Nonlinear correlation and fuzzy support vector machine. J. Power Source 2015, 281, 131–137. [Google Scholar] [CrossRef]
- Sahinoglu, G.O.; Pajovic, M.; Sahinoglu, Z.; Wang, Y.; Orlik, P.V.; Wada, T. Battery State-of-Charge Estimation Based on Regular/Recurrent Gaussian Process Regression. IEEE Trans. Ind. Electron. 2018, 65, 4311–4321. [Google Scholar] [CrossRef]
- Tulsyan, A.; Tsai, Y.; Gopaluni, R.B.; Braatz, R.D. State-of-charge estimation in lithium-ion batteries: A particle filter approach. J. Power Source 2016, 331, 208–223. [Google Scholar] [CrossRef]
- Xile, D.; Caiping, Z.; Jiuchun, J. Evaluation of SOC Estimation Method Based on EKF/AEKF under Noise Interference. Energy Procedia 2018, 152, 520–525. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Z.; Zhao, Z.; Wang, L.; Lai, C.S.; Wang, D. Robustness Evaluation of Extended and Unscented Kalman Filter for Battery State of Charge Estimation. IEEE Access 2018, 6, 27617–27628. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Sun, X. State of Charge and State of Health Estimation of Li-ion Batteries Based on Adaptive Square-root Unscented Kalman Filters. Proc. CSEE 2018, 38, 2384–2293+2548. [Google Scholar]
- Duong, T.Q. USABC and PNGV test procedures. J. Power Source 2000, 89, 244–248. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Ouyang, T.; Xu, P.; Chen, J.; Lu, J.; Chen, N. Improved parameters identification and state of charge estimation for lithium-ion battery with real-time optimal forgetting factor. Electrochim. Acta 2020, 353, 136576. [Google Scholar] [CrossRef]
- Fei, Y.; Xie, C.; Tang, Z.; Zeng, C.; Quan, S. State-of-Charge Estimation Based on Square Root Unscented Kalman Filter Algorithm for Li-ion Batteries. Proc. CSEE 2017, 37, 4514–4520+4593. [Google Scholar]
- Guo, L.; Hu, C.; Li, G. The SOC estimation of battery based on the method of improved Ampere-hour and Kalman filter. In Proceedings of the 2015 IEEE 10th Conference on Industrial Electronics and Applications (ICIEA), Auckland, New Zealand, 15–17 June 2015; pp. 1458–1460. [Google Scholar]
- Choi, W. A Study on State of Charge and State of Health Estimation in Consideration of Lithium-Ion Battery Aging. Sustainability 2020, 12, 10451. [Google Scholar] [CrossRef]
- Zheng, F.; Xing, Y.; Jiang, J.; Sun, B.; Kim, J.; Pecht, M. Influence of different open circuit voltage tests on state of charge online estimation for lithium-ion batteries. Appl. Energy 2016, 183, 513–525. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for electric vehicle batteries using unscented kalman filtering. Microelectron. Reliab. 2013, 53, 840–847. [Google Scholar] [CrossRef]
- Cao, X.; Fei, Y.; Sun, S.; Xie, C. SOC estimation of Lithium battery based on AUKF. Power Electron. 2017, 51, 69–72. [Google Scholar]
- Qingping, S.; Rongke, L. Weighted adaptive filtering algorithm for carrier tracking of deep space signal. Chin. J. Aeronaut. 2015, 28, 1236–1244. [Google Scholar]
- Junping, W.; Jingang, G.; Lei, D. An adaptive Kalman filtering based State of Charge combined estimator for electric vehicle battery pack. Energy Convers. Manag. 2009, 50, 3182–3186. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, X.; Sun, M.; Ding, J.; Yan, C. Adaptive UKF Filtering Algorithm Based on Maximum a Posterior Estimation and Exponential Weighting. Acta Autom. Sin. 2010, 36, 1007–1019. [Google Scholar] [CrossRef]
- Peng, S.; Chen, C.; Shi, H.; Yao, Z. State of Charge Estimation of Battery Energy Storage Systems Based on Adaptive Unscented Kalman Filter with a Noise Statistics Estimator. IEEE Access 2017, 5, 13202–13212. [Google Scholar] [CrossRef]
- An, Z.; Tian, M.; Zhao, L.; Chen, X.; Li, Y.; Si, X. SOC estimation of lithium battery based on adaptive untracked Kalman filter. Energy Storage Sci. Technol. 2019, 8, 856–861. [Google Scholar]
- Bian, X.; Wei, Z.; He, J.; Yan, F.; Liu, L. A two-step parameter optimization method for low-order model-based state of charge estimation. IEEE Trans. Transp. Electrif. 2020, 1–12. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, D.; He, H.; Cao, W.; Dong, G. A noise-tolerant model parameterization method for lithium-ion battery management system. Appl. Energy 2020, 268, 114932. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, L.; Zhao, X.; Wang, Y.; He, Z. Online state of charge estimation of Li-ion battery based on an improved unscented Kalman filter approach. Appl. Math. Model. 2019, 70, 532–544. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).