Lagrangian Relaxation Based on Improved Proximal Bundle Method for Short-Term Hydrothermal Scheduling

Abstract

Short-term hydrothermal scheduling (STHS) can improve water use efficiency, reduce carbon emissions, and increase economic benefits by optimizing the commitment and dispatch of hydro and thermal generating units together. However, limited by the large system scale and complex hydraulic and electrical constraints, STHS poses great challenges in modeling for operators. This paper presents an improved proximal bundle method (IPBM) within the framework of Lagrangian relaxation for STHS, which incorporates the expert system (ES) technique into the proximal bundle method (PBM). In IPBM, initial values of Lagrange multipliers are firstly determined using the linear combination of optimal solutions in the ES. Then, each time PBM declares a null step in the iterations, the solution space is inferred from the ES, and an orthogonal design is performed in the solution space to derive new updates of the Lagrange multipliers. A case study in a large-scale hydrothermal system in China is implemented to demonstrate the effectiveness of the proposed method. Results in different cases indicate that IPBM is superior to standard PBM in global search ability and computational efficiency, providing an alternative for STHS.

1. Introduction

According to the International Energy Agency, thermal power and hydropower are basic sources of electricity production in many countries [1]. Thus, short-term hydrothermal scheduling (STHS) is necessary in power system operations. The significance of STHS is to improve water use efficiency, reduce carbon emissions, and increase economic benefits by optimizing the commitment and generation level of hydro and thermal generating units together [2]. However, limited by complex hydraulic and electrical constraints, the nature of STHS is a large-scale nonconvex, nonlinear problem with integer variables, posing great challenges in modeling for operators [3].

Many approaches have been developed for STHS, such as mixed-integer linear programming (MILP) [4], nonlinear programming (NLP) [5], dynamic programming (DP) [6], and genetic algorithm (GA) [7]. Although these approaches have achieved success in practice, challenges still exist when dealing with large-scale systems. MILP depends on linearization strategies to accurately represent the system behavior. For NLP, a convex approximation is required to improve the global search ability, and global optimum is not guaranteed. DP suffers from the “curse of dimensionality”. GA falls into premature convergence easily. For large-scale systems, common approaches are based on decomposition techniques, such as the Lagrangian relaxation (LR) [8], Benders decomposition (BD) [9], and aggregation–disaggregation [10]. BD decomposes the primal problem into a master problem and some subproblems for dimension reduction. However, BD is sensitive to integer variables, of which the computational efficiency becomes very low for problems with many integer variables. The aggregation–disaggregation method has been successfully applied in the optimization of Brazilian hydropower system operations [11], while a loss of information in the aggregation step may result in undesirable errors in operations [12]. LR is suitable for large-scale nonconvex problems. In LR, the Lagrangian dual problem is introduced by relaxing linking constraints through Lagrange multipliers, which exhibits a decomposable structure [13]. By solving the dual problem, a lower bound of the primal problem is found, acting as a good starting point for heuristics to obtain feasible solutions [14].

Within the framework of LR, the key issue is to solve the Lagrangian dual, which is nonconvex and nonsmooth [15]. The proximal bundle method (PBM) is a classic method in nonsmooth optimization [16,17]. PBM gathers historical dual values and subgradients in a “bundle” to construct the cutting-planes model, and yields new iterates by solving a quadratic program per iteration [15]. To ensure high accuracy, an ascent condition is checked per iteration to decide whether to take a null step or a serious step. The iteration of PBM ends after the stopping rule is met. Although PBM is known for its stability and precision, the bundle size increases with the iteration, leading to a growing computational burden of solving the quadratic program [18]. Additionally, in the later iterations, a sufficient ascent in dual value is hard to satisfy. As a result, many null steps are declared, causing PBM to converge to a local optimum [19]. Some improvements of PBM were developed. The authors of [20] proposed a splitting bundle approach, which partitions the bundle into two subsets to capture the convex and concave behavior around the current point. The authors of [21] introduced the notion of gradient sampling into PBM to find the search direction, rather than using the subgradient information. The authors of [22] developed a redistributed PBM, which generates cutting-planes models of a local convexification of the objective function. However, solving a quadratic program per iteration is inevitable in these improvements.

The generation scenario of STHS changes slowly in a continuous period (e.g., the water level of reservoir decreases slowly in the dry season) and presents periodicity (e.g., the reservoir inflow changes periodically in a year). In this case, some inspiration can be obtained from historical operational records to guide the solution of a current problem. Therefore, an improved PBM (IPBM) is proposed in this paper, incorporating the expert system (ES) into the PBM. The ES is an important branch of artificial intelligence, which uses knowledge and reasoning processes to solve complex decision-making problems [23,24]. ES includes two parts: a knowledge base and inference engine [25]. The knowledge base stores knowledge expressions about the problem domain. To build the knowledge base of STHS, three steps are taken: (1) represent all historical generation scenarios by eigenvectors; (2) implement scenario clustering to yield representative scenarios; and (3) extract knowledge expressions from the PBM iterations of representative scenarios and save them in the database. The inference engine works based on the knowledge base. With the inference engine, initial values of multipliers are reasoned using the linear combination of optimal solutions in the knowledge base, which can accelerate the convergence of PBM. Then, when PBM declares a null step in iterations, the solution space is reasoned from the knowledge base, and the values of Lagrange multipliers are updated by performing an orthogonal design (OD) in the solution space [26,27]. The OD can not only avoid solving quadratic programming, but also behave like a “mutation operator” to increase the likelihood of reaching global optimum. The proposed IPBM is applied to a large-scale hydrothermal system in China to make daily generation schedules. Compared with standard PBM in different scenarios, IPBM can yield better objective function values in less time, verifying its superiority in global search ability and computational efficiency.

2. Problem Formulation

2.1. Study Area

The studied hydrothermal power system is in Guizhou Province, China, serving around 34.75 million people in an area of 176,000 km². Figure 1 illustrates the geographical distribution of the system. In the system, generating capacities of hydropower and thermal power are 9849 MW and 25,950 MW, respectively. The hydropower part includes 45 units in 13 hydropower plants, and the thermal part consists of 65 units in 22 thermal plants. The hydropower plants are located in the Wujiang river system, including 4 basins with 53 billion m³ average annual runoff. In the Wujiang river system, the wet season is in the period of May–October, and the dry season is in November–April. Since Guizhou is rich in coal resources, all the thermal plants are coal-fired plants. Detailed information about the system is presented in the appendix, including: (1) basic parameters of thermal units; and (2) basic characteristics of hydropower plants.

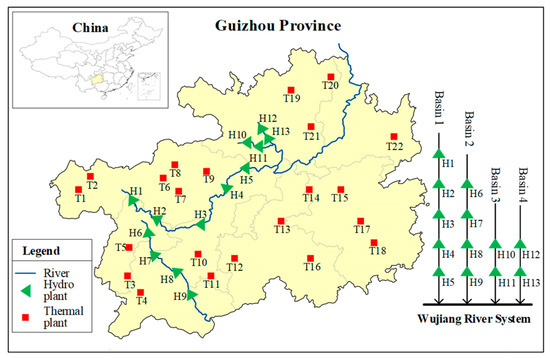
Figure 1. Geographical distribution of the studied hydrothermal power system.

Although these plants belong to different generation companies, they are operated by a central dispatching center in a centralized manner. Moreover, according to local government policy, the operation objective of the hydrothermal system is to minimize coal consumption to achieve energy-saving and emission reduction. For such a large system, a small improvement in operations will translate into huge benefits, making STHS an important problem.

2.2. Optimization Model

2.2.1. Objective Function

The objective function minimizes the coal consumption of the hydrothermal system over the whole scheduling horizon:

$$\underset{p_{i,j,t},p_{k,m,t},u_{i,j,t},u_{k,m,t}}{\min }{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{i=1}^{N_{TP}}{\displaystyle \sum _{j=1}^{N_{TU}^i}\left(a_{i,j}{p}_{i,j,t}^2+b_{i,j}{p}_{i,j,t}+c_{i,j}\right)u_{i,j,t}\Delta t}}}$$

(1)

where t, $i$, $j$, $k$, and $m$ = indices of time period, thermal plant, thermal unit, hydro plant, and hydro unit, respectively; $T$ = number of time periods; $N_{TP}$ = number of thermal plants; $N_{TU}^i$ = number of thermal units in plant $i$; $p_{i,j,t}$ = power output of thermal unit $j$ in plant $i$ at period $t$ (MW); $p_{k,m,t}$ = power output of hydro unit $m$ in plant k at period $t$ (MW); $u_{i,j,t}$ = binary variable indicating whether or not thermal unit j in plant i is operating at period $t$; $u_{k,m,t}$ = binary variable indicating whether or not hydro unit $m$ in plant $k$ is operating at period $t$; $a_{i,j}$ (t/MW2h), $b_{i,j}$ (t/MWh), and $c_{i,j}$ (t/h) = fuel consumption coefficients of thermal unit $j$ in plant $i$, respectively; $\Delta t$ = time conversion variable (h).

It is important to point out that because hydro units and thermal units are closely coupled by electrical constraints (Equations (2) and (3)), the schedules of both hydro units and thermal units will affect the objective function. Thus, the decision variables in Equation (1) are $p_{i,j,t}$, $p_{k,m,t}$, $u_{i,j,t}$, and $u_{k,m,t}$.

2.2.2. Constraints

In STHS, constraints that should be satisfied are grouped into system-wide electrical constraints, thermal power constraints, and hydropower constraints, which are formulated as follows.

1. System-wide electrical constraints

$${\displaystyle \sum _{i=1}^{N_{TP}}{\displaystyle \sum _{j=1}^{N_{TU}^i}{p}_{i,j,t}}}+{\displaystyle \sum _{k=1}^{N_{HP}}{\displaystyle \sum _{m=1}^{N_{HU}^k}{p}_{k,m,t}}}=D_t$$

(2)

$${\displaystyle \sum _{i=1}^{N_{TP}}{\displaystyle \sum _{j=1}^{N_{TU}^i}{p}_{i,j}^{\max }{u}_{i,j,t}}}+{\displaystyle \sum _{k=1}^{N_{HP}}{\displaystyle \sum _{m=1}^{N_{HU}^k}{p}_{k,m}^{\max }{u}_{k,m,t}}}\ge \left(1+\alpha \right)D_t$$

(3)

where $N_{HP}$ = number of hydro plants; $N_{HU}^k$ = number of hydro units in plant $k$; $D_t$ = system load demand at period $t$ (MW); $p_{i,j}^{\max }$ and $p_{k,m}^{\max }$ = the maximum output limits of thermal unit and hydro unit (MW), respectively; $\alpha$ = the constant representing the percentage of spinning reserve in load demand.

Equation (2) sets the power balance constraints. Equation (3) sets the spinning reserve constraints.

2.  Thermal power constraints

$$p_{i,j}^{\min }{u}_{i,j,t}\le p_{i,j,t}\le p_{i,j}^{\max }{u}_{i,j,t}$$

(4)

$$p_{i,j,t}\le p_{i,j}^{\max }\left(u_{i,j,t}-z_{i,j,t+1}\right)+S{D}_{i,j}{z}_{i,j,t+1}$$

(5)

$$p_{i,j,t}-p_{i,j,t-1}\le R{U}_{i,j}{u}_{i,j,t-1}+S{U}_{i,j}{y}_{i,j,t}$$

(6)

$$p_{i,j,t-1}-p_{i,j,t}\le R{D}_{i,j}{u}_{i,j,t}+S{D}_{i,j}{z}_{i,j,t}$$

(7)

$$y_{i,j,t}-z_{i,j,t}=u_{i,j,t}-u_{i,j,t-1}$$

(8)

$$y_{i,j,t}+z_{i,j,t}\le 1$$

(9)

$$y_{i,j,t}+{\displaystyle \sum _{\eta =t+1}^{t+T{A}_{i,j}-1}{z}_{i,j,\eta }}\le 1$$

(10)

$$z_{i,j,t}+{\displaystyle \sum _{\eta =t+1}^{t+T{B}_{i,j}-1}{y}_{i,j,\eta }}\le 1$$

(11)

where $p_{i,j}^{\min }$ = the minimum output limit of unit $j$ in plant $i$ (MW); $y_{i,j,t}$ = binary variable indicating whether or not the unit is started up at period $t$; $z_{i,j,t}$ = binary variable indicating whether or not the unit is shut down at period $t$; $S{U}_{i,j}$ and $S{D}_{i,j}$ = start-up and shut-down ramp rate limits of unit $j$ in plant $i$ (MW/h), respectively; $R{U}_{i,j}$ and $R{D}_{i,j}$ = ramp-up and ramp-down limits of unit $j$ in plant $i$ (MW/h), respectively; $T{A}_{i,j}$ and $T{B}_{i,j}$ = the minimum online and offline time periods of unit $j$ in plant $i$ (h), respectively.

Equation (4) sets the lower and upper bounds of each unit on power output. Equations (5)–(7) set the power ramping constraints of each unit, including the start-up ramp rate limit, shut-down ramp rate limit, and normal ramp-up and ramp-down limits. Equations (8) and (9) denote the logical status of unit commitment. Equations (10) and (11) set the minimum online and offline time periods of each unit, respectively.

3.  Hydropower constraints

$$Q_{k,t}=B_{k,t}+{\displaystyle \sum _{kh\in I{U}_k}{R}_{kh,t-{\tau }_{kh,k}}}$$

(12)

$$S_{k,t}=S_{k,t-1}+\left(Q_{k,t}-R_{k,t}\right)\Delta t$$

(13)

$$R_{k,t}=R_{k,t}^{\prime }+R_{k,t}^{″}={\displaystyle \sum _{m=1}^{N_{HU}^k}{R}_{k,m,t}^{\prime }}+R_{k,t}^{″}$$

(14)

$$\{\begin{array}{l}{R}_k^{\min }\le R_{k,t}\le R_k^{\max }\\ {\left(R_{k,m}^{\prime }\right)}^{\min }{u}_{k,m,t}\le R_{k,m,t}^{\prime }\le {\left(R_{k,m}^{\prime }\right)}^{\max }{u}_{k,m,t}\end{array}$$

(15)

$$S_k^{\min }\le S_{k,t}\le S_k^{\max }$$

(16)

$$Z_{k,t}=f_{zs}^k\left(S_{k,t}\right)$$

(17)

$$Z{T}_{k,t}=f_{zr}^k\left(R_{k,t}\right)$$

(18)

$$H_{k,t}=\frac{Z_{k,t-1}+Z_{k,t}}{2}-Z{T}_{k,t}-H_{k,t}^{loss}$$

(19)

$$H_{k,t}^{loss}=f_{hr}^k\left(R_{k,t}^{\prime }\right)$$

(20)

$$S_{k,0}=S_{k,beg}$$

(21)

$$S_{k,T}=S_{k,end}$$

(22)

$$p_{k,m,t}=f_{phr}^{k,m}\left(H_{k,t},R_{k,m,t}^{\prime }\right)$$

(23)

$$p_{k,m}^{\min }{u}_{k,m,t}\le p_{k,m,t}\le p_{k,m}^{\max }{u}_{k,m,t}$$

(24)

$$\left[p_{k,m,t}-p{s}_{k,m,vz}^{\max }\left(H_{k,t}\right)\right]\left[p_{k,m,t}-p{s}_{k,m,vz}^{\min }\left(H_{k,t}\right)\right]\ge 0$$

(25)

where $Q_{k,t}$, $B_{k,t}$, and $R_{k,t}$ = total inflow, natural inflow, and total release of plant $k$ at time $t$ (m³/s), respectively; $I{U}_k$ = the direct upstream plants set of plant $k$; $kh$ = the direct upstream plant index of plant $k$; ${\tau }_{kh,k}$ = water travel time from plant $kh$ to plant $k$ (h); $S_{k,t}$ = storage of plant $k$ at time $t$ (m³); $R_{k,t}^{\prime }$ and $R_{k,t}^{″}$ = total power release and spillage of plant $k$ at time $t$ (m³/s), respectively; $R_{k,m,t}^{\prime }$ = power release of unit $m$ in plant $k$ at time $t$ (m³/s); $R_k^{\min }$ and $R_k^{\max }$ = the minimum and maximum releases of plant $k$ (m³/s), respectively; ${\left(R_{k,m}^{\prime }\right)}^{\min }$ and ${\left(R_{k,m}^{\prime }\right)}^{\max }$ = the minimum and maximum power releases of unit $m$ in plant $k$ (m³/s), respectively; $S_k^{\min }$ and $S_k^{\max }$ = the minimum and maximum storages of plant $k$ (m³), respectively; $Z_{k,t}$ = forebay water level of plant $k$ at time $t$ (m); $f_{zs}^k(\cdot )$ = the function between storage and water level of plant $k$; $Z{T}_{k,t}$ = tailrace water level of plant $k$ at time $t$ (m); $f_{zr}^k(\cdot )$ = the function between tailrace water level and total release of plant $k$; $H_{k,t}$ = net water head of plant $k$ at time $t$ (m); $f_{hr}^k(\cdot )$ = the function between head loss and power release of plant $k$; $S_{k,beg}$ and $S_{k,end}$ = the initial and terminal storages of plant $k$ (m³), respectively; $f_{pqr}^{k,m}(\cdot )$ = power output as a function of unit power release and net head of unit $m$ in plant $k$; $p_{k,m}^{\min }$ and $p_{k,m}^{\max }$ = the minimum and maximum power outputs of unit $m$ in plant $k$ (MW), respectively; $p{s}_{k,m,vz}^{\max }\left(H_{k,t}\right)$ and $p{s}_{k,m,vz}^{\min }\left(H_{k,t}\right)$ = the upper and lower bounds of vibration zone $vz$ of unit $m$ in plant $k$ (MW), respectively. Both $p{s}_{k,m,vz}^{\max }\left(H_{k,t}\right)$ and $p{s}_{k,m,vz}^{\min }\left(H_{k,t}\right)$ are related to the net water head $H_{k,t}$.

Equations (12) and (13) set the water balance constraints. Equation (14) defines the total water release. Equations (15) and (16) set the discharge limit and storage limit, respectively. Equations (17) and (18) are forebay water level and storage function, and tailrace water level and release function, respectively, both of which are nonlinear and nonconvex. Equations (19) and (20) define the expression of the water head, where Equation (20) is nonlinear and convex. Equations (21) and (22) restrict the initial and terminal storages of each plant, respectively. Equation (23) is the hydropower production function, which is composed of a family of curves illustrating the nonlinear relationship between power output, water head, and power release. Equation (24) denotes the power output limit. Equation (25) sets the vibration zone limit.

3. Method Overview and Assumptions

3.1. Lagrangian Relaxation Framework

Within the LR framework, the first step is to construct a specific dual problem by relaxing linking constraints. Then, the next step consists of solving the dual problem. The obtained dual solution acts as a lower bound to the primal problem, and heuristics are adopted to convert the infeasible dual solution to a feasible solution. Through gradually narrowing the gap between dual solution and primal solution, a near-optimal solution will be finally found in multiple iterations.

In the context of STHS, Equations (1)–(25) are denominated the primal problem. The hydropower part and thermal power part are coupled by Equations (2) and (3). Therefore, the following dual function is constructed by relaxing Equations (2) and (3) via Lagrange multipliers ${\lambda }_{D_t}$ and ${\lambda }_{R_t}$ [28,29]:

$$LD\left({\lambda }_{D_t},{\lambda }_{R_t}\right)=\underset{\begin{array}{l}{p}_{i,j,t},p_{k,m,t}\\ u_{i,j,t},u_{k,m,t}\end{array}}{\min }\left[\begin{array}{l}F+{\displaystyle \sum _{t=1}^T{\lambda }_{D_t}\left(D_t-{\displaystyle \sum _{i=1}^{N_{TP}}{\displaystyle \sum _{j=1}^{N_{TU}^i}{p}_{i,j,t}}-{\displaystyle \sum _{k=1}^{N_{HP}}{\displaystyle \sum _{m=1}^{N_{HU}^k}{p}_{k,m,t}}}}\right)}\\ +{\displaystyle \sum _{t=1}^T{\lambda }_{R_t}\left(D_t+R_t-{\displaystyle \sum _{i=1}^{N_{TP}}{\displaystyle \sum _{j=1}^{N_{TU}^i}{p}_{i,j}^{\max }{u}_{i,j,t}}}-{\displaystyle \sum _{k=1}^{N_{HP}}{\displaystyle \sum _{m=1}^{N_{HU}^k}{p}_{k,m}^{\max }{u}_{k,m,t}}}\right)}\end{array}\right]$$

(26)

Subject to: Equations (4)–(25).

After regrouping relevant terms, independent thermal and hydro subproblems can be split from Equation (26). Detailed forms of these subproblems can be found in [15]. To solve the thermal and hydro subproblems, MILP is adopted [30]. The reasons for using MILP are as follows: (1) the nonlinearity in hydro and thermal subproblems can be eliminated with piecewise linear techniques; (2) MILP is efficient in solving small-scale problems; and (3) MILP is easily programmed based on general mathematical solvers.

Moreover, the heuristic technique in [31] is adopted to transform the dual solution into a feasible solution, which fixes the hydropower solution first and then adjusts the thermal unit schedule using a priority-list approach. Finally, the iteration of LR stops if any of Equations (27) and (28) are satisfied:

$$rd{g}_n=\frac{F_n^{*}-L{D}_n^{*}}{L{D}_n^{*}}\le RDG$$

(27)

$$\sqrt{{\displaystyle \sum _{t=1}^T\left[{\left({\lambda }_{D_t}^n-{\lambda }_{D_t}^{n-1}\right)}^2+{\left({\lambda }_{R_t}^n-{\lambda }_{R_t}^{n-1}\right)}^2\right]}}<\Delta \lambda$$

(28)

where $n$ = the iteration index; $rd{g}_n$, $F_n^{*}$ and $L{D}_n^{*}$ = the relative duality gap, the primal value (t), and the Lagrangian dual value (t) at iteration $n$, respectively; $RDG$ = the supplied minimum relative duality gap; ${\lambda }_{D_t}^n$ and ${\lambda }_{R_t}^n$ = the values of ${\lambda }_{D_t}$ and ${\lambda }_{R_t}$ at iteration $n$, respectively; $\Delta \lambda$ = the supplied minimum multiplier variation.

3.2. Standard Proximal Bundle Method

In the dual function (Equation (26)), subgradients with respect to ${\lambda }_{D_t}$ and ${\lambda }_{R_t}$ are

$$\{\begin{array}{l}{g}_{D_t}=D_t-{\displaystyle \sum _{i=1}^{N_{TP}}{\displaystyle \sum _{j=1}^{N_{TU}^i}{p}_{i,j,t}}-{\displaystyle \sum _{k=1}^{N_{HP}}{\displaystyle \sum _{m=1}^{N_{HU}^k}{p}_{k,m,t}}}}\\ g_{R_t}=D_t+R_t-{\displaystyle \sum _{i=1}^{N_{TP}}{\displaystyle \sum _{j=1}^{N_{TU}^i}{p}_{i,j}^{\max }{u}_{i,j,t}}}-{\displaystyle \sum _{k=1}^{N_{HP}}{\displaystyle \sum _{m=1}^{N_{HU}^k}{p}_{k,m}^{\max }{u}_{k,m,t}}}\end{array}$$

(29)

Let $n$ be the current iteration index. The notation is simplified by denoting $\mathsf{\lambda }=\left[{\lambda }_{D_1},\cdots ,{\lambda }_{D_T},{\lambda }_{R_1},\cdots ,{\lambda }_{R_T}\right]$ and $g=\left[g_{D_1}^{},\cdots ,g_{D_T}^{},g_{R_1}^{},\cdots ,g_{R_T}^{}\right]$. PBM generates two related iteration sequences: ${\left\{LD\left({\mathsf{\lambda }}^{nk}\right),g^{nk}\right\}}_{nk<n}$ and ${\left\{{\overline{\mathsf{\lambda }}}^{nk}\right\}}_{nk<n}$, where $nk$ = past iteration index; ${\mathsf{\lambda }}^{nk}$ and $g^{nk}$ = the multiplier vector and subgradient vector at iteration $nk$, respectively; $LD\left({\mathsf{\lambda }}^{nk}\right)$ = the dual value associated with ${\mathsf{\lambda }}^{nk}$; ${\overline{\mathsf{\lambda }}}^{nk}$ = the best multiplier vector so far at iteration nk, which provides the maximum dual value $LD\left({\overline{\mathsf{\lambda }}}^{nk}\right)$. The sequence ${\left\{LD\left({\mathsf{\lambda }}^{nk}\right),g^{nk}\right\}}_{nk<n}$ is the so-called “bundle”, while the sequence ${\left\{{\overline{\mathsf{\lambda }}}^{nk}\right\}}_{nk<n}$ denotes the stability centers in the bundle [32].

Having the bundle, a cutting-planes model is formulated at iteration $n$

$$L{\widehat{D}}_n\left(\mathsf{\lambda }\right)=\underset{nk<n}{\min }\left[LD\left({\mathsf{\lambda }}^{nk}\right)+g^{nk}{\left(\mathsf{\lambda }-{\mathsf{\lambda }}^{nk}\right)}^T\right]$$

(30)

Then, the next iterate ${\mathsf{\lambda }}^{n+1}$ is obtained by solving the quadratic programming [33]

$${\mathsf{\lambda }}^{n+1}=\arg \underset{\mathsf{\lambda }}{\max }\left[L{\widehat{D}}_n\left(\mathsf{\lambda }\right)+\frac{1}{2}{\mu }_n{\Vert \mathsf{\lambda }-{\overline{\mathsf{\lambda }}}^n\Vert }^2\right]$$

(31)

where ${\mu }_n$ = the penalty parameter, controlling the distance from ${\mathsf{\lambda }}^{n+1}$ to ${\overline{\mathsf{\lambda }}}^n$.

With the obtained ${\mathsf{\lambda }}^{n+1}$, the ascent condition is checked:

$$LD\left({\mathsf{\lambda }}^{n+1}\right)\ge LD\left({\overline{\mathsf{\lambda }}}^n\right)+\epsilon {\delta }^{n+1}$$

(32)

where $\epsilon$ = the parameter defining the minimum increase in dual value; ${\delta }^{n+1}=L\widehat{D}\left({\mathsf{\lambda }}^{n+1}\right)-LD\left({\overline{\mathsf{\lambda }}}^n\right)$ measuring the increase predicted by the cutting-planes model.

If Equation (32) holds, update the stability center sequence by setting ${\overline{\mathsf{\lambda }}}^{n+1}={\mathsf{\lambda }}^{n+1}$ (serious step). Otherwise, set ${\overline{\mathsf{\lambda }}}^{n+1}={\overline{\mathsf{\lambda }}}^n$ (null step). Invoke PBM iteratively in LR iterations until the stopping rule (Equations (27) and (28)) is met.

Although PBM is known for its stability and accuracy, there are still some drawbacks: (1) The time cost of solving quadratic programming. A quadratic programming problem in the form of Equation (31) needs to be solved at each iteration to generate a new iterate. The scale of the quadratic programming increases with the size of the bundle, which could be quite time-consuming in later iterations. (2) As the iteration proceeds, the ascent condition is hard to satisfy. As a result, many null steps are declared, causing PBM to easily fall into local optimum. (3) Initial values of Lagrange multipliers have an influence on the computational efficiency of PBM, which has not been fully discussed in the literature [33].

3.3. Improved Proximal Bundle Method

To overcome the difficulties of PBM, an IPBM incorporating the ES technique with PBM is proposed in this section. The ES component in IPBM mines information from historical operational records of hydrothermal units to guide the solution of a current problem. The ES consists of two parts: a knowledge base and inference engine, where the knowledge base is a repository of facts storing the knowledge about the STHS problem domain, and the inference engine provides reasoning about the information in the knowledge base to find a solution [25].

In the solution of Lagrangian dual, the main task is to determine the optimal values of Lagrange multipliers to reduce the relative duality gap (RDG). Thus, the trajectories of RDG and multiplier values in the iteration are regarded as a kind of knowledge. By extracting knowledge expressions and building the knowledge base, decision support can be provided for STHS from the inference engine. Specifically, initial values of multipliers can be obtained by using a linear combination of optimal multiplier values in the knowledge base, providing a good lower bound to the primal problem. Moreover, when a null step is claimed in IPBM, the solution space of STHS can be narrowed based on the knowledge base. Then, OD is carried out in the solution space to derive new updates of Lagrange multipliers, which can not only avoid solving quadratic programming, but also increase the likelihood of reaching a global optimum. Hence, the difficulties that standard PBM encountered are alleviated in IPBM.

Details about the ES technique are presented in the following.

3.3.1. Knowledge Base

To build the knowledge base, knowledge expressions are extracted from PBM iterations of historical scenarios. Since different generation scenarios correspond to different iteration processes, scenarios are firstly quantified by eigenvectors. Then, considering the large number of historical generation scenarios, cluster analysis is necessary to avoid the “scenario explosion” and the noise interference to the reasoning stage. Finally, knowledge expressions are extracted from the PBM iterations of representative scenarios and are stored in the database. Detailed steps of building the knowledge base are described as follows.

(1)  Representation of generation scenario

The generation scenario is characterized by operational constraints. Through interviewing experienced operators and analyzing the form of Equations (2)–(25), constraints and their associated factors are summarized in Table 1. In Table 1, constraints related to unit type and reservoir features usually do not change with scenario, or change slightly, while the rest of the constraints are dynamic. Therefore, the generation scenario is characterized by the load demand curve, natural inflows, and initial and terminal water levels of hydropower plants.

Table 1. Constraints and their associated factors.

Constraint	Associated Factor
(2), (3)	Load demand curve
(4)–(11)	Thermal unit type
(12)	Natural inflows
(13)–(20)	Reservoir features
(21), (22)	Initial and terminal water levels
(23)–(25)	Hydro unit type

To quantitatively represent the generation scenario, the following eigenvector $\mathsf{\eta }$ is formulated:

$$\mathsf{\eta }=\left[{\eta }_1,{\eta }_2,{\eta }_3,{\mathsf{\eta }}_4,{\mathsf{\eta }}_5\right]$$

(33)

$${\mathsf{\eta }}_4=\left[B_1,\cdots ,B_{hb},\cdots ,B_{HB}\right]$$

(34)

$${\mathsf{\eta }}_5=\left[P{E}_1,\cdots ,P{E}_{hb},\cdots ,P{E}_{HB}\right]$$

(35)

where ${\eta }_1$ = total energy demand (MWh); ${\eta }_2$ = peak load (MW); ${\eta }_3$ = peak–valley difference in the load demand curve; ${\mathsf{\eta }}_4$ = the vector of basin natural inflows; ${\mathsf{\eta }}_5$ = the vector of basin storage energy; $hb$ = hydro basin index; $B_{hb}$ = total natural inflows of hydro basin $hb$ over the whole planning horizon (m³/s); $HB$ = the number of hydro basins; $P{E}_{hb}$ = average storage energy of hydro basin $hb$ over the whole planning horizon (MWh).

In Equation (33), elements ${\eta }_1$, ${\eta }_2$, and ${\eta }_3$ depict the characteristics of the load demand curve; ${\mathsf{\eta }}_4$ denotes the natural inflows of basins; ${\mathsf{\eta }}_5$ means the average storage energy, which is a function of the initial and terminal water levels of hydropower plants [34].

(2)  Cluster analysis of historical generation scenarios

To obtain representative scenarios from massive historical generation scenarios, cluster analysis is necessary. First, the eigenvectors are normalized to eliminate the influence of dimension. Then, k-means clustering and silhouette coefficient are adopted to achieve scenario clustering [35]. By maximizing the silhouette coefficient of the clustering results, an optimal clustering result can be obtained. In each cluster, scenarios are sorted in ascending order according to the Euclidean distances from the centroid, and the scenario that has the minimum distance is selected as the representative scenario of the cluster.

(3)  Knowledge expression extraction

For each representative scenario, standard PBM is used to solve the Lagrangian dual. Knowledge expressions are extracted from the PBM iterations in the form of Equation (36):

$$K{E}_{nk}=\left[nk,rd{g}_{nk},{\mathsf{\lambda }}^{nk}\right],nk\le n{k}^{\max }$$

(36)

where $nk$ and $n{k}^{\max }$ = the iteration index and maximum iteration index in the process, respectively; ${\mathsf{\lambda }}^{nk}$ and $rd{g}_{nk}$ = the multiplier vector and relative duality gap at iteration $nk$, respectively.

Finally, all knowledge expressions and scenario eigenvectors are saved in the database to form the knowledge base, as illustrated in Figure 2.

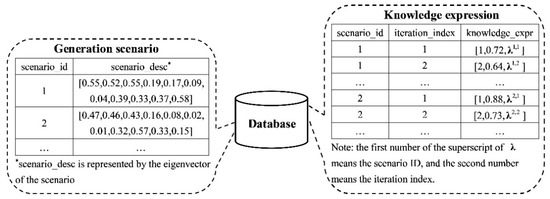
Figure 2. Database schema of the knowledge base.

3.3.2. Inference Engine

The inference engine works on the basis of the knowledge base. Similar generation scenarios mean that they have similar problem domains. Therefore, assuming that the PBM iterations of similar scenarios are alike, initial values of Lagrange multipliers, and new updates of Lagrange multipliers when null steps occur, can be reasoned by the inference engine.

(1)  Inferring the initial values of Lagrange multipliers

The similarity between two scenarios can be measured by the Euclidean distance between their eigenvectors:

$$\Delta d_{sn}=\sqrt{\left({\mathsf{\eta }}^{*}-{\mathsf{\eta }}^{sn}\right){\left({\mathsf{\eta }}^{*}-{\mathsf{\eta }}^{sn}\right)}^T}$$

(37)

where ${\mathsf{\eta }}^{*}$ = eigenvector of scenario to be solved; ${\mathsf{\eta }}^{sn}$ = scenario $sn$ in the knowledge base.

Initial values of multipliers can be obtained by using a linear combination of optimal multiplier values of different scenarios. The weighting coefficient is inversely proportional to the Euclidean distance and is determined as follows:

$$w_{sn}=\frac{1/\Delta d_{sn}}{{\displaystyle \sum _{sk\in SN}\left(1/\Delta d_{sk}\right)}}$$

(38)

where $SN$ = the set of scenarios in the knowledge base.

Hence, the initial values of multipliers are obtained (Figure 3a):

$${\mathsf{\lambda }}^{ini}={\displaystyle \sum _{sn\in SN}{w}_{sn}{\mathsf{\lambda }}_{sn}}$$

(39)

where ${\mathsf{\lambda }}_{sn}$ is the optimal multiplier vector of scenario $sn$.

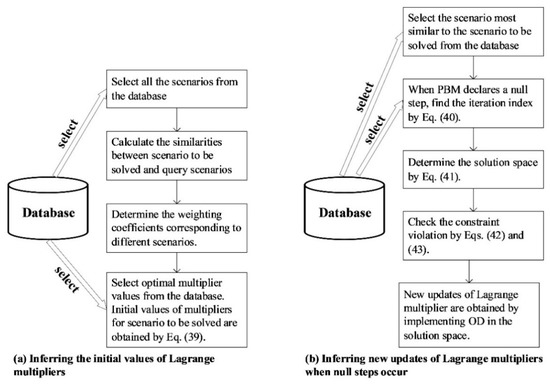
Figure 3. Procedures of the inference engine: (a) inferring the initial values of Lagrange multipliers; (b) inferring new updates of Lagrange multipliers when null steps occur.

(2)  Inferring new updates of Lagrange multipliers when null steps occur

In the iteration process of PBM, when Lagrange multipliers fail to improve the value of objective function sufficiently, a null step will be declared. Assume that a null step occurs at iteration $nu$; the relative duality gap is $rd{g}_{nu}$; and the most similar scenario in the knowledge base to the scenario to be solved is scenario $se$. The RDG measures the optimality of a dual solution. If two iterations have a close RDG, this means that they are at a similar stage in the whole iteration process. Therefore, $rd{g}_{nu}$ is used to match the knowledge expression in the knowledge base, as follows:

$$n{k}^{*}=\arg \underset{nk}{\min }\left|rd{g}_{nk}-rd{g}_{nu}\right|,nk\le NK$$

(40)

where $n{k}^{*}$ = the iteration index in scenario $se$ that has the closest RDG to $rd{g}_{nu}$; $NK$ = the maximum iteration index in the iterations of scenario $se$.

With the obtained iteration index $n{k}^{*}$, the range of multiplier values is derived:

$$\{\begin{array}{l}{\lambda }_l^{\max }=\max {\left\{{\lambda }_l^{nk}\right\}}_{n{k}^{*}\le nk\le NK}\\ {\lambda }_l^{\min }=\min {\left\{{\lambda }_l^{nk}\right\}}_{n{k}^{*}\le nk\le NK}\end{array}$$

(41)

where ${\lambda }_l^{\max }$ and ${\lambda }_l^{\min }$ = the upper and lower bounds of the $l\mathrm{th}$ element in vector $\mathsf{\lambda }$, respectively; ${\lambda }_l^{nk}$ = the value of the $l\mathrm{th}$ element in vector $\mathsf{\lambda }$ at iteration $nk$.

The obtained range is also the solution space of Lagrangian dual. Figure 3b depicts the procedure to infer new updates of Lagrange multipliers when null steps occur.

Having the solution space, a complete enumeration of state combinations of multiplier values can guarantee an optimum. However, the enumeration suffers from the “curse of dimensionality”. Supposing that each of the multipliers is discretized into $A$ states, there will be $A^{2T}$ state combinations to deal with, which is hard to deal with. Thus, the concept of orthogonal design (OD) is introduced. The OD is an experimental design method for multiple-factor experiments, which samples a representative subset from complete combinations based on the orthogonal array [36]. For an experiment of $X$ factors and $Y$ levels per factor, there exists an orthogonal array shown as $L_C\left(Y^X\right)={\left(a_{i,j}\right)}_{C\times X}$, where $L$ denotes the OD, $Y^X$ is the number of complete combinations, and $C$ is the number of combinations to be tested in the OD. $L_C\left(Y^X\right)$ is a matrix with $C$ rows and $X$ columns, and each row represents a combination of levels. Due to the orthogonality, the array $L_C\left(Y^X\right)$ ensures that the sample combinations are scattered uniformly in the state space. Figure 4 depicts the difference between complete and orthogonal combinations of an experiment that has three factors with three levels per factor. It can be observed that the orthogonal combinations are representative and uniformly distributed in the state space. Moreover, the scale of orthogonal combinations is much smaller than complete combinations.

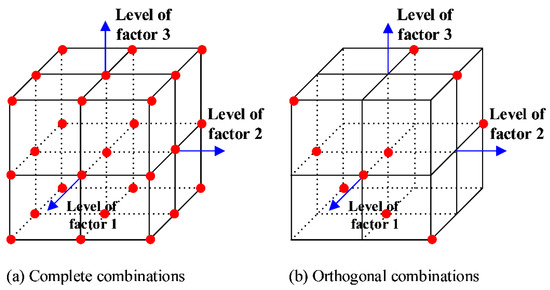
Figure 4. The difference between complete and orthogonal combinations: (a) complete combinations; (b) orthogonal combinations.

Additionally, before implementing the OD, constraint violation needs to be checked.

$$\left|g_{D_t}\right|\ge \kappa D_t$$

(42)

$$g_{R_t}<0$$

(43)

where $\kappa$ = the minimum power deviation (MW). If Equation (42) holds, it means that the power balance constraint at period $t$ is broken. If Equation (43) holds, it means that the spinning reserve constraint at period $t$ is broken.

Lagrange multipliers corresponding to broken constraints can be regarded as experiment factors. By scattering multipliers corresponding to broken constraints into several levels, a multiple-factor experiment is formed. Accordingly, an OD is executed to yield sample combinations. Keeping multipliers corresponding to unbroken constraints fixed, new updates of multipliers are obtained by combining sample combinations of broken multipliers with fixed unbroken multipliers. In this way, the computational burden of solving quadratic programming is avoided. More importantly, the OD behaves like a “mutation operator” to increase the likelihood of reaching global optimum. Then, after solving hydro and thermal subproblems with the obtained multiplier updates, arrange the dual values in ascending order, and update the bundle and stability centers sequences. Continue to solve the dual problem by PBM until a next null step is declared or the iteration stops.

3.4. Procedures of the Proposed IPBM

Procedures of the proposed IPBM within the LR framework are summarized as follows:

Step 1:

Build the knowledge base. First, represent historical generation scenarios by eigenvectors. Then, implement cluster analysis with k-means clustering and silhouette coefficient to obtain representative scenarios. Finally, extract knowledge expressions from PBM iterations of representative scenarios and save them in the database.

Step 2:

Relax linking constraints to form the Lagrangian dual by Equation (26).

Step 3:

Solve the dual problem.

(a)

Set the iteration index $n=1$.

(b)

If $n$ is equal to one, determine the initial values of multipliers by Equation (39). Otherwise, update the multipliers by PBM.

(c)

Solve hydro and thermal subproblems by MILP with the given multipliers. Then, set $n=n+1$. If $n$ is equal to two, go to Step 4.

(d)

If the ascent condition (Equation (32)) holds, a serious step is declared and go to Step 4. Otherwise, a null step is declared and update the multipliers by inference engine.

(e)

Solve the hydro and thermal subproblems by MILP. Then, according to the results, arrange the dual values in ascending order, and update the bundle and stability center sequences.

Step 4:

Primary recovery. Generate a feasible solution by the heuristic used.

Step 5:

Convergence test. If the stopping rule is met (Equations (27) and (28)), terminate the iteration. Otherwise, go to Step 3(b).

4. Case Study and Results

4.1. Parameter Settings and Performance Metrics of IPBM

The whole planning horizon of STHS is 24 h, with 1 h for each period. To build the knowledge base, historical operational data from 2013 to 2019 are used. There are 2380 generation scenarios at the daily scale after data correction, which are then clustered into 33 representative scenarios. Knowledge expressions are extracted from PBM iterations of these 33 representative scenarios. The knowledge base is based on MySQL Database 5.7 and structured query language. The proposed IPBM is encoded in Java language and implemented on a PC-Intel@2.60GHz. The MILP subproblems are solved with Gurobi 8.1.1 optimization solver. The OD is implemented using SPSS Statistics. Parameters associated with the computational simulation are set as follows: $RDG$ = 0.5%, $\Delta \lambda$ = 10⁻⁴, $\epsilon$ = 10⁻², and $\kappa ={10}^{-2}$.

To evaluate the performance of IPBM, three metrics are adopted: (1) dual value, representing the global search ability of IPBM; (2) primal value, representing the objective optimality after repairing the infeasible dual solution by heuristics; (3) computational time, representing the computational efficiency of IPBM. Among these metrics, the dual value is a positively oriented metric—the larger the better—while the remaining two metrics are negatively oriented metrics—the lower the better.

Based on the above settings, two improvements in IPBM, inferring initial values of Lagrange multipliers and inferring new updates of multipliers when null steps occur, are firstly tested. Then, the robustness of IPBM is demonstrated in comparison with standard PBM in 12 different cases.

4.2. Performance Testing of IPBM

A typical case in the spring of 2019 is selected as the generation scenario to manifest the performance of IPBM. In this scenario, water levels of hydropower plants are at the descending period before flood season. Both the load demand and water inflows are at a low level. The energy demand and peak load demand are 2.95 × 10⁵ MWh and 1.51 × 10⁴ MW, respectively. The peak–valley difference is 40.2%. Average natural inflow and total storage energy of hydropower plants are 264 m³/s and 4.65 × 10⁶ MWh, respectively.

4.2.1. Effects of Inferring the Initial Values of Lagrange Multipliers

Conventionally, initial values of multipliers are set to the marginal cost corresponding to the solution of a simplified economic dispatch, or set to zero directly. Therefore, to test the effect of initial multipliers, three techniques are compared:

(1)

Zero value (ZV), where multipliers are set to zero directly;

(2)

A simplified version of economic dispatch (SED), which relaxes the integer constraints and is described in [15];

(3)

The proposed method by expert system (ES1).

Moreover, to keep the single variable principle, PBM is adopted to update multipliers during the process.

Table 2 shows the comparison of different initial multiplier generation techniques. In the stage of initial multiplier generation, the initial dual value of ES1 is 103,000 t, far more than those of ZV and SED, which means that ES1 provides the best lower bound of dual value at the beginning period. In the stage of iterative calculations, dual values of three techniques converge to a close value, around 111,303 t. Figure 5 shows the evolution process of dual value by three techniques. In Figure 5, as the iteration proceeds, the difference in dual value caused by initial multipliers becomes smaller and smaller. However, the number of iterations differs a lot, causing the differences in computational time, which are 782 s, 423 s, and 359 s for ZV, SED, and ES1, respectively. Moreover, the primal values of the three techniques are basically the same. The primal value of ES1 is only 0.03% less than that of ZV.

Table 2. Comparisons of different initial multiplier generation techniques.

Stage	Item	ZV	SED	ES1
Initial multiplier generation	Dual value (t)	30,470	94,337	103,000
Iterative calculations	Dual value (t)	111,300	111,301	111,303
	Primal value (t)	113,796	113,780	113,761
	Time (s)	782	423	359

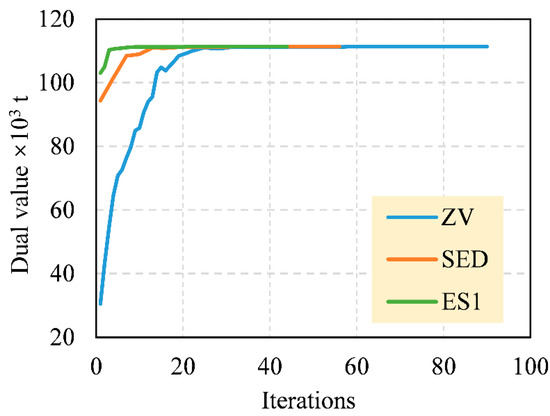
Figure 5. The evolution process of dual value by ZV, SED, and ES1.

Therefore, the conclusions are drawn: (1) the quality of initial values of multipliers has a significant influence on the computational time, but little influence on the final objective function value; and (2) initial values of Lagrange multipliers obtained by ES1 are better than those by ZV and SED, demonstrating the superiority of ES1.

4.2.2. Effects of Inferring New Updates of Multipliers When Null Steps Occur

To test the effect of multiplier updates when null steps occur, four techniques are compared:

(1)

Subgradient method (SG) (as in [37]);

(2)

Cutting-planes method (CP) (as in [38]);

(3)

Standard PBM;

(4)

The proposed method by expert system (ES2).

To keep the single variable principle, initial multiplier values of four techniques are given by ES1.

Table 3 lists the outcomes of the four techniques. Figure 6 illustrates the detailed evolution process of dual value. From Table 3, compared with SG and CP, PBM and ES2 can find better dual values and take less time. Figure 6 shows that the dual values of SG and CP oscillate violently during the iteration process, while PBM and IE2 present considerable stability. After using heuristics to obtain feasible solutions, the primal values of PBM and ES2 are less than those of SG and CP.

Table 3. Comparisons of different multiplier updating techniques.

Item	SG	CP	PBM	ES2
Dual value (t)	105,260	109,540	111,303	111,835
Primal value (t)	122,461	116,137	113,761	112,472
Time (s)	833	646	359	318

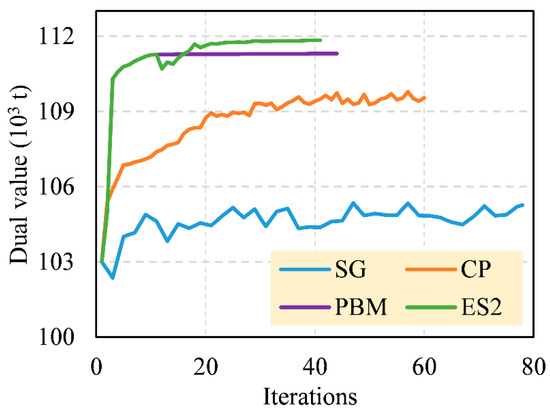
Figure 6. The evolution process of dual value by SG, CP, PBM, and ES2.

To further illustrate the superiority of ES2 over PBM, the effect of the expert system is analyzed. Table 4 lists the iterations of serious steps and null steps during the whole iteration process. ES2 converges in 41 iterations, while PBM takes 44 iterations. At the 11th and 32nd iterations of ES2, null steps occur. Subsequently, two orthogonal designs are executed, which are $L_{20}\left(2^{16}\right)$ and $L_8\left(2^7\right)$, respectively. In Table 4, the item $L_{20}\left(2^{16}\right)$ → [12–31] means that there are 16 broken constraints among the relaxed constraints. An experiment of 16 factors and 2 levels per factor is thus formed, where 20 multiplier combinations are sampled by the OD. These 20 multiplier combinations correspond to 20 iterations (from iteration 12 to 31) in the process. The item $L_8\left(2^7\right)$ → [33–40] in Table 4 has a similar meaning with the item $L_{20}\left(2^{16}\right)$ → [12–31].

Table 4. Detailed evolution steps of PBM and ES2.

Item	PBM	ES2
Serious steps	[1–10, 26]	[1–10]
Null steps	[11–25, 27–44]	[11, 32, 41]
Orthogonal design	/	$L_{20}\left(2^{16}\right)$ → [12–31] $L_8\left(2^7\right)$ → [33–40]

From Figure 7, during the first OD, the improvement of the dual value by ES2 is 407 t more than that by PBM. During the second OD, the two methods improve little. Finally, the dual value of ES2 converges to 111,835 t, 532 t more than PBM, which verifies the better global searchability of ES2. Moreover, since ES2 take less iterations and orthogonal designs in ES2 to avoid solving quadratic programming, the computational efficiency of ES2 is better than PBM.

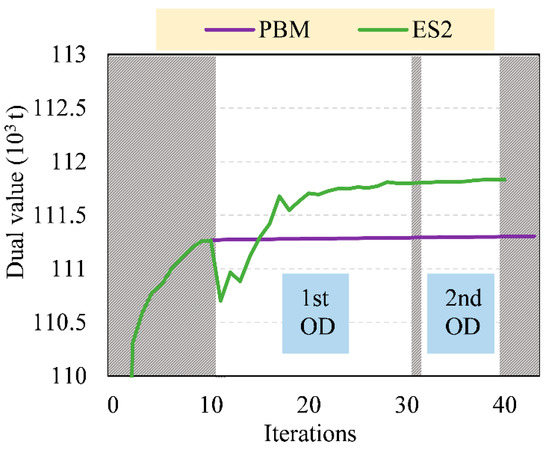
Figure 7. Detailed evolution process of dual value by ES2 and PBM.

In summary, compared with SG, CP, and PBM, ES2 shows extraordinary stability during the iteration process. Due to the advantage of the expert system, ES2 obtains the best objective function value in the least time, demonstrating its superiority in global search ability and computational efficiency.

4.3. Comparison with Standard PBM in Different Generation Scenarios

To demonstrate the robustness of IPBM, 12 typical generation scenarios from 2019 are chosen, of which the load demand and water inflow characteristics are summarized in Table 5. The scenarios are distinguished as follows: the first number refers to the scenario index (from 1 to 12), the second term is associated with the load demand level (LLD = low load demand; MLD = medium load demand; HLD = high load demand), and the third term means the water inflow condition (DS = dry season; WS = wet season). The conclusion is obtained by comparing the performance of IPBM with PBM in 12 scenarios.

Table 5. Description of 12 selected generation scenarios.

Generation Scenario	Load Demand Condition			Water Inflow Condition
	Energy Demand (105 MWh)	Peak Load (104 MW)	Peak–Valley Difference 1 (%)	Natural Inflows 2 (m3/s)	Storage Energy 3 (106 MWh)
1_LLD_DS	3.17	1.61	43.22	203.7	3.62
2_LLD_DS	2.82	1.47	49.04	233.9	3.27
3_LLD_DS	3.22	1.67	46.56	200.2	2.74
4_LLD_DS	2.98	1.49	42.31	189.5	1.99
5_LLD_DS	2.95	1.51	44.69	449.9	1.62
6_MLD_WS	3.32	1.72	45.33	3007.8	2.06
7_LLD_WS	2.75	1.45	50.61	2262.2	8.04
8_MLD_WS	3.61	1.83	42.88	1454.5	7.14
9_MLD_WS	3.72	1.89	40.45	1072.5	8.28
10_LLD_WS	3.26	1.72	46.56	955.5	7.42
11_HLD_DS	3.83	1.92	37.37	382.7	7.54
12_HLD_DS	4.61	2.33	40.37	247.6	6.65

¹ (Peak load—valley load)/peak load × 100%. ² The sum of natural inflows of four basins. ³ The sum of storage energy of four basins.

Table 6 lists the results for STHS by PBM and IPBM. From Table 6, it can be noticed that IPBM outperforms PBM in all scenarios in terms of dual value, primal value, and computational time. For dual value, the maximum and minimum relative differences are 0.64% in scenario 5_LLD_DS and 0.01% in scenario 4_LLD_DS, respectively, indicating that IPBM can provide a better lower bound for a primal problem. In terms of primal value, the average relative difference in 12 scenarios is −0.89%, which means that the average coal consumption reduction is 748 t by IPBM. Moreover, the computational time of IPBM is less than that of PBM in each scenario, verifying its high computational efficiency.

Table 6. Comparative analysis of 12 scenarios.

Generation Scenario	Dual Value (t)			Primal Value (t)			Time (s)
	PBM	IPBM	Rel. Diff. 1	PBM	IPBM	Rel. Diff. 1	PBM	IPBM	Rel. Diff. 1
1_LLD_DS	106,552	106,599	0.04%	108,430	107,409	−0.94%	491	400	−18.58%
2_LLD_DS	65,519	65,698	0.27%	66,816	66,418	−0.60%	541	448	−17.18%
3_LLD_DS	92,059	92,242	0.20%	94,027	93,359	−0.71%	465	377	−18.97%
4_LLD_DS	93,195	93,200	0.01%	94,708	94,183	−0.55%	499	342	−31.44%
5_LLD_DS	77,932	78,428	0.64%	79,516	78,961	−0.70%	392	330	−15.88%
6_MLD_WS	65,110	65,449	0.52%	66,687	65,780	−1.36%	553	382	−30.95%
7_LLD_WS	71,019	71,065	0.06%	72,631	71,879	−1.04%	361	326	−9.68%
8_MLD_WS	59,663	60,006	0.58%	61,109	60,497	−1.00%	527	421	−20.20%
9_MLD_WS	68,236	68,369	0.19%	69,897	69,276	−0.89%	548	379	−30.85%
10_LLD_WS	85,241	85,365	0.15%	86,673	85,862	−0.94%	442	301	−31.90%
11_HLD_DS	93,683	93,740	0.06%	95,179	94,329	−0.89%	568	448	−21.13%
12_HLD_DS	114,868	115,278	0.36%	117,465	116,203	−1.07%	550	375	−31.81%

¹ The relative difference between PBM and IPBM, calculated by (value of IPBM—value of PBM)/value of PBM × 100%.

Figure 8 illustrates the relative difference between the primal value and natural inflow in different scenarios. It can be observed that the relative difference is approximately positively correlated with the natural inflow. From scenario 2_LLD_DS to scenario 5_LLD_DS, both the natural inflow and relative difference are at a low level. From scenario 6_MLD_WS to scenario 10_LLD_WS, the natural inflow and relative difference are at a high level, and gradually decrease. The maximum relative difference is 1.36% in scenario 6_MLD_WS. The relative difference in the primal value reflects the improvement in the objective function of IPBM compared with PBM. Therefore, the improvement in the IPBM objective function is more significant in large-inflow scenarios. The reason is that when the natural inflow is high, the corresponding hydropower potential is large. IPBM can improve the water use efficiency and yield more hydropower energy. As a result, coal consumptions in large-inflow scenarios are greatly reduced.

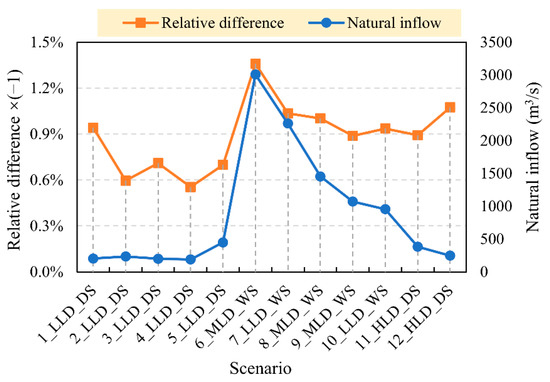
Figure 8. Relative differences of primal value and natural inflows in different scenarios.

5. Conclusions

Hydrothermal power accounts for a high proportion in power systems, making STHS a challenge for operators. To efficiently solve the STHS problem, an IPBM combining the ES technique and standard PBM within the LR framework is presented in this paper. In IPBM, the ES consists of two parts: a knowledge base and inference engine. The knowledge base is built by extracting knowledge expressions from historical generation scenarios. Based on the knowledge base, initial values of Lagrange multipliers and new updates of Lagrange multipliers when null steps occur are reasoned by the inference engine. In this way, the ES provides a good lower bound to the primal problem at the beginning period. Moreover, the ES avoids solving quadratic programs when a null step is declaimed and increases the likelihood of reaching global optimum. To verify the effectiveness of IPBM, a case study is conducted in a large-scale hydrothermal system in China. Results in different cases indicate that, compared with several common methods, IPBM can obtain generation schedules with less coal consumption in less time, demonstrating its superiority in global search ability, computational efficiency, and robustness. Hence, IPBM proves to be an effective method for STHS.

Due to the negative impact of dam construction on river ecosystems, the ecological dispatch of hydropower is attracting increasing attention from researchers. Therefore, for further studies, it is necessary to bring ecological flow constraints into the present solution framework.