Modelling and Prediction of Water Quality by Using Artificial Intelligence

Abstract

Artificial intelligence methods can remarkably reduce costs for water supply and sanitation systems and help ensure compliance with the quality of drinking and wastewater treatment. Therefore, modelling and predicting water quality to control water pollution has been widely researched. The novelty of the proposed system is presented to develop an efficient operation of monitoring drinking water to ensure a sustainable and friendly green environment. In this work, the adaptive neuro-fuzzy inference system (ANFIS) algorithm was developed to predict the water quality index (WQI). Feed-forward neural network (FFNN) and K-nearest neighbors were applied to classify water quality. The dataset has eight significant parameters, but seven parameters were considered to show significant values. The proposed methodology was developed based on these statistical parameters. Prediction results demonstrated that the ANFIS model was superior for the prediction of WQI values. Nevertheless, the FFNN algorithm achieved the highest accuracy (100%) for water quality classification (WQC). Furthermore, the ANFIS model accurately predicted WQI, and the FFNN model showed superior robustness in classifying the WQC. In addition, the ANFIS model showed accuracy during the testing phase, with a regression coefficient of 96.17% for predicting WQI, and the FFNN model achieved the highest accuracy (100%) for WQC. This proposed method, using advanced artificial intelligence, can aid in water treatment and management.

1. Introduction

With fast economic growth and increased urbanization, water pollution has become grimmer. Understanding the issues and patterns of water quality is also critical for water pollution reduction and regulation. Most countries around the world have started to develop environmental water management schemes to truly understand the quality of the marine ecosystem. Water is life’s most important substance. Although 71% of the Earth’s surface is covered with water, the vast majority of it (95%) is salt water [1]. Thus, conserving the quality of fresh water is essential. Almost one billion people do not have access to adequate drinking water sources, and two million people die every year from contaminated water and poor sanitation and hygiene [2].

Water quality is important to the sustainability of a diversion scheme. Predicting water quality involves forecasting variation patterns in the quality of a water system at a certain time. Water quality prediction is important for water quality preparation and regulation. Strategies for the prevention and regulation of water contamination can be developed by predicting future changes in water safety at varying levels of contamination and devising rational strategies to prevent and regulate water contamination. In water diversion schemes, the general consistency of water should be estimated. A large volume of water is transported to address everyday drinking issues. Thus, strategies should be investigated for forecasting water quality in current society [3].

Water of low quality can also be economically challenging, given that resources must be diverted to upgrade water delivery infrastructure any time a problem arises. For these purposes, the demand for improved water treatment and water quality control has been increasing to ensure clean drinking water at affordable rates. Systematic analyses of raw water, disposal systems, and organizational monitoring problems are required to resolve these challenges [4]. Achieving precise predictions of changes in water quality can immensely improve the efficiency of aquaculture. In general, water quality data are pre-processed before water quality parameters are predicted. Thus, this section consists of two stages. The first stage consists of the pre-treatment of water quality data and the performance of correlation analysis between different water quality parameters.

With advanced computing using artificial intelligence (AI) techniques, the modelling of water quality has been developed to resolve water quality issues. Artificial neural networks (ANNs) have aided in the monitoring of water quality systems by predicting changes in water quality [5]. They can immensely improve the efficiency of aquaculture. The simulation of water quality conditions has difficulties and challenges regarding the use of the hydrodynamic and water quality model, a relatively novel computational approach. ANNs have been widely established in many disciplines and provide an alternative technique for understanding and monitoring water quality in reservoirs. ANNs have been successfully applied to simulate and forecast water quality in water bodies. Numerous ANN methods, such as feed-forward neural networks [6], have been used in various applications. The fuzzy logic system has been developed to solve complex nonlinear systems [7]. ANN applications have been successfully used as tools to compute and predict the quality of water bodies [8,9,10,11,12]. ANN models require parameter values for designing predictions [13]. ANNs have numerous advantages, including their ability to learn, manage very complex nonlinear systems, and work with parallel processing. Shafi et al. [14] used support-vector machines, neural networks (NNs), deep NNs, and K-nearest neighbors (KNNs) to classify water quality using data from the Pakistan Council of Research in Water Resources (PCRWR) for drinking water.

Used a hybrid deep learning model convolutional neural network (CNN)-long short-term memory (LSTM) to predict water quality including total nitrogen, total phosphorous, and total organic carbon.

Reference [15], Liu et al. [16] used the long short-term memory (LSTM) network model to predict the quality of drinking water in the Yangtze River Basin. The LSTM model was developed using pH, dissolved oxygen (DO), chemical oxygen demand (COD), and NH3-N. It is noted that the LSTM model has promise for monitoring water quality.

Chen et al. [17] proposed artificial intelligence for modelling and predicting water quality. It is noted that the ANN model gave a better result. Singh [18] used the ANN model to compute dissolved oxygen (DO) and biological oxygen (BOD) parameters to predict the quality of river water. Zheng et al. [19] applied the immune practical swarm optimization (PSO) method, which employed a neural network with a hidden layer to predict sewage effluent water quality. Gao [20] enhanced the back-propagation (BP) neural network by using the grey correlation analysis method to predict water quality. Zhang et al. [21] combined ANNs with a genetic algorithm to predict water quality by using time data to enhance the stability of the forecasting results. Wang et al. [22] proposed a Genetic Regression Neural Network GA-GRNN model to develop an efficient method of predicting water quality to ensure water security in the south-to-north water diversion (SNWD) Project. Correlation coefficients were applied to investigate the relationship between significant parameters. Abyaneh [23] introduced ANNs and regression models to predict COD and bioche. The radial-basis-function was used as a kernel function of the ANN model [24,25]. Barzegar et al. [26] developed a hybrid convolutional neural network (CNN)–LSTM model to predict DO and chlorophyll-a (Chl-a) in Small Prespa Lake in Greece. It is observed that the deep learning model was outperformed compared with the traditional support-vector regression (SVR) model. Maiti et al. [27] predicted dissolved oxygen (DO) levels using the ANN model. Deep learning methods showed higher performance in predicting WQI compared to traditional machine learning techniques, as did AI techniques such as ANN, Bayesian NNs, and adaptive neuro-fuzzy [28]. Piazza et al. [29] presented a comparison between the proposed model’s numerical optimization approach and the results of an experimental campaign. The genetic algorithm with a hydraulic simulator was applied to test and evaluate water quality by monitoring it. Sambito et al. [30] developed a smart system based on the Internet of Things and a Bayesian decision network (BDN) for predicting wastewater. The proposed system was focused on analysis and soluble conservative pollutants such as metals, decision support systems, and auto-regressive moving averages, and was applied to predicting the water quality WQ of groundwater [31].

Currently, water quality is assessed by costly and time-consuming laboratory and statistical analyses that require sample collection, transportation to laboratories, and a lot of time and calculation, which is quietly unavailing because water is a completely transmissible medium and time is necessary if the water is contaminated with disease-causing waste. The catastrophic consequences of water contamination necessitate a faster and less expensive alternative. In this regard, we developed a real-time system to evaluate an alternative approach based on the advanced artificial intelligence method for modelling and predicting water quality. These mimicking models, however, face some challenges. For example, they do not consider factors affecting WQ. The contributions of the current study are presented to use an advanced AI Adaptive neural-fuzzy inference system ANFIS model that was developed to predict Water quality Index WQI. The Feed-forward neural network FFNN and KNN were used for the Water Quality Classification WQC. The highly efficient advanced AI can be generalized and then used to forecast the water pollution process, which will aid decision-makers in strategizing for timely decisions.

2. Materials and Methods

Figure 1 displays the framework of the methodology used.

2.1. Dataset

The datasets employed to conduct the research were acquired from different locations in India and contained 1679 simples from 666 different sources of rivers and lakes in the country. The data was collected between 2005 and 2014. The link to the datasets is attached. The datasets include eight important parameters: DO, pH, conductivity, biological oxygen demand, nitrate, fecal coliform, temp, and total coliform. However, seven parameters were considered to show significant values, and the developed models were evaluated based on some statistical parameters. All the experiments consisted of temp parameters. The Indian government collected these data to ensure the quality of the drinking water supplied. This dataset was obtained from Kaggle https://www.kaggle.com/anbarivan/indian-water-quality-data (accessed on 3 December 2020).

2.2. Data Preprocessing

The processing phase is very important in data analysis to improve data quality. In this phase, WQI was calculated from the most important parameters of the dataset. Then, water samples were classified on the basis of WQI values. The z-score method was used as a data normalization technique for superior accuracy.

2.2.1. Water Quality Index (WQI) Calculation

The WQI, which is calculated using several parameters that affect WQ [32], was used to measure water quality. The performance of the proposed system was evaluated on the published dataset, with seven important water quality parameters. The WQI was calculated using the following formula:

$$WQI= \frac{{{\displaystyle \sum }}_{i=1}^N{q}_i \times w_i}{{{\displaystyle \sum }}_{i=1}^N{w}_i}$$

(1)

where N denotes the total number of parameters included in the WQI formula, q_i denotes the quality estimate scale for each parameter i calculated by Formula (2), and w_i denotes the unit weight of each parameter in Formula (3).

$$q_i=100 \times (\frac{V_i- V_{Ideal}}{S_i- V_{Ideal}})$$

(2)

where V_i is a measured value that refers to the water samples tested, V_Ideal is an ideal value and indicates pure water (0 for all parameters except OD = 14.6 mg/L and pH = 7.0), and S_i is a standard value recommended for parameter i, as shown in

Table 1. Permissible limits of the parameters used in calculating the WQI [33].

Parameters	Permissible Limits
Dissolved oxygen, mg/L	10
pH	8.5
Conductivity, µS/cm	1000
Biological oxygen demand, mg/L	5
Nitrate, mg/L	45
Fecal coliform/100 mL	100
Total coliform/100 mL	1000

.

$$w_i= \frac{K}{S_i}$$

(3)

where K denotes the constant of proportionality, which is calculated using the following formula:

$$K= \frac{1}{{{\displaystyle \sum }}_{i=1}^N{S}_i}$$

(4)

Table 2. Water quality classification (WQC).

Water Quality Index Range	Classification
0–25	Excellent
26–50	Good
51–75	Poor
76–100	Very poor

and

Table 3. Parameters unit weights.

Parameter	Unit Weight (wi)
Dissolved Oxygen	0.2213
pH	0.2604
Conductivity	0.0022
Biological Oxygen Demand	0.4426
Nitrate	0.0492
Fecal Coliform	0.0221
Total Coliform	0.0022

represent the parameters of the unit weight and the WQC, respectively.

WQI can be used to calculate more parameters, including our selecting parameters. The WQI depends on the variable data. The proposed system can test any parameters with any water quality data.

2.2.2. Z-Score Normalization Method

Z-score a is used to normalize data by computing both the mean (μ) and standard deviation. The Z-score was applied to scale parameter values between 0 and 2. It is calculated using the following formula:

$$\mathrm{Z}-\mathrm{score}=\frac{\left(x-\mu \right)}{\sigma }$$

(5)

where x represents the tested sample in the dataset to be evaluated.

2.3. Adaptive Neuro-Fuzzy Inference System (ANFIS) Model

The ANFIS model is one of the types of ANN algorithms proposed by Jang [34,35]. This model was used to solve complex and nonlinear problems. The algorithm consists of a neural network and fuzzy logic and is, therefore, powerful. The algorithm is used to predict data and obtain the optimal membership function through an adaptive system in the input layer. The ANFIS model consists of five layers: fuzzification, antecedent, strength normalization, consequent, and inference [36]. Each layer contains many nodes. The ANFIS model is represented by two input parameters and an output parameter, as illustrated in Figure 2. The if-then rules are applied as follows:

$$Rule1:ifxis{A}_{1}andyis{B}_1,then{f}_1=p_{1}x+q_{1}y+r_1$$

(6)

$$Rule1:ifxis{A}_{2}andyis{B}_2,then{f}_1=p_{2}x+q_{2}y+r_2$$

(7)

where x and y are the input parameters for node $i$ and $A_1$,$A_2$,$B_1$, and $B_2$ are the fuzzy set. $p_{1,}{p}_2$, $q_1$, $q_2$, $r_1$ and $r_2$ are the consequent parameters. $f$ is the output of the ANFIS model.

• Layer 1 (Fuzzification Layer):

The first layer implements a membership function to convert the input data into a fuzzy set.

$$O_{1,i}=\mu A_i\left(x\right)\mathrm{for}i=1,2$$

(8)

$$O_{1,i}=\mu B_i\left(y\right)\mathrm{for}i=1,2$$

(9)

$$\mu A_i\left(x_1\right)=\frac{1}{1+{(\frac{x-c_i}{{\sigma }_i})}^{2b_i}}$$

(10)

where μ(x) and μ(y) are membership functions; A_i is the linguistic variable; and σ_i, b_i, and c_i are the parameters of the Bell function.

• Layer 2 (Antecedent Layer):

Nodes in the second layer are fixed nodes where inputs from the previous layer are multiplied with the node value to form an output signal for the second layer.

$$O_{2,i}=w_i=\mu A_i\left(x\right)\ast \mu B_i\left(y\right), i=1, 2$$

(11)

where w_i signal refers to the firing strength of the rule.

• Layer 3 (Strength Normalization Layer):

The ratio of $i_{th}$ is calculated to normalize firing strength.

$$O_{3,i} = {\overline{w}}_i= \frac{w_i}{w_{1+w_2}},i=1, 2$$

(12)

where O_3,i is the output of layer 3 and $\overline{w}$ is the normalized firing strength.

• Layer 4 (Consequent Layer):

The nodes of the fourth layer are adaptable, and the output of this layer is $O_{4,i}$. The node function of the fourth layer is defined in the following equation:

$$O_{4,i}={\overline{w}}_i·f_i={\overline{w}}_i·\left(p_{i}x+q_{i}y+r_i\right)$$

(13)

where $p_i, q_i$, and $r_i$ are consequent parameters used for the fuzzy inference system function ($f_i$).

• Layer 5 (Inference Layer):

This layer is applied to obtain the model output. The final output of a network is described as follows:

$$O_{5,i}overall output={{\displaystyle \sum }}^{}{\overline{w}}_i{f}_i=\frac{{{\displaystyle \sum }}_i{\overline{w}}_i{f}_i}{{{\displaystyle \sum }}_i{w}_i}$$

(14)

ANFIS is a back-propagation algorithm in which the error value between the expected and actual outputs, as well as the error function, are calculated. Weights are updated inversely from the fifth layer to the first, and the process continues until the lowest error rate is obtained. Figure 3 shows the framework of an FFNN model for predicting WQI.

The training data were divided into 70% for the training phase and 30% for the testing phase. The ANFIS model was processed based on the scatter partition fuzzy approach, which works by clustering to divide dimension vectors in the specific area of the fuzzy rules. The ANFIS model was developed by integrating fuzzy c-means clustering and back-propagation algorithms. The seven clusters and minimum improvement 10⁻⁵, partition matrix exponent 2, and number epoch 150 were appropriate.

2.4. Classification of Water Quality

In this section, two classification algorithms, namely, KNN and FFNN, were presented.

2.4.1. K-Nearest Neighbors (KNN) Model

The KNN algorithm is one of the traditional machine learning algorithms used for the classification of data. The KNN algorithms use K-neighbor values to find the closest point between the objects. The K-value is used to find the closest points in the feature vectors, and the value should be unique. In this study, three K-values were appropriated to obtain good results. The Euclidean distance function (Di) was applied to find the nearest neighbor in the features vector.

$${\mathrm{D}}_{\mathrm{i}}=\sqrt{\left({\mathrm{x}}_1-{\mathrm{x}}_2\right)+{({\mathrm{y}}_1-{\mathrm{y}}_2)}^2}$$

(15)

where x₁, x₂, y₁, and y₂ are variables for input data.

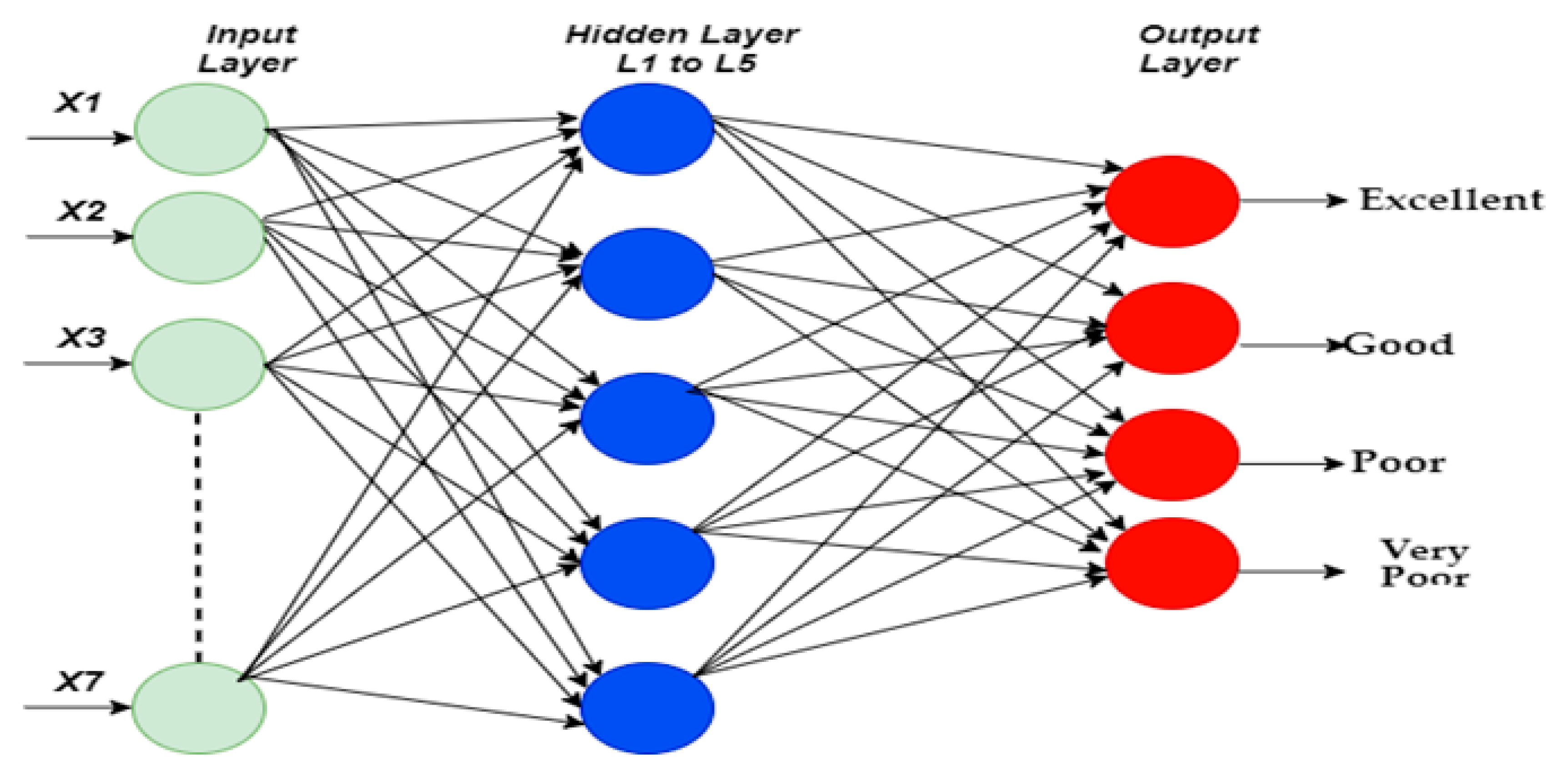
2.4.2. Artificial Neural Networks (ANNs)

The artificial neural network is a very powerful computation method for developing a number of real medical applications [37]. In general, ANN models are used as very powerful machine learning algorithms for time series prediction of different engineering applications. The ANN model consists of an input layer, hidden layers, and an output layer. Each hidden layer has weight and bias parameters to manage neurons. To transfer the data from the hidden layer into the output layer, the activation function is used. The learning algorithms are used to select the weights within the NN framework. The weight selection is based on minimum performance measures, such as mean square error (MSE). Figure 4 shows the architecture of FFNN for the classification water quality WQC.

In this study, the ANN algorithm was used to classify water quality. ANNs have three significant layers: input, hidden, and output. Five hidden layers were considered to transfer the input training from input to output to the sigmoid function. However, the output layer had three classes.

2.5. Performance Measurement

Performance measurement approaches, such as MSE, were applied to evaluate the ability of the proposed model to predict the WQI. Furthermore, the accuracy, specificity, sensitivity, precision, recall, and F-score performance measurements were determined to evaluate the FFNN and KNN classification algorithms to classify the WQC. The statistical methods used are defined as follows:

• Mean square error (MSE)

  $$MSE=\frac{1}{N} {\displaystyle \sum }_{i=1}^N{\left(y_i-{\widehat{y}}_i\right)}^2$$

  (16)

• Root mean square error (RMSE)

  $$RMSE=\sqrt{{\displaystyle \sum }_{i=1}^N\frac{{\left(y-\widehat{y}\right)}^2}{N}}$$

  (17)

  $$R=\frac{n{{\displaystyle \sum }}^{}\left(x\times y\right)-({{\displaystyle \sum }}^{}x)({{\displaystyle \sum }}^{}y)}{[n{{\displaystyle \sum }}^{}(x^2)-{{\displaystyle \sum }}^{}(x^2)]\times [n{{\displaystyle \sum }}^{}(y^2)-{{\displaystyle \sum }}^{}(y^2)]}\times 100\%$$

  (18)

  where R is Pearson’s correlation coefficient, x is the observation input data in the first set of the training data, y is the observation input data of the second set of the training data, and n is the total number of input variables.

• Accuracy

  $$Accuracy=\frac{TP+TN}{TP+FP+FN+TN}\times 100\%$$

  (19)

• Specificity

  $$Specificity=\frac{TN}{TN+FP}\times 100\%$$

  (20)

• Sensitivity

  $$Sensitivity=\frac{TP}{TP+FN}\times 100\%$$

  (21)

• Precision

  $$Precision=\frac{TP}{TP+FP}\times 100\%$$

  (22)

• F-score

  $$\mathrm{F}-\mathrm{score}=\frac{2\ast preision\ast \mathrm{Sensitivity}}{preision+\mathrm{Sensitivity}}\times 100\%$$

  (23)

  where TP, TN, FP, and FN are the true positive, true negative, false positive, and false negative, respectively.

3. Experimental Setup

The empirical results were analyzed in the MATLAB 2020 environment. The simulation was performed by employing a system with an i7 processor and 8 GB RAM to process all required tasks.

3.1. Prediction of WQI Using the ANFIS Model

The proposed methodology of the model was validated using 70% of the dataset for training and applying the ANFIS model to predict the WQI. The training results showed that the ANFIS model was highly optimal for predicting WQI.

Table 4. Performances of the ANFIS models to predict WQI.

Model		Training Dataset				Testing Data
	MSE	RMSE	Mean Errors	R (%)	MSE	RMSE	Mean Errors	R (%)
ANFIS	0.00336	0.0580	6.456 × 10−9	90.29	0.0029	0.0540	0.001330	92.39

summarizes the prediction results of the WQI obtained by the ANFIS model during the training and testing phases. The prediction results showed R% = 92.29%, which demonstrates the highly efficient performance of the proposed system. The prediction results of the ANFIS model in the testing showed R% = 92.39%, according to the correlation regression results. Figure 5 displays the time series plot for training and testing, showing that the target and prediction values were very close; the x-axis presents the numbers of samples; and the y-axis presents the scaling of data. The time steps are from 2005 to 2014, but we divided the dataset into training and testing for validation of the system. Splitting the data was done with a random function for selecting different simple points from the entire dataset. The testing phase is unseen data. It is a process used to validate the ANFIS model to predict the water quality. In the testing phase, the algorithm selects random values from the entire dataset to test the model.

The prediction results present the predicted values at the testing state. According to the evaluation metrics (MSE, RMSE, mean error, and R), the predicted values of the prediction values were very close to the experimental ones.

Figure 6 shows the histogram error of the predicted WQI values during the training and testing phases. The errors between the WQI prediction values and the WQI observation values were computed to generate an error histogram. These prediction errors can aid in determining how the predicted values deviate from the observation values. This is a histogram error for the training phase only. The maximum error was 0.01287 and the average error was 0.1178.

Figure 7 illustrates the regression plot of the ANFIS mode to predict WQI during the training and testing phases. The regression plot was used to determine the correlation between the predicted WQI and the observed WQI values using Pearson’s correlation. The target (x-axis) values represent the observation WQI data, and the output (y-axis) values represent the predicted WQI values generated by employing the ANFIS model. The target values are closest to the prediction values. The strong relationship between the observation values and the prediction values, which led to a good model, The correlation analysis revealed the highly efficient performance of the developed model.

The empirical results presented demonstrate the highly efficient performance of the ANFIS model.

3.2. Experiment Results of WQC Classification

This section presents the results of the classification algorithms used to predict the WQC.

Table 5. Performance of the machine learning models used to predict WQC.

Models	Accuracy (%)	Sensitivity (%)	Specificity (%)	Precision (%)	Recall (%)
FFNN	100	99.61	99.61	99.961	100
KNN	80.63	82.50	89.50	82.50	86.84

shows the results of the FFNN and KNN machine learning algorithms. The performance of the FFNN model was superior compared to that of the KNN algorithm. The accuracy, specificity, sensitivity, precision, recall, and F-score of the FFNN algorithm were 100%, 99.61%, 99.61%, 99.61%, and 100%, respectively. Notably, the performance of the FFNN outperformed that of the KNN algorithm. Figure 8 shows the confusion matrix of the FFNN model used to classify WQ. To validate the proposed system, we divided the dataset into 70% training and 30% testing. The numbers of false positives, false negatives, true positives, and true negatives were reported using a confusion matrix. The total number of samples of data was 1679, and we divided the data into 1119 samples as training, 280 as testing, and 280 as validation. It is observed that all sample data in both phases’ classification were true positive. The x-axis values represent class target and the y-axis values denote class output. The classes are categorized into 1 (excellent), 2 (good), 3 (poor), and 4 (very poor).

Figure 9 shows the histogram error of the predicted WQI values at the training and testing phases. The maximum error was 0.0228.

The receiver operating characteristic (ROC) was used as a metric to display the FFNN confusion metric properties, such as true positive and false positive, for WQC. Figure 10 shows the ROC for measuring the validity of the FFNN model based on the real standard dataset. All graphs for the testing, training, and validation of the system are presented. The last graph shows the overall ROC of the system. Notably, the detection rate was very high, and the misclassification rate was very low. The x- and y-axis represent the false positive rate (misclassification) and true positive rate, respectively. The results demonstrate the highly efficient performance of the FFNN model for WQC.

A performance plot was used to identify the MSE in the network of WQC. The performance of the FFNN model is illustrated in Figure 11. The best validation achieved by the FFNN model was 2.24613 × 10⁻⁶ at epoch 52. In the performance of the FFNN model, the MSE decreased rapidly as it learns. The blue, green and red lines represent the training process, validation error and training error, respectively. Increased numbers of epochs indicate that the training data had small errors. When the validation error stops, the training stops.

4. Discussion

Modelling and the prediction of water quality have played a pivotal and significant role in saving time and consumption in lab analysis. Artificial intelligence algorithms were explored as an alternative method to estimate and predict water quality. This study used the experimental data of 1679 samples from 666 different water bodies of rivers and lakes from different states in India. The dataset includes seven selected important parameters: DO, pH, conductivity, BOD, nitrate, fecal coliform, and total coliform.

Table 6. Comparison of the proposed system with existing models.

Authors	Water Body	Place of Study	Models		Number of Parameters	Purpose of System		Results of WQI		Results of WQC
			Model Prediction of WQI	Model for Classification of WQC		WQI	WQC	MSE	R%	Accuracy (%)
Ahmed et al. [38]	River	Malaysia	FFNN	Not used	25	Yes	No	0.1156	97.7	No
Gazzaz et al. [39]	River	Malaysia	ANNs	Not used	23	Yes	No	9.25	77.0	No
Sakizadeh et al. [40]	Groundwater	Iran	ANNs	Not used	16	Yes	No	9.25	77.0	No
Rankovic et al. [41]	River	Serbia	FFNN	Not used	10	Yes	No	0.9923	87.4	No
Umair Ahmed et al. [42]	River	Pakistan	Polynomial regression	Multi-layer perceptron (MLP)	4	Yes	Yes	7.9467	-	85.07
Proposed system	Rivers and lakes	India	ANFIS	FFNN	7	Yes	Yes	0.0029	96.17	100

summarizes the existing model results against our proposed system. There are various studies that used machine learning models for modelling and predicting WQ. Ahmed et al. [38] applied the FFNN model to predict WQI, and 25 parameters were used as input data. Gazzaz et al. [39] applied machine learning to predict WQI, and 23 input parameters were considered. Sakizadeh [40] employed 16 parameters. Rankovic et al. [41] proposed an artificial intelligence model to predict WQ using 10 input parameters. Umair Ahmed et al. [42] used various machine learning models for WQI and WQC, and four parameters were used as input data. It is noted that the polynomial regression model is good for predicting WQI, whereas the multi-layer perceptron (MLP) model is suitable for classifying WQC.

Although fewer parameters were used in this investigation, the results of this research are superior to others. Selecting few parameters is suitable for expensive real-time systems. In this study, seven significant parameters were used for modelling and predicting WQI, with superior results (having a very low error prediction (MSE = 0.00336), and a high value for the correlation regression (R = 96.17%).

Moreover, using the FFNN model, a system to detect WQC was developed with the highest accuracy (100%). The proposed method is presented to use only seven water quality parameters for predicting and classifying water quality, so the empirical results confirmed the effectiveness of the model, whereas previous research used machine learning models but with less accuracy.

This system can monitor drinking water and contaminated water with high accuracy. This study suggests that the combined approach of the artificial intelligence techniques proposed in the current study should be applied as a promising tool to accurately simulate water level and quality. The developed model has shown acceptable performance when compared with the available ones, as presented in Table 6.

The ultimate goal of this work is to serve and directly align with Sustainable Development Goal (SDG) 6, which aims to ensure access to clean water for all. The developed model can be used easily and inexpensively to predict water quality and index and thus water quality classification with high accuracy. In addition, this kind of model is robust and can forecast water contamination and thus guide the authorized governments/agencies to develop effective strategies for better water sustainability and management through the removal of the contamination source and/or seek for an alternative source of pure water to meet the community demand.

5. Conclusions

Modelling and predicting water quality using AI algorithms is very important for the protection of the environment. The artificial intelligence models were developed to predict and classify water quality for drinking by employing data from rivers collected from different locations in Indian states. WQI was applied to calculate seven important parameters: DO, pH, conductivity, biological oxygen demand, nitrate, fecal coliform, and total coliform. These were considered significant parameters for water quality. Developing new methodologies using advanced AI ANFIS algorithms can help ensure a safe environment. In this proposed methodology, advanced ANFIS algorithms were used to predict WQI. The FFNN algorithm was used to classify the WQC data. The proposed methodology was statistically evaluated and tested. The following conclusions can be drawn by using advanced AI to monitor WQ:

• First, the present study explored an alternative method of artificial intelligence to predict water quality by employing minimal and available water quality parameters. The datasets employed to conduct the research were acquired from different locations in India and contained 1679 samples from 666 different sources of rivers and lakes in the country. Artificial intelligence models were applied to predict and classify WQI.
• Second, an advanced AI ANFIS model can be developed to predict WQI by selecting important parameters from a standard dataset. Notably, prediction values were very close to the observation values.
• Third, machine learning algorithms, namely, FFNN and KNN, can be developed for WQC. The FFNN outperformed KNN in WQC. The classification results of FFNN were superior to those of the KNN algorithm.
• Fourth, the system will help reduce people’s consumption of poor-quality water and consequently curtail horrific diseases such as typhoid and diarrhea. In this case, our application can improve water pollution in different water bodies. The robustness and efficiency of the proposed model in predicting WQI can be examined in future works. The developed models can be implemented to predict the quality of different types of water in Saudi Arabia.