Variable Neighborhood Search for Major League Baseball Scheduling Problem
Abstract
1. Introduction
2. Literature Review
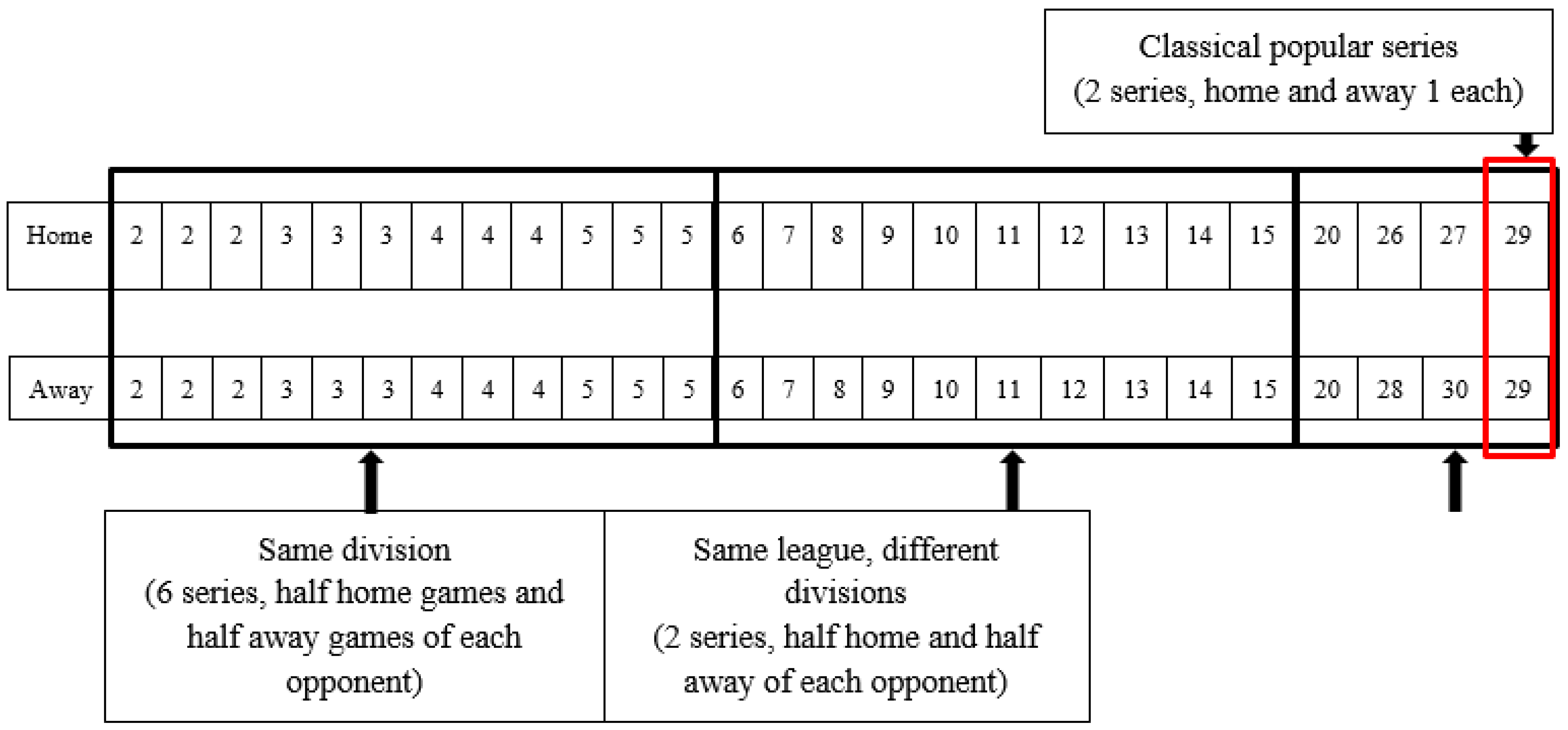
3. Problem Description and Formulation
4. Methodology
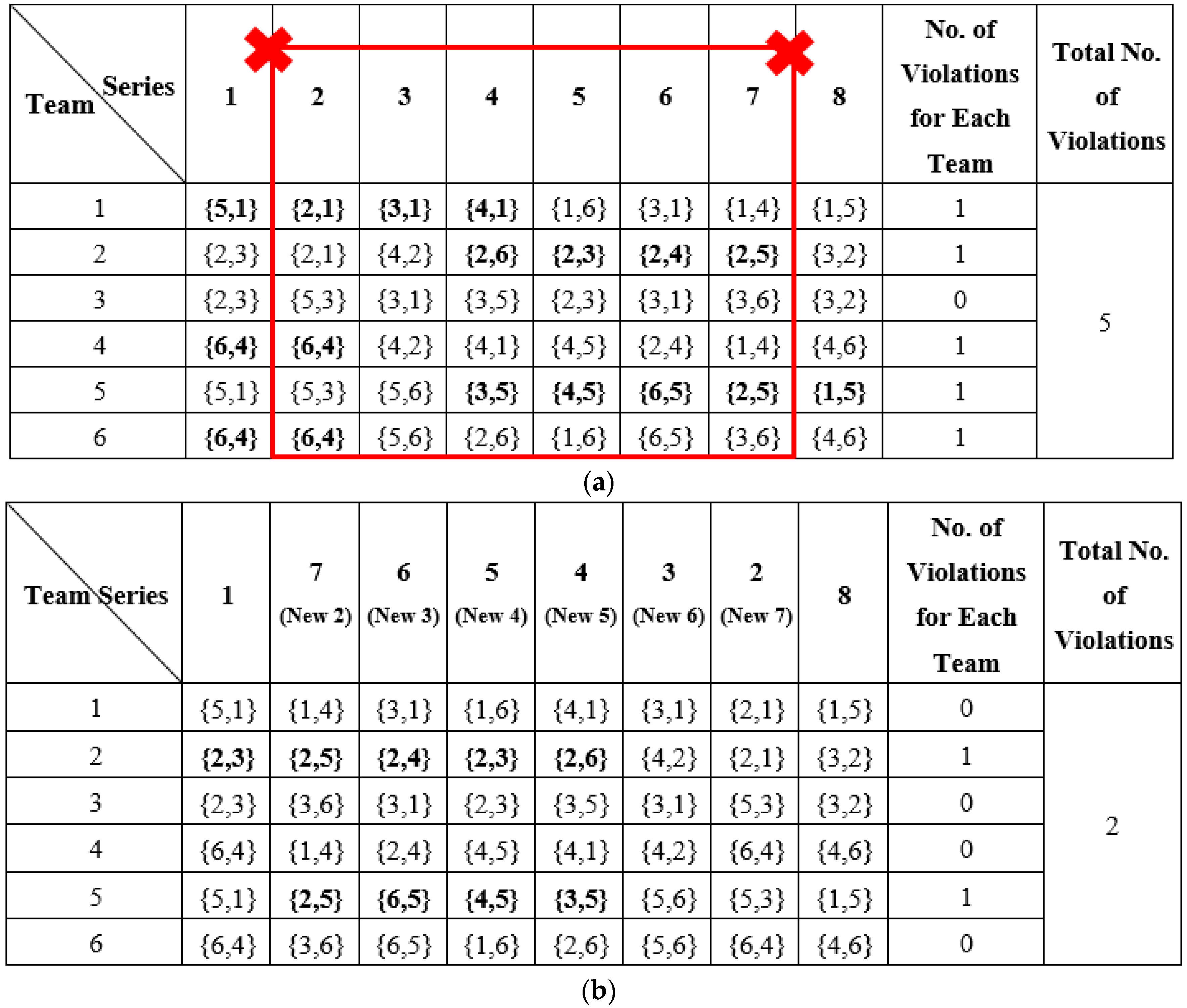
4.1. Initial Schedule Generation
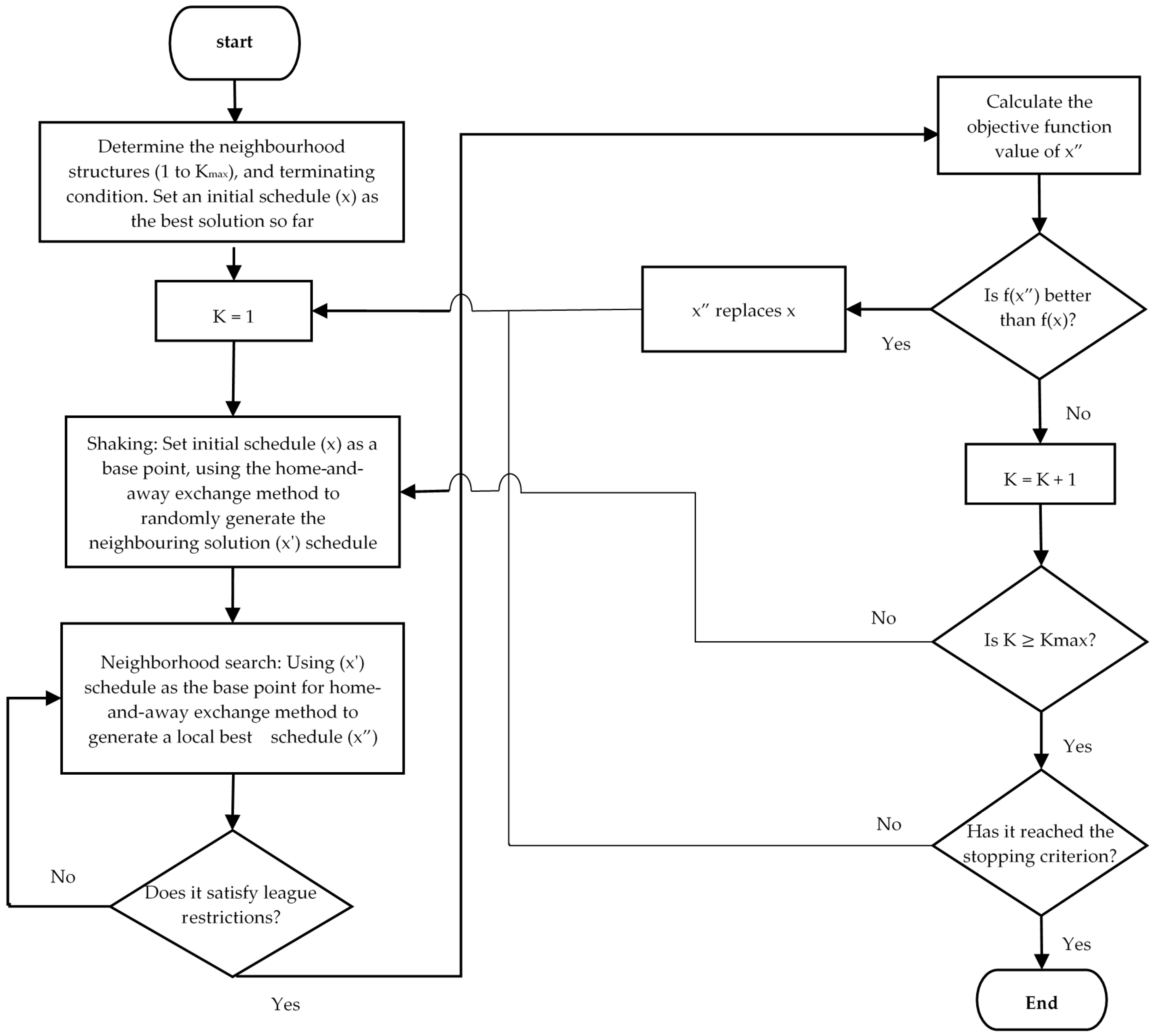
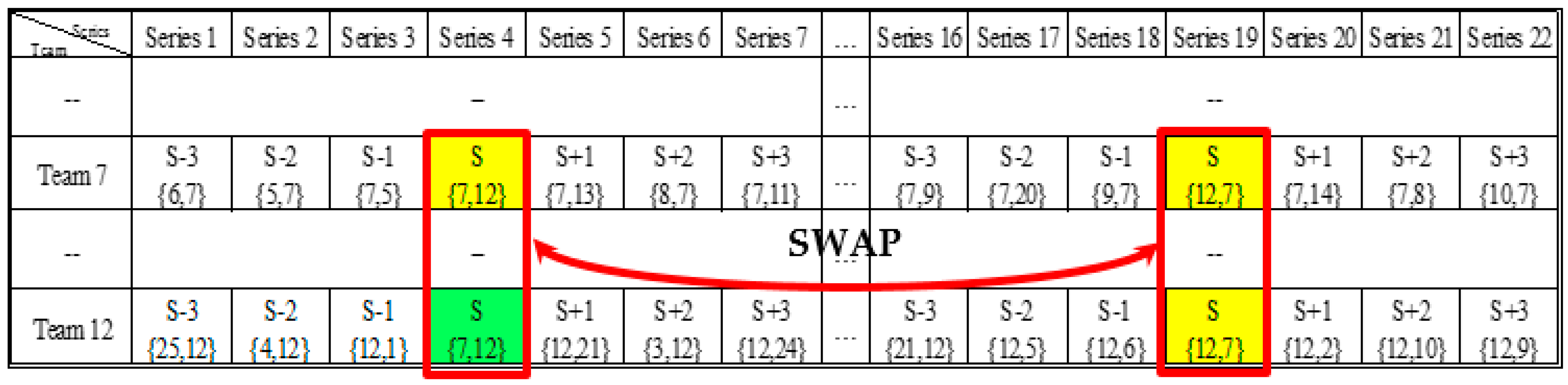
4.2. Schedule Optimization
5. Case Study Results and Discussions
5.1. Case Instance
5.2. Parameter Settings
5.3. Result Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bartsch, T.; Drexl, A.; Kröger, S. Scheduling the professional soccer leagues of Austria and Germany. Comput. Oper. Res. 2006, 33, 1907–1937. [Google Scholar] [CrossRef]
- Rasmussen, R.V.; Trick, M.A. A Benders approach for the constrained minimum break problem. Eur. J. Oper. Res. 2007, 177, 198–213. [Google Scholar] [CrossRef]
- Nurmi, K.; Goossens, D.; Bartsch, T.; Bonomo, F.; Briskorn, D.; Duran, G.; Kyngäs, J.; Marenco, J.; Ribeiro, C.C.; Spieksma, F.; et al. A Framework for a Highly Constrained Sports Scheduling Problem. In Proceedings of the International MultiConference of Engineers and Computer Scientists (IMECS 2010), Hong Kong, 17–19 March 2010; International Association of Engineers: London, UK, 2010; Volume III, pp. 1991–1997. [Google Scholar]
- Kendall, G.; Knust, S.; Ribeiro, C.C.; Urrutia, S. Scheduling in sports: An annotated bibliography. Comput. Oper. Res. 2010, 37, 1–19. [Google Scholar] [CrossRef]
- Ribeiro, C.C. Sports scheduling: Problems and applications. Int. Trans. Oper. Res. 2012, 19, 201–226. [Google Scholar] [CrossRef]
- Goossens, D.R.; Spieksma, F.C. Soccer Schedules in Europe: An Overview. J. Sched. 2012, 15, 641–651. [Google Scholar] [CrossRef]
- Wright, M.B. OR Analysis of Sporting Rules–A survey. Eur. J. Oper. Res. 2014, 232, 1–8. [Google Scholar] [CrossRef]
- Easton, K.; Nemhauser, G.; Trick, M. The traveling tournament problem description and benchmarks. In Proceedings of the 7th International Conference on Principles and Practice of Constraint Programming, Paphos, Cyprus, 26 November–1 December 2001; pp. 580–584. [Google Scholar]
- Anagnostopoulos, A.; Michel, L.; Van Hentenryck, P.; Vergados, Y. A simulated annealing approach to the traveling tournament problem. J. Sched. 2006, 9, 177–193. [Google Scholar] [CrossRef]
- Chen, P.-C.; Kendall, G.; Berghe, G.V. An Ant Based Hyper-heuristic for the Travelling Tournament Problem. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Scheduling (CI-Sched 2007), Honolulu, Hawaii, USA, 1–5 April 2007; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2007; pp. 19–26. [Google Scholar]
- Di Gaspero, L.; Schaerf, A. A composite-neighborhood tabu search approach to the traveling tournament problem. J. Heuristics 2007, 13, 189–207. [Google Scholar] [CrossRef]
- Trick, M.A. Sports Scheduling. Hybrid Optim. 2011, 45, 489–508. [Google Scholar]
- Cáceres, L.P.; Riff, M.C. AISTTP: An Artificial Immune Algorithm to Solve Traveling Tournament Problems. Int. J. Comput. Intell. Appl. 2012, 11, 1250008. [Google Scholar] [CrossRef]
- Januario, T.; Urrutia, S. A new neighborhood structure for round robin scheduling problems. Comput. Oper. Res. 2016, 70, 127–139. [Google Scholar] [CrossRef]
- Khelifa, M.; Boughaci, D. A Variable Neighborhood Search Method for Solving the Traveling Tournaments Problem. Electron. Notes Discret. Math. 2015, 47, 157–164. [Google Scholar] [CrossRef]
- Khelifa, M.; Boughaci, D. Hybrid harmony search combined with variable neighborhood search for the traveling tournament problem. In Proceedings of the International Conference on Computational Collective Intelligence, Halkidiki, Greece, 28–30 September 2016; Springer: Cham, Switzerland, 2016; pp. 520–530. [Google Scholar]
- Januario, T.; Urrutia, S.; Ribeiro, C.C.; De Werra, D. Edge coloring: A natural model for sports scheduling. Eur. J. Oper. Res. 2016, 254, 1–8. [Google Scholar] [CrossRef]
- Alarcón, F.; Durán, G.; Guajardo, M.; Miranda, J.; Muñoz, H.; Ramírez, L.; Ramírez, M.; Sauré, D.; Siebert, M.; Souyris, S.; et al. Operations Research Transforms the Scheduling of Chilean Soccer Leagues and South American World Cup Qualifiers. Interfaces 2017, 47, 52–69. [Google Scholar] [CrossRef]
- Khelifa, M.; Boughaci, D.; Aimeur, E. An enhanced genetic algorithm with a new crossover operator for the traveling tournament problem. In Proceedings of the 2017 4th International Conference on Control, Decision and Information Technologies (CoDIT), Barcelona, Spain, 5–7 April 2017; Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2017; pp. 1072–1077. [Google Scholar]
- Durán, G.; Guajardo, M.; Sauré, D. Scheduling the South American Qualifiers to the 2018 FIFA World Cup by integer programming. Eur. J. Oper. Res. 2017, 262, 1109–1115. [Google Scholar] [CrossRef]
- Durán, G. Sports scheduling and other topics in sports analytics: A survey with special reference to Latin America. Top 2021, 29, 125–155. [Google Scholar] [CrossRef]
- Trick, M.A.; Yildiz, H. Benders’ cuts guided large neighborhood search for the traveling umpire problem. Nav. Res. Logist. 2011, 58, 771–781. [Google Scholar] [CrossRef]
- Trick, M.A.; Yildiz, H. Locally Optimized Crossover for the Traveling Umpire Problem. Eur. J. Oper. Res. 2012, 216, 286–292. [Google Scholar] [CrossRef]
- Trick, M.A.; Yildiz, H.; Yunes, T. Scheduling Major League Baseball Umpires and the Traveling Umpire Problem. Interfaces 2012, 42, 232–244. [Google Scholar] [CrossRef][Green Version]
- Xue, L.; Luo, Z.; Lim, A. Two exact algorithms for the traveling umpire problem. Eur. J. Oper. Res. 2015, 243, 932–943. [Google Scholar] [CrossRef]
- Toffolo, T.A.M.; Christiaens, J.; Spieksma, F.C.R.; Berghe, G.V. The sport teams grouping problem. Ann. Oper. Res. 2017, 275, 223–243. [Google Scholar] [CrossRef]
- Westphal, S. Scheduling the German Basketball League. Interfaces 2014, 44, 498–508. [Google Scholar] [CrossRef]
- Goossens, D. Optimization in Sports League Scheduling: Experiences from the Belgian Pro League Soccer. In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems, Funchal, Madeira, Portugal, 24–26 January 2018; Springer: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Günneç, D.; Demir, E. Fair-fixture: Minimizing carry-over effects in football leagues. J. Ind. Manag. Optim. 2019, 15, 1565–1577. [Google Scholar] [CrossRef]
- Çavdaroğlu, B.; Atan, T. Determining matchdays in sports league schedules to minimize rest differences. Oper. Res. Lett. 2020, 48, 209–216. [Google Scholar] [CrossRef]
- Gotzes, U.; Hoppmann, K. Bounding the final rank during a round robin tournament with integer programming. Oper. Res. 2020, 1–9. [Google Scholar] [CrossRef]
- Lambrechts, E.; Ficker, A.M.C.; Goossens, D.R.; Spieksma, F.C.R. Round-robin tournaments generated by the Circle Method have maximum carry-over. Math. Program. 2018, 172, 277–302. [Google Scholar] [CrossRef]
- Melouk, S.H.; Keskin, B.B. Team assignments and scheduling for the NCAA basketball tournament. J. Oper. Res. Soc. 2012, 63, 620–630. [Google Scholar] [CrossRef]
- Nemhauser, G.L.; Trick, M.A. Scheduling A Major College Basketball Conference. Oper. Res. 1998, 46, 1–8. [Google Scholar] [CrossRef]
- Henz, M. Scheduling a Major College Basketball Conference—Revisited. Oper. Res. 2001, 49, 163–168. [Google Scholar] [CrossRef][Green Version]
- Faella, M.; Sauro, L. Irrelevant matches in round-robin tournaments. Auton. Agents Multi-Agent Syst. 2021, 35, 1–34. [Google Scholar] [CrossRef]
- Robinson, L.W. Baseball playoff eliminations: An application of linear programming. Oper. Res. Lett. 1991, 10, 67–74. [Google Scholar] [CrossRef]
- Gusfield; Martel The Structure and Complexity of Sports Elimination Numbers. Algorithmica 2002, 32, 73–86. [CrossRef]
- Rutjanisarakul, T.; Jiarasuksakun, T. A Sport Tournament Scheduling by Genetic Algorithm with Swapping Method. arXiv 2017, arXiv:1704.04879. [Google Scholar]
- Raof, A.R.A.; Sudin, S.; Mahrom, N.; Rosli, A.N.C. Sport Tournament Automated Scheduling System. MATEC Web Conf. EDP Sci. 2018, 150, e05027. [Google Scholar] [CrossRef]
- Della Croce, F.; Dragotto, G.; Scatamacchia, R. On fairness and diversification in WTA and ATP tennis tournaments generation. Ann. Oper. Res. 2020, 1–13. [Google Scholar] [CrossRef]
- Burrows, W.; Tuffley, C. Maximising Common Fixtures in a Round Robin Tournament with Two Divisions. arXiv 2015, arXiv:1502.06664. [Google Scholar]
- Davari, M.; Goossens, D.; Beliën, J.; Lambers, R.; Spieksma, F.C. The multi-league sports scheduling problem, or how to schedule thousands of matches. Oper. Res. Lett. 2020, 48, 180–187. [Google Scholar] [CrossRef]
- Lim, A.; Rodrigues, B.; Zhang, X. A simulated annealing and hill-climbing algorithm for the traveling tournament problem. Eur. J. Oper. Res. 2006, 174, 1459–1478. [Google Scholar] [CrossRef]
- Wright, M. Scheduling fixtures for Basketball New Zealand. Comput. Oper. Res. 2006, 33, 1875–1893. [Google Scholar] [CrossRef]
- Van Hentenryck, P.; Vergados, Y. Population-Based Simulated Annealing for Traveling Tournaments. In Proceedings of the 22nd National Conference on Artificial Intelligence, Vancouver, Canada, 22–26 July 2007; AAAI Press: Palo Alto, CA, USA, 2007; pp. 267–272. [Google Scholar]
- Khelifa, M.; Boughaci, D. A Cooperative Local Search Method for Solving the Traveling Tournament Problem. Comput. Inform. 2019, 37, 1386–1410. [Google Scholar] [CrossRef]
- Van Bulck, D.; Goossens, D.R.; Spieksma, F.C.R. Scheduling a non-professional indoor football league: A tabu search based approach. Ann. Oper. Res. 2018, 275, 715–730. [Google Scholar] [CrossRef]
- Uthus, D.C.; Riddle, P.J.; Guesgen, H.W. An ant colony optimization approach to the traveling tournament problem. In Proceedings of the 11th Annual Conference on Genetic and Evolutionary Computation—GECCO ’09, Montreal, Canada, 8–12 July 2009; ACM: New York, NY, USA, 2009; pp. 81–88. [Google Scholar]
- Guiqian, T. The Optimization of Professional Sporting Management System Based on Gene Algorithm. In Advanced Technology in Teaching, Proceedings of the 2009 3rd International Conference on Teaching and Computational Science (WTCS 2009), Shenzhen, China, 19–20 December 2009; Advances in Intelligent and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2012; Volume 116, pp. 679–687. [Google Scholar]
- Biajoli, F.L.; Lorena, L.A.N. Clustering search approach for the traveling tournament problem. In Advances in Artificial Intelligence. Lecture Notes in Computer Science; Gelbukh, A., Kuri Morales, Á.F., Eds.; Springer: Berlin, Heidelberg, Germany, 2007; Volume 4827, pp. 83–93. [Google Scholar]
- Russell, R.A.; Leung, J.M.Y. Devising a Cost Effective Schedule for a Baseball League. Oper. Res. 1994, 42, 614–625. [Google Scholar] [CrossRef]
- Hoshino, R.; Kawarabayashi, K.I. A Multi-round Generalization of the Traveling Tournament Problem and its Application to Japanese Baseball. Eur. J. Oper. Res. 2011, 215, 481–497. [Google Scholar] [CrossRef]
- Hoshino, R.; Kawarabayashi, K.I. Generating Approximate Solutions to the TTP using a Linear Distance Relaxa-tion. J. Artif. Intell. Res. 2012, 45, 257–286. [Google Scholar] [CrossRef]
- Yeh, C.W. Tabu search algorithm for major league baseball scheduling. Master’s Thesis, Department of Industrial Engineering and Management, Yuan Ze University, Taoyuan City, Taiwan, 2013. [Google Scholar]
- Lin, W.-B.; Chen, M.-Y. A study of efficiency monitoring systems for match-fixing players in the Chinese Professional Baseball League. Eur. Sport Manag. Q. 2015, 15, 301–322. [Google Scholar] [CrossRef]
- Ko, Y.D.; Jung, S.H.; Kim, S.H.; Lee, S.W. Sustainable Sport Scheduling Approach Considering Team Equity for the Korean Professional Baseball League. Sustainability 2018, 10, 429. [Google Scholar] [CrossRef]
- Kim, T. Optimal approach to game scheduling of multiple round-robin tournament: Korea professional baseball league in focus. Comput. Ind. Eng. 2019, 136, 95–105. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N. An Introduction to Variable Neighbourhood Search. Metaheuristic; Springer: Boston, MA, USA, 1999; pp. 433–458. [Google Scholar]
- Mladenović, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]

| League | Division | Team |
|---|---|---|
| American | East | Baltimore Orioles |
| Boston Red Sox | ||
| New York Yankees | ||
| Tampa Bay Rays | ||
| Toronto Blue Jays | ||
| Central | Chicago White Sox | |
| Cleveland Indians | ||
| Detroit Tigers | ||
| Kansas City Royals | ||
| Minnesota Twins | ||
| West | Houston Astros | |
| Los Angeles Angels | ||
| Oakland Athletics | ||
| Seattle Mariners | ||
| Texas Rangers | ||
| National | East | Atlanta Braves |
| Miami Marlins | ||
| New York Mets | ||
| Philadelphia Phillies | ||
| Washington Nationals | ||
| Central | Chicago Cubs | |
| Cincinnati Reds | ||
| Milwaukee Brewers | ||
| Pittsburgh Pirates | ||
| St. Louis Cardinals | ||
| West | Arizona Diamondbacks | |
| Colorado Rockies | ||
| Los Angeles Dodgers | ||
| San Diego Padres | ||
| San Francisco Giants |
| Source | DF | SS | MS | F-Value | p-Value |
|---|---|---|---|---|---|
| VNS Type | 1 | 1.56322 × 1012 | 1.56322 × 1012 | 7807.68 | 0.000 |
| Error | 142 | 2.84306 × 1010 | 2.00215 × 108 | ||
| Total | 143 | 1.59165 × 1012 | |||
| S = 14150 R-Sq = 98.21% R-Sq(adj) = 98.20% | |||||
| Source | DF | SS | MS | F-Value | p-Value |
| VNS-I_Shaking | 2 | 2.81981 × 109 | 1.40990 × 109 | 16.36 | 0.000 |
| Error | 69 | 5.94718 × 109 | 8.61910 × 107 | ||
| Total | 71 | 8.76699 × 109 | |||
| S = 9284 R-Sq = 32.16% R-Sq(adj) = 30.20% | |||||
| Source | DF | SS | MS | F-Value | p-Value |
| VNS-II_No. N. S. 1 | 2 | 3.01533 × 109 | 1.50767 × 109 | 6.25 | 0.003 |
| Error | 69 | 1.66483 × 1010 | 2.41279 × 108 | ||
| Total | 71 | 1.96636 × 1010 | |||
| S = 15533 R-Sq = 15.33% R-Sq(adj) = 12.88% | |||||
| Source | DF | SS | MS | F-Value | p-Value |
| VNS-II_N1 | 5 | 5.21903 × 109 | 1.04381 × 109 | 4.77 | 0.001 |
| Error | 66 | 1.44446 × 1010 | 2.18857 × 108 | ||
| Total | 71 | 1.96636 × 1010 | |||
| S = 13366 R-Sq = 38.22% R-Sq(adj) = 35.49% | |||||
| Source | DF | SS | MS | F-Value | p-Value |
| VNS-II_N2 | 5 | 7.51511 × 109 | 2.50504 × 109 | 14.02 | 0.000 |
| Error | 66 | 1.21485 × 1010 | 1.78654 × 108 | ||
| Total | 71 | 1.96636 × 1010 | |||
| Source | DF | SS | MS | F-Value | p-Value |
| VNS-II_N3 | 5 | 3.23669 × 109 | 6.47337 × 108 | 2.60 | 0.033 |
| Error | 66 | 1.64269 × 1010 | 2.48892 × 108 | ||
| Total | 71 | 1.96636 × 1010 | |||
| S = 15776 R-Sq = 16.46% R-Sq(adj) = 10.13% | |||||
| Parameter | VNS-I | VNS-II |
|---|---|---|
| Number of Shakings | 50 | 1 |
| Number of Neighboring Solutions | 100 | 50 |
| Number of Neighborhoods (Kmax) | 3 | 3 |
| Neighborhood Structure (N1) | 5 teams | 1 team |
| Neighborhood structure (N2) | 10 teams | 5 teams |
| Neighborhood structure (N3) | 15 teams | 10 teams |
| Stopping criterion | Max. No. of Iterations = 60,000 | |
| Number of runs | 10 | |
| Team | MLB 2016 Schedule | VNS-I | VNS-II | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Avg. | Best | Avg. Gap (%) | Best Gap (%) | Avg. | Best | Avg. Gap (%) | Best Gap (%) | ||
| Baltimore Orioles | 37,803 | 47,301 | 38,408 | 25.12 | 1.60 | 40,608 | 37,367 | 7.42 | −1.15 |
| Boston Red Sox | 44,846 | 52,571 | 52,456 | 17.23 | 16.97 | 43,987 | 41,584 | −1.92 | −7.27 |
| New York Yankees | 41,135 | 44,986 | 44,576 | 9.36 | 8.37 | 41,903 | 40,972 | 1.87 | −0.40 |
| Tampa Bay Rays | 44,004 | 55,200 | 58,443 | 25.44 | 32.81 | 43,683 | 42,013 | −0.73 | −4.52 |
| Toronto Blue Jays | 51,993 | 58,109 | 53,295 | 11.76 | 2.50 | 48,473 | 51,584 | −6.77 | −0.79 |
| Chicago White Sox | 31,236 | 35,675 | 37,654 | 14.21 | 20.55 | 31,396 | 30,705 | 0.51 | −1.70 |
| Cleveland Indians | 30,445 | 33,718 | 29,758 | 10.75 | −2.26 | 30,128 | 29,120 | −1.04 | −4.35 |
| Detroit Tigers | 30,907 | 35,293 | 33,611 | 14.19 | 8.75 | 29,930 | 30,956 | −3.16 | 0.16 |
| Minnesota Twins | 34,919 | 38,143 | 37,780 | 9.23 | 8.19 | 34,212 | 34,037 | −2.02 | −2.53 |
| Kansas City Royals | 35,294 | 37,640 | 37,123 | 6.65 | 5.18 | 34,265 | 34,784 | −2.92 | −1.45 |
| Houston Astros | 46,728 | 54,729 | 59,696 | 17.12 | 27.75 | 44,898 | 41,686 | −3.92 | −10.79 |
| Los Angeles Angels | 53,971 | 61,335 | 57,801 | 13.64 | 7.10 | 52,154 | 51,311 | −3.37 | −4.93 |
| Oakland Athletics | 49,342 | 63,922 | 54,734 | 29.55 | 10.93 | 51,494 | 48,913 | 4.36 | −0.87 |
| Seattle Mariners | 58,909 | 68,710 | 66,227 | 16.64 | 12.42 | 59,642 | 57,200 | 1.24 | −2.90 |
| Texas Rangers | 49,390 | 50,948 | 49,098 | 3.15 | −0.59 | 44,649 | 45,074 | −9.60 | −8.74 |
| Atlanta Braves | 33,826 | 41,702 | 42,894 | 23.28 | 26.81 | 34,748 | 33,948 | 2.73 | 0.36 |
| New York Mets | 41,003 | 49,457 | 51,546 | 20.62 | 25.71 | 38,554 | 37,154 | −5.97 | −9.39 |
| Miami Marlins | 31,211 | 41,560 | 44,343 | 33.16 | 42.07 | 32,784 | 32,503 | 5.04 | 4.14 |
| Philadelphia Phillies | 33,398 | 40,636 | 41,324 | 21.67 | 23.73 | 30,298 | 30,197 | −9.28 | −9.58 |
| Washington Nationals | 28,557 | 36,587 | 35,516 | 28.12 | 24.37 | 29,267 | 28,390 | 2.49 | −0.58 |
| Chicago Cubs | 28,184 | 36,211 | 37,321 | 28.48 | 32.42 | 29,397 | 29,056 | 4.30 | 3.09 |
| Cincinnati Reds | 28,956 | 35,377 | 33,955 | 22.18 | 17.26 | 28,529 | 28,704 | −1.47 | −0.87 |
| Milwaukee Brewers | 30,350 | 38,242 | 38,823 | 26.00 | 27.92 | 31,421 | 30,140 | 3.53 | −0.69 |
| Pittsburgh Pirates | 30,425 | 39,632 | 41,773 | 30.26 | 37.30 | 30,493 | 30,781 | 0.22 | 1.17 |
| St. Louis Cardinals | 30,753 | 38,264 | 39,716 | 24.42 | 29.15 | 31,892 | 31,003 | 3.70 | 0.81 |
| Arizona Diamondbacks | 42,220 | 51,811 | 51,221 | 22.72 | 21.32 | 41,904 | 41,829 | −0.75 | −0.93 |
| Colorado Rockies | 39,051 | 51,181 | 39,402 | 31.06 | 0.90 | 39,607 | 39,697 | 1.42 | 1.65 |
| Los Angeles Dodgers | 48,245 | 53,286 | 50,780 | 10.45 | 5.25 | 47,615 | 46,589 | −1.31 | −3.43 |
| San Diego Padres | 46,125 | 55,377 | 51,893 | 20.06 | 12.51 | 46,062 | 46,401 | −0.14 | 0.60 |
| San Francisco Giants | 45,795 | 58,373 | 56,229 | 27.47 | 22.78 | 45,299 | 46,098 | −1.08 | 0.66 |
| Total Distance | 1,179,021 | 1,405,976 | 1,367,396 | 19.25 | 13.78 | 1,169,292 | 1,149,796 | −0.83 | −2.48 |
| Average distance | 39,301 | 46,866 | 45,580 | 19.25 | 13.78 | 38,976 | 38,327 | −0.83 | −2.48 |
| Standard Deviation | 8592 | 9700 | 9122 | 12.89 | 5.81 | 8197 | 7986 | −4.60 | −7.06 |
| Max Distance | 58,909 | 68,710 | 66,227 | 59,642 | 57,200 | ||||
| Min Distance | 28,184 | 33,718 | 29,758 | 28,529 | 28,390 | ||||
| Team | MLB 2019 Schedule | VNS-I | VNS-II | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Avg. | Best | Avg. Gap (%) | Best Gap (%) | Avg. | Best | Avg. Gap (%) | Best Gap (%) | ||
| Baltimore Orioles | 34,070 | 47,301 | 38,408 | 38.83 | 12.73 | 40,608 | 37,367 | 19.19 | 9.68 |
| Boston Red Sox | 39,657 | 52,571 | 52,456 | 32.56 | 32.27 | 43,987 | 41,584 | 10.92 | 4.86 |
| New York Yankees | 35,317 | 44,986 | 44,576 | 27.38 | 26.22 | 41,903 | 40,972 | 18.65 | 16.01 |
| Tampa Bay Rays | 50,374 | 55,200 | 58,443 | 9.58 | 16.02 | 43,683 | 42,013 | −13.28 | −16.60 |
| Toronto Blue Jays | 56,357 | 58,109 | 53,295 | 3.11 | −5.43 | 48,473 | 51,584 | −13.99 | −8.47 |
| Chicago White Sox | 33,102 | 35,675 | 37,654 | 7.77 | 13.75 | 31,396 | 30,705 | −5.15 | −7.24 |
| Cleveland Indians | 35,216 | 33,718 | 29,758 | −4.25 | −15.50 | 30,128 | 29,120 | −14.45 | −17.31 |
| Detroit Tigers | 29,360 | 35,293 | 33,611 | 20.21 | 14.48 | 29,930 | 30,956 | 1.94 | 5.44 |
| Minnesota Twins | 37,802 | 38,143 | 37,780 | 0.90 | −0.06 | 34,212 | 34,037 | −9.50 | −9.96 |
| Kansas City Royals | 36,627 | 37,640 | 37,123 | 2.77 | 1.35 | 34,265 | 34,784 | −6.45 | −5.03 |
| Houston Astros | 46,755 | 54,729 | 59,696 | 17.05 | 27.68 | 44,898 | 41,686 | −3.97 | −10.84 |
| Los Angeles Angels | 50,407 | 61,335 | 57,801 | 21.68 | 14.67 | 52,154 | 51,311 | 3.47 | 1.79 |
| Oakland Athletics | 52,523 | 63,922 | 54,734 | 21.70 | 4.21 | 51,494 | 48,913 | −1.96 | −6.87 |
| Seattle Mariners | 55,161 | 68,710 | 66,227 | 24.56 | 20.06 | 59,642 | 57,200 | 8.12 | 3.70 |
| Texas Rangers | 46,093 | 50,948 | 49,098 | 10.53 | 6.52 | 44,649 | 45,074 | −3.13 | −2.21 |
| Atlanta Braves | 38,157 | 41,702 | 42,894 | 9.29 | 12.41 | 34,748 | 33,948 | −8.93 | −11.03 |
| New York Mets | 46,374 | 49,457 | 51,546 | 6.65 | 11.15 | 38,554 | 37,154 | −16.86 | −19.88 |
| Miami Marlins | 39,029 | 41,560 | 44,343 | 6.48 | 13.62 | 32,784 | 32,503 | −16.00 | −16.72 |
| Philadelphia Phillies | 33,665 | 40,636 | 41,324 | 20.71 | 22.75 | 30,298 | 30,197 | −10.00 | −10.30 |
| Washington Nationals | 36,546 | 36,587 | 35,516 | 0.11 | −2.82 | 29,267 | 28,390 | −19.92 | −22.32 |
| Chicago Cubs | 32,065 | 36,211 | 37,321 | 12.93 | 16.39 | 29,397 | 29,056 | −8.32 | −9.38 |
| Cincinnati Reds | 33,516 | 35,377 | 33,955 | 5.55 | 1.31 | 28,529 | 28,704 | −14.88 | −14.36 |
| Milwaukee Brewers | 34,060 | 38,242 | 38,823 | 12.28 | 13.98 | 31,421 | 30,140 | −7.75 | −11.51 |
| Pittsburgh Pirates | 36,323 | 39,632 | 41,773 | 9.11 | 15.00 | 30,493 | 30,781 | −16.05 | −15.26 |
| St. Louis Cardinals | 31,735 | 38,264 | 39,716 | 20.57 | 25.15 | 31,892 | 31,003 | 0.49 | −2.31 |
| Arizona Diamondbacks | 43,262 | 51,811 | 51,221 | 19.76 | 18.40 | 41,904 | 41,829 | −3.14 | −3.31 |
| Colorado Rockies | 35,568 | 51,181 | 39,402 | 43.90 | 10.78 | 39,607 | 39,697 | 11.36 | 11.61 |
| Los Angeles Dodgers | 43,275 | 53,286 | 50,780 | 23.13 | 17.34 | 47,615 | 46,589 | 10.03 | 7.66 |
| San Diego Padres | 50,478 | 55,377 | 51,893 | 9.71 | 2.80 | 46,062 | 46,401 | −8.75 | −8.08 |
| San Francisco Giants | 50,592 | 58,373 | 56,229 | 15.38 | 11.14 | 45,299 | 46,098 | −10.46 | −8.88 |
| Total Distance | 1,223,466 | 1,405,976 | 1,367,396 | 14.92 | 11.76 | 1,169,292 | 1,149,796 | −4.43 | −6.02 |
| Average distance | 40,782 | 46,866 | 45,580 | 14.92 | 11.76 | 38,976 | 38,327 | −4.43 | −6.02 |
| Standard Deviation | 7820 | 9700 | 9122 | 26.15 | 18.63 | 8197 | 7986 | 6.60 | 3.85 |
| Max Distance | 56,357 | 68,710 | 66,227 | 59,642 | 57,200 | ||||
| Min Distance | 29,360 | 33,718 | 29,758 | 28,529 | 28,390 | ||||
| Number of Iterations | VNS-I | VNS-II |
|---|---|---|
| 1 | 1,519,607 | 1,525,334 |
| 10,000 | 1,389,212 | 1,163,451 |
| 20,000 | 1,386,232 | 1,150,402 |
| 30,000 | 1,385,316 | 1,150,402 |
| 40,000 | 1,379,673 | 1,149,796 |
| 50,000 | 1,373,940 | 1,149,796 |
| 60,000 | 1,367,396 | 1,149,796 |
| CPU time (seconds) | 646 | 720 |
| Initial solution distance (miles) | 1,519,607 | 1,525,334 |
| Distance after optimization (miles) | 1,367,396 | 1,149,796 |
| Improvement from the initial solution (%) | 10.02% | 24.62% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.-C.; Lin, Y.-Y.; Chen, A.H.-L.; Chen, W.-S. Variable Neighborhood Search for Major League Baseball Scheduling Problem. Sustainability 2021, 13, 4000. https://doi.org/10.3390/su13074000
Liang Y-C, Lin Y-Y, Chen AH-L, Chen W-S. Variable Neighborhood Search for Major League Baseball Scheduling Problem. Sustainability. 2021; 13(7):4000. https://doi.org/10.3390/su13074000
Chicago/Turabian StyleLiang, Yun-Chia, Yen-Yu Lin, Angela Hsiang-Ling Chen, and Wei-Sheng Chen. 2021. "Variable Neighborhood Search for Major League Baseball Scheduling Problem" Sustainability 13, no. 7: 4000. https://doi.org/10.3390/su13074000
APA StyleLiang, Y.-C., Lin, Y.-Y., Chen, A. H.-L., & Chen, W.-S. (2021). Variable Neighborhood Search for Major League Baseball Scheduling Problem. Sustainability, 13(7), 4000. https://doi.org/10.3390/su13074000






