Multimodal Data Based Regression to Monitor Air Pollutant Emission in Factories
Abstract
1. Introduction
- Our paper firstly discovers the linear relationship between the air pollutant (PM 2.5) and the energy consumption in a factory (Section 3 Preliminary Study), which is monitored by the power plant and government and cannot be modified by factory owners. Despite the difficulty to collect the true emission of pollutants, the indirect factors (energy consumption) are usually easy to obtain. The intuition is that we could recover the missing or mislabeled air quality values from those indirect features, which is referred to as Single-location recovery. Supporting vector regression (SVR) model is used to establish the relationship between the emission of pollutants and the indirect factors of energy consumption and material balance. Specifically, we use the data to train the SVM model and then apply this model to estimate the emission of pollutants of a factory given the indirect factors of this factory.
- To further improve the precision of air pollutant emission estimation, we combine the spatial interpolation based multiple-location recovery model and the single-location recovery model to obtain the precise air pollutant emission estimation. Specifically, we apply the gaussian process regression (GPR) model to generate an accurate air quality map at each timestamp and recover the missing or mislabeled air quality values at unknown locations. To combine the recovered air quality values from the above mentioned two models, a weighted scheme is applied.
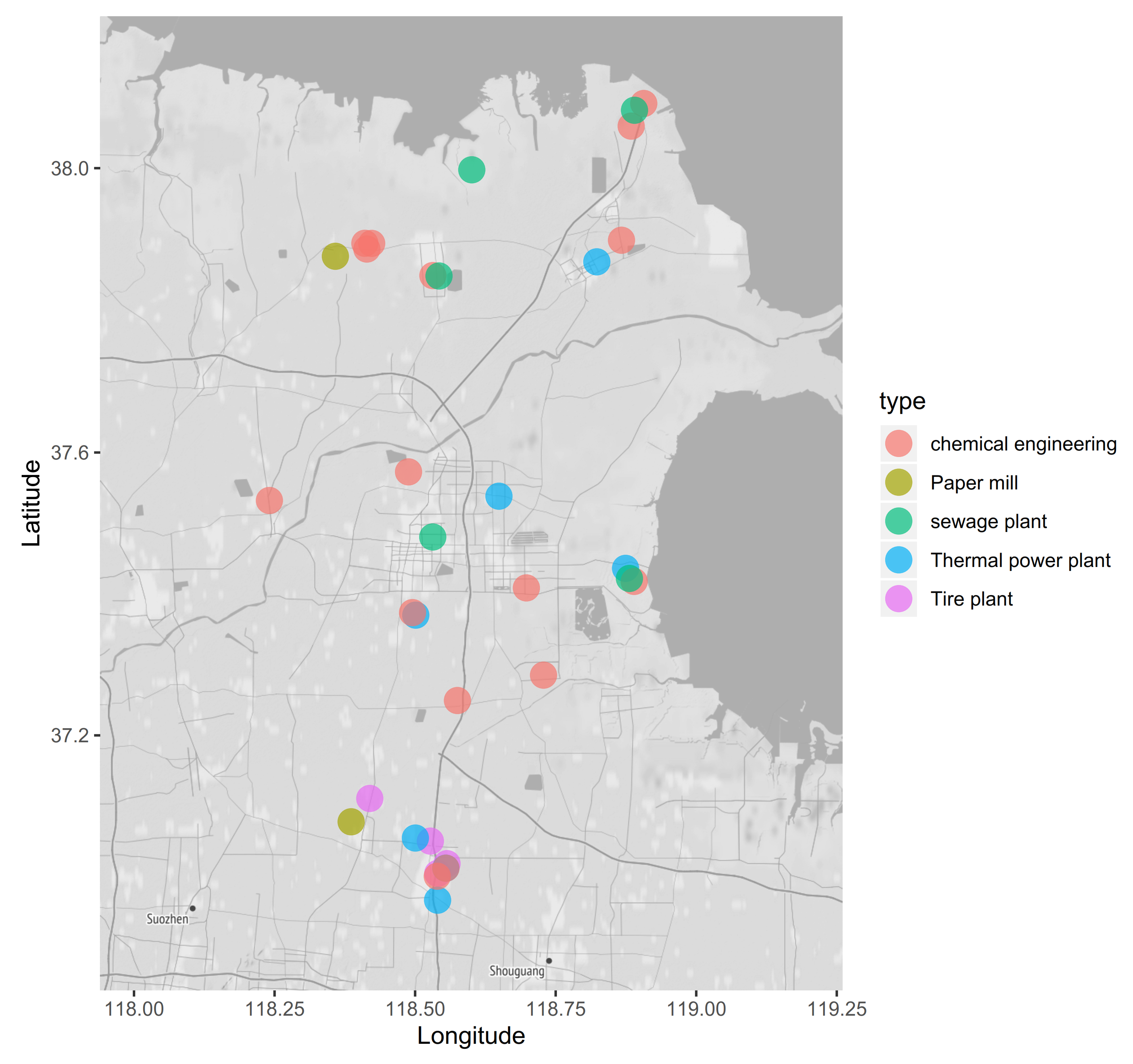
- We evaluate the proposed models using real-world data in Shandong Province, China, which contains 33 factories categorized into 5 types and each has a co-located air quality monitoring station. We also compare our model with the existing spatial interpolation based models and evaluate our model under different seasons. To the best of our knowledge, this paper is the first data-driven pollution emission estimation model for Chinese factories.
2. Literature Review
3. Preliminary Study
- Single-location recovery. Given the local factory production data, such as Total energy consumption, Water, Desalted water, Electricity, Steam, Plant-wide fuel, Natural gas, Refinery dry gas, etc., we can find a function to estimate the air pollution levels from those indirect data. Namely, Predicting the missing air quality readings at a target location from those indirect factory production features, which are strongly correlated to the local air pollution emission. We denote this approach as Single-location recovery.
- Multiple-location recovery. We can also borrow the idea from the air quality spatial interpolation research area. Assuming that the air quality readings at a target location are missing, but accurate air quality readings from surrounding locations are available, we can apply the spatial interpolation method to predict the air quality readings from all other available and accurate data. Based on this intuition, we name this method as Multiple-location recovery.
- The overall relationship between PM 2.5 and energy consumption is positive-related, namely, more energy consumption leads to more produced air pollution.
- Using single-location indirect features, such as energy consumtion, is not enough to recover the air quality readings accurately and reliably.
4. Methods
4.1. Support Vector Regression for Single-Location Recovery
4.2. Gaussian Process Regression for Multiple-Location Recovery
4.3. Combined Model
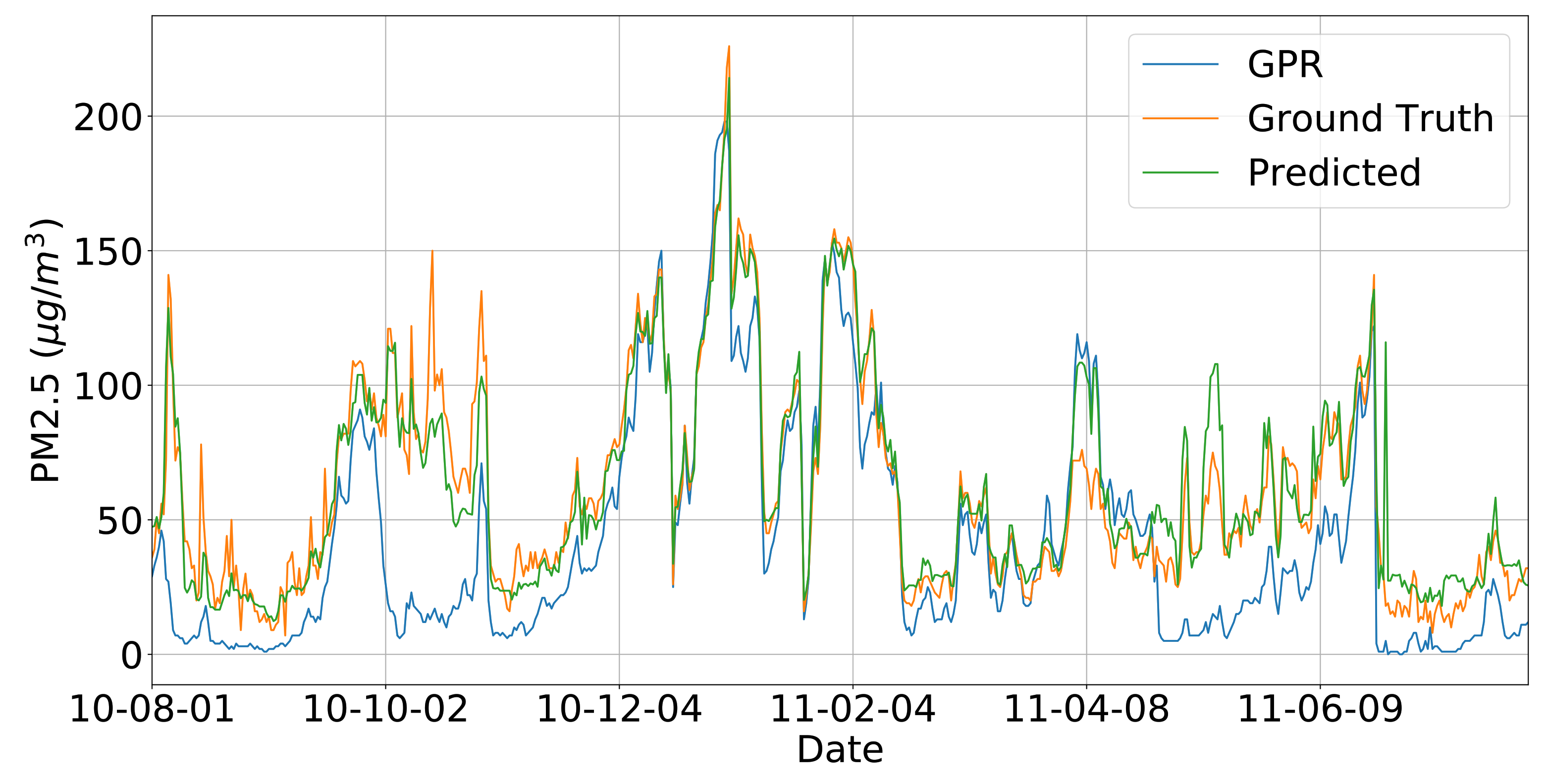
5. Results
5.1. Dataset and Setup
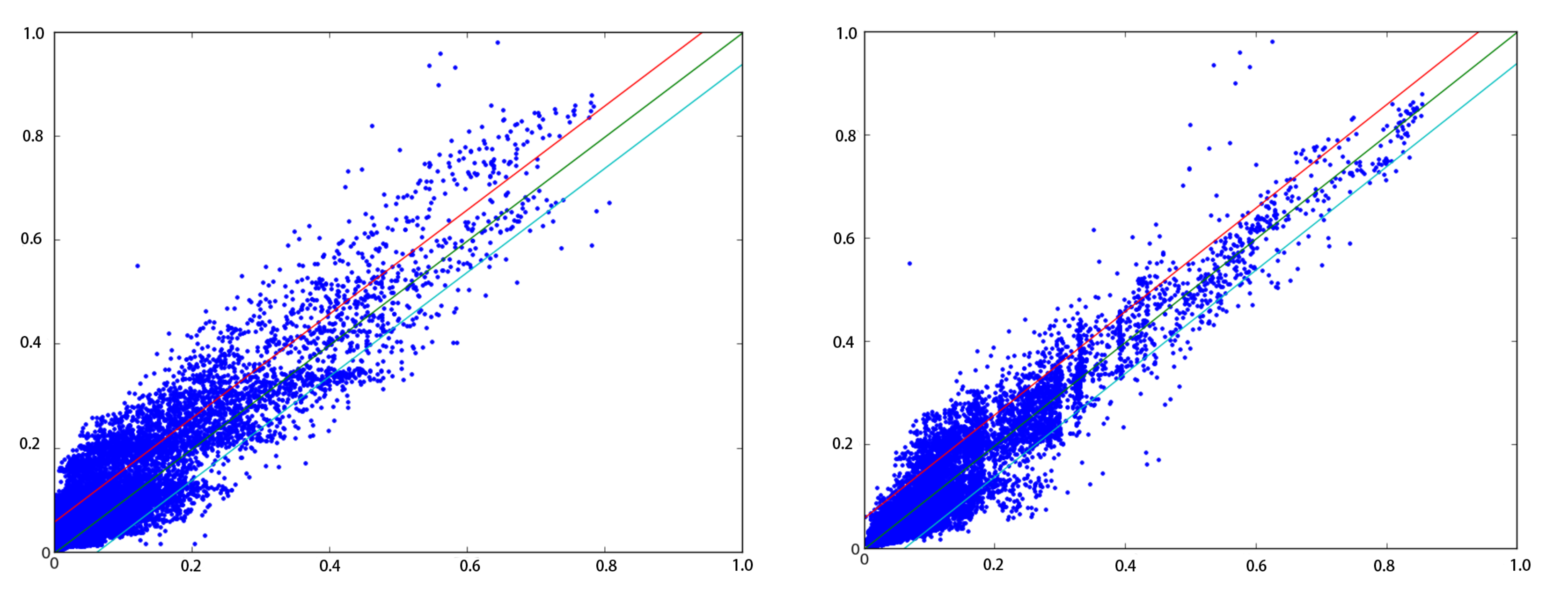
5.2. Single-Location Recovery
5.3. Multiple-Location Recover
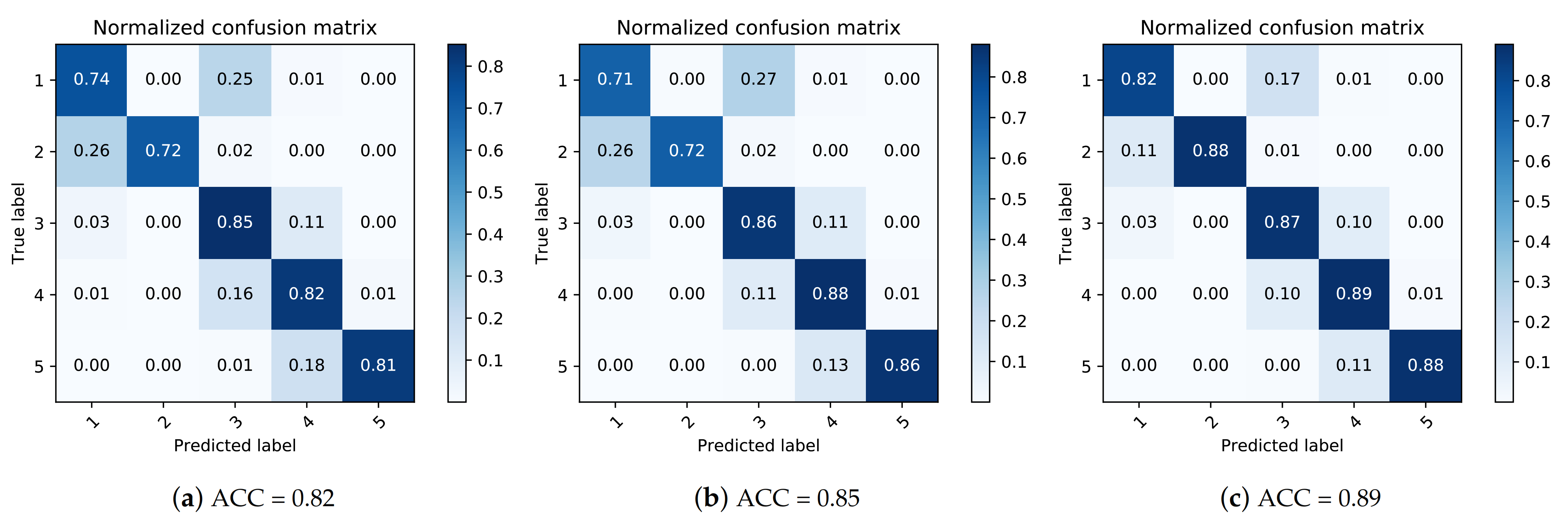
5.4. Impact of Season
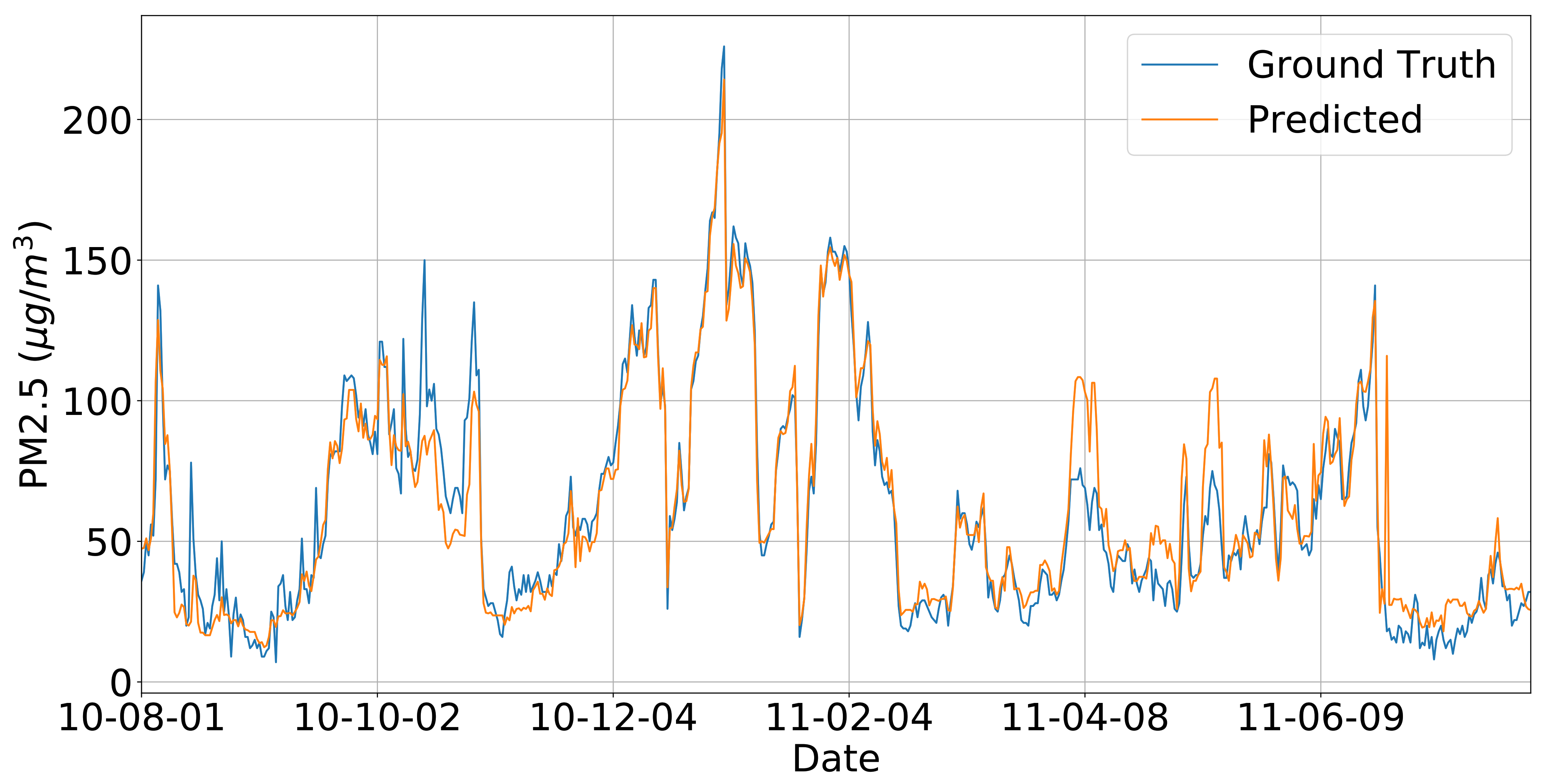
5.5. Overall Recovery
6. Discussion and Suggestion
- Prepare a multi-departmental collaborative implementation plan for related information such as supporting equipment, information processing, information technology, human resources, and implementation procedures.
- Establish a multi-source database covering basic enterprise information, industrial chain information, and enterprise emergency environmental accident cases, based on which the factories are classified and managed to improve the quality and efficiency of exhaust emission supervision.
- Adjust pollutant discharge management institutions according to the nature of the industry, implement refined and standardized management of pollution discharge surveys, inspections and assessments, and discharge volume verification in key industries, generate discharge data supervision reports on schedule, and conduct dynamic management and evaluation of supervision content.
- Establish a data sharing platform among multiple government departments such as the Environment Bureau, the Taxation Bureau, and the Bureau of Industry and Information Technology to break the phenomenon of “information islands” and “data conflicts”, and realize real-time sharing of data related to surrounding monitoring point sources and corporate pollution.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Boretti, A.; Rosa, L. Reassessing the projections of the world water development report. NPJ Clean Water 2019, 2, 1–6. [Google Scholar] [CrossRef]
- Li, X.; Jin, L.; Kan, H. Air pollution: A global problem needs local fixes. Nature 2019, 570, 437–439. [Google Scholar] [CrossRef]
- Boamah, K.B.; Du, J.; Boamah, A.J.; Appiah, K. A study on the causal effect of urban population growth and international trade on environmental pollution: Evidence from China. Environ. Sci. Pollut. Res. 2017, 25, 5862–5874. [Google Scholar] [CrossRef] [PubMed]
- He, P.; Sun, Y.; Shen, H.; Jian, J.; Yu, Z. Does Environmental Tax Affect Energy Efficiency? An Empirical Study of Energy Efficiency in OECD Countries Based on DEA and Logit Model. Sustainability 2019, 11, 3792. [Google Scholar] [CrossRef]
- Krass, D.; Nedorezov, T.; Ovchinnikov, A. Environmental taxes and the choice of green technology. Prod. Oper. Manag. 2013, 22, 1035–1055. [Google Scholar] [CrossRef]
- Kemp, R.; Pontoglio, S. The innovation effects of environmental policy instruments—A typical case of the blind men and the elephant? Ecol. Econ. 2011, 72, 28–36. [Google Scholar] [CrossRef]
- Choi, T. Local sourcing and fashion quick response system: The impacts of carbon footprint tax. Transp. Res. Part E Logist. Transp. Rev. 2013, 55, 43–54. [Google Scholar] [CrossRef]
- Onofrei, M.; Vintilă, G.; Dascalu, E.D.; Roman, A.; Firtescu, B.N. The impact of environmental tax reform on greenhouse gas emissions: Empirical evidence from European countries. Environ. Eng. Manag. J. 2017, 16, 2843–2849. [Google Scholar] [CrossRef]
- Agnolucci, P. The effect of the German and British environmental taxation reforms: A simple assessment. Energy Policy 2009, 37, 3043–3051. [Google Scholar] [CrossRef]
- Gulia, S.; Khanna, I.; Shukla, K.; Khare, M. Ambient air pollutant monitoring and analysis protocol for low and middle income countries: An element of comprehensive urban air quality management framework. Atmos. Environ. 2019, 222, 117120. [Google Scholar] [CrossRef]
- Chalabi, Z.; Milojevic, A.; Doherty, R.M.; Stevenson, D.S.; MacKenzie, I.A.; Milner, J.; Vieno, M.; Williams, M.; Wilkinson, P. Applying air pollution modelling within a multi-criteria decision analysis framework to evaluate UK air quality policies. Atmos. Environ. 2017, 167, 466–475. [Google Scholar] [CrossRef]
- Boyce, J.K.; Pastor, M. Clearing the air: Incorporating air quality and environmental justice into climate policy. Clim. Chang. 2013, 120, 801–814. [Google Scholar] [CrossRef]
- Cai, H.; Xie, S. Traffic-related air pollution modeling during the 2008 beijing olympic games: The effects of an odd-even day traffic restriction scheme. Sci. Total Environ. 2011, 409, 1935–1948. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Yuan, Z.; Liu, X.; Xia, X.; Huang, X.; Dong, Z. Improving air pollution control policy in China—A perspective based on cost–benefit analysis. Sci. Total Environ. 2016, 543, 307–314. [Google Scholar] [CrossRef]
- Yang, S.; Chen, B.; Wakeel, M.; Hayat, T.; Alsaedi, A.; Ahmad, B. PM2.5 footprint of household energy consumption. Appl. Energy 2018, 227, 375–383. [Google Scholar] [CrossRef]
- Wang, S.; Kim, S.M.; He, T. Symbol-level cross-technology communication via payload encoding. In Proceedings of the IEEE 38th International Conference on Distributed Computing Systems (ICDCS), Vienna, Austria, 2–5 July 2018; pp. 500–510. [Google Scholar]
- Chae, Y.; Wang, S.; Kim, S.M. Exploiting wifi guard band for safeguarded zigbee. In Proceedings of the 16th ACM Conference on Embedded Networked Sensor Systems, Shenzhen, China, 4–7 November 2018; pp. 172–184. [Google Scholar]
- Li, K.; Wang, S. Electric vehicle charging station deployment for minimizing construction cost. In Proceedings of the International Conference on Big Data Analytics and Knowledge Discovery, Lyon, France, 28–31 August 2017; pp. 471–485. [Google Scholar]
- Jeong, W.; Jung, J.; Wang, Y.; Wang, S.; Yang, S.; Yan, Q.; Yi, Y.; Kim, S.M. SDR receiver using commodity wifi via physical-layer signal reconstruction. In Proceedings of the 26th Annual International Conference on Mobile Computing and Networking, London, UK, 25–26 March 2020; pp. 1–14. [Google Scholar]
- Ji, Z.; Wang, S. Online truthfully incentive mechanisms with budget constraint for multiple overlapped tasks crowdsourced sensing. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 December 2017; pp. 999–1003. [Google Scholar]
- Eronat, A.H.; Bengil, F.; Neser, G. Shipping and ship recycling related oil pollution detection in candarh bay (Turkey) using satellite monitoring. Ocean. Eng. 2019, 187, 106157.1–106157.8. [Google Scholar] [CrossRef]
- Aliyu, Y.A.; Botai, J.O. Appraising city-scale pollution monitoring capabilities of multi-satellite datasets using portable pollutant monitors. Atmos. Environ. 2018, 179, 239–249. [Google Scholar] [CrossRef]
- Khaki, M.; Awange, J. The application of multi-mission satellite data assimilation for studying water storage changes over south america. Sci. Total Environ. 2018, 647, 1557–1572. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Chaoa, C.Y.; Chien, C.H.; Biswas, P. Integrating low-cost air quality sensor networks with fixed and satellite monitoring systems to study ground-level pm2.5. Atmos. Environ. 2020, 223, 117293. [Google Scholar] [CrossRef]
- Dewinter, J.L.; Brown, S.G.; Seagram, A.F.; Landsberg, K.; Eisinger, D.S. A national-scale review of air pollutant concentrations measured in the u.s. near-road monitoring network during 2014 and 2015. Atmos. Environ. 2018, 183, 94–105. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, X.; Li, Z.; Jiang, S.; Jiang, X. Fine-Grained Air Quality Monitoring Based on Gaussian Process Regression. In Proceedings of the International Conference on Neural Information Processing, Kuching, Malaysia, 3–6 November 2014. [Google Scholar]
- Cheng, Y.; Li, X.; Li, Z.; Jiang, S.; Li, Y.; Jia, J.; Jiang, X. AirCloud: A cloud-based air-quality monitoring system for everyone. In Proceedings of the 12th ACM Conference on Embedded Network Sensor Systems, Memphis, Tennessee, 3–6 November 2014; pp. 251–265. [Google Scholar]
- Gao, M.; Beig, G.; Song, S.; Zhang, H.; Hu, J.; Ying, Q.; McElroy, M.B. The impact of power generation emissions on ambient PM2.5 pollution and human health in China and India. Environ. Int. 2018, 121, 250–259. [Google Scholar] [CrossRef]
- Fahimnia, B.; Sarkis, J.; Choudhary, A.; Eshragh, A. Tactical supply chain planning under a carbon tax policy scheme: A case study. Int. J. Prod. Econ. 2015, 164, 206–215. [Google Scholar] [CrossRef]
- Hariga, M.; As’ ad, R.; Shamayleh, A. Integrated economic and environmental models for a multi stage cold supply chain under carbon tax regulation. J. Clean. Prod. 2017, 166, 1357–1371. [Google Scholar] [CrossRef]
- Chen, Y.J.; Sheu, J. Environmental-regulation pricing strategies for green supply chain management. Transp. Res. Part -Logist. Transp. Rev. 2009, 45, 667–677. [Google Scholar] [CrossRef]
- Keoleian, G.A.; Volk, T.A. Renewable energy from willow biomass crops: Life cycle energy, environmental and economic performance. Crit. Rev. Plant Sci. 2005, 24, 385–406. [Google Scholar] [CrossRef]
- Bjorklund, A.E.; Finnveden, G. Life cycle assessment of a national policy proposal—The case of a Swedish waste incineration tax. Waste Manag. 2007, 27, 1046–1058. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Feng, Y.; Yu, G.; Liu, L.; Li, J.; Xiong, Y.; Li, F. Development of an imaging gas correlation spectrometry based mid-infrared camera for two-dimensional mapping of CO in vehicle exhausts. Opt. Express 2018, 26, 8239–8251. [Google Scholar] [CrossRef]
- Li, T.; Winnel, M.; Lin, H.; Panther, J.; Liu, C.; O’Halloran, R.; Zhao, H. A reliable sewage quality abnormal event monitoring system. Water Res. 2017, 121, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Gallardo-Gonzalez, J.; Baraket, A.; Boudjaoui, S.; Metzner, T.; Hauser, F.; Rößler, T.; Bausells, J. A fully integrated passive microfluidic Lab-on-a-Chip for real-time electrochemical detection of ammonium: Sewage applications. Sci. Total Environ. 2019, 653, 1223–1230. [Google Scholar] [CrossRef]
- Marchant, C.; Leiva, V.; Christakos, G.; Cavieres, M.F. Monitoring urban environmental pollution by bivariate control charts: New methodology and case study in Santiago, Chile. Environmetrics 2019, 30, e2551. [Google Scholar] [CrossRef]
- Wang, S.; Jeong, W.; Jung, J.; Kim, S.M. X-MIMO: Cross-technology multi-user MIMO. In Proceedings of the 18th Conference on Embedded Networked Sensor Systems, Yokohama, Japan, 16 November 2020; pp. 218–231. [Google Scholar]
- McKercher, G.R.; Vanos, J.K. Low-cost mobile air pollution monitoring in urban environments: A pilot study in Lubbock, Texas. Environ. Technol. 2018, 39, 1505–1514. [Google Scholar] [CrossRef]
- Hswen, Y.; Qin, Q.; Brownstein, J.S.; Hawkins, J.B. Feasibility of using social media to monitor outdoor air pollution in London, England. Prev. Med. 2019, 121, 86–93. [Google Scholar] [CrossRef] [PubMed]
- Pourshahabi, S.; Rakhshandehroo, G.; Talebbeydokhti, N.; Nikoo, M.R.; Masoumi, F. Handling Uncertainty in Optimal Design of Reservoir Water Quality Monitoring Systems. Environ. Pollut. 2020, 266, 115211. [Google Scholar] [CrossRef]
- Martin, C.; Parkes, S.; Zhang, Q.; Zhang, X.; McCabe, M.F.; Duarte, C.M. Use of unmanned aerial vehicles for efficient beach litter monitoring. Mar. Pollut. Bull. 2018, 131, 662–673. [Google Scholar] [CrossRef] [PubMed]
- Bian, X.; Li, X.; Qi, P.; Chi, Z.; Ye, R.; Lu, S.; Cai, Y. Quantitative design and analysis of marine environmental monitoring networks in coastal waters of China. Mar. Pollut. Bull. 2019, 143, 144–151. [Google Scholar] [CrossRef]
- Ripoll, A.; Viana, M.; Padrosa, M.; Querol, X.; Minutolo, A.; Hou, K.M.; García-Vidal, J. Testing the performance of sensors for ozone pollution monitoring in a citizen science approach. Sci. Total Environ. 2018, 651, 1166–1179. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. In Summer School on Machine Learning; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin, Germany, 2003; pp. 63–71. [Google Scholar]
- Murphy, K.P. Machine learning: A probabilistic perspective. In Machine Learning: A Probabilistic Perspective; Springer: Boston, MA, USA, 2012. [Google Scholar]
- Cheng, Y.; He, X.; Zhou, Z.; Thiele, L. MapTransfer: Urban Air Quality Map Generation for Downscaled Sensor Deployments. In Proceedings of the 2020 IEEE/ACM Fifth International Conference on Internet-of-Things Design and Implementation (IoTDI), Sydney, Australia, 21–24 April 2020; pp. 14–26. [Google Scholar]
- Cheng, Y.; Li, X.; Li, Y. Finding dynamic co-evolving zones in spatial-temporal time series data. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Riva del Garda, Italy, 19–23 September 2016; pp. 129–144. [Google Scholar]
- Cheng, Y.; He, X.; Zhou, Z.; Thiele, L. Ict: In-field calibration transfer for air quality sensor deployments. In Proceedings of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, Austin, TX, USA, 9–13 November 2019; pp. 1–19. [Google Scholar]
- Einsiedler, J.; Cheng, Y.; Papst, F.; Saukh, O. Interpretable and Transferable Models to Understand the Impact of Lockdown Measures on Local Air Quality. arXiv 2020, arXiv:2011.10144. [Google Scholar]
- Bellinger, C.; Mohomed Jabbar, M.S.; Zaïane, O.; Osornio-Vargas, A. A systematic review of data mining and machine learning for air pollution epidemiology. BMC Public Health 2017, 17, 907. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, C.; Wang, S.; Li, S. Impacts of energy consumption structure, energy intensity, economic growth, urbanization on PM2. 5 concentrations in countries globally. Apply Energy 2018, 230, 94–105. [Google Scholar] [CrossRef]
- Xie, X.; Ai, H.; Deng, Z. Impacts of the scattered coal consumption on PM2.5 pollution in China. J. Clean. Prod. 2020, 245, 118922. [Google Scholar] [CrossRef]




| Categories | Features | No. |
|---|---|---|
| hour of day, day of week, month and is Holiday | 4 | |
| temperature, humidity, pressure, wind speed and wind power | 5 | |
| Factory Indirect Features: Total energy consumption, Water, Desalted water, Electric, Steam, Plant-wide fuel, Natural gas, Refinery dry gas, etc. | 20 |
| Chemical Engineering | Paper Mill | Sewage Plant | Thermal Power Plant | Tire Plant | |
|---|---|---|---|---|---|
| SVR | 8.12 | 9.43 | 10.14 | 9.22 | 10.22 |
| GPR | 12.15 | 14.33 | 9.23 | 10.21 | 9.21 |
| AirCloud | 12.83 | 14.52 | 9.31 | 10.62 | 9.32 |
| Combined | 7.21 | 8.64 | 8.34 | 7.29 | 8.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Gao, X. Multimodal Data Based Regression to Monitor Air Pollutant Emission in Factories. Sustainability 2021, 13, 2663. https://doi.org/10.3390/su13052663
Wu H, Gao X. Multimodal Data Based Regression to Monitor Air Pollutant Emission in Factories. Sustainability. 2021; 13(5):2663. https://doi.org/10.3390/su13052663
Chicago/Turabian StyleWu, Hao, and Xinwei Gao. 2021. "Multimodal Data Based Regression to Monitor Air Pollutant Emission in Factories" Sustainability 13, no. 5: 2663. https://doi.org/10.3390/su13052663
APA StyleWu, H., & Gao, X. (2021). Multimodal Data Based Regression to Monitor Air Pollutant Emission in Factories. Sustainability, 13(5), 2663. https://doi.org/10.3390/su13052663






