Environmental Regulation, Resource Misallocation and Industrial Total Factor Productivity: A Spatial Empirical Study Based on China’s Provincial Panel Data
Abstract
1. Introduction
2. Literature Review
3. Research Hypotheses
3.1. Environmental Regulation and TFP
3.2. Resource Misallocation and TFP
3.3. Environmental Regulation, Resource Misallocation and TFP
4. Model Specification and Data Source
4.1. Model Specification
4.2. Variable Selection, Data Source and Processing
4.2.1. Environmental Regulation Intensity
4.2.2. Degree of Resource Misallocation
4.2.3. Industrial TFP
4.2.4. Control Variables
5. Regression Results and Discussions
5.1. The Impact of Environmental Regulation on Industrial TFP
5.2. The Impact of Resource Misallocation on Industrial TFP
5.3. The Resource Reallocation Effects of Environmental Regulation and Its Impact on Industrial TFP
5.4. Robustness Test
6. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Calculation of the Degree of Resource Misallocation at the Provincial Level in China
Appendix B. Spatial Distribution of Resource Misallocation in China
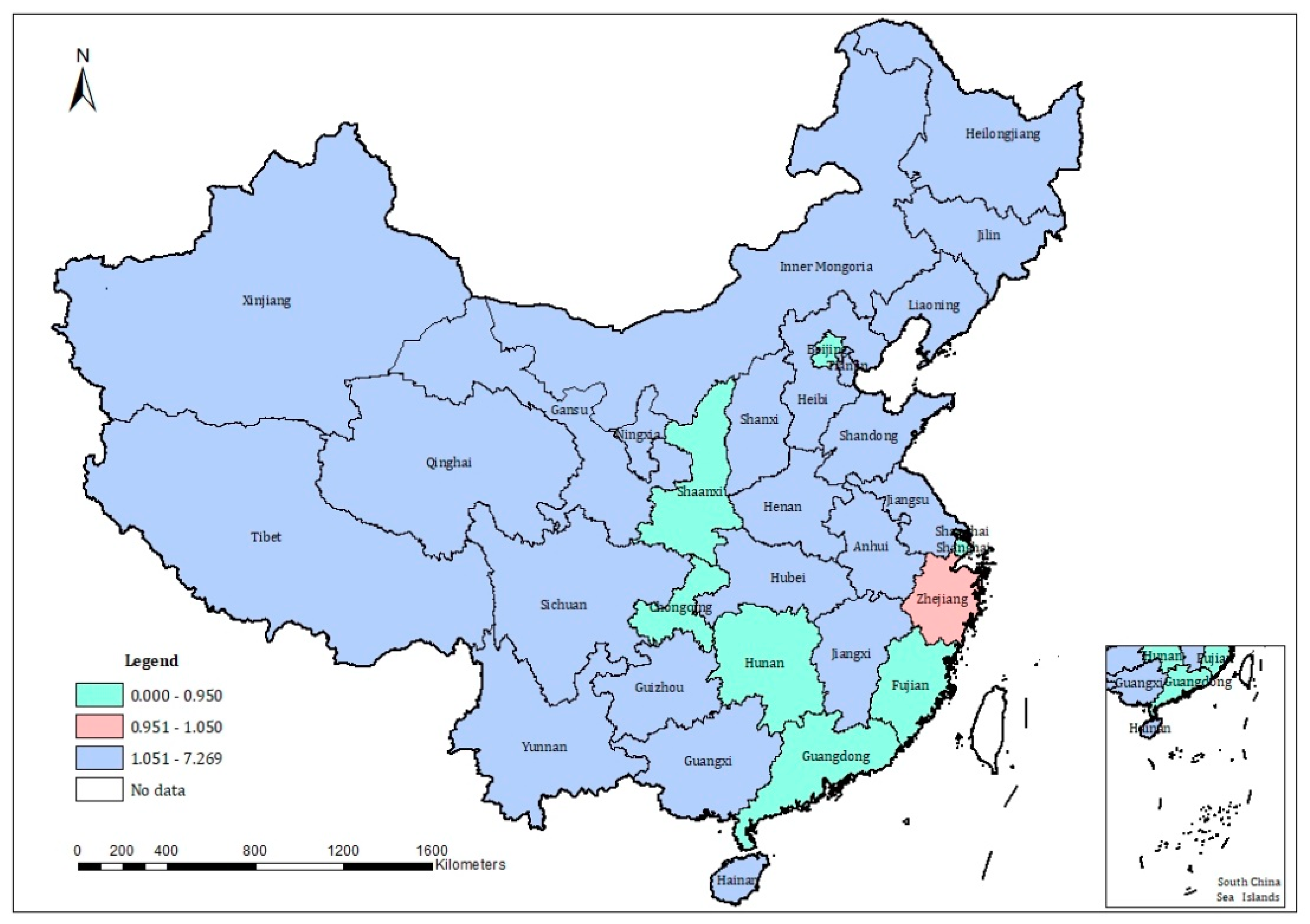
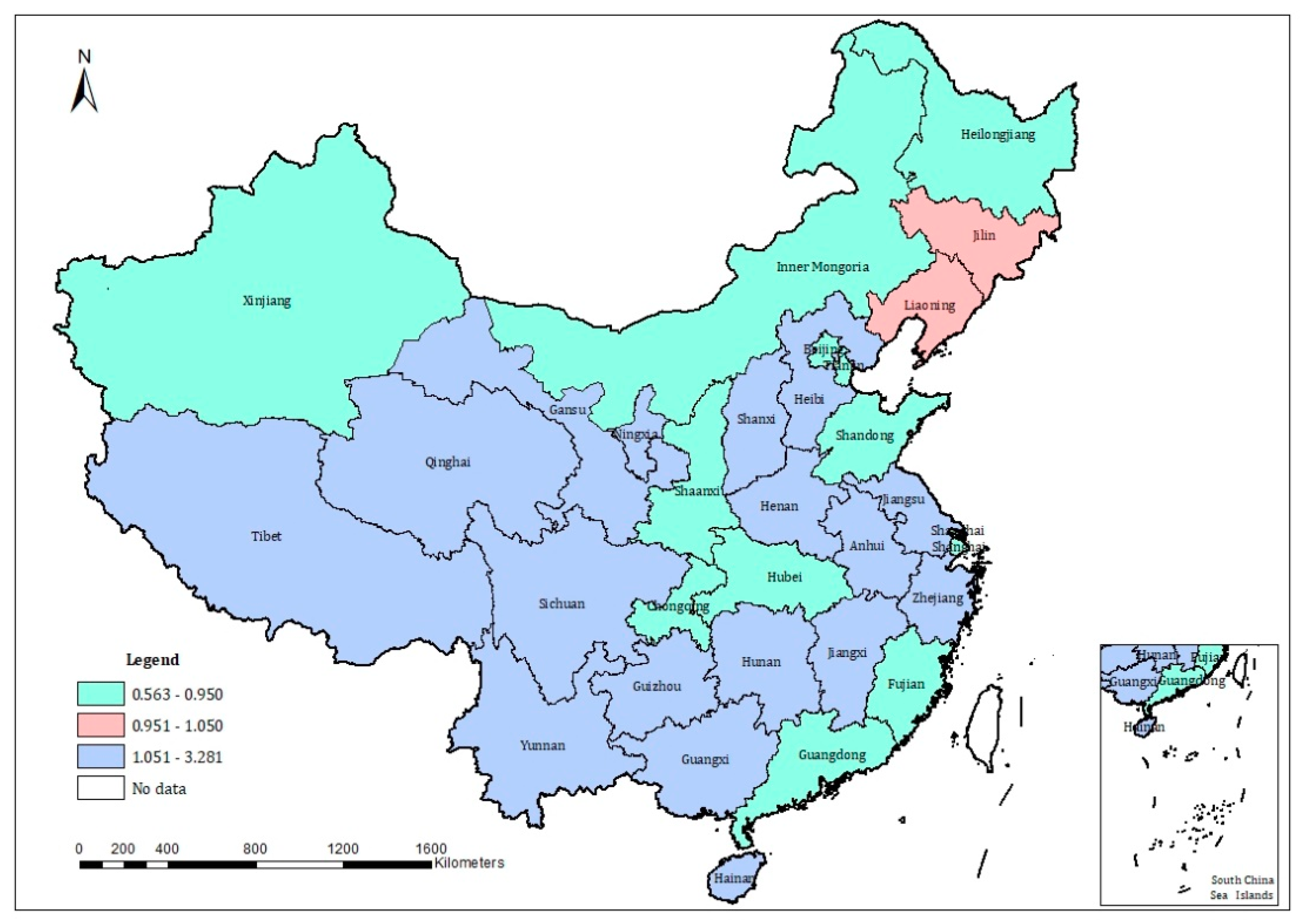
Appendix C. Variation Trend of Industrial TFP for Each Province during 1997–2017
| 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 1.14 | 1.42 | 1.67 | 2.04 | 2.22 | 2.28 | 2.61 | 2.89 | 2.89 | 3.06 | 3.21 | 3.23 | 3.50 | 4.00 | 3.80 | 3.96 | 4.02 | 4.17 | 4.05 | 4.09 | 3.93 |
| Tianjin | 1.14 | 1.08 | 1.40 | 1.62 | 1.89 | 2.21 | 2.47 | 2.89 | 3.29 | 3.59 | 3.80 | 4.18 | 4.81 | 5.36 | 6.02 | 6.58 | 7.05 | 7.60 | 8.70 | 10.57 | 10.81 |
| Hebei | 1.15 | 1.30 | 1.55 | 1.71 | 1.89 | 2.08 | 2.24 | 2.45 | 2.67 | 2.95 | 3.26 | 3.51 | 3.66 | 3.94 | 4.27 | 4.55 | 4.76 | 4.85 | 4.94 | 5.08 | 5.16 |
| Shanxi | 1.10 | 1.15 | 1.22 | 1.26 | 1.31 | 1.41 | 1.47 | 1.49 | 1.48 | 1.49 | 1.62 | 1.63 | 1.53 | 1.67 | 1.82 | 1.97 | 2.06 | 2.09 | 2.02 | 2.01 | 2.16 |
| Inner Mongoria | 1.18 | 1.51 | 1.67 | 1.96 | 2.38 | 2.67 | 2.73 | 3.03 | 3.26 | 3.77 | 4.19 | 4.87 | 5.58 | 6.04 | 6.52 | 6.95 | 6.91 | 7.40 | 8.78 | 10.23 | 11.73 |
| Liaoning | 1.11 | 1.23 | 1.39 | 1.57 | 1.75 | 2.03 | 2.12 | 2.33 | 2.53 | 2.78 | 3.19 | 3.65 | 4.13 | 4.70 | 5.36 | 5.86 | 5.94 | 6.31 | 6.55 | 6.23 | 6.58 |
| Jilin | 1.15 | 1.66 | 1.95 | 2.38 | 2.82 | 3.17 | 3.07 | 3.27 | 3.32 | 3.51 | 3.77 | 4.14 | 4.67 | 5.49 | 6.31 | 6.90 | 7.11 | 7.33 | 7.74 | 8.45 | 9.05 |
| Heilongjiang | 1.07 | 1.38 | 1.53 | 1.84 | 2.07 | 2.43 | 2.94 | 3.10 | 3.33 | 3.51 | 3.54 | 3.72 | 3.96 | 4.37 | 4.69 | 5.00 | 5.17 | 4.86 | 5.09 | 4.73 | 4.67 |
| Shanghai | 1.13 | 1.29 | 1.42 | 1.63 | 2.28 | 2.44 | 2.90 | 3.51 | 3.79 | 4.15 | 4.45 | 3.96 | 4.11 | 4.70 | 5.02 | 5.32 | 5.80 | 5.92 | 6.18 | 6.34 | 7.09 |
| Jiangsu | 1.11 | 1.23 | 1.37 | 1.54 | 1.72 | 1.96 | 2.26 | 2.62 | 2.97 | 3.36 | 3.81 | 4.31 | 4.80 | 5.38 | 6.03 | 6.71 | 7.40 | 8.02 | 8.68 | 9.26 | 9.91 |
| Zhejiang | 1.13 | 1.29 | 1.55 | 1.43 | 1.53 | 1.69 | 1.78 | 1.94 | 2.10 | 2.34 | 2.53 | 2.71 | 2.74 | 2.88 | 3.06 | 3.21 | 3.46 | 3.65 | 3.81 | 4.01 | 4.33 |
| Anhui | 1.13 | 1.26 | 1.38 | 1.53 | 1.70 | 1.86 | 1.94 | 2.01 | 2.13 | 2.09 | 2.08 | 2.09 | 2.19 | 2.45 | 2.77 | 2.94 | 3.06 | 3.15 | 3.26 | 3.37 | 3.54 |
| Fujian | 1.13 | 1.28 | 1.42 | 1.53 | 1.62 | 1.75 | 1.86 | 2.02 | 2.04 | 2.15 | 2.30 | 2.41 | 2.53 | 2.72 | 3.07 | 3.40 | 3.69 | 3.98 | 4.17 | 4.34 | 4.57 |
| Jiangxi | 1.19 | 1.33 | 1.38 | 1.42 | 1.49 | 1.54 | 1.52 | 1.44 | 1.35 | 1.25 | 1.17 | 1.10 | 1.04 | 1.05 | 1.18 | 1.26 | 1.33 | 1.42 | 1.48 | 1.55 | 1.65 |
| Shandong | 1.13 | 1.33 | 1.43 | 1.62 | 1.77 | 2.00 | 2.40 | 2.49 | 2.76 | 3.10 | 3.45 | 4.07 | 4.53 | 4.93 | 5.36 | 5.75 | 6.22 | 6.62 | 6.81 | 7.07 | 7.48 |
| Henan | 1.09 | 1.18 | 1.30 | 1.45 | 1.58 | 1.73 | 1.92 | 2.09 | 2.19 | 2.30 | 2.43 | 2.66 | 2.72 | 2.93 | 3.17 | 3.32 | 3.39 | 3.55 | 3.60 | 3.70 | 3.85 |
| Hubei | 1.14 | 1.51 | 1.70 | 2.03 | 2.31 | 2.51 | 2.51 | 2.80 | 3.15 | 3.53 | 3.87 | 4.26 | 4.78 | 5.81 | 6.94 | 7.89 | 8.80 | 9.70 | 10.55 | 11.40 | 12.24 |
| Hunan | 1.14 | 1.30 | 1.44 | 1.57 | 1.68 | 1.74 | 1.75 | 1.76 | 1.68 | 1.68 | 1.69 | 1.69 | 1.67 | 1.76 | 1.81 | 1.95 | 2.06 | 2.15 | 2.26 | 2.35 | 2.54 |
| Guangdong | 1.16 | 1.33 | 1.50 | 1.71 | 1.89 | 2.04 | 2.27 | 2.57 | 2.70 | 3.01 | 3.42 | 3.70 | 3.81 | 4.12 | 4.33 | 4.44 | 4.54 | 4.64 | 4.67 | 4.70 | 4.75 |
| Guangxi | 1.08 | 1.21 | 1.28 | 1.36 | 1.47 | 1.67 | 1.78 | 1.89 | 1.88 | 1.82 | 1.71 | 1.70 | 1.54 | 1.56 | 1.55 | 1.67 | 1.78 | 1.72 | 1.82 | 1.91 | 2.02 |
| Hainan | 1.04 | 1.44 | 1.64 | 1.86 | 2.06 | 2.37 | 2.74 | 2.99 | 3.19 | 3.72 | 4.61 | 4.37 | 4.61 | 4.95 | 4.84 | 4.37 | 3.94 | 4.07 | 4.17 | 4.21 | 4.34 |
| Chongqing | 1.08 | 1.12 | 1.25 | 1.39 | 1.56 | 1.72 | 1.94 | 2.04 | 1.97 | 1.92 | 1.96 | 2.03 | 2.10 | 2.29 | 2.35 | 2.40 | 2.44 | 2.50 | 2.53 | 2.61 | 2.79 |
| Sichuan | 1.10 | 1.20 | 1.28 | 1.37 | 1.47 | 1.58 | 1.73 | 1.94 | 2.18 | 2.42 | 2.62 | 2.86 | 3.06 | 3.57 | 4.19 | 4.60 | 4.95 | 5.18 | 5.42 | 5.68 | 6.00 |
| Guizhou | 1.10 | 1.22 | 1.36 | 1.41 | 1.42 | 1.51 | 1.80 | 1.91 | 1.84 | 1.76 | 1.77 | 1.69 | 1.63 | 1.67 | 1.73 | 1.76 | 1.75 | 1.75 | 1.77 | 1.74 | 1.76 |
| Yunnan | 1.13 | 1.28 | 1.56 | 1.69 | 1.80 | 1.99 | 2.17 | 2.00 | 1.85 | 1.86 | 1.87 | 1.81 | 1.74 | 1.74 | 1.81 | 1.84 | 1.84 | 1.92 | 2.04 | 2.10 | 2.29 |
| Tibet | 0.96 | 0.94 | 0.94 | 0.90 | 0.90 | 0.90 | 0.64 | 0.55 | 0.43 | 0.37 | 0.38 | 0.35 | 0.35 | 0.28 | 0.29 | 0.20 | 0.20 | 0.20 | 0.15 | 0.09 | 0.07 |
| Shaanxi | 1.12 | 1.25 | 1.36 | 1.45 | 1.56 | 1.72 | 1.77 | 1.99 | 2.01 | 1.95 | 1.89 | 1.86 | 1.66 | 1.64 | 1.66 | 2.13 | 2.22 | 2.27 | 2.29 | 2.34 | 2.46 |
| Gansu | 1.10 | 1.32 | 1.40 | 1.64 | 1.84 | 2.00 | 2.05 | 2.20 | 2.40 | 2.59 | 2.83 | 2.88 | 2.99 | 3.27 | 3.61 | 3.94 | 4.23 | 4.60 | 4.98 | 5.33 | 5.31 |
| Qinghai | 1.18 | 1.32 | 1.49 | 2.16 | 2.50 | 2.33 | 2.81 | 3.16 | 3.67 | 3.95 | 4.40 | 5.23 | 5.63 | 6.15 | 10.50 | 11.36 | 10.93 | 12.11 | 13.15 | 17.04 | 14.04 |
| Ningxia | 1.10 | 1.30 | 1.38 | 1.57 | 1.68 | 1.83 | 1.85 | 1.89 | 2.06 | 2.15 | 2.32 | 2.60 | 2.63 | 3.01 | 4.16 | 4.62 | 4.76 | 4.32 | 4.74 | 5.23 | 5.42 |
| Xinjiang | 1.13 | 1.17 | 1.33 | 1.71 | 2.00 | 2.14 | 2.03 | 2.19 | 1.98 | 2.32 | 2.48 | 2.81 | 2.96 | 3.10 | 3.05 | 3.32 | 3.26 | 3.60 | 4.04 | 4.36 | 4.33 |
Appendix D. Robustness Test Results
| Variable | TFP | |||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| ER | −1.234 ** (0.483) | −1.286 *** (0.486) | ||
| ER2 | 0.337 (0.264) | 0.347 (0.266) | ||
| MisK | −0.718 *** (0.114) | −0.671 *** (0.105) | ||
| MisL | −0.403 ** (0.180) | −0.189 ** (0.081) | ||
| Lnpgdp | 1.680 *** (0.425) | 2.130 *** (0.514) | 1.019 ** (0.518) | 1.174 ** (0.488) |
| Indstrc | −10.452 *** (1.915) | −8.907 *** (2.371) | −5.242 ** (2.306) | −4.199 * (2.084) |
| Lnfdi | −0.86 3*** (0.076) | −0.853 *** (0.079) | −0.678 *** (0.079) | −0.582 *** (0.071) |
| Lnexpdt | 0.962 *** (0.299) | 1.008 ** (0.482) | 0.378 (0.473) | 0.364 (0.426) |
| W × ER | −6.689 *** (2.433) | |||
| W × ER2 | 3.483 *** (0.982) | |||
| W × MisK | −3.277 *** (1.088) | |||
| W × MisL | 4.399 ** (2.067) | |||
| W × Lnpgdp | −5.025 *** (1.339) | −5.541 * (3.256) | ||
| W × Indstrc | −13.606 ** (5.476) | −82.951 *** (12.643) | ||
| W × Lnfdi | 0.745 ** (0.361) | 3.938 *** (0.745) | ||
| W × Lnexpdt | 3.005 *** (0.980) | 0.044(3.477) | ||
| Spatial | 0.118 ** (0.051) | 0.239 * (0.157) | ||
| R2 | 0.769 | 0.783 | 0.795 | 0.842 |
| N. Observation | 651 | 651 | 651 | 651 |
| fixed effects of provinces | Yes | Yes | Yes | Yes |
| fixed effects of years | No | No | Yes | Yes |
| Robust LM-lag | 1.907 [0.167] | 32.604 *** [0.000] | ||
| Robust LM-error | 3.957 ** [0.047] | 45.565 *** [0.000] | ||
| LR spatial FE | 565.545 *** [0.000] | 549.485 *** [0.000] | ||
| LR year FE | 10.828 [0.966] | 35.878 ** [0.023] | ||
| Wald spatial lag | 33.068 *** [0.000] | 168.791 *** [0.000] | ||
| Wald spatial error | 31.044 *** [0.000] | 163.145 *** [0.000] | ||
| Hausman test | 98.976 *** [0.000] | 150.216 *** [0.000] |
| Direct Effect | Spatial Spillover Effect | Total Effect | ||
|---|---|---|---|---|
| (1) | ER --> TFP | −1.286 ** (0.497) | −6.850 *** (2.475) | −8.136 *** (2.512) |
| (2) | ER2 --> TFP | 0.349 (0.262) | 3.546 *** (0.980) | 3.895 *** (1.001) |
| (3) | MisK --> TFP | −0.704 *** (0.108) | −2.829 *** (0.981) | −3.533 *** (0.984) |
| (4) | MisL --> TFP | −0.191 ** (0.076) | 3.609 ** (1.865) | 3.418 *** (1.910) |
| (5) | ER --> MisK | −0.508 *** (0.099) | −0.080 (0.343) | −0.588 * (0.350) |
| (6) | ER --> MisL | −0.096 (0.062) | −0.251 ** (0.119) | −0.347 * (0.197) |
| Variable | MisK | MisL | ||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| ER | −0.597 *** (0.097) | −0.458 *** (0.094) | −0.087 (0.061) | −0.105 *(0.059) |
| Lnpgdp | −0.115 *** (0.019) | −0.853 *** (0.191) | −1.181 *** (0.119) | −1.177 *** (0.119) |
| Indstrc | 5.359 *** (0.890) | 5.349 *** (0.870) | 2.688 *** (0.561) | 2.461 *** (0.545) |
| Lnfdi | 0.171 *** (0.030) | 0.147 ***(0.030) | 0.084 *** (0.019) | 0.081 *** (0.019) |
| Lnexpdt | −1.308 *** (0.181) | −1.232 *** (0.176) | −0.496 *** (0.114) | −0.498 *** (0.110) |
| W × ER | −0.088 (0.470) | −0.397 ** (0.196) | ||
| W × Lnpgdp | 1.223 (1.295) | 1.534 * (0.839) | ||
| W × Indstrc | −5.147 (4.959) | −1.387 (3.114) | ||
| W × Lnfdi | 0.486 *** (0.033) | 0.152 *** (0.024) | ||
| W × Lnexpdt | −2.996 ** (1.471) | −2.190 ** (0.910) | ||
| Spatial | 0.512 *** (0.174) | 0.640 *** (0.178) | ||
| R2 | 0.899 | 0.905 | 0.835 | 0.846 |
| N. Observation | 651 | 651 | 651 | 651 |
| fixed effects of provinces | Yes | Yes | Yes | Yes |
| fixed effects of years | Yes | Yes | Yes | Yes |
| Robust LM-lag | 8.654 *** [0.003] | 5.148 ** [0.023] | ||
| Robust LM-error | 10.351 *** [0.001] | 8.262 *** [0.004] | ||
| LR spatial FE | 1153.430 *** [0.000] | 948.556 *** [0.000] | ||
| LR year FE | 81.025 *** [0.000] | 160.132 *** [0.000] | ||
| Wald spatial lag | 16.134 *** [0.000] | 16.852 *** [0.000] | ||
| Wald spatial error | 16.251 *** [0.000] | 19.275 *** [0.000] | ||
| Hausman test | 28.204*** [0.003] | 32.363 *** [0.000] |
| Variable | TFP | ||
|---|---|---|---|
| (1) | (2) | (3) | |
| ER | −0.811 *** (0.212) | −0.749 *** (0.220) | −0.783 *** (0.213) |
| MisK | −0.733 *** (0.093) | −0.675 *** (0.104) | |
| MisL | −0.494 *** (0.159) | −0.431 *** (0.168) | |
| Lnpgdp | 1.077 ** (0.437) | 1.066 ** (0.490) | 1.225 ** (0.486) |
| Indstrc | −3.799 * (2.063) | −7.351 *** (2.089) | −4.032 * (2.064) |
| Lnfdi | −0.569 *** (0.070) | −0.642 *** (0.072) | −0.576 *** (0.070) |
| Lnexpdt | 0.599 (0.417) | 0.658 (0.418) | 0.443 (0.423) |
| W × ER | 0.618 (1.068) | 1.063 (1.119) | 0.931 (1.083) |
| W × MisK | 4.716 *** (0.867) | 3.351 *** (1.079) | |
| W × MisL | 10.206 *** (1.726) | 4.140 * (2.081) | |
| W × Lnpgdp | −8.764 *** (2.974) | −5.232 ** (2.359) | −6.426 * (3.264) |
| W × Indstrc | −85.306 *** (12.372) | −68.761 *** (12.087) | −80.904 *** (12.512) |
| W × Lnfdi | 3.630 *** (0.737) | 4.286 *** (0.766) | 3.835 *** (0.742) |
| W × Lnexpdt | 0.564 (3.456) | 1.395 (3.422) | 0.402 (3.461) |
| Spatial | 0.208 *** (0.057) | 0.385 *** (0.161) | 0.202 *** (0.054) |
| R2 | 0.844 | 0.834 | 0.845 |
| N. Observation | 651 | 651 | 651 |
| fixed effects of provinces | Yes | Yes | Yes |
| fixed effects of years | Yes | Yes | Yes |
| Wald spatial lag | 173.920 *** [0.000] | 161.405 *** [0.000] | 172.680 *** [0.000] |
| Wald spatial error | 165.728 *** [0.000] | 159.462 *** [0.000] | 165.269 *** [0.000] |
| Hausman test | 128.040 *** [0.000] | 109.473 *** [0.000] | 128.343 *** [0.000] |
References
- Liu, H.W.; Zheng, S.L.; Zuo, W.T. The Influence Mechanism of Environmental Regulation on TFP of Enterprises. Sci. Res. Manag. 2016, 37, 33–41. [Google Scholar]
- Boyed, G.A.; McClelland, J.D. The Impact of Environmental Constraints on Productivity Improvement in Integrated Paper Plants. J. Environ. Econ. Manag. 1999, 38, 121–142. [Google Scholar] [CrossRef]
- Tanguay, G.A.; Rajaonson, J.; Lefebvre, J.-F.; Lanoie, P. Measuring the Sustainability of Cities: An Analysis of the Use of Local Indicators. Ecol. Indic. 2010, 10, 407–418. [Google Scholar] [CrossRef]
- Greenstone, M.; List, J.A.; Syverson, C. The Effects of Environmental Regulation on the Competitiveness of U.S. Manufacturing; NBER Working Paper No. 18392; 2012; Available online: https://www.nber.org/papers/w18392.2012 (accessed on 12 November 2020).
- Zhu, Y.; Wang, Z.; Qiu, S.; Zhu, L. Effects of Environmental Regulations on Technological Innovation Efficiency in China’s Industrial Enterprises: A Spatial Analysis. Sustainability 2019, 11, 2186. [Google Scholar] [CrossRef]
- Hou, B.Q.; Wang, B.; Du, M.Z.; Zhang, N. Does the SO2 Emissions Trading Scheme Encourage Green Total Factor Productivity? An Empirical Assessment on China’s Cities. Environ. Sci. Pollut. Res. 2020, 27, 6375–6388. [Google Scholar] [CrossRef] [PubMed]
- Porter, M.E.; Van der Linde, C. Toward a New Conception of the Environment-Competitiveness Relationship. J. Econ. Perspect. 1995, 9, 97–118. [Google Scholar] [CrossRef]
- Hamamoto, M. Environmental Regulation and the Productivity of Japanese Manufacturing Industries. Resour. Energy Econ. 2006, 28, 299–312. [Google Scholar] [CrossRef]
- Ambec, S.; Cohen, M.A.; Elgie, S.; Lanoie, P. The Porter Hypothesis at 20: Can Environmental Regulation Enhance Innovation and Competitiveness. Rev. Environ. Econ. Policy. 2013, 7, 2–22. [Google Scholar] [CrossRef]
- Jorge, M.L.; Madueño, J.H.; Martínez-Martínez, D.; Sancho, M.P.L. Competitiveness and Environmental Performance in Spanish Small and Medium Enterprises: Is there a Direct Link? J. Clean. Prod. 2015, 101, 26–37. [Google Scholar] [CrossRef]
- Sun, X.M.; Wang, J. Environmental Regulation, Induced R&D and Firms’ TFP—Porter Hypothesis Reexamined. J. Xi’an Jiaotong Univ. (Soc. Sci.) 2016, 36, 10–16. [Google Scholar]
- Shen, Y.C.; Yue, S.J.; Sun, S.Q.; Guo, M.Q. Sustainable Total Factor Productivity Growth: The Case of China. J. Clean. Prod. 2020, 256, 120727. [Google Scholar] [CrossRef]
- Lou, Y.; Tian, Y.; Tang, X. Does Environmental Regulation Improve and Enterprise’s Productivity?—Evidence from China’s Carbon Reduction Policy. Sustainability 2020, 12, 6742. [Google Scholar] [CrossRef]
- Zhao, M.L.; Liu, F.Y.; Sun, W.; Tao, X. The Relationship between Environmental Regulation and Green Total Factor Productivity in China: An Empirical Study Based on the Panel Data of 177 Cities. Int. J. Environ. Res. Public Health 2020, 17, 5287. [Google Scholar] [CrossRef] [PubMed]
- Johnstone, N.; Managi, S.; Rodriguez, M.C.; Hascic, I.; Fujii, H.; Souchier, M. Environmental Policy Design, Innovation and Efficiency Gains in Electricity Generation. Energy Econ. 2017, 63, 106–115. [Google Scholar] [CrossRef]
- He, Y.M.; Luo, Q. Environmental Regulation, Technological Innovation and Industrial Total Factor Productivity of China—Reexamination of the Strong Potter Hypothesis. Soft Sci. 2018, 32, 20–25. [Google Scholar]
- Li, B.; Peng, X.; Ouyang, M.K. Environmental Regulation, Green Total Factor Productivity and the Transformation of China’s Industrial Development Mode—Analysis Based on Data of China’s 36 Industries. China Ind. Econ. 2013, 4, 56–68. [Google Scholar]
- Elgin, C.; Oztunali, O. Environmental Kuznets Curve for the Informal Sector of Turkey (1950–2009). Panoeconomicus 2014, 61, 471–485. [Google Scholar] [CrossRef]
- Albrizio, S.; Kozluk, T.; Zipperer, V. Environmental Policies and Productivity Growth: Evidence across Industries and Firms. J. Environ. Econ. Manag. 2017, 81, 209–226. [Google Scholar] [CrossRef]
- Zhao, X.M.; Liu, C.J.; Yang, M. The Effects of Environmental Regulation on China’s Total Factor Productivity: An Empirical Study of Carbon-Intensive Industries. J. Clean. Prod. 2018, 179, 325–334. [Google Scholar] [CrossRef]
- Wang, J.; Liu, B. Environmental Regulation and Enterprises’ TFP—An Empirical Analysis Based on China’s Industrial Enterprises Data. China Ind. Econ. 2014, 3, 44–56. [Google Scholar]
- Jin, Y.G.; Chang, R. Environmental Regulation and Industrial Total Factor Productivity: An Empirical Study on the Dynamic Panel Data of 280 Prefecture Level Cities. J. Econ. Prob. 2016, 11, 18–23. [Google Scholar]
- Tong, J.; Liu, W.; Xue, J. Environmental Regulation, Factor Input Structure and Industrial Transformation. Econ. Res. J. 2016, 51, 43–57. [Google Scholar]
- Barbera, A.J.; McConnell, V.D. The Impact of Environmental Regulations on Industry Productivity: Direct and Indirect Effects. J. Environ. Econ. Manag. 1990, 18, 50–65. [Google Scholar] [CrossRef]
- Zhao, X.M.; Liu, C.J.; Sun, C.W.; Yang, M. Does Stringent Environmental Regulation Lead to a Carbon Haven Effect? Evidence from Carbon-intensive Industries in China. Energy Econ. 2020, 86, 104631. [Google Scholar] [CrossRef]
- Chen, C.F.; Han, J.; Mao, Y.L. Environmental Regulation, Industrial Heterogeneity and Industrial Green Growth in China—a Nonlinear Test from the Perspective of Total Factor Productivity. J. Shanxi Univ. Financ. Econ. 2018, 40, 65–80. [Google Scholar]
- Ju, K.Y.; Zhou, D.J.; Wu, J.M. Can Environmental Regulation a “Win-Win” Strategy?—Strong Porter Hypothesis Research on China’s Industry. J. Beijing Inst. Technol. (Soc. Sci. Ed.) 2020, 22, 21–28. [Google Scholar]
- Lee, E. Environmental Regulation and Financial Performance in China: An Integrated View of the Porter Hypothesis and Institutional Theory. Sustainability 2020, 12, 10183. [Google Scholar] [CrossRef]
- Berman, E.; Bui, L.T.M. Environmental Regulation and Productivity: Evidence from Oil Refineries. Rev. Econ. Stat. 2001, 83, 498–510. [Google Scholar] [CrossRef]
- Piot-Lepetit, I.; Le Moing, M. Productivity and Environmental Regulation: The Effect of the Nitrates Directive in the French Pig Sector. Environ. Resour. Econ. 2007, 38, 433–446. [Google Scholar] [CrossRef]
- Lanoie, P.; Patry, M.; Lajeunesse, R. Environmental Regulation and Productivity: Testing the Porter Hypothesis. J. Prod. Anal. 2008, 30, 121–128. [Google Scholar] [CrossRef]
- Hancevic, P.I. Environmental Regulation and Productivity: The Case of Electricity Generation under the CAAA-1990. Energy Econ. 2016, 60, 131–143. [Google Scholar] [CrossRef]
- Manello, A. Productivity Growth, Environmental Regulation and Win-win Opportunities: The Case of Chemical Industry in Italy and Germany. Eur. J. Oper. Res. 2017, 262, 733–743. [Google Scholar] [CrossRef]
- Guner, N.; Ventura, G.; Xu, Y. Macroeconomic Implications of Size-Dependent Policies. Rev. Econ. Dyn. 2008, 11, 721–744. [Google Scholar] [CrossRef]
- Song, S.; Yi, D.T. The Fundraising Efficiency in U.S. Non-Profit Art Organizations: An Application of a Bayesian Estimation Approach using the Stochastic Frontier Production Model. J. Prod. Anal. 2011, 35, 171–180. [Google Scholar] [CrossRef]
- Buera, F.J.; Shin, Y. Financial Frictions and the Persistence of History: A Quantitative Exploration. J. Political Econ. 2013, 121, 221–272. [Google Scholar] [CrossRef]
- Fontagne, L.; Santoni, G. Agglomeration Economies and Firm-Level Labor Misallocation. J. Econ. Geogr. 2019, 19, 251–272. [Google Scholar] [CrossRef]
- Buera, F.J.; Kaboski, J.P.; Shin, Y. Finance and Development: A Tale of Two Sectors. Am. Econ. Rev. 2011, 101, 1964–2002. [Google Scholar] [CrossRef]
- Jovanovic, B. Misallocation and Growth. Am. Econ. Rev. 2014, 104, 1149–1171. [Google Scholar] [CrossRef]
- Qian, X.; Cai, Y. A Survey on Measurements of Resource Misallocation. J. Beijing Technol. Bus. Univ. (Soc. Sci.) 2014, 29, 116–126. [Google Scholar]
- Hsieh, C.T.; Klenow, P.J. Misallocation and Manufacturing TFP in China and India. Quart. J. Econ. 2009, 124, 1403–1448. [Google Scholar] [CrossRef]
- Aoki, S. A Simple Accounting Framework for the Effect of Resource Misallocation on Aggregate Productivity. J. Jpn. Int. Econ. 2012, 26, 473–494. [Google Scholar] [CrossRef]
- Bartelsman, E.; Haltiwanger, J.; Scarpetta, S. Cross-Country Differences in Productivity: The Role of Allocation and Selection. Am. Econ. Rev. 2013, 103, 305–334. [Google Scholar] [CrossRef]
- Midrigan, V.; Xu, D.Y. Finance and Misallocation: Evidence from Plant-Level Data. Am. Econ. Rev. 2014, 104, 422–458. [Google Scholar] [CrossRef]
- Tombe, T.; Winter, J. Environmental Policy and Misallocation: The Productivity Effect of Intensity Standards. J. Environ. Econ. Manag. 2015, 72, 137–163. [Google Scholar] [CrossRef]
- Han, C.; Zhang, W.G.; Feng, Z.B. How Does Environmental Regulation Remove Resource Misallocation—An Analysis of the First Obligatory Pollution Control in China. China Ind. Econ. 2017, 4, 115–134. [Google Scholar]
- Dong, Z.Q.; Hu, S.M.; Wang, L.H. Misallocation of Innovation Factors: A Comparative Study Based on the Spatial Spillover Effects. Zhejiang Acad. J. 2020, 2, 136–145. [Google Scholar]
- Li, G.; Dong, M.J.; Shen, K.T. The Impact of Intensified Environmental Regulations Policies on China’s Economic Growth—An Assessment Based on CGE Model. China Ind. Econ. 2012, 11, 5–17. [Google Scholar] [CrossRef]
- Li, L.; Tao, F. Selection of Optimal Environmental Regulation Intensity for Chinese Manufacturing Industry—Based on the Green TFP Perspective. China Ind. Econ. 2012, 5, 70–82. [Google Scholar]
- Anselin, L.; Bera, A.K.; Florax, R.; Yoon, M.J. Simple Diagnostic Tests for Spatial Dependence. Reg. Sci. Urban. Econ. 1996, 26, 77–104. [Google Scholar] [CrossRef]
- LeSage, J.P.; Pace, R.K. Introduction to Spatial Econometrics; Taylor and Francis: Boca Raton, FL, USA, 2009. [Google Scholar]
- Wang, Y.; Li, J.M. Measurement of Environmental Regulation Intensity, Potential Problems and its Correction. Collect. Essays Financ. Econ. 2015, 194, 98–106. [Google Scholar]
- Jin, L.Q. Analysis of Resources Misallocation among Regions from 1992 to 2015. Soc. Sci. Beijing 2018, 1, 57–66. [Google Scholar]
- Zhang, J.Q.; Gong, E.Z.; Sun, Y.Y. How Will Environmental Regulation Effect TFP of Manufacturing in Yangtze River Economic Belt? Stud. Sci. Sci. 2019, 37, 1558–1569. [Google Scholar]
- Kumar, S.; Managi, S. Environmental Productivity and Kuznets Curve. Ecol. Econ. 2008, 65, 432–440. [Google Scholar]
- Elhorst, J.P. Spatial Econometrics: From Cross-Sectional Data to Spatial Panels; Springer: New York, NY, USA, 2014. [Google Scholar]
- Shapiro, J.S.; Walker, R. Why Is Pollution from US Manufacturing Declining? The Roles of Environmental Regulation, Productivity, and Trade. Am. Econ. Rev. 2018, 108, 3814–3854. [Google Scholar] [CrossRef]
- Restuccia, D.; Rogerson, R. Policy Distortions and Aggregate Productivity with Heterogeneous Establishments. Rev. Econ. Dyn. 2008, 11, 707–720. [Google Scholar] [CrossRef]
- Kim, H.; Kim, D.; Paul, C.; Lee, C.K. The Spatial Allocation of Hospitals With Negative Pressure Isolation Rooms in Korea: Are We Prepared for New Outbreaks? Int. J. Health Policy Manag. 2020, 9, 475–483. [Google Scholar]
- Brandt, L.; Tombe, T.; Zhu, X. Factor Market Distortions across Time, Space and Sectors in China. Rev. Econ. Dyn. 2013, 16, 39–58. [Google Scholar] [CrossRef]
| Variable | Description | Mean | Std.Dev | Min | Max |
|---|---|---|---|---|---|
| TFP | Industrial total factor productivity | 3.028 | 2.179 | 0.066 | 17.041 |
| ER | Environmental regulation intensity | 0.281 | 0.241 | 0.023 | 2.548 |
| MisK | Degree of capital misallocation | 1.500 | 1.236 | 0.234 | 9.840 |
| MisL | Degree of labor misallocation | 1.154 | 0.610 | 0.341 | 4.042 |
| Lnpgdp | The level of economic development | 9.828 | 0.913 | 7.719 | 11.768 |
| Indstrc | Industrial structure | 0.865 | 0.074 | 0.622 | 0.996 |
| Lnfdi | Degree of openness | 11.792 | 2.000 | 0.693 | 15.090 |
| Lnexpdt | Government regulation and control ability | 6.941 | 1.270 | 3.515 | 9.618 |
| Variable | TFP | |||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| ER | −1.234 ** (0.483) | −1.184 ** (0.485) | ||
| ER2 | 0.337 (0.264) | 0.277 (0.264) | ||
| MisK | −0.718 *** (0.114) | −0.726 *** (0.117) | ||
| MisL | −0.403 ** (0.180) | −0.368 ** (0.175) | ||
| Lnpgdp | 1.680 *** (0.425) | 2.972 *** (0.557) | 1.019 ** (0.518) | 1.200 ** (0.544) |
| Indstrc | −10.452 *** (1.915) | −11.808 *** (2.329) | −5.242 ** (2.306) | −6.430 *** (2.287) |
| Lnfdi | −0.863 *** (0.076) | −0.832 *** (0.079) | −0.678 *** (0.079) | −0.662 *** (0.074) |
| Lnexpdt | 0.962 *** (0.299) | 0.660 (0.502) | 0.378 (0.473) | 0.254 (0.473) |
| W×ER | −1.760 * (0.970) | |||
| W×ER2 | 1.335 *** (0.515) | |||
| W×MisK | −1.142 *** (0.240) | |||
| W×MisL | 0.011 * (0.006) | |||
| W×Lnpgdp | −3.929 *** (0.742) | −2.857 *** (0.918) | ||
| W×Indstrc | −7.950 ** (3.287) | −14.848 *** (4.377) | ||
| W×Lnfdi | 0.367 ** (0.156) | 0.903 *** (0.163) | ||
| W×Lnexpdt | 2.118 *** (0.635) | 0.166(0.909) | ||
| Spatial | 0.098 * (0.054) | 0.187 *** (0.053) | ||
| R2 | 0.769 | 0.791 | 0.795 | 0.826 |
| N. Observation | 651 | 651 | 651 | 651 |
| fixed effects of provinces | Yes | Yes | Yes | Yes |
| fixed effects of years | No | No | Yes | Yes |
| Robust LM-lag | 1.907 [0.167] | 32.604 *** [0.000] | ||
| Robust LM-error | 3.957 ** [0.047] | 45.565 *** [0.000] | ||
| LR spatial FE | 565.545 *** [0.000] | 549.485 *** [0.000] | ||
| LR year FE | 10.828 [0.966] | 35.878 ** [0.023] | ||
| Wald spatial lag | 60.682 *** [0.000] | 99.919 *** [0.000] | ||
| Wald spatial error | 55.955 *** [0.000] | 78.281 *** [0.000] | ||
| Hausman test | 32.119 *** [0.002] | 80.843 *** [0.000] |
| Direct Effect | Spatial Spillover Effect | Total Effect | ||
|---|---|---|---|---|
| (1) | ER --> TFP | −1.221 ** (0.477) | −2.040 * (1.064) | −3.261 *** (1.114) |
| (2) | ER2 --> TFP | 0.304 (0.271) | 1.474 *** (0.571) | 1.778 *** (0.641) |
| (3) | MisK --> TFP | −0.678 *** (0.124) | −1.195 *** (0.284) | −1.873 *** (0.312) |
| (4) | MisL --> TFP | −0.372 ** (0.176) | 0.015 ** (0.007) | −0.357 *** (0.097) |
| (5) | ER --> MisK | −0.381 *** (0.096) | −0.092 (0.202) | −0.473 ** (0.223) |
| (6) | ER --> MisL | −0.083 (0.061) | −0.243 ** (0.121) | −0.325 ** (0.133) |
| Variable | MisK | MisL | ||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| ER | −0.597 *** (0.097) | −0.338 *** (0.093) | −0.087 (0.061) | −0.083 (0.060) |
| Lnpgdp | −0.115 *** (0.019) | −0.788 *** (0.208) | −1.181 *** (0.119) | −1.212 *** (0.133) |
| Indstrc | 5.359 *** (0.890) | 6.519 *** (0.893) | 2.688 *** (0.561) | 2.503 *** (0.577) |
| Lnfdi | 0.171 *** (0.030) | 0.144 *** (0.030) | 0.084 *** (0.019) | 0.087 *** (0.019) |
| Lnexpdt | −1.308 *** (0.181) | −0.822 *** (0.188) | −0.496 *** (0.114) | −0438 *** (0.121) |
| W × ER | −0.097(0.189) | −0.253 ** (0.122) | ||
| W × Lnpgdp | 2.176 *** (0.331) | 2.090 * (1.132) | ||
| W × Indstrc | −1.151 (1.757) | −0.262 (0.227) | ||
| W × Lnfdi | 0.185 *** (0.067) | 0.136 *** (0.044) | ||
| W × Lnexpdt | −2.141 *** (0.365) | −0.317 (0.231) | ||
| Spatial | 0.529 *** (0.057) | 0.046 ** (0.021) | ||
| R2 | 0.899 | 0.907 | 0.835 | 0.841 |
| N. Observation | 651 | 651 | 651 | 651 |
| fixed effects of provinces | Yes | Yes | Yes | Yes |
| fixed effects of years | Yes | Yes | Yes | Yes |
| Robust LM-lag | 8.654 *** [0.003] | 5.148 ** [0.023] | ||
| Robust LM-error | 10.351 *** [0.001] | 8.262 *** [0.004] | ||
| LR spatial FE | 1153.430 *** [0.000] | 948.556 *** [0.000] | ||
| LR year FE | 81.025 *** [ 0.000] | 160.132 *** [0.000] | ||
| Wald spatial lag | 50.950 *** [0.000] | 16.761 *** [0.005] | ||
| Wald spatial error | 50.965 *** [0.000] | 16.401 *** [0.006] | ||
| Hausman test | 81.895 *** [0.000] | 31.947 *** [0.002] |
| Variable | TFP | ||
|---|---|---|---|
| (1) | (2) | (3) | |
| ER | −0.849 *** (0.222) | −0.820 *** (0.234) | −0.803 *** (0.225) |
| MisK | −0.852 *** (0.095) | −0.729 *** (0.111) | |
| MisL | −1.028 *** (0.150) | −0.358 ** (0.173) | |
| Lnpgdp | 1.598 *** (0.510) | 2.010 *** (0.492) | 1.947 *** (0.479) |
| Indstrc | −6.250 *** (2.262) | −9.7605 *** (2.183) | −5.776 *** (2.173) |
| Lnfdi | −0.671 *** (0.073) | −0.680 *** (0.075) | −0.631 *** (0.073) |
| Lnexpdt | 0.442 (0.466) | 0.180 (0.352) | −0.103 (0.353) |
| W × ER | 0.581 (0.455) | 0.746 (0.486) | 0.660 (0.468) |
| W × MisK | 1.225 *** (0.207) | 0.936 *** (0.229) | |
| W × MisL | 1.629 *** (0.339) | 1.385 *** (0.381) | |
| W × Lnpgdp | −2.597 *** (0.823) | −2.189 *** (0.860) | −2.155 *** (0.837) |
| W × Indstrc | −16.768 *** (4.311) | −8.839 ** (4.287) | −13.192 *** (4.225) |
| W × Lnfdi | 0.855 *** (0.162) | 0.839 *** (0.160) | 0.891 *** (0.155) |
| W × Lnexpdt | 0.125 (0.900) | −0.028 (0.736) | 0.101 (0.761) |
| Spatial | 0.196 *** (0.052) | 0.121 ** (0.053) | 0.174 ***(0.051) |
| R2 | 0.829 | 0.696 | 0.719 |
| N. Observation | 651 | 651 | 651 |
| fixed effects of provinces | Yes | No | No |
| fixed effects of years | Yes | Yes | Yes |
| Wald spatial lag | 105.767 *** [0.000] | 98.668 *** [0.000] | 96.965 *** [0.000] |
| Wald spatial error | 81.402 *** [0.000] | 85.108 *** [0.000] | 76.138 *** [0.000] |
| Hausman test | 20.138 * [0.092] | 7.287 [0.887] | 19.705 [0.184] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, X.; Yang, Y.; Zhao, X.; Feng, Y.; Liu, C. Environmental Regulation, Resource Misallocation and Industrial Total Factor Productivity: A Spatial Empirical Study Based on China’s Provincial Panel Data. Sustainability 2021, 13, 2390. https://doi.org/10.3390/su13042390
Dong X, Yang Y, Zhao X, Feng Y, Liu C. Environmental Regulation, Resource Misallocation and Industrial Total Factor Productivity: A Spatial Empirical Study Based on China’s Provincial Panel Data. Sustainability. 2021; 13(4):2390. https://doi.org/10.3390/su13042390
Chicago/Turabian StyleDong, Xu, Yali Yang, Xiaomeng Zhao, Yingjie Feng, and Chenguang Liu. 2021. "Environmental Regulation, Resource Misallocation and Industrial Total Factor Productivity: A Spatial Empirical Study Based on China’s Provincial Panel Data" Sustainability 13, no. 4: 2390. https://doi.org/10.3390/su13042390
APA StyleDong, X., Yang, Y., Zhao, X., Feng, Y., & Liu, C. (2021). Environmental Regulation, Resource Misallocation and Industrial Total Factor Productivity: A Spatial Empirical Study Based on China’s Provincial Panel Data. Sustainability, 13(4), 2390. https://doi.org/10.3390/su13042390







