A Fuzzy-AHP Methodology for Planning the Risk Management of Natural Hazards in Surface Mining Projects
Abstract
1. Introduction
- -
- A hazard is a potentially damaging physical event, phenomenon, or human activity that may cause the loss of life or injury, property damage, social and economic disruption, or environmental degradation;
- -
- A disaster is a severe disruption of the functioning of a community or a society causing widespread human, material, economic or environmental losses which exceed the ability of the affected community or society to cope using its resources;
- -
- Risk is the probability of occurrence of an uncertain event multiplied by the resulting cost or benefit, if this event takes place.
- Drastic changes of natural terrains relief, landscape, and topography,
- Reduction of soil cohesion resulting from intensive excavations and pits opening,
- Soil liquefaction related to the use of explosives and vibrations generated by heavy-duty excavation equipment and means for transportation of ore (shovels, belt conveyors, wagons, etc.),
- Soil disturbance due to the opening of access roads and site grading/levelling works,
- Modifications of hydrology, according to mine development and closure,
- Lowering of soil consistency caused by the removal of topsoil and planation systems,
- Effects on slope stability [1],
- Disposal of excavated ore piles, waste material, surplus soil or aggregates,
- Intensive and extended utilization of technical means/machinery for increasing ore production,
- Reduction of the mining system environmental sustainability.
2. Risk Management: Problems and Research Questions
- (a)
- The validity of risk analysis depends on the availability and reliability of actual data (frequency, intension, duration, location, meteorological parameters, etc.) collected through various methods and at different levels of accuracy. Often, these data are insufficient, heterogeneous, or less appropriate for use [36,37,38].
- (b)
- Each mine has its own meteorological, topographical, geological, environmental, and hydrological features. For example, one mine at a long distance from the sea is less prone to extreme sea water movements (e.g., tsunamis), while another mine might operate at a location prone to seismic activity. Therefore, the criticality and impact of identified hazards differ significantly from one mine to another [12,13,14].
- (c)
- The vulnerability of a particular mine depends on the efficiency of proactive measures taken against potential disasters. It relates to the efficiency of safety measures [39] for quick evacuation of personnel, transfer of valuable machinery at safer locations, or saving of expensive field equipment, in cases of emergency. Mining industry experience shows that not all mines have the same level of readiness for withstanding natural hazards.
- (d)
- The phase of the life cycle that a surface mine operates is another aspect related to the magnitude of risks. For instance, due to the extended geoenvironmental changes, a mine entering the closing phase seems to be likely more vulnerable and highly exposed to natural hazards than another mine running the exploitation, or early development phase [13,14].
- (1)
- How should the natural hazard risks be assessed based on scientific reasoning and acquisition of empirical evidence, judgement, and knowledge from mining experts?
- (2)
- Is it possible to organize and execute the prevention of mine disasters in terms of a project embodying the theoretical background and practices of project and risk management?
- (3)
- Are there any methods, tools, or techniques appropriate for a mathematically consistent determination of the probability that a natural hazard event will occur with effects to mining operations and for a proactive risk impact analysis as well?
- (4)
- Is it possible to define the elements at risk and to use them in disastrous scenarios analyses?
- (5)
- Is there any substantial methodology for quantitative evaluations of time and cost overruns required for a useful pre-disaster management project and the implementation of post-disaster recovery and restoration measures/means/actions in a mine?
3. Materials and Methods
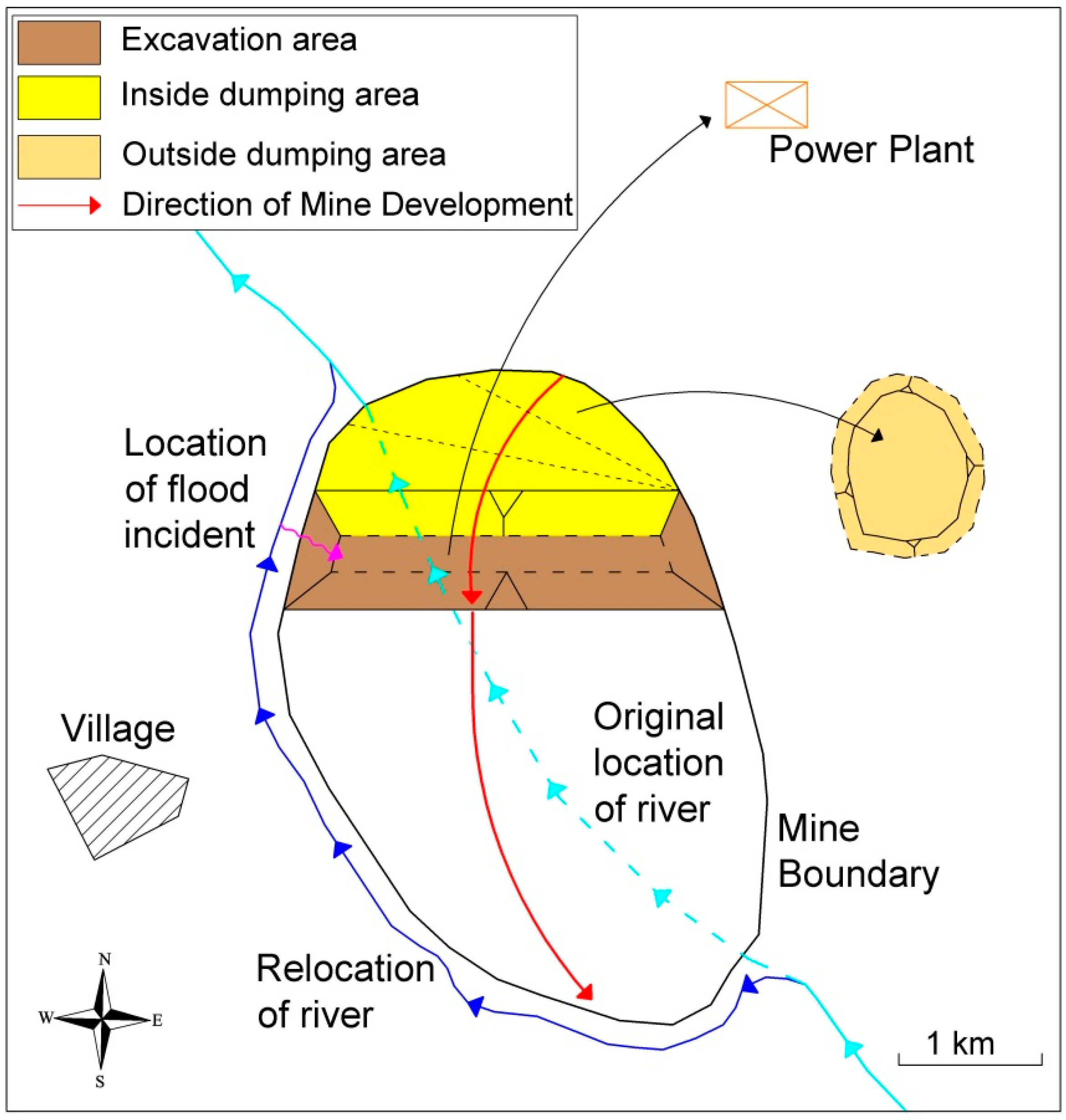
3.1. Surface Mining Project Setting
3.2. Proposed Methodology
3.2.1. General Concept
- (a)
- Understanding the origin, content, magnitude, and potential impacts of natural hazards.
- (b)
- Determination of the probability, in the form of weight factors and sub-factors, that natural hazards risk will occur, by applying the Fuzzy Analytical Hierarchy Process (FAHP) method. The mathematical calculations of FAHP embody data collected from empirical evidence and aggregation of knowledge from experts in the mining industry.
- (c)
- Structuring a risk and impact severity matrix enabling the multidisciplinary evaluation and classification of impacts to the elements at risk of a typical surface mining system.
- (d)
- Development of a hazardous scenario for a surface mine and elaboration of a techno-economic analysis of post-disaster cost and time overruns, using the Expected Value (EV) function for prediction of the restoration cost using also the Monte Carlo simulation and Program Evaluation Review Technique PERT technique for the prediction of critical cost and time parameters.
3.2.2. AHP and Fuzzy AHP
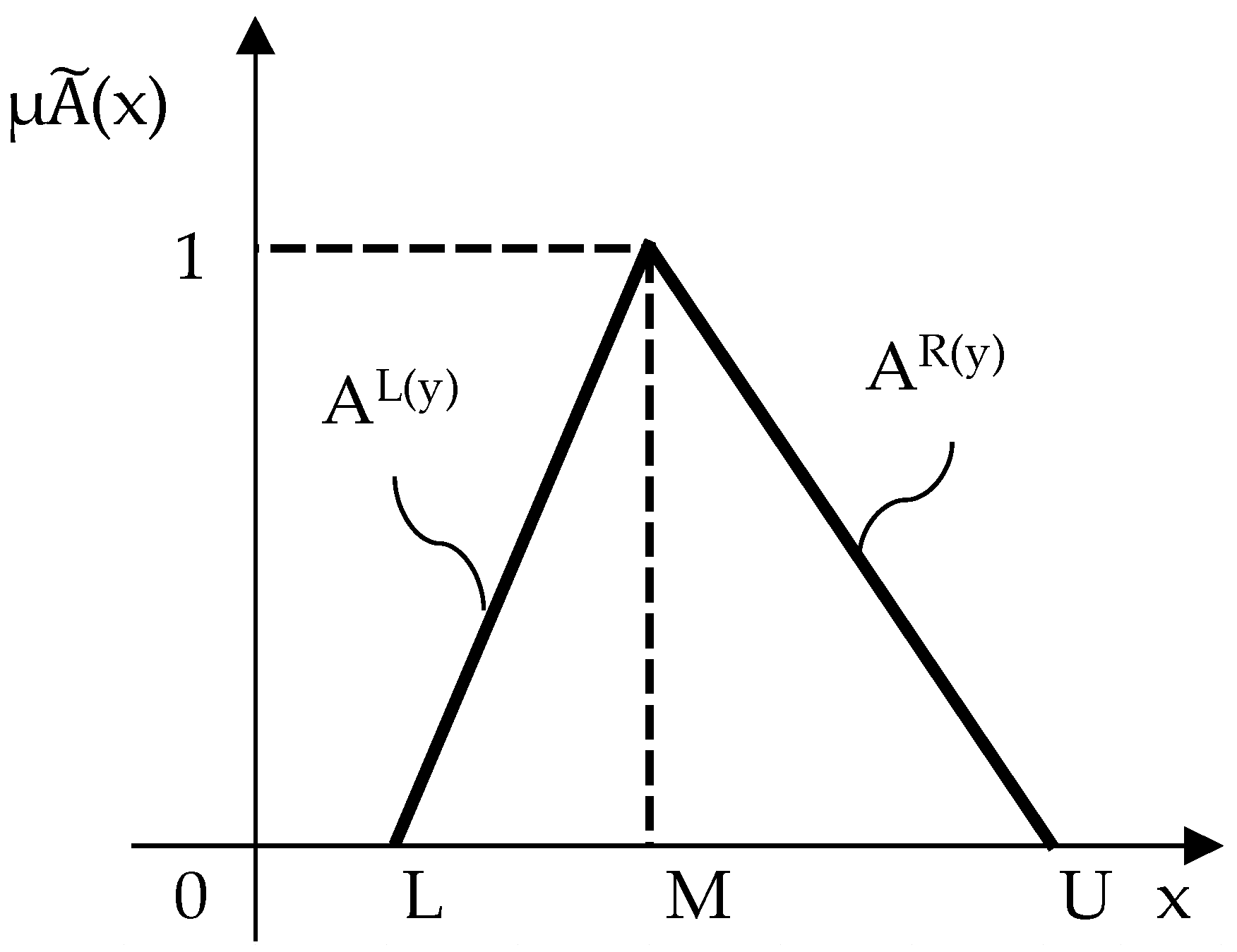
3.2.3. Mathematical Definitions and Operations
- (a)
- DefinitionsR: the set of real numbers; N: the set of natural numbersL1 > 0; L2 > 0; M1 > 0; M2 > 0; U1 > 0; U2 > 0; p ∈ R; p > 0; q ∈ R; q ≠ 0;{Lm, Mm, Um} ∈ R; L < M < U; m ∈ N;
- (b)
- Addition of two TFNs ⊕:
- (c)
- Multiplication of two TFNs ⊗:
- (d)
- Subtraction of two TFNs ⊖:Division of two TFNs ⊘:
- (e)
- Multiplication of a TFN by a constant p:
- (f)
- Division of a TFN by a constant q:
3.2.4. The Triangular FAHP Method
- Step-1:
- Formulation of a team of experts consisted of two (2) experts from a surface mine operating in northern Greece and one (1) expert from an engineering company involved with projects of the energy sector. The experts filled up a questionnaire properly structured for making a linguistic evaluation of the probability, as risk factor and sub-factor, that each hazard will occur;
- Step-2:
- Setting up the goal, the hierarchy, and identity of each risk factor and sub-factor;
- Step-3:
- Construction of the pair-wise comparison matrix, [ak], the elements of which aijk represent the kth experts’ preference of the risk factor i over the risk factor j; i, j ∈ N. The fundamental relationship between the elements of the reciprocal matrix is (aij).(aji)=1;
- Step-4:
- Production of the average pair-wise comparison matrix, [a] with elements the average values of experts’ preferences by applying Equation (10):
- Step-5:
- Construction of the fuzzy pairwise comparison matrix [] [ã] with elements the fuzzy values, ãij using the linguistic scale of membership function and the operations of TFNs numerical conversion (Table 2).
- Step-6:
- Calculation of the fuzzy geometric mean value of each risk factor i, according to Buckley’s approach (Equation (11)):Upon determination of geometric means, the vector of fuzzy geometric risk factors is formulated (Equation (12)):
- Step-6:
- Step-7: Definition of the fuzzy risk factors (i.e., the fuzzy relative weights) i, as follows (Equation (13)):
- Step-6:
- Step-8: De-fuzzification of the fuzzy relative weights i, to determine the crisp values Wi, using the Centre of the Area (CoA) method by applying Equation (14) [72]:
- Step-6:
- Step-9: Normalisation of the De-fuzzified relative weights i by applying Equation (15):
- Step-6:
- Step-10: Determination of the Consistency Index (CI) value of the FAHP using Equation (16):where λmax is the largest eigenvalue of the pair-wise comparison matrix.
- Step-6:
- Step-11: determination of the Consistency Ratio (CR) using Equation (17):where RI(n) is a Random Index shown in Table 3 [51,73] that depends on the number of risk factors, n. If CR < 0.1, the pair-wise comparison matrix is mathematically consistent and acceptable [51], and the calculated risk factors can be used to analyse disastrous scenarios. Otherwise, a new loop for the questionnaire review by experts is required until the mathematical consistency has been achieved.
3.2.5. Risk Breakdown Structure
4. Results
4.1. Application of FAHP
4.2. Risk Assessment
- -
- Partial destruction of electrical installations and equipment
- -
- Damage to the roofs of building facilities
- -
- Two (2) weeks stoppage of lignite production caused by the forced shutdown of mining activities
- -
- Destruction of pit surfaces, trenches and slopes (4% of the mine surface)
- -
- Loss of lignite material (7% of the mine surface) at descended locations
- -
- Complete destruction of two (2) mining equipment units
- -
- Complete destruction of two (2) belt conveyor lines
4.3. Pre-Disaster Analysis
5. Discussion
- (a)
- FAHP is a group decision-making method widely used in mining research as a stand-alone method or combined with other methods [38,58]. FAHP, being more sophisticated and requiring calculations of higher complexity to those of simple AHP, enables the transformation of decision-making problems into objective evaluations. The experts participating in these evaluations use linguistic expressions to explicitly convey their knowledge, which in turn becomes transformable into numerical form via the mathematical rules and operations of fuzzy logic theory. The use of questionnaires ensures confidentiality, objectivity, and quick collection of primary data and validation of the produced results. If so required, several rounds of questionnaire delivery can be arranged for improvement of performance and consistency. The FAHP results can be communicated in simplified forms of presentation, allowing mining executives and operations managers an easy understanding of the problem of natural hazards and the consequences these hazards are entailing for sustainable mining planning.On the other hand, FAHP has its weaknesses, such as computational complexity, mostly when the model of trapezoid membership function has chosen, misalignments of experts’ opinions in the pair-wise comparisons, and lowering of the whole performance insofar as the number of the criteria (in our case study: risk factors and sub-factors) under evaluation are getting increased. Notwithstanding the popularity, flexibility, practicality, and low development cost of FAHP, there are also other appropriate decision-making methods for risks quantification e.g., VIKOR (VIekriterijumsko KOmpromisno Rangiranje), DEMATEL(Decision Making Trial and Evaluation Laboratory), PROMETHEE, etc. or other combined methods like AHP/TOPSIS, FAHP/TOPSIS, AHP/PROMETHEE, which can produce results of similar reliability [12].It should be noted that the selection of the appropriate MCDM method for the determination of the risk factors/sub-factors depends on the philosophy and technical preferences of risk analysts. The FAHP Consistency Ratio (CR = 0.091) is marginally acceptable (i.e., Δ = 0.1 − 0.091 = 9.0 × 10−3), although the questionnaires sent twice to experts aiming to achieve the maximum alignment in the definition of values of the initial pre-fuzzy reciprocal matrix. This result might be seen as a gap attributable to perceptional inflexibility, subjectivity, or bias of each expert on how a particular natural hazard is figured out and how frequently it is expected to appear in a complex mining system of long-term exploitation life. For bridging this gap, one approach might be the enlargement of experts group by engaging experts from other scientific disciplines (geologists, meteorologists, etc.) with analogous skills and qualifications so that the average values of the elements in the initial pre-fuzzy reciprocal matrix become as objective as possible. However, the performance of this approach requires previous in-depth research and validation in conditions of real problem-solving assessments with different levels of complexity.
- (b)
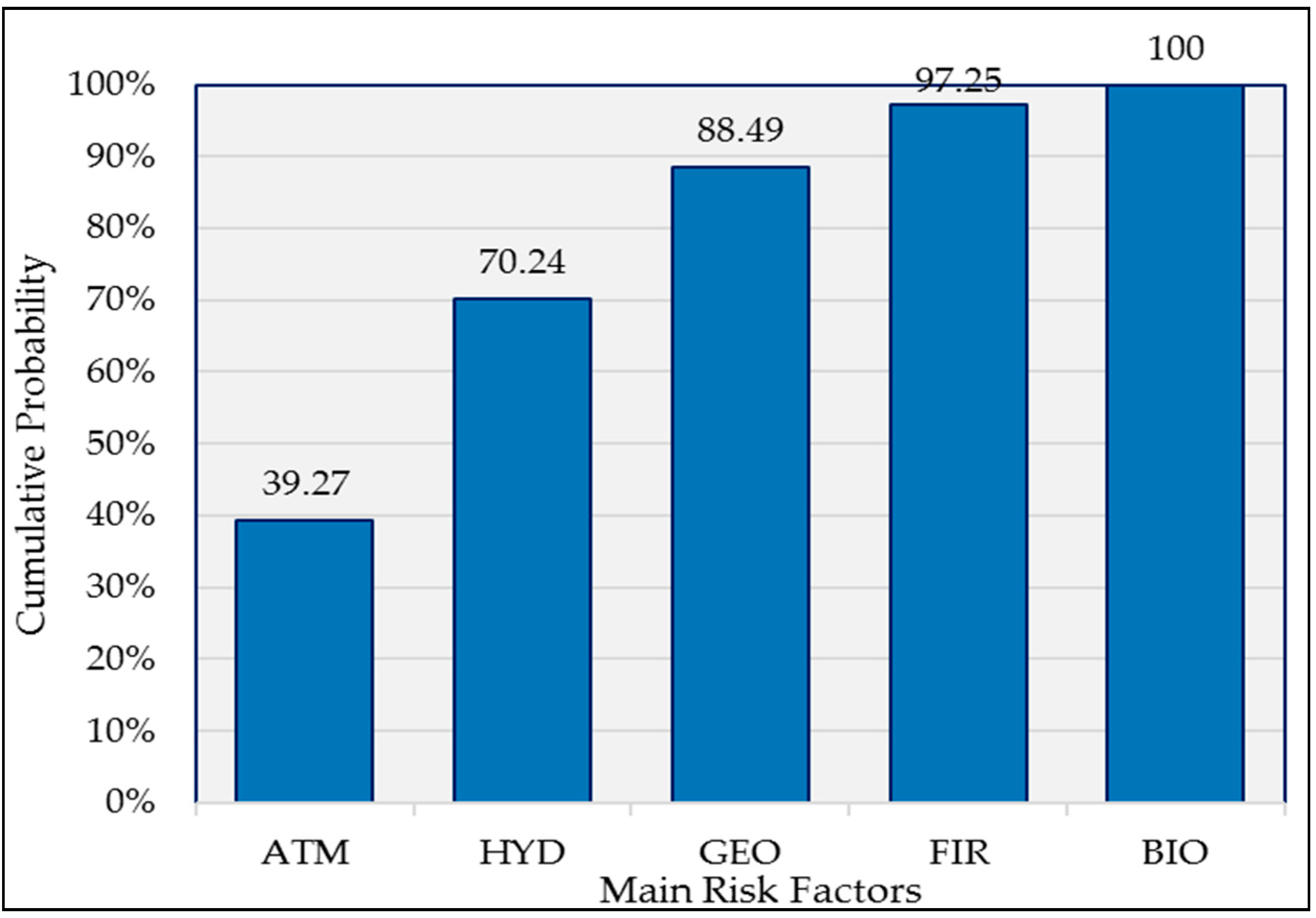
- Another remarkable observation is the high score of the cumulative probability of the meteorological and hydrological risks, which equals to 70.24% (Figure 4). This finding reflects the serious concerns of experts on the effects of climate change that might constitute an emerging and high consequence risk factor as reported in the literature in mine damages of a large scale [44,45,80]. Finally, the biological factors, although evaluated as of meagre probability score (2.75%), require further investigation with a focus on the widespread impacts in the mining industry, and beyond to the energy economy, as lessons of the COVID-19 pandemic crisis are dictating.
- (c)
- A pre-disaster planning project, to meet its objectives, requires a detailed analysis of all risks that might insert time and cost impacts, as well as safety and health problems for the working personnel in the mine. To this regard, FAHP has been a valuable tool for exploring and collecting expert’s knowledge that is particularly useful in quantifying the probability of risks with hazardous effects in mines [38,42,57]. Except for the contribution of FAHP in the determination of risk probabilities, the experts’ knowledge and the collection of data (cost and recovery time) from mining archives, contribute to the quantitative analysis of all potential disastrous scenarios and the definition of appropriate proactive and reactive activities and measures to be early taken in a mine [6]. Thus, the scope and capital expenditures (CAPEX) of a pre-disaster project can be reasonably estimated providing the basis with the mining executives to approve the implementation of such a project, under the condition that all other techno-economic parameters (net present value, internal rate of return, benefit/cost ratio-BCR, etc.) reflect the feasibility of the entire project.The pre-disaster projects must be organised and planned in terms of practicality, efficiency, efficacy, and cost-effectiveness, ensuring fast response in emergency conditions, whenever a disastrous event occurs. The essential functions of an integrated pre-disaster project planning are [30]:
- -
- Project definition (scope, time, budget, resources, limitations, and constraints)
- -
- Project development (planning, organisation, execution, monitoring, feedback, closeout)
- -
- Cost breakdown, budgetary and financial/investment analysis
- -
- Project hazardousness analysis and risk assessment
- -
- Analysis of the mine sustainability in normal and in post-hazard operation conditions
- -
- Pre-disaster preparedness management (functions, mechanisms, infrastructures, equipment, resources)
- -
- Post-disaster initiations and action planning (emergency plans, mitigation, relief, recovery, restoration and repairing actions, solutions for maintaining the mine sustainability, etc.)
- -
- Stakeholder management (mining staff, communities, authorities)
- -
- Health, safety, security, and environmental management (HSSE)
- -
- Project disclosure management
- -
- Training and readiness simulations for mining operators
To this viewpoint, the suggested methodology might be seen as a low cost and rapid development and performance tool for mining executives and managers constituting an adding value element in frameworks of pre-disaster projects planning. Moreover, it is a tool providing an effective response on issues related to several components of sustainable mining either directly, such as risk management, health and safety performance and prevention of environmental damages, or indirectly, such as responsible design and respect to the right of local communities. - (d)
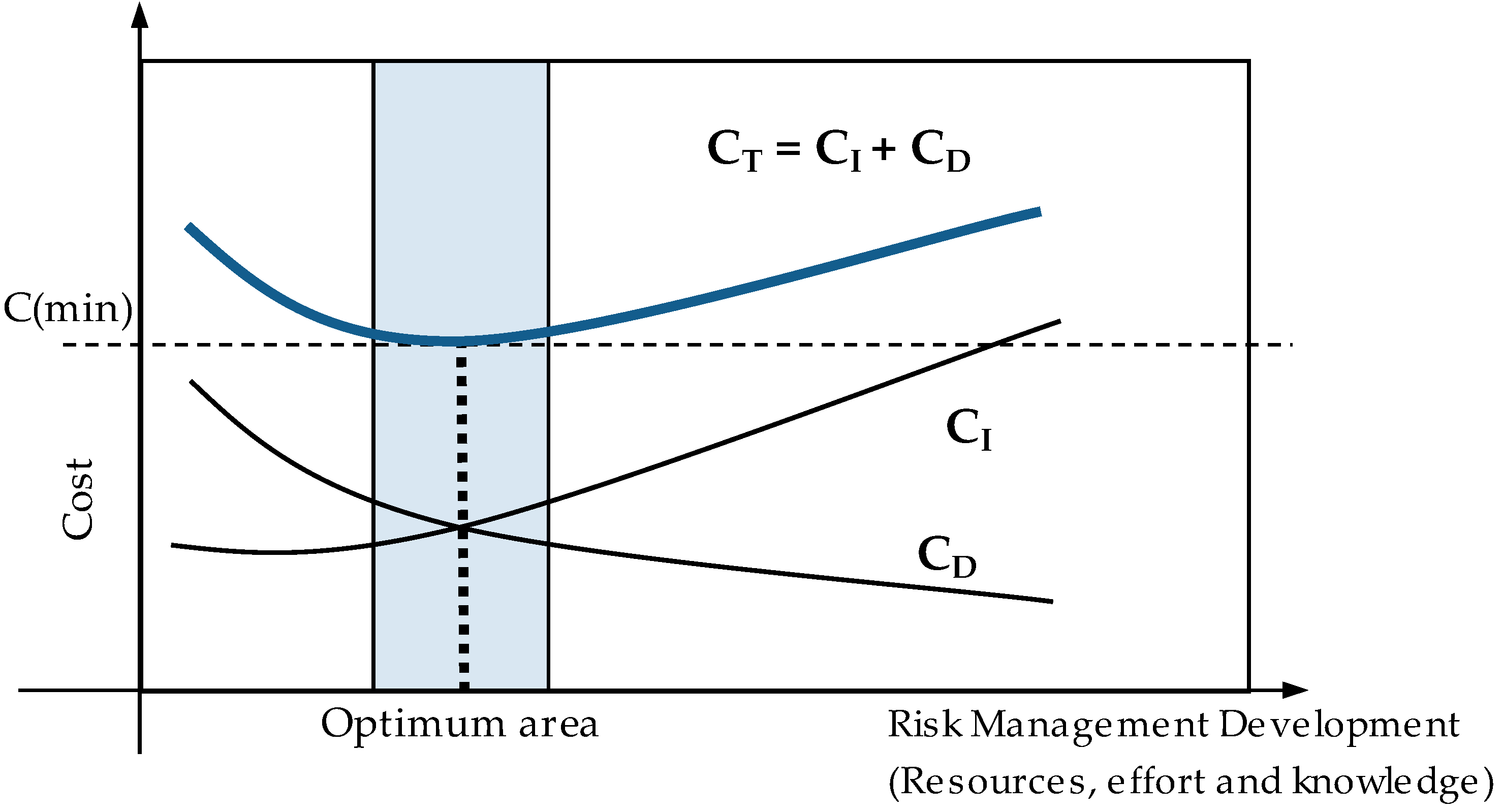
- The development of risk-based natural hazards analysis in mines has considerable techno-economic views. It is a matter of fact that risk analysis is an indispensable tool of project management and critical for the cost and extent of proactive/preventive measures to be taken in terms of efficient pre-disaster project development. Practice, however, dictates that indirect costs, CI, required for the development of risk and quality management (knowledge, resources, quality control, etc.) of a pre-disaster planning project, must be reasonable to enable the balance with the direct costs, CD, related to expenses for the prevention and readiness measures (availability of means and equipment, personnel training, mechanisms). In this way, the total cost of pre-disaster management that corresponds to an efficient level of quality and performance, CT, will obtain a minimum value, as explained by the following Equation (21):CT = CI + CD
6. Conclusions and Perspectives for Further Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Knabe, W. Methods and Results of Strip-Mine Reclamation in Germany. Ohio J. Sci. 1964, 64, 74–105. [Google Scholar]
- Chuman, T. Restoration Practices used on Post mining Sites and Industrial Deposits in the Czech Republic with an Example of Natural Restoration of Granodiorite Quarries and Spoil Heaps. J. Landsc. Ecol. 2015, 8, 29–46. [Google Scholar] [CrossRef]
- Kavvadas, M.; Roumpos, C.; Schilizzi, P. Investigation of the Stability of Deep Excavation Slopes in Continuous Surface Lignite Mines. In Proceedings of the 14th International Symposium of Continuous Surface Mining (ISCSM), Thessaloniki, Greece, 23–26 September 2018; pp. 377–393. [Google Scholar]
- UN-ISDR. Terminology of Disaster Risk reduction. United Nations; International Strategy for Disaster Reduction: Geneva, Switzerland, 2004. [Google Scholar]
- ADPC. Building Disaster Risk Reduction in Asia: A Way Forward ADPC Looks Ahead to 2015; Asian Disaster Preparedness Center: Bangkok, Thailand, 2004. [Google Scholar]
- Moe, T.L.; Pathranarakul, P. An integrated approach to natural disaster management. Disaster Prev. Manag. 2006, 15, 396–413. [Google Scholar] [CrossRef]
- Van Westen, C.J. Remote Sensing and GIS for Natural Hazards Assessment and Disaster Management; Schroder, J.F., Bishop, M.P., Eds.; Academic Press: San Diego, CA, USA, 2013. [Google Scholar]
- Hewitt, K. , Burton, I. The Hazardousness of a Place: A Regional Ecology of Damage Events; University of Toronto Press: Toronto, ON, Canada, 1971. [Google Scholar] [CrossRef]
- Dey, B.; Singh, R.B. Natural Hazards and Disaster Management. Central Board of Secondary Education (CBSE), 1st ed.; Central Board of Secondary Education: Delhi, India, 2006. [Google Scholar]
- Nelson, S. Natural Disasters & Assessing Hazards and Risk, Course Handout for Earth and Environmental Sciences 3050: Natural Disasters; Tulane University, Earth and Environmental Sciences Department: New Orleans, LA, USA, 2014. [Google Scholar]
- Roumpos, C.; Spanidis, P.-M. A project management approach to open – pit lignite mine planning and exploitation [open-pit project management]. World Coal 2003, 55–61. [Google Scholar]
- Spanidis, P.M.; Roumpos, C.; Pavloudakis, F. A Multi-Criteria Methodology for Low-Risk Evaluation of Mine Closure Restoration in Continuous Surface Lignite Mining Projects. In Proceedings of the 14th International Symposium of Continuous Surface Mining (ISCSM), Thessaloniki, Greece, 23–26 September 2018; pp. 563–578. [Google Scholar]
- Roumpos, C.; Spanidis, P.-M.; Pavloudakis, F. Land reclamation planning of continuous surface lignite mines in closure phase: A risk-based investigation. In Proceedings of the 14th International Symposium of Continuous Surface Mining (ISCSM), Thessaloniki, Greece, 23–26 September 2018; pp. 551–562. [Google Scholar]
- Pavloudakis, F.; Spanidis, P.-M.; Roumpos, C. Investigation of Natural and Technological Hazards and associated Risks in Surface Lignite Mines. In Proceedings of the 2nd International Conference on Natural Hazards & Infrastructure (ICONHIC), Chania, Crete, Greece, 23–26 June 2019. [Google Scholar]
- EM-DAT. The OFDA/CRED International Disaster Database; Universite Catholique de Louvain: Brussels, Belgium, 2009. [Google Scholar]
- Tischew, S.; Krimer, A.; Lorenz, A. Alternative Restoration Strategies in Former Lignite Mining Areas of Eastern Germany, Biodiversity: Structure and Function; EOLSS Publishers Co Ltd.: Oxford, UK, 2009. [Google Scholar]
- Kasztelewicz, Z. Approaches to post-mining land reclamation in Polish Opencast lignite mining. Civ. Environ. Eng. Rep. 2014, 12, 55–67. [Google Scholar] [CrossRef]
- Iannacchione, A.; Varley, F.; Brady, T. The Application of Major Hazard Risk Assessment (MHRA) to Eliminate Multiple Fatality Occurrences in the US Minerals Industry; Dept. of Health & Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, Spokane Research Laboratory Spokane: Washington, USA, 2008. [Google Scholar]
- Tripathy, D.P.; Ala, C.K. Identification of safety hazards in Indian underground coal mines. J. Sustain. Min. 2018, 17, 175–183. [Google Scholar] [CrossRef]
- Abbasi, S. Defining Safety Hazards & Risks in Mining Industry: A Case-Study in United States. Asian J. Appl. Sci. Technol. (AJAST) 2018, 2, 1071–1078. [Google Scholar]
- Domingues, C.R.; Martinez, I.V.; Pena, P.M.P.; Ochoa, A.R. Analysis and evaluation of risks in underground mining using the decision matrix risk-assessment (DMRA) technique, in Guanajuato, Mexico. J. Sustain. Min 2019, 18, 52–59. [Google Scholar] [CrossRef]
- Donoghue, A.M. Occupational health hazards in mining: An overview. Occup. Med. 2004, 54, 283–289. [Google Scholar] [CrossRef]
- Wang, Y.I.; Yang, W.; Li, M.; Liu, X. Risk assessment of floor water inrush in coal mines based on secondary fuzzy comprehensive evaluation. Int. J. Rock Mech. Min. Sci. 2012, 52, 50–55. [Google Scholar] [CrossRef]
- Pavloudakis, F.; Roumpos, C.; Galetakis, M. Public acceptance of surface mining projects and the determination of the marginal environmental cost. Int. J. Min. Reclam. Environ. 2012, 26, 292–308. [Google Scholar] [CrossRef]
- Azhari, A.; Ozbay, U. Investigating the effect of earthquakes on open pit mine slopes. Int. J. Rock Mech. Min. Sci. 2017, 100, 218–228. [Google Scholar] [CrossRef]
- Park, J.H.; Edraki, M.; Baumgartl, T. A practical testing approach to predict the geochemical hazards of in-pit coal mine tailings and rejects. CATENA 2017, 148, 3–10. [Google Scholar] [CrossRef]
- Kasap, Y.; Subaşı, E. Risk assessment of occupational groups working in open pit mining: Analytic Hierarchy Process. J. Sustain. Min. 2017, 16, 38–46. [Google Scholar] [CrossRef]
- Ferrari, F.; Giacomini, A.; Thoeni, K.; Lambert, C. Qualitative evolving rockfall hazard assessment for high-walls. Int. J. Rock Mech. Min. Sci. 2017, 98, 98–101. [Google Scholar] [CrossRef]
- McQuillan, A.; Canbulat, I.; Payne, D.; Oh, J. New risk assessment methodology for coal mine excavated slopes. Int. J. Min. Sci. Technol. 2018, 28, 583–592. [Google Scholar] [CrossRef]
- Lemly, A.D. Environmental hazard assessment of Benga Mining’s proposed Grassy Mountain Coal Project. Environ. Sci. Policy 2019, 96, 105–113. [Google Scholar] [CrossRef]
- Dos Santos, T.B.; Lana, M.S.; Pereira, T.C.; Canbulat, I. Quantitative hazard assessment system (Has-Q) for open pit mine slopes. Int. J. Min. Sci. Technol. 2019, 29, 419–427. [Google Scholar] [CrossRef]
- PMI. A Guide to Project Management Body of Knowledge (PMBOK), 6th ed.; Project Management Institute, Inc.: Newtown Square, PA, USA, 2019. [Google Scholar]
- O’Keefe, P.; Westgate, K.; Wisner, B. Taking the naturalness out of natural disasters. Nature 1976, 260, 566–567. [Google Scholar] [CrossRef]
- Baroudi, B.; Rapp, R. A project management approach to disaster response and recovery operations. In Proceedings of the 36th Australasian University Building Educators Association (AUBEA) Conference, Gold Coast, Australia, 27 April 2011; pp. 17–28. [Google Scholar]
- FEMA. HAZUS-MH. FEMA’s Methodology for Estimating Potential Losses from Disasters; US Federal Emergency Management Agency: Hyattsville, USA, 2004. [Google Scholar]
- Brundl, M.; Romang, H.E.; Bischof, N.; Rheinberger, C.M. The Risk concept and its application in Natural Hazard Risk Management in Switzerland. Nat. Hazards Earth Syst. Sci. 2009, 9, 801–813. [Google Scholar] [CrossRef]
- Yazdani-Chamzini, A.; Yakhchali, S.H. Handling equipment selection in open pit mines based on group decision making. Int. J. Ind. Eng. Comput. 2012, 3, 907–924. [Google Scholar] [CrossRef]
- Mahase, M.J.; Musingwini, C.; Nhleko, A.S. A survey of applications of multi-criteria decision analysis methods in mine planning and related case studies. J. South. Afr. Inst. Min. Metall. 2016, 116, 1051–1056. [Google Scholar] [CrossRef][Green Version]
- Vlachos, T. A Review of the effectiveness of Health & Safety Management Systems according to OHSAS 18001 standard at PPC’S lignite mines. In Proceedings of the 14th International Symposium of Continuous Surface Mining (ISCSM), Thessaloniki, Greece, 23–26 September 2018; pp. 428–436. [Google Scholar]
- Wang, S.Q.; Dulaimi, M.F.; Aguria, M.Y. Risk Management framework for Construction Projects in Developing Countries. Constr. Manag. Econ. 2004, 22, 237–252. [Google Scholar] [CrossRef]
- Kwak, Y.H.; Anbari, F.T. Analysing Project Management research: Perspectives from Top Management Journals. Int. J. Proj. Manag. 2009, 27, 435–446. [Google Scholar] [CrossRef]
- Dey, P.K. Project risk management using multiple criteria decision-making technique and decision tree analysis: A case study of Indian oil refinery. Prod. Plan. Control 2011, 1–19. [Google Scholar] [CrossRef]
- Pavloudakis, F.; Galetakis, M.; Roumpos, C. A spatial decision support system for the optimal environmental reclamation of open-pit coal mines in Greece. Int. J. Min. Reclam. Environ. 2009, 23, 291–303. [Google Scholar] [CrossRef]
- Ignjatović, D.; Jovančić, P.; Pavlović, V. Estimation of Damage on the Equipment during the Floods in Opencast Mines Tamnava-West Field and Veliki Crljeni. In Proceedings of the 13th International Symposium of Continuous Surface Mining (ISCSM), Belgrade, Serbia, 13–14 September 2016; pp. 137–148. [Google Scholar]
- Pavlović, N.; Ignjatović, D.; Pavlović, V. Control of Social and Environmental Risks during Opencast Lignite Mining. In Proceedings of the 14th International Symposium of Continuous Surface Mining (ISCSM), Thessaloniki, Greece, 23–26 September 2018; pp. 413–427. [Google Scholar]
- Spanidis, P.-M.; Roumpos, C.; Pavloudakis, F. A Methodology for Natural Hazards Risk Management in continuous Surface Lignite Mines. In Proceedings of the 2nd International Conference on Natural Hazards & Infrastructure (ICONHIC), Chania, Greece, 23–26 June 2019. [Google Scholar]
- Anawar, H.M. Impact of climate change on acid mine drainage generation and contaminant transport in water ecosystems of semi-acid and acid mining areas. Phys. Chem. Earth Parts A/B/C 2013. [Google Scholar] [CrossRef]
- Candeias, C.; Ávila, P.; Coelho, P.; Teixeira, J.P. Reference Module in Earth Systems and Environmental Sciences. Mining Activities: Health Impacts; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Liu, R.; Cheng, W.; Yua, Y.; Xu, Q. Human factors analysis of major coal mine accidents in China based on the HFACS-CM model and AHP method. Int. J. Ind. Ergon. 2018, 68, 270. [Google Scholar] [CrossRef]
- Hassan, T.; Moidu, S.; Riyasa, J.; Kuenzerb, C. Remote sensing of coal fires in India: A review. Earth-Sci. Rev. 2018, 187, 338–355. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process; McGraw-Hill International: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. Application of the AHP in project management. Int. J. Proj. Manag. 2008, 19, 19–27. [Google Scholar]
- Velasquez, M.; Hester, P.T. An Analysis of Multi-Criteria Decision Making Methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Oreski, D. Strategy development by using SWOT-AHP. TEM J. 2012, 1, 283–291. [Google Scholar]
- Triantaphyllou, E.; Shu, B.; Sanchez-Nieto, S.; Ray, T. Multi-Criteria Decision Making: An Operations Research Approach. In Encyclopedia of Electrical and Electronics Engineering; Webster, J.G., Ed.; John Wiley & Sons: New York, NY, USA, 1998; Volume 15, pp. 175–186. [Google Scholar]
- Gupta, V. Comparative performance of contradictory and non- contradictory judgement matrices in AHP under qualitative and quantitative metrics. Int. J. Decis. Support Syst. Technol. 2018, 10, 21–38. [Google Scholar] [CrossRef]
- Dey, P.K. Project Risk Management: A Combined Analytic Hierarchy Process and Decision Tree Approach. Cost Eng. 2002, 44, 13–26. [Google Scholar]
- Spanidis, P.-M.; Roumpos, C.; Pavloudakis, F. A Multi-Criteria Approach for the Evaluation of Low Risk Restoration Projects in Continuous Surface Lignite Mines. Energies 2020, 13, 2179. [Google Scholar] [CrossRef]
- Tah, J.; Carr, V. A proposal for Construction Project Risk Assessment using Fuzzy Logic. Constr. Manag. Econ. 2000, 18, 491–500. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Chang, D.Y. Applications of the extent analysis method on Fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Chen, C.T. Extensions of the TOPSIS for group decision making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Esmaeli, A.; Kahnali, R.A.; Rostamzadeh, R.; Zavadskas, E.K.; Sepahvand, A. The Formulation of Organizational Strategies through Integration of Freeman Model SWOT and Fuzzy MCDM Methods: A Case Study of Oil Industry. Transform. Bus. Econ. 2014, 13, 602–627. [Google Scholar]
- Chen, Y.-H.; Wang, T.-C.; Wu, C.-Y. Strategic decisions using the fuzzy PROMETHEE for IS outsourcing. Expert Syst. Appl. 2011, 38, 13216–13222. [Google Scholar] [CrossRef]
- Kannan, G.; Roohollah, K.; Jafarian, A. A fuzzy multi criteria approach for measuring sustainability performance of a supplier based on triple bottom line approach. J. Clean. Prod. 2013, 47, 345–354. [Google Scholar] [CrossRef]
- Moslem, S.; Duleba, S. Sustainable Urban Transport Development by Applying a Fuzzy-AHP Model: A case Study from Mersin, Turkey. Urban Sci. 2019, 3, 55. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy Sets. Information and Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Do, Q.H.; Chen, J.-F.; Hsieh, H.-N. Trapezoidal Fuzzy AHP and Fuzzy Comprehensive Evaluation Approaches for evaluating Academic Library Service. WSEAS Trans. Comput. 2015, 14, 607–619. [Google Scholar]
- Zimmerman, H.J. Fuzzy Set Theory and Its Applications; Kluwer: Boston, MA, USA, 1992. [Google Scholar]
- Lima, F.R.; Osiro, L.; Carpinetti, L.C.R. A comparison between Fuzzy AHP and Fuzzy TOPSIS methods to supplier selection. Appl. Soft Comput. 2014, 21, 194–209. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Erkan, T.E. Selection of Academic staff using the Fuzzy AHP: A pilot study. Tech. Vjesn. 2012, 19, 923–929. [Google Scholar]
- Chou, S.-W.; Chang, Y.-C. The implementation factors that influence the ERP (Enterprise Resource Planning) Benefits. Decision Support Systems 2008, 1, 149–157. [Google Scholar] [CrossRef]
- Golden, B.; Wasil, E.; Harker, P. (Eds.) The Analytic Hierarchy Process: Applications and Studies; Springer-Verlag: Heidelberg, Germany, 1989. [Google Scholar]
- Hillson, D. Use a Risk Breakdown Structure (RBS) to Understand Your Risks. In Proceedings of the Project Management Institute Annual Seminars & Symposium, San Antonio, TX, USA, 3–10 October 2002. [Google Scholar]
- Carter, B.; Hanckok, T.; Morin, J.-M.; Robins, N. Introducing RISKMAN; Blackwell: Oxford, UK, 1994. [Google Scholar]
- Project Management Body of Knowledge (PMBOK), 5th ed; Project Management Institute: Newtown Square, PA, USA, 2013.
- Brink, D. Essential of Statistics; BookBoon: London, UK, 2008. [Google Scholar]
- Meredith, J.; Mantel, S., Jr. Project Management—A Managerial Approach, 7th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Τaha, H.A. Operations Research. Macmillan Publishing Co., Inc.: Indianapolis, IN, USA, 1987; pp. 468–487. [Google Scholar]
- Phillips, J. Climate change and surface mining: A review of environment-human interactions and their spatial dynamics. Appl. Geogr. 2016, 74, 95–108. [Google Scholar] [CrossRef]
- Teli, S.N.; Magali, V.S.; Bushi, U.M. In Proceedings of the Role of Cost of Quality in the Automotive Industry. National Conference on Recent Trends in Mechanical Engineering (NCRTME), Datta Meghe College of Engineering, NaviMumbai, India, 28–29 August 2010. [Google Scholar]
- Opricovic, S.; Tzeng, G.-H. The Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Brans, J.P.; Vincke, P. A preference ranking organisation method: The PROMETHEE method for MCDM. Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Bernard, R. Classement et choix en présence de points de vue multiples (la méthode ELECTRE). Rev. d’Informatique Rech. Opérationelle (RIRO) 1968, 8, 57–75. [Google Scholar]

| Saaty Scale | Definition of Linguistic Terms | Triangular Fuzzy Numbers Scale |
|---|---|---|
| 1 | Equal (EQ) | (1, 1, 1) |
| 3 | Moderate (MD) | (2, 3, 4) |
| 5 | Strong (ST) | (4, 5, 6) |
| 7 | Very Strong (VS) | (6, 7, 8) |
| 9 | Extremely Strong (ES) | (9, 9, 9) |
| 2 | Intermediate Values | (1, 2, 3) |
| 4 | (3, 4, 5) | |
| 6 | (5, 6, 7) | |
| 8 | (7, 8, 9) |
| Saaty Scale | Definition (Linguistic Terms) | TFNs Values | Reverse Values | TFNs Conversion |
|---|---|---|---|---|
| 1 | Equal (EQ) | (1, 1, 1) | 1/1 | (1/1, 1/1, 1/1) |
| 3 | Moderate (MD) | (2, 3, 4) | 1/3 | (1/4, 1/3, 1/2) |
| 5 | Strong (ST) | (4, 5, 6) | 1/5 | (1/6, 1/5, 1/4) |
| 7 | Very Strong (VS) | (6, 7, 8) | 1/7 | (1/8, 1/7, 1/6) |
| 9 | Extremely Strong (ES) | (9, 9, 9) | 1/9 | (1/9, 1/9, 1/9) |
| 2 | Intermediate Values | (1, 2, 3) | 1/2 | (1/3, 1/2, 1/1) |
| 4 | (3, 4, 5) | 1/4 | (1/5, 1/4, 1/3) | |
| 6 | (5, 6, 7) | 1/6 | (1/7, 1/6, 1/5) | |
| 8 | (7, 8, 9) | 1/8 | (1/9, 1/8, 1/7) |
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|
| RI(n) | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 | 1.51 |
| Risk ID | Risk Factors & Sub-Factors | Probability of Occurrence | |
|---|---|---|---|
| Factors P(i) | Sub-Factors P(i, j) | ||
| R-1.00 | ATMOSPHERIC (ATM) | P(1.00) = 0.393 | |
| R-1.01 | Lightning | P(1.01) = 0.039 | |
| R-1.02 | Windstorms | P(1.02) = 0.043 | |
| R-1.03 | Winter Storms | P(1.03) = 0.047 | |
| R-1.04 | Snow Avalanches | P(1.04) = 0.013 | |
| R-1.05 | Extreme Rainfalls | P(1.05) = 0.141 | |
| R-1.06 | Extreme Frost | P(1.06) = 0.004 | |
| R-1.07 | Extreme Snowfalls | P(1.07) = 0.004 | |
| R-1.08 | Hailstorms | P(1.08) = 0.004 | |
| R-1.09 | Tornados | P(1.09) = 0.000 | |
| R-1.10 | Cyclones | P(1.10) = 0.000 | |
| R-1.11 | Extreme Summers | P(1.11) = 0.098 | |
| R-2.00 | GEOLOGICAL (GEO) | P(2.00) = 0.183 | |
| R-2.01 | Earthquakes | P(2.01) = 0.002 | |
| R-2.02 | Soil & Rock mass movements | P(2.02) = 0.037 | |
| R-2.03 | Volcanic eruptions | P(2.03) = 0.000 | |
| R-2.04 | Landslides | P(2.04) = 0.040 | |
| R-2.05 | Erosion | P(2.05) = 0.047 | |
| R-2.06 | Soil Subsidence | P(2.06) = 0.057 | |
| R-3.00 | HYDROLOGICAL (HYD) | P(3.00) = 0.310 | |
| R-3.01 | Floods | P(3.01) = 0.201 | |
| R-3.02 | Droughts | P(3.02) = 0.025 | |
| R-3.03 | Mudslides | P(3.03) = 0.077 | |
| R-3.04 | Extreme sea movements | P(3.04) = 0.000 | |
| R-3.05 | Sea erosion | P(3.05) = 0.006 | |
| R-4.00 | FIRES (FIR) | P(4.00) = 0.088 | |
| R-4.01 | Fires by external sources | P(4.01) = 0.018 | |
| R-4.02 | Forest Fires | P(4.02) = 0.053 | |
| R-4.03 | Bush Fires | P(4.03) = 0.018 | |
| R-5.00 | BIOLOGICAL (BIO) | P(5.00) = 0.028 | |
| R-5.01 | Epidemic crises | P(5.01) = 0.003 | |
| R-5.02 | Pollution by biological factors | P(5.02) = 0.025 | |
| ΣP(i) = 1.000 | ΣP(i. j) = 1.000 | ||
| Risk ID | Risk Factors | ATM | GEO | HYD | FIR | BIO |
|---|---|---|---|---|---|---|
| R-1.00 | ATM | 1.00 | 3.00 | 2.00 | 4.00 | 8.00 |
| R-2.00 | GEO | 1/3 | 1.00 | 1/3 | 4.00 | 8.00 |
| R-3.00 | HYD | 1/2 | 3.00 | 1.00 | 4.00 | 8.00 |
| R-4.00 | FIR | 1/4 | 1/4 | 1/4 | 1.00 | 6.00 |
| R-5.00 | BIO | 1/8 | 1/8 | 1/8 | 1/6 | 1.00 |
| Risk ID | Risk Factors | ATM | GEO | HYD | FIR | BIO |
|---|---|---|---|---|---|---|
| R-1.00 | ATM | (1, 1, 1) | (2, 3, 4) | (1, 2, 3) | (3, 4, 5) | (7, 8, 9) |
| R-2.00 | GEO | (1/4, 1/3, 1/2) | (1, 1, 1) | (1/4, 1/3, 1/2) | (3, 4, 5) | (7, 8, 9) |
| R-3.00 | HYD | (1/3, 1/2, 1/1) | (2, 3, 4) | (1, 1, 1) | (3, 4, 5) | (7, 8, 9) |
| R-4.00 | FIR | (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1/5, 1/4, 1/3) | (1, 1, 1) | (5, 6, 7) |
| R-5.00 | BIO | (1/9, 1/8, 1/7) | (1/9, 1/8, 1/7) | (1/9, 1/8, 1/7) | (1/7, 1/6, 1/5) | (1, 1, 1) |
| Risk-ID | Risk Factors | Fuzzy Geometric Mean Values | Fuzzy Values | Defuzzified Values | Normalised Values | Probability of Occurrence P(i) |
|---|---|---|---|---|---|---|
| R-1.00 | ATM | 3.519 | 0.632 | 0.423 | 0.393 | P(1.00) = 39.3% |
| R-2.00 | GEO | 1.623 | 0.291 | 0.197 | 0.183 | P(2.00) = 18.3% |
| R-3.00 | HYD | 2.825 | 0.507 | 0.333 | 0.310 | P(3.00) = 31.0% |
| R-4.00 | FIR | 0.763 | 0.137 | 0.094 | 0.088 | P(4.00) = 8.8% |
| R-5.00 | BIO | 0.226 | 0.040 | 0.030 | 0.028 | P(5.00) = 2.8% |
| Consistency Control: n = 5; CI = 0.102; RI(n) = 1.12; CR = CI/RI = 0.091 < 0.10 | 1.000 | ΣP(i) = 100% | ||||
| Elements at Risk | Probability of Occurrence (1) | ||||||
|---|---|---|---|---|---|---|---|
| People | Assets (2) | Environment (3) | P(A) | P(B) | P(C) | P(D) | P(E) |
| No injury | No damage, d = 0€ | No impact | none | none | none | none | none |
| First aid treatment | d ≤ 200 k€ | Negligible area ≤ 2% | L | L | L | L | L |
| Lost workday injury ≤ 3 days | 200 k€ < d ≤ 2M€ | Minor 2% < area ≤ 5% | L | L | L | M | M |
| Lost workday Injury > 3 days | 2 M€ < d ≤ 20M€ | Severe5% < area ≤ 10% | L | L | M | M | H |
| Permanent disability | 20M€ < d ≤ 200M€ | Major 10% < area ≤ 20% | M | M | M | H | H |
| Fatality | d > 200 M€ | Catastrophic area >20% | M | M | H | H | H |
| (1) Classification of the Probability of Occurrence: | |||||||
| P(A)-Remote | 0 < P < 0.05 | Never occurred in the mining industry | |||||
| P(B)-Unlikely | 0.05 < P < 0.10 | Has occurred in the mining industry | |||||
| P(C)-Occasional | 0.10 < P < 0.20 | Occurred at the mine the last 25 years | |||||
| P(D)-Probable | 0.20 < P < 0.50 | Occurred at the mine once per year | |||||
| P(E)-Frequent | 0.50 < P | Occurred at the mine more than once per year | |||||
| Risk IDs | Affected Elements at Risk (Field Inspection Findings) | Risk Factors/Sub-Factors | Probability of Occurrence–P(i, j) | Probability Classification | Impact Analysis (2) | Restoration and Recovery Actions |
|---|---|---|---|---|---|---|
| R-1.00 | ATMOSPHERIC (ATM) | |||||
| R-1.01 | Destruction of electrical installations and equipment | Lightning | P(1.01) = 0.039 | P(A) Remote | Low | Repairing works including materials and erection |
| R-1.02 | Damages to the roofs of building facilities | Windstorm | P(1.02) = 0.043 | P(B) Unlikely | Low | Repairing works including materials and erection |
| R-1.05 | Stoppage of lignite production in a mine sector | Extreme Rainfall | P(1.05) = 0.141 | P(C) Occasional | Medium | Filed dewatering: diversion of stagnant water |
| R-2.00 | GEOLOGICAL (GEO) | |||||
| R-2.04 | Collapse of pit surfaces in the 4% of the mine surface | Landslide | P(2.04) = 0.040 | P(A) Remote | Low | Slope stabilisation- Concrete supports and retaining |
| R-2.05 | Loss of lignite material in the 7% of the mine surface | Erosion | P(2.05) = 0.047 | P(A) Remote | Low | Environmental restoration -Removal of affected soil(s) |
| R-3.00 | HYDROLOGICAL (HYD) | |||||
| R-3.01 | Disaster of one (1) mining shovel of 135 tn | Flood | P(3.01) = 0.201 | P(D) Probable | High | Procurement of new shovels |
| R-3.03 | Disaster of two (2) bucket wheel excavators | Mudslide | P(3.03) = 0.077 | P(A) Remote | Medium | Procurement of new excavators |
| Restoration Cost [k€]– (Monte Carlo Simulation) | Recovery Time [Weeks]– (PERT Method) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Risk IDs | Risk Factors/Sub-Factors (2) P(i)–P(i, j) | Probability of Occurrence P(i, j) | Cmin | Cmax | Mean Cost CM (3) | Expected (Partial) Cost Overrun EVC(i, j) | Optimistic Time [To] | Pessimistic Time [Tp] | Most Likely Time [TML] | Mean Time [TM] (4) | Expected (Partial) Time Overrun EVT(i, j) |
| R-1.00 | ATMOSPHERIC | (0.393) | |||||||||
| R-1.01 | Lightning | 0.039 | 45.00 | 50.00 | 47.58 | 1.87 | 1.50 | 3.50 | 2.50 | 2.50 | 0.10 |
| R-1.02 | Windstorms | 0.043 | 20.00 | 35.00 | 29.57 | 1.28 | 3.00 | 6.00 | 4.50 | 4.50 | 0.19 |
| R-1.03 | Extreme Rainfalls | 0.141 | 2500 | 2900 | 2761 | 388.18 | 16.00 | 21.00 | 19.00 | 18.83 | 2.65 |
| R-2.00 | GEOLOGICAL | (0.183) | |||||||||
| R-2.04 | Landslides | 0.040 | 400 | 600 | 478 | 19 | 16.00 | 24.00 | 20.00 | 20.00 | 0.80 |
| R-2.05 | Erosions | 0.047 | 1000 | 1300 | 1217 | 58 | 28.00 | 40.00 | 35.00 | 34.67 | 1.65 |
| R-3.00 | HYDROLOGICAL | (0.310) | |||||||||
| R-3.01 | Floods | 0.201 | 4000 | 5000 | 4469 | 900 | 20.00 | 30.00 | 27.00 | 26.33 | 5.30 |
| R-3.02 | Mudslides | 0.077 | 3000 | 4000 | 3744 | 290 | 31.00 | 50.00 | 43.00 | 42.17 | 3.26 |
| Cost Overrun: | EV(C) = | 1658.33 | mil [€] | ||||||||
| Time Overrun: | EV(T) = | 13.95 | weeks (5) | ||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spanidis, P.-M.; Roumpos, C.; Pavloudakis, F. A Fuzzy-AHP Methodology for Planning the Risk Management of Natural Hazards in Surface Mining Projects. Sustainability 2021, 13, 2369. https://doi.org/10.3390/su13042369
Spanidis P-M, Roumpos C, Pavloudakis F. A Fuzzy-AHP Methodology for Planning the Risk Management of Natural Hazards in Surface Mining Projects. Sustainability. 2021; 13(4):2369. https://doi.org/10.3390/su13042369
Chicago/Turabian StyleSpanidis, Philip-Mark, Christos Roumpos, and Francis Pavloudakis. 2021. "A Fuzzy-AHP Methodology for Planning the Risk Management of Natural Hazards in Surface Mining Projects" Sustainability 13, no. 4: 2369. https://doi.org/10.3390/su13042369
APA StyleSpanidis, P.-M., Roumpos, C., & Pavloudakis, F. (2021). A Fuzzy-AHP Methodology for Planning the Risk Management of Natural Hazards in Surface Mining Projects. Sustainability, 13(4), 2369. https://doi.org/10.3390/su13042369








