Advanced Flight Planning and the Benefit of In-Flight Aircraft Trajectory Optimization

Abstract

The implementation of Trajectory-Based Operations, invented by the Single European Sky Air Traffic Management Research program SESAR, enables airlines to fly along optimized waypoint-less trajectories and accordingly to significantly increase the sustainability of the air transport system in a business with increasing environmental awareness. However, unsteady weather conditions and uncertain weather forecasts might induce the necessity to re-optimize the trajectory during the flight. By considering a re-optimization of the trajectory during the flight they further support air traffic control towards achieving precise air traffic flow management and, in consequence, an increase in airspace and airport capacity. However, the re-optimization leads to an increase in the operator and controller’s task loads which must be balanced with the benefit of the re-optimization. From this follows that operators need a decision support under which circumstances and how often a trajectory re-optimization should be carried out. Local numerical weather service providers issue hourly weather forecasts for the coming hour. Such weather data sets covering three months were used to re-optimize a daily A320 flight from Seattle to New York every hour and to calculate the effects of this re-optimization on fuel consumption and deviation from the filed path. Therefore, a simulation-based trajectory optimization tool was used. Fuel savings between 0.5% and 7% per flight were achieved despite minor differences in wind speed between two consecutive weather forecasts in the order of $0.5$ m s${}^{-1}$. The calculated lateral deviations from the filed path within 1 nautical mile were always very small. Thus, the method could be easily implemented in current flight operations. The developed performance indicators could help operators to evaluate the re-optimization and to initiate its activation as a new flight plan accordingly.

1. Introduction

Trajectory-Based Operations (TBO) are a promising solution to the increasing requirements on safety, efficiency, and environmental compatibility of the air traffic system. TBO describes four-dimensional trajectories with mandatory time targets to enable airlines to achieve individual multi-criteria optimized flight planning without constraints on the path, speeds, or altitudes. For TBOs to be safe and efficient, aircraft should communicate with each other and separate themselves from each other. Alternatively, Air Traffic Control (ATC) needs access to the separation-required position data of all aircraft [1,2,3] which are already provided by most aircraft via Automatic Dependent Surveillance-Broadcast (ADS-B). In addition, ATC requires a short term-trajectory prediction tool [4,5,6]. Under these circumstances, optimized trajectories may be obtained in the form of a compromise between all air traffic stakeholders [7] considering the collaboration of several stakeholders with different intentions. Recently, the FAA and NASA conducted research into a Collaborative Trajectory Options Program (CTOP) to ease the burden of areas with too much traffic. Here, aircraft can be rerouted through or around Flow Constrained Areas (FCAs) according to FAA Order JO 7210.3BB based on a Trajectory Options Set (TOS) consisting of five routes and a corresponding Relative Trajectory Cost (RTC). A TOS significantly increases flexibility in the implementation of efficient routes and is also considered for use as a means of in-flight optimization in the future [8].

For a successful implementation of optimized routes in TBOs, waypoint-less free routes are indispensable. The establishment of such operations is planned in Free Route Airspaces (FRA) [9], where aircraft can follow a freely planned route between defined entry and exit points and intermediate points, without constraints by the air traffic services (ATS) route network, but under “control by exception” by ATC [1]. Without knowing the intended 4D trajectory, ATC would hardly be able to monitor the airspace, if those trajectories were to be implemented [1].

The operation of optimized free routes would be an efficient stepping-stone towards approaching the ambitious goals of the Single European Sky ATM research program (SESAR) and to increase the airspace capacity [10,11,12], but only if the operator follows the optimum trajectory [13]. During the flight planning phase, this optimum is non-predictable due to the major influence of actual weather conditions, which are relatively erratic. Especially when considering the large time horizon of a long-haul flight (about five hours) the predictability of the real weather conditions state a challenge for all stakeholders in the Air Traffic Management (ATM) [14].

Global weather data services, e.g., the Global Forecast System (GFS) provide hourly weather forecasts and indicators of the reliability of the forecast in terms of so-called ensemble forecast data with different look-ahead times [14]. Often, the prediction accuracy of the one-hour forecast is within 3%, compared to the next six-hour modeled actual weather state [14]. For predictions of more than one hour ahead, the prediction error increases significantly and does not provide satisfying input data for trajectory optimization [15]. The modeled state, in turn, describes the real atmospheric state with an accuracy of approximately 5% [14].

Hence, using the one-hour forecast during the flight to recalculate the trajectory, for instance on an Elelctronic Flight Bag (EFB), and downlink to ATC for clearance is an option that must be considered. Within Lufthansa, the idea to share the vertical optimized trajectory with an Air Navigation Service Provider (ANSP) is called “Trajectory Intents”. Today, the procedure is hampered by a certified software for the downlink to ATC, due to safety issues.

The procedure, however, would increase both the pilot’s and the controller’s task loads, considering that trajectories in the airspace would be updated hourly. Nevertheless, it completely describes the idea, intended by ICAO and SESAR with TBOs. Perhaps an hourly trajectory intent is unnecessary if there are only small changes in the weather forecast. To help the pilot decide whether to activate the newly optimized trajectory, the pilot needs an evaluation of the prospective trajectory and a comparison with the presently activated trajectory under the new weather conditions. If the new trajectory represents an improvement in fuel consumption or arrival time, this must be indicated to the pilot. This paper investigates the benefit of a dynamic, hourly trajectory optimization during a flight between Seattle and New York considering hourly weather forecasts issued on 93 consecutive days. In this study, these hourly weather updates are used to re-optimize the trajectory during the flight and emphasize the benefit of activating a re-optimized flight plan as soon as a new trajectory is available is investigated and underlined. Thereby, for every hour of the cruise phase of the flight, the TOolchain for Multicriteria Aircraft Trajectory Optimization (TOMATO) [10,16] is applied to the dynamic input variables to re-optimize the trajectory, and the recently activated trajectory is recalculated with the new input variables to calculate the benefit of the re-optimization. TOMATO provides multi-criteria optimized 4D trajectories beginning at an arbitrary position along the trajectory [16,17], considering frequently updated input data sets [14] and, if desired, also the respective statistical accuracy as a frequency distribution [6,18].

2. State of the Art

2.1. Today’s Flight Planning

Today’s flight planning procedure for civil air traffic following the instrument flight rules involves filing the flight as a static route no later than one hour before departure. The filed flight is defined as a string of waypoints, airways, times, altitudes (flight levels), and speeds and is provided to the pilot as an Operational Flight Plan (OFP).

Today, the development of the flight plan has to comply with capacity constraints, flight performance limitations, and airline intentions (e.g., the cost index CI). Capacity constraints are defined by the sector load laid down by the Air Traffic Flow Management (ATFM) units, which is defined in ICAO Doc. 4444 PANS-ATM [19] for the Network Manager in Europe. Furthermore, capacity is limited by minimum separation as defined by the Required Navigation Performance (RNP) in ICAO’s Performance-based Navigation (PBN) concept [20] considering the lateral and vertical separation of aircraft. Performance limitations range from minimum/maximum speeds, climb/descent rates, loads and maximum thrust settings and are mostly defined in the aircraft-type-specific as well as the airline-specific Flight Crew Operational Manual (FCOM) and in the airline-specific Operations Manual Part B (OM-B) or in the Flight Operations Manual Flight Operations Manual (FOM). The airline intentions describing the current cost balance between time costs (especially passenger-sensitive delay costs and crew costs) and fuel costs may vary from flight to flight [21]. In accordance with these boundary conditions, the dispatcher calculates the operational flight plan. The OFP is used for the airspace demand-to-capacity balancing. The calculation is frequently updated up to one hour before scheduled off block time, considering the most recent weather data. Finally, the OFP is submitted to the Network Manager and provided to the pilot [22].

2.2. Today’s Flight Execution

Already today, no flight is flown as planned. There are a variety of factors that can lead to a deviation from the flight plan. Deviations can be vertical, lateral, or relate to speed. To comply with ICAO Doc. 4444 PANS-ATM [19], deviations from the planned speed must be reported to ATC if they deviate from the True Air speed (TAS) 5% or are Mach $0.01$ above the crossover altitude during cruise flight. Any lateral or vertical deviation from the OFP, initiated by the pilot, requires approval from ATC before the deviation is executed.

In most cases, instructions to deviate from the OFP are issued by ATC (e.g., directs, altitude changes, speed changes), especially during the departure or arrival phases in the vicinity of an airport, where highly dynamic air traffic guidance is necessary. Often, however, the flight crew has reason to deviate from the filed flight plan. One example is the failure to reach the first planned flight level. This can happen if the aircraft departs with a higher takeoff mass than that assumed in the planning phase. There can be various reasons for this, for instance, additional short-term express freight or a higher fuel load. The latter in particular is an important issue. The decision on the final fuel is made during the briefing, when the flight has already been filed; it rests solely with the commander. A high amount of extra fuel, e.g., due to adverse weather at the destination, results in a higher takeoff mass. This might lead to a lower first flight level than originally filed due to aircraft performance reasons. A lower flight level has to be communicated to ATC at an early stage to allow respective coordination. Another typical deviation from the OFP is due to heavy weather, such as thunderstorms and turbulence areas. Apart from the main task of conducting a safe flight, the crew also has the task of executing a flight economically. An economic flight execution not only includes an ideal trajectory but also on-time-performance and passenger satisfaction. In today’s flight operation, the information available to the crew is usually insufficient for accomplishing this task. With regard to the trajectory, the main guideline for conducting a flight is the OFP. Apart from the North Atlantic air space, which stipulates that a constant Mach number must be flown, flights are usually calculated according to an airline-specific cost index that converts marginal time costs and fuel costs into an additional virtual fuel flow. The flight planning system converts this into an optimum speed. Flying with a constant cost index means a change in speed during the flight when there is a reduction in weight due to fuel burn. The flight, airline, and aircraft-specific cost index is indicated in the OFP. Although the OFP has been calculated based on well-known optimization algorithms, it is full of constraints. The main constraints are airspace restrictions, published by the ANSP using the Route Availability Document (RAD). They are implemented in the flight planning software and lead inevitably to laterally and vertically non-optimal trajectories.

In addition to the OFP, the crew has access to information from the onboard Flight Management and Guidance System (FMGS). The FMGS provides information about optimum altitude and fuel flow based on the temperature and winds, which can be inserted in the respective FMGS pages. The pilot can enter wind data for up to five altitudes for the climb and descent phases and up to four flight levels for the cruise portion. Additionally, the temperature of each waypoint can be entered. Once the temperature and winds are inserted, the FMGS computes the International Standard Atmosphere (ISA) profile and displays the forecast wind profile by linear interpolation and propagation. In daily flight operation, these insertions are carried out manually. The data can be automatically received and inserted into the FMGS through the onboard Aircraft Communications, Addressing, and Reporting System Aircraft Communications Addressing and Reporting System (ACARS). Wind data are updated at 4 a.m., 10 a.m., 4 p.m. and 10 p.m. UTC. The update has to be initiated by the pilot. FMGS-functions such as “secondary flightplan” allow the crew a limited comparison of route alternatives during flight. In addition to the FMGS, the onboard library contains some information, for instance, flight level optimization and fuel vs altitude trade-off diagrams. It is hardly necessary to mention that the use of such paper tables is very inconvenient and is practically not done during the flight. A very convenient and versatile solution for flight optimization results from the widespread use of Electronic Flight Bag (EFB). Highly sophisticated software solutions by a third-party supplier are capable of calculating optimized trajectories in real-time. The software delivers an unconstrained vertically and laterally optimized route. Thus, the flight crew knows which is the optimum and tries to reach it as closely as possible. A frequent point of criticism concerning this onboard optimization arises from ATC. The optimization of a single flight event from the pilot’s perspective does not take into account the overall air traffic system. This point of criticism is certainly justified to some extend and has to be discussed between the ANSPs and the airspace users.

Assuming a global weather update frequency of six hours, the calculation of the filed flight plan may be obsolete since the weather data may already be outdated at take-off.

2.3. Today’s 4D Trajectory Optimization Methods

Two approaches of trajectory optimization arise from the described uncertainties in weather prediction. First, a stochastic treatment of weather input data and the search for a robust solution would be possible in the pre-flight planning phase. Second, a trajectory re-optimization and dynamic adaption of the flight plan during the flight represents a greater optimization potential but is an operational challenge.

Often, the first option is theoretically solved as a (dynamic) optimal control problem where stochastic equations are transferred to equivalent deterministic differential equations [23]. Here, uncertainties can only be represented by one variable, and large-scale problems are hard to compute. With these limitations, a robust optimal control calculation of trajectories with weather uncertainties are possible [24]. The influence of wind uncertainties and a realistic interpolation in the robust trajectory has been focused in [25], whereas the shortest path algorithm for a robust trajectory considering a variety of forecast ensembles has been implemented as cluster analysis [26]. A Mixed-Integer Linear Programming approach has been implemented to provide a trade-off between minimum flight time and minimum arrival time uncertainty considering weather uncertainties derived from ensemble weather forecasts [27]. The approach was enhanced by a probabilistic fuel consumption with a simplified flight performance model [28]. Robust trajectories were also used for recommendations for decision making in uncertain weather situations [29]. The restricted applicability of this approach towards a realistic treatment of weather uncertainties lies in the fact, that only a single variable has to describe the uncertainties.

The second option poses a challenge for operators and for the trajectory optimization tool. Theoretically, we could already show a benefit of a frequently re-optimized lateral trajectory in terms of fuel costs by approximately 1% [14,15]. Note, after each weather update, the current aircraft position might not be optimal anymore. The fuel, required for flying to the next optimal position, hampers the theoretical fuel benefit. Practically, in 2019, a test flight with the Boeing EcoDemonstrator proved the feasibility of in-flight-optimized trajectories with TOMATO. Furthermore, the NASA Traffic Aware Strategic Aircrew Requests (TASAR) procedure already combines lateral and vertical trajectory recalculation to avoid convective weather cells and thereby considers the surrounding air traffic [30]. From this follows, that there are already ways to operate along dynamically re-optimized trajectories. However, it remains to be clarified how this dynamic optimum is calculated.

Commercial products for a dynamic optimum, such as Lido Flight 4D by Lufthansa or the Air Traffic Simulator (TAAM) by Jeppesen have been developed and are daily applied for re-routing because of dangerous weather situations and for support for diversions. Both tools are rarely used for a routine optimization of the trajectory. With both systems, the operator chooses an airline-specific cost index (i.e., the weighting between fuel costs and time costs) and yields an optimized 4D trajectory. The optimization is restricted to the current navaid-infrastructure and to the mentioned target functions time and fuel. However, efficient TBOs need the degrees of freedom that result from free route optimization, without airways restrictions and fixed flight levels. Furthermore, the environmental impact of the flight is not considered in these software applications. The importance of a multi-criteria trajectory optimization gains in importance with the prospect of a sustainable future air traffic system.

Non-commercial applications for a dynamic trajectory optimum solve the resulting non-linear optimization function with conflictive goals. For example, Matthes et al. [31] developed a performance model for the development of environmentally friendly trajectories based on BADA performance tables. These tables pose the opportunity to consider aircraft-type-specific fuel consumption. The engine-type-specific combustion process, however, is not described. Hence, emissions cannot be estimated with sufficient granularity [12]. The model of Matthes et al. optimizes all flight phases and has been extended by Yamashita et al. [32], to more precisely estimate the impact of the approximated emissions on the Earth–atmosphere System. However, the quantification of the emissions is still an approximate estimation.

In contrast to the model of Matthes et al., other mathematical trajectory optimization approaches often focus on cruise phase [33,34,35,36,37,38] with a single optimization function and utilize the BADA performance model [34,35,39]. Due to the mathematical complexity, speed and altitude are not part of the optimization and are defined as state parameters. For example, by using the optimal control approach for vertical trajectory optimization and reducing the modeling of the flight performance to a manageable number of parameters [34,35,39], or by focusing on a lateral path optimization [33,36,37,38].

All these approaches are restricted to three ways: first, constant weather conditions considering the beginning of the flight are assumed. Second, a fixed waypoint grid is used. Third, the approaches are not simultaneously covering all optimization target functions which are relevant for the authors. For this reason, a multi-criteria trajectory optimization algorithm considering dynamic input variables for a 4D trajectory optimization called TOMATO has been developed and tested on individual cases [40,41]. The tool-chain TOMATO is also able to re-optimize the trajectory during the flight. In recent applications of TOMATO [40,41], the benefit of re-optimization, compared to the optimized trajectory using the former input variables has not been calculated for a large variety of weather scenarios. Here, TOMATO is used to determine a mean advantage of dynamic optimization, by investigating the influence of weather changes during a flight on the optimal flight over several months.

3. Methodology

3.1. Weather Data

The dynamic in-flight trajectory optimization requires precise and frequently updated weather information [22,41]. For this purpose, three different sources of weather information are available [41]. The weather data sources are depicted in Figure 1.

First, surrounding aircraft measure atmospheric state parameters (e.g., pressure p and temperature T) and calculate wind direction and wind speed. This data is transmitted to a receiving Aircraft Meteorological Data Relay (AMDAR) station on the ground. After data analysis, cleansing and post-processing, the data is distributed to airlines, weather services, and other users [42]. Therewith, a significantly better temporal and spatial resolution of weather data is provided, especially in areas with increased air traffic. This local weather data source is shown at the bottom of Figure 1.

Second, numerical weather models push AMDAR and radiosonde data into continuous calculations of the current global atmospheric state. Every six hours, the Global Forecast System (GFS) provides a binary coded global weather data set in so-called cycles 0, 6, 12 and 18. The data are compressed in a GRIdded Binary (GRIB) format with a maximum size of 16 Mb. The data is easy to transfer and to read. The cycles are shown in Figure 1 as GFS${}_0$, GFS${}_6$,…GFS${}_{18}$, Subsequently, the National Weather Service (NWS) of the National Oceanic and Atmospheric Administration (NOAA) forecasts the global weather with different time horizons. These forecasts are also calculated every six hours for the next 384 h. The forecasts are indicated as GFS${}_0,1$, GFS${}_0,2$,…GFS${}_6,6$ in Figure 1. For each of the 384 h, a global data set is published. Additionally, the National Centers for Environmental Prediction (NCEP) provide 21 Global Ensemble Forecast System (GEFS) ensemble forecasts to quantify the amount of uncertainty in a GFS forecast [43]. These ensembles and the prediction accuracy have been analyzed in [14] and are not used in this study.

Third, the numerical weather forecast model Rapid Refresh (RAP) hourly provides short term weather forecasts with a high spatial resolution of 13 km (lateral) and 50 vertical layers up to a pressure altitude of 10 hPa, covering the United States. RAP is also performed by the NOAA NCEP and is fed by the GFS with the boundary conditions. Every hour, the model provides hourly forecast outputs for the next 18 hours. The data is indicated as RAP${}_0,1$, RAP${}_0,2$,... RAP${}_6,6$ in Figure 1. The high resolution and the high accuracy of RAP is used in this study to show the potential of an hourly aircraft trajectory optimization.

The resolution, distribution, and differences in weather forecasts within two hours are shown in Figure 2.

From each RAP forecast $W_t$

$$W_t=\{p_t,T_t,{\rho }_t,r{H}_t,u_t,v_t,w_t\},$$

(1)

a set of pressure p [Pa], temperature T [K], density $\rho$ [kg m${}^{-3}$], relative humidity $rH$ [-], horizontal wind component from West u, from South v, and vertical wind component w [m s${}^{-1}$] as functions of longitude, latitude and altitude is used by TOMATO as input variables. The index ${}_t$ denotes the prediction cycle with a discretization of one hour. This means that $W_{t-1}$ describes the forecast updated one hour ago and $W_{t+1}$ describes the forecast that will occur in one hour.

3.2. Multi-Criteria Trajectory Optimization

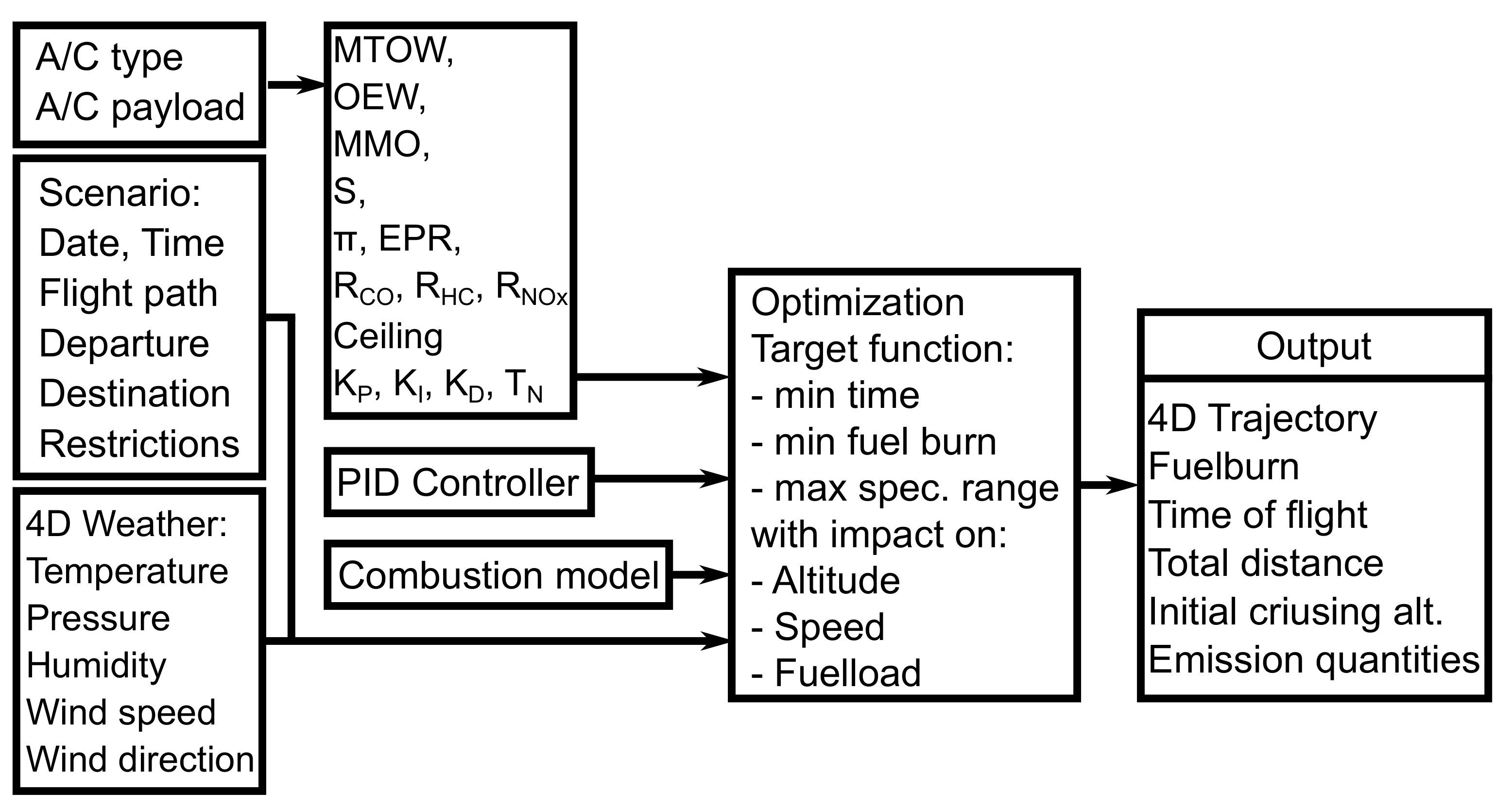
In this study, the TOolchain for Multi-criteria Aircraft Trajectory Optimization (TOMATO) [16,17] is used, based on an iterative simulation-based optimization mechanism to optimize single trajectories. TOMATO consists of three main modules (see Figure 3): First, a pathfinding algorithm optimizes the lateral path using arbitrary cost layers with wind information, overfly charges, restricted areas, turbulence- and traffic information, and environmentally sensitive areas. Here, the cruising altitude varies between FL 310 and FL 400 considering the imported weather forecasts. Additionally, the aerodynamic optimum altitude is calculated [44]. The optimum path is based on a polarized map with a resolution of 0.2°.

Second, a flight performance model with an included combustion chamber model calculates the vertical profile along the initially optimized lateral path. The Compromized Aircraft performance model with Limited Accuracy (COALA) calculates the fuel flow based on the integration of the equation of motion and quantifies the emissions [44]. Third, the trajectory is assessed regarding the defined target functions. After the assessment, the weightings for each target function are adapted. Each trajectory is calculated individually by using the constant input variables and first guesses of the controlled input variables, and a defined objective function. This function can either be analytically solvable, nonlinear, or a multi-criteria combination of several aspects. After a first optimization, the trajectory is assessed regarding operational, time-based, and environmental costs. In case a scenario of several trajectories is optimized, the airspace demand, potential conflicts, and the expected controller taskload are also calculated and assessed. The outcome of the assessment is used to manipulate the weighting functions of those costs in the controlled input variables of the next iteration loop (see Figure 3 for more details). TOMATO has been validated [45] and applied to various applications [11].

Today, operational constraints often prevent aircraft to follow freely optimized routes (compare Section 2.1 and literature therein [19,20,22]). To meet these capacity constraints, different grids have been applied to follow the current navaid structure or airway structure [7,17]. To perform in trajectory-based operations, COALA has been successfully applied to fixed waypoints at fixed time steps as well [7,46]. The implementation of these constraints are necessary for trajectory prediction for all stakeholders, but always induces a deviation from the optimum. Each trajectory is described as a set of

$$T_i=\{{\mathrm{lon}}_i,{\mathrm{lat}}_i,{\mathrm{alt}}_i,{\mathrm{TAS}}_i,{\mathrm{Phase}}_i,{\dot{m}}_{f,i},m_{\mathrm{gas}},\mathrm{i}\}$$

(2)

with longitude $\mathrm{lon}$ [°], latitude $\mathrm{lat}$ [°], altitude $\mathrm{alt}$ [m], speed $\mathrm{TAS}$ [m s${}^{-1}$], flight phase $\mathrm{Phase}$ [a.u.], fuel flow ${\dot{m}}_f$ [kg s${}^{-1}$], and emissions $m_{\mathrm{gas}}$ [kg s${}^{-1}$]. The emissions are described as set of

$$m_{\mathrm{gas}},\mathrm{i}=\{m_{\mathrm{CO}}2,\mathrm{i},m_{\mathrm{H}}2\mathrm{O},\mathrm{i},m_{\mathrm{SO}}2,\mathrm{i},m_{\mathrm{NO}}\mathrm{x},\mathrm{i},m_{\mathrm{HC}},\mathrm{i},m_{\mathrm{CO}},\mathrm{i},m_{\mathrm{BC}},\mathrm{i}\}$$

(3)

where ${\mathrm{CO}}_2$, ${\mathrm{H}}_2\mathrm{O}$, ${\mathrm{SO}}_2$, ${\mathrm{NO}}_{\mathrm{x}}$, $\mathrm{HC}$, $\mathrm{CO}$, and $\mathrm{BC}$ denote emissions of carbon dioxide, water vapor, sulfur dioxide, nitrogen oxides, hydrocarbons, carbon monoxide and black carbon, respectively.

In Equations (2) and (3), the index ${}_i$ denotes the time discretization of one second. Hence, $T_{i=1}$ denote the first second of the trajectory $T_i$ and $T_{i=j}$ denotes the last last second of trajectory $T_i$.

3.3. Flight Performance Model COALA

The aircraft performance model COALA calculates and optimizes physically possible 4D aircraft trajectories for 16 different aircraft types. In COALA, the equation of motion is solved analytically. The model differs from other aircraft performance models in the consideration of the forces of acceleration and inertia each time step by a PID controller, which controls the true airspeed and uses the lift coefficient as a regulative variable. The parameters of the controller are aircraft type-specific. Therewith, COALA is based solely on physical functions, except for the drag polar, which is approximated by the BADA model [47,48]. That’s why COALA contains the “limited accuracy” in its name. The aircraft type-specific behavior, modeled with COALA, has been demonstrated in [44,49].

For trajectory optimization, the cruising altitude and the true airspeed are effective variables to consider the cost index $CI$ in trajectory optimization. Therewith, a manipulated speed and a corresponding altitude can be provided as target functions to the PID controller. COALA contains target functions for true airspeed and cruising altitude for a maximum climb rate, a maximum specific range, minimum fuel, or minimum time of flight. These target functions are controlled by the PID controller and allow mass-specific changes in speed and altitude. Since these aerodynamic target functions cannot be generalized for all aircraft types, especially not under real weather conditions, individual aircraft type-specific target functions depending on the drag polar, maximum Mach number, and operating empty weight are derived iteratively. In this study, true airspeed and the corresponding cruising altitude are optimized towards a maximum specific range. Hence, weather-driven deviations from the aerodynamically optimized cruising altitude are not considered.

COALA contains a combustion chamber model to quantify the emissions as products of complete combustion (e.g., ${\mathrm{CO}}_2$, ${\mathrm{H}}_2\mathrm{O}$ and ${\mathrm{SO}}_2$) and incomplete combustion (e.g., ${\mathrm{NO}}_{\mathrm{x}}$, $\mathrm{HC}$, $\mathrm{CO}$ and black carbon). These additional Key performance indicators allow a multi-criteria trajectory optimization. In cooperation with the simulation environment TOMATO [16,17,50] COALA has already been used for multi-criteria trajectory optimization. Here, emissions were included in the target function. Therefore, performance indicators have been transformed into costs by using the aviation-specific global warming potential of each emission [51] and the emission trading scheme [52]. The methodical procedure within COALA is shown in Figure 4.

3.4. On-Board Dynamic Trajectory Optimization

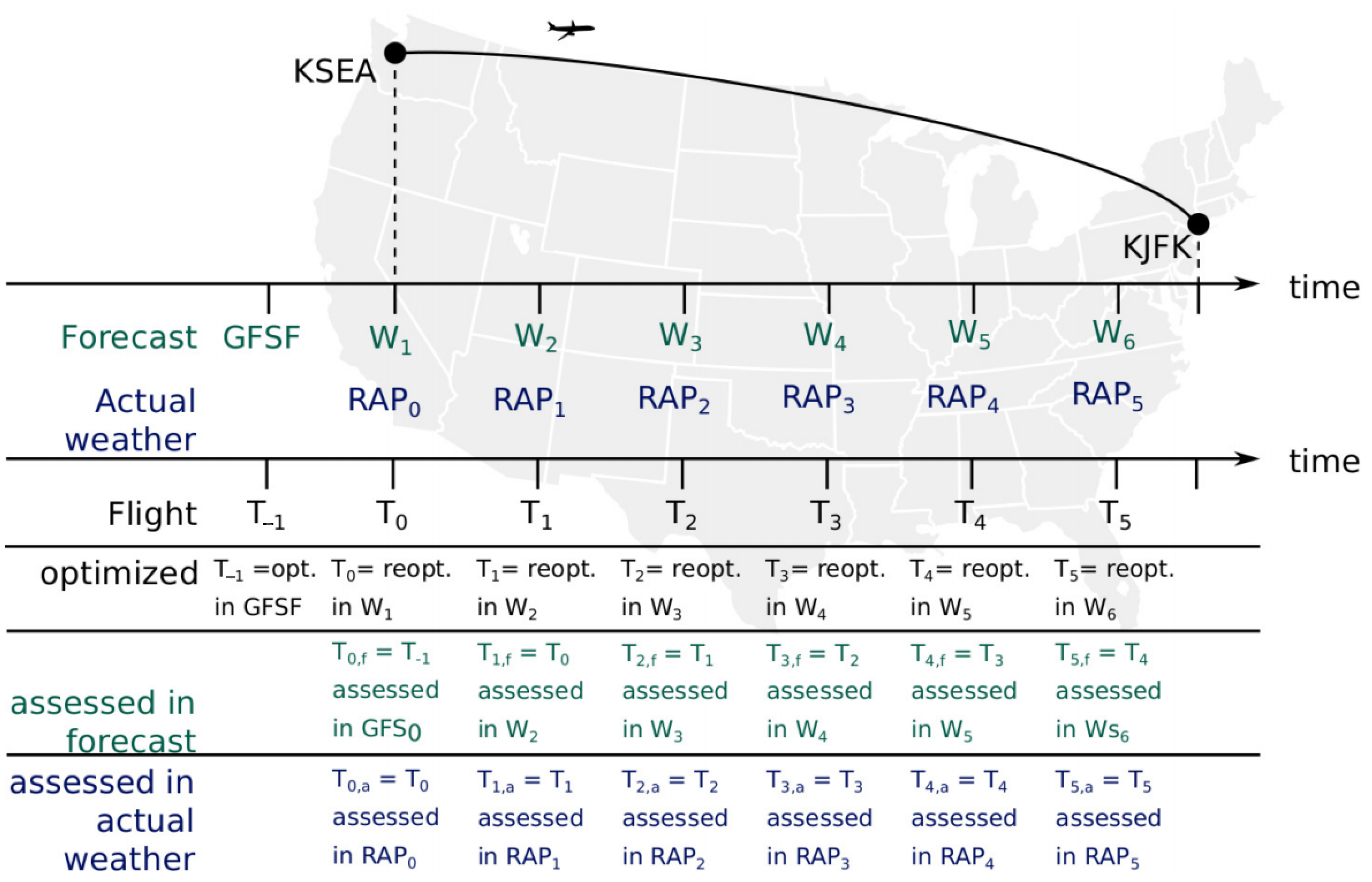
TOMATO can also be used to optimize an aircraft trajectory between two arbitrary points in time and space, as long as the boundary conditions

$$T_{i=1}=\{{\mathrm{lon}}_{i=1},{\mathrm{lat}}_{i=1},{\mathrm{alt}}_{i=1},{\mathrm{TAS}}_{i=1},{\mathrm{Phase}}_{i=1}\}$$

(4)

are completely defined. Therewith, TOMATO can be applied to different weather data sets t depending on time of flight. In this study, 93 A320 flights from Seattle (KSEA) to New York (KJFK) with a payload of $14.5$ tons and a fuel load of 11 tons starting at midnight UTC (=4 p.m. local time) are calculated and assessed. Weather data are taken from January, July, and August 2019 to cover different weather conditions.

Each day, GFS weather forecasts ${\mathrm{GFS}}_0$ are used for pre-planning. Therefore, five global weather data sets ${\mathrm{GFS}}_0,t=1$…${\mathrm{GFS}}_0,t=5$, each valid for a specific hour t are used.

After take-off, each hour t, TOMATO re-optimizes the flight $T_t=f\left(W_t\right)$, using the weather data update of the actual hour $W_t$ (see also Figure 5). Weather forecast updates $(W_t$ are provided by the NCEP of the North American continent with a grid size of 13 km [41] (see also Figure 2).

With each re-optimization, we calculate the flight to the destination airport. The process is symbolized in Figure 5.

The state $T_{i=60}\left(W_{t-1}\right)\{{\mathrm{lon}}_{i=60}(t-1),{\mathrm{lat}}_{i=60}(t-1),{\mathrm{alt}}_{i=60}(t-1),{\mathrm{TAS}}_{i=60}(t-1),{\mathrm{Phase}}_{i=60}(t-1)\}$ of the aircraft at the end of each hour is used as the initial state for the re-optimization of the next hour $T_{i=1}\left(W_t\right)$ with the new weather data set $W_t$. Again, the optimization is done iteratively. First, the pathfinding algorithm searches for the optimum path, second the flight performance model calculates a target function for true airspeed and quantifies the emissions, fuel flow, and time of flight, and third, the assessment tool compares the quantified emissions and fuel flow and time of flight. In the next iteration loop, the altitude is varied in the pathfinding algorithm, until the assessment is satisfied.

Since in the new weather situation $W_{t+1}$ the current state of the aircraft $T_t$ no longer needs to be optimal, the path optimized in the previous weather data set would deviate from the optimum in the new weather data set. The difference between both optimizations should help the pilot to decide to request clearance from ATC for the newly optimized trajectory $T_{t+1}\left(W_{t+1}\right)$ and finally activate it in the FMGS.

3.5. On-Board Trajectory Assessment

To determine the difference between the current $T_t$ and the previous $T_{t-1}$ optimization, the trajectory of the previous optimization $T_{t-1}$ must be modelled in the new weather data set $T_{t-1}=f\left(W_t\right)$. This step is symbolized in Figure 5 as green $T_{t,f}$. For this purpose, the trajectory is discretized in intervals of seconds ${}_i$. The discretized state variables of $T_{t-1}$ $\{{\mathrm{lon}}_i,{\mathrm{lat}}_i,{\mathrm{alt}}_i,{\mathrm{TAS}}_i,{\mathrm{Phase}}_i\}$ are provided to the flight performance model COALA as objective functions. COALA calculates $T_{t-1}=f\left(W_t\right)$ using the new weather forecast $W_t$. Subsequently, the $T_{t-1}=f\left(W_t\right)$ is assessed regarding emissions, fuel flow and time of flight. The assessment of $T_{t-1}=f\left(W_t\right)$ is compared with the assessment of $T_t=f\left(W_t\right)$. The benefit of $T_t=f\left(W_t\right)$ compared to $T_{t-1}=f\left(W_t\right)$ serves as a decision support for the pilot to activate the new trajectory and is statistically analyzed in the following. Note, although the whole trajectory is modeled, only the future part of the trajectory $T_{t-1}=f\left(W_t\right)$ is assessed to ensure, that the expected fuel benefit was not reached in the already flown (past) part of the trajectory.

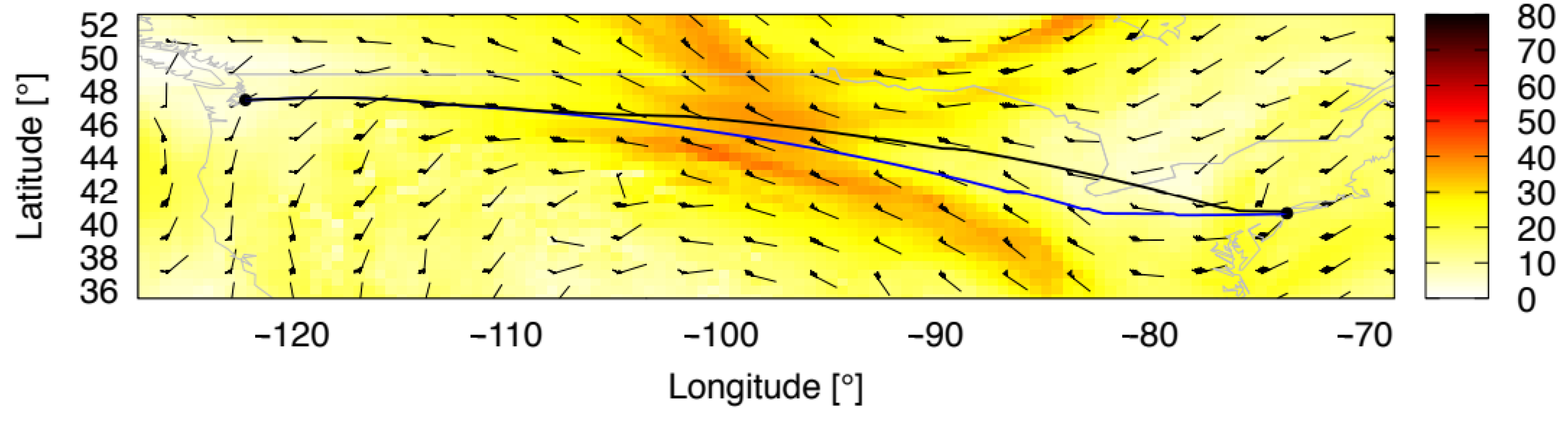
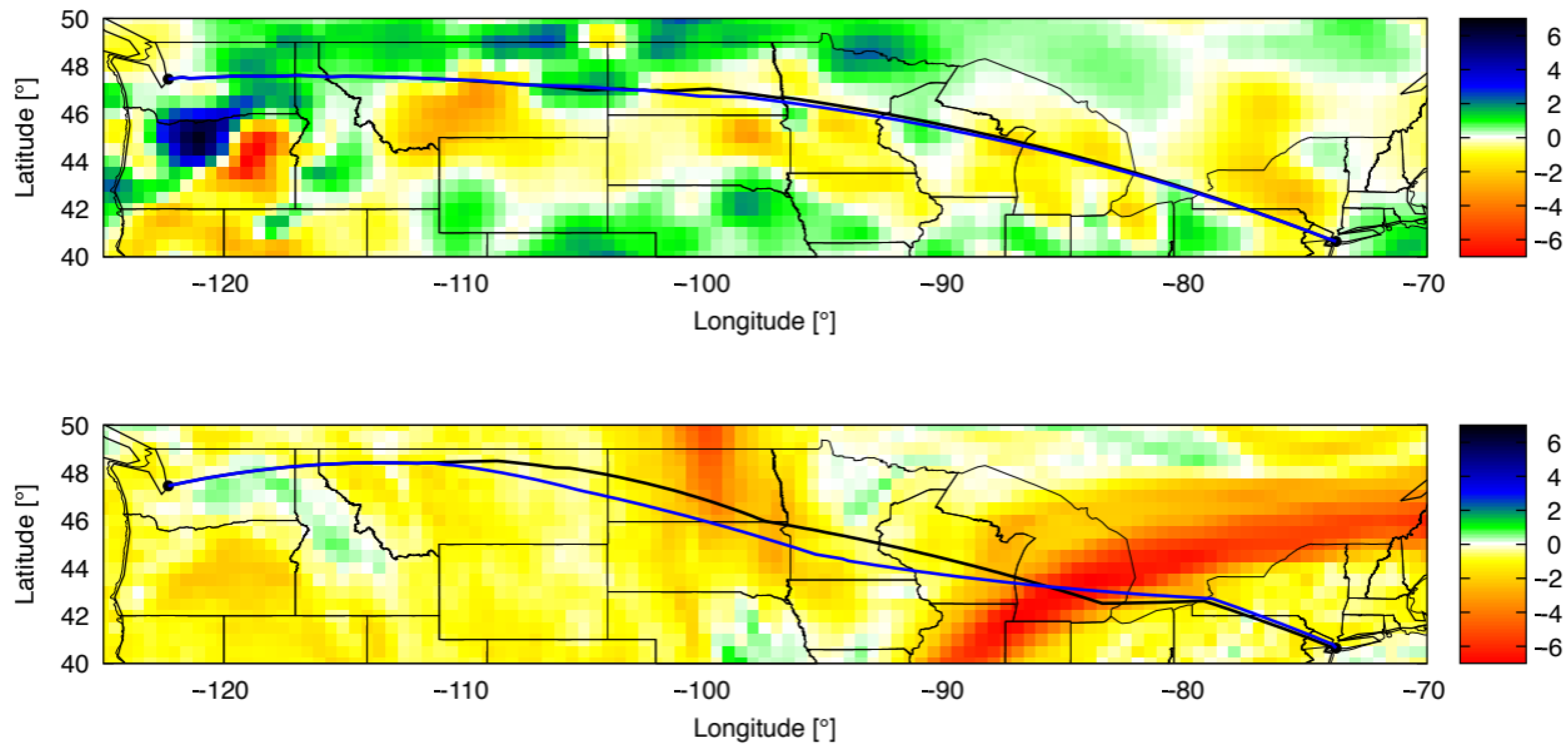
Figure 6 shows an example of two optimizations with different weather data sets on 8 August 2019, 1 p.m. UTC. In this case, activation of the trajectory after the first flight hour yields a fuel benefit of 163 kg, which is $\approx 1.5\%$ of the total fuel burn.

Figure 6 might indicate significant fuel savings of the black path due to direct routing. However, the wind conditions of the previous weather forecast resulted in a “cheaper” flight along the blue path with obviously strong tailwind components. Besides a trajectory assessment considering the latest weather forecast, the trajectory can be modeled in the actual weather situation. This step allows an indication of the accuracy of the weather forecast and thus the applicability of the forecast in dynamic trajectory optimization. The actual weather is also provided hourly by RAP. This step is symbolized in Figure 5 as blue $T_{t,a}$. The accuracy of the RAP forecast for the next hour compared to actual weather provided by RAP has been analyzed in [14]. Therein, a forecast precision in wind speed of ≈3 $\mathrm{m}{\mathrm{s}}^{-1}$ has been identified.

4. Advantage of Hourly Trajectory Optimization

The 93 simulated A320 flights from KSEA to KJFK had a mean fuel burn of $10,309.8$ kg fuel and a mean flight time of $4.8$ h ($17,352$ s). We re-optimized each flight a total of four times, namely after every full hour. Mean fuel burn values for the remaining flight time after each hour are listed in

Table 1. Mean fuel burn and mean fuel burn benefit of the remaining A320 flight from KSEA to KJFK after each flight hour. Additionally, the number of flights (out of 93) with a fuel benefit larger than $0.5$, $1.0$ and $2\%$ are listed. The relative benefit, compared to the mean required fuel for the remaining flight increases.

Flight Hour	Fuel Burn [kg]	Mean Benefit		No. of Flights with Benefit
		[kg]	[%]	>$0.5$ %	>$1.0$ %	>$2.0$ %
0	$10,309.8$	−	−	−	−	−
1	$7228.3$	$33.5$	$0.49$	32	9	2
2	$5045.9$	$23.9$	$0.47$	39	11	1
3	$2939.1$	$15.3$	$0.52$	37	14	4
4	$908.9$	$11.1$	$1.22$	85	45	16

. The mean benefit of re-optimization depending on the remaining flight time was between 0.5% and $1.2\%$ (see also Table 1). However, more than 50% of the flights achieved savings of only 70 kg or less during the entire flight, which corresponds to relative savings of $0.6$% of total fuel for these flights. From this follows, taking into account the task load for controllers and pilots when deviating from the filed route, not every optimization is worthwhile.

Table 1 lists the mean fuel burn of the remaining flight after each hour. Considering this fuel burn the relative advantage of re-optimization increases with increasing flight hours (or decreasing distance to destination). For example, 16 out of 93 flights gained a benefit in fuel burn of more than two percent, when re-optimizing the path after the fourth flight hour. This is due to the lower remaining fuel burn, which compares the savings in kg. From this follows, on average, frequent re-optimization increases the total savings in fuel burn.

For convenience, the flight on 8 August 2019 shown in Figure 6 is elaborated in detail in

Table 2. Fuel burn and fuel burn benefit of the remaining A320 flight on 8 August 2019 from KSEA to KJFK with re-optimization after each flight hour.

Flight Hour	Fuel Burn [kg]	Fuel Burn Benefit
		[kg]	[%]
0	$10,186.7$	−	−
1	$7086.6$	$163.6$	$2.3$
2	$4891.9$	$23.8$	$0.48$
3	$2782.6$	$8.5$	$0.3$
4	$879.9$	$27.3$	$3.1$

. The fuel burn benefit as a consequence of a re-optimization after each flight hour is defined as the difference between the required fuel after re-optimization in the new weather and the calculated fuel along the trajectory, optimized one hour ago, modeled in the new weather data set. For a single flight, the absolute fuel benefit after each hour varies strongly and so does the relative fuel burn benefit, compared to the required fuel for the remaining flight after each flight hour. On 8 August 2019, the first and the last re-optimization have been most beneficial. Probably, It would have been sufficient to only optimize after the first and the fourth hour.

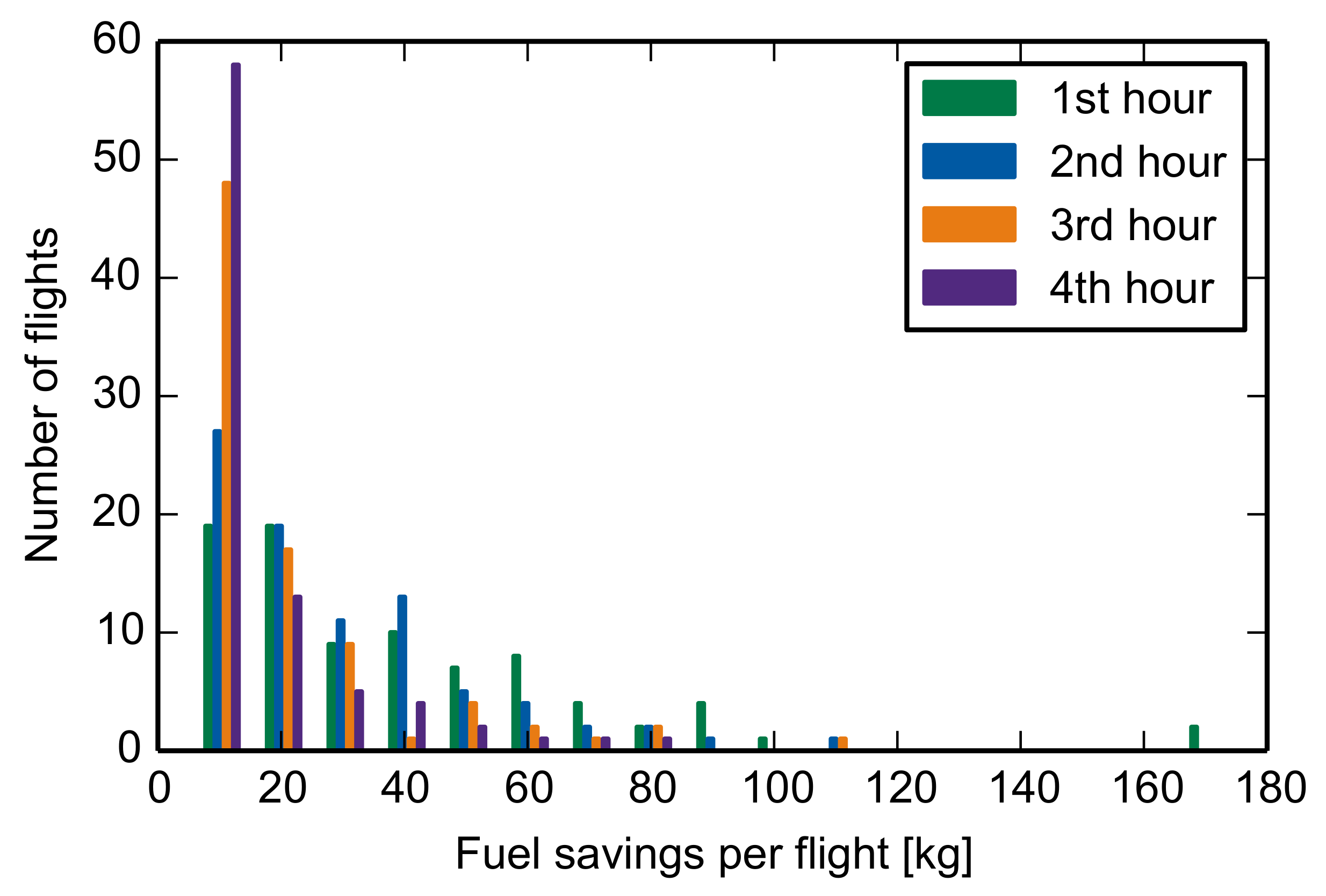
The absolute benefit of hourly trajectory optimization and activation decreases with decreasing distance to the destination. In Figure 7, the differences in fuel burn have been analyzed for each hour, separated by color. Most frequently, benefits between 5 and 15 kg can be reached each hour. This corresponds to $\approx 1\%$ of the total fuel of the whole flight. After the first optimization, at least 20 of 93 flights still gained a benefit of 25 kg, corresponding to $\approx 2\%$ of the whole flight’s total fuel. On average, this benefit seems sufficient to be considered for a re-optimization during the flight.

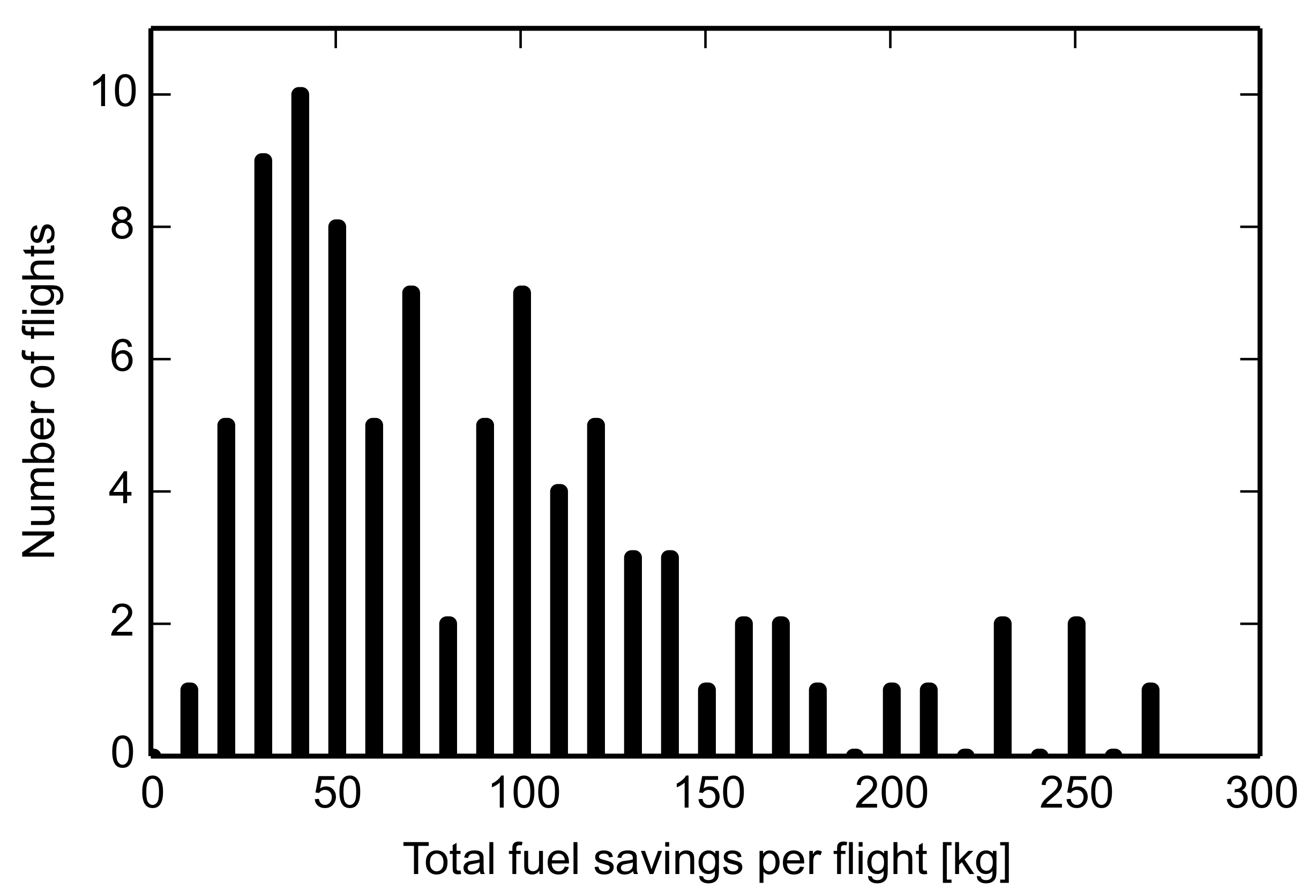
If you add up all the hourly benefits of a flight, you can see that 10% of flights save more than 170 kg of fuel. This corresponds to 1.64% of the total fuel consumption. 20% of the flights save more than 130 kg of fuel, which corresponds to 1.26% of the total fuel consumption. 30% of all flights still save more than 110 kg of fuel, which corresponds to 1.07% of the total fuel consumption (see Figure 8).

The differences between two subsequent optimizations in the lateral path are sometimes quite small (compare Figure 9) and do not always correspond with changes in wind speed $\Delta u$ [m s${}^{-1}$] only. For example, on 10 August 2019, the re-optimized path only deviates from the former optimized one by 328 m on average, although differences in wind speed along the path reach maximum values of 6 m s${}^{-1}$ (compare Figure 9, top). On 4 January 2020, the re-optimized trajectory deviate by 1902 m on average, whereas differences in wind speed along the path are quite small ($-2\le \Delta u\le +2$ m s${}^{-1}$), with one exception at $-85$ Longitude (see Figure 9, bottom).

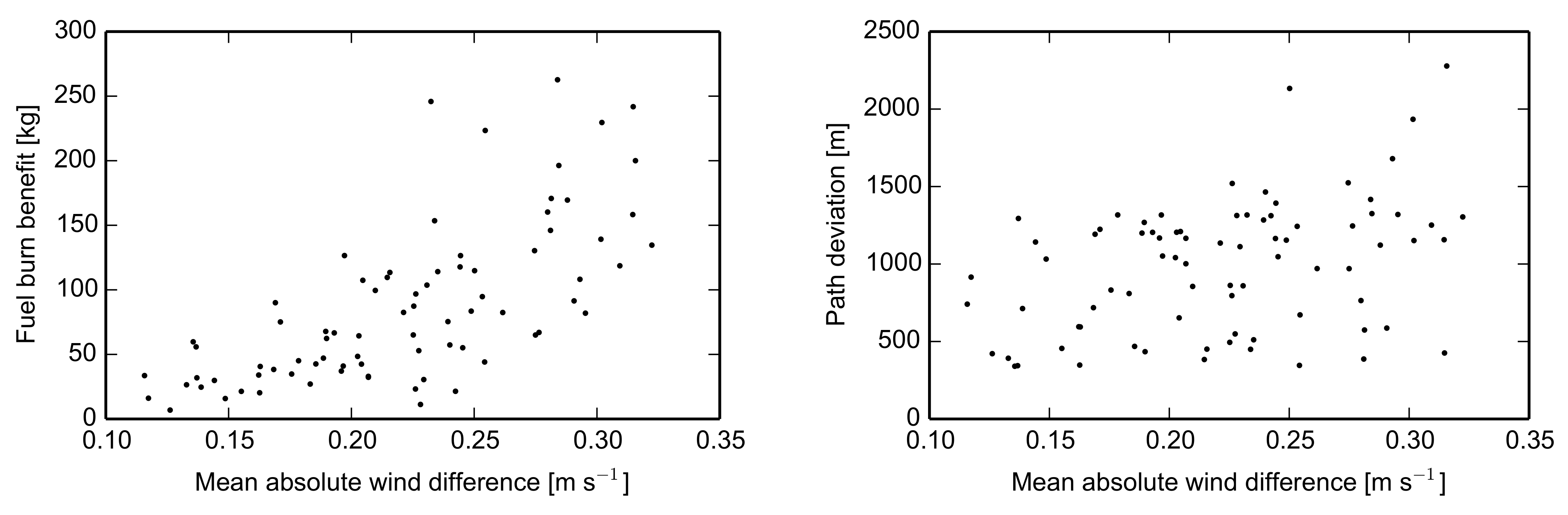
Mean differences in the path of all subsequent optimizations are analyzed and compared with the corresponding differences in wind speed along the path in Figure 10. Differences in wind speed $\Delta u$ along the path between two subsequent RAP forecasts are $-7\le \Delta u\le +9$ m s${}^{-1}$ with an average value of $\Delta u=0.5$ m s${}^{-1}$. However, averaged along the path, small differences in wind speed of $\overline{\Delta u}=0.25$ m s${}^{-1}$ are estimated. Figure 10 shows a weak positive correlation between differences in wind speed and fuel burn benefit after re-optimization. This correlation might be weak because of three reasons: (i) additional cost functions in the multi-criteria trajectory optimization, despite from wind speed, (ii) a non-optimum aircraft position, from which the re-optimization starts and (iii) because of the limited number of analyzed flights and weather scenarios. From this follows that increasing differences in wind speed increase the necessity and the benefit in fuel burn of an in-flight trajectory optimization.

The resulting lateral deviation from the former optimized path does not significantly correlate with changes in wind speed. Considering the applied weather data of three months, the lateral deviations of the path between two subsequent optimizations are surprisingly small. Averaged over the entire flight, the great circle distance between the geographical positions of the path each second are between 328 m on 8 August 2019 and 2277 m on 1 July 2019 (see also Figure 10, right). Averaged over all flights, the difference in a path between two subsequent optimizations were 1322 m, which corresponds to less than 1 nautical mile. Figure 10 does not show a clear correlation between the path deviation and the difference in wind speed between two subsequent re-optimizations. It follows from Figure 10 that strong changes in wind speed do not necessarily induce a large change in the lateral path during trajectory re-optimization. The small, but often efficient deviations from the lateral path increase the probability of ATC clearance to activate the re-optimized trajectory.

The question of how often or at what intervals an optimization can be triggered from the operator’s point of view depends on several issues: While the workload in the cockpit is very high during takeoff and landing, several optimizations could be triggered during the cruise portion of a medium- or long-haul flight. Besides the workload in the cockpit, the workload of the air traffic controller also plays a role, as an optimized trajectory must be coordinated and requested with ATC. Although the air traffic controller’s workload is not directly visible to the flight crew, an experienced pilot can guess the workload based on the volume and speed of radio communication traffic. Since the majority of the trajectory optimization concerns the cruise portion of the flight and thus the Enroute-Controller, a limitation of optimization triggers with a subsequent ATC-coordination should not be a workload problem.

Another important issue is the usability of the optimization tool. The question of optimization frequency of flights in daily flying will rather be the pilots’ acceptance of the optimization tool, which is directly related to its usability. If an optimization tool generates trajectory data that must first be entered into the aircraft’s FMGS by the pilots by hand, this will be perceived as a time-consuming procedure. However, if the optimization requests were sent to a ground station for calculation, e.g., the airline’s dispatch, which sends a result via ACARS directly into the FMGS for acceptance by the flight crew, the usage of the tool, and hence the frequency of possible optimization requests, would be increased.

In summary, using an appropriate tool, hourly optimizations are typically possible during cruise flight from a pilot’s point of view.

5. Conclusions

In this study, the benefit of hourly re-optimizing the aircraft trajectory during the flight has been analyzed and the method was embedded in the context of current flight procedures. A flight from Seattle to New York has been analyzed, optimized, and assessed on 93 days with five hourly weather forecasts per day. Therefore, the TOolchain for Multi-criteria Aircraft Trajectory Optimization (TOMATO) has been used for a dynamic 4D trajectory optimization. Additionally, the differences between the weather forecasts and their impact on fuel burn and lateral path deviation have been analyzed. The amount of fuel saved due to an hourly re-optimization has been estimated by comparing the newly optimized flight with a former modeled flight in the new weather forecast. On the 93 days examined, fuel savings between $0.5$% and 7% per flight were achieved despite minor differences in wind speed between two consecutive weather forecasts in the order of $0.5$ m s${}^{-1}$. The fuel-saving assessment should help the operator to decide whether or not to activate the proposed re-optimized trajectory.

The lateral deviations from the filed path were always below 1 nautical mile and thus very small. In this study, deviations in cruising altitude and true airspeed were neglected, because the optimizer always chose an aerodynamically optimized cruising altitude and cruising speed for a maximum specific range. Therewith, the aircraft followed a continuous cruise climb profile with deviations in true airspeed far below 5%.

The simulation-based optimization method within TOMATO is a resource-intensive approach and limits the number of variables to optimize. For example, the aircraft speed cannot be optimized considering the optimum utilization of all future tailwind components during the remaining flight. For that reason, target functions for the ground speed are missing, but target functions for the true airspeed are considered. Furthermore, wind optimum cruising altitudes can only be determined iteratively which is resource-intensive. For that reason, in this study, the aerodynamic optimum altitude is chosen which is not necessarily the fuel optimum altitude. Nevertheless, in this study, only hourly trajectory updates were analyzed, because of hourly weather updates.

In this study, the re-optimization was restricted to the cruise phase for the following reasons: First, the operator’s task load in the climb and descent phase might be higher and second, because TOMATO calculates additional fuel costs for level flights and speed brakes usage in a descent phase, different from continuous descent operations (CDO). For this reason, the ground distance of the CDO is fixed, as soon as the aircraft reaches the iteratively calculated top of descent. A path variation in this flight phase would induce additional costs in the current state of TOMATO.

Unfortunately, the authors are not able to validate the results of this study, because there is no comparable study considering the disadvantage of frequent weather data updates and frequent re-optimizations in trajectory optimization. All other studies did not consider on-time weather updates during the flight. For this reason, the calculated fuel consumptions are smaller than expected with constant weather, which are in the order of 2 to 5% per flight [22,31].

The fuel-saving potential of the small path deviations allows an easy implementation of the method in today’s flight procedures and does not require a fully developed Free Route Airspace Concept. However, the impact of this concept on the operator’s and controller’s taskload has not been considered in this study. The evaluation of the additional taskload due to the re-optimization for both stakeholders will be the focus of the next study.

Besides the consideration of the controller’s and operator’s taskload, we will investigate in an optimum trajectory update frequency, averaged over several weather scenarios. This optimum depends on differences in weather input data between two subsequent updates and in the taskload. To simplify operational feasibility, optimum trajectories along the current navaid infrastructure will additionally be calculated and compared with the optimized free routes.