Abstract
A data envelopment analysis was used to evaluate the efficiency of 18 primary healthcare centres in a health district of the Valencian Community, Spain. Factor analysis was used as a first step in order to identify the most explanatory variables to be incorporated in the models. Included as variable inputs were the ratios of general practitioners, nurses, and costs; as output variables, those included were consultations, emergencies, avoidable hospitalisations, and prescription efficiency; as exogenous variables, those included were the percentage of population over 65 and a multimorbidity index. Confidence intervals were calculated using bootstrapping to correct possible biases. Efficient organisations within the set were identified, although the results depend on the models used and the introduction of exogenous variables. Pharmaceutical expenditure showed the greatest slack and room for improvement in its management. Data envelopment analysis allows an evaluation of efficiency that is focussed on achieving better results and a proper distribution and use of healthcare resources, although it needs the desired goals of the healthcare managers to be clearly identified, as the perspective of the analysis influences the results, as does including variables that measure the achievements and outcomes of the healthcare services.
1. Introduction
Health care is one of the pillars of the Welfare State, together with education, the pension system, and social services. Health expenditure in developed countries amounts on average to 8.8% of the Gross Domestic Product GDP [1]. Spain, at 6.4% (74,000 million Euros of public health expenditure in 2017, 1594 per capita) [2], is below the European average, although with an upward trend due to population ageing and the incorporation of better but more expensive technology.
The Spanish National Health System is structured into two health care levels, primary care and specialist care, in which there is an inverse relationship between accessibility and technological complexity. The main care facilities are the health care centres, staffed by multidisciplinary teams comprising general practitioners, paediatricians, nurses, and administrative staff. Since primary health care services are located within the community, they also deal with health promotion and disease prevention [3].
Within the healthcare services, primary health care (PHC) represents the entry point for the healthcare system, therefore its correct functioning determines that of specialised care and directly impacts on the health of the population [4,5].
Among the main objectives of the Spanish National Health System is the promotion of health in an environment of high health expenditure and its progressive increase [3], which makes it necessary to adopt containment measures so that the quality of health services is not impaired. Evaluation of the efficiency of PHC services is relevant, therefore, to detect the set of varied problems that affect its ability to offer high quality services to the population within the restraints of the healthcare expenditure. Furthermore, evaluation and analysis of this will allow for a better distribution and use of healthcare resources.
The recent pandemic caused by SARS-CoV-2 has revealed many of the weaknesses of healthcare systems, both European and worldwide, as well as the need to introduce changes in the organisations and give PHC the importance it deserves [6,7,8,9]. In some countries, the PHC network constitutes a pillar sustaining the containment measures [10].
Although alternative methods exist to measure the efficiency of service organisations, such as the parametric, one of the most widely used is data envelopment analysis (DEA), which is applicable to the case of healthcare services as it measures the production and efficiency of these organisational units, which use numerous resources to produce multiple results.
DEA was developed with the goal of evaluating performance in the public sector from the point of view of production efficiency, a sector in which there was neither a "market" to select the most efficient organisational units, nor a regulatory model that guaranteed greater efficiency [11,12]. Each unit evaluated (or Decision Making Unit (DMU)) uses multiple inputs to produce multiple outputs. DEA models seek to determine which of the “n” DMUs compared constitute the efficient frontier (or enveloping surface) from a Pareto-Koopmans perspective: a DMU is on the efficient frontier if and only if there is no other observed DMU that improves any input or output without the worsening of other inputs or outputs. Once the DMUs with the best practices are identified, the DEA models construct an empirical production frontier.
This methodology holds the advantage that it does not presuppose any production function, nor the need for economic evaluation of many outputs that are sometimes difficult to quantify.
DEA has been used to analyse efficiency in the service sector in general. In the healthcare field, it has been used to evaluate healthcare systems [13,14,15,16], reform [17], hospital services [17,18,19,20,21,22] and, to a lesser degree, primary health care. In a recent systematic review, 54 studies were identified that used DEA to evaluate the efficiency of primary health centres [23].
One of the first applications of DEA to PHC was carried out by Goñi-Legaz (1998), differentiating in clusters the rural PHC from the urban [24].
Filipe Amado and Dyson (2008) indicate that performance evaluation and improvement in primary health care should include structure, process, products, and results [25], that evaluation in primary care should be formative, involving the stakeholders if unintended consequences are to be avoided and performance is to be improved; and, in principle, DEA provides the basis for an appropriate methodology [26,27]. In this sense, Romano and Choi (2016) concluded that it is necessary to introduce quality indicators in the models [28].
On the other hand, Cordero et al. (2015) stated that in the measure of efficiency, exogenous variables should be introduced because this has a modulating effect on efficiency. It is not the same to estimate the efficiency of a health centre with a very aged population compared to others with younger population, for example [29].
Other authors use these models to measure the trade-off between efficiency and equality in healthcare systems, taking as reference the case of New Zealand, where there are differences between ethnic subpopulations, attempting to maximise gains in health care while minimising inequalities [16].
In the studies that apply DEA to PHC evaluation, we must consider the input and output variables used and the models. One of the most important aspects is the selection of the best input and output variables to be included in the model and the exploration of the effect of the exogenous variables [30]. Regarding the outputs, discussion with primary health centre managers focusses on whether greater weight should be given to the productivity variables or those that reflect health outcomes. This last has been little explored in the literature, as access to this kind of information is difficult and the majority of studies focus on the so-called “activity oriented” outputs and models, not on healthcare results measured, for example, in hospitalisations or avoided mortality. The most used input variables in these studies were identified as personnel costs, gross expenditure, referrals and hospitalisation days, pharmaceutical prescription, and research carried out. Outputs include consultations or visits, patients registered, procedures, treatments, and services, and also, instead of being considered as inputs, variables such as prescriptions and research. Some of these studies incorporate variables of quality as outputs, which in the majority of cases refer to compliance with protocols or standards, experience of professionals, patient satisfaction, or the accessibility and equality of attention, but few of them use variables that measure results in patient health. The studies use different DEA models without having a standard focus that allows comparison of results [23].
Regarding the models, Cordero Ferrera et al. (2014) used an input orientation in primary care centre efficiency measurements because managers can determine only those resources attributed to each primary care centre and the demand for health services cannot be controlled [31,32]. Other authors justify the use of output-oriented models, considering that the health care sector is very specific and that health care services should concentrate on increasing the outputs, that is achieving the best healthcare outcome, and it is assumed that greater output is associated with technical efficiency [33].
In this work, real world data from the basic health units (BHU) of PHC in a health district of the Valencian Community are used, from which the output variables, input, and exogenous variables are elaborated in order to develop and compare useful models to measure the efficiency of the BHUs that will be the DMUs in this study. The objective is to verify how the variables that are introduced in the models with the DEA methodology influence the efficiency measurement, to evaluate the usefulness of the methodology, as well as to examine the requirements and limitations to be considered in improving the measurement of efficiency.
2. Materials and Methods
2.1. Data and Variables
The Valencian Community (east of Spain) health map is composed of 24 health districts with each divided into a number of basic health units (BHU) that may vary from one health district to another. The Valencia Clínico–La Malvarrosa Health District is one of the biggest health districts of the Valencian Community. It covers a wide geographical area and very diverse zones. It contains 18 BHUs serving an approximate population of 320,000 inhabitants. These are the BHUs that were incorporated in the analysis. Each BHU consists of one or more primary care centres.
The BHUs of the district analysed vary widely in terms of size and characteristics of the population they serve, their location (urban and rural), etc. Although the intention was to introduce more health districts into the efficiency analysis, at this time only the data for this health district is available for evaluation.
As well as the information system of the Regional Ministry of Health (Conselleria de Sanitat i Salut Pública) and the Hospital Clínico Universitario of Valencia (Valencian Community), the information sources used were: the electronic outpatient clinical records (ABUCASIS), which include the Ambulatory Information System (SIA) and the Pharmacy Prescriptions Manager (GAIA); the Hospital Minimum Data Set (MDS); the Population Information System (SIP); the Economic Information System (SIE); the database of emergencies from the Hospital Information System (HIS); and the databases for Hospital Pharmacy of the Regional Ministry of Health.
For this analysis of efficiency, the data of the year 2015 of each BHU have been used, since, although more recent data have been requested, at the moment only the data corresponding to the year 2015 are correctly validated and available. The data gathered for 2015 from each BHU is explained in Appendix A.
The variables used as inputs and outputs in the evaluation of efficiency were compiled from the original data or developed specifically in each BHU.
In order to mitigate the difference in size, ratios per 10,000 inhabitants are used.
The percentage of population over 65 and a multimorbidity index (case-mix) are included as exogenous variables, as they do not directly participate in the production process and cannot be controlled, but do affect it, given that the organisations’ activity and healthcare results are conditioned by the characteristics of the population they serve [30].
Some of these variables were taken directly from the data provided by the BHUs, while others needed to be compiled, such as the case-mix, avoidable hospitalisations, and the efficiency indicator in pharmaceutical prescription.
Furthermore, three of the available output variables (emergencies, avoidable hospitalisations, and mortality) constitute undesirable health results, due to which they cannot be used directly in the DEA, as this methodology maximises results and in these cases it is important that their values be as low as possible. To correct this effect, a factor is applied to invert them [34]. The corrected ratio of hospital emergencies is obtained from the emergencies in the population assigned to each BHU as 10,000 minus hospital emergencies. The corrected ratio of avoidable hospitalisations is calculated as 100 minus the avoidable hospitalisation rate for each BHU. The corrected mortality rate is calculated a 1000 minus the mortality rate of each BHU. In this way, these corrected variables become favourable outputs of the BHUs.
The data obtained were anonymised and the study has strictly complied with the current personal data protection regulations, specifically Regulation 2016/679 of the European Parliament and of the Council of 27 April 2016 on the protection of natural persons with regard to the processing of personal data and on the free movement of such data, as well as the Organic Law 3/2018, of December 5 concerning protection of personal data and guarantee of digital rights.
2.2. Methodology
DEA is used in the measurement of efficiency with the principle goal of finding the frontier of efficient production formed by those resource combinations that optimise the amount of services produced while minimising resources used [35]. The variable return to scale (VRS) method was used. Unlike the constant return to scale (CRS) method, VRS does not assume that all the BHUs have the same scale of production and therefore it takes into account the different dimensions that may be found in each of them. This method has some advantages over others in regard to the heterogeneity of magnitudes, the lack of need for normality, and in not requiring all the variables to be evaluated in economic units. Nevertheless, it does have a restriction on the maximum number of variables that can be introduced as inputs and outputs in the models, established at one third of the BHUs evaluated. This limitation requires that the variables included in the models are very carefully chosen in such a way that they best detect the differences in efficiency of the BHUs. To choose the variables, factor analysis was used prior to DEA to avoid correlations and conveniently select the definitive inputs and outputs.
Public health service organizations in Spain are very rigid in modifying resources, especially with regard to the allocation of health personnel, which constitutes a high percentage of cost, and the management of the centres has little room to modify this. For this reason, the output orientation has been selected in this work, since the objective of these BHUs must be to obtain the best possible result with the resources available.
For each production unit, an input series x and an output series y are considered. The DEA estimator of the production of the set of n units, can be defined as:
For each specific unit, given inputs x0 and outputs y0, the estimation of the output orientated efficiency, , is given by:
Thus, indicates the technically efficient units, and denotes inefficiency in the unit. Considering the inverse of , the efficiency score between 0 and 1 is obtained, with values inferior to 1 denoting the degree of unit inefficiency in relation to the technically efficient units.
DEA efficiency scores may be biased upwards, due to the omission of important variables in the models or due to measurement errors in the data used. In this way, the empirical frontier may fail to incorporate unobservable but very efficient units [36]. To avoid the possibility of biases in the estimations, we employ the DEA bootstrap methodology described in Simar and Wilson [36] to calculate the bias-correction of technical efficiency scores of the analysed models as well as the 95% confidence intervals [37].
In addition, to account for the influence of environmental or exogenous variables not controlled by BHUs (percentage of population over 65 or case-mix), we use a two-stage procedure and implement bootstrap bias correction, following the methodology of Simar and Wilson’s second algorithm [38]. To explore the influence of these variables in the models, their corrected values have been used as the number of elderly and/or multimorbid people assigned to a BHU entails an increment of resources.
DEA with VRS and output orientation was used. Software R was used when exogenous variables were introduced in the model and STATA if they were not included [35].
3. Results
3.1. Factor Analysis
The analysed BHUs have very different sizes, with an average assigned population of 17,831 patients (maximum 37,497 and minimum 7148). Table 1 shows the descriptive statistics of the variables considered in the analysis and their type of variable, input, output, or exogenous.

Table 1.
Descriptive statistics of variables.
Due to the limitation on the number of variables that can be incorporated in a DEA model, it is necessary to choose the inputs and outputs to be used that best detect differences in efficiency between the BHUs.
Factor analysis is used as a first step in the construction of DEA models. The choice of the most suitable variables is based on the relations observed between them, their discriminatory or explanatory power of the variability and, furthermore, by taking into account the availability of the variables (the possibility of obtaining the information) and the interest of the administration in the results of the BHUs that they wish to evaluate. This analysis allows us to determine which variables are most correlated with the factors or dimensions that have the greatest explanatory power of the variance and to avoid, as far as possible, those variables that are correlated with each other.
Four factors that explain 86.11% of the total variation in the data were identified by the factor analysis (Table 2). However, only variables related with the first three factors were selected, as even though the fourth factor achieved an eigenvalue greater than 1, it only increases the percentage of explained total variance 7.73% and the objective of this analysis is, due to the limitation in the number of variables that is possible to introduce in the models, to select those variables with greater explanatory power.

Table 2.
Explained total variance.
The composition of each factor is shown in Table 3.

Table 3.
Matrix of rotated components.
The factor or dimension that most differentiates the BHUs is Factor 1, which explains 42.76% of the variance and concerns healthcare activity. It correlates to general practitioners’ and nursing consultations, referrals to specialised care and the corrected emergencies, pharmaceutical expenditure, and prescription efficiency. It is determined that those BHUs with a high number of general practitioners’ and nursing consultations, referrals, and pharmaceutical expenditure—that is, with high activity and low prescription efficiency—have a lower number of corrected emergencies. This indicates, therefore, that if the patients are well controlled by their general practitioners (which involves a greater number of consultations and higher pharmaceutical expenditure) there should be fewer emergencies. Factor 2 explains 21.99% and correlates to human resources, both in number and cost. Lastly, Factor 3 explains 13.63% and concerns patient morbidity. Those BHUs with a high percentage of people over 65 will have higher case-mix and a greater ratio of avoidable hospitalisations (or lower ratio of corrected avoidable hospitalisations). Both avoidable hospitalisations and the mortality ratio are clearly related to age and to a greater clinical complication in the patients.
If we analyse the factorial scores for each of the BHUs, in factor 1, which is related to healthcare activity, BHUs 12, 13, and 3 stand out as having the lowest factor 1 values and therefore few consultations, emergencies, referrals, and pharmaceutical expenditure. On the other hand, at the opposite end of the scale, with a high level of activity, are BHUs 6, 17, 4, and 5.
From this first factor, the variables pharmaceutical expenditure and prescription efficiency have been selected to use in the models and general practitioners’ and nursing consultations have been grouped into a single variable.
With respect to factor 2, BHUs 10 and 18 stand out, with fewer human resources (medical staff, nurses, and personnel expenditure), while BHUs 9 and 13 are those that obtain the highest scores in this factor.
From the second factor, the number of general practitioners and nursing has been introduced.
Factor 3, related to an older population, greater clinical complexity, and a higher ratio of avoidable hospitalizations, is found with the lowest scores in BHUs 12, 13, and 3. At the other extreme, BHUs 4, 5, 6, and 17 stand out.
From the third factor, corrected avoidable hospitalizations are taken into account in the models as an output and, later, as exogenous variables, the percentage of population over 65 years and the case-mix.
Finally, BHU 12 stands out as having the lowest burden of factors 1 and 2; that is, less aged population and less activity. BHU 4 is that with the highest load of factor 1 and factor 3, and therefore has a more aged population, morbidity, and less activity.
3.2. Data Envelopment Analysis
From the results of the factor analysis, the following models for evaluation by DEA are established (Table 4): Model 1, in which the healthcare results of the patient (emergencies and avoidable hospitalisations) and prescription quality were introduced as outputs and the ratio of general practitioners, ratio of nurses, and ratio of pharmaceutical cost as inputs; and Model 2, which includes the same inputs, but substitutes ratio of emergencies with general practitioners’ and nursing consultations, that is to say, the data for healthcare activity (consultations) is introduced. General practitioners’ and nursing consultations are included aggregated as a single variable.

Table 4.
Composition of models.
Several models with different combination of inputs and outputs were implemented, but we only show the results of the two models that obtained the best results and show the greatest differences between the BHUs.
After applying the selected models (Table 4), the efficiency value is obtained (Table 5). The efficiency score obtained is in general quite high, as in the majority of cases it is above 90%.

Table 5.
Efficiency obtained with models 1 and 2 for variable return to scale (VRS).
In Model 1, the range of efficiency is between 0.789 and 1. Those units that are inefficient need to reduce their consumption of inputs proportionally between 2.9% and 21.1% for their level of outputs. On introducing healthcare activity (number of consultations) (Model 2), all the BHUs improve with the exception of one and the number of BHUs reaching the efficient frontier increases from 6 to 8. The range is between 0.777 and 1. In this model, the inefficient units need to reduce their inputs proportionally between 1% and 22.3%. Some BHUs, such as 1, 3, 11, 12, and 13 are shown to be efficient in both models, independently of the outputs used. On the other hand, BHUs 5 and 15 obtain the worst results, needing to reduce their inputs between 15% and 21% to reach the frontier, depending on the model.
On the other hand, information is also obtained on the slack of the inputs (islacks) and outputs (oslacks) that the inefficient BHUs should increase or decrease to place them on the efficient frontier (Table 6 and Table 7). This information is useful for decision making, as it allows identification of what each BHU must improve and if any of them are oversized for the results obtained.

Table 6.
Input and output slack of Model 1 VRS.

Table 7.
Input and output slack of Model 2 VRS.
In Model 1 (Table 6) the unit with the greatest slack in human resources is BHU9, both in general practitioners and nursing. This unit also presents one of the highest amounts of slack in pharmaceutical expenditure, although the worst unit is BHU6. Regarding the outputs, BHU4 is the most in need of increasing its corrected emergencies, that is, it is the one that should most reduce the number of emergencies attended. BHU7 should most reduce its avoidable hospitalisations and BHU15 should most increase its prescription efficiency.
The slacks found in Model 1 are greater than those of Model 2, where the variable ratio of emergencies is changed for that of consultations. In this model (Table 7), BHUs 5 and 17 are the only ones that should reduce their general practitioners, while BHU2 is the one that should most reduce its nursing personnel. In pharmaceutical expenditure, the unit most in need of improving management is BHU15. Regarding outputs, no slack was observed in the number of consultations, and only BHU15 needs to reduce avoidable hospitalisations. In prescription efficiency, BHUs 16 and 18 have the greatest margin for improvement.
Among the input and output variables, the one that most influences achieving the efficient frontier, together with human resources, is pharmaceutical expenditure, which represents the greatest cost for the BHUs (around 60% of the total cost of the primary healthcare centres, as also suggested by similar studies [39,40]). Among the inefficient units, there is a need to reduce pharmaceutical expenditure by between 93,415 and 751,928 Euros per 10,000 inhabitants, which entails, on average, a reduction of over 20%.
Figure 1 represents the efficiency value of the different BHUs in Model 1 with respect to the exogenous variables of percentage of population over 65 and case-mix. It shows the units situated on the efficient frontier (value 1) and the distance of those that fall below it. It shows which units serve more aged population and with higher morbidity, such as BHUs 5 and 15, and that both exogenous variables are highly correlated, with a correlation of 0.67 obtained in the factor analysis.
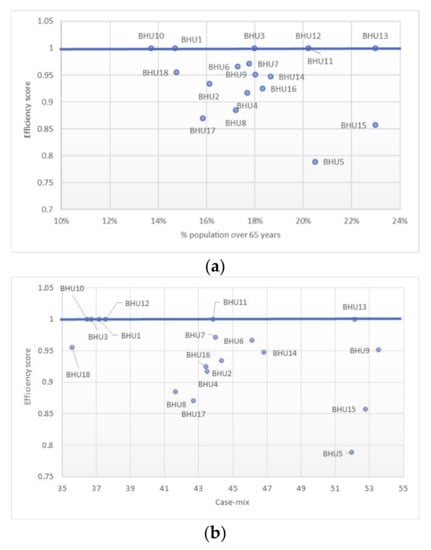
Figure 1.
(a) Efficiency frontier of Model 1 VRS output orientation with regard to percentage of population over 65. (b) Efficiency frontier of Model 1 VRS output orientation with regard to case-mix.
It can be seen that the results for efficiency obtained with this methodology depend on the variables introduced as inputs and outputs in the established models. Thus, Model 1, where the variable ratio of corrected emergencies is introduced as output, gives worse results for efficiency than Model 2, where this variable is substituted by ratio of consultations. This fact implies that emergencies are worse managed than consultations, as many of the BHUs need to lower their ratio of emergencies to be efficient. Certain BHUs are efficient in both models, while other BHUs are always inefficient. It can be seen that the worst rated BHUs in the set are 5 and 15, as these are in the worst place in the efficiency rankings of both models.
The results also show which input and output to improve in each BHU, but the models reach different results. Pharmaceutical expenditure is the input with greatest amount of slack and is most open to better management and control by healthcare professionals in order to reach efficiency. Use of human resources is the second.
Table 8 shows the results of technical efficiency scores in comparison to technical efficiency bias-corrected (by bootstrapping) and the bootstrap confidence intervals (BCI).

Table 8.
Original efficiency scores and bias-corrected obtained with models 1 and 2 for VRS.
Once the bootstrapping has been carried out, the results indicate lower efficiency scores for every BHU, confirming, as other authors have stated, that the standard procedure may be biased upwards [36]. However, those BHUs that were previously efficient continue to be those with higher results in both models and are almost the only ones that could achieve the efficient frontier (score equal to 1) according to the confidence intervals.
The biggest differences with the original scores are achieved by BHUs 3, 10, 11, 12, 13, and 18, and these differences are superior in model 1.
The variables collected that can be used as exogenous variables are the case-mix and the percentage of population over 65. Incorporating these variables (which take into account the characteristics of the assigned population) into the models leads to different results in bias-corrected efficiency scores by bootstrap (Table 9), and therefore needs to be considered in correctly evaluating the BHUs.

Table 9.
Bias-corrected efficiency scores (by bootstrap) obtained with models 1 and 2 for VRS including exogenous variables.
Including one exogenous variable or the other leads to slightly different results. Using case-mix allows the units to obtain, in most cases, better results. It is important, however, to bear in mind that the percentage of population over 65 is always available, while the case-mix may not be (as it is obtained from the CRG classification, which is not implemented in other regions). Furthermore, as has been determined in other studies, both variables show a high correlation and therefore could provide similar information in the models [41,42].
If we compare the results including the exogenous variables with those obtained in Table 8, in Model 1 with percentage of population over 65, eleven units achieve better results. When introducing case-mix as the exogenous variable, one unit more improves its score. In Model 2 with percentage of population over 65, half of the units show worse efficiency results and the other half improve their scores. If instead we use case-mix, BHUs 3 and 4, which get worse results when using percentage of people over 65, now improve their scores, while BHU 18 shows the opposite effect.
BHUs 5 and 15, which achieved the worst results in the original models (Table 5), and have more aged population and higher morbidity, show the greatest increase in their efficiency scores when including both exogenous variables, especially in Model 1. Contrarily, BHUs 7 and 14 obtain a higher decrease, more pronounced in Model 2.
By introducing the case-mix exogenous variable, better efficiencies are obtained generally than with that of population over 65. These variables have a high correlation (0.67 in the factor analysis and are related to the same factor (Table 3)), so they similarly affect the efficiency of the BHUs, although the case-mix has a greater influence.
There is no clear combination of inputs and outputs that allow the units to obtain higher results, but it is clear that the characteristics of the population they serve affect their performance to some extent.
Some units achieve, in general, the best results (higher scores) in all the models, no matter which combination of inputs and outputs and exogenous variable are included, such as BHUs 1 and 10. The majority, though, show differences in their performance depending on the variables used in the evaluation.
4. Discussion
DEA is a useful methodology for the evaluation of efficiency of BHUs and provides very valuable information for managers, but it does have some disadvantages and limitations that are not always easily overcome. The objective is to find the BHUs that are on the efficient frontier, which will be those with the highest efficiency scores, and, for those BHUs that fall short, determine in what they are failing; that is, which resources they should reduce or which results to improve and by how much.
It must be borne in mind that the efficiency found using this methodology only allows comparison within the set of considered BHUs. In this case, no great differences were observed between the components of the group in the efficiency rating obtained, which implies they all function similarly [31]. However, if they are compared with BHUs from other health districts, the results may be completely different. It must be further taken into account that the efficient frontier is not static, as it depends on the evaluated BHUs and will change with time as the medical technology used evolves. It would therefore be convenient to also analyse the evolution of the results obtained by the same BHUs in successive years as the data for those years become available.
The majority of the inputs employed by healthcare organisations in their daily activity are predetermined (personnel, equipment, etc.) and not easily controllable from the primary healthcare centres and BHUs. For this reason, output orientation is used, and the most efficient BHU is considered to be that with the best results regarding health care, measured by quality of attention. This is contrary to other studies which consider that activity is conditioned by demand and that it is the inputs that should be reduced [30].
The DEA scores depend on the choice of input and output variables, as other authors have also established [23]. From the point of view of healthcare activity, nearly all the BHUs obtain high efficiency scores. Due to this, the model to measure efficiency needs to introduce other variables that offer greater information on the quality of the health care, such as satisfaction surveys of the users, the ratio of avoidable mortality, or, as exogenous variable, the vulnerability index of the population assigned to the BHU. The inclusion of performance indicators for professionals must be interpreted with caution unless it is accompanied by care outcome indicators [43]. This would allow different results to be obtained that would contribute to proposing recommendations for the management of the BHUs and thus achieve more efficient and higher quality health care. To this purpose, it is necessary to involve the healthcare managers in the analysis, so their preferences can be incorporated through deliberation of the variables used as inputs and outputs, allowing them to become measures of utility [44].
The number of variables that can be used in the models is limited, as for reliable results it is recommended that the total of inputs and outputs does not exceed one third of the BHUs analysed. This entails an appropriate selection of the variables, and requires, in some cases, prior use of other methodologies, such as factor analysis. As more BHUs are incorporated into the analysis, the restrictions on the number of variables that can be introduced decrease. However, the results show that weighting is needed for the correct management of BHU activity, since the aim is to improve the health of the population with services of quality rather than the pure activity quantified by the number of consultations. These issues will be addressed in the continuation of this work.
In order to achieve more reliable results, and following the methodology used by other authors [37,38], bias-corrected efficiency scores were obtained by bootstrap. This technique allows for correction if outliers exist and improves the model specification and its validity.
It is observed that the characteristics of the population introduced as exogenous variables have a significant influence on the effectiveness scores of the centres, so it is very important to include them in the models [29,30]. Regarding this, although this study has the case-mix variable which measures the burden of chronic disease, the most suitable and easily available exogenous variable for measuring efficiency is the percentage of over-65s, which further has a high correlation with the case-mix.
Furthermore, information systems need to be improved to provide quality data, as the evaluation of efficiency of the different healthcare services will continue to be a necessary field of research and of great importance for healthcare management. This would directly contribute to achieving efficient health care, entail higher quality in delivery of services, and translate into an increase in satisfaction by the population.
Some of the limitations found in this methodology for evaluating primary health care are the following: (1) the undesirable results in health, such as the number of emergencies or avoidable hospitalisations, in many cases entail using corrected variables. Some authors choose to use the inverse of the data [34], while others incorporate them with a negative sign or even consider them as inputs [45]. Some of these solutions are more restrictive than others, in the sense that they make it more difficult for the BHUs to be efficient and lead to different results [46]. The different options for correction lead to different evaluations of efficiency, due to which the most suitable conversion is not clearly defined; (2) Incorporating data with different scales or magnitudes can produce unreliable results [47]. It can be seen that when a BHU is efficient owing to an output with high value, such as may be the number of consultations, incorporating other variables into the model does not result in changes to its efficiency values. The use of ratios or standardised variables may help in this aspect; (3) In the analysis, the variables with greater magnitudes than the others (pharmaceutical expenditure for the inputs and number of medical and nursing consultations for the outputs) dominate. This aspect is a serious hindrance in the evaluation of efficiency when it is the quality of care that you wish to consider, as the goal is not to achieve a high level of care activity, but that these consultations are efficient, that is, they manage to avoid deaths, hospitalisations, emergencies, and unnecessary referrals to specialised care; (4) Lastly, how to calculate the slacks and introduce the exogenous variables simultaneously has not been resolved in this work.
Another limitation of the work is not having more up-to-date data and a greater range of years for analysis. Therefore, the efficiency results may vary for the present, although the data analysed are of high quality in terms of accuracy and reliability, and have served to validate the model. For future studies, comparative models will be conducted and the challenge will be to include in these the changes that have occurred in primary care clinical practice during management of the pandemic.
5. Conclusions
This work has used real world data from the 18 BHUs of the Clínico—Malvarrosa Health District in the Valencian Community, Spain. One of the principle contributions to the study of efficiency in primary health care is to consider the population health outcomes instead of outputs strictly for activity, for which some variables, such as avoidable hospitalisations or quality of pharmaceutical prescription, needed to be specially compiled for this study. This is a pilot test applied to a single health district with the aim of developing efficiency evaluation models and identifying deficiencies in them, to be later extended to other health districts.
DEA is a useful methodology, but it is observed that the variables that are introduced in the models influence the efficiency results. It will be necessary to choose the most appropriate inputs and outputs to evaluate the efficiency according to the objectives pursued, or to increase the number of evaluated units, which would allow more variables to be included in the models, always weighting the most important. Thus, future research needs to consider more suitable variables for the measurement of efficiency according to the degree of importance given to them by the managers, which would allow for different results that would contribute to the proposal of more useful recommendations for decision-making.
On the other hand, the exogenous variables determine the results of the BHUs and must be incorporated in the models, taking into account that the results will vary according to which variable is introduced. The case-mix seems to be the most appropriate, although, if this is not available, the variable of ageing population could be used, as it is linearly correlated with the case-mix.
The pandemic caused by SARS-CoV-2 has significantly affected the activity of primary healthcare centres and introduced changes in their management. It is still too soon to determine which of these changes will be lasting, but without doubt there will be an effect when it comes to measuring inefficiency and some of the variables may no longer be useful, not only while the pandemic lasts, but for the more or less near future. Therefore, a more profound analysis is needed together with the compilation of new data that allow the models to be re-evaluated and to incorporate the necessary modifications.
Finally, given the limitations of this methodology and considering the importance of primary care within the health system and its financial sustainability, further studies on efficiency evaluation are needed to identify an appropriate DEA model to measure the performance of PHC and achieve reliable and useful results.
Author Contributions
Conceptualization, D.V.-C. and I.B.-M.; methodology, D.V.-C. and I.B.-M.; software, S.G.-d.-J.; validation, R.U.-T. and Á.B.-P.; formal analysis, S.G.-d.-J.; investigation, S.G.-d.-J.; resources, S.G.-d.-J.; data curation, R.U.-T.; writing—original draft preparation, S.G.-d.-J. and I.B.-M.; writing—review and editing, S.G.-d.-J. and I.B.-M.; supervision, D.V.-C. and R.U.-T.; project administration, I.B.-M. and D.V.-C.; funding acquisition, I.B.-M., D.V.-C. and R.U.-T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by “Conselleria de Hacienda y Modelo Económico de la Comunitat Valenciana (Spain)”, file number HIECPU/2019/1, in the context of the Project “Desarrollo de un Modelo para el análisis de la eficiencia en las Unidades Básicas de Salud de atención primaria en un departamento de Salud perteneciente al mapa sanitario de la Comunidad Valenciana”.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Ethics Committee of HOSPITAL CLINICO UNIVERSITARIO DE VALENCIA (protocol code 2020/170 and date of approval 25 June 2020).
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Inma Saurí and José Luis Trillo for his helpful assistance in the collection and elaboration of the variables and to Javier Díaz Carnicero for his help in the mathematical models. We would like to thank John Wright for help with English editing.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The data collected for 2015 from each BHU were as follows.
- Assigned population for each BHU.
Healthcare resources (inputs):
- General practitioners and nursing personnel assigned to each BHU.
- Costs for personnel assigned to each BHU (personnel expenditure).
- Examinations expenditure, including costs of laboratory tests and imaging diagnoses performed on the assigned population of each BHU.
- Pharmaceutical expenditure. This includes the cost of medications prescribed and dispensed by general practitioners.
Activity (outputs):
- Number of consultations with general practitioners and nursing staff.
- Number of referrals to specialised care.
- Number of emergencies attended for patients who are part of the assigned population.
Healthcare results (outputs):
- Number of avoidable hospitalisations. This refers to the number of hospital admissions of the population over 40 years old caused by pathologies that should be controlled from the primary health centres [48] and as such should not result in an admission.
- Mortality. Number of persons of each BHU dying in a year.
- Indicator of prescription efficiency. The quality of pharmaceutical prescription, or indicator of prescription efficiency, is measured with the prior development of other indicators which consider that, for a group of pathologies (which constitute a high percentage of the total pharmaceutical expenditure) there has been correct prescription of the drugs for the patient to be controlled and at the same time, these are the most economic and efficient in their therapeutic group.
Exogenous variables:
- Percentage of population over 65 for each BHU.
- Case-mix, that is, a measure of the multimorbidity or the level of patients with multiple chronic conditions assigned to each BHU, is obtained from the Clinical Risk Group (CRG) classification of the population assigned to each BHU. The CRG assigns a weight to each health condition, related to the clinical complexity, in economic terms, of treatment.
References
- Organisation for Economic Co-operation and Development Health Resources. Health Spending—OECD. Available online: https://data.oecd.org/healthres/health-spending.htm (accessed on 20 July 2020).
- Ministerio de Sanidad Portal Estadístico del SNS. Sanidad en Datos. Available online: https://www.mscbs.gob.es/estadEstudios/sanidadDatos/home.htm (accessed on 20 July 2020).
- Ministerio de Sanidad. Servicios Sociales e Igualdad Sistema Nacional de Salud en España. In Monografía en Internet.; 2012. Available online: http://www.msssi.gob.es/organizacion/sns/docs/sns2012/SNS012__Espanol.pdf (accessed on 1 December 2020).
- Starfield, B.; Shi, L.; Macinko, J. Contribution of primary care to health systems and health. Milbank Q. 2005, 83, 457–502. [Google Scholar] [CrossRef]
- Caminal, J.; Starfield, B.; Sánchez, E.; Casanova, C.; Morales, M. The role of primary care in preventing ambulatory care sensitive conditions. Eur. J. Public Health 2004, 14, 246–251. [Google Scholar] [CrossRef]
- Sarti, T.D.; Lazarini, W.S.; Fontenelle, L.F.; Almeida, A.P.S.C. Qual o papel da Atenção Primária à Saúde diante da pandemia provocada pela COVID-19? Epidemiol. Serv. Rev. Sist. Unico Saude Bras. 2020, 29, e2020166. [Google Scholar] [CrossRef]
- Saint-Lary, O.; Gautier, S.; Le Breton, J.; Gilberg, S.; Frappé, P.; Schuers, M.; Bourgueil, Y.; Renard, V. How GPs adapted their practices and organisations at the beginning of COVID-19 outbreak: A French national observational survey. BMJ Open 2020, 10, e042119. [Google Scholar] [CrossRef]
- Wynn, A.; Moore, K.M. Integration of primary health care and public health during a public health emergency. Am. J. Public Health 2012, 102, e9. [Google Scholar] [CrossRef]
- Joy, M.; Mcgagh, D.; Jones, N.; Liyanage, H.; Sherlock, J.; Parimalanathan, V.; Akinyemi, O.; Van Vlymen, J.; Howsam, G.; Marshall, M.; et al. Reorganisation of primary care for older adults during COVID-19: A cross-sectional database study in the UK. Br. J. Gen. Pr. 2020, 70, e540–e547. [Google Scholar] [CrossRef]
- Lim, W.H.; Wong, W.M. COVID-19: Notes from the front line, Singapore’s primary health care perspective. Ann. Fam. Med. 2020, 18, 259–261. [Google Scholar] [CrossRef] [PubMed]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring efficiency of decision-making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Sherman, H.D.; Zhu, J. Service Productivity Management: Improving Service Performance Using Data Envelopment Analysis (DEA); Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Del Rocío Moreno-Enguix, M.; Gómez-Gallego, J.C.; Gómez Gallego, M. Analysis and determination the efficiency of the European health systems. Int. J. Health Plann. Manag. 2018, 33, 136–154. [Google Scholar] [CrossRef] [PubMed]
- Dlouhý, M. Measuring geographic inequalities: Dealing with multiple health resources by data envelopment analysis. Front. Public Health 2018, 6, 53. [Google Scholar] [CrossRef] [PubMed]
- Sandiford, P.; Vivas Consuelo, D.; Rouse, P.; Bramley, D. The trade-off between equity and efficiency in population health gain: Making it real. Soc. Sci. Med. 2018, 212, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Sandiford, P.; Consuelo, D.J.J.V.; Rouse, P. How efficient are New Zealand’s District Health Boards at producing life expectancy gains for Māori and Europeans? Aust. N. Z. J. Public Health 2017. [Google Scholar] [CrossRef] [PubMed]
- Caballer-Tarazona, M.; Moya-Clemente, I.; Vivas-Consuelo, D.; Barrachina-Martínez, I. A model to measure the efficiency of hospital performance. Math. Comput. Model. 2010, 52, 1095–1102. [Google Scholar] [CrossRef]
- Pérez-Romero, C.; Ortega-Díaz, M.I.; Ocaña-Riola, R.; Martín-Martín, J.J. Análisis de la eficiencia técnica en los hospitales del Sistema Nacional de Salud español. Gac. Sanit. 2017, 31, 108–115. [Google Scholar] [CrossRef] [PubMed]
- Tabanera, L.H.; Martín, J.J.; González, M.D.P.L.D.A. Eficiencia técnica de los hospitales públicos y de las empresas públicas hospitalarias de Andalucía. Gac. Sanit. 2015, 29, 274–281. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Siciliani, L. Estimating technical efficiency in the hospital sector with panel data: A comparison of parametric and non-parametric techniques. Appl. Health Econ. Health Policy 2006, 5, 99–116. [Google Scholar] [CrossRef]
- Martin Martin, J.J.; González, M.D.P.L.D.A. La medida de la eficiencia en las organizaciones sanitarias. Presup. Público 2007, 49, 139–161. [Google Scholar]
- Mancuso, P.; Valdmanis, V.G. Care Appropriateness and health productivity evolution: A non-parametric analysis of the Italian regional health systems. Appl. Health Econ. Health Policy 2016, 14, 595–607. [Google Scholar] [CrossRef]
- Zakowska, I.; Godycki-Cwirko, M. Data envelopment analysis applications in primary health care: A systematic review. Fam. Pract. 2020, 37, 147–153. [Google Scholar] [CrossRef]
- Goñi-Legaz, S. El análisis envolvente de datos como sistema de evaluaclón de la eficiencia técnica de las organizaciones del sector público: Aplicación en los equipos de atención primaria. Rev. Esp. Financ. Contab. 1998, 27, 979–1004. [Google Scholar]
- Donabedian, A. The Definition of Quality and Approaches to Its Assessment and Monitoring; Health Administration Press: Chicago, IL, USA, 1980; Volume 1. [Google Scholar]
- Filipe Amado, C.A.; Dyson, R.G. On comparing the performance of primary care providers. Eur. J. Oper. Res. 2008, 185, 915–932. [Google Scholar] [CrossRef]
- Amado, C.A.; Santos, S.P. Challenges for performance assessment and improvement in primary health care: The case of the Portuguese health centres. Health Policy 2009, 91, 43–56. [Google Scholar] [CrossRef] [PubMed]
- Romano, J.; Choi, Á. Medida de la eficiencia de la atención primaria en Barcelona incorporando indicadores de calidad. Gac. Sanit. 2016, 30, 359–365. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Cordero, J.M.; Alonso-Morán, E.; Nuño-Solinis, R.; Orueta, J.F.; Arce, R.S. Efficiency assessment of primary care providers: A conditional nonparametric approach. Eur. J. Oper. Res. 2015, 240, 235–244. [Google Scholar] [CrossRef]
- Cordero-Ferrera, J.M.; Crespo-Cebada, E.; Murillo-Zamorano, L.R. Measuring technical efficiency in primary health care: The effect of exogenous variables on results. J. Med. Syst. 2011, 35, 545–554. [Google Scholar] [CrossRef]
- Pelone, F.; Kringos, D.S.; Romaniello, A.; Archibugi, M.; Salsiri, C.; Ricciardi, W. Primary care efficiency measurement using data envelopment analysis: A systematic review. J. Med. Syst. 2015, 39. [Google Scholar] [CrossRef]
- Cordero Ferrera, J.M.; Cebada, E.C.; Murillo Zamorano, L.R. The effect of quality and socio-demographic variables on efficiency measures in primary health care. Eur. J. Health Econ. 2014, 15, 289–302. [Google Scholar] [CrossRef]
- Oikonomou, N.; Tountas, Y.; Mariolis, A.; Souliotis, K.; Athanasakis, K.; Kyriopoulos, J. Measuring the efficiency of the Greek rural primary health care using a restricted DEA model; the case of southern and western Greece. Health Care Manag. Sci. 2016, 19, 313–325. [Google Scholar] [CrossRef]
- Cordero, J.M.; Nuño-Solinís, R.; Orueta, J.F.; Polo, C.; del Río-Cámara, M.; Alonso-Morán, E. Evaluación de la eficiencia técnica de la atención primaria pública en el País Vasco, 2010-2013. Gac. Sanit. 2016, 30, 104–109. [Google Scholar] [CrossRef]
- Ji, Y.; Lee, C. Data Envelopment analysis in stata. Stata J. 2010, 10, 267–280. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P. Sensitivity analysis of efficiency scores: How to bootstrap in nonparametric frontier models. Manag. Sci. 1998, 44, 49–61. [Google Scholar] [CrossRef]
- Tapia, J.A.; Salvador, B.; Rodríguez, J.M. Data envelopment analysis with estimated output data: Confidence intervals efficiency. Meas. J. Int. Meas. Confed. 2020, 152. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Estimation and inference in two-stage, semi-parametric models of production processes. J. Econ. 2007, 136, 31–64. [Google Scholar] [CrossRef]
- Caballer-Tarazona, V.; Guadalajara-Olmeda, N.; Vivas-Consuelo, D. Predicting healthcare expenditure by multimorbidity groups. Health Policy 2019, 123, 427–434. [Google Scholar] [CrossRef]
- Vivas-Consuelo, D.; Usó-Talamantes, R.; Guadalajara-Olmeda, N.; Trillo-Mata, J.-L.; Sancho-Mestre, C.; Buigues-Pastor, L. Pharmaceutical cost management in an ambulatory setting using a risk adjustment tool. BMC Health Serv. Res. 2014, 14. [Google Scholar] [CrossRef] [PubMed]
- Caballer Tarazona, V.; Guadalajara Olmeda, N.; Vivas Consuelo, D.; Clemente Collado, A. Impact of Morbidity on Health Care Costs of a Department of Health through Clinical Risk Groups. Valencian Community, Spain. Rev. Esp. Salud Publica 2016, 90, e1–e15. [Google Scholar]
- Carreras, M.; Ibern, P.; Coderch, J.; Sánchez, I.; Inoriza, J.M. Estimating lifetime healthcare costs with morbidity data. BMC Health Serv. Res. 2013, 13. [Google Scholar] [CrossRef]
- Orueta, J.F.; García-Alvarez, A.; Grandes, G.; Nuño-Solinís, R. Variability in potentially preventable hospitalisations: An observational study of clinical practice patterns of general practitioners and care outcomes in the Basque Country (Spain). BMJ Open 2015, 5. [Google Scholar] [CrossRef]
- Gouveia, M.C.; Dias, L.C.; Antunes, C.H. Additive DEA based on MCDA with imprecise information. J. Oper. Res. Soc. 2008, 59, 54–63. [Google Scholar] [CrossRef]
- Jahanshahloo, G.R.; Vencheh, A.H.; Foroughi, A.A.; Matin, R.K. Inputs/outputs estimation in DEA when some factors are undesirable. Appl. Math. Comput. 2004, 156, 19–32. [Google Scholar] [CrossRef]
- Scheel, H. Undesirable outputs in efficiency valuations. Eur. J. Oper. Res. 2001, 132, 400–410. [Google Scholar] [CrossRef]
- Dyson, R.G.; Allen, R.; Camanho, A.S.; Podinovski, V.V.; Sarrico, C.S.; Shale, E.A. Pitfalls and protocols in DEA. Eur. J. Oper. Res. 2001, 132, 245–259. [Google Scholar] [CrossRef]
- Angulo-Pueyo, E.; Ridao-López, M.; Martínez-Lizaga, N.; García-Armesto, S.; Peiró, S.; Bernal-Delgado, E. Factors associated with hospitalisations in chronic conditions deemed avoidable: Ecological study in the Spanish healthcare system. BMJ Open 2017, 7, e011844. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).