Artificial Neural Networks to Forecast Failures in Water Supply Pipes
Abstract
:1. Introduction
- The accuracy of ANNs as classification systems to predict pipe failures in water supply networks is evaluated and, in particular, the use of a specific machine-learning software named Weka.
- The effectiveness of two sampling methods, under-sampling and over-sampling, are compared for the first time in this type of problem.
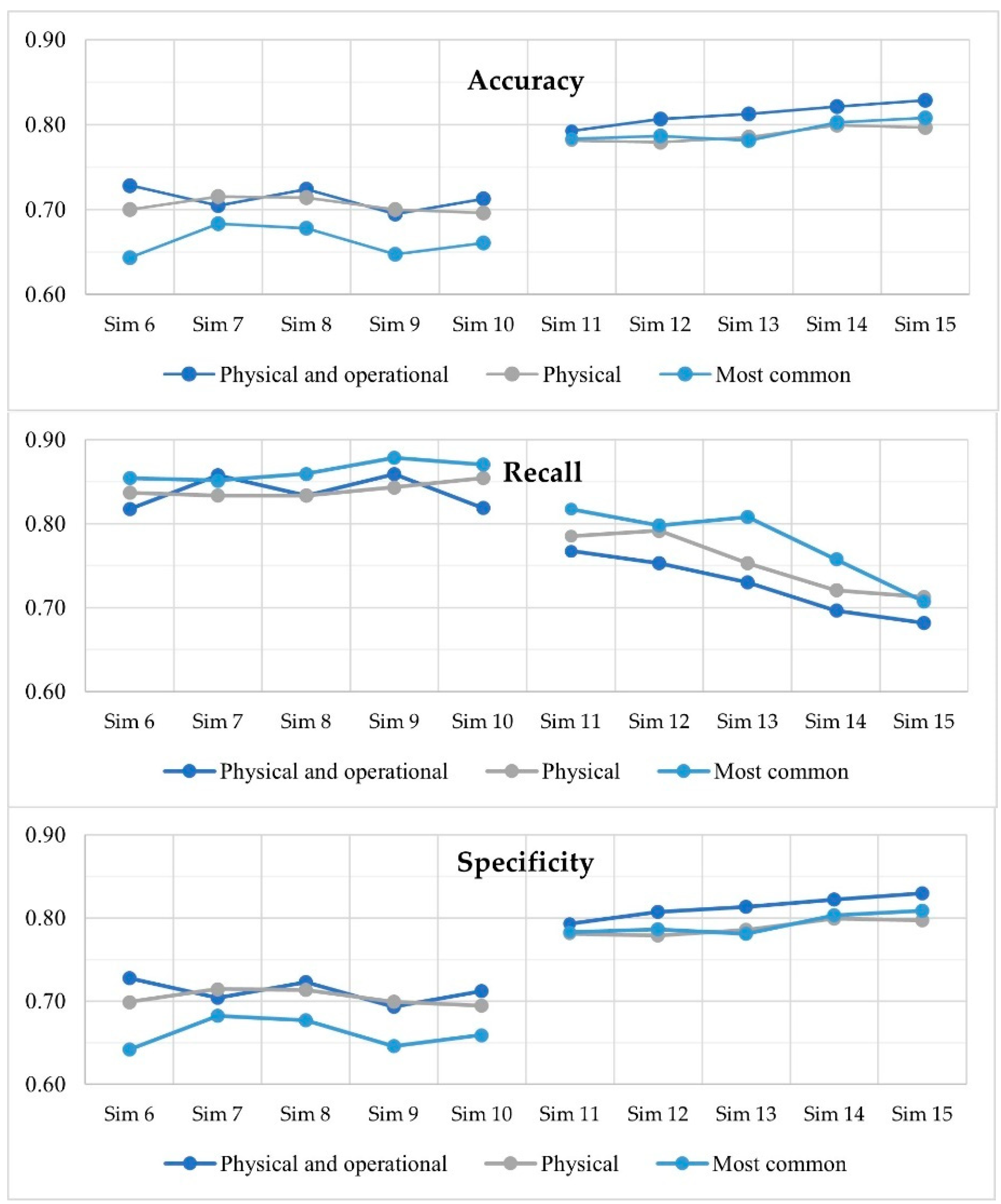
- The influence of physical and operational variables is also tested and discussed.
2. Methodology: Artificial Neural Networks
3. Implementation and Results
3.1. Case Study: The Water Supply Network of Seville (Spain)
3.2. Implementation
3.3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Acknowledgments
Conflicts of Interest
References
- ISO/FDIS 24516-1: Guidelines for the Management of Assets of Water Supply and Wastewater Systems; ISO: Geneva, Switzerland, 2016.
- Giraldo-González, M.M.; Rodríguez, J.P. Comparison of Statistical and Machine Learning Models for Pipe Failure Modeling in Water Distribution Networks. Water 2020, 12, 1153. [Google Scholar] [CrossRef] [Green Version]
- Almheiri, Z.; Meguid, M.; Zayed, T. Intelligent Approaches for Predicting Failure of Water Mains. J. Pipeline Syst. Eng. Pract. 2020, 11, 1–15. [Google Scholar] [CrossRef]
- Christodoulou, S.; Deligianni, A. A Neurofuzzy Decision Framework for the Management of Water Distribution Networks. Water Resour. Manag. 2010, 24, 139–156. [Google Scholar] [CrossRef]
- Sattar, A.M.A.; Ertuğrul, Ö.F.; Gharabaghi, B.; McBean, E.A.; Cao, J. Extreme learning machine model for water network management. Neural Comput. Appl. 2019, 31, 157–169. [Google Scholar] [CrossRef]
- Shirzad, A.; Tabesh, M.; Farmani, R. A comparison between performance of support vector regression and artificial neural network in prediction of pipe burst rate in water distribution networks. KSCE J. Civ. Eng. 2014, 18, 941–948. [Google Scholar] [CrossRef]
- Tabesh, M.; Soltani, J.; Farmani, R.; Savic, D. Assessing pipe failure rate and mechanical reliability of water distribution networks using data-driven modeling. J. Hydroinf. 2009, 11, 1–17. [Google Scholar] [CrossRef]
- Li, D.; Cong, A.; Guo, S. Sewer damage detection from imbalanced CCTV inspection data using deep convolutional neural networks with hierarchical classification. Autom. Constr. 2019, 101, 199–208. [Google Scholar] [CrossRef]
- Sousa, V.; Matos, J.P.; Matias, N. Evaluation of artificial intelligence tool performance and uncertainty for predicting sewer structural condition. Autom. Constr. 2014, 44, 84–91. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn and Tensor Flow; O’Reilly Media, Inc.: Newton, MA, USA, 2017. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sze, V.; Chen, Y.-H.; Yang, T.-J.; Emer, J.S. Efficient Processing of Deep Neural Networks: A Tutorial and Survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef] [Green Version]
- Robles-Velasco, A.; Cortés, P.; Muñuzuri, J.; Onieva, L. Prediction of pipe failures in water supply networks using logistic regression and support vector classification. Reliab. Eng. Syst. Saf. 2020, 196, 106754. [Google Scholar] [CrossRef]
- Robles-Velasco, A.; Cortés, P.; Muñuzuri, J.; Barbadilla-Martín, E. Aplicación de la regresión logística para la predicción de roturas de tuberías en redes de abastecimiento de agua. Dir. Organ. 2020, 70, 78–85. [Google Scholar] [CrossRef]
- Frank, E.; Hall, M.A.; Witten, I.H. Data Mining: Practical Machine Learning Tools and Techniques; Morgan Kaufmann Publishers, Inc.: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Velasco, A.R.; Muñuzuri, J.; Onieva, L.; Palero, M.R. Trends and applications of machine learning in water supply networks management. J. Ind. Eng. Manag. 2021, 14, 45–54. [Google Scholar] [CrossRef]
- Winkler, D.; Haltmeier, M.; Kleidorfer, M.; Rauch, W.; Tscheikner-Gratl, F. Pipe failure modelling for water distribution networks using boosted decision trees. Struct. Infrastruct. Eng. 2018, 14, 1402–1411. [Google Scholar] [CrossRef] [Green Version]


| Variable | Type | Min | Max | Mean | Std |
|---|---|---|---|---|---|
| MAT—Material | Categorical | CI, DI, AC, CON and PE | |||
| DIA—Diameter (mm) | Numerical | 20 | 1700 | 152.32 | 142.09 |
| AGE—Age (years) | Numerical | 0 | 118 | 24.91 | 17.15 |
| LEN—Length of the segment (m) | Numerical | 0.5 | 4295 | 42.86 | 79.28 |
| CON—Connections per km | Numerical | 0 | 11.44 | 0.05 | 0.22 |
| N_type—Network type | Categorical | Transport and Secondary | |||
| ∆PRE—Pressure fluctuation (m) | Numerical | 0 | 27.24 | 2.88 | 2.16 |
| NOPF—Number of Previous Failures | Numerical | 0 | 10 | 0.04 | 0.28 |
| Sim. | HL | Sampling Method | Acc. | Rec. | Spec. | Prec. | Runtime (s) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | None | 0.993 | 0.000 | 1.000 | 0.000 | 110.5 |
| 2 | 5 | None | 0.993 | 0.002 | 1.000 | 0.111 | 223.5 |
| 3 | 10 | None | 0.993 | 0.002 | 1.000 | 0.100 | 385.0 |
| 4 | 50 | None | 0.993 | 0.005 | 1.000 | 0.250 | 1885.0 |
| 5 | 100 | None | 0.993 | 0.005 | 1.000 | 0.176 | 3716.1 |
| 6 | 1 | Under-sampling | 0.728 | 0.817 | 0.728 | 0.020 | 2.0 |
| 7 | 5 | Under-sampling | 0.705 | 0.858 | 0.704 | 0.020 | 3.6 |
| 8 | 10 | Under-sampling | 0.724 | 0.834 | 0.723 | 0.021 | 6.4 |
| 9 | 50 | Under-sampling | 0.694 | 0.859 | 0.693 | 0.019 | 29.3 |
| 10 | 100 | Under-sampling | 0.691 | 0.864 | 0.690 | 0.019 | 58.8 |
| 11 | 1 | Over-sampling | 0.793 | 0.767 | 0.793 | 0.025 | 263.9 |
| 12 | 5 | Over-sampling | 0.807 | 0.753 | 0.807 | 0.026 | 502.1 |
| 13 | 10 | Over-sampling | 0.813 | 0.730 | 0.813 | 0.026 | 883.6 |
| 14 | 50 | Over-sampling | 0.822 | 0.696 | 0.822 | 0.027 | 4154.3 |
| 15 | 100 | Over-sampling | 0.828 | 0.682 | 0.829 | 0.027 | 8416.1 |
| Input Variables | |
|---|---|
| Physical and operational | MAT, DIA, AGE, LEN, CON, N_type, ∆PRE and NOPF |
| Physical | MAT, DIA, AGE, LEN, CON and N_type |
| Most common | DIA, AGE, LEN and NOPF |
| Input Variables | Under-Sampling | Over-Sampling |
|---|---|---|
| Physical and operational | 0.781 | 0.780 |
| Physical | 0.775 | 0.785 |
| Most common | 0.768 | 0.800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robles-Velasco, A.; Ramos-Salgado, C.; Muñuzuri, J.; Cortés, P. Artificial Neural Networks to Forecast Failures in Water Supply Pipes. Sustainability 2021, 13, 8226. https://doi.org/10.3390/su13158226
Robles-Velasco A, Ramos-Salgado C, Muñuzuri J, Cortés P. Artificial Neural Networks to Forecast Failures in Water Supply Pipes. Sustainability. 2021; 13(15):8226. https://doi.org/10.3390/su13158226
Chicago/Turabian StyleRobles-Velasco, Alicia, Cristóbal Ramos-Salgado, Jesús Muñuzuri, and Pablo Cortés. 2021. "Artificial Neural Networks to Forecast Failures in Water Supply Pipes" Sustainability 13, no. 15: 8226. https://doi.org/10.3390/su13158226
APA StyleRobles-Velasco, A., Ramos-Salgado, C., Muñuzuri, J., & Cortés, P. (2021). Artificial Neural Networks to Forecast Failures in Water Supply Pipes. Sustainability, 13(15), 8226. https://doi.org/10.3390/su13158226








