Abstract
With increasing availability of alternative mobility options for city transportation system, it is necessary to better understand how emerging mobility options are impacting the travel demand and consumer-social surplus. However, few study have been conducted to evaluate the social welfare effects of the range of vacant trips in ride-sourcing service modes. This paper identified the vacant trip and loading rate evaluation model under the ride-sourcing service mode to enhance the effective operation of the different mobility services under numerical illustrations. The solution can also offer some beneficial guidance and theoretical basis for ride-sourcing systems in regard to planning and management aspects.
1. Introduction
Considering many disruptive phenomena, such as growing environmental pollution, terrible congestion, and economic concerns, many planners and managers of modern cities are looking for low-carbon and sustainable transportation development modes (e.g., transit-oriented development; self-driving transit; ride-sharing) [1]. One kind of technological innovation in the taxi ride-sourcing service (RSS) market, an app-based e-hailing service (AES) (e.g., Didi in China), has developed tremendously due to the advances in smart mobile and GPS technologies. This has been at the center of attention as an efficiency-oriented mode of urban mobility. Otherwise, some incentive transport policies are being used to encourage commuters to change from driving alone to ride-sharing (e.g., the priority mechanism for high-occupancy vehicle/toll (HOV/HOT) lanes, price compensation and security enhancement). Therefore, many researchers regard AES as an alternative solution to the future urban traffic development [2,3]. Meanwhile, owing to emphasizing and encouraging the low-carbon concept of sharing travel, E-reserved carpooling services (ECS) have also attracted extensive attention of researchers. They together with the traditional cruising taxis service (TCTS), constitute a new ride-sourcing system in urban mobility, which provide a feasible solution to the problem of high private car mode share as the main cause for the high transport energy usage in cities [4,5].
Social welfare consists of consumer surplus and producer surplus in the process of traffic system analysis. The first attempt to describe the social welfare (many studies also call it system performance) was made by Douglas [6], in which an aggregate model in terms of social welfare was proposed to study the price regulation and service standard of the TCTS market. In the RSS market introduced by this research, the social welfare mainly shows the surplus value of both drivers and passengers, Ensuring consumer surplus (we regard the waiting time as a major factor of consumer surplus, which can also reflect the vacant cruising distance of RSS vehicles) can improve passenger satisfaction and producer surplus (the profitability of being a taxi driver) is conducive to the sustainable development of the RSS market. In an overview of countries around the world, the RSS industry is always an important field that gives consideration to both efficiency and fairness. Sometimes, additional attention needs to be paid to the welfare and fairness of participants especially in China. Thus, the administrators of the cities not only apply for various subsidies for the RSS operators but also formulate strict control policies to ensure the maximization of social welfare. However, such a situation is broken by market-oriented AES and ECS modes. Therefore, it is necessary to re-analyze the efficiency and welfare of the new hybrid RSS market.
The studies of RSS can be broadly classified into two types: one, modeling equilibrium of trip-based demand assignment considering different properties [7,8,9,10] (these methods are often formulated as a network optimization problem); and the other, analysis of operational efficiency [11] and social welfare [12,13].
In the studies of the trip-based travel demand equilibrium mechanism, they have become better understood with continuous efforts by many researchers [14,15]. Unlike the modeling process for the TCTS mode above, some methods of machine learning are also used to estimate the app-based RSS supply-demand condition with multiple data sources (e.g., history AES or ECS orders, weather condition and real-time traffic data) to achieve better system utilities [16,17].
In studies of operational efficiency, many studies show that AES and ECS modes can be a cost-effective way to reduce urban congestion when compared with more traditional road network optimization approaches (e.g., road price or increasing road capacity) [18], because they not only decrease the waiting time of passengers but also reduce the vacant cruising trips of app-based taxis. Some app-based RSS platforms also proclaim that they aim to transfer the inefficient cruise-street hailing mode to convenient matching-waiting mode by breaking the asymmetric demand-supply information in the traditional taxi market. Therefore, they think that an AES mode can achieve the objective of decreasing inefficient cruising trips and pollution emissions. However, the continuous competition in mobility market produces many bad results. Recent evidence shows that the expansion of app-based RSS markets has already contributed substantially to the deteriorating traffic conditions in some major cities because of AES drivers’ profitable selfishness [19].
Besides, in the research fields of social welfare, ref. [20] developed a social welfare maximization decision model to investigate the effects of fare adjustments and fleet size restriction in the competitive RSS market, and to decide how the government should regulate taxi markets in the presence of such competition from the perspective of social welfare maximization [21,22]. Focused on the design of prices and subsidies on two-sides of the AES/TCTS market, they suggest that AES platforms should carry out a strong incentive to encourage sharing via subsidies in order to obtain the maximum social welfare. Meanwhile, ref. [23] introduces a price competition model between AES and TCTS markets, and the results of social welfare analysis show that win-win outcomes can be achieved by a dynamic payout ratio.
Considering that AES and ECS have recently been at the center of attention as the most disruptive modes in urban transport systems, and the maximum social welfare of the participants and the minimum empty driving distance are the guarantee for the sustainable development of transportation. In this paper, we develop a Cobe-Douglas model to describe the supply-demand relationship in RSS markets. On this foundation, an efficiency-based model of vacant trip analysis and a social welfare analysis model are established to discuss the effect of entrants (AES mode and ECS mode) for operational efficiency and social welfare in hybrid RSS markets.
The rest of this paper is organized as follows. Section 2 presents the mobility network structure and the vacant trips formulations for three different mobility modes. In Section 3, the social welfare and loading rate in TCTS, AES and ECS systems are discussed, respectively. Section 4 examines and analyzes the performance of mobility systems under different loading rates, numerical illustrations and verification are also presented in this section. Finally, we give the conclusion.
2. Modeling Structure
As mentioned before, the major factors in the RSS system are passenger-vehicle matching and occupied/empty vehicle movements over urban road networks. Thus, the analyses should involve not only the mobility system itself but also the urban road network.
2.1. Mobility Network Presentation
Three types of mobility service, traditional cruising taxis service (TCTS), App-based E-hailing service (AES) and e-reserved carpooling service (ECS), are conducted driving in a road network . Here represents the set of nodes and is the set of links in the network. Correspondingly, there are also three groups of ride-sourcing demands to exist in the network: street-hailing passengers (SHPs), and e-hailing passengers (EHPs), e-reserved rider-sharing passengers (ERRSPs). The passenger-vehicle matching modes among different service are shown in Figure 1. In any given time, the number of customers demanding rides from the origin zone sets to destination zone sets is . In this paper, is assumed to be a function of customer-waiting time at the origin zone , and the monetary price and travel time cost for traffic from zone to zone , Moreover, the directed links are weighted with routing probabilities for different trip modes to describe the distance of routing choices by vehicles. In general, there are several paths between each pair of zones and (for each type of service separately). Each path goes over several links (in general). Each path has its total distance (sum of lengths of all links on the path). We can calculate the probability of each path (using a logit model, for example). One of the paths (in general) is optimal. The optimal path has the smallest total distance (), and it satisfies . By making and as the sets of customer origin and destination zones, respectively, which yields , then we have the following trip end constraints when achieving system matching equilibrium between a customer and ride-sourcing service.
where and , are respectively the total traffic supply in origin zone and demand for destination zone , meanwhile, is the different groups of traffic mobility, , , indicate the different mobility types of demand for the TCTS, AES and ECS from origin zone to destination zone . Obviously, the sum of , and equals .
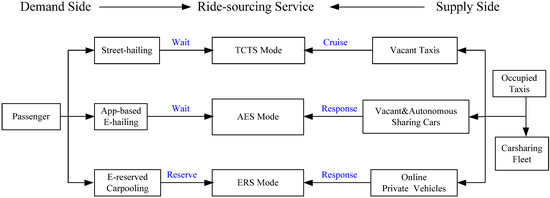
Figure 1.
The competitive ride-sourcing mobility market.
2.2. Mobility Demand Description
A passenger demand for mobility trips is assumed to be related to the trip price, and to a proxy for service quality. The aspect of service quality of particular interest in this paper is the expected delay/waiting time incurred. By engaging a mobility mode we can obtain the demand; increased prices and waiting times will inhibit passenger demand, according to the research [14,24]. The waiting time is determined by the total vacant mobility-hours available. A higher the more vacant cruising mileage will lead to the greatest of the probability that the vacant taxi moves on the road, and it will be easier for passenger-taxi matching. Assuming the total customer demand of trip mileage, , to be a strictly decreasing and convex function of the trip fare and passengers’ waiting time , then we can obtain the Cobe-Douglas form of the demand function as below.
where is the waiting time for different groups of passengers who have the demand from origin to destination . In this paper, , and represent SHPs, EHPs and ERRSPs, respectively. Therefore, can be regarded individually as the street-hailing, e-hailing and e-reserved ridesharing waiting time in TCTS, AES and ECS modes. Furthermore, is the empty mileage of different mobility service mode in the same OD matching pair, and let be defined as the elasticity of price, waiting time and empty mileage respectively. According to the Cobe-Douglas production function [6] and the realistic knowledge, we can conclude that the parameter yields . and represent the demand elasticity coefficient, which can be determined by the economic and consumer condition, spatial layout, road network characteristics and other factors of the city. Combining Formulas (3) and (4), we can obtain the Cobe-Douglas production demand function in ride-sourcing mobility markets.
We also consider a realistic mobility fare structure consisting of three components: a flag-fall or a constant initial flat charge, a distance-based charge, and a delay-based charge. Let () be the initial flag-fall charge per ride, maximum mileage for flag-fall charge, fare charge per occupied unit mileage and fare charge per congestion delay time for different matching modes, respectively. Further, let be the ride time from region to region . Considering the punctual arrival time, we have congestion delay times . Then, the mobility fare in single trip for different modes can be described as below.
The different fares for three modes of matching can be established into varied combinations to satisfy different demand conditions. For the TCTS trips, we have the charging function:
For the AES trips, we have the charging function:
where is the minimum fare charge for single trips. Meanwhile, let be the service frequency during the carpooling drivers’ whole own trip, and let be the coefficient of ride-sharing service frequency for initial flag-fall charge per ride. It is worth noting that the ECS mode encourages passengers to regard this service as a long distance trip, it is not suitable if passengers get on and off of the carpooling vehicle frequently, so initial flag-fall charge will increase with the parameter . Then, we have the charging function of the ECS trips.
2.3. Mobility Vacant Trips Analysis
In this section, we will discuss the difference of vacant trips among TCTS, RSS and ECS. The vacant trips develop because of the spatial distance between the next pickup point and last drop off point. The cruising taxi drivers search and match passenger by the experienced characteristics of demand distribution, the by contrast, ride-sourcing drivers can select the optimal matching result to minimize their empty miles (maximize their trip utilities) by obtaining the OD information of potential passengers in advance. The e-reserved ride-sharing mode will follow the dispatch of the platform, it is more effective to attract more potential private vehicles and passengers using ride-sourcing services by matching the similar OD route.
2.3.1. TCTS Vacant Trips
The destination choice of the TCTS mode mainly depends on the choice behavior of the taxi drivers. It is assumed here that, taxi drivers are completely rational, and that they always make a choice according to the principle of maximum passengers matching probability with the minimum vacant mileages. There is a maximum of four neighboring target search zones in four directions for TCTS drivers. For example, in the morning peak there is more demand from suburbs to the city center, and it could be expected that taxi drivers would return to the suburbs once they have dropped their passengers. In this paper, drivers are assumed to attempt to minimize individual expected vacant time/distance to match the next customer once the last ride is completed. The TCTS drivers will meet two choice strategies seeking the next customer: empiricism cruising and random cruising. For the first one, TCTS drivers prefer cruising the zone where there are maximum traffic demands among the other three regions. For the second mode, the expected search time in each zone is a random variable due to variations in perceptions of taxi drivers and the random arrival of customers. This random variable is assumed to be identically distributed with a density function. With these behavior assumptions, the probability that a vacant taxi originating at zone chooses to meet a customer at the zone is specified by the following logic discrete choice model.
When represents the probability of a cruising taxi that takes a customer to zone to search and meet the next customer in the same zone, and is a non-negative parameter which can reflect the degree of uncertainty on customer demand and mobility services. The probability is in turn affected by the customer demand Equation (5); therefore, it can also reflect a driver’s trade-off between customer demand and proximity. is the conversion coefficient from the traffic demand to traffic mileage.
The total expectation of vacant cruising mileage for taxi cruising from the zone to the zone is:
According to the Equation (2), the occupied taxis will change to a vacant one, and the new vacant vehicle in zone after one OD trip can be expressed as:
Combining Equations (11) and (13), we can obtain the cruising-based vacant mileage.
2.3.2. AES Vacant Trips
We assume that the AES mode can only carry one passenger in each trip service, the vacant sharing cars usually choose the shortest path to reach the pickup zone when they respond to the trip demand by fully communicating with the passengers in advance with the smart phone app, and the empty mileage will not affect by the uncertain cruise behavior. At the same time, the ride-sourcing service mode can master the OD information and the congestion condition of road networks through the ride-sourcing service, to help them ignore the impact of uncertainties (the uncertainties parameter cannot be taken into account). Referring to Equation (11), it can be obtained that the probability and the expectation empty mileage for AES originating at zone choosing to meet a customer at zone is:
Combining Equations (1), (15) and (16), we can obtain the vacant cruising mileage of AES.
2.3.3. ECS Vacant Trips
The ECS mode can be regarded as one of the shared mobility, the matching willingness of ECS will become stronger during the rush hour of long-distance commute. Unlike TCTS or AES modes, drivers can provide three or four empty seats, with an even greater frequency of getting on and off ride-sharing occupancy during their own trips in this mode. The maximized utilities for carpooling driver are a higher service frequency under the less deviation from their own original shortest route. We know can express the service frequency/ride-sharing number during ride-sharing trip in ERS. Therefore the total expectation of empty mileage for vacant private cars cruising from the zone to the zone in ERS mode can be expressed as below:
3. Social Welfare and Loading Rate Analysis
3.1. Social Welfare Analysis Model
Considering that the social welfare in RSS markets consists of passenger surplus and driver surplus, and the higher the surplus values there are on both sides, the more sustainable this is for the development of the RSS market. In this section, we introduce a aggregate producer-consumer surplus theory based on the Douglas model [6] to analyze and improve the performance of the RSS mobility market.
According to the theory above, the production surplus, , is equal to the difference between total revenue and total cost, we can obtain the total mobility production surplus function for three mobility services:
where represents the production surplus of TCTS, AES and ECS, respectively. And is the operation cost function for different mobility service modes, which satisfied the conditions as below.
where is the unit energy cost of trip mileage, and the unit energy cost is different among different mobility services, for example, the source of energy is natural gas in traditional TCTS mode, while electric vehicles are mainly engaged in AES mode and drives have the pressure of high-gasoline prices in the ECS network. Thus, follows .
According to passenger demand Function (5), we can obtain the relationship between the fare price and travel demand as shown in Function (18), and the total trip fare, P, can be denoted as below.
Then we can get the consumer surplus function of passengers.
Although we can observe the occurrence in some situations of the price elasticity coefficient of , but it will be closer to the reality when the price elasticity meets the condition of .
This paper denies social welfare of the mobility service market as the summation of net benefits as given by the aggregate producer-consumer surplus.
From Function (24), it can be seen that the social welfare of the RSS mobility market has nothing to do with the payment fee, which means that the passenger payment fee has been transferred in the mobility system, and the variable of social welfare function is only the vacant trip and passenger demand.
3.2. Loading Rate Analysis Model
The optimal loading rate (OLA) of the mobility service is the result of the comprehensive function of price, service level and other modes in the mobility market. A reasonable loading rate is related to the parameters of fare charging level, waiting time and vacant mileage; an excessive loading rate will lead to a long waiting time for passengers, which easily results in a sharp decline of the mobility service level, while a lower level will affect the initiative of mobility service providers, causing the idle mobility resources. Therefore, it is necessary to explore the optimal loading rate of mobility market under the maximum social welfare conditions in order to achieve the objective of sustainable development.
We can specify a point of constrained maximized welfare (S) for the system:
Combining Functions (25) and (26), we can calculate the optimal trip mileage, , and optimal vacant mileage, , with the maximum social welfare:
The loading rate can be adopted as below:
4. Numerical Analysis
4.1. Network and Key Parameters
The proposed model was tested in a real-life network section (in Shenzhen, China), which be seen in Figure 2. The urban expressway (Haibin Road) in this network divides the network into six zones (all zones can be regard as origins and destinations). Otherwise, the OD demand is assumed to be normally distributed, please see them in Table 1 and the optimal travel distances between the six zones are shown in Table 2. The probability of different search directions and related parameters are set out in Table 3, Table 4, Table 5 and Table 6.
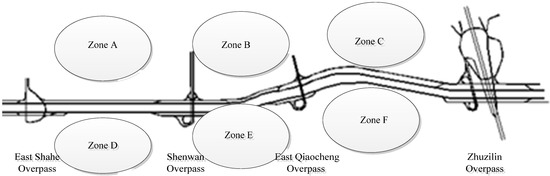
Figure 2.
Part of Shenzhen Network (Haibin Road).

Table 1.
The OD demand of zones (A, B, C, D, E and F) in the network.

Table 2.
The optimal travel distance of zones (A, B, C, D, E and F) in the network.

Table 3.
The probability of different search directions in TCTS.

Table 4.
The probability of different search directions in AES.

Table 5.
The probability of different search directions in ECS.

Table 6.
The key parameters of Shenzhen city taxi market.
According to the travel data of Shenzhen in China (https://pta.jtys.sz.gov.cn/ accessed on 20 June 2021), we know that the number of issued vehicles in the mobility modes of TCTS, AES and ECS is 62313, 21489 and 7890 in the total year of 2019, respectively. For AES mode, the order of each ECS vehicle is about 9.3 in one day, the daily average driving mileage and loading mileage is about 84.0 km and 73.2 km, respectively. Meanwhile, the daily average order operation amount of each car is about ¥ 296.2. By contrast, for ECS mode the daily average order of TCTS is about 35.1, the daily loading mileage is about 384.5 km, and the daily average order operation amount of each car is about ¥ 1027. Referring to some parameters definitions, the key parameters can be shown in Table 6.
According to the analysis model in Section 3 above, the app-based mobility mode such as ACS and ECS shortens the vacant driving time, improves the loading rate and reduces the waiting time of passengers. However, it can be seen from Table 7 above that compared results among different modes, that the production surplus in AES and ECS had a slight increase, while in contrast, the consumer surplus of passengers had a significant increase, which makes the social welfare of the group in AES and ECS modes much higher than that in the TCTS mode. It also demonstrates from the mathematical point of view why the application of mobile travel has been popularized rapidly in recent years. The essence is to enhance the residual value of both the supply and demand sides and create a win-win strategy.

Table 7.
The social welfare situation (the case of Shenzhen).
4.2. Network and Key Parameters
In order to show the impact of the mobility loading rate on social welfare more intuitively, we obtain the change of mobility market surplus in different modes, which can be shown in Figure 3, Figure 4 and Figure 5, respectively. As shown in Figure 3, the mobility service surplus is negative in different service modes when the loading rate is low, but it increases first with the increase of the real load rate, and then achieves a maximum value in loading rate is 70–80% of TCTS, AES and ECS. This indicates the optimal loading rate for mobility service. Otherwise, it can be seen from Figure 4 that consumer surplus of passengers decreases continuously with the increase of loading rate in different modes and the range tends to be stable. This is because the decrease of vacant mileages will lead to the longer waiting time and less mobility demand. It can also be shown that the lowest benefit loading rate in TCTS, AES and ECS is 29.2%, 42.5% and 54.2% from Figure 3 when mobility service surplus is zero. For the group social welfare in the Figure 5, when the loading rate of TCTS mode is very low (under 10%), the social welfare TCTS mode will increase, but this state is unstable and rarely exists in practice (at this time, the TCTS mode is unprofitable). The total social welfare in AES and ECS is higher than that of the TCTS mode no matter what the loading rate is, which proves the role of information and self- driving technology in promoting the social welfare of users.
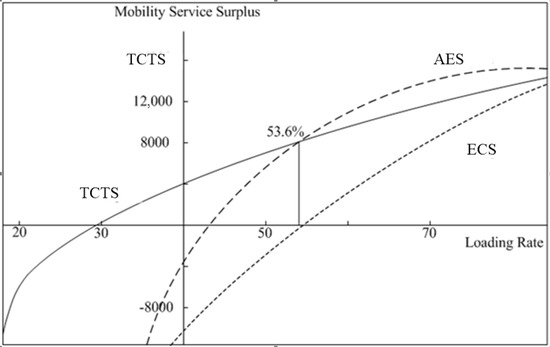
Figure 3.
Dynamic mobility service surplus in different service modes.
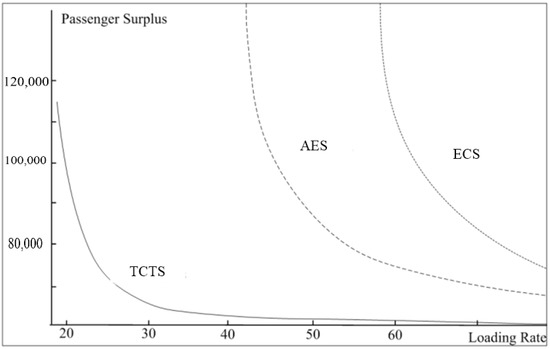
Figure 4.
Dynamic passenger’s surplus in different service modes.
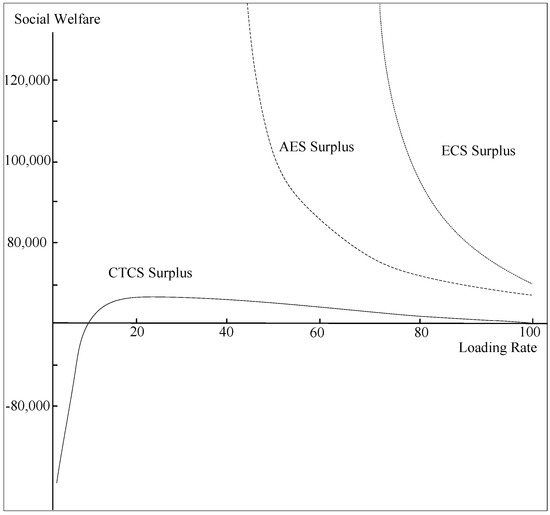
Figure 5.
Dynamic social welfare in different service modes.
5. Conclusions
With growing congestion and seemingly constant disruption in our cities, many researchers think that car-based mobility services are a way to address the lack of capacity in our infrastructure network. There are also many studies that show this. This paper aims to advance the doubt about whether the well-established and emerging RSS services are a sustainable way to enhance the social welfare and operational efficiency. To achieve this, a conventional Cobe-Douglas technique was combined to analyze social welfare and operational efficiency of the emerging RSS service.
The maximized social welfare and operational efficiency of RSS services has been presented with the use of examples and real data of Shenzhen city to illustrate their capabilities. Firstly, the numerical simulation results show that the surplus value of TCTS increases greatly, the passenger residual value decreases slowly, and the overall social welfare is slightly reduced with the increase of the ride-sourcing service. Secondly, through the evaluation of the vacant cruising trip and loading rate, the total social welfare in AES and ECS is higher than that of the TCTS mode no matter what the loading rate is.
Significantly, the app-based RSS mode generates massive vacant trips while providing additional services than road capacity during peak hours, this adverse phenomenon is particularly prominent in the AES mode. Furthermore, AES mode also brings some negative impacts upon the TCTS and AES markets; it reduces the demand for TCTS market and increases the cruising mileage of TCTS drivers, In the end, it reduces the welfare of the TCTS market. Loss of TCTS staff increases protest activities, contradictions between customers, and driver price. It is a top priority issue for the government to balance the system among TCTS, RSS and passengers. These results can build upon the dynamically evolving market of new business models and new technologies aiming at satisfying the mobility needs of urban dwellers.
Author Contributions
Conceptualization, Z.Z. and N.Z.; methodology, Z.Z.; validation, Z.Z. and N.Z.; formal analysis, Z.Z.; investigation, Z.Z.; resources, Z.Z.; data curation, Z.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z. and N.Z.; visualization, Z.Z.; supervision, N.Z.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Research program on the integration of civil aviation and other modes of transportation in China, grant number: 54422601.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data of ride-sourcing in Shenzhen are collected from (https://pta.jtys.sz.gov.cn/ (accessed on 25 May 2021)).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ma, J.; Xu, M.; Meng, Q.; Cheng, L. Ridesharing user equilibrium problem under OD-based surge pricing strategy. Transp. Res. Part B Methodol. 2020, 134, 1–24. [Google Scholar] [CrossRef]
- Wang, J.-P.; Ban, X.; Huang, H.-J. Dynamic ridesharing with variable-ratio charging-compensation scheme for morning commute. Transp. Res. Part B Methodol. 2019, 122, 390–415. [Google Scholar] [CrossRef]
- Xu, M.; Meng, Q. Fleet sizing for one-way electric carsharing services considering dynamic vehicle relocation and nonlinear charging profile. Transp. Res. Part B Methodol. 2019, 128, 23–49. [Google Scholar] [CrossRef]
- Dingil, A.E.; Schweizer, J.; Rupi, F.; Stasiskiene, Z. Updated Models of Passenger Transport Related Energy Consumption of Urban Areas. Sustainability 2019, 11, 4060. [Google Scholar] [CrossRef] [Green Version]
- Brownstone, D.; Golob, T.F. The impact of residential density on vehicle usage and energy consumption. J. Urban Econ. 2009, 65, 91–98. [Google Scholar] [CrossRef] [Green Version]
- Douglas, G.W. Price regulation and optimal service standards: The taxi cab industry. J. Transp. Econ. Policy 1972, 6, 116–117. [Google Scholar]
- Tirachini, A.; Chaniotakis, E.; Abouelela, M.; Antoniou, C. The sustainability of shared mobility: Can a platform for shared rides reduce motorized traffic in cities? Transp. Res. Part C Emerg. Technol. 2020, 117, 102707. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y. Optimizing flexible one-to-two matching in ride-hailing systems with boundedly rational users. Transp. Res. Part E Logist. Transp. Rev. 2021, 150, 102329. [Google Scholar] [CrossRef]
- Zha, L.; Yin, Y.; Xu, Z. Geometric matching and spatial pricing in ride-sourcing markets. Transp. Res. Part C Emerg. Technol. 2018, 92, 58–75. [Google Scholar] [CrossRef]
- Yang, H.; Qin, X.; Ke, J.; Ye, J. Optimizing matching time interval and matching radius in on-demand ride-sourcing markets. Transp. Res. Part B Methodol. 2020, 131, 84–105. [Google Scholar] [CrossRef]
- Beojone, C.V.; Geroliminis, N. On the inefficiency of ride-sourcing services towards urban congestion. Transp. Res. Part C Emerg. Technol. 2021, 124, 102890. [Google Scholar] [CrossRef]
- Dong, T.; Xu, Z.; Luo, Q.; Yin, Y.; Wang, J.; Ye, J. Optimal contract design for ride-sourcing services under dual sourcing. Transp. Res. Part B Methodol. 2021, 146, 289–313. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Zhang, S. Optimal pricing of customized bus services and ride-sharing based on a competitive game model. Omega 2021, 103, 102413. [Google Scholar] [CrossRef]
- Wong, K.; Wong, S.; Yang, H.; Wong, K.; Wong, S.; Yang, H. Modeling urban taxi services in congested road networks with elastic demand. Transp. Res. Part B Methodol. 2001, 35, 819–842. [Google Scholar] [CrossRef]
- Yang, H.; Ye, M.; Tang, W.H.; Wong, S.C. Regulating taxi services in the presence of congestion externality. Transp. Res. Part A Policy Pract. 2005, 39, 17–40. [Google Scholar] [CrossRef]
- Zhou, T.; Shi, W.; Liu, X.; Tao, F.; Qian, Z.; Zhang, R. A Novel Approach for Online Car-Hailing Monitoring Using Spatiotemporal Big Data. IEEE Access 2019, 7, 128936–128947. [Google Scholar] [CrossRef]
- Wang, D.; Cao, W.; Li, J.; Ye, J. DeepSD: Supply-Demand Prediction for Online Car-Hailing Services Using Deep Neural Networks. In Proceedings of the 2017 IEEE 33rd International Conference on Data Engineering (ICDE), San Diego, CA, USA, 19–22 April 2017. [Google Scholar]
- Zhang, Z.; Zhang, N. The Morning Commute Problem with Ridesharing When Meet Stochastic Bottleneck. Sustainability 2021, 13, 6040. [Google Scholar] [CrossRef]
- Erhardt, G.D.; Roy, S.; Cooper, D.; Sana, B.; Chen, M.; Castiglione, J. Do transportation network companies decrease or increase congestion? Sci. Adv. 2019, 5, eaau2670. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Szeto, W. Modeling and analyzing a taxi market with a monopsony taxi owner and multiple rentee-drivers. Transp. Res. Part B Methodol. 2021, 143, 1–22. [Google Scholar] [CrossRef]
- Sun, L.; Teunter, R.H.; Babai, M.Z.; Hua, G. Optimal pricing for ride-sourcing platforms. Eur. J. Oper. Res. 2019, 278, 783–795. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Yang, H.; Wang, D.; Ye, J. Customer behavioural modelling of order cancellation in coupled ride-sourcing and taxi markets. Transp. Res. Procedia 2019, 38, 853–873. [Google Scholar] [CrossRef]
- Ramezani, M.; Nourinejad, M. Dynamic modeling and control of taxi services in large-scale urban networks: A macroscopic approach. Transp. Res. Part C Emerg. Technol. 2018, 94, 203–219. [Google Scholar] [CrossRef]
- Djavadian, S.; Chow, J. An agent-based day-to-day adjustment process for modeling ‘Mobility as a Service’ with a two-sided flexible transport market. Transp. Res. Part B Methodol. 2017, 104, 36–57. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).