Inequalities in the European Union—A Partial Order Analysis of the Main Indicators
Abstract
1. Introduction
“The intercountryal community has made significant strides towards lifting people out of poverty. The most vulnerable countrys—the least developed countries, the landlocked developing countries and the small island developing states—continue to make inroads into poverty reduction. However, inequality still persists, and large disparities remain in access to health and education services and other assets” [6].
2. Methodology
2.1. Why Partial Order?
2.2. Basics of Partial Order Theory
2.3. Product Order
2.3.1. Notation
2.3.2. Zeta Matrix
2.3.3. Concepts of Partial Ordering
- (1)
- Max(X): the set of objects of X, where no other object y can be found with y > x. This is the set of maximal objects of a poset. If x is the only maximal object, it is called the “greatest” object.
- (2)
- Min(X): the set of objects of X, where no other object y can be found with y < x. This is the set of minimal objects of a poset. If x is the only minimal object, x is called the “least” object.
- (3)
- Iso(X): the set of objects of X which are at the same time objects of Max(X) and Min(X).
- (1)
- Chain: A subset C of X, where each object is mutually comparable with others of C.
- (2)
- Antichain: A subset AC of X, where each object of AC is mutually incomparable with others in AC.
- (3)
- Let x be an object of C, then l(x,C) is the length of the chain C including x and is the number of objects in C which are <= x. As x may be a member of several chains at once, it is meaningful to define the height h(x) as the max{l(x,C)} taken over all chains, where x is a member.
- (4)
- Level: The subset of X, where all objects have the same height h(x).
2.3.4. The Hasse Diagram
- (1)
- Because of transitivity relation the fact x < y and y < z does not need a line for x < z, because the lines for x < y and y < z are sufficient.
- (2)
- In a Euclidean plane objects such as x < y is located in that manner that y is located above x. By this convention the use of arrows is superfluous.
- (3)
- The drawing by a computer program assumes a grid where all objects are positioned, following rule 2, so that the representation is as symmetric as possible.
- (4)
- Isolated objects are drawn in that vertical height, where the maximal objects are located too.
2.4. Elaborate Analyses
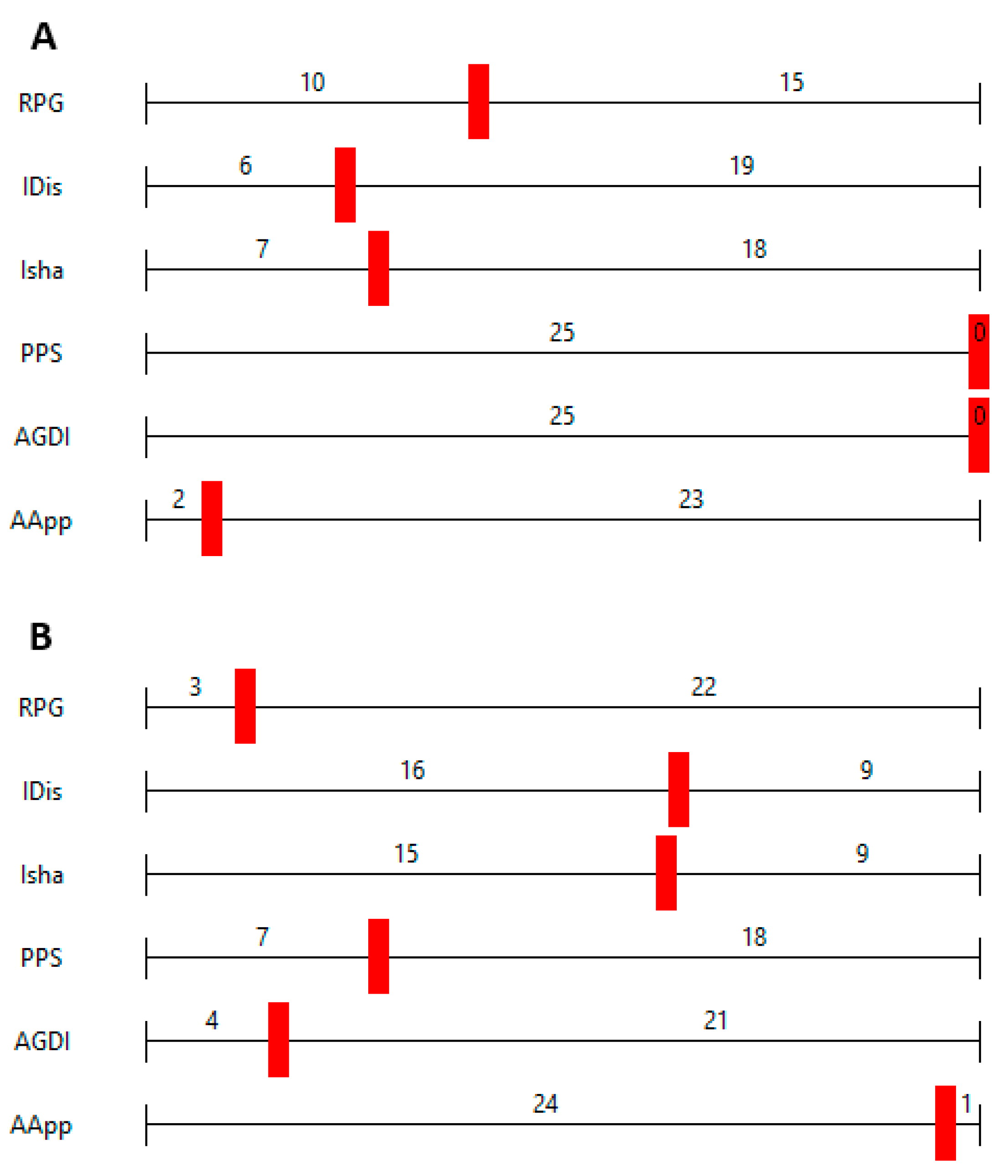
2.4.1. Sensitivity Analysis
Motivation
Procedure
2.4.2. Single Object Analysis
Motivation
Procedure
Remark
2.4.3. Isolated Object Analysis
Motivation
Procedure
Remark
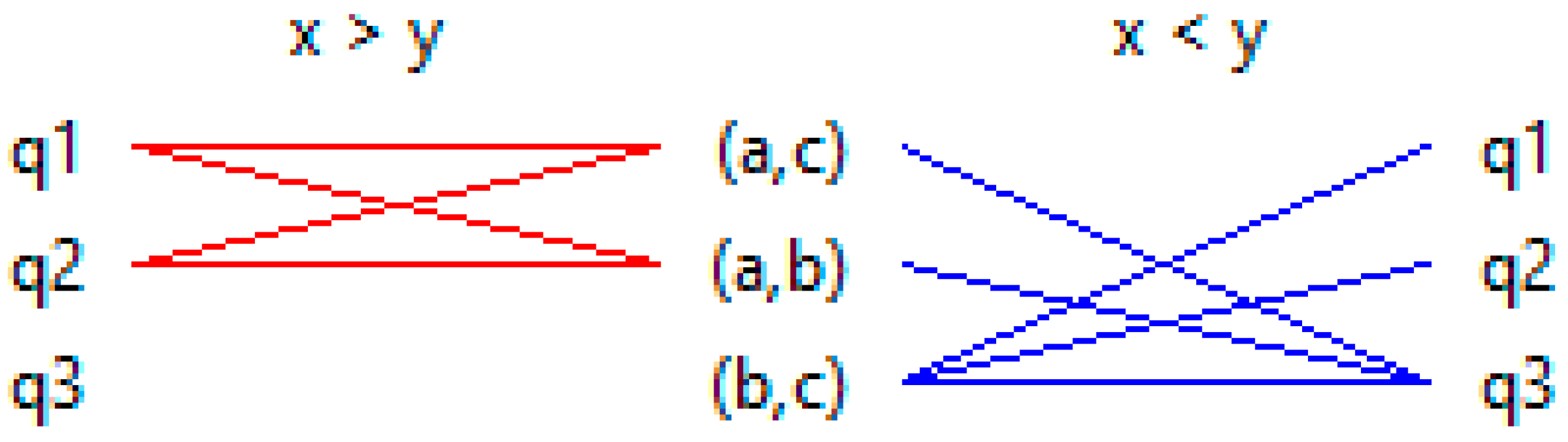
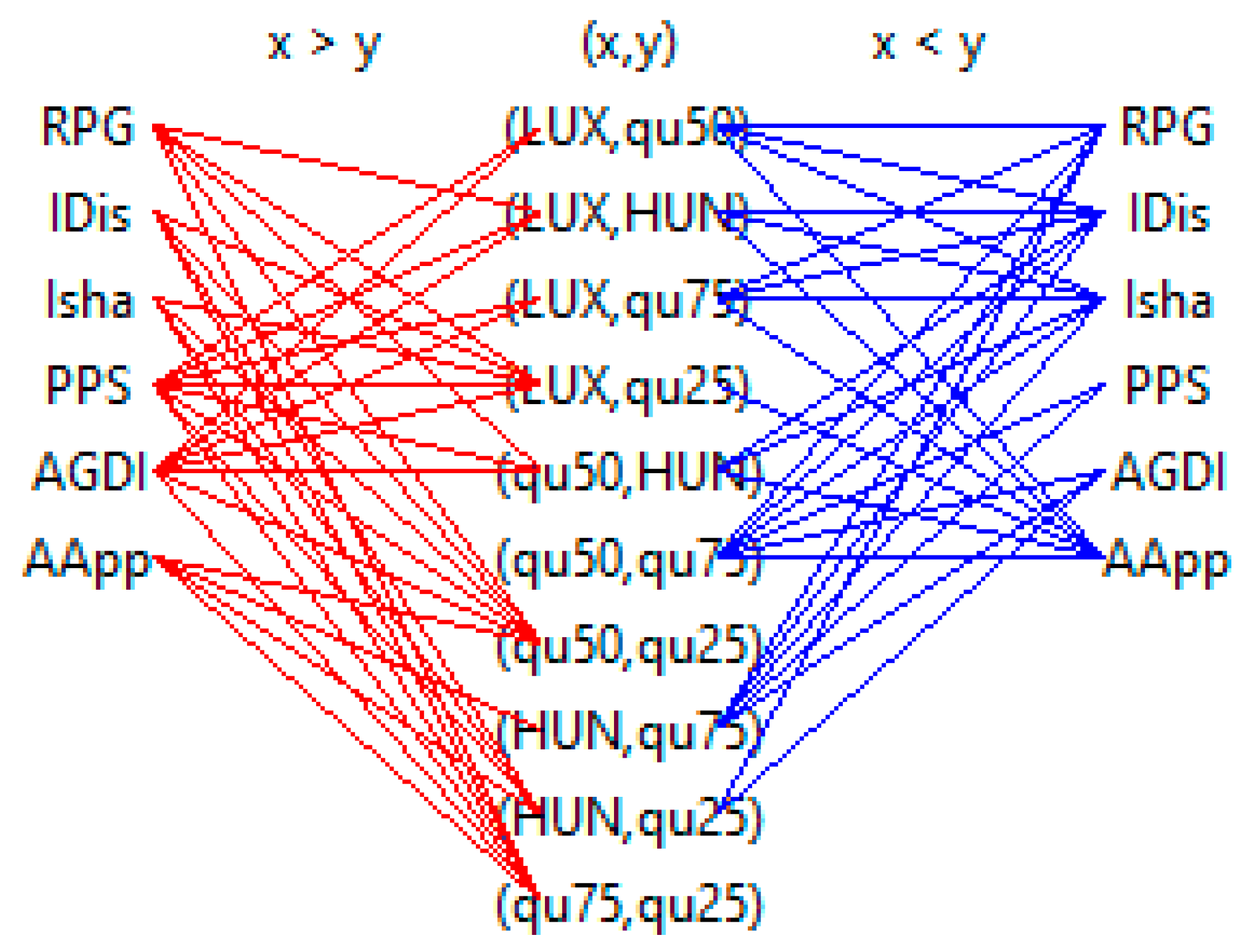
2.4.4. Tripartite Graph
Motivation
Procedure
- (1)
- vertically oriented list of indicator names in the left side of the diagram
- (2)
- vertically oriented list of object pairs, generated from Xac and
- (3)
- vertically oriented list of indicator names on the very right side.
Remarks
2.4.5. Average Ranks
Motivation
Procedure
Remark
2.5. Indicators and Data
2.5.1. The Indicators
2.5.2. The Data
2.6. Software
3. Results and Discussion
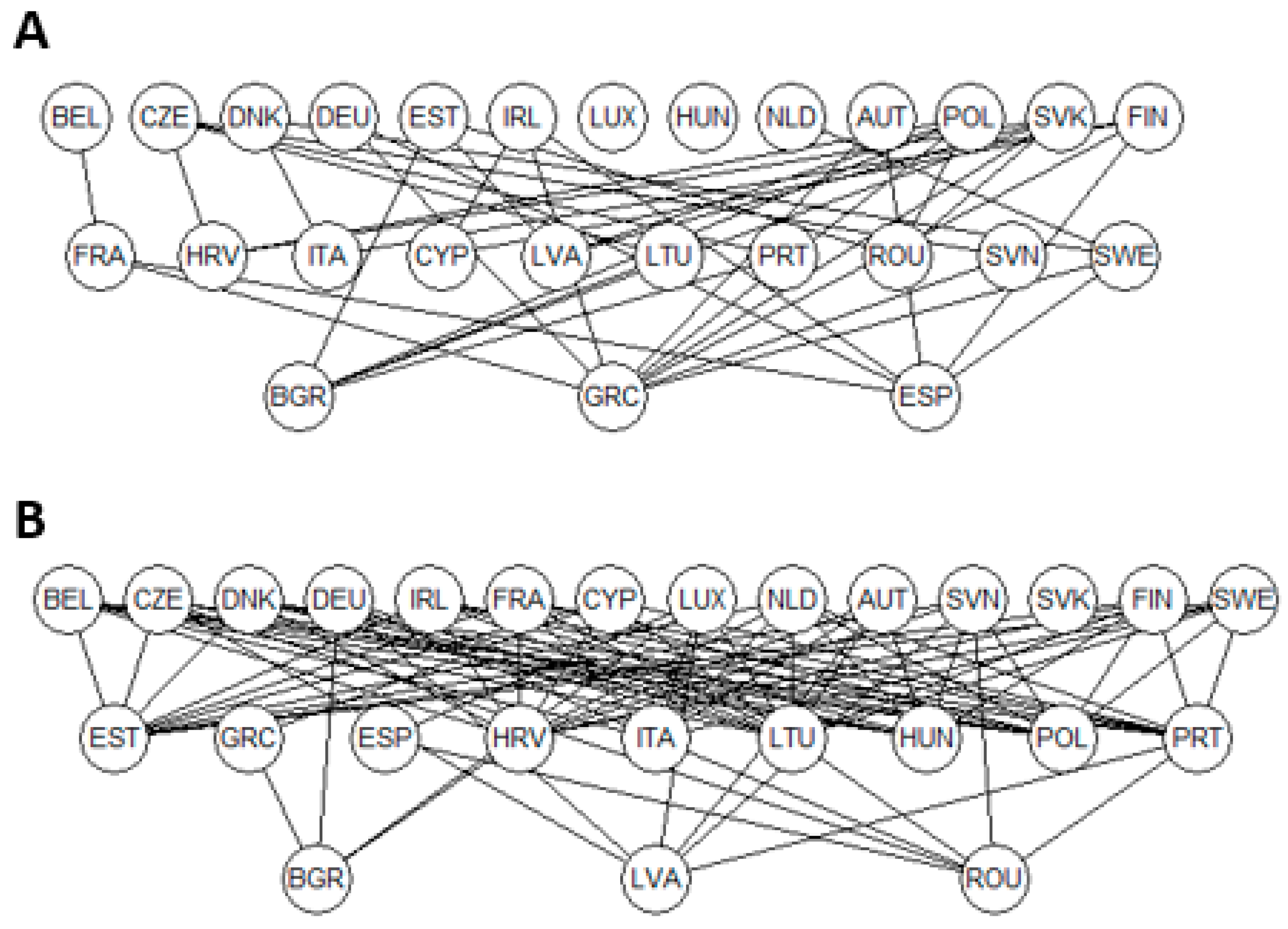
3.1. Analysis without AApp
3.2. Analysis Including AApp
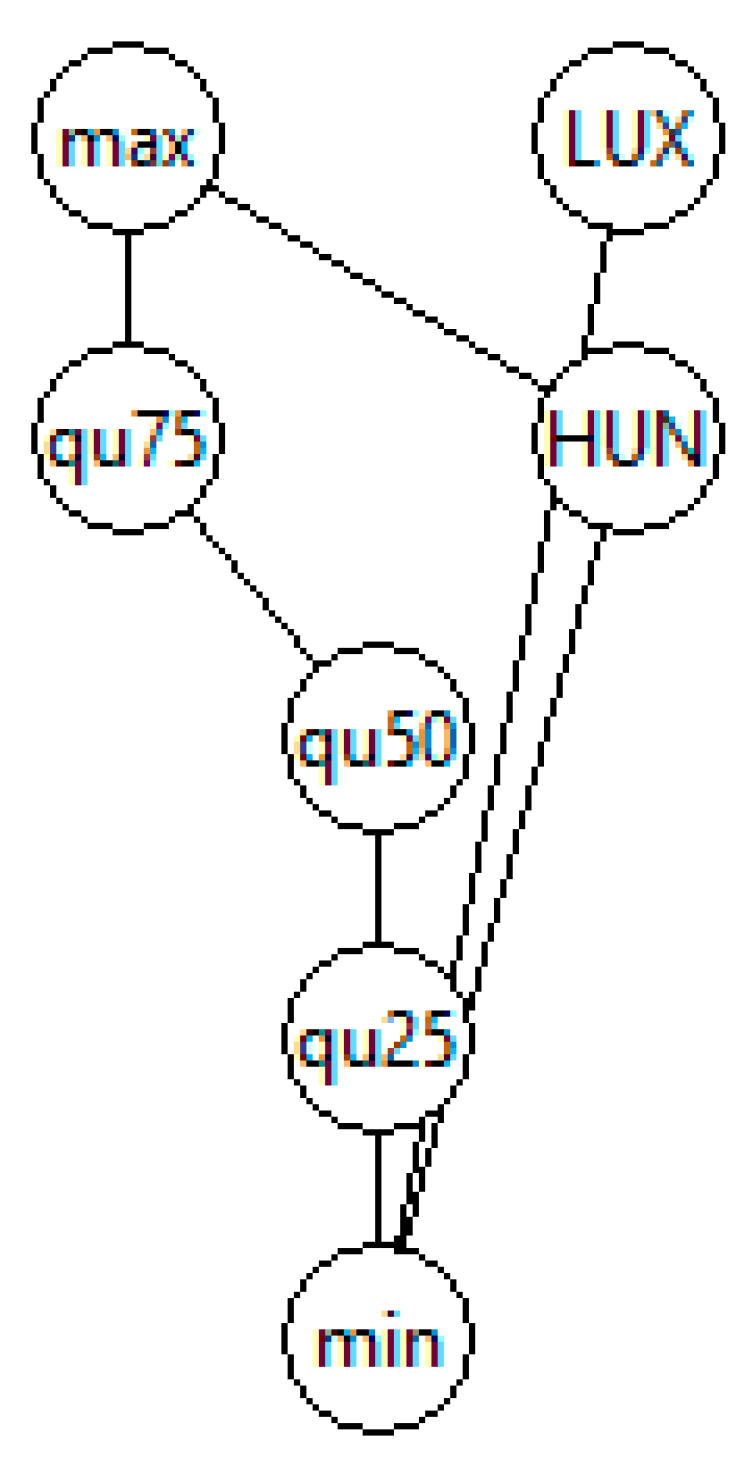
- (1)
- Why are LUX and HUN mutually incomparable? and
- (2)
- Why are HUN and LUX not connected, i.e., incomparable to all other countries.
3.3. Additional Indicators
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Resolution Adopted by the General Assembly on 25 September 2015. Transforming Our World: The 2030 Agenda for Sustainable Development, General Assembly, Seventieth Session Agenda Items 15 and 116, Oct. 21st, United Nations. 2015. Available online: https://www.un.org/ga/search/view_doc.asp?symbol=A/RES/70/1&Lang=E (accessed on 31 March 2021).
- The 17 Goal, United Countrys, Department of Economic and Social Affairs Sustainable Development. 2021. Available online: https://sdgs.un.org/goals (accessed on 31 March 2021).
- Global Indicator Framework for the Sustainable Development Goalsand Targets of the 2030 Agenda for Sustainable Development, A/RES/71/313E/CN.3/2018/2. 2018. Available online: https://unstats.un.org/sdgs/indicators/Global%20Indicator%20Framework%20after%20refinement_Eng.pdf (accessed on 31 March 2021).
- Measuring Progress towards the Sustainable Development Goals, SDG Tracker. 2018. Available online: https://sdg-tracker.org/ (accessed on 31 March 2021).
- The Three Pillars of Sustainability, Future Learn. 2021. Available online: https://www.futurelearn.com/info/courses/sustainability-society-and-you/0/steps/4618 (accessed on 31 March 2021).
- Reduce Inequality within and among Countries, SDG Tracker. 2018. Available online: https://sdg-tracker.org/inequality#targets (accessed on 31 March 2021).
- Sustainable Development in the European Union. Monitoring Report on Progress towards the SDGs in an EU Context, 2020 Edition, Eurostat. 2020. Available online: https://ec.europa.eu/eurostat/documents/3217494/11011074/KS-02-20-202-EN-N.pdf/334a8cfe-636a-bb8a-294a-73a052882f7f?t=1592994779000 (accessed on 31 March 2021).
- Tosato, M.L.; Marchini, S.; Passerini, L.; Pino, A.; Eriksson, L.; Lindgren, F.; Hellberg, S.; Jonsson, J.; Sjöström, N.; Skagerberg, B.; et al. QSARs based on statistical design and their use for identifying chemicals for further biological testing. Environ. Tox. Chem. 1990, 9, 265–277. [Google Scholar] [CrossRef]
- Bock, H.H. Automatische Klassifikation; Vandenhoeck&Ruprecht: Göttingen, Germany, 1974. [Google Scholar]
- Bock, H.H. Clusteranalyse mit unscharfen Partitionen. In Studien zur Klassifikation, Bd 6 Klassifikation und Erkenntnis III—Numerische Klassifikation; Bock, H.H., Ed.; Gesellschaft für Klassifikation: Frankfurt, Germany, 1979; pp. 137–163. [Google Scholar]
- Mucha, H.-J.; Bartel, H.-G.; Dolata, J. Techniques of Rearrangements in Binary Trees (Dendrograms) and Applications. Match Commun. Math. Comput. Chem. 2005, 54, 561–582. [Google Scholar]
- Marshall, A.W.; Olkin, I. Inequalities: Theory of Majorization and Its Applications; Academic Press: San Diego, CA, USA, 1979. [Google Scholar]
- Bruggemann, R.; Patil, G.P. Ranking and Prioritization for Multi-indicator Systems—Introduction to Partial Order Applications; Springer: New York, NY, USA, 2011. [Google Scholar]
- Annoni, P.; Fattore, M.; Bruggemann, R. A Multi-Criteria Fuzzy Approach for Analyzing Poverty structure. Stat. Appl. 2011, 2011, 7–30. [Google Scholar] [CrossRef]
- Beycan, T.; Suter, C. Application of Partial Order Theory to Multidimensional Poverty Analysis in Switzerland. In Partial Order Concepts in Applied Sciences; Marco Fattore, R.B., Ed.; Springer: Cham, Switzerland, 2017; pp. 135–150. [Google Scholar]
- Fattore, M. Partially Ordered Sets and the Measurement of Multidimensional Ordinal Deprivation. Soc. Indic. Res. 2016, 128, 835–858. [Google Scholar] [CrossRef]
- Halfon, E.; Reggiani, M.G. On Ranking Chemicals for Environmental Hazard. Environ. Sci. Technol. 1986, 20, 1173–1179. [Google Scholar] [CrossRef]
- Voigt, K.; Welzl, G.; Brüggemann, R. Data analysis of environmental air pollutant monitoring systems in Europe. Environmetrics 2004, 15, 577–596. [Google Scholar] [CrossRef]
- Davey, B.A.; Priestley, H.A. Introduction to Lattices and Order; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Prömel, H.J.; Steger, A.; Taraz, A. Phase Transitions in the evolution of Partial Orders. J. Combin. Theory 2001, 94, 230–275. [Google Scholar] [CrossRef][Green Version]
- Bruggemann, R.; Voigt, K. Antichains in partial order, example: Pollution in a German region by Lead, Cadmium, Zinc and Sulfur in the herb layer. MATCH Commun. Math. Comput. Chem. 2012, 67, 731–744. [Google Scholar]
- Carlsen, L.; Bruggemann, R.; Kenessova, O.; Erzhigitov, E. Evaluation of analytical performance based on partial order methodology. Talanta 2015, 132, 285–293. [Google Scholar] [CrossRef] [PubMed]
- Winkler, P. Average height in a partially ordered set. Discr. Math. 1982, 39, 337–341. [Google Scholar] [CrossRef]
- Bubley, R.; Dyer, M. Faster random generation of linear extensions. Discr. Math. 1999, 201, 81–88. [Google Scholar] [CrossRef]
- Bruggemann, R.; Sørensen, P.B.; Lerche, D.; Carlsen, L. Estimation of Averaged Ranks by a Local Partial Order Model. J. Chem. Inf. Comp. Sci. 2004, 44, 618–625. [Google Scholar] [CrossRef] [PubMed]
- Bruggemann, R.; Carlsen, L. An Improved Estimation of Averaged Ranks of Partially Orders. MATCH Commun. Math. Comput. Chem. 2011, 65, 383–414. [Google Scholar]
- De Loof, K.; De Meyer, H.; De Baets, B. Exploiting the Lattice of Ideals Representation of a Poset. Fundam. Inform. 2006, 71, 309–321. [Google Scholar]
- De Loof, K.; Rademaker, M.; Bruggemann, R.; De Meyer, H.; Restrepo, G.; De Baets, B. Order Theoretical Tools to Support Risk Assessment of Chemicals. MATCH Commun. Math. Comput. Chem. 2012, 67, 213–230. [Google Scholar]
- PyHasse. 2020. Available online: www.pyhasse.org (accessed on 31 March 2021).
- Carlsen, L. Gender inequality and development. Sustain. Sci. 2020, 15, 759–780. [Google Scholar] [CrossRef]
- Bruggemann, R.; Carlsen, L.; Voigt, K.; Wieland, R. PyHasse Software for Partial Order Analysis: Scientific Background and Description of Selected Modules. In Multi-indicator Systems and Modelling in Partial Order; Bruggemann, R., Carlsen, L., Wittmann, J., Eds.; Springer: New York, NY, USA, 2014; pp. 389–423. [Google Scholar] [CrossRef]
- Bruggemann, R.; Kerber, A.; Koppatz, P.; Pratz, V. PyHasse, a Software Package for Application Studies of Partial Orderings. In Measuring and Understanding Complex Phenomena; Brüggemann, R., Carlsen, L., Beycan, T., Suter, C., Maggino, F., Eds.; Indicators and Their Analysis in Different Scientific Fields; Springer Nature: Cham, Switzerland, 2021; pp. 291–307. [Google Scholar] [CrossRef]
- Bruggemann, R.; Carlsen, L. Uncertainty in weights for composite indicators generated by weighted sums. In Measuring and Understanding Complex Phenomena; Brüggemann, R., Carlsen, L., Beycan, T., Suter, C., Maggino, F., Eds.; Indicators and Their Analysis in Different Scientific Fields; Springer Nature: Cham, Switzerland, 2021; pp. 45–62. [Google Scholar] [CrossRef]
- Formal Concept Analysis: Foundations and Applications; Ganter, B., Stumme, G., Wille, R., Eds.; Springer: Berlin, Germany, 2005. [Google Scholar]
- Bruggemann, R.; Kerber, A. Evaluations as Sets over Lattices—Application point of view. In Measuring and Understanding Complex Phenomena; Bruggemann, R., Carlsen, L., Beycan, T., Suter, C., Maggino, F., Eds.; Indicators and Their Analysis in Different Scientific Fields; Springer Nature: Cham, Switzerland, 2021; pp. 91–101. [Google Scholar] [CrossRef]
- Kerber, A.; Bruggemann, R. Problem Orientable Evaluations as L-subsets. In Measuring and Understanding Complex Phenomena; Bruggemann, R., Carlsen, L., Beycan, T., Suter, C., Maggino, F., Eds.; Indicators and Their Analysis in Different Scientific Fields; Springer Nature: Cham, Switzerland, 2021; pp. 83–89. [Google Scholar] [CrossRef]



| Fictitious Object | q1 | q2 | q3 |
|---|---|---|---|
| “Min” | |||
| “qu25” | 25%-quartile from | 25%-quartile from | 25%-quartile from |
| “qu50” | qu50 of | qu50 of | qu50 of |
| “qu75” | 75%-quartile from | 75%-quartile from | 75%-quartile from |
| “Max” |
| Indicator | Short | Description (Adopted from the References) | Orientation |
|---|---|---|---|
| Relative median at-risk-of-poverty gap 1 | RPG | The indicator is calculated as the distance between the median equivalised total net income of persons below the at-risk-of-poverty threshold and the at-risk-of-poverty threshold itself, expressed as a percentage of the at-risk-of-poverty threshold. This threshold is set at 60% of the countryal median equivalised disposable income of all people in a country | Lower: better |
| Income distribution 2 | IDis | The indicator is a measure of the inequality of income distribution. It is calculated as the ratio of total income received by the 20% of the population with the highest income (the top quintile) to that received by the 20% of the population with the lowest income (the bottom quintile). | Lower: better |
| Income share of the bottom 40% of the population 3 | Isha | The indicator measures the income share received by the bottom 40% of the population. The income concept used is the total disposable household income. | Higher: better |
| Purchasing power adjusted GDP per capita 4 | PPS | Gross domestic product (GDP) is a measure for the economic activity…. Basic figures are expressed in purchasing power standards (PPS), which represents a common currency that eliminates the differences in price levels between countries to allow meaningful volume comparisons of GDP. | Higher: better |
| Adjusted gross disposable income of households per capita 5 | AGDI | The indicator reflects the purchasing power of households and their ability to invest in goods and services or save for the future, by accounting for taxes and social contributions and monetary in-kind social benefits. | Higher: better |
| Asylum applications by state of procedure 6 | AApp | The indicator shows the number of first-time asylum applicants per million inhabitants | Not unambiguous (cf. discussion in text) |
| Indicator | Short | Description (Adopted from the References) | Orientation |
|---|---|---|---|
| Early leavers from education and training, by citizenship 1 | EL | The indicator measures the share of the population aged 18 to 24 with at most lower secondary education who were not involved in any education or training during the four weeks preceding the survey. | Lower: better |
| Young people neither in employment nor in education and training (NEET), by citizenship 2 | NEET | The indicator measures the share of the population aged 15 to 29 who are not employed and not involved in education or training. The numerator of the indicator refers to persons who meet the following two conditions: (a) they are not employed (i.e., unemployed or inactive according to the Intercountryal Labour Organisation definition) and (b) they have not received any education or training (i.e., neither formal nor non-formal) in the four weeks preceding the Labour Force Survey (LFS). | Lower: better |
| Employment rate, by citizenship 3 | ER | The indicator measures the share of the population aged 20 to 64 which are employed. Employed persons are defined as all persons who, during a reference week, worked at least one hour for pay or profit or were temporarily absent from such work. | Higher: better |
| 2010 | 2015 | 2019 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Country | ID | RPG | IDis | Isha | PPS | AGDI | AApp | RPG | IDis | Isha | PPS | AGDI | AApp | RPG | IDis | Isha | PPS | AGDI | AApp |
| Austria | AUT | 21.8 | 4.34 | 22.6 | 31,800 | 24,232 | : | 20.5 | 4.05 | 23.1 | 35,900 | 26,818 | 9893 | 23.9 | 4.17 | 22.9 | 39,400 | 28,177 | 1237 |
| Belgium | BEL | 18 | 3.92 | 23.2 | 30,200 | 22,369 | 1979 | 17.4 | 3.83 | 23.2 | 33,200 | 25,401 | 3458 | 16.3 | 3.61 | 23.9 | 36,700 | 27,082 | 2009 |
| Bulgaria | BGR | 29.6 | 5.86 | 19.5 | 11,000 | 7880 | : | 30.3 | 7.11 | 17.8 | 13,200 | 10,272 | 2809 | 27.5 | 8.1 | 16.4 | 16,500 | 10,875 | 297 |
| Croatia | HRV | 27.6 | 5.54 | 20.0 | 15,000 | 11,202 | : | 26.4 | 5.16 | 20.3 | 16,500 | 12,876 | 33 | 26.2 | 4.76 | 21.3 | 20,300 | 14,969 | 311 |
| Cyprus | CYP | 18 | 4.54 | 21.9 | 25,300 | 19,099 | 3418 | 19.8 | 5.20 | 20.1 | 22,900 | 17,648 | 2483 | 16 | 4.58 | 21.5 | 27,900 | 20,765 | 14,394 |
| Czechia | CZE | 21.1 | 3.47 | 24.9 | 21,000 | 14,957 | 36 | 19.2 | 3.51 | 24.8 | 24,400 | 17,385 | 117 | 14.1 | 3.34 | 25 | 28,900 | 20,017 | 147 |
| Denmark | DNK | 21.6 | 4.41 | 23.0 | 32,600 | 21,037 | 913 | 22 | 4.08 | 23.2 | 35,300 | 23,774 | 3664 | 18.8 | 4.09 | 23.2 | 40,500 | 25,529 | 448 |
| Estonia | EST | 23.2 | 5.01 | 20.6 | 16,500 | 11,557 | 23 | 21 | 6.21 | 18.5 | 21,200 | 15,227 | 171 | 22 | 5.08 | 20.2 | 26,100 | 17,786 | 75 |
| Finland | FIN | 13.8 | 3.61 | 24.2 | 29,500 | 21,472 | : | 13.2 | 3.56 | 24.2 | 30,500 | 24,035 | 5867 | 14.9 | 3.69 | 23.8 | 34,700 | 25,848 | 443 |
| France | FRA | 19.5 | 4.43 | 22.2 | 27,200 | 22,671 | 741 | 15.7 | 4.29 | 22.6 | 29,400 | 24,852 | 1060 | 16.5 | 4.27 | 22.7 | 33,100 | 26,158 | 2062 |
| Germany | DEU | 20.7 | 4.49 | 22.0 | 30,000 | 23,864 | 504 | 22 | 4.80 | 21.4 | 34,200 | 27,658 | 5409 | 23.2 | 4.89 | 21.7 | 37,500 | 30,333 | 1714 |
| Greece | GRC | 23.4 | 5.61 | 19.8 | 21,100 | 17,175 | : | 30.6 | 6.51 | 18.7 | 19,200 | 15,212 | 1051 | 27 | 5.11 | 20.7 | 20,700 | 15,904 | 6990 |
| Hungary | HUN | 16.5 | 3.41 | 24.8 | 16,400 | 11,925 | : | 21.8 | 4.30 | 22.4 | 19,200 | 14,094 | 17,722 | 28.9 | 4.23 | 22.7 | 22,800 | 16,099 | 48 |
| Ireland | IRL | 15.5 | 4.7 | 21.2 | 32,800 | 19,983 | 420 | 18.4 | 4.50 | 21.6 | 49,700 | 20,021 | 695 | 14.8 | 4.03 | 22.8 | 60,200 | 22,541 | 961 |
| Italy | ITA | 24.8 | 5.38 | 20.2 | 26,400 | 21,426 | 169 | 29.3 | 5.84 | 19.7 | 26,500 | 21,417 | 1363 | 30 | 6.01 | 19.5 | 29,800 | 22,878 | 580 |
| Latvia | LVA | 28.9 | 6.84 | 17.9 | 13,400 | 10,278 | 29 | 25.5 | 6.51 | 18.1 | 17,900 | 13,478 | 167 | 28.2 | 6.54 | 18.3 | 21,500 | 15,519 | 94 |
| Lithuania | LTU | 32.6 | 7.35 | 17.7 | 15,200 | 12,603 | 119 | 26 | 7.46 | 17.3 | 20,700 | 16,528 | 95 | 26 | 6.44 | 18.2 | 26,000 | 19,798 | 224 |
| Luxembourg | LUX | 18.6 | 4.1 | 22.5 | 64,700 | 29,509 | : | 17.4 | 4.26 | 22.4 | 74,600 | 33,089 | 4143 | 24.6 | 5.34 | 20.4 | 81,000 | 33,332 | 3548 |
| Malta | MLT | 17.3 | 4.33 | 22.2 | 21,700 | : | 350 | 17.5 | 4.15 | 22.3 | 26,900 | : | 3809 | 17.1 | 4.18 | 22.3 | 31,100 | : | 7965 |
| Netherlands | NLD | 16.2 | 3.65 | 24.2 | 34,100 | 23,175 | 800 | 16.8 | 3.82 | 23.7 | 36,200 | 24,958 | 2540 | 17.1 | 3.94 | 23.4 | 39,900 | 26,496 | 1296 |
| Poland | POL | 22.2 | 4.98 | 20.9 | 15,800 | 12,451 | 114 | 22.3 | 4.92 | 21.1 | 19,100 | 15,253 | 270 | 22 | 4.37 | 22.3 | 22,700 | 17,306 | 73 |
| Portugal | PRT | 22.7 | 5.56 | 19.7 | 20,600 | 16,740 | 15 | 29 | 6.01 | 19.4 | 21,300 | 17,630 | 84 | 22.4 | 5.16 | 20.7 | 24,700 | 19,569 | 169 |
| Romania | ROU | 31.3 | 6.11 | 19.0 | 12,800 | 9962 | : | 38.2 | 8.32 | 16.8 | 15,500 | 11,749 | 62 | 33 | 7.08 | 17.8 | 21,700 | 16,608 | 127 |
| Slovakia | SVK | 25.7 | 3.8 | 23.9 | 18,900 | 14,040 | 58 | 28.9 | 3.54 | 24.8 | 21,500 | 15,898 | 50 | 25.2 | 3.34 | 25.1 | 21,900 | 16,866 | 39 |
| Slovenia | SVN | 20.2 | 3.42 | 24.9 | 21,100 | 15,940 | 95 | 20.3 | 3.60 | 24.4 | 22,700 | 17,027 | 126 | 18.2 | 3.39 | 24.9 | 27,700 | 19,548 | 1731 |
| Spain | ESP | 26.8 | 6.16 | 19.2 | 24,000 | 17,797 | 55 | 33.8 | 6.87 | 18.2 | 25,100 | 19,202 | 314 | 29.1 | 5.94 | 19.3 | 28,400 | 20,346 | 2444 |
| Sweden | SWE | 19.9 | 3.85 | 23.6 | 32,000 | 21,589 | 3389 | 19.9 | 4.06 | 22.9 | 35,300 | 24,700 | 15,931 | 21.7 | 4.33 | 22.4 | 37,000 | 25,089 | 2250 |
| Country | ID | EL | NEET | ER |
|---|---|---|---|---|
| Austria | AUT | 5.5 | 6.3 | 78.3 |
| Belgium | BEL | 7.3 | 10.6 | 71.8 |
| Bulgaria | BGR | 14 | 16.7 | 75 |
| Croatia | HRV | 3 | 14.2 | 66.8 |
| Cyprus | CYP | 4.9 | 12.7 | 75.8 |
| Czechia | CZE | 6.7 | 9.7 | 80.2 |
| Denmark | DNK | 9.6 | 9.3 | 79.4 |
| Estonia | EST | 9.4 | 9.4 | 81.2 |
| Finland | FIN | 7.1 | 9.3 | 77.9 |
| France | FRA | 7.8 | 12.2 | 72.8 |
| Germany | DEU | 7.6 | 5.7 | 82.7 |
| Greece | GRC | 3 | 16.9 | 61.5 |
| Hungary | HUN | 11.8 | 13.2 | 75.3 |
| Ireland | IRL | 5.2 | 11.2 | 75 |
| Italy | ITA | 11.3 | 21.2 | 63.4 |
| Latvia | LVA | 8.7 | 9.8 | 78.6 |
| Lithuania | LTU | 4 | 11 | 78.2 |
| Luxembourg | LUX | 4.7 | 5.6 | 70.1 |
| Malta | MLT | 15.2 | 6.7 | 76.1 |
| Netherlands | NLD | 7.2 | 5.2 | 81 |
| Poland | POL | 5.3 | 12 | 73 |
| Portugal | PRT | 10.2 | 9 | 76.2 |
| Romania | ROU | 15.4 | 16.8 | 70.9 |
| Slovakia | SVK | 8.4 | 14.5 | 73.4 |
| Slovenia | SVN | 4.1 | 7.6 | 76.6 |
| Spain | ESP | 14.7 | 13.1 | 68.7 |
| Sweden | SWE | 4.8 | 5.5 | 84.5 |
| 2010 | 2015 | 2019 | |
|---|---|---|---|
| rank | rank | rank | |
| AUT | 5 | 7 | 7 |
| BEL | 6 | 5 | 1 |
| BGR | 24.5 | 25 | 26 |
| CYP | 14 | 13 | 14 |
| CZE | 11 | 3 | 6 |
| DEU | 9 | 10.5 | 8 |
| DNK | 10 | 10.5 | 2.5 |
| ESP | 21 | 20 | 20 |
| EST | 19.5 | 19 | 17 |
| FIN | 3 | 5 | 4 |
| FRA | 12 | 5 | 10 |
| GRC | 17.5 | 24 | 23 |
| HRV | 22 | 22 | 22 |
| HUN | 13 | 16 | 21 |
| IRL | 7 | 9 | 5 |
| ITA | 15 | 15 | 18 |
| LTU | 23 | 21 | 19 |
| LUX | 2 | 2 | 9 |
| LVA | 26 | 23 | 24 |
| NLD | 1 | 1 | 2.5 |
| POL | 19.5 | 17 | 15 |
| PRT | 17.5 | 18 | 16 |
| ROU | 24.5 | 26 | 25 |
| SVK | 16 | 14 | 13 |
| SVN | 4 | 12 | 12 |
| SWE | 8 | 8 | 11 |
| A | 2015 | 2019 | B | 2015 | 2019 |
|---|---|---|---|---|---|
| rank | rank | rank | rank | ||
| AUT | 11 | 10.5 | AUT | 5.5 | 10 |
| BEL | 11 | 7 | BEL | 2.5 | 1.5 |
| BGR | 26 | 24 | BGR | 20 | 25 |
| CYP | 20 | 20 | CYP | 14 | 3 |
| CZE | 1 | 1 | CZE | 10 | 12 |
| DEU | 22 | 10.5 | DEU | 7.5 | 13 |
| DNK | 21 | 4 | DNK | 7.5 | 7 |
| ESP | 13.5 | 25 | ESP | 21 | 16 |
| EST | 18 | 6 | EST | 18 | 23 |
| FIN | 11 | 5 | FIN | 2.5 | 7 |
| FRA | 3 | 12 | FRA | 9 | 4.5 |
| GRC | 24 | 26 | GRC | 22 | 15 |
| HRV | 8 | 21 | HRV | 25 | 19 |
| HUN | 25 | 14.5 | HUN | 11 | 21 |
| IRL | 4 | 9 | IRL | 12 | 7 |
| ITA | 16 | 19 | ITA | 15 | 18 |
| LTU | 13.5 | 14.5 | LTU | 23 | 20 |
| LUX | 7 | 14.5 | LUX | 1 | 8 |
| LVA | 18 | 22.5 | LVA | 24 | 24 |
| NLD | 2 | 8 | NLD | 4 | 1.5 |
| POL | 18 | 2.5 | POL | 17 | 22 |
| PRT | 9 | 14.5 | PRT | 19 | 17 |
| ROU | 23 | 22.5 | ROU | 26 | 26 |
| SVK | 5 | 2.5 | SVK | 16 | 14 |
| SVN | 6 | 17 | SVN | 13 | 11 |
| SWE | 15 | 18 | SWE | 5.5 | 4.5 |
| RPG | IDis | Isha | PPS | AGDI | AApp | |
|---|---|---|---|---|---|---|
| min | −33.0 | −8.1 | 16.4 | 16,500.0 | 10,875.0 | −14,394.0 |
| qu25 | −27.0 | −5.9 | 19.5 | 21,900.0 | 16,866.0 | −2009.0 |
| qu50 | −22.2 | −4.5 | 22.0 | 28,150.0 | 20,181.5 | −514.0 |
| qu75 | −16.5 | −3.9 | 23.4 | 37,000.0 | 25,848.0 | −147.0 |
| max | −14.1 | −3.3 | 25.1 | 60,200.0 | 30,333.0 | −39.0 |
| Isolated objects | ||||||
| LUX | −24.6 | −5.34 | 20.4 | 81,000.0 | 33,332.0 | −3548.0 |
| HUN | −28.9 | −4.23 | 22.7 | 22,800.0 | 16,099.0 | −48.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carlsen, L.; Bruggemann, R. Inequalities in the European Union—A Partial Order Analysis of the Main Indicators. Sustainability 2021, 13, 6278. https://doi.org/10.3390/su13116278
Carlsen L, Bruggemann R. Inequalities in the European Union—A Partial Order Analysis of the Main Indicators. Sustainability. 2021; 13(11):6278. https://doi.org/10.3390/su13116278
Chicago/Turabian StyleCarlsen, Lars, and Rainer Bruggemann. 2021. "Inequalities in the European Union—A Partial Order Analysis of the Main Indicators" Sustainability 13, no. 11: 6278. https://doi.org/10.3390/su13116278
APA StyleCarlsen, L., & Bruggemann, R. (2021). Inequalities in the European Union—A Partial Order Analysis of the Main Indicators. Sustainability, 13(11), 6278. https://doi.org/10.3390/su13116278






