On Spatially Dependent Risk Preferences: The Case of Nigerian Farmers
Abstract
1. Introduction
2. Materials and Methods
2.1. The Theoretical Model
2.2. Source of Data
Order of Presentation
- Instruction for small gain one and large gain one treatments
- Instruction for small gain two and large gain two treatments
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Bank. Agriculture for Development: Overview, World Development Report 2008; The World Bank: Washington, DC, USA, 2007; Available online: https://www.openknowledge.worldbank.org (accessed on 10 September 2015).
- Tshoni, S. Analysis of Smallholders’ farm diversity and risk attitudes in the Stellenbosch local municipal area. In Family Farming Knowledge Platform; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2015; pp. 1–88. Available online: http://scholar.sun.ac.za/bitstream/handle/10019.1/96677/tshoni_analysis_2015.pdfsequence=3&isAllowed=y (accessed on 10 January 2021).
- Binswanger, H.P. Attitudes toward risk: Experimental measurement in rural India. Am. J. Agric. Econ. 1980, 62, 395–407. [Google Scholar] [CrossRef]
- Binswanger, H.P. Attitudes toward risk: Theoretical implications of an experiment in rural India. Econ. J. 1981, 91, 867–890. [Google Scholar] [CrossRef]
- Wik, M.; Aragie Kebede, T.; Bergland, O.; Holden, S.T. On the measurement of risk aversion from experimental data. Appl. Econ. 2004, 36, 2443–2451. [Google Scholar] [CrossRef]
- Yesuf, M. Risk, Time and Land Management under Market Imperfections: Applications to Ethiopia. Ph.D. Thesis, Goteborg University, Gothenburg, Sweden, 2004. [Google Scholar]
- Harrison, G.W.; Humphrey, S.J.; Verschoor, A. Choice under Uncertainty in Developing Countries, CEDEX Discussion Paper Series, No. 2005-18, 2005. Available online: http://www.nottingham.ac.uk/economics/cedex/papers (accessed on 12 November 2014).
- Yesuf, M.; Bluffstone, R.A. Poverty, risk aversion, and path dependence in low-income countries: Experimental evidence from Ethiopia. Am. J. Agric. Econ. 2009, 91, 1022–1037. [Google Scholar] [CrossRef]
- Harrison, G.W.; Humphrey, S.J.; Verschoor, A. Choice under uncertainty: Evidence from Ethiopia, India and Uganda. Econ. J. 2010, 120, 80–104. [Google Scholar] [CrossRef]
- Tanaka, T.; Camerer, C.F.; Nguyen, Q. Risk and time preferences: Linking experimental and household survey data from Vietnam. Am. Econ. Rev. 2010, 100, 557–571. [Google Scholar] [CrossRef]
- Brick, K.; Visser, M.; Burns, J. Risk aversion: Experimental evidence from South African fishing communities. Am. J. Agric. Econ. 2012, 94, 133–152. [Google Scholar] [CrossRef]
- Reardon, T.; Taylor, J.E. Agroclimatic shock, income inequality, and poverty: Evidence from Burkina Feso. World Dev. 1996, 24, 901–914. [Google Scholar] [CrossRef]
- Humphrey, S.J.; Verschoor, A. Decision-making under risk among small farmers in East Uganda. J. Afr. Econ. 2004, 13, 44–101. [Google Scholar] [CrossRef]
- Nguyen, Q.; Leung, P. Do fishermen have different attitudes toward risk? An application of prospect theory to the study of Vietnamese fishermen. J. Agric. Resour. Econ. 2009, 34, 518–538. [Google Scholar]
- Nguyen, Q. Does nurture matter: Theory and experimental investigation on the effect of working environment on risk and time preferences. J. Risk Uncertain. 2011, 43, 245–270. [Google Scholar] [CrossRef]
- Tanaka, Y.; Munro, A. Regional variation in risk and time preferences: Evidence from a large-scale field experiment in rural Uganda. J. Afr. Econ. 2014, 23, 151–187. [Google Scholar] [CrossRef]
- Nguyen, Q.; Leung, P. How nurture can shape preferences: An experimental study on risk preferences of Vietnamese fishers. Environ. Dev. Econ. 2010, 15, 609–631. [Google Scholar] [CrossRef]
- Roe, B.; Irwin, E.G.; Sharp, J.S. Pigs in space: Modeling the spatial structure of hog production in traditional and nontraditional production regions. Am. J. Agric. Econ. 2002, 84, 259–278. [Google Scholar] [CrossRef]
- Case, A. Neighborhood Influence and Technological Change. Reg. Sci. Urban Econ. 1992, 22, 491–508. [Google Scholar] [CrossRef]
- Holloway, G.; Shankar, B.; Rahmanb, S. Bayesian spatial probit estimation: A primer and an application to HYV rice adoption. Agric. Econ. 2002, 27, 383–402. [Google Scholar] [CrossRef]
- Krishnan, P.; Patnam, M. Neighbors and extension agents in Ethiopia: Who matters more for technology adoption? Am. J. Agric. Econ. 2014, 96, 308–327. [Google Scholar] [CrossRef]
- Läpple, D.; Kelley, H. Spatial dependence in the adoption of organic drystock farming in Ireland. Eur. Rev. Agric. Econ. 2015, 42, 315–337. [Google Scholar] [CrossRef]
- Tessema, Y.M.; Asafu-Adjaye, J.; Kassie, M.; Mallawaarachchi, T. Do neighbours matter in technology adoption? The case of conservation tillage in Northwest Ethiopia. Afr. J. Agric. Resour. Econ. 2016, 11, 211–225. [Google Scholar]
- Holloway, G.; Lapar, M.; Lucila, A. How big is your neighbourhood? Spatial implications of market participation among Filipino smallholders. J. Agric. Econ. 2007, 58, 37–60. [Google Scholar] [CrossRef]
- Benirschka, M.; Binkley, J.K. Land price volatility in a geographically dispersed market. Am. J. Agric. Econ. 1994, 76, 185–195. [Google Scholar] [CrossRef]
- Bockstael, N.E. Modeling economics and ecology: The importance of a spatial perspective. Am. J. Agric. Econ. 1996, 78, 1168–1180. [Google Scholar] [CrossRef]
- Weiss, M.D. Precision farming and spatial economic analysis: Research challenges and opportunities. Am. J. Agric. Econ. 1996, 78, 1275–1280. [Google Scholar] [CrossRef]
- Areal, F.J.; Balcombe, K.; Tiffin, R. Integrating spatial dependence into stochastic frontier analysis. Aust. J. Agric. Resour. Econ. 2012, 56, 521–541. [Google Scholar] [CrossRef]
- Kim, C.W.; Phipps, T.T.; Anselin, L. Measuring the benefits of air quality improvement: A spatial hedonic approach. J. Environ. Econ. Mgt. 2003, 45, 24–39. [Google Scholar] [CrossRef]
- Anselin, L. Under the hood issues in the specification and interpretation of spatial regression models. Agric. Econ. 2002, 27, 247–267. [Google Scholar] [CrossRef]
- LeSage, J.P.; Pace, R.K. Introduction to Spatial Econometrics; Balakrishnan, N., William, S.R., Eds.; CRC Press: London, UK, 2009; pp. 1–313. [Google Scholar]
- Charness, G.; Gneezy, U.; Imas, A. Experimental methods: Eliciting risk preferences. J. Econ. Behav. Org. 2013, 87, 43–51. [Google Scholar] [CrossRef]
- Bocqueho, G.; Jacquet, F.; Reynaud, A. Expected utility or prospect theory maximisers? Assessing farmers’ risk behaviour from field-experiment data. Eur. Rev. Agric. Econ. 2014, 41, 135–172. [Google Scholar] [CrossRef]
- Anselin, L. Lagrange multiplier test diagnostics for spatial dependence and spatial heterogeneity. Geogr. Anal. 1988, 20, 1–17. [Google Scholar] [CrossRef]
- LeSage, J.P. An introduction to spatial econometrics. Rev. d'économie Ind. 2008, 123, 19–44. [Google Scholar] [CrossRef]
- Fox, J.; Kleiber, C.; Zeileis, A. ivreg: Two-Stage Least-Squares Regression with Diagnostics. R Package Version 0.5-0. 2020. Available online: https://CRAN.R-project.org/package=ivreg (accessed on 5 April 2021).
- Liu, E.M. Time to change what to sow: Risk preferences and technology adoption decisions of cotton farmers in China. Rev. Econ. Stat. 2013, 95, 1386–1403. [Google Scholar] [CrossRef]
- Ihli, H.J.; Chiputwa, B.; Musshoff, O. Do Changing Probabilities or Payoffs in Lottery-Choice Experiments Matter? Evidence from Rural Uganda. Global Food Discussion Papers No. 24; Transformation of Global Agri-Food Systems: Trends, Driving Forces and Implications for Developing Countries; Georg-August-University of Göttingen: Göttingen, Germany, 2013. [Google Scholar]
- Galarza, F. Choices under Risk in Rural Peru. Munich Personal RePEc Archive (MPRA); Working Paper No. 17708. October 2009. Available online: http://mpra.ub.uni-muenchen.de/17708/ (accessed on 25 May 2015).
- Liebenehm, S.; Waibel, H. Simultaneous estimation of risk and time preferences among small-scale cattle farmers in West Africa. Am. J. Agric. Econ. 2014, 96, 1420–1438. [Google Scholar] [CrossRef]
- Schubert, R. Analyzing and managing risks-on the importance of gender differences in risk attitudes. Manag. Financ. 2006, 32, 706–715. [Google Scholar] [CrossRef]
- Charness, G.; Gneezy, U. Strong evidence for gender differences in risk taking. J. Econ. Behav. Org. 2012, 83, 50–58. [Google Scholar] [CrossRef]
- Bannier, C.E.; Neubert, M. Gender differences in financial risk taking: The role of financial literacy and risk tolerance. Econ Lett. 2016, 145, 130–135. [Google Scholar] [CrossRef]
- Fisher, P.J.; Yao, R. Gender differences in financial risk tolerance. J. Econ. Psychol. 2017, 61, 191–202. [Google Scholar] [CrossRef]
- Harris, C.R.; Jenkins, M.; Glaser, D. Gender differences in risk assessment: Why do women take fewer risks than men? Judgm. Decis. Mak. 2006, 1, 48. [Google Scholar]
- Stark, O.; Zawojska, E. Gender differentiation in risk-taking behavior: On the relative risk aversion of single men and single women. Econ. Lett. 2015, 137, 83–87. [Google Scholar] [CrossRef]
- Ward, P.S.; Singh, V. Risk and Ambiguity Preferences and the Adoption of New Agricultural Technologies: Evidence from Field Experiment in Rural India. International Food Policy Research Institute (IFPRI) Discussion Paper 01324 (February 2014). Available online: https://ssrn.com/abstract=2392762 (accessed on 5 May 2021).
- Sabater-Grande, G.; Georgantzís, N. Accounting for risk aversion in repeated prisoners’ dilemma games: An experimental test. J. Econ. Behav. Org. 2002, 48, 37–50. [Google Scholar] [CrossRef]
- García Gallego, A.; Georgantzís, N.; Jaramillo-Gutiérrez, A.; Parravano, M. The lottery-panel task for bi-dimensional parameter-free elicitation of risk attitudes. Rev. Int. Sociol. Spec. Issue Behav. Exp. Econ. 2012, 70, 53–72. [Google Scholar]
- Attanasi, G.; Georgantzis, N.; Rotondi, V.; Vigani, D. Lottery- and survey-based risk attitudes linked through a multichoice elicitation task. Theory Decis. 2018, 84, 341–372. [Google Scholar] [CrossRef]
- Barreda-Tarrazona, I.; Jaramillo-Gutierrez, A.; Navarro-Martinez, D.; Sabater-Grande, G. Risk attitude elicitation using a multi-lottery choice task: Real vs. hypothetical incentives. Span. J. Financ. Account. 2011, 40, 609–624. [Google Scholar] [CrossRef]
- Barreda-Tarrazona, I.; Sabater-Grande, G.; Georgantzis, N. Risk Elicitation through the S-GG Lottery Panel Task: Implementation note; Working Paper 2020/23; LEE and Economics Department, Universitat Jaume I: Castellón, Spain, 2020. [Google Scholar]
- Harrison, G.W.; Rutstrom, E.E. Risk aversion in the laboratory, Risk aversion in experiments. Res. Exp. Econ. 2008, 12, 41–196. [Google Scholar]
- Bell, K.P.; Bockstael, N.E. Applying the generalized-moments estimation approach to spatial problems involving micro-level data. Rev. Econ. Stat. 2000, 82, 72–82. [Google Scholar] [CrossRef]
- Tobler, W.R.A. Computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Lawrance, E.C. Poverty and the rate of time preference: Evidence from panel data. J. Pol. Econ. 1991, 99, 54–77. [Google Scholar] [CrossRef]
- Guiso, L.; Paiella, M. Risk aversion, wealth and background risk. J. Eur. Econ. Assoc. 2008, 6, 1109–1150. [Google Scholar] [CrossRef]
- Bezabih, M.; Sarr, M. Risk preferences and environmental uncertainty: Implications for crop diversification decisions in Ethiopia. Environ. Resour. Econ. 2012, 53, 483–505. [Google Scholar] [CrossRef]
- Shee, A.; Azzarri, C.; Haile, B. Farmers’ willingness to pay for improved agricultural technologies: Evidence from a field experiment in Tanzania. Sustainability 2020, 12, 216. [Google Scholar] [CrossRef]
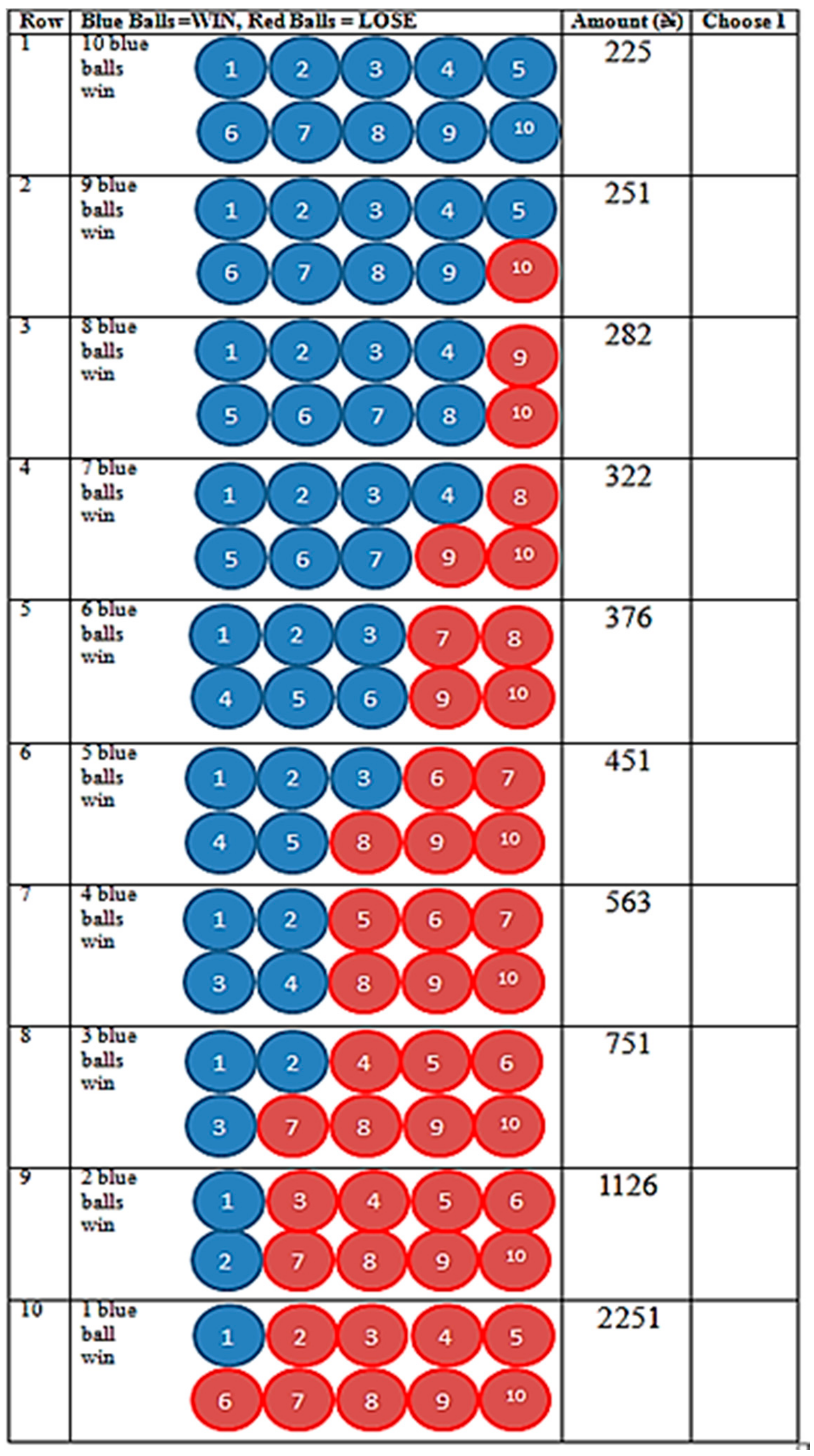
| Panel Lotteries for Four Treatments (Currency in Naira) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | |
| Panel 1 | 225 | 251 | 282 | 322 | 376 | 451 | 563 | 751 | 1126 | 2251 |
| Panel 2 | 225 | 251 | 282 | 322 | 376 | 451 | 564 | 753 | 1129 | 2259 |
| Panel 3 | 225 | 251 | 283 | 324 | 379 | 455 | 570 | 762 | 1145 | 2295 |
| Panel 4 | 225 | 252 | 284 | 326 | 382 | 460 | 578 | 774 | 1165 | 2340 |
| Panel 1 | 0 | 26 | 57 | 97 | 151 | 226 | 338 | 526 | 901 | 2026 |
| Panel 2 | 0 | 26 | 57 | 97 | 151 | 226 | 339 | 528 | 904 | 2034 |
| Panel 3 | 0 | 26 | 58 | 99 | 154 | 230 | 345 | 537 | 920 | 2070 |
| Panel 4 | 0 | 27 | 59 | 101 | 157 | 235 | 353 | 549 | 940 | 2115 |
| Panel 1 | 22,500 | 25,002 | 28,128 | 32,148 | 37,507 | 45,010 | 56,265 | 75,024 | 112,540 | 225,090 |
| Panel 2 | 22,500 | 25,012 | 28,150 | 32,186 | 37,567 | 45,100 | 56,400 | 75,234 | 112,900 | 225,900 |
| Panel 3 | 22,500 | 25,056 | 28,250 | 32,358 | 37,834 | 45,500 | 57,000 | 76,167 | 114,500 | 229,500 |
| Panel 4 | 22,500 | 25,112 | 28,375 | 32,572 | 38,167 | 46,000 | 57,750 | 77,334 | 116,500 | 234,000 |
| Panel 1 | 0 | 2502 | 5628 | 9648 | 15,007 | 22,510 | 33,765 | 52,524 | 90,040 | 202,590 |
| Panel 2 | 0 | 2512 | 5650 | 9686 | 15,067 | 22,600 | 33,900 | 52,734 | 90,400 | 203,400 |
| Panel 3 | 0 | 2556 | 5750 | 9858 | 15,334 | 23,000 | 34,500 | 53,667 | 92,000 | 207,000 |
| Panel 4 | 0 | 2612 | 5875 | 10,072 | 15,667 | 23,500 | 35,250 | 54,834 | 94,000 | 211,500 |
| Variables | Definition | Mean (SD) | Min | Max |
|---|---|---|---|---|
| SG1 | Small gain one probability index | 0.80 (0.15) | 0.10 | 1.00 |
| SG2 | Small gain two probability index | 0.60 (0.13) | 0.10 | 1.00 |
| LG1 | Large gain one probability index | 0.70 (0.15) | 0.10 | 1.00 |
| LG2 | Large gain two probability index | 0.60 (0.16) | 0.10 | 1.00 |
| Age | Age of the farmer in years | 47.00 (12.50) | 20.00 | 80.00 |
| Education | Years of formal schooling | 4.60 (4.50) | 0.00 | 16.00 |
| Male | 1 if male, 0 if female | 0.68 | 0.00 | 1.00 |
| Christian | 1 if Christian, 0 otherwise | 0,56 | 0.00 | 1.00 |
| Married | 1 if married, 0 otherwise | 0.94 | 0.00 | 1.00 |
| Household size | Number of household members | 6.00 (3.00) | 1.00 | 21.00 |
| Farm size | Rice farm area in hectares | 1.90 (1.50) | 0.20 | 16.00 |
| Bad road | 1 if farmers live in untarred, poorly accessible road areas, 0 otherwise | 0.37 | 0.00 | 1.00 |
| Variables | SG1 | SG2 | LG1 | LG2 |
|---|---|---|---|---|
| Spatial Dependence | ||||
| Spatial lag | 0.0016 *** (0.0002) | 0.0019 *** (0.0002) | 0.0019 *** (0.0002) | 0.0019 *** (0.0002) |
| Farm- and Farmer-Specific Factors | ||||
| Age | 0.0032 *** (0.0009) | 0.0021 *** (0.0008) | 0.0022 ** (0.0010) | 0.0019 ** (0.0008) |
| Education | 0.0043 (0.0025) | 0.0002 (0.0025) | 0.0035 (0.0026) | 0.0037 (0.0024) |
| Christian | 0.0498 ** (0.0217) | 0.0498 *** (0.0185) | −0.0263 (0.0207) | 0.0217 (0.0191) |
| Household size | 0.0021 (0.0031) | 0.0027 (0.0034) | 0.0016 (0.0034) | 0.0004 (0.0037) |
| Farm size | −0.0163 ** (0.0075) | −0.0047 (0.0056) | −0.0155 * (0.0081) | −0.0074 (0.0069) |
| Male | 0.0559 ** (0.0234) | 0.0498 *** (0.0196) | 0.0616 *** (0.0217) | 0.0580 *** (0.0210) |
| Married | 0.3103 *** (0.0611) | 0.2214 *** (0.0556) | 0.3089 *** (0.0587) | 0.2137 *** (0.0509) |
| Location/Infrastructure | ||||
| Bad roads | 0.1097 *** (0.0206) | 0.0549 *** (0.0186) | 0.1123 *** (0.0208) | 0.0595 *** (0.0195) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ambali, O.I.; Areal, F.J.; Georgantzis, N. On Spatially Dependent Risk Preferences: The Case of Nigerian Farmers. Sustainability 2021, 13, 5943. https://doi.org/10.3390/su13115943
Ambali OI, Areal FJ, Georgantzis N. On Spatially Dependent Risk Preferences: The Case of Nigerian Farmers. Sustainability. 2021; 13(11):5943. https://doi.org/10.3390/su13115943
Chicago/Turabian StyleAmbali, Omotuyole Isiaka, Francisco Jose Areal, and Nikolaos Georgantzis. 2021. "On Spatially Dependent Risk Preferences: The Case of Nigerian Farmers" Sustainability 13, no. 11: 5943. https://doi.org/10.3390/su13115943
APA StyleAmbali, O. I., Areal, F. J., & Georgantzis, N. (2021). On Spatially Dependent Risk Preferences: The Case of Nigerian Farmers. Sustainability, 13(11), 5943. https://doi.org/10.3390/su13115943







