Abstract
ORC technology is one of the most promising technologies for the use of residual energy in the generation of electrical energy, offering simple and environmentally friendly alternatives. In this field, the selection of working fluids plays an important role in the operation of the cycle, whether in terms of the energy efficiency or the minimization of environmental impacts. Therefore, in this paper, a comprehensive review is presented on the use of R1234yf refrigerant and its mixtures as working fluids in ORC systems. These fluids are used in low- and medium-temperature applications for the use of residual energy generated from solar energy, geothermal energy, and internal combustion engines. It was concluded that R1234yf and its mixtures are competitive as compared with conventional refrigerants used in ORC.
1. Introduction
Global energy demand grew by 2.3% in 2018, almost double the average annual growth rate since 2010, with about 75% of this increase being due to oil, gas, and coal consumption [1]. In this regard, it is well known that the energy obtained from the combustion of fossil fuels has negative effects on the environment; in addition, fossil fuels are limited and their use is not sustainable [2].
Among the alternatives that are promoted to mitigate environmental, access, and sustainability problems represented by the use of electrical energy is the use of the organic Rankine cycle (ORC). The Rankine steam cycle has been considered as the main technology used to convert high-temperature heat into electricity [3]; however, low- to medium-temperature heat sources have received less attention due to technical difficulties in the exploitation of these resources [4]. ORCs use organic working fluids, which have lower boiling points and higher steam pressures than water, allowing an ORC to operate at lower temperatures than conventional systems [5]. Organic working fluids used in ORC systems have larger molecular masses, which allow compact designs, high mass flow rates, and higher turbine efficiencies (up to 80–85%) [6,7]. In addition, heat recovery using ORCs is considered an important technology among renewable energy processes because of its ability to generate energy from available waste heat and from natural heat sources such as solar radiation [8], ocean thermal sources [9], geothermal sources [10], biomass combustion [11], or waste heat recovery from industrial processes [12] or from internal combustion engines [13].
In the industrial sector, the amount of rejected heat is estimated at 50% of the initial load of heat used [14]; therefore, a significant part of this waste heat can be recovered. For this heat source, most of the waste heat is found at temperatures below 200 °C [15], which confirms the interest in the use of ORC systems. The energy production levels of commercial ORCs range from 10 kW to 10 MW for a heat source temperature range of between 100 and 300 °C [16]. Several studies on ORC technology have been carried out over the past few years. For example, Vélez et al. [17] presented an overview of the technical and economic aspects, as well as the evolution in the market of ORC technologies. They concluded that the ORC is a promising trend for the conversion of low, and medium-temperature thermal energy into small-scale electrical or mechanical energy. Other works have reviewed applications of ORCs in solar pond energy systems, solar reverse osmosis desalination systems, and Rankine duplex cooling systems [18].
On the other hand, the use of certain working fluids in ORCs contributes to global warming (GWP) and even to the destruction of the ozone layer (ODP). As examples of such refrigerants, R245fa, R11, R134a, and R123 can be mentioned, among others. The use of substances with high GWP has been limited by various regulations in recent years. Among the most recent regulations is the Kigali [19] agreement, the main objective of which is to keep global warming below 1.5 °C to 2 °C by reducing and eliminating the use of high-GWP substances. For this reason, several studies have been carried out with the aim of developing fluids that have a low GWP, and whose thermophysical properties have adequate energy efficiency [16].
The selection of refrigerants for energy generation is a complex issue, as several aspects must be considered. In the case of an ORC, research on the use of pure fluids and certain mixtures began years ago in order to achieve better energy efficiency, as well as to minimize the environmental impacts. In this sense, a new refrigerant belonging to the family of hydrofluoroolefins (HFOs), called R1234yf, exhibits more environmentally friendly properties than conventional refrigerants such as hydrochlorofluorocarbons (HCFCs) and hydrofluorocarbons (HFCs). Thus, R1234yf has been considered an excellent replacement for the R134a refrigerant [20], mainly in automotive air conditioning applications [21]. In fact, Spatz and Minor [22] reported that R1234yf has excellent environmental properties, such as a low GWP, zero ODP, and a minimal life time in the atmosphere. They also highlighted that the toxicity and thermodynamic properties of R1234yf are very similar to those of R134a.
Regarding the use of R1234yf in ORC, Yamada et al. [23] reported the feasibility of the R1234yf for five cycle configurations. The authors found that ORC using R1234yf and R134a had similar thermal efficiencies; thus, they noted that R1234yf could be considered a prime candidate to replace R134a. Jung et al. [24] analyzed an ORC using several working fluids for heat recovery from exhaust gases in internal combustion engines. For a low compression ratio, R134a and R1234yf showed high efficiencies. Liu et al. [4] investigated several HFOs as possible working fluids in an ORC for power generation using geothermal energy. It was concluded that R1234yf presented the best performance characteristics at the lowest temperature of 120 °C.
Thus, the use of ORC systems in low-temperature applications using R1234yf refrigerant could be a suitable approach. Therefore, this paper presents a comprehensive review of ORC systems using R1234yf as a pure refrigerant at some of its most representative mixtures for low- and medium-temperature applications. In the review, the impacts of this refrigerant on the performance of ORC systems and the various ORC applications based on solar energy, geothermal energy, and heat recovery from internal combustion engines is discussed. Finally, this paper aims to provide a fairly comprehensive overview of the current situation for R1234yf and its future prospects in ORC systems.
The review is organized as follows. Section 2 describes the methodology followed for the presentation of this review. Section 3 presents the main characteristics of R1234yf, either in pure form or as a mixture. In addition, emphasis is placed on ORC systems based on solar energy, geothermal energy, and waste heat recovery from internal combustion engines where R1234yf is listed as a working fluid. Section 4 presents a general discussion on the main results in the study on ORC systems from energetic, exergetic, and economic perspectives. Finally, Section 5 presents a summary.
2. Methodology
To prepare this review, emphasizing the main applications of the use of R1234yf refrigerant in ORC systems, an exhaustive search was carried out in databases of scientific articles and technical journals. Thus, a classification was made of the main applications of ORC systems based on the use of residual energy sources, which were grouped into three widely developed technologies in this field, namely solar energy, geothermal energy, and waste heat from internal combustion engines.
In particular, for each investigated study, information was available on the most relevant characteristics of the refrigerant, such as its intrinsic properties, thermal operating conditions in the ORC system, cycle configurations, materials, component selection, and thermal and exergetic efficiency, among others. Such information was reviewed in order to highlight the feasibility of using R1234yf and its mixtures as working fluids in ORC systems.
Finally, this classification is intended to provide a source of information for research work on R1234yf in proposals for new configurations of ORC systems, which seek to take advantage of residual energy from various processes, thus having less impact on the environment due to the use of alternative low GWP refrigerants.
3. Use of R1234yf Refrigerant in ORC Systems
In ORCs, the working fluid plays an important role in the operation of the system. This fluid must match the temperature range of the specific application and must be non-toxic and non-flammable. When using low-temperature heat sources, two properties stand out that influence the operation and performance of the system, the critical temperature and the nature of the fluid. Critical temperature shows the most direct relationship with cycle performance; that is, how the fluid evaporation process matches the heat source in the subcritical ORC. For some low-temperature heat sources, working fluids with low critical temperatures may be preferred, as more electrical energy can be produced [25]. R1234yf has a low critical temperature (as shown in Table 1) compared to other fluids commonly used in the operation of ORC systems (R134a, R141b, R152a, R245fa, R600, R600a, R1234ze(E)). Since it does not present a high critical temperature, the condensation pressure does not decrease as much compared to fluids with high critical temperatures, causing a higher specific volume in the turbine exhaust, and therefore causing a high cost for this component [26]. Concerning the nature of R1234yf, it is categorized as an isentropic refrigerant, which along with other dry fluids is more appropriate than wet fluids, since they overheat even after an isentropic expansion; therefore, partial condensation is eliminated in the final part of the expansion process within the cycle [27].

Table 1.
Properties of R1234yf and of the most common refrigerants used in ORC systems.
R1234yf is a potential candidate for ORC applications, especially for low- to medium-temperature heat sources. Thus, R1234yf has been proposed as a replacement candidate for HFCs, mainly from an environmental perspective, which is a determining factor in the selection of refrigerant fluids for this type of systems. Table 1 shows a comparison between the main characteristics and thermophysical properties of R1234yf with some of the most common HFCs and HCs in ORC systems. Hydrocarbons are found to be highly flammable according to the ASHRAE standard [28]. It should be noted that R1234yf is classified as A2L or low on the flammability index according to the ISO [29] flammability classification due to its low combustion speed, low heat of combustion, and high minimum ignition energy. The critical pressure, Pcrit; temperature, Tcrit; and normal boiling point, NBP, are included as feasibility indicators in typical ORC applications.
ORC power systems have been used to generate electricity from waste heat for several decades. In addition to the configuration of the standard ORC subcritical cycle, another configuration consisting of a transcritical cycle has been investigated. Table 2 summarizes the advantages and disadvantages for each ORC power system configuration [30].

Table 2.
Advantages and disadvantages for two ORC power system configurations.
The following sections discuss the studies that have been carried out for the different applications of ORC and the different sources of heat that have used R1234yf as a pure substance in comparison with other refrigerants.
3.1. R1234yf as a Pure Fluid
The use of R1234yf in ORC systems has been investigated in applications for the use of low- and medium-temperature heat sources. Working fluids for ORC systems can be classified according to the slope of the vapor saturation line in a T-s diagram [27]. For example, R1234yf is an isentropic fluid and has a vertical slope in its saturation curve; that is, the ratio of change of entropy with respect to temperature is constant, as shown in Figure 1. Therefore, isentropic fluids do not require superheating, since the fluid at the outlet of the evaporator has a saturated or superheated vapor state, thus stopping the fluid entering during the expansion in the turbine from being two-phase, which is a favorable characteristic compared to other fluids used in ORCs [31]. Similarly, the environmentally friendly characteristics of the R1234yf suggest that it is a possible candidate for use in systems that take advantage of solar energy, geothermal heat, and waste heat.
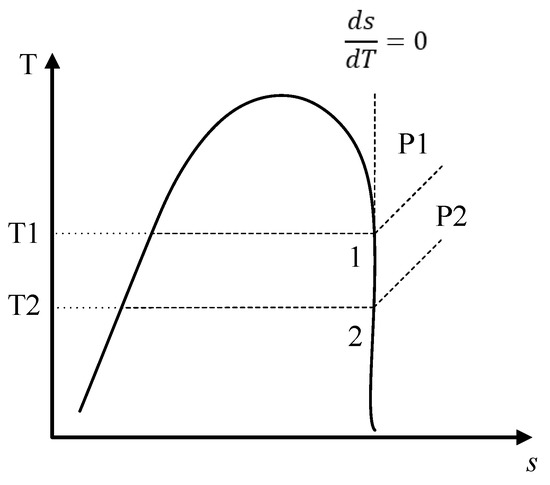
Figure 1.
Scheme of the T-s diagram for an isentropic fluid.
Several studies on temperature-based ORC energy systems, whose heat sources are between 50 and 250 °C and which operate with R1234yf as a pure substance, have focused primarily on energy analysis. The parameters of greatest interest are the thermal efficiency and power generated by the cycle. Table 3 shows an overview of these studies, as well as the most relevant characteristics.

Table 3.
Summary of ORC systems that operate with R1234yf to take advantage of different heat sources.
3.1.1. ORC Power Systems Based on Solar Energy
Solar energy has several advantages, including its availability in many regions of the world and it being a clean energy source because it does not emit polluting gases during operation. This type of renewable energy represents one of the most promising and viable options for energy generation currently and in the future [41]. The studies on solar-based ORC energy systems have typically been limited to heat source temperatures between 80 and 150 °C [42].
A solar-powered ORC system consists of a subsystem that collects solar energy to activate an ORC. The use of these systems with R1234yf has been based on two types of technology, as shown in Figure 2. The thermal energy of the sun is used by a solar collector that acts as an evaporator to heat the working fluid of the ORC, either directly (Figure 2a) or indirectly through the use of a heating fluid (Figure 2b) [32,34,41].
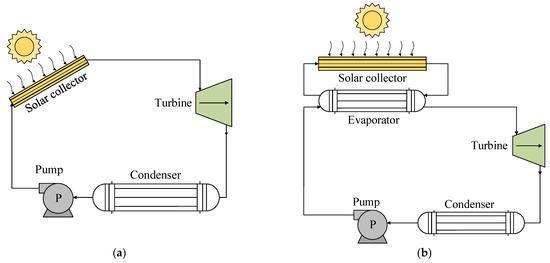
Figure 2.
Scheme showing technologies for the use of solar energy: (a) direct steam generation; (b) indirect generation.
Figure 3a presents a schematic of a basic ORC consisting of the following processes: (1–2 s) isentropic pumping, (2–3) addition of heat at constant pressure and temperature, (3–4 s) isentropic expansion, and (4 s−1) heat rejection at constant pressure and temperature. Figure 3b shows the T-s diagram for the representation of an ORC for a pure fluid, where the different thermodynamic states are indicated.
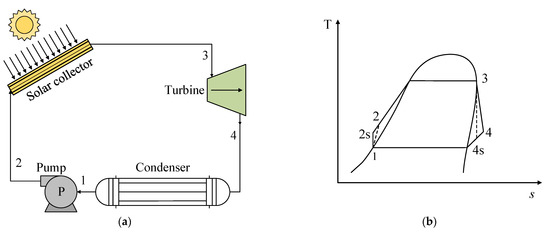
Figure 3.
(a) Scheme of the operation of an ORC system for the use of solar energy. (b) Scheme of the T-s diagram of the basic ORC system.
Additionally, Table 4 shows the different solar collector technologies commonly used in ORC, their typical temperature ranges, and the corresponding capacity of each temperature range. The working fluids can be heated in the low-temperature range below 240 °C through flat plate collectors or parabolic collectors. Concentrating collectors such as parabolic troughs and Fresnel type collectors can heat the working fluid to medium temperature ranges between 240 and 400 °C [41]. The use of the R1234yf stands out, as it is suitable for the temperature ranges in which concentrating solar collectors are most commonly used for high-capacity installations, as their efficiency is reasonable in the medium and high temperature ranges. In contrast, non-concentrated solar collectors are more suitable for low-capacity installations.

Table 4.
Operational characteristics of solar thermal collectors.
With the aim of improving cycle performance, some researchers have evaluated the effects of coupling a regenerator or internal heat exchanger (IHX) in the cycle. In this regard, Baldasso et al. [32] incorporated three heat exchangers into the ORC cycle operating with R1234yf and cyclohexane—a heat exchanger on the low-temperature side, a preheater, and a superheater in the evaporation stage. The capture of the heat source was achieved using a solar collector of parabolic cylinders. The cycle efficiency with R1234yf presented a reduction of 27.5% compared to cyclohexane. Barbazza et al. [33] performed small-scale Rankine cycle optimization for domestic solar applications. They analyzed two case studies, in the first using flat plate solar collectors to obtain hot water at 75 °C, while in the second using parabolic solar collectors to obtain hot water at 120 °C. As for the cycle of operation, they included an economizer in the ORC as an additional element, which operated as a preheater of the fluid before entering the evaporator. For the 75 °C heat source, the R1234yf presented the best performance, obtaining output power values of 2 to 4.5 kW. The optimum evaporation temperature of the R1234yf was 57 °C and the cycle efficiency ranged from 4.3 to 4.7%. For the highest temperature heat source, the best performance was offered by R1234ze(E), another HFO that the authors analyzed in the operation of the system. Zheng et al. [34] investigated an ORC system, which powered a vapor compression cycle for cooling. This system used a different approach, whereby the source of the solar energy was used to directly power a refrigeration system. In this work, the authors used R1234yf and a zeotropic mixture. The use of pure R1234yf showed an 8.5% lower cycle efficiency relative to the use of R600a. Regarding the COP achieved for the refrigeration cycle, R1234yf represented the lowest performance.
3.1.2. ORC Power Systems Based on Geothermal Energy
The use of geothermal resources has emerged as a measure to address environmental impacts. The geothermal heat source is one of the forms of renewable energy with which a sustainable type of energy can be achieved. The studies that have focused on ORC systems for the use of geothermal heat have been based on low to medium operating temperatures, which oscillate between 70 and 150 °C, a range in which R1234yf can operate according to its characteristics and thermophysical properties.
The system used for geothermal energy sources is based on the basic cycle of an ORC, which integrates four main components: an evaporator, a turbine or generator, a condenser, and a pump (Figure 4). It should also be noted that many studies on the use of this type of energy seek to improve the efficiency of the cycle by integrating equipment with a particular function in the regeneration process, such as a recuperator or a liquid heater in the feeding stage of the evaporator. As with solar energy, the geothermal energy source integrated into an ORC can be used in two configurations: (1) direct heat exchange between the waste heat source and the working fluid and (2) a secondary circuit to transfer the heat from the waste heat site to the evaporator.
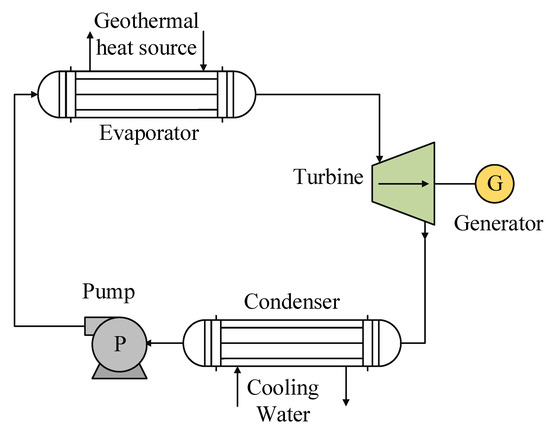
Figure 4.
General scheme of the ORC system used for geothermal heat sources.
One of the investigations of the use of R1234yf in ORC systems without modification to the cycle and intended for the use of a medium-temperature geothermal energy source (180 °C) was carried out by Quoilin et al. [35]. The R1234yf presented 2.54 kW of net work output, which was 47.6% lower than that produced by n-butane. Liu et al. [4] investigated several HFOs in an ORC for power generation using a geothermal energy source. A preheater was included in the system cycle. The authors varied the temperature of the heat source over the range of 120 to 200 °C and found that the highest performance for R1234yf was at 120 °C; this performance was the highest at this operating point among all of the fluids evaluated. However, as the temperature of the heat source increased, the performance of the R1234yf decreased considerably, becoming less suitable for this operating range. As for the pressure range (20–30 bar), the R1234yf showed the best performance, being up to 83% higher than the efficiency of R1225ye(E) at a pressure of 30 bar.
Yang et al. [36] optimized the economic performance of an ORC for geothermal applications with low-GWP fluids. In the modeling of the cycle, they added a reheater and established a 100 °C heat source. The ORC working with R1234yf presented the best performance among the fluids evaluated, with a production rate of 335.65 kW, being higher by 2.5% and 2.4% than R1234ze (E) and R600a, respectively. The authors also reported that R1234yf resulted in the highest operating costs as compared to the other working fluids.
3.1.3. ORC Power Systems Based on Waste Heat Recovery from Internal Combustion Engines
Another focus in this area is based on the residual energy of internal combustion engines. It is estimated that about 60–70% of total fossil fuel is consumed by internal combustion engines, of which 40–50% is used in the automotive sector [43]. In general, in conventional vehicles, 40% of the fuel’s energy is converted into useful energy for driving a vehicle, while the remaining 60% is wasted in the exhaust gases and in the refrigeration system. The waste heat from the exhaust gases reaches temperatures above 200 °C, while that from the refrigeration system is in the range of 80 to 120 °C [44]. The technology that recovers this heat and converts it into useful energy is known as waste heat recovery (WHR). The use of an ORC system adapted for WHR is considered a promising method due to the simple setup and high efficiency [45].
One of the ORC systems adapted for the use of waste heat in internal combustion engines is shown in Figure 5, which presents the use of mainly exhaust gases from a diesel engine [46], one of the applications that has highlighted R1234yf as working fluid. For the use of waste heat in such engines, the working fluid absorbs heat from the exhaust gases of the engine in the evaporator, where the working fluid is converted into vapor at high temperature and pressure. This vapor then flows into the expander to produce energy. After this, a low-pressure superheated vapor enters the condenser and condenses to liquid. Finally, the refrigerant in liquid state is pumped back into the evaporator and a new cycle begins.
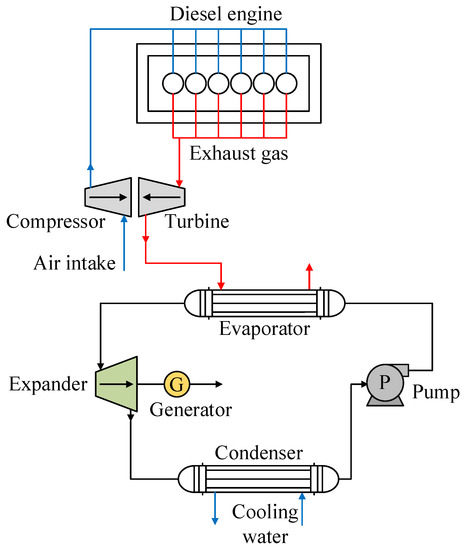
Figure 5.
Scheme showing a diagram of an ORC using the energy from the exhaust gases of an internal combustion engine.
In addition to the basic cycle for recovery of waste heat from exhaust gases, research on the performance of R1234yf has also been carried out on ORC systems, which in addition to recovering heat from exhaust gases, recover waste heat from the engine refrigeration system [37]. In Figure 6, it can be observed that the refrigerant absorbs heat from the engine cooling fluid in the evaporator, and therefore becomes a saturated vapor. Afterwards, the refrigerant heats up during its passage through the exchanger, where the exhaust gases of the engine circulate, becoming a superheated steam, then later passing through the turbine and generating energy. The above can also be seen reflected in the T-s diagram. It can be seen that between the points (2–3), the use of the residual heat of the engine refrigerant is shown, as well as the use of the residual heat of the exhaust gases (3–4). Thus, the working fluid in the ORC reaches a temperature higher than its critical temperature (4), producing a favorable effect in the expansion process and positively impacting the power generation of the cycle [37].
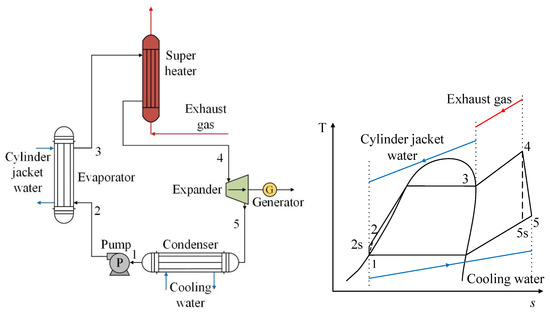
Figure 6.
Scheme of an ORC system using two heat sources from an internal combustion engine.
According to the thermophysical properties of R1234yf, in this type of system the refrigerant offers acceptable vapor density and latent vaporization heat, good thermal conductivity, and a low specific heat from the liquid. These characteristics result in a decrease in the size of the system equipment, low energy consumption in the pump, and an increase in the output power. Several studies are found in the literature for the use of this waste heat source in ORC-R1234yf systems. For example, Yang et al. [37] thermoeconomically optimized an ORC for heat recovery from a diesel engine for marine applications. Under optimal operating conditions and a turbine inlet temperature of 110 °C, R1234yf showed better behavior than the other analyzed fluids, whereby the net power generated at these conditions was 320.3 kW, with a thermal efficiency of 9.45%, which was the highest. For the pressure range of 0.4 to 3 MPa, R1234yf offered the highest output power values; however, the operating costs for R1234yf in such conditions were the highest within the group of fluids evaluated.
Some studies have focused on the use of a dual-loop system for the use of waste heat from internal combustion engines, commonly called a dual-loop organic Rankine cycle (DORC). Unlike the commonly used single-loop system, two cycles occur in the DORC: the first cycle, where the high-temperature waste heat from the exhaust gases is used; and the second cycle, where the waste heat from the engine cooling fluid is recovered. In the high-temperature cycle, it is more convenient to operate with high critical point refrigerants; conversely, fluids with low critical point properties are more suitable for the low-temperature cycle. For this last cycle, the investigations using R1234yf are interesting. An example is the study by Yang et al. [40], who carried out a multiobjective optimization process from a thermoeconomic point of view for a DORC system using R600 and R245fa in the high-temperature cycle, with the use of R1234yf as one of the fluids used in the low-temperature cycle. However, the lowest performance was obtained when using the combination of R1234yf-R600 and R1234yf-R245fa in relation to the other refrigerant compositions used. This study took into account the net power output, the total investment cost, the cost of electricity production, and the heat transfer area.
Among the investigations that have included the incorporation of other components into the cycle, in their search to improve the performance of the ORC, Tian et al. [38] added a preheater and a superheater. In the thermoeconomic evaluation they carried out for a group of working fluids, R1234yf presented lower thermal efficiency within a range of 1.2 to 3 MPa as compared to R142b. Yang et al. [39] evaluated the incorporation of three heat exchangers for greater recovery of residual heat when using R1234yf as the working fluid in an ORC. The results showed that with input temperature variation (110 to 140 °C) in the expansion device, the thermal efficiency of the cycle increased, whereby the largest output power value occurred at 120°C. On the other hand, from an economic point of view and with a temperature range at the entrance of the expander of 125 to 130 °C, the lowest operating costs for the cycle were achieved using R1234yf.
3.2. R1234yf Mixtures in ORC Systems
The use of the R1234yf in ORC systems was discussed in the previous sections. However, there are some considerable deficiencies in the heat transfer process in ORC heat exchange equipment as a consequence of the constant temperature behavior of the pure fluid when it undergoes a phase change. The constant temperature in the evaporation stage leads to a significant temperature difference between the source and the working fluid, which causes a greater amount of exergy destruction [47]. Figure 7 shows the thermal behavior between the fluid (pure and mixed) and the heat source in ORC systems.
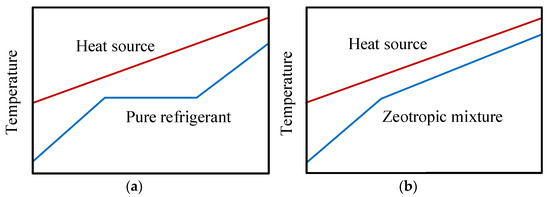
Figure 7.
Scheme of the thermal behavior between the fluid and the source: (a) pure fluid; (b) zeotropic fluid mixture.
The main advantages of the use of mixtures is that they allow a decrease in irreversibility in the heat transfer processes, thus improving the work output in the heat source [48]. Unlike when using R1234yf as a pure refrigerant, the zeotropic mixture has non-isothermal phase change lines at high and low-temperatures, thus leading to an improvement in the overlap between the lines of the heat source and the mixture in evaporation and condensation processes. Figure 7 shows the differences in thermal behavior between the pure fluid and the zeotropic mixture, whereby the use of zeotropic mixtures reduces the thermal difference between the refrigerant and the heat source, resulting in a reduction in the irreversibility of the heat exchangers.
In addition, Figure 8 shows a T-s diagram comparison of the behavior in the phase change process in the heat exchange equipment for both the pure fluid and a zeotropic mixture in an ORC. The red line represents the heat source and the blue line represents the current in the heat dissipation process; therefore, this figure illustrates the “glide” present in the phase change processes of the zeotropic mixture.
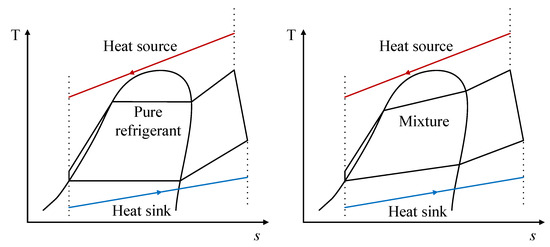
Figure 8.
T-s diagrams showing the differences between a pure fluid and a zeotropic mixture.
There are very few studies on the use of R1234yf-based mixtures for ORC applications. The most representative studies in this area are mentioned below. For example, Kang et al. [49] evaluated zeotropic mixtures R1234yf/R600a and R1234yf/R601a for a heat source input temperature of 110 °C. The authors varied the mass fraction of R1234yf in each one of the analyzed mixtures, aiming to obtain the most effective proportion in the operation of the analyzed system. For the R1234yf/R601a mixture, with a mass fraction of 0.7 for R1234yf, the highest net power output was achieved for an evaporation temperature range of 55 to 95 °C. For the R1234yf/R600a mixture, with a mass fraction of 0.8 for R1234yf, the best power values for low evaporation temperatures were obtained. The R1234yf/R601a mixture also achieved the best performance for the entire evaporation temperature range under study.
In the use of solar energy as a heat source, minimal studies have been performed on R1234yf mixtures. As such, one study stands out in which the researchers implemented a configuration focused on the use of solar energy by directly coupling a vapor compression refrigeration system [34]. This coupling is known as organic Rankine cycle–vapor compression cycle (ORC-VCC) coupling. The authors used the same mixture in both cycles and incorporated an internal heat exchanger (IHX) in the ORC. Figure 9 shows the scheme of the system with the respective T-s diagrams of both cycles; the coupling between the axes of the ORC expander and the VCC compressor can be noticed. The authors analyzed the R1234yf/R600a mixture under certain operating conditions, demonstrating that this mixture gave the lowest performance with this system, with a 50:50 composition ratio being the most suitable mixture. However, the incorporation of the IHX contributed positively to the efficiency of the system, resulting in a viable alternative for this type of ORC-VCC system.
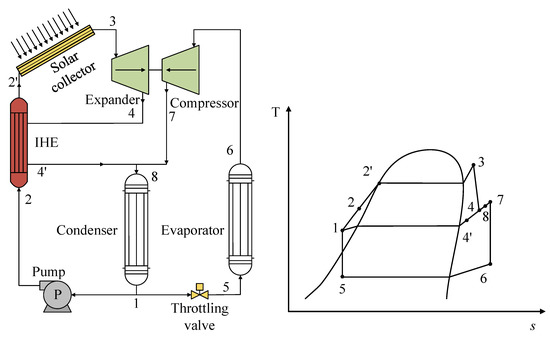
Figure 9.
General scheme and T-s diagram of an ORC-VCC system based on solar energy.
Luo et al. [16] evaluated the behavior of R1234yf, as well as different mixtures, among which R365mfc/R1234yf stood out. The ORC model consisted of a basic system using a low-temperature energy source. The analysis conditions were based on a heating fluid (water) temperature of 138 °C, with a temperature of 15 °C for the heat dissipator. For a mass concentration at a ratio of 5:95 for the R365mfc/R1234yf mixture, a power value of 28.8 kW was obtained, with this result being 10% greater than the best behavior obtained for R1234yf. Among the causes of this favorable result was the operation of the R365mfc/R1234yf mixture above the critical point.
The use of R1234yf mixtures has also been investigated with the use of waste heat produced by internal combustion engines. For this type of energy source, one of the prominent configurations is a DORC, such as the one used by Zhou et al. [50], configuration of which is shown in Figure 10. For the high-temperature circuit corresponding to the source of residual heat from engine exhaust gases, the authors used water as the working fluid in order to avoid the decomposition of an organic fluid at high temperatures. For the low-temperature cycle, they analyzed three mixtures, namely RC318/R1234yf, R600/R1234yf, and RC318/R245fa, which have a lower critical temperature and are more suitable for the working temperature range. In this part of the cycle, the waste heat from the cooling water and the waste heat from the high-temperature cycle are recovered. Evaluating the performance of the R1234yf mixtures in the low-temperature cycle, the authors found the maximum thermal efficiency for the R600/R1234yf mixture, which was 8.4% for mass fractions of 0.64:0.36. When they varied the mass fraction from 0 to 1, they observed that all of the mixtures offer better efficiency in relation to the pure fluids as a consequence of better adaptation of the temperature lines of the mixture and of the heat exchange source in the condensation process. In terms of heat recovery in the cooling water, the RC318/R1234yf mixture was able to increase this by up to 17.3%. This was also reflected in relation to the efficiency of the system, since the R600/R1234yf mixture presented the highest exergetic efficiency at close to 55%.
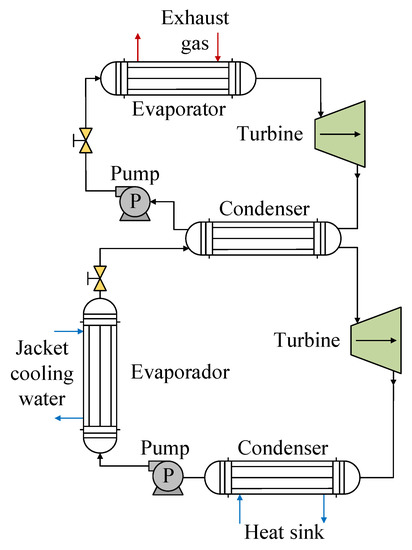
Figure 10.
Scheme of the DORC heat recovery system for R1234yf mixtures.
Among the studies that have investigated mixtures with R1234yf in transcritical organic Rankine cycle (TORC) systems, in the study conducted by Yang et al. [51], the authors used a mixture of two low-GWP refrigerants, namely R1234yf and R32. This type of system operates in conditions above the critical level of the refrigerant fluid. Figure 11 shows the configuration of the cycle that the authors worked on, as well as a T-s diagram of the TORC system. The figure shows the energy transfer of the heat source under transcritical conditions for the working mixture, due to the fact that the fluids that work near or above the critical point often lead to high use of heat. For a heat source of 180 °C, the authors evaluated the influence of the mass fractions of the refrigerants in the composition of the mixture, finding an optimal mass of R32, whereby the results reflected a substantial improvement in the use of the R1234yf/R32 mixture compared to using these refrigerants as pure fluids.
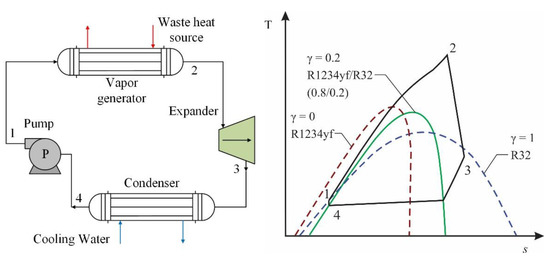
Figure 11.
General scheme and T-s diagram for a TORC system with R1234yf/R32 fluid [51].
Following research on ORC systems in conditions above the critical point of working fluids, in the study by Dai et al. [52], the authors used CO2 (R744) as the base refrigerant and varied the second component to experiment with different mixtures, among which R744/R1234yf stood out. The system they analyzed was a basic ORC system involving the use of low-temperature energy sources. Additionally, they took into account the adaptation of a regenerator with the aim of achieving an improvement in cycle performance. The best ratio for the R744/R1234yf mixture that the authors found was 0.4:0.6 for the mass fraction, which provided a thermal efficiency of 9.75%. Furthermore, with the coupling of a regenerator they managed to significantly improve the thermal efficiency of the cycle, especially for medium–high concentrations of R744 in each of the mixtures.
4. General Discussion
Most of the research on the use of the R1234yf refrigerant and its different zeotropic mixtures have focused mainly on analysis of the thermal performance of different ORC configurations, with few studies having focused on or that include the exergetic and economic aspects. However, within the revised literature, there are results for certain operating conditions in which ORC systems provide a greater perspective on the operability of R1234yf and its mixtures.
The feasibility of R1234yf and its respective mixtures depends on the cycle configuration, for example the incorporation of heat exchange equipment into the basic cycle, such as preheaters, reheaters, or an internal heat exchanger. In addition, as described in previous sections, the operating conditions and intrinsic characteristics of the fluid determine the system performance. Among these factors are the temperature of the heat source, the evaporation pressure, and the critical temperature of the fluid.
4.1. Energy Aspects
In this section, the reviewed studies focus on comparing the performance of R1234yf as a pure fluid and its mixtures in different ORC systems, with the most common evaluation parameters being energy aspects, the thermal efficiency of the cycle, and the net power output. Table 5 shows comparisons between different ORC systems that use R1234yf as a working fluid, as well as R1234yf mixtures.

Table 5.
Energy behavior of R1234yf and its mixtures in ORC systems.
From an energy point of view, the use of geothermal energy in ORC systems using R1234yf provides adequate energy performance under certain operating conditions when coupled with a reheater [36]. In this sense, there are few studies on the use of this type of energy source that have included R1234yf among the fluids of interest. Figure 12 shows a summary of the energy assessments in ORC systems for a fixed 100 °C heat source [36]. It can be observed that R1234yf shows the best energy performance, as well as greater energy production, as compared to the other refrigerants that are currently being investigated for their environmental characteristics. Thus, R1234yf is shown to be a viable alternative under operating conditions involving a heat source and a low temperature range. In addition, the inclusion of the reheaters is advantageous in improving the performance of the R1234yf in such systems.
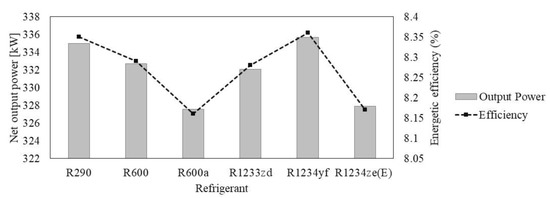
Figure 12.
Scheme of the energy performance parameters in an ORC system involving the use of geothermal energy.
According to the reviewed literature, R1234yf and its mixtures show the best energy efficiency performance when used in an ORC system operating in the low-temperature range as the heat source, thus representing a competitive alternative to traditional refrigerants; in addition, it has environmentally friendly characteristics. An IHX or reheater can also be incorporated in the ORC configuration, contributing to improvements in thermal efficiency and power output.
4.2. Exergy Aspects
The zeotropic mixtures with R1234yf have shown improvements in the use of the heat source; for example, Figure 13 compares the exergetic aspects of a DORC system. The use of organic fluids is viable in the low-temperature cycle, while the use of water is commonly viable in the high temperature cycle. It can also be observed that for certain conditions, R1234yf generates the best performance at an exergetic level, surpassing refrigerants that are used in different systems for the use of residual energy.
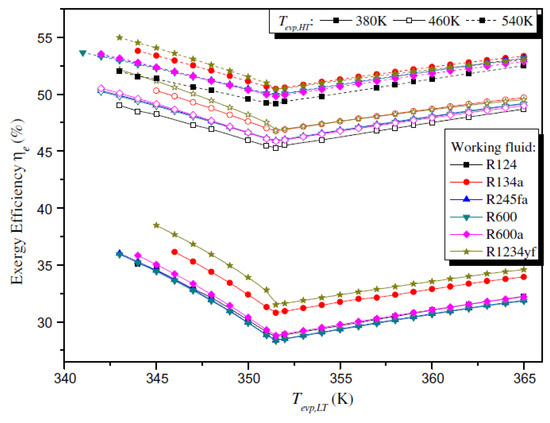
Figure 13.
Scheme showing the exergy efficiency variation in a DORC system [43].
Other aspects not often analyzed in ORC systems involving the use of R1234yf are the concepts of exergy destruction and exergetic efficiency. Figure 14 analyzes each component within a DORC. It can be seen that the turbine makes the greatest contribution to the irreversibility of the entire system, while the pump contributes least. In the same figure it can be seen that the heat exchange processes between the working fluid, the exhaust gases, and the engine refrigerant have a more significant influence on the exergetic performance of the system, making this heat exchange equipment the main optimization focus [43].
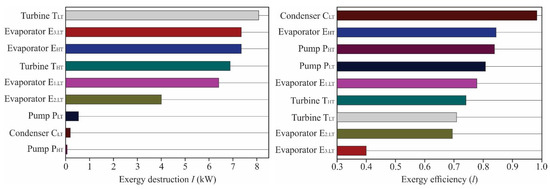
Figure 14.
Scheme showing the exergy destruction and exergy efficiency of a DORC system using R1234yf [43].
Another study involved similar conditions to the previous one but with the use of R1234yf mixtures, as presented in Figure 15, which shows the exergy loss distribution in each of the components of the DORC system, while the recovery of residual energy is presented in an ICE. It can clearly be seen that the heat exchange equipment generates the highest values in terms of exergy destruction. However, through the use of R1234yf mixtures, an improvement on exergetic performance can be seen.
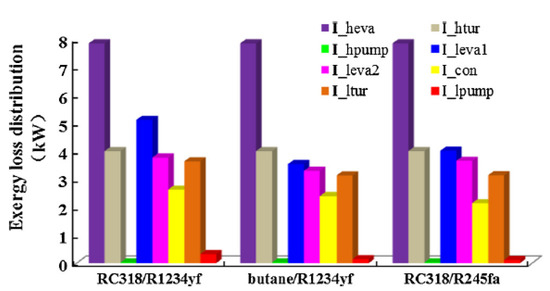
Figure 15.
Scheme of the exergy loss distribution in a DORC system used to recover residual energy from an ICE [50].
4.3. Economic Aspects
Economic aspects are scarcely studied in ORC systems. Fluid mixtures often offer better thermodynamic performance, however in certain cases their performance is lower than that of R1234yf in terms of the heat exchange area, which represents an associated investment cost [42]. The use of residual energy sources from ICE has been the subject of a greater number of studies using R1234yf. This is highlighted in Figure 16, which offers a comparison of the output power of the system by operating cost of the cycle. The system is based on an ORC with a superheater, which uses the energy from the exhaust gases of a marine diesel engine. In the figure, an evaluation of the power connected to the cycle cost factor is presented for different water inlet temperatures in the motor shroud. It can be observed that R1234yf produces the highest power level by operating cost in relation to the other fluids studied. Similarly, there are operating factors such as the temperature of the cooling water that directly influence the optimization of the economic resources in the cycle.
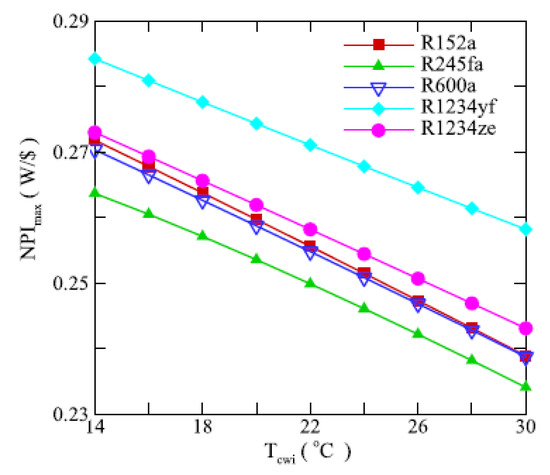
Figure 16.
Scheme of the net power per operating cost for an ORC system with a reheater based on residual energy from a diesel ICE [37].
Finally, it can be concluded that the highest investment cost is for the ORC configuration that involves additional equipment such as preheaters, IHXs, and reheaters.
4.4. Research Perspectives
According to the review, it has been observed that for a residual energy source, ORC systems using R1234yf refrigerant or R1234yf mixtures operating near or above the critical point have achieve better use of the heat source. This causes a greater generation of power; in addition, there is a pairing between the thermal profiles of the heat source and the working fluid, which is favorable in the reduction of irreversibilities generated in the energy transfer stage. This is one of the focal factors that make R1234yf and its mixtures competitive against conventional refrigerants, thus contributing to a larger area of research.
On the other hand, to achieve better operating conditions for the ORC the incorporation of heat exchangers is common, which should lead to more comprehensive studies in terms of energetic, exergetic, economic, and environmental aspects, which will more clearly reflect the advantages and disadvantages of coupling energy exchange equipment and other factors in an ORC.
Optimization is another area to be explored in ORC configurations involving the use of environmentally friendly fluids such as R1234yf in order to achieve maximum power and performance under certain operating conditions.
5. Summary
This paper has presented a detailed review of the use of R1234yf refrigerant and its mixtures in ORC systems. The main results of the different studies that have investigated R1234yf using residual energy from various heat sources were discussed, as well as the operating conditions and technologies or typical configurations of these systems. The main conclusions on the applicability of R1234yf in ORC systems are list below.
R1234yf represents an environmentally friendly alternative due to its low GWP in relation to the conventional refrigerants used in ORC systems. In addition, it allows safer operating conditions in relation to its lower flammability index.
Among the applications that offer the best energy performance when taking into account the thermal efficiency and the net output power of the ORC are systems based on the recovery of residual energy from internal combustion engines. This area represents a major research focus in terms of the performance of R1234yf.
The redesign or coupling of components, such as preheaters, reheaters, or IHX, in a basic ORC system plays an important role in the use of heat sources, where the properties of R1234yf have resulted in improvements in thermal performance, allowing R1234yf and its mixtures to become alternatives to HFCs.
Regarding ORC systems based on solar energy, the research is limited, however unfavorable results have been achieved for R1234yf in comparison with other fluids. However, redesigns of the cycle or even the use of mixtures based on R1234yf has resulted in competitive results. In addition, for the application range of R1234yf in this technology, which is set at medium temperatures, the system costs can be reduced, since the investment in terms of the solar collection system for this temperature range is usually the most economical.
The use of R1234yf and its mixtures is suitable in ORC systems where medium temperature ranges are handled for the heat source, making R1234yf suitable for solar and geothermal applications. Regarding the technology used in the recovery of residual heat from internal combustion engines, due to the fact that the exhaust gases present high temperatures, the DORC configuration is the most appropriate.
Finally, the mixtures involving R1234yf are more favorable compared to the pure R1234yf refrigerant, which is true for the three most prominent technologies in solar, geothermal, and WHR of combustion engines, in relation to the energy efficiency of ORC systems. However, in ORC system applications, in the recovery of residual heat from internal combustion engines, there are higher costs associated with the exchangers.
Author Contributions
Conceptualization, J.J.G.-P.; methodology and writing of the paper, J.M.B.-F.; analysis of the information, investigation, and writing of the paper, D.M.-M.; review and editing, J.M.B.-M. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We acknowledge the University of Guanajuato and Federal University of Itajubá (UNIFEI) for their sponsorship of this work.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| P | Pressure, bar |
| s | Entropy, kJ/kg K |
| T | Temperature, °C |
| Greek symbols | |
| γ | mass fraction |
| Subscript | |
| cond | condenser |
| crit | critical |
| evap | evaporator |
| hs | heat source |
| in | inlet |
| rec | reheater |
| t | turbine |
| w | water |
| Acronyms | |
| COP | Coefficient of Performance |
| DORC | Dual-Loop Organic Rankine Cycle |
| GWP | Global Warming Potential |
| HC | Hydrocarbon |
| HFC | Hydrofluorocarbon |
| HFO | Hydrofluoroolefin |
| ICE | Internal Combustion Engine |
| IHE | Internal Heat Exchanger |
| NBP | Normal Boiling Point |
| ODP | Ozone Depletion Potential |
| ORC | Organic Rankine Cycle |
| TORC | Transcritical Organic Rankine Cycle |
References
- Karmaker, A.K.; Rahman, M.; Hossain, A.; Ahmed, R. Exploration and corrective measures of greenhouse gas emission from fossil fuel power stations for Bangladesh. J. Clean. Prod. 2020, 244, 118645. [Google Scholar] [CrossRef]
- Abam, F.; Ekwe, E.; Effiom, S.; Ndukwu, M. A comparative performance analysis and thermo-sustainability indicators of modified low-heat organic Rankine cycles (ORCs): An exergy-based procedure. Energy Rep. 2018, 4, 110–118. [Google Scholar] [CrossRef]
- Xin, T.; Xu, C.; Yang, Y. A general and simple method for evaluating the performance of the modified steam Rankine cycle: Thermal cycle splitting analytical method. Energy Convers. Manag. 2020, 210, 112712. [Google Scholar] [CrossRef]
- Liu, W.; Meinel, D.; Wieland, C.; Spliethoff, H. Investigation of hydrofluoroolefins as potential working fluids in organic Rankine cycle for geothermal power generation. Energy 2014, 67, 106–116. [Google Scholar] [CrossRef]
- Schuster, A.; Karellas, S.; Kakaras, E.; Spliethoff, H. Energetic and economic investigation of Organic Rankine Cycle applications. Appl. Therm. Eng. 2009, 29, 1809–1817. [Google Scholar] [CrossRef]
- Mavrou, P.; Papadopoulos, A.I.; Stijepovic, M.Z.; Seferlis, P.; Linke, P.; Voutetakis, S. Novel and conventional working fluid mixtures for solar Rankine cycles: Performance assessment and multi-criteria selection. Appl. Therm. Eng. 2015, 75, 384–396. [Google Scholar] [CrossRef]
- Mavrou, P.; Papadopoulos, A.I.; Seferlis, P.; Linke, P.; Voutetakis, S. Selection of working fluid mixtures for flexible Organic Rankine Cycles under operating variability through a systematic nonlinear sensitivity analysis approach. Appl. Therm. Eng. 2015, 89, 1054–1067. [Google Scholar] [CrossRef]
- Villarini, M.; Bocci, E.; Moneti, M.; Di Carlo, A.; Micangeli, A. State of Art of Small Scale Solar Powered ORC Systems: A Review of the Different Typologies and Technology Perspectives. Energy Procedia 2014, 45, 257–267. [Google Scholar] [CrossRef]
- Wang, M.; Jing, R.; Zhang, H.; Meng, C.; Li, N.; Zhao, Y. An innovative Organic Rankine Cycle (ORC) based Ocean Thermal Energy Conversion (OTEC) system with performance simulation and multi-objective optimization. Appl. Therm. Eng. 2018, 145, 743–754. [Google Scholar] [CrossRef]
- Eyerer, S.; Dawo, F.; Wieland, C.; Spliethoff, H. Advanced ORC architecture for geothermal combined heat and power generation. Energy 2020, 205, 117967. [Google Scholar] [CrossRef]
- Qiu, G.; Shao, Y.; Li, J.; Liu, H.; Riffat, S.B. Experimental investigation of a biomass-fired ORC-based micro-CHP for domestic applications. Fuel 2012, 96, 374–382. [Google Scholar] [CrossRef]
- Baccioli, A.; Antonelli, M. Control variables and strategies for the optimization of a WHR ORC system. Energy Procedia 2017, 129, 583–590. [Google Scholar] [CrossRef]
- Lion, S.; Michos, C.N.; Vlaskos, I.; Rouaud, C.; Taccani, R. A review of waste heat recovery and Organic Rankine Cycles (ORC) in on-off highway vehicle Heavy Duty Diesel Engine applications. Renew. Sustain. Energy Rev. 2017, 79, 691–708. [Google Scholar] [CrossRef]
- Mahmoudi, A.; Fazli, M.; Morad, M.R. A recent review of waste heat recovery by Organic Rankine Cycle. Appl. Therm. Eng. 2018, 143, 660–675. [Google Scholar] [CrossRef]
- Papapetrou, M.; Kosmadakis, G.; Cipollina, A.; La Commare, U.; Micale, G. Industrial waste heat: Estimation of the technically available resource in the EU per industrial sector, temperature level and country. Appl. Therm. Eng. 2018, 138, 207–216. [Google Scholar] [CrossRef]
- Luo, D.; Mahmoud, A.M.; Cogswell, F.J. Evaluation of Low-GWP fluids for power generation with Organic Rankine Cycle. Energy 2015, 85, 481–488. [Google Scholar] [CrossRef]
- Vélez, F.; Segovia, J.J.; Martín, M.C.; Antolín, G.; Chejne, F.; Quijano, A. A technical, economical and market review of organic Rankine cycles for the conversion of low-grade heat for power generation. Renew. Sustain. Energy Rev. 2012, 16, 4175–4189. [Google Scholar] [CrossRef]
- Tchanche, B.F.; Lambrinos, G.; Frangoudakis, A.; Papadakis, G. Low-grade heat conversion into power using organic Rankine cycles—A review of various applications. Renew. Sustain. Energy Rev. 2011, 15, 3963–3979. [Google Scholar] [CrossRef]
- Baffoe, G.; Ahmad, S.; Bhandari, R. The road to sustainable Kigali: A contextualized analysis of the challenges. Cities 2020, 105, 102838. [Google Scholar] [CrossRef]
- Jarall, S. Study of refrigeration system with HFO-1234yf as a working fluid. Int. J. Refrig. 2012, 35, 1668–1677. [Google Scholar] [CrossRef]
- Pabon, J.J.; Khosravi, A.; Belman-Flores, J.; Machado, L.; Revellin, R. Applications of refrigerant R1234yf in heating, air conditioning and refrigeration systems: A decade of researches. Int. J. Refrig. 2020, 118, 104–113. [Google Scholar] [CrossRef]
- Spatz, M.; Minor, B. HFO_1234yf low GWP refrigerant: A global sustainable solution for mobile air conditioning, Honeywell/DuPont Join Collaboration. In Proceedings of the SAE 2008 Alternate Refrigerant Systems Symposium, Scottsdale, AZ, USA, 10–12 June 2008. [Google Scholar]
- Yamada, N.; Mohamad, N.A.; Kien, T.T. Study on thermal efficiency of low- to medium-temperature organic Rankine cycles using HFO−1234yf. Renew. Energy 2012, 41, 368–375. [Google Scholar] [CrossRef]
- Jung, D.; Park, S.; Min, K. Selection of appropriate working fluids for Rankine cycles used for recovery of heat from exhaust gases of ICE in heavy-duty series hybrid electric vehicles. Appl. Therm. Eng. 2015, 81, 338–345. [Google Scholar] [CrossRef]
- Wang, D.; Ling, X.; Peng, H.; Liu, L.; Tao, L. Efficiency and optimal performance evaluation of organic Rankine cycle for low grade waste heat power generation. Energy 2013, 50, 343–352. [Google Scholar] [CrossRef]
- Astolfi, M.; Romano, M.C.; Bombarda, P.; Macchi, E. Binary ORC (organic Rankine cycles) power plants for the exploitation of medium–low temperature geothermal sources—Part A: Thermodynamic optimization. Energy 2014, 66, 423–434. [Google Scholar] [CrossRef]
- Chintala, V.; Kumar, S.; Pandey, J.K. A technical review on waste heat recovery from compression ignition engines using organic Rankine cycle. Renew. Sustain. Energy Rev. 2018, 81, 493–509. [Google Scholar] [CrossRef]
- Ashrae Standard. Designation and Safety Classifications of Refrigerants; American Society of Heating, Refrigerating and Air-Conditioning Engineers: Peachtree Corners, GA, USA, 2007. [Google Scholar]
- Refrigerants—Designation and Safety Classification; ISO 817:2014; International Organization for Standardization: Geneva, Switzerland, 2014.
- Dumont, O.; Dickes, R.; De Rosa, M.; Douglas, R.; Lemort, V. Technical and economic optimization of subcritical, wet expansion and transcritical Organic Rankine Cycle (ORC) systems coupled with a biogas power plant. Energy Convers. Manag. 2018, 157, 294–306. [Google Scholar] [CrossRef]
- Saleh, B.; Koglbauer, G.; Wendland, M.; Fischer, J. Working fluids for low-temperature organic Rankine cycles. Energy 2007, 32, 1210–1221. [Google Scholar] [CrossRef]
- Baldasso, E.; Andreasen, J.G.; Modi, A.; Haglind, F.; Stoppato, A. Performance analysis a of solar driven organic Rankine cycle using multi-component working fluids. In Proceedings of the ECOS 2015—The 28th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Paris, France, 29 June–3 July 2015. [Google Scholar]
- Barbazza, L.; Pierobon, L.; Haglind, F.; Mirandola, A. Multi-objective optimization of small scale organic Rankine cycles for domestic solar applications. In Proceedings of the 8th Conference on Sustainable Development of Energy, Water and Environment Systems, Dubrovnik, Croatia, 22–27 September 2013. [Google Scholar]
- Zheng, N.; Wei, J.; Zhao, L. Analysis of a solar Rankine cycle powered refrigerator with zeotropic mixtures. Sol. Energy 2018, 162, 57–66. [Google Scholar] [CrossRef]
- Quoilin, S.; Declaye, S.; Tchanche, B.F.; Lemort, V. Thermo-economic optimization of waste heat recovery Organic Rankine Cycles. Appl. Therm. Eng. 2011, 31, 2885–2893. [Google Scholar] [CrossRef]
- Yang, M.-H.; Yeh, R.-H. Economic performances optimization of an organic Rankine cycle system with lower global warming potential working fluids in geothermal application. Renew. Energy 2016, 85, 1201–1213. [Google Scholar] [CrossRef]
- Yang, M.-H.; Yeh, R.-H. Thermo-economic optimization of an organic Rankine cycle system for large marine diesel engine waste heat recovery. Energy 2015, 82, 256–268. [Google Scholar] [CrossRef]
- Tian, H.; Shu, G.; Wei, H.; Liang, X.; Liu, L. Fluids and parameters optimization for the organic Rankine cycles (ORCs) used in exhaust heat recovery of Internal Combustion Engine (ICE). Energy 2012, 47, 125–136. [Google Scholar] [CrossRef]
- Yang, M.-H. Thermal and economic analyses of a compact waste heat recovering system for the marine diesel engine using transcritical Rankine cycle. Energy Convers. Manag. 2015, 106, 1082–1096. [Google Scholar] [CrossRef]
- Yang, F.; Cho, H.; Zhang, H.; Zhang, J. Thermoeconomic multi-objective optimization of a dual loop organic Rankine cycle (ORC) for CNG engine waste heat recovery. Appl. Energy 2017, 205, 1100–1118. [Google Scholar] [CrossRef]
- Aboelwafa, O.; Fateen, S.-E.K.; Soliman, A.; Ismail, I.M. A review on solar Rankine cycles: Working fluids, applications, and cycle modifications. Renew. Sustain. Energy Rev. 2018, 82, 868–885. [Google Scholar] [CrossRef]
- Modi, A.; Haglind, F. A review of recent research on the use of zeotropic mixtures in power generation systems. Energy Convers. Manag. 2017, 138, 603–626. [Google Scholar] [CrossRef]
- Shu, G.; Liu, L.; Tian, H.; Wei, H.; Yu, G. Parametric and working fluid analysis of a dual-loop organic Rankine cycle (DORC) used in engine waste heat recovery. Appl. Energy 2014, 113, 1188–1198. [Google Scholar] [CrossRef]
- Wang, E.; Yu, Z.; Zhang, H.; Yang, F. A regenerative supercritical-subcritical dual-loop organic Rankine cycle system for energy recovery from the waste heat of internal combustion engines. Appl. Energy 2017, 190, 574–590. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, E.; Fan, B. A performance analysis of a novel system of a dual loop bottoming organic Rankine cycle (ORC) with a light-duty diesel engine. Appl. Energy 2013, 102, 1504–1513. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, H.; Song, S.; Bei, C.; Wang, H.; Wang, E. Thermoeconomic multi-objective optimization of an organic Rankine cycle for exhaust waste heat recovery of a diesel engine. Energy 2015, 93, 2208–2228. [Google Scholar] [CrossRef]
- Sadeghi, M.; Nemati, A.; Ghavimi, A.; Yari, M. Thermodynamic analysis and multi-objective optimization of various ORC (organic Rankine cycle) configurations using zeotropic mixtures. Energy 2016, 109, 791–802. [Google Scholar] [CrossRef]
- Abadi, G.B.; Kim, K.C. Investigation of organic Rankine cycles with zeotropic mixtures as a working fluid: Advantages and issues. Renew. Sustain. Energy Rev. 2017, 73, 1000–1013. [Google Scholar] [CrossRef]
- Kang, Z.; Zhu, J.; Lu, X.; Li, T.; Wu, X. Parametric optimization and performance analysis of zeotropic mixtures for an organic Rankine cycle driven by low-medium temperature geothermal fluids. Appl. Therm. Eng. 2015, 89, 323–331. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, Y.; Li, F.; Yu, L. Performance analysis of zeotropic mixtures for the dual-loop system combined with internal combustion engine. Energy Convers. Manag. 2016, 118, 406–414. [Google Scholar] [CrossRef]
- Yang, M.-H.; Yeh, R.-H.; Hung, T.-C. Thermo-economic analysis of the transcritical organic Rankine cycle using R1234yf/R32 mixtures as the working fluids for lower-grade waste heat recovery. Energy 2017, 140, 818–836. [Google Scholar] [CrossRef]
- Dai, B.; Li, M.; Ma, Y. Thermodynamic analysis of carbon dioxide blends with low GWP (global warming potential) working fluids-based transcritical Rankine cycles for low-grade heat energy recovery. Energy 2014, 64, 942–952. [Google Scholar] [CrossRef]
- Shu, G.; Liu, L.; Tian, H.; Wei, H.; Xu, X. Performance comparison and working fluid analysis of subcritical and transcritical dual-loop organic Rankine cycle (DORC) used in engine waste heat recovery. Energy Convers. Manag. 2013, 74, 35–43. [Google Scholar] [CrossRef]
- Yang, M.-H. Optimizations of the waste heat recovery system for a large marine diesel engine based on transcritical Rankine cycle. Energy 2016, 113, 1109–1124. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).